Как найдите площадь закрашенного сектора круга

3 октября 2013

В этом уроке мы разберем еще одну задачу B5 на площади секторов из ЕГЭ по математике, однако будьте очень внимательны: на первый взгляд все считается очень просто. Но в самом конце решения многие ученики допускают очень обидную ошибку. Сейчас вы поймете, о чем идет речь. Итак, задача:

Задача. Найдите площадь S закрашенного сектора, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как решать такую задачу? В первую очередь, поскольку речь идет о площади сектора, нам нужно знать формулу площади круга:

S = πR²

где R — радиус круга. Следовательно, для решения нам потребуется найти этот самый радиус. В данной задаче все очень просто: проводим вертикальный радиус и считаем клеточки.

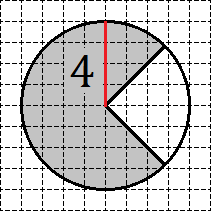
Отсюда сразу получаем, что радиус R = 4. Таким образом, площадь круга S равна:

S = π · 4² = 16π

Обратите внимание: нам очень повезло с радиусом. Потому что в настоящих задачах далеко не всегда верхняя точка окружности лежит в узлах координатной сетки. Однако где-то на окружности обязательно найдется точка с целочисленными координатами, которая точно будет лежать в узле сетки. Вот ее и надо использовать для вычисления радиуса. Давайте посмотрим, каким образом.

Для этого нам потребуется отдельная сетка. Отметим на ней центр окружности (точку O) и некую гипотетическую точку A, которая должна лежать на нашей окружности. Допустим, это будет выглядеть следующим образом:

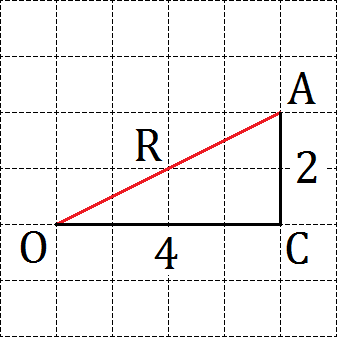
Тогда отрезок OA будет радиусом этой окружности. Как его найти? Достроим до прямоугольного треугольника наш отрезок. Если двигаться вдоль линий координатной сетки, мы получим прямоугольный треугольник OAC с прямым углом C. Разумеется, полученная таким образом точка C не будет лежать на окружности — она лежит где-то внутри. Но этого нам и не требуется. Главное, что мы легко можем найти катеты: OC = 4, AC = 2.

Тогда мы можем найти радиус R (он же — отрезок OA) по теореме Пифагора:

R² = 4² + 2² = 16 + 4 = 20

И тогда получилось бы, что вместо 16π площадь всего круга равнялась бы 20π. В остальном решение было бы полностью аналогичным, поэтому возвращаемся к нашей исходной задаче. Мы только что нашли площадь круга, а нам надо найти площадь сектора. Давайте схематично перерисуем круг и разделим его на 8 равных частей, как пиццу (стандартная практика в задачах B5). Затем закрашиваем на получившемся рисунке те сектора, которые на исходном чертеже также были закрашены:

Получаем, что закрашенных кусочков было k = 6, а всего их изначально n = 8. Поскольку все части равные, мы можем найти площадь каждого маленького сектора, разделив общую площадь круга на 8:

S_sec = 16π/8 = 2π

А поскольку в закрашенном секторе таких кусочков k = 6, то искомая площадь будет равна

S = 6 · S_sec = 6 · 2π = 12π

Но в задаче B5 от нас требуется найти не просто площадь сектора, а величину S/π. Поэтому выполняем последний шаг. Подставляем и получаем:

12π : π = 12

Это и есть ответ. Так в чем же главная ошибка учеников, которые решают подобные задачи? Дело в том, что многие начинают считать площадь меньшего из секторов, изображенных на рисунке. Однако этот сектор не закрашен. В результате при правильных по существу расчетах многие ученики получают неправильный ответ. Согласитесь, обидная ошибка?

Поэтому рекомендация следующая: внимательно читайте условие задачи B5! Если требуется найти площадь закрашенного сектора, то именно закрашенный сектор и нужно искать. Даже если на чертеже он занимает большую часть круга. А если требуется найти площадь незакрашенного сектора, то об этом обязательно будет указано в условии. Поэтому прежде чем записывать ответ, еще раз проверьте, что от вас требуется: закрашенный сектор или незакрашенный? И тогда дополнительный балл на ЕГЭ по математике вам гарантирован.:)

Смотрите также:

1. Задача B5: площадь кольца
2. Задача B5: площадь сектора
3. Как сдать ЕГЭ по математике
4. Метод коэффициентов, часть 1
5. Задача B5: метод узлов
6. Сфера, описанная вокруг куба

Сайты, меню, вход, новости

Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.

Для решения обеих задач надо определить величину соответствующего ему центрального угла.

Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.

Самые простые задания этого вида — те, в которых центральный угол — прямой.  90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.

Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).

Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).

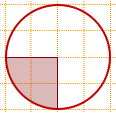
1) На клетчатой бумаге изображён круг площадью 60.

Найти площадь заштрихованного сектора.

Решение:

Так как центральный угол, соответствующий данному сектору, равен 90º, то

S_{сектора}=S_круга:4=60:4=15.

Обратная задача.

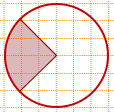2) На клетчатой бумаге изображён круг.

Какова площадь круга, если площадь заштрихованного сектора равна 17?

Решение:

Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.

Следовательно, площадь сектора составляет 1/4 от площади круга: S_круга=S_{сектора}:(1/4)=17·4=68.

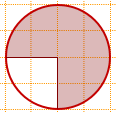3) Найти площадь круга, если площадь заштрихованного сектора равна 21.

Решение:

Площадь заштрихованного сектора составляет 3/4 площади круга.

Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

S_круга=S_{сектора}:(3/4)=21: (3/4)=21·4:3=28.

4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?

Решение:

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).

Так как 45° составляет от 360° 1/8 часть, то

S_круга=S_{сектора}:(1/8)=11: (1/8)=11·8=88.

5) На клетчатой бумаге изображен круг площадью 96.

Найдите площадь заштрихованного сектора.

Решение:

Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.

S_{незакрашенного сектора}=S_круга:8=96:8=12.

S_{закрашенного сектора}=S_{незакрашенного сектора}-S_круга=96-12=84.

А как определить на клетчатой бумаге центральные углы в 60° и 30°?

Можно рассуждать следующим образом.

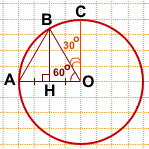Рассмотрим треугольник ABC.

Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.

Но AO=BO (как радиусы).

Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.

∠BOC=∠AOC-∠AOB=90°-60°=30°.

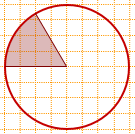6) Найти площадь заштрихованного сектора, если площадь круга равна 30.

Решение:

Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и S_{сектора}=S_круга:6=30:6=5.

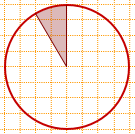7) Найти площадь круга, если площадь заштрихованного сектора равна 24.

Решение:

Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.

S_круга=S_{сектора}:(1/12)=24: (1/12)=24·12=288.

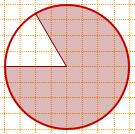8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.

Решение:

Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.

Следовательно, на площадь закрашенной части приходится 5/6 круга:

S_круга=S_{сектора}:(5/6)=60: (5/6)=60·6:5=72°.

В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.

9) 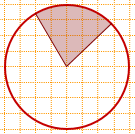Центральный угол равен 30+45=75°,

площадь заштрихованного сектора составляет

1/12+1/8=5/24 площади круга, то есть

S_{сектора}=S_круга·(5/24)=S_круга:24·5,

S_круга=S_{сектора}:(5/24)=S_круга: 5·24.

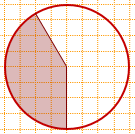10) Центральный угол равен 180-30=150°,

площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,

S_{сектора}=S_круга·(5/12),

S_круга=S_{сектора}:(5/12).

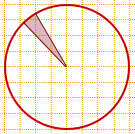11) Центральный угол равен 60-45=15°,

площадь заштрихованного сектора составляет 1/24 площади круга

и т.д.

12) Центральный угол равен 15+90=105°

(либо 180-30-45=105°),

площадь заштрихованного сектора составляет

1/24+1/4=7/24 и т.д.

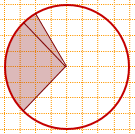
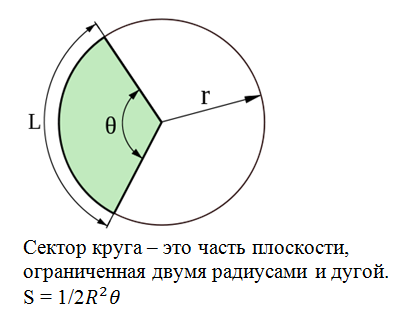
Нахождение площади сектора круга

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.

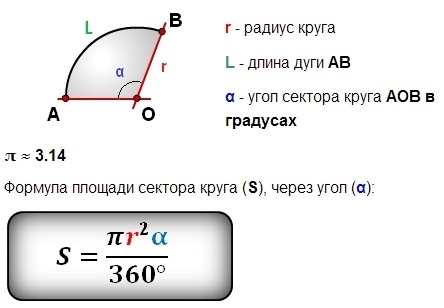
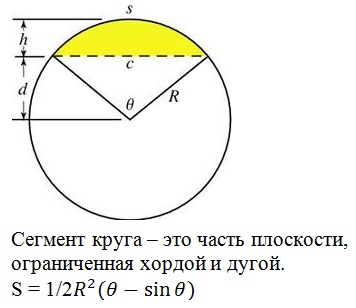
Определение сектора круга

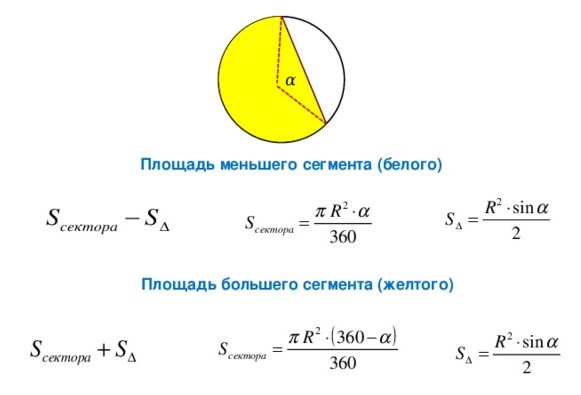
Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.

• AB – дуга сектора;
• R (или r) – радиус круга;
• α – это угол сектора, т.е. угол между двумя радиусами. Также его иногда называют центральным углом.

Формулы нахождения площади сектора круга

Через длину дуги и радиус круга

Площадь (S) сектора круга равняется одной второй произведения длины дуги сектора (L) и радиуса круга (r).

Через угол сектора (в градусах) и радиус круга

Площадь (S) сектора круга равняется площади круга, умноженной на угол сектора в градусах ( α°) и деленной на 360°.

Через угол сектора (в радианах) и радиус круга

Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (a_рад) и квадрата радиуса круга.

Примеры задач

Задание 1
Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.

Решение
Воспользуемся первой формулой, подставив в нее заданные значения:

Задание 2
Найдите угол сектора, если известно, что его площадь равна 78 см 2 , а радиус круга – 8 см.

Решение
Выведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше:

Площадь закрашенного сектора окружности

На клетчатой бумаге с размером клетки 1 × 1 изображён вписанный в окружность угол ABC. Найдите его градусную величину.

Аналоги к заданию № 27890: 26237 27891 509571 Все

На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

Отрежем от закрашенной фигуры сектор, отмеченный синим цветом, и добавим к ней сектор, выделенный красным цветом. Указанные секторы равны, поэтому площадь фигуры не изменилась. Следовательно, она равна трём четвертям площади круга, радиус которого см. Поэтому

см 2 .

Хотелось бы более “научного” доказательства. Аргумент “это видно” не достаточен, так как всем видно разное. Спасибо!

На рисунке ВИДНО, что они равны. Или задайте прямые уравнениями и и найдите угол между ними. Но то, что уравнения именно такие, тоже ВИДНО по рисунку. Задания на работу с рисунками предполагают считывание информации с рисунка.

На клетчатой бумаге с размером клетки 1 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.

Треугольник прямоугольный, значит, радиус описанной вокруг него окружности равен половине гипотенузы.

Площадь сектора круга – формулы и примеры расчетов

Выполняя инженерные расчёты при проектировании различных объектов строительства, создании роботов, автоматизированных систем, станков, машин, самолётов, ракет, современных средств вооружения часто бывает необходимо найти площадь сектора круга.

Геометрия помогает при этом решать задачи на нахождение центра тяжести (центр масс), вычислять его координаты для плоских пластин, имеющих, в частности, форму правильного многоугольника.

Измерять и вычислять величины считается базовым умением. Оно включено в первую часть профильной программы выпускного экзамена ЕГЭ и ОГЭ по математике.

Сектор круга

Существует несколько определений, каждое из которых отличается только формулировкой, не меняющей подход к рассмотрению понятия:

Часть плоскости, ограниченная центральным углом и соответствующей дугой окружности.

Часть круга, заключённая между двумя радиусами.

Часто эту формулировку заменяют похожей, описывающей построение непосредственно: часть круга, лежащего внутри соответствующего центрального угла.

Площадь сектора круга через радиус и длину дуги

Пусть известны радиус круга R, длина дуги l. Как в этом случае определить площадь сектора, стягиваемого данной дугой?

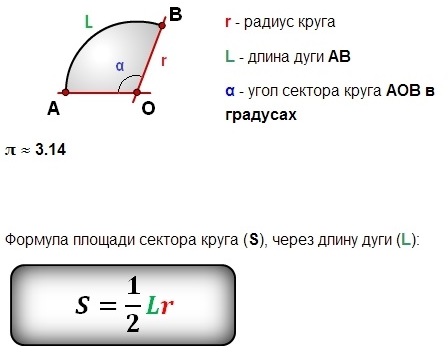
Для ответа на вопрос понадобится формула нахождения длины окружности:

Определение, представленное через третью формулировку, даёт возможность соотнести численные величины понятий: сектор и круг, дуга и окружность, центральный и полный углы.

Поскольку отношения постоянны, то для ответа на поставленный вопрос достаточно найти отношение части к целому, затем умножить полученный результат на площадь круга S = πR 2 .

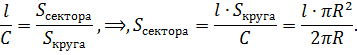
После сокращения дроби получают формулу:

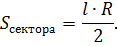
Примеры решения задач

Задача №1

Найти площадь сектора круга радиусом 2 см, имеющего длину дуги 4 см.

Подставляя имеющиеся величины в формулу, получаем:

S_сект = (4 * 2) / 2 = 4.

Ответ: S_сект = 4 см 2 .

Задача №2

Подставив известные данные в формулу, получим:

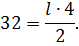
Тот же результат получился бы при первоначальной работе в «общем виде»:

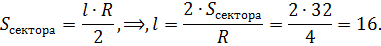
Площадь сектора круга через радиус и угол сектора

Если известна градусная мера центрального угла (n°), то, находя отношение её к полному кругу (к 360º), также умножают результат на площадь круга:

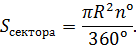
Задача №3

Чему равна площадь фигуры, изображённой на рисунке?

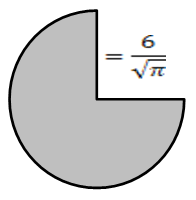
Центральный угол изображённого сектора равен

Подставляя в формулу величины, несложно получить искомый результат:

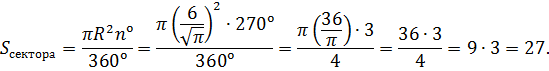
Ответ: S_сект = 27 см 2 .

Также аналогичным образом решаются обратные задачи.

Площадь сектора круга через угол сектора в радианах

Пусть центральный угол задан своей радианной мерой. Учитывая, что

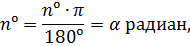
несложно получить искомую формулу:

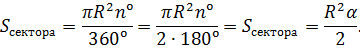
Задача №4

Чему равен центральный угол сектора в радианах (рад.), если его площадь равна 32, а радиус – 4?

Выразив α, затем подставив числовые данные, легко получить результат:

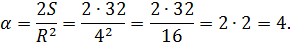
Благодаря этой формуле, несложно доказать, что площади двух секторов с равными центральными углами относятся как квадраты радиусов соответствующих окружностей:

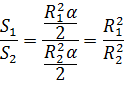
С другой стороны, площадь части кольца находится из условия:

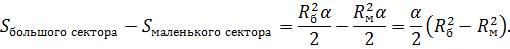
Сегмент круга

Существует два подхода к определению понятия:

Геометрическая фигура, являющаяся общей частью круга и полуплоскости, называется сегментом круга.

Часть плоскости, заключённая между хордой и окружностью.

Оба определения характеризуют один и тот же объект с разных сторон, выражая, по сути одно и то же.

Иногда проводится описательное построение. В этом случае второй вариант быстрее приводит к данному термину.

Площадь сегмента круга по хорде и высоте

Пусть градусная мера ограничивающей дуги мала, длина хорды равна a, h – высота сегмента (перпендикуляр, опущенный из точки на окружности к середине хорды). Примечание: часто высота сегмента называется «стрелкой».

Тогда можно приближённо считать, что

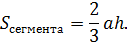
Погрешность такого вычисления уменьшается вместе с отношением

В частности, когда дуга содержит угол, меньший 50º, то есть,

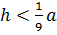
погрешность оказывается менее 1%.

Более точной является формула для любого сегмента меньшего полукруга:

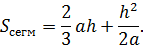
Точный расчёт производится, исходя из свойства нахождения сложной фигуры, являющейся суммой или разностью двух и более объектов.

Сегмент является частью сектора, к которому либо добавлен треугольник, содержащий центральный угол (для дуг больших 180º), либо убран (соответствующий центральный угол меньше 180º).

Отсюда следует, что

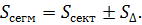
Задача №5

Вычислить стрелку и площадь сегмента, если центральный угол содержит 60º, а

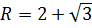
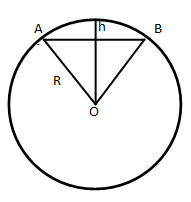
Для нахождения стрелки достаточно из радиуса вычесть высоту треугольника AOB. Поскольку угол AOB по условию равен 60º, то треугольник AOB равносторонний. Поэтому его высота в √3/2 раз отличается от стороны (от радиуса).

Отсюда следует, что:

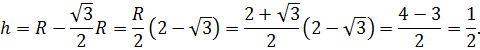
Площадь по первой формуле будет приблизительно равна

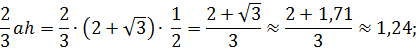
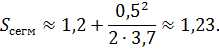
Применяя точную формулу и учитывая, что

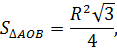
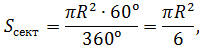
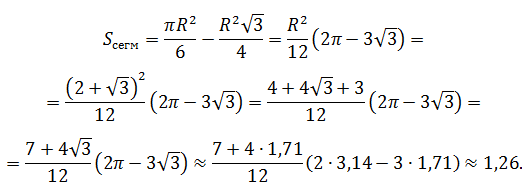
Ответ: S_сегм = 1,26 см 2 .

Площадь сегмента круга через синус угла

Рассматривая точную формулу, площадь треугольника можно находить, используя половину произведения сторон на синус угла между ними. А значит:

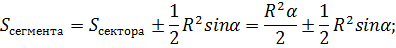
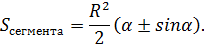
Многие вычисления помогает провести онлайн калькулятор. Достаточно ввести исходные данные и запросить результат.

[spoiler title=”источники:”]

http://ege.sdamgia.ru/test?theme=123

http://nauka.club/matematika/geometriya/ploshchad-sektora-kruga.html

[/spoiler]

Задачи на клетчатой бумаге интересны тем, что можно их решать различными способами – и через дополнительное построение, и через различные геометрические формулы. Так как задач таких сейчас полно в сети, ещё раз обозначу себе картинкой условие:

У нас нет ничего в условии кроме длины клетки, равной 1/√π

Как найти площадь?

Например, по такой формуле, где альфа – размер угла.

Но у нас нет ни угла, ни радиуса.

Значит, находим радиус. На глаз тут 4,5 клетки, но мы будем точнее, если нарисуем вот такой треугольник прямоугольник, в котором радиус будет гипотенузой и через теорему Пифагора его найдём.

(4/√π)2 + (2/√π)2 = 16/π+4/π = √(20/π)

Как найти угол? Если разделить всю окружность на 4 части, то видно, что закрашенная часть составит целую четверть и ещё её половинку. То бишь, 1/4+0,5Х1/4 Это не что иное как 3/8

Теперь считаем угол: 360Х3/8=135 градусов.

Теперь, когда у нас есть все данные, подставляем в формулу.

S=135/360 Х π Х (√(20/π))2

Квадрат и корень квадратный сокращаются, получаем 135/360 Х π Х 20/π

Следом сокращается и п, остаётся 135/360 Х 20/1 = 135/18 = 7,5

Поскольку площадь измеряется в квадратных сантиметрах в нашей задаче, то и ответ будет 7,5 кв.см