Задания
Версия для печати и копирования в MS Word
Тип 18 № 311914 

i
Найдите синус острого угла трапеции, изображённой на рисунке.
Спрятать решение
Решение.
Введем обозначения, как показано на рисунке и проведём высоту трапеции СH. В прямоугольном треугольнике BCH длины катетов равны 3 и 4, поэтому гипотенуза равна Следовательно, искомый синус острого угла B, равный отношению противолежащего углу катета CH к гипотенузе BC, равен
Ответ: 0,8.
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Помощь
ЗАДАЧА
Прежде чем приступить к решению задачи, мы:
– рассмотрим трапецию, вспомним ее основные характеристики;
– перенесем данные задачи на чертеж;
– внимательно прочитаем вопрос.
Как мы видим нам дана трапеция АВСD. Что мы знаем об этой фигуре? Давайте рассуждать:
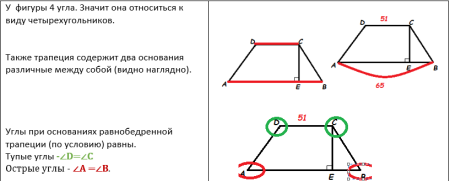
По условию задачи СЕ- высота трапеции.
Проведем ещё одну высоту из точки D. Что нам это даст? Во- первых отметим ,что эти высоты равны друг другу. Во- вторых, построенная нами высота «отрезает» из нижнего основания кусочек равный 51. Наглядно это выглядит так;
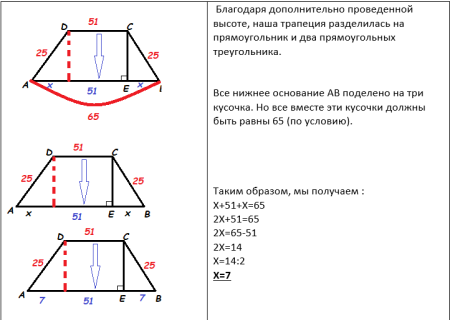
Напомню, по условию, нам нужно найти синус острого угла трапеции. В нашей трапеции, как мы определили ранее, острые углы – А и В. Рассмотрим подробнее угол В в прямоугольном треугольнике СЕВ. Также вспомним, что синус острого угла – это отношение противоположного катета к гипотенузе прямоугольного ∆. Продолжение решения…..
![]()
Углы равнобедренной трапеции. Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?
Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.

Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):

Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:
![]()
*И ещё! В задачах не введены буквенные обозначения. Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.
Рассмотрим задачи:

27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:

В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.
По теореме Пифагора указанный катет равен:
![]()
Таким образом:

Ответ: 0,96

27440. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.
Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:

Ответ: 21

27441. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.
Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):

Можем вычислить высоту трапеции, а затем найти катет:

По теореме Пифагора вычисляем катет:

Таким образом, меньшее основание равно:
![]()
Ответ: 22

27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.
Построим высоты и отметим данные в условии величины. Нижнее основание разбивается на отрезки:

Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:
![]()
Ответ: 10

27443. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.
Строим высоты и вычисляем чему равен катет:

Таким образом большее основание будет равно:
![]()
Ответ: 71

27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:

По определению тангенса:

Ответ: 0,4

77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:

Выразим гипотенузу обозначенную как х через косинус:

Из основного тригонометрического тождества найдём cosα
![]()
Таким образом:

Ответ: 5

27818. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 500? Ответ дайте в градусах.

Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 1800. В нашем случае это
![]()
C условии сказано, что разность противолежащих углов равна 500, то есть
![]()
Так как у равнобедренной трапеции углы при основании равны, то есть угол А равен углу В, то можем записать
![]()
Имеем два уравнения с двумя неизвестными, можем решить систему:

*Конечно, эту задачу можно было легко решить просто перебирая пары углов )

27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 600. Найдите меньшее основание.

Построим высоты DE и CF:

Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:

Так как AE=FB=5, то EF=25–5–5=15. Следовательно и DC=15.
Ответ: 15

27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 450. Найдите высоту трапеции.

Из точек D и C опустим две высоты:

Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.
В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 450. Отсюда следует, что высота трапеции будет равна 3.
Ответ: 3
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Расскажите о сайте в социальных сетях!
khilsonglyo95
Вопрос по геометрии:
Как найти синус острого угла трапеции?
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 2
lenghantede21
Провести высоту из вершины тупого угла, Найти отношение Этой высоты к боковой стороне . и это будет синус острого угла трапеции
hoplyediclfe311
Таак, ну если провести из вершины высоту, то тогда получится ПРЯМОУГОЛЬНЫЙ треугольник. если смотреть на угол треугольник при основании, то синус=противолеж.катет(он же высота) : на гипотенузу(она же боковая сторона)
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.
Источник: mathege
Решение:
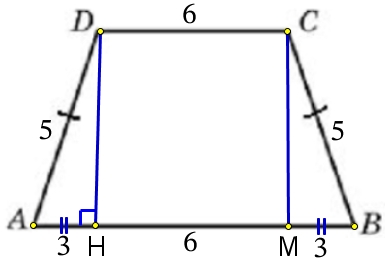
Проведём высоты DH и СМ равнобедренной трапеции, тогда DCMH – прямоугольник:
DC = HM = 6
В прямоугольном ΔАНD найдём DH:
Синус острого угла прямоугольного треугольника – это отношение противолежащего катета к гипотенузе. Найдём синус острого угла трапеции:
Ответ: 0,8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
