Содержание:
- Координаты вектора
- Направляющие косинусы
- Сумма двух векторов, заданных координатами
- Умножение вектора на число
- Основное свойство направляющих косинусов
Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении
и длине.
Координаты вектора
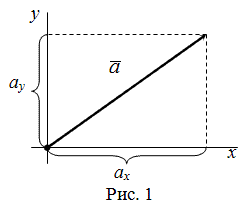
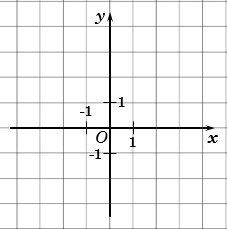
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$
и произвольный вектор $overline{a}$, начало которого совпадает
с началом системы координат (рис. 1).
Определение
Координатами вектора $overline{a}$ называются проекции
$a_{x}$ и $a_{y}$
данного вектора на оси $O x$ и
$O y$ соответственно:
$$a_{x}=Пр_{O x} bar{a}, a_{y}=Пр_{O y} bar{a}$$
Величина $a_{x}$ называется абсциссой вектора
$overline{a}$, а число $a_{y}$
– его ординатой. То, что вектор $overline{a}$ имеет координаты
$a_{x}$ и $a_{y}$,
записывается следующим образом: $overline{a}=left(a_{x} ; a_{y}right)$.
Пример
Запись $overline{a}=(5 ;-2)$ означает, что вектор $overline{a}$
имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Сумма двух векторов, заданных координатами
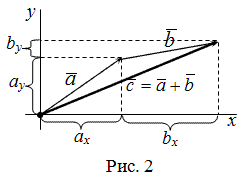
Пусть заданы $overline{a}=left(a_{x} ; a_{y}right)$ и $overline{b}=left(b_{x} ; b_{y}right)$,
тогда вектор $overline{c}=overline{a}+overline{b}$ имеет координаты
$left(a_{x}+b_{x} ; a_{y}+b_{y}right)$ (рис. 2).
Определение
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заданы $overline{a}=(-3 ; 5)$
и $overline{b}=(0 ;-1)$. Найти координаты вектора $overline{c}=overline{a}+overline{b}$
Решение. $overline{c}=overline{a}+overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$
Умножение вектора на число
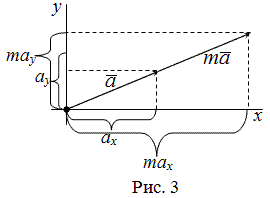
Если задан $overline{a}=left(a_{x} ; a_{y}right)$, то тогда вектор
$m overline{a}$ имеет координаты
$m overline{a}=left(m a_{x} ; m a_{y}right)$, здесь
$m$ – некоторое число (рис. 3).
Определение
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное
число.
Пример
Задание. Вектор $overline{a}=(3 ;-2)$.
Найти координаты вектора 2$overline{a}$
Решение. $2 overline{a}=2 cdot(3 ;-2)=(2 cdot 3 ; 2 cdot(-2))=(6 ;-4)$
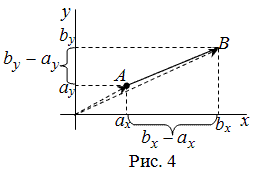
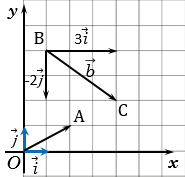
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две
точки $Aleft(a_{x} ; a_{y}right)$ и $Bleft(b_{x} ; b_{y}right)$.
Тогда координаты вектора $overline{A B}=left(x_{1} ; y_{1}right)$ находятся по формулам (рис. 4):
$x_{1}=b_{x}-a_{x}, y_{1}=b_{y}-a_{y}$
Определение
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат
конца отнять соответствующие координаты начала.
Пример
Задание. Найти координаты вектора $overline{A B}$,
если $A(-4 ; 2), B(1 ;-3)$
Решение. $overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$
Направляющие косинусы
Определение
Направляющими косинусами вектора называются косинусы углов, образованных вектором с
положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для
единичного вектора направляющие косинусы
равны его координатам.
Если в пространстве задан вектор $overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$, то
его направляющие косинусы вычисляются по формулам:
$cos alpha=frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos beta=frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, cos gamma=frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$
Здесь $alpha$, $beta$ и
$gamma$ – углы, которые составляет вектор с положительными
направлениями осей $O x$, $O y$ и
$O z$ соответственно.
Основное свойство направляющих косинусов
Определение
Сумма квадратов направляющих косинусов равна единице.
1
$cos ^{2} alpha+cos ^{2} beta+cos ^{2} gamma=1$
Если известны направляющие косинусы вектора $overline{a}=left(a_{x} ; a_{y}right)$,
то его координаты могут быть найдены по формулам:
$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta$
Аналогичные формулы имеют место и в трехмерном случае – если известны направляющие косинусы вектора
$overline{a}=left(a_{x} ; a_{y} ; a_{z}right)$,
то его координаты могут быть найдены по формулам:
$a_{x}=|overline{a}| cos alpha, a_{y}=|overline{a}| cos beta, a_{z}=|overline{a}| cos gamma$
Читать дальше: длина (модуль) вектора.
Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $overline$, начало которого совпадает с началом системы координат (рис. 1).
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $Aleft(a_ ; a_right)$ и $Bleft(b_ ; b_right)$. Тогда координаты вектора $overline=left(x_ <1>; y_<1>right)$ находятся по формулам (рис. 4):
Направляющие косинусы
Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.
Здесь $alpha$, $beta$ и $gamma$ – углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.
Основное свойство направляющих косинусов
Сумма квадратов направляющих косинусов равна единице.
Сложение и вычитание векторов
Формулы сложения и вычитания векторов
Формулы сложения и вычитания векторов для плоских задач
В случае плоской задачи сумму и разность векторов a = < ax ; ay > и b = < bx ; by > можно найти, воспользовавшись следующими формулами:
Формулы сложения и вычитания векторов для пространчтвенных задач
В случае пространственной задачи сумму и разность векторов a = < ax ; ay ; az > и b = < bx ; by ; bz > можно найти, воспользовавшись следующими формулами:
Формулы сложения и вычитания n -мерных векторов
В случае n -мерного пространства сумму и разность векторов a = < a 1 ; a 2 ; . ; an > и b = < b 1 ; b 2 ; . ; bn > можно найти, воспользовавшись следующими формулами:
Примеры задач на сложение и вычитание векторов
Примеры плоских задач на сложение и вычитание векторов
Примеры пространственных задач на сложение и вычитание векторов
Примеры задач на сложение и вычитание векторов с размерностью большей 3
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Планиметрия. Страница 8
1 2 3 4 5 6 7 8 9 10 11 12
1.Вектор и его абсолютная величина
Вектором называется направленный отрезок определенной длины. Любой вектор имеет начальную и конечную точки. Начало и конец вектора обозначаются заглавными буквами, например вектор
. Сам вектор обозначается прописной буквой, например:
. Каждый вектор имеет определенную длину и направление. Например, вектора
имеют одинаковое направление. А вектора
Абсолютной величиной вектора или модулем вектора называется длина отрезка, представляющего собой вектор.
Если начало вектора совпадает с его концом, то такой вектор называется нулевым.
Если два вектора имеют одинаковое направление и равные абсолютные величины, то такие векторы называются равными.
Рис.1 Обозначение векторов.
Координаты вектора
Любой вектор имеет свои координаты. Координатами вектора называются числа x2-x1 и y2-y1. Например, координаты вектора
с начальной точкой А (1;1) и конечной точкой В (4;3) будут:
Координаты нулевого вектора равны нулю.
Абсолютная величина вектора – это его длина. А следовательно, ее можно определить как расстояние между двумя точками, начальной и конечной. Т.е.
Два вектора называются равными, если у них соответствующие координаты равны.
Рис.2 Координаты вектора.
2.Сложение векторов
Пусть заданы два вектора со своими координатами
(b1;b2). Тогда суммой двух векторов будет вектор с координатами
В векторной форме можно записать так:
Для сложения векторов используются два метода: метод треугольника и метод параллелограмма.
Для сложения векторов методом треугольника необходимо перенести вектор
параллельным переносом так, чтобы конец вектора
совпадал с началом вектора
. Тогда начало вектора
и конец вектора
и будет сумма векторов
По методу параллелограмма, если два вектора
имеют общее начало, то суммой двух векторов будет диагональ параллелограмма, построенного на этих векторах, т.е. вектор
Разностью двух векторов
называется такой вектор
, который нужно прибавить к вектору
, чтобы получить вектор
Рис.3 Сложение векторов.
3.Умножение вектора на число
Любой вектор с координатами (x;y) можно умножить на простое число, например λ. (Рис.3) Тогда произведением вектора на число λ будет называться вектор с координатами (λx;λy). Абсолютная величина вектора будет равна:
Для любых двух векторов
число λ можно вынести за скобку λ (
Если λ > 0, то направление вектора не изменяется, а если λ 2 и называется скалярным квадратом. Отсюда следует, что
Теорема. Скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними.
Доказательство. Пусть даны два вектора а и b и угол между ними α. Тогда квадрат суммы двух векторов равен:
Следовательно, скалярное произведение двух векторов не зависит от выбора системы координат, а зависит только от их абсолютных величин. (Рис.5)
Так как координаты вектора
(b cos α; b sin α), то скалярное произведение двух векторов
Рис.5 Скалярное произведение векторов.
Отсюда вытекает следующий вывод:
если два вектора перпендикулярны, то их скалярное произведение равно нулю.
если скалярное произведение двух ненулевых векторов равно нулю, то векторы перпендикулярны.
6.Пример 1
Четырехугольник ABCD – параллелограмм. Докажите равенство векторов
Доказательство:
Пусть ABCD данный параллелограмм (Рис.6). Необходимо доказать, что вектора
параллельному переносу таким образом, чтобы точка А совпала с точкой D. При таком перемещении точка А смещается по прямой AD и переходит в точку D. Это значит, что точка В переместится по параллельной прямой ВС в точку С.
Таким образом, при параллельном переносе прямая АВ переходит в параллельную прямую DC, а вектор
переходит в вектор
. А это значит, что эти вектора равны.
Действительно, так как при перемещении прямая АВ переходит в параллельную прямую DC, а точка А переходит в точку D, то на луче DC можно отложить только один вектор, равный вектору
Рис.6 Задача. Четырехугольник ABCD – параллелограмм.
Пример 2
Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2). Докажите равенство векторов
Доказательство:
Найдем координаты векторов
Таким образом, координаты векторов следующие:
А так как равные вектора имеют равные соответствующие координаты и xAB = xCD, yAB = yCD, то вектора
Рис.7 Задача. Даны точки А(1;1), B(3;1), C(2;-2), D(4;-2).
Пример 3
В треугольнике АВС проведена медиана AM. Докажите, что
Доказательство:
, равный и параллельный вектору
от точки С. И отложим вектор
, равный и параллельный вектору
от точки В (Рис.8).
Тодга получим параллелограмм, в котором вектор
, так же как вектор
. А так как диагонали параллелограмма пересекаются в точке М и делятся этой точкой пополам, то
Отсюда можно сделать вывод: так как
Рис.8 Задача. В треугольнике АВС проведена медиана AM.
Пример 4
(-3;-2). Найдите вектор
и его абсолютную величину.
Решение:
, то найдем его координаты:
Теперь найдем его абсолютную величину:
| 2 = (-1) 2 + (-4) 2 = 17
| =
(-3;-2). ” alt=”Задача. Даны векторы
Рис.9 Задача. Даны векторы
Пример 5
Найдите угол между векторами
Решение:
По определению, скалярное произведение двух векторов равно произведению их абсолютных величин на косинус угла между ними. Отсюда можно найти косинус угла между ними по формуле:
Следовательно, cos α = 2 / 2 = 1 /
Таким образом, угол между векторами
(1;-1) и b (2;0).” alt=”Задача. Найдите угол между векторами
(1;-1) и b (2;0).” src=”http://www.mathtask.ru/page-0056/pl21.png”/>
Рис.10 Задача. Найдите угол между векторами
[spoiler title=”источники:”]
Сложение векторов
Формула
Чтобы складывать вектора нужно найти суммы соответствующих координат данных векторов. Например, пусть есть векторы на плоскости $ overline{a} = (x_1;y_1) $ и $ overline{b}=(x_2;y_2) $, тогда их сумму можно найти по формуле: $$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2)$$
Если векторы заданы в пространстве тремя координатами $ overline{a} = (x_1;y_1;z_1) $ и $ overline{b}=(x_2;y_2;z_2) $, то выполнить сложение нужно по другой формуле:
$$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2; z_1+z_2) $$
При сложении первая координата первого вектора складывается с первой координатой второго вектора, вторая координата первого вектора складывается со второй координатой второго вектора и так далее в зависимости от размерности векторов. Стоит отметить, что складывать векторы можно только одинаковой размерности.
Примеры решений
| Пример |
| Даны два вектора $ overline{a} = (1,3) $ и $ overline{b} = (2,4) $. Нужно сложить два вектора. |
| Решение |
|
Итак, как складывать вектора по координатам? К первой прибавляем первую, вторую ко второй: $$ overline{a}+overline{b} = (1+2;3+4) = (3;7) $$ В этой задаче векторы заданы в двумерном пространстве и имеют только две координаты. Если бы координат было бы три, то применять нужно вторую формулу для трехмерной задачи. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a}+overline{b} = (3;7) $$ |
Всего: 20 1–20
Добавить в вариант
Найдите сумму координат вектора 
Вектор с концом в точке B(5; 4) имеет координаты (3; 1). Найдите сумму координат точки A.
Найдите квадрат длины вектора 

Найдите сумму координат вектора
Вектор
с началом в точке A(3; 6) имеет координаты (9; 3). Найдите сумму координат точки B.
Найдите сумму координат вектора
Найдите сумму координат вектора
Вектор с началом в точке A(−22; −1) имеет координаты (8; 7). Найдите сумму координат точки B.
Дана правильная треугольная призма ABCA1B1C1 со стороной основания 12 и высотой 3. Точка K — середина BC, точка L лежит на стороне A1B1 так, что В1L = 5. Точка М — середина A1C1. Через точки K и L проведена плоскость таким образом, что она параллельна прямой AC.
а) Докажите, что указанная выше плоскость перпендикулярна прямой MB.
б) Найдите объем пирамиды с вершиной в точке В, у которой основанием является сечение призмы плоскостью.
Источник: ЕГЭ — 2016. Основная волна 06.06.2016. Центр
Точки E и K — соответственно середины сторон CD и AD квадрата ABCD. Прямая BE пересекается с прямой CK в точке O.
а) Докажите, что вокруг четырёхугольника ABOK можно описать окружность.
б) Найдите AO, если сторона квадрата равна 1.
В правильной треугольной призме ABCA1B1C1 все рёбра равны 2. Точка M — середина ребра AA1.
а) Докажите, что прямые MB и B1C перпендикулярны.
б) Найдите расстояние между прямыми MB и B1C.
В правильной треугольной призме ABCA1B1C1 сторона основания равна 4, а боковое ребро равно 2. Точка M — середина ребра A1C1, а точка O — точка пересечения диагоналей боковой грани ABB1A1.
а) Докажите, что точка пересечения диагоналей четырёхугольника, являющегося сечением призмы ABCA1B1C1 плоскостью AMB, лежит на отрезке OC1.
б) Найдите угол между прямой OC1, и плоскостью AMB.
Всего: 20 1–20
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Метод координат
- Координаты вектора
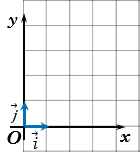
Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.
На рисунке выше оси 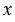
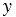
Отложим от начала координат О единичные векторы 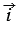
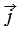
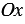
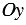
Векторы 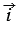
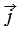
Координатные векторы не коллинеарны, поэтому любой вектор 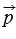
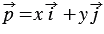
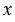
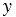
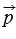
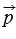
Координаты вектора записывают в фигурных скобках после обозначения вектора: 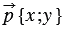
На рисунке выше 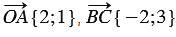
Нулевой вектор можно представить в виде 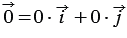
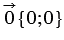
Если векторы 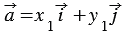
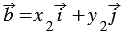
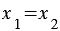
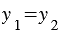
Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:
10. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
Доказательство
Дано: 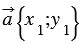
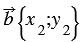
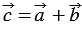
Доказать: 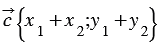
Доказательство:
По условию 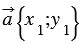
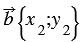
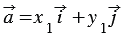
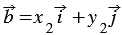
Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим: 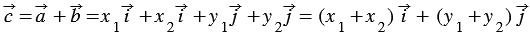
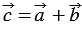

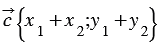
20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Доказательство
Дано: 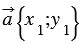
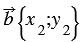
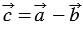
Доказать: 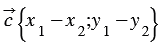
Доказательство:
По условию 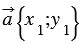
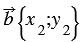
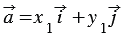
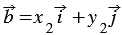
Вычтем из равенства (1) равенство (2) и применим свойства сложения векторов и умножения вектора на число, получим: 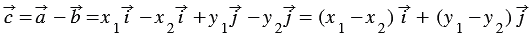
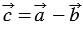
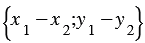
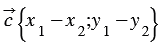
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Доказательство
Дано: 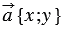
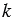
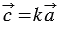
Доказать: 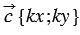
Доказательство:
По условию 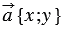
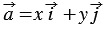
Умножим последнее равенство на число 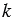
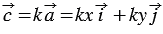
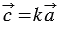
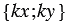
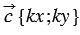
Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Пример
Найти координаты вектора 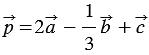
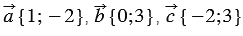
Решение:
По правилу 30 вектор 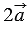
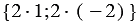
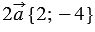
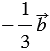
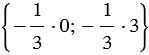
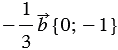
Так как 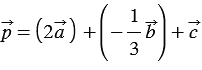
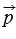
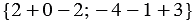
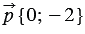
Ответ: 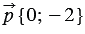
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Связь между координатами вектора его начала и конца
Простейшие задачи в координатах
Уравнение линии на плоскости
Уравнение окружности
Уравнение прямой
Взаимное расположение двух окружностей
Метод координат
Правило встречается в следующих упражнениях:
7 класс
Задание 933,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 943,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 952,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 953,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник