Алгебра логики
Алгебра логики
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Основоположником алгебры логики является английский математик и логик Дж. Буль (1815–1864), положивший в основу своего логического учения аналогию между алгеброй и логикой. Любое высказывание он записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и др.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Например, «3 умножить на 3 равно 9», «Архангельск севернее Вологды» — истинные высказывания, а «Пять меньше трех», «Марс — звезда» — ложные.
Очевидно, что не всякое предложение может быть логическим высказыванием, т. к. не всегда есть смысл говорить о его ложности или истинности. Например, высказывание «Информатика — интересный предмет» неопределенно и требует дополнительных сведений, а высказывание «Для ученика 10-А класса Иванова А. А. информатика — интересный предмет» в зависимости от интересов Иванова А. А. может принимать значение «истина» или «ложь».
Кроме двузначной алгебры высказываний, в которой принимаются только два значения — «истинно» и «ложно», существует многозначная алгебра высказываний. В такой алгебре, кроме значений «истинно» и «ложно», употребляются такие истинностные значения, как «вероятно», «возможно», «невозможно» и т. д.
В алгебре логики различаются простые (элементарные) высказывания, обозначаемые латинскими буквами (A, B, C, D, …), и сложные (составные), составленные из нескольких простых с помощью логических связок, например таких, как «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний.
Обозначим как А высказывание «Алгебра логики успешно применяется в теории электрических схем», а через В — «Алгебра логики применяется при синтезе релейно-контактных схем».
Тогда составное высказывание «Алгебра логики успешно применяется в теории электрических цепей и при синтезе релейно-контактных схем» можно кратко записать как А и В; здесь «и» — логическая связка. Очевидно, что поскольку элементарные высказывания А и В истинны, то истинно и составное высказывание А и В.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
1. Логическое отрицание, инверсия (лат. inversion — переворачивание) — логическая операция, в результате которой из данного высказывания (например, А) получается новое высказывание (не А), которое называется отрицанием исходного высказывания, обозначается символически чертой сверху ($A↖{-}$) или такими условными обозначениями, как ¬, ‘not’, и читается: «не А», «А ложно», «неверно, что А», «отрицание А». Например, «Марс — планета Солнечной системы» (высказывание А); «Марс — не планета Солнечной системы» ($A↖{-}$); высказывание «10 — простое число» (высказывание В) ложно; высказывание «10 — не простое число» (высказывание B ) истинно.
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
или
Высказывание $A↖{-}$ ложно, когда А истинно, и истинно, когда А ложно.
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖{-}$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.
2. Конъюнкция (лат. conjunctio — соединение) — логическое умножение, операция, требующая как минимум двух логических величин (операндов) и соединяющая два или более высказываний при помощи связки «и» (например, «А и В»), которая символически обозначается с помощью знака ∧ (А ∧ В) и читается: «А и В». Для обозначения конъюнкции применяются также следующие знаки: А ∙ В; А & В, А and В, а иногда между высказываниями не ставится никакого знака: АВ. Пример логического умножения: «Этот треугольник равнобедренный и прямоугольный». Данное высказывание может быть истинным только в том случае, если выполняются оба условия, в противном случае высказывание ложно.
Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.
3. Дизъюнкция (лат. disjunction — разделение) — логическое сложение, операция, соединяющая два или более высказываний при помощи связки «или» (например, «А или В»), которая символически обозначается с помощью знака ∨ (А ∨ В) и читается: «А или В». Для обозначения дизъюнкции применяются также следующие знаки: А + В; А or В; А | B. Пример логического сложения: «Число x делится на 3 или на 5». Это высказывание будет истинным, если выполняются оба условия или хотя бы одно из условий.
Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
4. Дизъюнкция строго-разделительная, сложение по модулю два — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле, которая символически обозначается с помощью знаков ∨ ∨ или ⊕ (А ∨ ∨ В, А ⊕ В) и читается: «либо А, либо В». Пример сложения по модулю два — высказывание «Этот треугольник тупоугольный или остроугольный». Высказывание истинно, если выполняется какое-то одно из условий.
Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
или
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
5. Импликация (лат. implisito — тесно связываю) — логическая операция, соединяющая два высказывания при помощи связки «если…, то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность». Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием. Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь. Например, «Если 3 * 3 = 9 (А), то Солнце — планета (В)», результат импликации А → В — ложь.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
6. Эквивалентность, двойная импликация, равнозначность (лат. aequalis — равный и valentis — имеющий силу) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В, которое читается: «А эквивалентно B». Для обозначения эквивалентности применяются также следующие знаки: ⇔, ∼. Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Примером эквивалентности является высказывание: «Треугольник будет прямоугольным тогда и только тогда, когда один из углов равен 90 градусам».
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖{-} ∧B) ∧ (A ∧ B↖{-})$ |
| Импликация | А → В | $A↖{-} ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖{-} ∧ B↖{-}) ∨ (A ∧ B)$ |
Приоритет выполнения логических операций следующий: отрицание («не») имеет самый высокий приоритет, затем выполняется конъюнкция («и»), после конъюнкции — дизъюнкция («или»).
С помощью логических переменных и логических операций любое логическое высказывание можно формализовать, т. е. заменить логической формулой. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определять истинность или ложность составного высказывания. Например, высказывание «Если пять больше двух (А), то вторник всегда наступает после понедельника (В)» — импликация А → В, и результат операции в данном случае — «истина». В логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Рассмотрим, например, построение составного высказывания из высказываний А и В, которое было бы ложно тогда и только тогда, когда оба высказывания истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А высказывание может быть, например, таким: «Этот мяч полностью красный или полностью синий». Следовательно, если утверждение А «Этот мяч полностью красный» — истина, и утверждение В «Этот мяч полностью синий» — истина, то составное утверждение — ложь, т. к. одновременно и красным, и синим мяч быть не может.
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X < 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Решение. Последовательность выполнения операций следующая: сначала выполняются операции сравнения в скобках, затем дизъюнкция, и последней выполняется операция импликации. Операция дизъюнкции ∨ ложна тогда и только тогда, когда оба операнда ложны. Таблица истинности для импликации имеет вид
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда получаем:
1) для X = 1:
((1 > 3) ∨ (1 < 3)) → (1 < 4) = ложь ∨ истина → истина = истина → истина = истина;
2) для X = 12:
((12 > 3) ∨ (12 < 3) → (12 < 4) = истина ∨ ложь → ложь = истина → ложь = ложь;
3) для X = 3:
((3 > 3) ∨ (3 < 3)) → (3<4) = ложь ∨ ложь → истина = ложь → истина = истина.
Пример 2. Указать множество целых значений X, для которых истинно выражение ¬((X > 2) → (X > 5)) .
Решение. Операция отрицания применена ко всему выражению ((X > 2) → (X > 5)) , следовательно, когда выражение ¬((X > 2) → (X > 5)) истинно, выражение ((X > 2) →(X > 5)) ложно. Поэтому необходимо определить, для каких значений X выражение ((X > 2) → (X > 5)) ложно. Операция импликации принимает значение «ложь» только в одном случае: когда из истины следует ложь. А это выполняется только для X = 3; X = 4; X = 5.
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Под логическим выражением следует понимать такую запись, которая может принимать логическое значение «истина» или «ложь». При таком определении среди логических выражений необходимо различать:
- выражения, которые используют операции сравнения («больше», «меньше», «равно», «не равно» и т. п.) и принимают логические значения (например, выражение а > b , где а = 5 и b = 7, равно значению «ложь»);
- непосредственные логические выражения, связанные с логическими величинами и логическими операциями (например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина).
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a – π/b) < 1 ∧ ¬B ∧ ¬(b^a + a^b > a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) ba + ab > a + b, после подстановки получим: 32 + 23 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (ba + ab > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
4) sin(π/a – π/b) < 1 = sin(π/2 – π/3) < 1 = истина.
После этих вычислений окончательно получим: истина ∨ А ∧ истина ∧ ¬В ∧ ¬истина.
Теперь должны быть выполнены операции отрицания, затем логического умножения и сложения:
5) ¬В = ¬ложь = истина; ¬истина = ложь;
6) A ∧ истина ∧ истина ∧ ложь = истина ∧ истина ∧ истина ∧ ложь = ложь;
7) истина ∨ ложь = истина.
Таким образом, результат логического выражения при заданных значениях— «истина».
Примечание. Учитывая, что исходное выражение есть, в конечном итоге, сумма двух слагаемых, и значение одного из них 1 ≤ a = 1 ≤ 2 = истина, без дальнейших вычислений можно сказать, что результат для всего выражения тоже «истина».
Тождественные преобразования логических выражений
В алгебре логики выполняются основные законы, позволяющие производить тождественные преобразования логических выражений.
| Закон | Для ∨ | Для ∧ |
| Переместительный | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Сочетательный | A ∨ (B ∨ C) = (B ∨ A) ∨ C | A ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Распределительный | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) | A ∨ B ∧ C = (A ∨ B) ∧ (A ∨ C) |
| Правила де Моргана | ${A ∨ B}↖{-}$ = $A↖{-} ∧ B↖{-}$ | ${A ∧ B}↖{-}$ = $A↖{-} ∨ B↖{-}$ |
| Идемпотенции | A ∨ A = A | A ∧ A = A |
| Поглощения | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Склеивания | (A ∧ B) ∨ (A↖{-} ∧ B) = B | (A ∨ B) ∧ (A↖{-} ∨ B) = B |
| Операция переменной с ее инверсией | $A ∨ A↖{-}$ = 1 | $A ∧ A↖{-}$ = 0 |
| Операция с константами | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Двойного отрицания | $A↖{=}$ = A |
Доказательства этих утверждений производят на основании построения таблиц истинности для соответствующих записей.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определенному виду путем использования основных законов алгебры логики. Под упрощением формулы, не содержащей операций импликации и эквивалентности, понимают равносильное преобразование, приводящее к формуле, которая содержит либо меньшее по сравнению с исходной число операций, либо меньшее число переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т. п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Рассмотрим на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2 .
Для преобразования здесь можно применить закон идемпотенции, распределительный закон; операцию переменной с инверсией и операцию с константой.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1 .
Здесь для упрощения применяется закон поглощения.
3) ¬(X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1 .
При преобразовании применяются правило де Моргана, операция переменной с ее инверсией, операция с константой
Примеры решения задач
Пример 1. Найти логическое выражение, равносильное выражению A ∧ ¬(¬B ∨ C) .
Решение. Применяем правило де Моргана для В и С: ¬(¬B ∨ C) = B ∧ ¬C .
Получаем выражение, равносильное исходному: A ∧ ¬(¬B ∨ C) = A ∧ B ∧ ¬C .
Ответ: A ∧ B ∧ ¬C.
Пример 2. Указать значение логических переменных А, В, С, для которых значение логического выражения (A ∨ B) → (B ∨ ¬C ∨ B) ложно.
Решение. Операция импликации ложна только в случае, когд а из истинной посылки следует ложь. Следовательно, для заданного выражения посылка A ∨ B должна принимать значение «истина», а следствие, т. е. выражение B ∨ ¬C ∨ B , — «ложь».
1) A ∨ B — результат дизъюнкции — «истина», если хотя бы один из операндов — «истина»;
2) B ∨ ¬C ∨ B — выражение ложно, если все слагаемые имеют значение «ложь», т. е. В — «ложь»; ¬C — «ложь», а следовательно, переменная С имеет значение «истина»;
3) если рассмотреть посылку и учесть, что В — «ложь», то получим, что значение А — «истина».
Ответ: А — истина, В — ложь, С — истина.
Пример 3. Каково наибольшее целое число X, при котором истинно высказывание (35 < X · X) → (X < (X – 3)) ?
Решение. Запишем таблицу истинности для операции импликации:
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Выражение X < (X – 3) ложно при любых положительных значениях X. Следовательно, для того чтобы результатом импликации была «истина», необходимо и достаточно, чтобы выражение 35 < X · X также было ложно. Максимальное целое значение X, для которого 35 < X · X ложно, равно 5.
Ответ: X = 5.
Использование логических выражений для описания геометрических областей
Логические выражения могут быть использованы для описания геометрических областей. В этом случае задача формулируется так: записать для заданной геометрической области такое логическое выражение, которое принимает значение «истина» для значений x, y тогда и только тогда, когда любая точка с координатами (x; y) принадлежит геометрической области.
Рассмотрим описание геометрической области с помощью логического выражения на примерах.
Пример 1. Задано изображение геометрической области. Записать логическое выражение, описывающее множество точек, принадлежащих ей.
1) 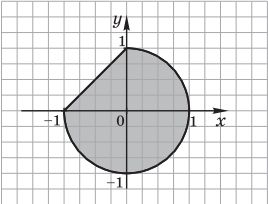
Решение. Заданную геометрическую область можно представить в виде набора следующих областей: первая область — D1 — полуплоскость ${x}/{-1} +{y}/{1} ≤ 1$, вторая — D2 — круг с центром в начале координат $x^2 + y^2 ≤ 1$. Их пересечение D1 $∩$ D2 представляет собой искомую область.
Результат: логическое выражение ${x}/{-1}+{y}/{1} ≤ 1 ∧ x^2 + y^2 ≤ 1$.
2)
Эту область можно записать так: |x| ≤ 1 ∧ y ≤ 0 ∧ y ≥ -1 .
Примечание. При построении логического выражения используются нестрогие неравенства, а это значит, что границы фигур также принадлежат заштрихованной области. Если использовать строгие неравенства, то границы учитываться не будут. Границы, не принадлежащие области, обычно изображаются пунктиром.
Можно решить обратную задачу, а именно: нарисовать область для заданного логического выражнения.
Пример 2. Нарисовать и заштриховать область, для точек которой выполняется логическое условие y ≥ x ∧ y + x ≥ 0 ∧ y < 2 .
Решение. Искомая область представляет собой пересечение трех полуплоскостей. Строим на плоскости (x, y) прямые y = x; y = –x; y = 2. Это границы области, причем последняя граница y = 2 не принадлежит области, поэтому ее наносим пунктирной линией. Для выполнения неравенства y ≥ x нужно, чтобы точки находились слева от прямой y = x, а неравенство y = –x выполняется для точек, которые находятся справа от прямой y = –x. Условие y < 2 выполняется для точек, лежащих ниже прямой y = 2. В результате получим область, которая изображена на рис.:
Использование логических функций для описания электрических схем
Логические функции очень удобны для описания работы электрических схем. Так, для схемы, представленной на рис., где значение переменной X — это состояние выключателя (если он включен, значение X — «истина», а если выключен — «ложь»), это значение Y — это состояние лампочки (если она горит — значение «истина», а если нет — «ложь»), логическая функция запишется так: Y = X . Функцию Y называют функцией проводимости.
Для схемы, представленной на рис., логическая функция Y имеет вид: Y = X1 ∪ X2, т. к. достаточно одного включенного выключателя, чтобы горела лампочка. В схеме на рис., для того чтобы горела лампочка, должны быть включены оба выключателя, следовательно, функция проводимости имеет вид: Y = X1 ∧ X2 .
Для более сложной схемы функция проводимости будет иметь вид: Y = (X11 ∨ (X12 ∧ X13)) ∧ X2 ∧ (X31 ∨ X32).
Схема также может содержать контакты на замыкание. В этом случае размыкаемый контакт как выключатель обеспечивает загорание лампочки, когда кнопка отпущена, а не нажата. Для таких схем размыкающий выключатель описывается отрицанием.
Две схемы называются равносильными, если через одну из них ток проходит тогда, когда он проходит и через другую. Из двух равносильных схем более простой считается схема, функция проводимости которой содержит меньшее число элементов. Задача нахождения наиболее простых схем среди равносильных очень важна.
Использование аппарата алгебры логики при проектировании логических схем
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера. Любая информация при обработке на компьютере представляется в двоичной форме, т. е. кодируется некоторой последовательностью 0 и 1. Обработку двоичных сигналов, соответствующих 0 и 1, выполняют в компьютере логические элементы. Логические элементы, которые выполняют основные логические операции И, ИЛИ, НЕ, представлены на рис.
Условные обозначения логических элементов являются стандартными и используются при составлении логических схем компьютера. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу компьютера.
Технически компьютерный логический элемент реализуется в виде электрической схемы, которая представляет собой соединение различных деталей: диодов, транзисторов, резисторов, конденсаторов. На вход логического элемента, который называют также вентилем, поступают электрические сигналы высокого и низкого уровней напряжения, на выход выдается один выходной сигнал также либо высокого, либо низкого уровня. Эти уровни соответствуют одному из состояний двоичной системы: 1 — 0; ИСТИНА — ЛОЖЬ. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических схем описывают с помощью таблиц истинности. Условное обозначение на схеме ИЛИ знак «1» — от устаревшего обозначения дизъюнкции как «>=1» (значение дизъюнкции равно 1, если сумма двух операндов больше или равна 1). Знак «&» на схеме И является сокращенной записью английского слова and.
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы ${X1}↖{-} ∧ X2 ∨ {X1 ∨ X2}↖{-} ∨ X1$.
| X1 | X2 | ${X1}↖{-}$ | ${X1}↖{-}$ X2 | X1 ∧ X2 | ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
- в таблице истинности функции выбирают наборы аргументов, для которых логические формы равны 1 («истина»);
- все выбранные логические наборы как логические произведения аргументов записывают, последовательно соединив их между собой операцией логической суммы (дизъюнкции);
- для аргументов, которые являются ложными, в построенной записи проставляют операцию отрицания.
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Ответ: F(X1, X2) = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
- в таблице истинности выбирают наборы аргументов, для которых логические формы равны 0 («ложь»);
- все выбранные логические наборы как логические суммы аргументов записывают последовательно, соединив их между собой операцией логического произведения (конъюнкции);
- для аргументов, которые являются истинными, в построенной записи проставляют операцию отрицания.
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Ответ: X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2 = X1 ∧ ${X1}↖{-}$ ∨ X1 ∧ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ ${X2}↖{-}$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ 0 = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 = X2 ∧ (X1 ∨ ${X1}↖{-}$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ ${X3}↖{-}$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∪ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∨ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ = X2 ∧ X3 ∧ (X1 ∨ ${X1}↖{-}$) ∨ X1 ∧ ${X3}↖{-}$ ∧ (X2 ∨ ${X2}↖{-}$) = X2 ∧ X3 ∨ X1 ∧ ${X3}↖{-}$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
Решение. Очевидно, что результатом решения будет таблица, в которой искомая функция Y(X1, X2, X3) будет иметь значение «истина», если какие-либо две переменные имеют значение «истина».
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Из условия 4 следует, что Борис не увлекается ни лыжами, ни теннисом, а из условий 3 и 5, что Петр не умеет играть в футбол, хоккей, теннис и бадминтон. Следовательно, любимые виды спорта Петра — лыжи и плавание. Занесем это в таблицу, а оставшиеся клетки столбцов «Лыжи» и «Плавание» заполним нулями.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
Из условий 1 и 2 следует, что Борис не футболист. Таким образом, в футбол играет Алексей. Продолжим заполнять таблицу. Внесем в пустые ячейки строки «Алексей» нули.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.
Логические выражения и таблица истинности
Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2n, где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Пример 1. Для формулы A/ (B / ¬B /¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
Пример 2. Определите истинность логического выражения F(А, В) = (А/ В)/(¬А/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А/ В; 2) ¬А; 3) ¬В; 4) ¬А/¬В; 5) (А/ В)/(¬А/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
|
А |
В |
А/ В |
¬А |
¬В |
¬А/¬В |
F |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A/ B) / ¬С
- В данной функции три логические переменные – А, В, С
- количество строк таблицы = 23 =8
- В формуле 3 логические операции.
- Расставляем порядок действий
1) А/ В; 2) ¬С; 3) (AVB) / ¬С .
- количество столбцов таблицы = 3 + 3 = 6
|
А |
В |
С |
A/B |
¬С |
(A/B) / ¬С |
|
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
Пример 4. Определите истинность формулы: F = ((С /В) => В) / (А / В) => В.
Построим таблицу истинности этой формулы.
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
|
X |
Y |
Z |
F |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
Какое выражение соответствует F?
1) ¬X/¬Y/Z 2) ¬X/¬Y/Z 3) X/Y/¬Z 4) X/Y/Z
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
|
X |
Y |
Z |
F |
¬X |
¬Y |
¬Z |
¬X/¬Y/Z |
¬X/¬Y/Z |
X/Y/¬Z |
X/Y/Z |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
Очевидно, что значения заданной функции F совпадают со значениями выражения X/Y/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/¬Y/Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X/¬Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X/Y/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X/Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
Содержание:
- Свойства логических операций
- Законы алгебры логики могут быть доказаны с помощью таблиц истинности
- Примеры с решением
Построение таблиц истинности для логических выражений
Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:
- подсчитать п — число переменных в выражении;
- подсчитать общее число логических операций в выражении;
- установить последовательность выполнения логических операций с учётом скобок и приоритетов;
- определить число столбцов в таблице: число переменных + число операций;
- заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в п. 3;
- определить число строк в таблице (не считая шапки таблицы):
;
- выписать наборы входных переменных с учётом того, что они представляют собой ряд целых п-разрядных двоичных чисел от 0 до
;
- провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Построим таблицу истинности для логического выражения 

- Наборы входных переменных — это целые числа от 0 до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Заполненная таблица истинности имеет вид:

Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение 
Возможно вам будут полезны данные страницы:
Свойства логических операций
Рассмотрим основные свойства логических операций, называемые также законами алгебры логики.
1. Переместительный (коммутативный) закон:
• для логического умножения:
• для логического сложения:
2. Сочетательный (ассоциативный) закон:
• для логического умножения:
• для логического сложения:
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
3. Распределительный (дистрибутивный) закон:
• для логического умножения:
• для логического сложения:
4. Закон двойного отрицания:
Двойное отрицание исключает отрицание.
5. Закон исключённого третьего:
• для логического умножения:
• для логического сложения:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
6. Закон повторения:
• для логического умножения:
• для логического сложения:
7. Законы операций с 0 и 1:
• для логического умножения:
• для логического сложения:
8. Законы общей инверсии:
• для логического умножения:
• для логического сложения:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности
Докажем распределительный закон для логического сложения:
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Примеры с решением
Пример 1.
Найдём значение логического выражения 
Решение:
При X = 0 получаем следующее логическое выражение: 
Для решения задач вам понадобится знание таблиц истинности логических операций:

Порядок выполнения логических операций задается круглыми скобками
Сначала выполняется операция отрицания НЕ
затем И
после И выполняется ИЛИ
затем следование
и в последнюю очередь — эквивалентность.
Задача 1
Дан фрагмент таблицы истинности выражения F:

Решение:
Чтобы определить верное выражение, надо значения А,В,С каждой из строк таблицы подставить в очередное выражение, определить его результат выполнения и сравнить со значением F соответствующей строки.
То выражение, значения которого совпадут со значениями столбца F, и будет искомым. Решение:
Ответ: 4
Задача 2
Дан фрагмент таблицы истинности выражения F:

Решение:
Обратите внимание:
1) В каждом из приведенных выражений логические переменные связывает только один тип логической операции. В 1 и 3 вариантах это операция И (

2) По столбцу F видно, что выражение для двух комбинаций данных истинно, а для одной — ложно. Следовательно, выражение не может быть логическим умножением (И), так как логическое умножение истинно только для одной комбинации данных, а в таблице две истины. Следовательно, искомое выражение является логическим сложением (ИЛИ) значений логических переменных.
Поэтому, в качестве ответа может быть 2 или 4 вариант. Рассмотрим их.
1) 2-й вариант: В первой строке таблицы истинности отображены только значения х1, хЗ, х5, и все они равны 0. Но в формуле 2го варианта у нас х5 отрицается, то есть значение х5 будет изменено на 1, и в результате всё выражение должно быть истинным. Что не соответствует заданной таблице. Остаётся 4-й вариант.
2) Как мы видим, переменные х1, хЗ и х5 в 4-м варианте ответа не отрицаются, что соответствует первой строке заданной таблицы.
Ответ: 4
Задача 4
Какое из приведенных имен сказочных героев удовлетворяет логическому условию:

1) АРТЕМОН
2) БАЗИЛИО
3) БУРАТИНО
4) МАЛЬВИНА
Решение:
Составим для каждого из предложенных ответов схему соответственно заданной логической формуле. Ищем истинное значение.
1) АРТЕМОН
Первая буква согласная – НЕТ (0)
Вторая буква не А – ДА (1)
Последняя буква гласная – НЕТ (0) / у
Предпоследняя буква гласная – ДА (1) X” ‘”X X”
Подставляем полученные значения в формулу и решаем ее: н 0 ->1 ) л 0 -> 1 ),= О
И так с каждым вариантом ответа, пока не найдете истину.
Задача 5
Логическая функция F задаётся выражением
Определите, какому столбцу таблицы истинности функции F соответствует каждая из

Решение 1:
Последней операцией выполнения является операция 

Рассмотрим все случаи, когда F = 1 (это значения в строках 1 и 3):
– не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.

- две единицы в 3-м столбце => это значения X
- два нуля в 1-м столбце => это значения Y
- ноль единица во 2-м столбце => это значения Z
Ответ: YZX
Решение 2:
Последней операцией выполнения является операция 

Выражение F равно 1 в 1й и Зй строках, в этих же строках только “Перем.3”=1, следовательно, значение X находится в 3-м столбце.
Теперь рассмотрим построчно значения 1-х двух столбцов:
(помним, что 1 -> 0 = 0, в остальных комбинациях =1)
1 строка: 0 и О, Y = Z. Поэтому Y и Z для столбцов не определить.
2 строка: 0 и 1. Независимо будет ли Y=0 Z=1 или Y=1 Z=0, функция F=0 т.к. уже
Х=0. Поэтому Y и Z для столбцов не определить.
3 строка: 0 и 1. В этой строке функция F=1, значит 
невозможна, иначе F будет = 0. Комбинация 
Ответ: YZX
Лекции:
- Элементы векторной алгебры
- Асимптоты графика функции
- Разложение в ряд маклорена
- Частные производные второго порядка
- Тройной интеграл
- Производная синуса
- Дифференциальные уравнения в полных дифференциалах
- Тригонометрические неравенства
- Найти неопределенный интеграл: примеры решения
- Векторы и операции с ними
Задания 2. Значение логического выражения
Примеры для
разбора взяты с сайта https://inf-oge.sdamgia.ru, где решение
приведено логически рассуждая, а в данной работе с использованием таблиц
истинности.
1.
Для какого из приведённых значений числа X ложно
высказывание:
НЕ (X< 6) ИЛИ (X<
5)?
1) 7 2) 6 3) 5 4)
4
Решение.
1
способ
Логическое «ИЛИ» ложно только тогда, когда ложны оба высказывания.
Запишем выражение в виде
(X>=
6) ИЛИ (X< 5)
и проверим
все варианты ответа.
1) Истинно, поскольку истинно первое высказывание: 7 больше 6.
2) Истинно, поскольку истинно первое высказывание: 6 не меньше 6.
3) Ложно, поскольку ложны оба высказывания: 5 не больше 6 и 5 не
меньше 5.
4) Истинно, поскольку истинно второе высказывание: 4 меньше 5.
2
способ
Пусть А=(X<
6) и В=(X< 5), тогда по условию НЕ (X<
6) ИЛИ (X<
5)=0.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
А=1 X< 6 В=0 X>=5, |
Правильный ответ указан под номером 3.
2.
Для какого из приведённых значений числа X истинно
высказывание:
НЕ (X < 6) И (X < 7)?
1) 5 2) 6 3) 7 4)
8
Решение.
Пусть А=
(X< 6) и В= (X< 7), тогда по условию НЕ (X<
6) И (X<
7)=1.
Строим таблицу
истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 X>= 6 B=1 X< 7, сл-но X=6 |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 2.
3.
Для какого из приведённых значений числа X истинно
высказывание:
(X < 8) И НЕ (X <
7)?
1) 9 2) 8 3) 7 4) 6
Решение.
Пусть А=
(X< 8) и В= (X< 7), тогда по условию A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
A И HE B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
A=1 X<8 B=0 X>=7, сл-но X=7 |
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 3.
4.
Для какого из приведённых значений числа X истинно
высказывание:
НЕ (X > 5) И (X >
4)?
1) 4 2) 5 3) 6 4) 7
Решение.
Пусть А=
(X>5) и В= (X>4), тогда по условию НЕ A И B=1.
Строим таблицу
истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 X<= 5 B=1 X>4, сл-но X=2 |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 2.
5.
Для какого из приведённых значений числа X истинно
высказывание:
НЕ (X <
5) И (X <
6)?
1) 6 2) 5 3) 4 4) 3
Решение.
Пусть А=
(X<5) и В= (X<6), тогда по условию НЕ A И B=1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 X>= 5 B=1 X<6, сл-но X=5 |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 2.
6.
Для какого из приведённых значений числа X истинно
высказывание:
(X < 7) И НЕ (X <
6)?
1) 4 2) 5 3) 6 4) 7
Решение.
Пусть А=
(X<7) и В= (X<6), тогда по условию A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
A И HE B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
A=1 X<7 B=1 X>=6, |
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 3.
7.
Для какого из приведённых значений числа X ложно
высказывание:
НЕ (X <
7) ИЛИ (X <
6)?
1) 4 2) 5 3) 6 4) 7
Решение.
Пусть А=
(X<7) и В= (X<6), тогда по условию НЕ A ИЛИ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
HE A ИЛИ B |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
A=1 X<7 B=0 X>=6, |
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 3.
8.
Для какого из приведённых чисел истинно высказывание:
НЕ (число < 100) И НЕ (число
чётное)?
1) 123 2) 106 3) 37 4) 8
Решение.
Пусть А=
(число < 100) и В= (число чётное), тогда по условию НЕ A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
НЕ |
НЕ |
HE A И НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (число > 100) B=0 (число нечётное), сл-но 123 |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный ответ указан под номером 1.
9.
Для какого из приведённых чисел истинно высказывание:
(число < 100) И НЕ (число
чётное)?
1) 156 2) 105 3) 23 4) 10
Решение.
Пусть А=
(число < 100) и В= (число чётное), тогда по условию A И НЕ B=1.
Строим таблицу
истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
A И НЕ B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
A=1 (число < 100) B=0 (число нечётное), сл-но 23 |
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 3.
10.
Для какого из приведённых чисел истинно высказывание:
НЕ (число <50) И (число
чётное)?
1) 24 2) 45 3) 74 4) 99
Решение.
Пусть А=
(число < 50) и В= (число чётное), тогда по условию НЕ A И B=1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
НЕ A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (число >50) B=1 (число чётное), сл-но 74 |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 3.
11.
Для какого из приведённых чисел истинно высказывание:
(число <75) И НЕ (число
чётное)?
1) 46 2) 53 3) 80 4) 99
Решение.
Пусть А=
(число < 75) и В= (число чётное), тогда по условию A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
A И НЕ B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
A=1 (число <75) B=0 (число нечётное), сл-но 53 |
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 2.
12.
Для какого из приведённых чисел ложно высказывание:
НЕ (число <10) ИЛИ НЕ (число
чётное)?
1) 123 2) 56 3) 9 4) 8
Решение.
Пусть А=
(число < 10) и В= (число чётное), тогда по условию НЕ A ИЛИ НЕ B=0.
Строим таблицу
истинности:
Условию задачи соответствует 4-я строка
|
A |
B |
НЕ |
НЕ |
НЕ A ИЛИ НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
0 |
A=1 (число <10) B=1 (число чётное), сл-но 8 |
Правильный ответ указан под номером 4.
13.
Для какого из приведённых чисел ложно высказывание:
(число < 40) ИЛИ НЕ (число
чётное)?
1) 123 2) 56 3) 9 4) 8
Решение.
Пусть А=
(число < 40) и В= (число чётное), тогда по условию A ИЛИ НЕ B=0.
Строим
таблицу истинности:
Условию задачи соответствует2-я строка
|
A |
B |
НЕ |
A ИЛИ НЕ B |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
A=0 (число >40) B=1 (число чётное), сл-но 56 |
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 2.
14.
Для какого из приведённых чисел ложно высказывание:
НЕ (число > 50) ИЛИ (число
чётное)?
1) 123 2) 56 3) 9 4) 8
Решение.
Пусть А=
(число >50) и В= (число чётное), тогда по условию НЕ A ИЛИ B=0.
Строим
таблицу истинности:
Условию задачи соответствует3-я строка
|
A |
B |
НЕ |
НЕ A ИЛИ B |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
A=1 (число >50) B=0 (число нечётное), сл-но 123 |
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 1.
15.
Для какого из приведённых значений числа X истинно
высказывание:
НЕ (X <
3) И (X <
4)?
1) 5 2) 2 3) 3 4) 4
Решение.
Пусть А=
(X<3) и В= (X<4), тогда по условию НЕ A И B=1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 X>=3 B=1 X<6, |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 3.
16.
Для какого из приведённых значений числа X истинно
высказывание:
(X < 5) И НЕ (X <
4)?
1) 5 2) 2 3) 3 4) 4
Решение.
Пусть А=
(X<5) и В= (X<4), тогда по условию A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
A И HE B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
A=1 X< 5 B=0 X>=4, |
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 4.
17.
Для какого из приведённых чисел истинно высказывание:
НЕ (Первая цифра чётная) И (Последняя
цифра нечётная)?
1) 1234 2) 6843 3) 3561 4) 4562
Решение.
Пусть А=
(Первая цифра чётная) и В= (Последняя цифра нечётная), тогда по условию НЕ
A И B=1.
Строим
таблицу истинности:
Условию задачи соответствует2-я строка
|
A |
B |
НЕ |
НЕ A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (Первая цифра нечётная) B=1 (Последняя цифра нечётная), сл-но 3561 |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 3.
18.
Для какого из приведённых имён истинно высказывание:
НЕ (Первая буква гласная) И
НЕ (Последняя буква согласная)?
1) Инна 2) Нелли 3) Иван 4) Потап
Решение.
Пусть А=
(Первая буква гласная) и В= (Последняя буква согласная), тогда по условию НЕ
A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует1-я строка
|
A |
B |
НЕ |
НЕ |
НЕ A И НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (Первая буква согласная) B=0 (Последняя буква гласная), |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный ответ указан под номером 2.
19.
Для какого из приведённых имён истинно высказывание:
НЕ (Первая буква гласная) И
НЕ (Последняя буква согласная)?
1) Анна 2) Роман 3) Олег 4) Татьяна
Решение.
Пусть А=
(Первая буква гласная) и В= (Последняя буква согласная), тогда по условию НЕ
A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует1-я строка
|
A |
B |
НЕ |
НЕ |
НЕ A И НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (Первая буква согласная) B=0 (Последняя буква гласная), |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный ответ указан под номером 4.
20.
Для какого из приведённых имён истинно высказывание:
НЕ (Первая буква согласная) И
НЕ (Последняя буква гласная)?
1) Ольга 2) Михаил 3) Валентина 4) Ян
Решение.
Пусть А=
(Первая буква согласная) и В= (Последняя буква гласная), тогда по условию НЕ
A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует1-я строка
|
A |
B |
НЕ |
НЕ |
НЕ A И НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (Первая буква гласная) B=0 (Последняя буква согласная), |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный ответ указан под номером 4.
21.
Для какого из приведённых имён истинно высказывание:
НЕ (Первая буква согласная) И
НЕ (Последняя буква гласная)?
1)
Юлиан 2) Константин 3) Екатерина 4) Светлана
Решение.
Пусть А=
(Первая буква согласная) и В= (Последняя буква гласная), тогда по условию НЕ
A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует1-я строка
|
A |
B |
НЕ |
НЕ |
НЕ A И НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (Первая буква гласная) B=0 (Последняя буква согласная), |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный
ответ указан под номером 1.
22.
Для какого из приведённых имён ложно высказывание:
НЕ (Первая буква гласная) ИЛИ
НЕ (Последняя буква согласная)?
1) Арина 2) Владимир 3) Раиса 4) Ярослав
Решение.
Пусть А=
(Первая буква гласная) и В= (Последняя буква согласная), тогда по условию НЕ
A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует1-я строка
|
A |
B |
НЕ |
НЕ |
НЕ A И НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (Первая буква согласная) B=0 (Последняя буква гласная), |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный
ответ указан под номером 3.
23. Для какого из приведённых имён ложно высказывание:
НЕ (Первая буква гласная) ИЛИ НЕ (Последняя буква согласная)?
1)
Эдуард 2) Ангелина 3) Карина 4) Никон
Решение.
Пусть А=
(Первая буква гласная) и В= (Последняя буква согласная), тогда по условию НЕ
A ИЛИ НЕ B=0.
Строим
таблицу истинности:
Условию задачи соответствует4-я строка
|
A |
B |
НЕ |
НЕ |
НЕ A ИЛИ НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
0 |
A=1 (Первая буква гласная) B=1 (Последняя буква согласная), |
Правильный
ответ указан под номером 1.
24.
Для какого из приведённых имён ложно высказывание:
НЕ (Первая буква согласная) ИЛИ
НЕ (Последняя буква гласная)?
1) Пимен 2) Кристина 3) Ирина 4) Александр
Решение.
Пусть А=
(Первая буква согласная) и В= (Последняя буква гласная), тогда по условию НЕ
A ИЛИ НЕ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 4-я строка
|
A |
B |
НЕ |
НЕ |
НЕ A ИЛИ НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
0 |
A=1 (Первая буква согласная) B=1 (Последняя буква гласная), |
Правильный
ответ указан под номером 2.
25.
Для какого из приведённых имён ложно высказывание:
НЕ (Первая буква согласная) ИЛИ
НЕ (Последняя буква гласная)?
1)
Егор 2) Тимур 3) Вера 4) Любовь
Решение.
Пусть А=
(Первая буква согласная) и В= (Последняя буква гласная), тогда по условию НЕ
A ИЛИ НЕ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 4-я строка
|
A |
B |
НЕ |
НЕ |
НЕ A ИЛИ НЕ B |
|
|
0 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
0 |
A=1 (Первая буква согласная) B=1 (Последняя буква гласная), |
Правильный
ответ указан под номером 3.
26.
Для какого из приведённых имён ложно высказывание:
НЕ ((Первая буква гласная) И (Последняя
буква согласная))?
1)
Валентина 2) Герман 3) Анастасия 4) Яков
Решение.
Пусть А=
(Первая буква гласная) и В= (Последняя буква согласная), тогда по условию НЕ
(A И B)=0.
Строим
таблицу истинности:
Условию задачи соответствует 4-я строка
|
A |
B |
A И B |
НЕ (A И B) |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
A=1 (Первая буква гласная) B=1 (Последняя буква согласная), сл-но |
Правильный
ответ указан под номером 4.
27. Для
какого из приведённых имён ложно высказывание:
НЕ ((Первая буква согласная) И (Последняя
буква гласная))?
1) Дарья 2) Павел 3) Абрам 4) Анфиса
Решение.
Пусть А=
(Первая буква согласная) и В= (Последняя буква гласная), тогда по условию НЕ
(A И B)=0.
Строим
таблицу истинности:
Условию задачи соответствует 4-я строка
|
A |
B |
A И B |
НЕ (A И B) |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
1 |
0 |
1 |
|
|
1 |
0 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
A=1 (Первая буква согласная) B=1 (Последняя буква гласная), |
Правильный
ответ указан под номером 1.
28. Для
какого из данных слов истинно высказывание:
НЕ (оканчивается на мягкий знак) И (количество
букв чётное)?
1)
сентябрь 2) август 3) декабрь 4) май
Решение.
Пусть А=
(оканчивается на мягкий знак) и В= (количество букв чётное), тогда по условию НЕ
A И B
=1.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
НЕ A |
НЕ A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (не оканчивается на мягкий знак) B=1 (количество букв чётное), |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный
ответ указан под номером 2.
29. Для
какого из данных слов истинно высказывание:
(оканчивается на мягкий знак) И НЕ (количество
букв чётное)?
1) сентябрь 2) август 3) декабрь 4) май
Решение.
Пусть А=
(оканчивается на мягкий знак) и В= (количество букв чётное), тогда по условию A И НЕ B
=1.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
НЕ В |
A И НЕ B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
A=1 (оканчивается на мягкий знак) B=0 (количество букв чётное), |
|
1 |
1 |
0 |
0 |
Правильный
ответ указан под номером 1.
30. Для
какого из данных слов истинно высказывание:
НЕ (есть шипящие) И (оканчивается
на гласную)?
Шипящие звуки — это [ж], [ш], [ч’], [щ’].
1) любовь 2) отвращение 3) забота 4)
отчуждённость
Решение.
Пусть А=
(есть шипящие) и В= (оканчивается на гласную), тогда по условию НЕ A И B =1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ А |
НЕ A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (нет шипящих) B=1 (оканчивается на гласную), сл-но забота |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный
ответ указан под номером 3.
31. Для
какого из данных слов истинно высказывание:
НЕ (есть шипящие) И НЕ (оканчивается
на гласную)?
Шипящие звуки — это [ж], [ш], [ч’], [щ’].
1) любовь 2) отвращение 3) забота 4)
отчуждённость
Решение.
Пусть А=
(есть шипящие) и В= (оканчивается на гласную), тогда по условию НЕ A И НЕ B
=1.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
НЕ А |
НЕ В |
НЕ A И НЕ В |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (нет шипящих) B=0 (не оканчивается на гласную), |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный
ответ указан под номером 1.
32. Для
какого из данных слов истинно высказывание:
НЕ (ударение на первый слог) И (количество
букв чётное)?
1)
корова 2) козел 3) кошка 4) конь
Решение.
Пусть А=
(ударение на первый слог) и В= (количество букв чётное), тогда по условию НЕ
A И B
=1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ А |
НЕ A И НЕ В |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (ударение не на первый слог) B=1 (количество букв чётное), |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный
ответ указан под номером 1.
33. Для
какого из данных слов истинно высказывание:
(ударение на первый слог) И НЕ (количество
букв чётное)?
1)
корова 2) козел 3) кошка 4) конь
Решение.
Пусть А=
(ударение на первый слог) и В= (количество букв чётное), тогда по условию A И НЕ B
=1.
Строим
таблицу истинности:
Условию задачи соответствует 4-я строка
|
A |
B |
НЕ В |
A И НЕ В |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
A=1 (ударение на первый слог) B=1 (количество букв чётное), сл-но конь |
Правильный
ответ указан под номером 4.
34. Для
какого из приведённых названий ложно высказывание:
НЕ (Количество букв чётное) ИЛИ (Первая
буква согласная)?
1) Омск 2) Иваново 3) Москва 4) Кировск
Решение.
Пусть А=
(Количество букв чётное) и В= (Первая буква согласная), тогда по условию НЕ
A ИЛИ B
=0.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ А |
НЕ A ИЛИ В |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
A=1 (Количество букв чётное) B=0 (Первая буква гласная), сл-но Омск |
|
1 |
1 |
0 |
1 |
Правильный
ответ указан под номером 1.
35. Для
какого из приведённых названий ложно высказывание:
(Количество букв чётное) ИЛИ (Последняя
буква гласная)?
1) Москва 2) Омск 3) Дубна 4) Новокунецк
Решение.
Пусть А=
(Количество букв чётное) и В= (Первая буква гласная), тогда по условию A ИЛИ B =0.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
A ИЛИ В |
|
|
0 |
0 |
0 |
A=0 (Количество букв нечётное) B=0 (Последняя буква согласная), сл-но Новокузнецк |
|
0 |
1 |
1 |
|
|
1 |
0 |
1 |
|
|
1 |
1 |
1 |
Правильный
ответ указан под номером 4.
36. Для
какого из приведённых чисел ложно высказывание:
НЕ (число > 50) ИЛИ (число
чётное)?
1) 123 2) 56 3) 9 4) 8
Решение.
Пусть А=
(число > 50) и В= (число чётное), тогда по условию НЕ A ИЛИ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
HE A ИЛИ B |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
A=1 число > 50 B=0 число нечётное, сл-но 123 |
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 1.
37. Для
какого из данных слов истинно высказывание:
НЕ (третья буква гласная) И (последняя
согласная)?
1) слива 2) инжир 3) ананас 4) киви
Решение.
Пусть А=
(третья буква гласная) и В= (последняя согласная), тогда по условию НЕ A И B=1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (третья буква согласная) B=1 (последняя согласная), сл-но инжир |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 2.
38. Для
какого из данных слов истинно высказывание:
НЕ (третья буква гласная) И НЕ (последняя
согласная)?
1) слива 2) инжир 3) ананас 4) киви
Решение.
Пусть А=
(третья буква гласная) и В= (последняя согласная), тогда по условию НЕ A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
НЕ |
НЕ |
HE A И HE B |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (третья буква согласная) B=0 (последняя гласная), сл-но киви |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный ответ указан под номером 4.
39. Для
какого из приведённых чисел истинно высказывание:
НЕ (число > 10) И (число
нечётное)?
1) 22 2) 13 3) 9 4) 6
Решение.
Пусть А=
(число > 10) и В= (число нечётное), тогда по условию НЕ A И B=1.
Строим таблицу
истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (число < 10) B=1 (число нечётное), сл-но 9 |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 3.
40. Для
какого из приведённых чисел истинно высказывание:
НЕ (число < 10) И (число
нечётное)?
1) 22 2) 13 3) 9 4) 6
Решение.
Пусть А=
(число < 10) и В= (число нечётное), тогда по условию НЕ A И B=1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (число > 10) B=1 (число нечётное), сл-но 13 |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 2.
41.
Для какого из приведённых значений числа X ложно высказывание: (X
= 9) ИЛИ НЕ (X
< 10)?
1) 8 2) 9 3) 10 4) 11
Решение.
Пусть А=
(X = 9) и В= (X < 10), тогда по условию A ИЛИ НЕ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
A ИЛИ HE B |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
A=0 (X = 9) B=1 (X < 10), сл-но 8 |
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 1.
42.
Для какого из приведённых значений числа X ложно высказывание: НЕ (X
= 5) ИЛИ (X >
6)?
1) 4 2) 5 3) 6 4) 7
Решение.
Пусть А=
(X = 5) и В= (X > 6), тогда по условию НЕ A ИЛИ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
HE A ИЛИ B |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
A=1 (X = 5) B=0 (X < 6), сл-но 5 |
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 2.
43.
Для какого из приведённых чисел ложно высказываие: НЕ (число
> 30) ИЛИ (число
нечётное)?
1) 28 2) 34 3) 17 4) 45
Решение.
Пусть А=
(число > 30) и В= (число нечётное), тогда по условию НЕ A ИЛИ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
HE A ИЛИ B |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
A=1 (число > 30) B=0 (число чётное), сл-но 34 |
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 2.
44.
Для какого из приведённых чисел ложно высказывание: НЕ (число >
30) ИЛИ (число чётное)?
1) 28 2) 34 3) 17 4) 45
Решение.
Пусть А=
(число > 30) и В= (число чётное), тогда по условию НЕ A ИЛИ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ |
HE A ИЛИ B |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
A=1 (число > 30) B=0 (число нечётное), сл-но 45 |
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 4.
45.
Для какого из приведённых чисел истинно высказывание: НЕ (число
< 20) И (число
чётное)?
1) 8 2) 15 3) 21 4) 36
Решение.
Пусть А=
(число < 20) и В= (число чётное), тогда по условию НЕ A И B=1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (число > 20) B=1 (число чётное), сл-но 36 |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 4.
46.
Для какого из приведённых чисел истинно высказывание: НЕ (число
< 20) И (число нечётное)?
1) 8 2) 15 3) 21 4) 36
Решение.
Пусть А=
(число < 20) и В= (число нечётное), тогда по условию НЕ A И B=1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И B |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (число > 20) B=1 (число нечётное), сл-но 21 |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 3.
47.
Для какой из перечисленных ниже фамилий русских писателей и поэтов
истинно высказывание:
НЕ (количество гласных букв чётно) И НЕ (первая буква согласная)?
1) Есенин
2) Одоевский
3) Толстой
4) Фет
Решение.
Пусть А=(количество
гласных букв чётно) и
В= (первая буква согласная), тогда по условию НЕ A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
НЕ |
НЕ |
HE A И НЕ В |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (количество гласных букв нечётно) B=0 (первая буква гласная), |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный ответ указан под номером 2.
48.
Для какой из перечисленных ниже фамилий русских писателей и поэтов
истинно высказывание:
НЕ (количество гласных букв нечётно) И НЕ (первая буква
согласная)?
1) Есенин 2) Одоевский 3) Толстой 4) Фет
Решение.
Пусть А=( количество
гласных букв нечётно) и
В= (первая буква согласная), тогда по условию
НЕ A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
НЕ |
НЕ |
HE A И НЕ В |
|
|
0 |
0 |
1 |
1 |
1 |
A=0 (количество гласных букв чётно) B=0 (первая буква гласная), |
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
0 |
Правильный ответ указан под номером 1.
49.
Для какого из приведённых имён истинно высказывание:
НЕ (Третья буква гласная) И (Последняя буква согласная)?
1) Иван 2) Ксения 3) Марина 4) Матвей
Решение.
Пусть А=(Третья буква
гласная) и В= (Последняя
буква согласная), тогда по условию
НЕ A И B=1.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ |
HE A И НЕ В |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
A=0 (Третья буква гласная) B=0 (Последняя буква гласная), |
|
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 2.
50.
Для какого из приведённых имён ложно высказывание:
(Третья буква гласная) ИЛИ НЕ (Последняя буква гласная)?
1) Елена 2) Татьяна 3) Максим 4) Станислав
Решение.
Пусть А=(Третья буква
гласная) и В= (Последняя
буква гласная), тогда по условию
A ИЛИ НЕ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 2-я строка
|
A |
B |
НЕ В |
A ИЛИ НЕ В |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
A=0 (Третья буква согласная) B=1 (Последняя буква гласная), |
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 2.
51.
Для какого из указанных значений числа X истинно высказывание: (X
< 3) И НЕ (X < 2)?
1) 1 2) 2 3) 3 4) 4
Решение.
Пусть А=( X < 3) и В= (X < 2), тогда по условию
A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ В |
A И НЕ В |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
A=1 (X < 3) B=0 (X >=2), сл-но X=2 |
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 2.
52.
Для какого из приведённых значений числа X ложно высказывание: НЕ
(X < 7) ИЛИ (X < 6)?
1) 4 2) 5 3) 6 4) 7
Решение.
Пусть А=( X < 7) и В= (X < 6), тогда по условию
НЕ A ИЛИ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ А |
НЕ A ИЛИ В |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
A=1 (X < 7) B=0 (X >=6), сл-но X=6 |
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 3.
53. Для
какого из приведённых чисел истинно высказывание:
(Первая цифра чётная) И НЕ(Сумма
цифр чётная)?
1) 648 2) 452 3) 357 4) 123
Решение.
Пусть А=(Первая цифра
чётная) и В= (Сумма
цифр чётная), тогда по условию
A И НЕ B=1.
Строим
таблицу истинности:
Условию задачи соответствует 3-я строка
|
A |
B |
НЕ В |
A И НЕ В |
|
|
0 |
0 |
1 |
0 |
|
|
0 |
1 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
A=1 (Первая цифра чётная) B=0 (Сумма цифр нечётная), |
|
1 |
1 |
0 |
0 |
Правильный ответ указан под номером 2.
54. Для
какого из приведённых имён истинно высказывание:
НЕ((Первая буква согласная) ИЛИ (Последняя
буква гласная))?
1) Иван 2) Семён 3) Никита 4) Михаил
Решение.
Пусть А=(Первая буква
согласная) и В= (Последняя
буква гласная), тогда по условию
НЕ (A ИЛИ B)=1.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
А |
НЕ (А ИЛИ В) |
|
|
0 |
0 |
0 |
1 |
A=0 (Первая буква гласная) B=0 (Последняя буква согласная), сл-но Иван |
|
0 |
1 |
1 |
0 |
|
|
1 |
0 |
1 |
0 |
|
|
1 |
1 |
1 |
0 |
Правильный ответ указан под номером 1.
55. Для
какого из приведённых имён ЛОЖНО высказывание:
НЕ(Первая буква гласная) ИЛИ (Последняя буква гласная)?
1) Анна 2) Максим 3) Татьяна 4) Егор
Решение.
Пусть А=(Первая буква гласная) и В= (Последняя буква гласная),
тогда по условию
НЕ A ИЛИ B=0.
Строим
таблицу истинности:
Условию задачи соответствует 1-я строка
|
A |
B |
НЕ |
НЕ А ИЛИ В |
|
|
0 |
0 |
0 |
0 |
A=0 (Первая буква согласная) B=0 (Последняя буква гласная), сл-но Татьяна |
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
1 |
|
|
1 |
1 |
0 |
1 |
Правильный ответ указан под номером 1.
Список используемой
литературы:
1. https://inf-oge.sdamgia.ru
Информатика. Учебник для 9 класса по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень
§11. Логические выражения.
Формализация
Ключевые слова:
• формализация • логическое выражение • таблица истинности • вычислимое выражение • тождественно истинное выражение • тождественно ложное выражение • равносильные выражения • логическая схема
Обозначив простые высказывания буквами — логическими переменными и используя логические операции, можно записать любое высказывание в виде логического выражения.
Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь).
Например, пусть система сигнализации должна дать аварийный сигнал, если вышли из строя два из трёх двигателей самолёта. Обозначим высказывания:
А = Первый двигатель вышел из строя;
В = Второй двигатель вышел из строя;
С = Третий двигатель вышел из строя;
X = Аварийная ситуация.
Тогда логическое высказывание X можно записать в виде логического выражения (логической формулы):
X = (А и В) или (А и С) или (В и С).
Это выражение может быть записано с помощью других обозначений:
X = (А • В) + (А • С) + (В • С). (*)
Таким образом, мы выполнили формализацию.
Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.
При вычислении логических выражений установлен такой порядок выполнения операций:
1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.
Можно ли убрать скобки в выражении (*)? Почему?
Уберите лишние скобки в логических выражениях:
а) X = (А + (В • С) • (А + С));
б) X = (А + B) • (C • А) • (А + (B + C))).
Вычислите значение логического выражения X = (А • В + С) • (А + C) при:
а) А = О, В = О, С = 1;
б) А = О, В = 1, С = 1;
в) А = 1, В = 1, С = 0.
Таблицы истинности
Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения
X = А и не В или не А и B,
которое можно также записать в виде
X = А • B + А • В.
Сколько строк в таблице истинности выражения с двумя переменными?
Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).

Рис. 2.18
Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.
Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.
Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.
Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?
Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.
Сколько строк в таблице истинности выражения с тремя переменными?
Постройте таблицу истинности логического выражения
Х = А • В + А • С + В • С.
Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).

Рис. 2.19
Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?
Всего в таблице истинности функции от трёх переменных 23 = 8 строк, для каждой из них нужно знать, чему равно значение функции. В нашем примере пять значений функции неизвестны, причём каждое из них может быть равно 0 или 1, т. е. у нас есть 5 свободных бит.
Сколько различных значений можно закодировать с помощью 5 бит?
Как вы нашли это значение?
Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:
а) А + В + C;
б) A • С + В;
в) А + B • С;
г) А • В • C;
д) A • B + C.
Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.
Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке. Для второй строки A • С + В = 1 • 1 + 1 = 1, значит, эта функция тоже не подходит.
Проверьте самостоятельно, подходят ли остальные варианты.
Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:
а) А + B + C;
б) A • С • В;
в) А • B • C;
г) A + В + С;
д) A + B + C.
Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).

Рис. 2.20
Выясним, какие из следующих функций могут соответствовать этой таблице:
а) A + В + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + В + C.
Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные). Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:
а) 1 + В + 0;
в) 0 + B + 0;
д) 0 + В + 0.
Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.
Кратко решение можно записать так:
1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;
2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;
3) этим условиям удовлетворяют функции в) и д).
Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).

Рис. 2.21
Выясните, какие из следующих функций могут соответствовать этой таблице:
а) А • B + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + B + C.
Составление условий
Логические выражения часто используются при решении математических задач с помощью компьютеров.
Построим условия (логические выражения), соответствующие заштрихованным областям на числовой оси (рис. 2.22).

Рис. 2.22
На рисунке 2.22, а выделен отрезок [3; 6]. Для того чтобы определить такую область, нужно ограничить значение х с двух сторон: оно должно быть больше или равно трём и меньше или равно шести, причем эти два условия должны выполняться одновременно, т. е. их нужно связать с помощью операции И:
(3 ? х) и (х ? 6).
Область на рис. 2.22, б — это объединение двух отрезков. Мы можем отдельно записать условия для каждого отрезка и связать их с помощью операции ИЛИ:
(1 ? х) и (х ? 3) или (5 ? х) и (х ? 8).
Запишите условие, которое определяет область на рис. 2.22, в.
Теперь рассмотрим задачу с областью на плоскости. Запишем условие, соответствующее заштрихованной части (рис. 2.23).

Рис. 2.23
Требуется составить логическое выражение, зависящее от переменных х и у, которое будет равно 1 (истинно) внутри заштрихованной области и равно 0 вне её.
Выделенная область находится справа от вертикальной линии х = -1, поэтому должно выполняться условие х ? -1, которое определяет полуплоскость (рис. 2.24).

Рис. 2.24
Кроме того, все точки области находятся выше горизонтальной линии у = -1 и ниже наклонной прямой у = —х, что даёт ещё два условия: у ? -1 и у ? -х. Все три простых условия должны выполняться одновременно, поэтому их нужно связать с помощью двух операций И:
(х ? -1) и (у ? -1) и (у ? -х).
Запишите условие, которое определяет области на рисунках (рис. 2.25).

Рис. 2.25
Построим логическое выражение для области на рис. 2.26.

Рис. 2.26
Можно разделить заштрихованную область на две части (рис. 2.27).

Рис. 2.27Обе области находятся внутри круга радиуса 1 с центром в начале координат, т. е. в области х2 + у2 ? 1. Первая область описывается выражением
(х2 + у2 ? 1) и (х ? 0),
а вторая — выражением
(х2 + у2 ? 1) и (х ? 0) и (у ? -х).
Поскольку нам нужно «сложить» две области, эти выражения нужно объединить с помощью операции логического сложения (ИЛИ):
(х2 + у2 ? 1) и (х ? 0) или (х2 + у2 ? 1) и (х ? 0) и (у ? -х).
Общее условие х2 + у2 ? 1 можно вынести за скобки:
(х2 + у2 ? 1) и ((х ? 0) или (х ? 0) и (у ? -х)).
Попробуйте ещё упростить полученное условие.
Запишите условие, которое определяет области на рисунках (рис. 2.28).

Рис. 2.28
Логические схемы
Вернёмся снова к примеру с системой аварийной сигнализации самолёта. Предположим, что на каждом двигателе установлен логический датчик, который выдаёт условный сигнал 1 (например, высокий уровень напряжения), если двигатель неисправен, и условный сигнал 0, если двигатель исправен. Требуется построить логическую схему — схему логического устройства, — которая при аварии выдаёт условный сигнал 1, а в режиме нормальной работы — сигнал 0.
Сигналы от трёх двигателей назовём А, Б и С. В начале параграфа мы уже составили логическое выражение для запуска аварийной сигнализации:
Х = А • В + А • С + В • С.
Здесь три логических умножения и два логических сложения. Сначала выполняются все операции умножения (слева направо), а затем — все операции сложения (тоже слева направо). Расставим номера операций:
| 1 | 4 | 2 | 5 | 3 | ||||||||
| Х | = | А | • | В | + | А | • | С | + | В | • | С. |
Последней выполняется вторая операция сложения. Поэтому последний элемент в схеме — это элемент логического сложения ИЛИ (рис. 2.29).

Рис. 2.29
На первый вход этого элемента ИЛИ подаётся сигнал А • В + А • С, в этом выражении последняя операция — логическое сложение, добавляем ещё один элемент ИЛИ (рис. 2.30).

Рис. 2.30
Три операции логического умножения добавляют в схему три элемента И (рис. 2.31).

Рис. 2.31
Запишите в тетради логическое выражение по логической схеме (рис. 2.32).

Рис. 2.32
Постройте логическую схему, соответствующую выражению:
a) X = A • С + В • C;
б) Y = А • С + B • C;
в) Z = A • B + A • B • C.
Работа в парах. Один из вас пусть нарисует логическую схему для выражения X = A + В • С (черта сверху обозначает, что операция отрицания применяется ко всему выражению), а второй — для выражения Y = (А + В) (А + С). Постройте таблицы истинности для своих выражений и сравните их. Какую формулу вы сейчас вместе доказали?
Работа в парах. Запишите логическое выражение, включающее 5-6 операций, и предложите соседу нарисовать логическую схему. Проверьте и обсудите с ним его решение.
Путешествуя по Зазеркалью, Алиса увидела дверь с тремя кнопками, которые были отмечены буквами А, В и С. На двери висела схема (рис. 2.33).

Рис. 2.33
На какую (одну!) из трёх кнопок нужно нажать Алисе, чтобы открыть дверь?
Выводы
• Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.
• В логических выражениях операции выполняются в следующем порядке:
1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.
Для изменения порядка действий используются скобки.
• Таблица истинности логического выражения показывает, чему равно значение выражения при всех возможных комбинациях значений исходных переменных.
• Логические выражения, истинность которых зависит от значений исходных переменных, называют вычислимыми.
• Логическое выражение, которое всегда истинно, называется тождественно истинным или тавтологией. Выражение, которое всегда ложно, называют тождественно ложным или противоречием. Пример тождественно истинного выражения: А + А, пример тождественно ложного: А • А.
• Два выражения, принимающие одинаковые значения при всех значениях переменных, называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Что можно сделать для того, чтобы изменить порядок выполнения действий в логических выражениях?
2. Поясните разницу между терминами «логическое выражение» и «логическая функция».
3. Как можно доказать (или опровергнуть) логическую формулу?
4. Можно ли сказать, что таблица истинности однозначно определяет: а) логическое выражение; б) логическую функцию?
5. Что такое вычислимое логическое выражение?
6. Что такое равносильные выражения?
7. Выполните по указанию учителя задания в рабочей тетради.
Оглавление
§10. Другие логические операции.
§11. Логические выражения.
§12. Множества и логика.
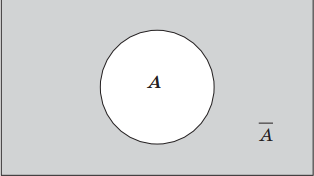
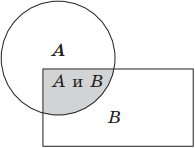
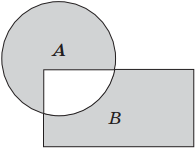
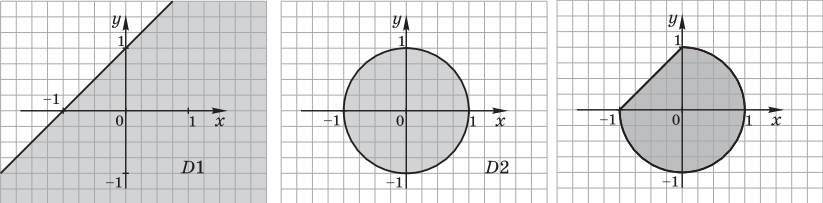
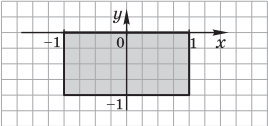
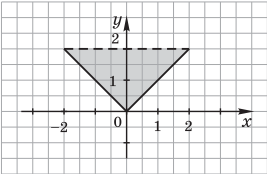
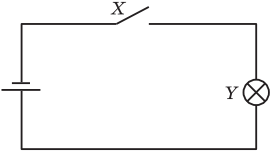
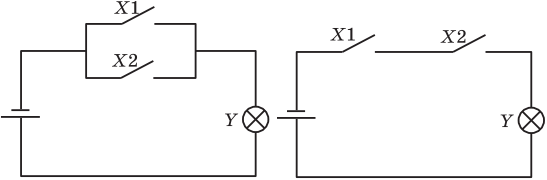

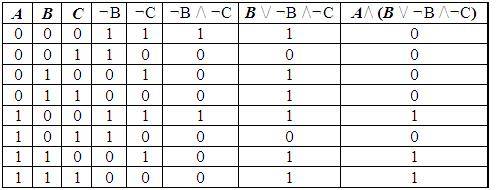
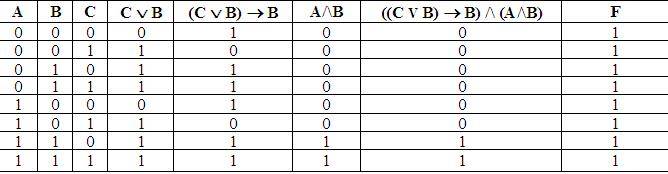
 ;
; ;
;























 – не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.
– не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.



