Как найти 2 четверть на координатной точки

((0;-) (frac<π><2>) ()) – четвертая четверть

Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.

Как расположены четверти на числовой окружности

Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.

Единичной окружностью называют окружность радиуса 1.

Общий вид числовой окружности.

1) Ее радиус принимается за единицу измерения.

2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.

3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:

первая четверть – это дуга AB

вторая четверть – дуга BC

третья четверть – дуга CD

четвертая четверть – дуга DA

4) Начальная точка числовой окружности – точка А.

Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.

Числовая окружность на координатной плоскости.

Центр радиуса числовой окружности соответствует началу координат (числу 0).

Горизонтальный диаметр соответствует оси x, вертикальный – оси y.

Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).

Значения x и y в четвертях числовой окружности:

x 0, y Основные величины числовой окружности:

Величина
в радианах

Величина
в радиусах

Имена и местонахождение основных точек числовой окружности:

Как запомнить имена числовой окружности.

Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.

Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.

1) Начнем с крайних точек на осях координат.

Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).

Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.

Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.

Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.

2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.

Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:

– Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.

– Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.

Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.

– Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.

Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.

3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.

Особенности числовой окружности. Сравнение с числовой прямой.

Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.

На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:

Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.

Отсюда формула:

Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число:

M(t) = M(t + 2πk),

где k ∈ Z.

Число k называется параметром.

Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., – спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac<4>=frac<2pi r><4>=frac<pi r><2>.) Тогда радианная мера угла: $$ angle AOB=frac>=frac<pi r><2cdot r>=frac<pi> <2>$$

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M – искомая. При t Например:

Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<pi><4>, frac<pi><2>, frac<2pi><3>, pi), а также (-frac<pi><6>, -frac<pi><4>, -frac<pi><2>, -frac<2pi><3>, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<13pi><6>, frac<25pi><6>), и (-frac<11pi><6>). Все четыре точки совпадают, т.к. begin Mleft(frac<pi><6>right)=Mleft(frac<pi><6>+2pi kright)\ frac<pi><6>-2pi=-frac<11pi><6>\ frac<pi><6>+2pi=frac<13pi><6>\ frac<pi><6>+4pi=frac<25pi> <6>end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -frac<pi> <6>lt t lt frac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi klt tltfrac<pi><3>+2pi k $$
Интервал
$$ -frac<pi> <6>leq t leq frac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi kleq tleqfrac<pi><3>+2pi k $$
Полуинтервал
$$ -frac<pi> <6>leq t ltfrac<pi> <3>$$ а также, с учетом периода $$ -frac<pi><6>+2pi kleq tltfrac<pi><3>+2pi k $$

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^<circ>=frac<pi><6>.\ EC=60^<circ>=frac<pi><3>.\ AE=EC+CD=90^<circ>+30^<circ>=120^<circ>=frac<2pi><3>.\ ED=EC+CD=60^<circ>+90^<circ>=150^<circ>=frac<5pi><6>. end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<pi><2>; frac<3pi><4>; frac<7pi><6>; frac<7pi><4>).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac<pi><2>=-90^<circ>, frac<3pi><4>=135^<circ>\ frac<7pi><6>=210^<circ>, frac<7pi><4>=315^ <circ>end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<11pi><2>; 5pi; frac<17pi><6>; frac<27pi><4>).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk – четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac<11pi><2>=frac<-12+1><2>cdotpi=-6pi+frac<pi><2>rightarrow frac<pi><2>=90^<circ>\ 5pi=4pi+pirightarrow pi=180^<circ>\ frac<17pi><6>=frac<18-1><6>pi=3pi-frac<pi><6>rightarrow pi-frac<pi><6>=frac<5pi><6>\ frac<27pi><4>=frac<28-1><4>pi=7pi-frac<pi><4>rightarrow pi-frac<pi><4>=frac<3pi> <4>end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac<3,14><2>=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac<3pi><2>approx frac<3cdot 3,14><2>=4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac<3pi> <2>Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac<3pi><2>lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

[spoiler title=”источники:”]

http://raal100.narod.ru/index/0-287

http://reshator.com/sprav/algebra/10-11-klass/edinichnaya-chislovaya-okruzhnost-na-koordinatnoj-ploskosti/

[/spoiler]

Чтобы найти на плоскости какой-то объект, его описывают двумя значениями. Так каждое место в зале кинотеатра имеет два параметра: ряд и место. Каждая клетка на шахматной доске или при игре в «морской бой» описывается номером строки и буквой, обозначающей столбец. 

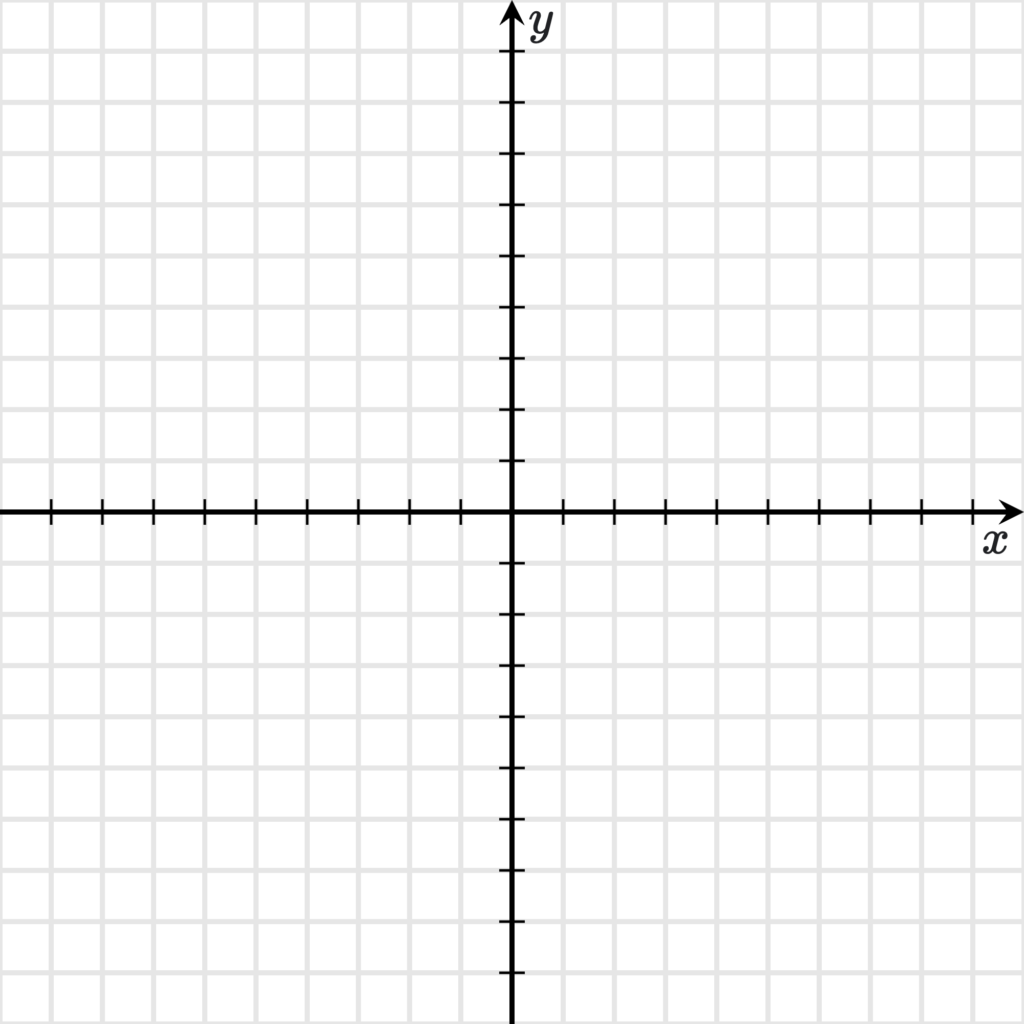
В математике определение местоположения объекта на плоскости придумали быстро находить с помощью системы координат, образованной двумя прямыми, называемых координатными осями (или осями координат).

Абсцисса, ордината, начало координат и единичный отрезок

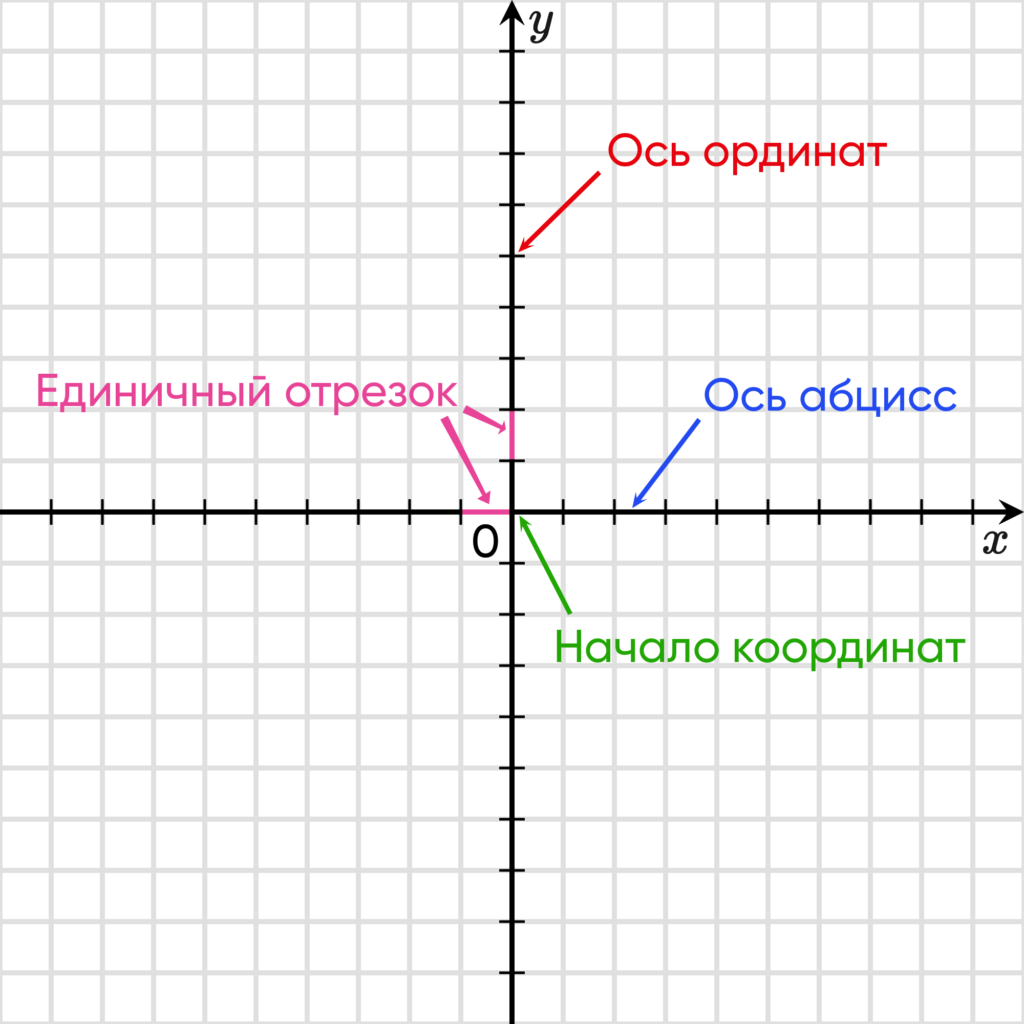
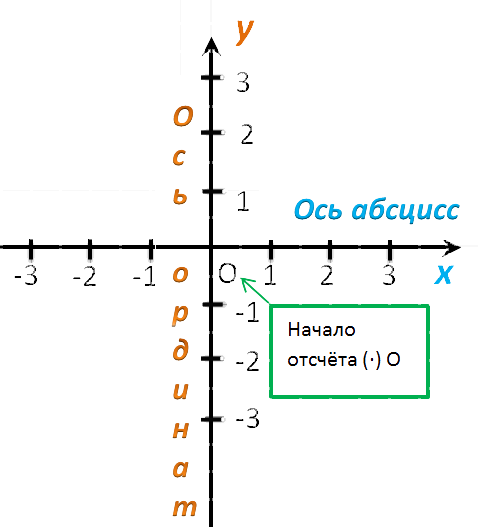
Эти оси имеют общепринятые наименования. А именно, горизонтальную ось именуют осью абсцисс и на письме обозначают $Оx$

Вертикальную ось называют осью ординат и на письме обозначают $Оy$

Оси пересекаются под прямым углом перпендикулярно друг к другу, поэтому такая система координат и называется прямоугольной.

Место пересечения осей координат является началом отсчета. Обычно эту точку обозначают буквой $О$ и называют началом координат. Ее называют еще иногда нулевой точкой.

На каждой оси выбирается единичный отрезок, с помощью которого вычисляются координаты объекта. Длиной единичного отрезка может выступать любая единица измерения, но она должна быть одинаковой на каждой из осей. То есть, если единичный отрезок на оси абсцисс задан, например, равным 1 см, то и на оси ординат единичный отрезок тоже должен быть равен одному сантиметру.

Положительное и отрицательное направление

У осей стрелкой задается положительное направление: 

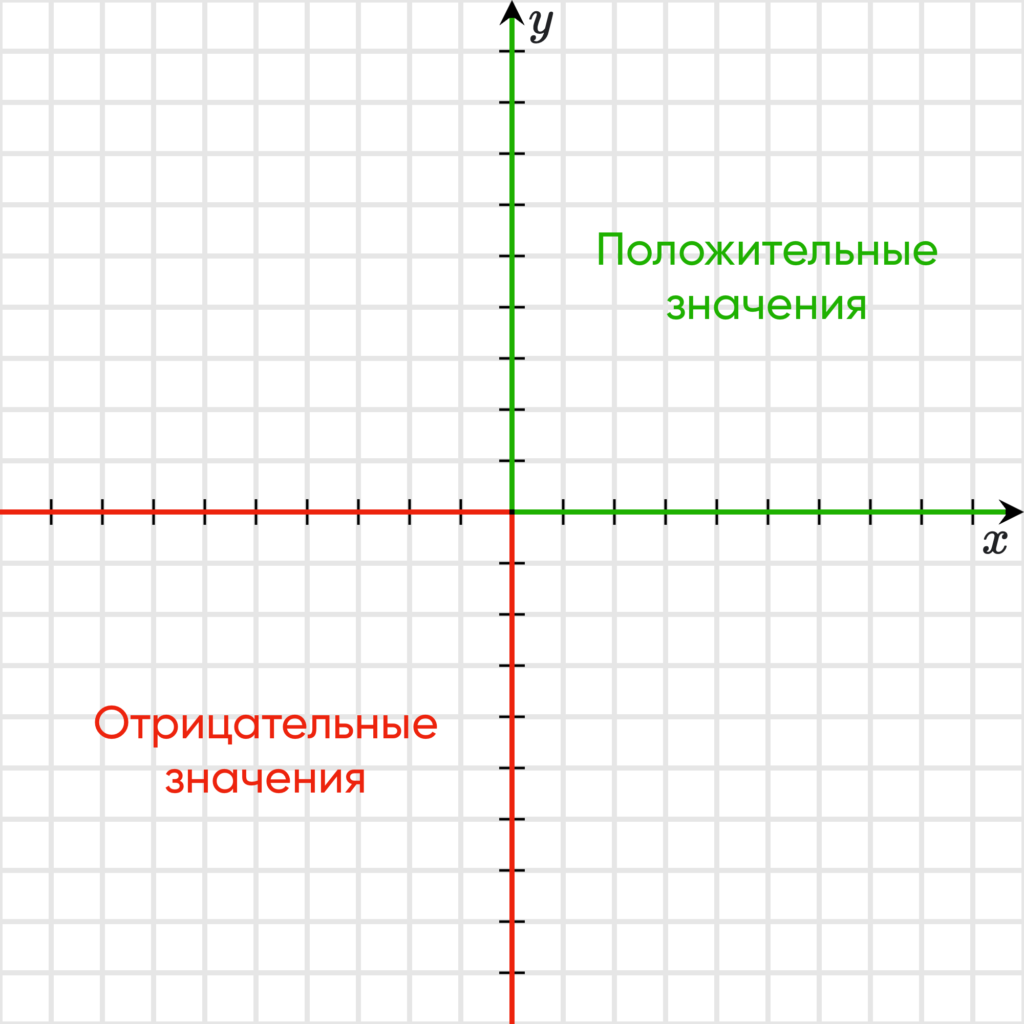
• так обычно у оси $Оx$ положительным считается направление вправо;
• у оси $Оy$ положительным считается направление снизу вверх.

В таком случае часть прямой $Оx$ левее точки $О$ будет принимать отрицательные значения. Аналогично часть прямой $Оy$ ниже точки отсчета $О$ будет также принимать отрицательные значения.

Таким образом, все вместе:

• начало координат $О$
• пересекающиеся под прямым углом оси $Оx$ и $Оy$ с заданными направлениями
• заданный единичный отрезок

образуют в математике прямоугольную систему координат, плоскость называют координатной. 

Или другими словами:

Прямоугольная система координат – это две взаимно перпендикулярные координатные оси с заданными направлениями, единицей длины и точкой отсчета в месте их пересечения.

На письме система координат обозначается $Оxy$

Четверти

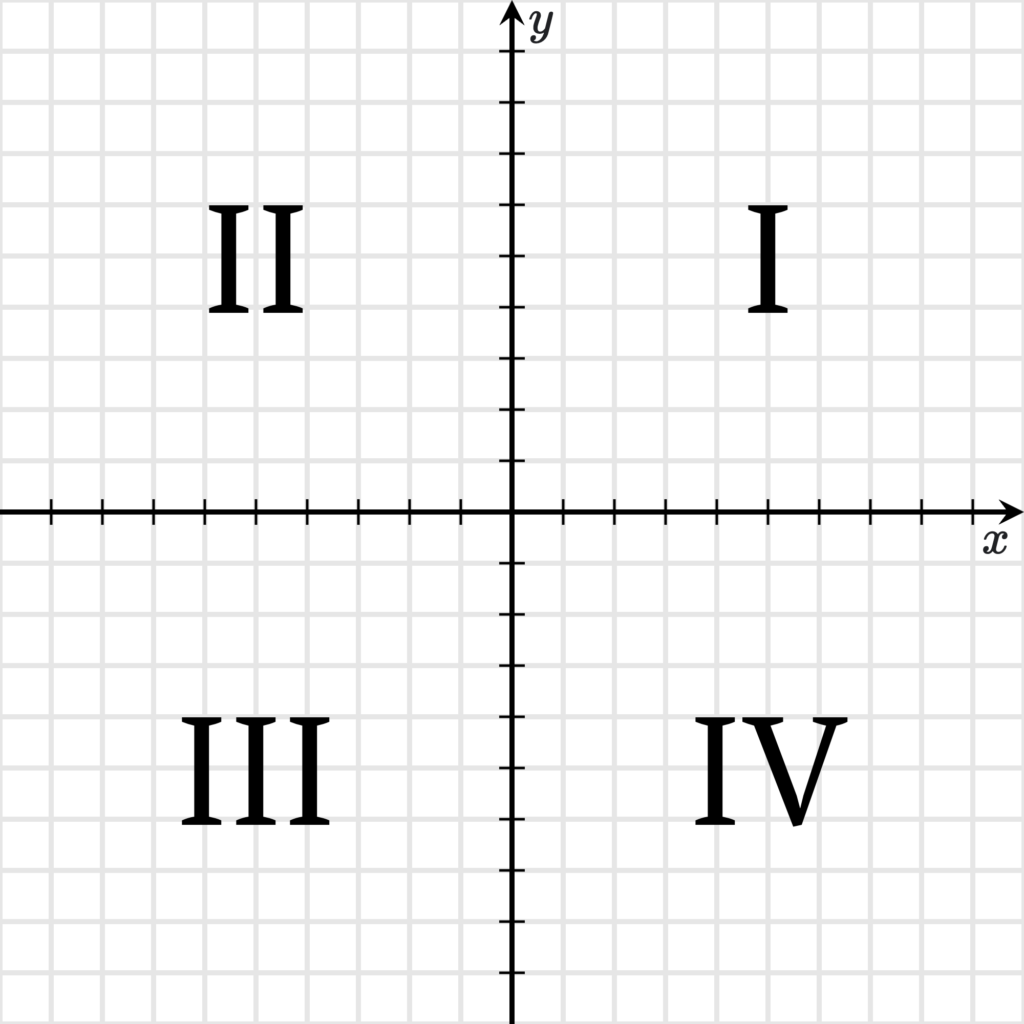
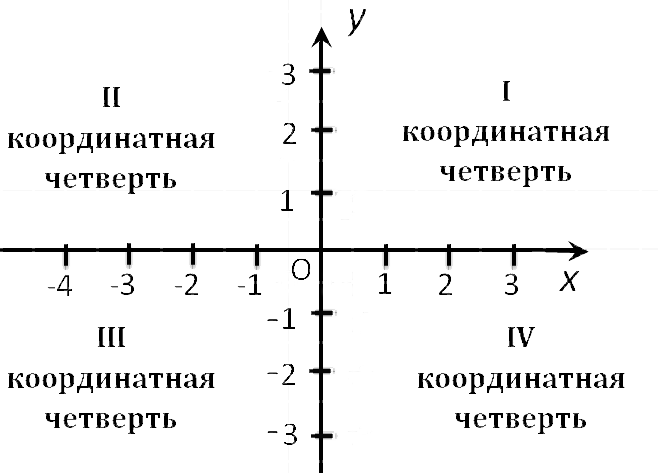
Осями координат плоскость делится на 4 части, их обозначают римскими цифрами. Каждая часть называется «квадрант». Другие названия: «координатный угол» или «четверть». Нумерация четвертей принята против часовой стрелки в том порядке, в котором указано на рисунке ниже.

В квадранте I значения $x$ и $y$ будут положительными. Отсюда следует, что если координаты объекта $x$ и $y$ – числа положительные, то он находится в I квадранте.

В квадранте II значение $y$ будет положительными, а $x$ отрицательным.

В квадранте III обе координаты $x$ и $y$ будут иметь отрицательные значения.

В последнем IV квадранте значение $x$ будет положительным, а $y$ отрицательным. 

Немного из истории

В латинском языке слово «координаты» получилось из двух других: co – «совместно» и ordinatus – «определенный», «упорядоченный».

Впервые необходимость нахождения координат объектов возникла в географии и астрономии. Для этого использовали широту и долготу, определяющие расположение точки на небесной сфере или на поверхности земного шара.

Таким образом начали вычислять координаты точек еще в 14 веке. Но упорядочил и систематизировал все знания в 17 веке французский математик по имени Рене Декарт. Поэтому прямоугольную систему координат также называют еще и «декартовой».

В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты».
В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.

Координаты могут обозначаться самыми разными наборами цифр или букв.

Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого
она города и кто ёё владелец.

Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте,
запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.

Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или
других символов, мы задаём координаты объекта.

Декартова система координат

Французкий математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.

Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.

• На плоскости такими ориентирами будут служить две числовые оси. На чертеже обычно первую ось рисуют горизонтально, её
  называют осью АБСЦИСС и обозначают буквой «X», записывают ось
  «Ox». Положительное направление на оси абсцисс выбирают
  слева направо и
  показывают стрелкой.
• Вторую ось проводят вертикально, её называют
  осью ОРДИНАТ и обозначают буквой «Y», записывают ось
  «Oy».
  Положительное направление на оси ординат выбирают
  снизу вверх и
  показывают стрелкой.

Оси взаимно перпендикулярны (т.е. угол между ними равен 90°) и
пересекаются в точке, которую обозначают «O».
Точка «O» является началом отсчёта для каждой из осей.

Координатные оси — это прямые, образующие систему координат.

Ось абсцисс «Ox» — горизонтальная ось.

Ось ординат «Oy» — вертикальная ось.

Координатная плоскость — плоскость, в которой построена система координат.
Обозначается плоскость как «x0y».

Обращаем ваше внимание на выбор длины единичных отрезков по осям.

Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева
от оси «Oy». Цифры
на оси «Ox», как правило, пишут внизу под осью.

Обычно единичный отрезок на оси «0y» равен единичному
отрезку на оси «0x». Но бывают случаи,
когда они не равны друг другу.

Оси координат делят плоскость на 4 угла, которые называют координатными четвертями. Четверть, образованная положительными
полуосями (правый верхний угол), считают первой I.

Отсчитываем четверти (или координатные углы) против часовой стрелки.

Ваши комментарии

Оставить комментарий:

Перейти к содержанию

var x,y: integer;

begin

    readln(x,y);

    if (x>0) and (y>0) then 

        writeln('I quadrant')

    else

        if (x<0) and (y>0) then 

            writeln('II quadrant')

        else

            if (x<0) and (y<0) then 

                writeln('III quadrant')

            else

                if (x>0) and (y<0) then 

                    writeln('IV quadrant');

end.

-5 3 

II quadrant

#include 

 
main() {

    int x,y;

    scanf("%d%d",&x,&y);

    if (x>0 && y>0) printf("I");

    else

        if (x<0 && y>0) printf("II");

        else 

            if (x<0 && y<0) printf("III");

            else

                if (x>0 && y<0) printf("IV");

    printf("n");

}

x = int(input("x="))

y = int(input("y="))

if x>0 and y>0:

    print('I')

elif x<0 and y>0:

    print('II')

elif x<0 and y<0:

    print('III')

elif x>0 and y<0:

    print('IV')

x=-3

y=-2

III

алг координатная четверть

нач

  цел x,y

  ввод x,y

  если x>0 и y>0 то вывод "I"

   иначе

    если x<0 и y>0 то вывод "II"

     иначе

      если x<0 и y<0 то вывод "III"

       иначе

        если x>0 и y<0 то вывод "IV" все

      все

    все

  все

кон

input x

input y

if x>0 and y>0 then

    print "I четверть"

else

    if x<0 and y>0 then

        print "II четверть"

    else

        if x<0 and y<0 then

            print "III четверть"

        else

            if x>0 and y<0 then print "IV четверть"

        endif

    endif

endif

7 

-2

IV четверть