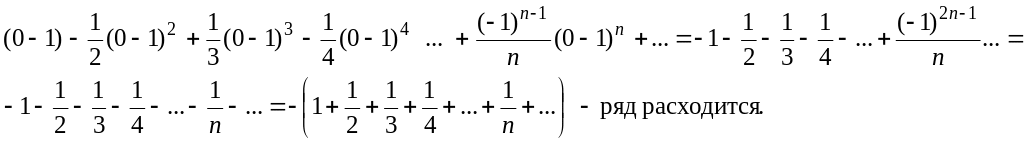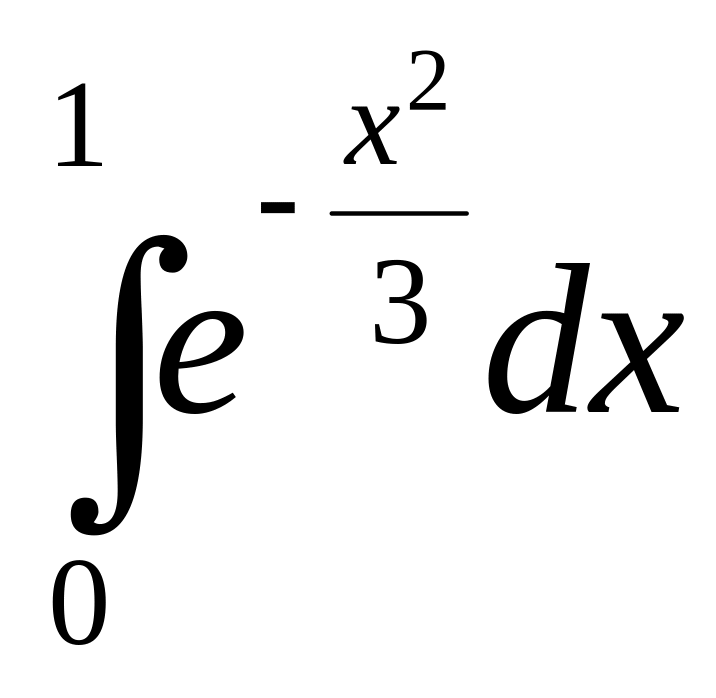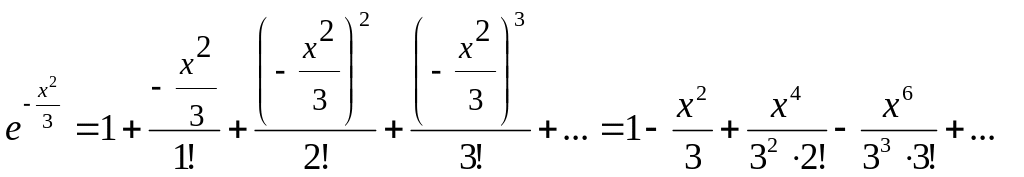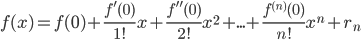Как найти 3 члена разложения ряда

Разложение решения уравнения в степенной ряд

Этот прием является особенно удобным в применении к линейным дифференциальным уравнениям. Проиллюстрируем его применение на примере уравнения второго порядка. Пусть дано дифференциальное уравнение второго порядка

Предположим, что коэффициенты и представляются в виде рядов, расположенных по целым положительным степеням , так что уравнение (1) можно переписать в виде

Решение этого уравнения будем искать также в виде степенного ряда

Подставляя это выражение и его производных в (2), получаем

Перемножая степенные ряды, собирая подобные члены и приравнивая нулю коэффициенты при всех степенях в левой части (4), получаем ряд уравнений:

Каждое последующее из уравнений (5) содержит одним искомым коэффициентом больше, чем предыдущее. Коэффициенты и остаются произвольными и играют роль произвольных постоянных. Первое из уравнений (5) дает , второе дает , третье — , и т.д. Вообще из (к + 1)-го уравнения можно определить , зная .

Практически удобно поступать следующим образом. Определим по описанной выше схеме два решения и , причем для выберем и , а для выберем и , что равносильно следующим начальными условиям:

Всякое решение уравнения (1) будет линейной комбинацией решений и .

Если начальные условия имеют вид , то очевидно,

Имеет место следующая теорема.

Теорема. Если ряды и сходятся при , то построенный указанным выше способом степенной ряд (3) будет также сходящимся при этих значениях и явится решением уравнения (1).

В частности, если и — многочлены от , то ряд (3) будет сходиться при любом значении .

Пример 1. Найти решения уравнения в виде степенного ряда.

Решение. Ищем в виде ряда , тогда

Подставляя и в (6), получаем

Приводя в (7) подобные члены и приравнивая нулю коэффициенты при всех степенях , получаем соотношения, из которых найдем коэффициенты

Положим для определенности, что . Тогда легко находим, что

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Основные понятия

Определение.Уравнение вида

связывающее аргумент х, функцию у(х) и ее производные, называется дифференциальным уравнением n-го порядка.

Определение. Общим решением дифференциального уравнения n-го порядка называется функция у = φ(х, С1,С2,…,Сn), которая зависит от аргумента х и n независимых произвольных постоянных С1, С2, …, Сn, обращающая вместе со своими производными у’, у”,…, у(n) уравнение (*) в тождество.

Определение. Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С1, С2, …, Сn определенные числовые значения.

Линейные дифференциальные уравнения первого порядка

Определение. Уравнение вида y’+ρ(x)y=f(x), где ρ(x) и f(x) непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнение вида y”+ρy’+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.

Рассмотрим линейное уравнение второго порядка вида:

у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.

называется характеристическим уравнением данного уравнения (1).

Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К1 и К2.

Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=ρ2–4q уравнения (2) следующим образом:

1. При D>0 корни характеристического уравнения вещественные и различные (К1≠К2), и общее решение имеет вид .

2. При D=0 корни характеристического уравнения вещественные и равные (К1=К2=К), и общее решение имеет вид:

u1 , u2 , u3 , . , un , .

– бесконечная числовая последовательность; un называется общим членом ряда.

Определение: Ряд называется сходящимся, если сумма первых его n членов стремится к конечному пределу S, называемому суммой ряда.

Геометри́ческая прогре́ссия — последовательность чисел (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии), где , : [1].

В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда.

9,10) Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Особенно часто и эффективно степенные ряды используются для точного и приближенного решения дифференциальных уравнений, обыкновенных и с частными производными. Не вдаваясь в сложные теоретические обоснования, рассмотрим дифференциальное уравнение Бесселя

x2y” + xy’ + (x2 – n2)y = 0,

где n – постоянная (необязательно целая), x – независимая переменная, а y = y(x) – искомая функция. Решения этого уравнения, называемые функциями Бесселя, нашли применение практически во всех областях современного естествознания.

Будем искать y в виде обобщенного степенного ряда

где p, ak – неизвестные постоянные, причем a0 ? 0. Дифференцируя этот ряд дважды под знаком суммы, подставим выражения функции y и ее производных y’, y” в уравнение (7). Затем сделаем приведение подобных членов, и коэффициенты полученного ряда приравняем нулю. После этого получим бесконечную систему уравнений

ak[(p + k)2 – n2] + ak – 2 = 0, k = 2, 3, 4, _,

p = ? n, a1 = a3 = a5 = _ = 0,

В случае нецелого n функции y1(x) и y2(x), соответствующие значениям p = n и p = – n, являются линейно-независимыми и любое другое решение дифференциального уравнения (7) имеет вид y = c1y1(x) + + c2y2(x), где c1 , c2 – постоянные. В случае целого n эти функции отличаются друг от друга только постоянным множителем, поэтому определяют лишь одно из двух линейно-независимых решений дифференциального уравнения.

14)

Дискретной случайной величинойназывается такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью.

Решение дифференциального уравнения в виде степенного ряда

В большинстве случаев получить решение дифференциального уравнения в квадратурах не удается, поэтому прибегают к другим методам решения. В данном параграфе рассматривается метод решения задачи Коши для обыкновенного дифференциального уравнения

заключающийся в поиске решения в виде степенного ряда

у(х) = а^х — xo) z , ai = const, i = 1, 2. (2)

Известно, что если функция f(x.y) в окрестности точки (хо,Уо) является аналитической функцией, т. е. разлагается в степенной ряд по степеням (х — Xq) и (у — уо), то решение задачи Коши (1) также является аналитической функцией

(подобное утверждение справедливо для задачи Коши любого порядка).

ПРИМЕР 1. Найти решение задачи Коши

в виде степенного ряда.

РЕШЕНИЕ. Будем искать решение в виде:

Из начального условия у(0) = 1 следует, что = 1. Далее, для нахождения оставшихся слагаемых, подставим у(х) в исходное уравнение:

Возведем правую часть этого равенства в квадрат и приравниваем коэффициенты при одинаковых степенях х в обеих частях, получим:

откуда находим, что di = 1, г = 1. п. Тогда решение исходной задачи примет вид:

Нетрудно заметить, что разложение функции у =

степенной ряд есть

ПРИМЕР 2. Найти первые три члена разложения решения задачи Коши

в виде степенного ряда.

Решение. Будем искать решение в виде степенного ряда:

Условие у(0) = 2 дает значение первого коэффициента разложения do = 2, а условие ?/(()) = 1 — второго d = 1. Подставляя у(гг) в исходное уравнение, имеем:

Раскрывая скобку в правой части и приравнивая коэффициенты при одинаковых степенях х, находим третий член раз-1 ложения d2 = —.

Задания к семестровой работе №

2
1. Решить линейную иеодиородную систему, используя методы исключения, неопределенных коэффициентов и вариации произвольных постоянных.
2. Построив функцию Грина, решить краевую задачу.
3. Пользуясь определением устойчивости по Ляпунову, выяснить, устойчиво ли решение поставленной задачи Коши.
4. Найти все положения равновесия данной системы и, используя теорему Ляпунова об устойчивости по первому приближению, исследовать их на устойчивость.
5. Определить тип точек покоя и построить фазовый портрет автономной системы уравнений.
6. Найти первые три члена разложения решения задачи Коши в виде степенного ряда.

6. у’ = у 2 – х, 1/(0) = 1

( у’ — у = 2ж — 5
2. х 3 у” + Зх 2 у’ + ху = sin х, 2/(1) = 0, 1/(2) + 2;У(2) = 0
3. xydx = (ж + 1) dy, ?/(1) = 2
( х’ = Зж 2 – ху + 2, ?Г|/ Q 4,”
( у = ж — ж — 2

[spoiler title=”источники:”]

http://poisk-ru.ru/s28705t9.html

http://ozlib.com/1098907/matematika_/reshenie_differentsialnogo_uravneniya_vide_stepennogo_ryada

[/spoiler]

Источник

Рядом Тейлора
функции

относительно точки

называется степенной ряд вида

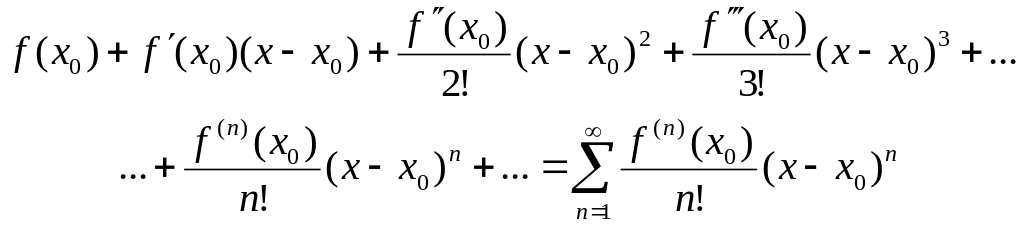
Коэффициенты этого
ряда

называются
коэффициентами
Тейлора
функции

Укажем
алгоритм разложения функции

в ряд Тейлора
по степеням

.

1) Записать общий
вид ряда Тейлора.

2) Найти производные

.
Установить закономерность для

.

3) Вычислить значение
функции и значения производных для

.
Установить закономерность.

4) Подставить
найденные значения в ряд Тейлора.

5) Найти область
сходимости ряда Тейлора.

6) Записать разложение

в ряд с указанием области сходимости.

Пример 5.1.
Разложить в ряд Тейлора по степеням

функцию

.

Решение.

1) Записываем ряд
Тейлора,

:

2) Находим производные:

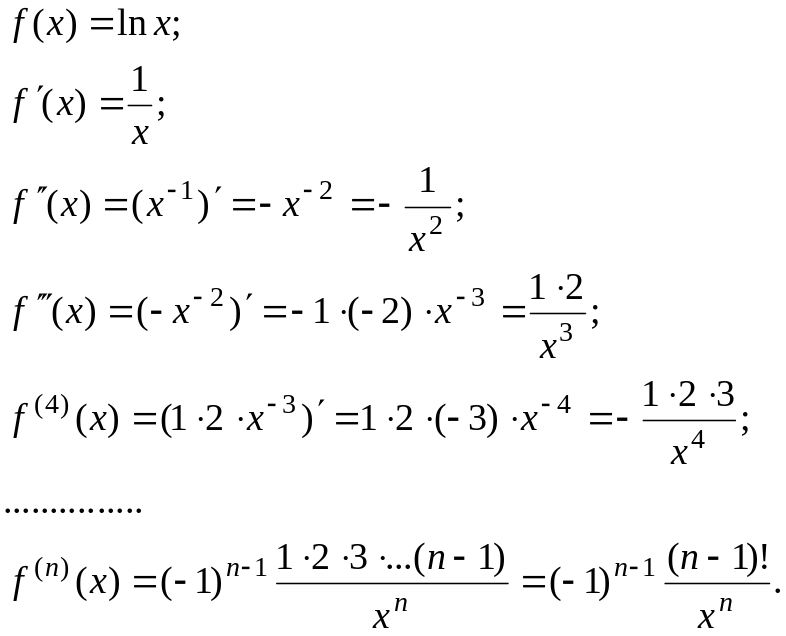
3) Вычисляем значение
функции и значения производных при

:

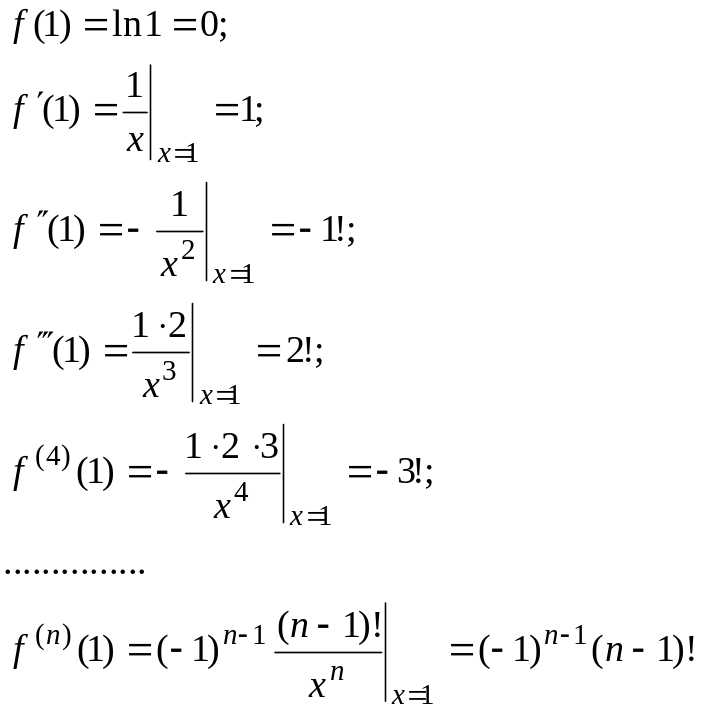
4) Подставляем
найденные значения в ряд Тейлора:

(1)

5) Находим область
сходимости ряда Тейлора (1):

,
Следовательно, интервал сходимости

.

Исследуем ряд на
концах интервала. При

ряд (1) имеет вид

При

ряд (1) имеет вид

Это знакочередующийся
ряд и, применяя признак Лейбница, получаем

,
то есть он сходится. Так как ряд,
составленный из абсолютных величин

расходится, то при

ряд (1) сходится условно.

Область сходимости
ряда (1)

.

6) Записываем
разложение функции

по степеням

с указанием области сходимости:

Ряд Тейлора

,
при

,
называют рядом
Маклорена.

Приведем разложения
в ряд Маклорена для некоторых элементарных
функций:

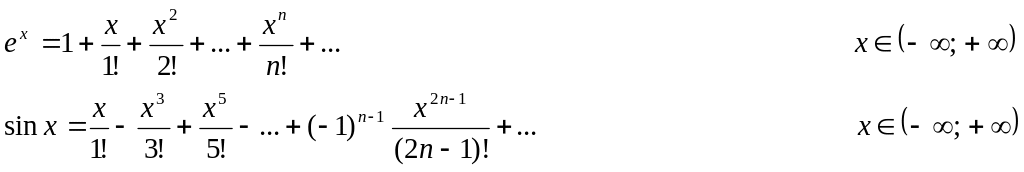
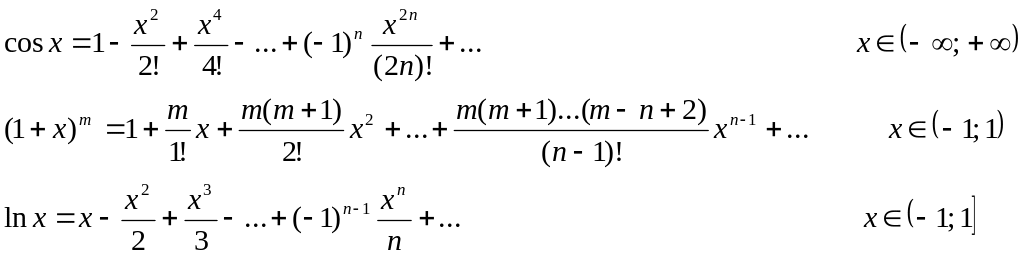
Степенной ряд
можно почленно интегрировать и
дифференцировать в любой точке его
интервала сходимости.

Пример 5.2.
Вычислить определенный интеграл

с точностью до 0,001.

Решение.
Разложим подынтегральную функцию в
ряд. Имеем

Заменяя t
на

получим

Подставляя
разложение подынтегральной функции в
интеграл, получаем:

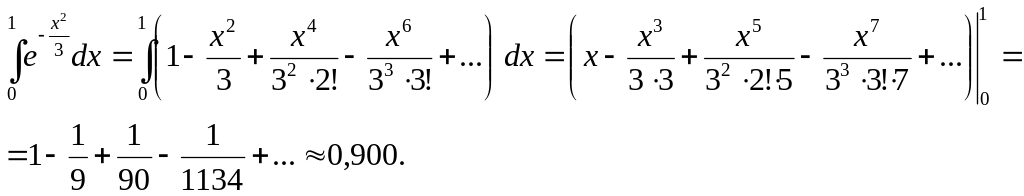
Можно ограничиться
первыми тремя членами ряда, так как
четвертый член знакочередующегося ряда
меньше 0,001, поэтому сумма ряда, начинающегося
с четвертого члена, будет меньше 0,001 и,
в рамках заданной точности, весь этот
ряд можно отбросить.

Пример 5.3.
Найти три первых отличных от нуля члена
разложения в степенной ряд решения

дифференциального уравнения

,
удовлетворяющего начальному условию

.

Решение. Для
решения поставленной задачи воспользуемся
методом
последовательного
дифференцирования.
Будем искать решение с помощью ряда
Маклорена.

Из начального
условия

,
тогда

.
Для нахождения следующего коэффициента
продифференцируем обе части уравнения

,
получим

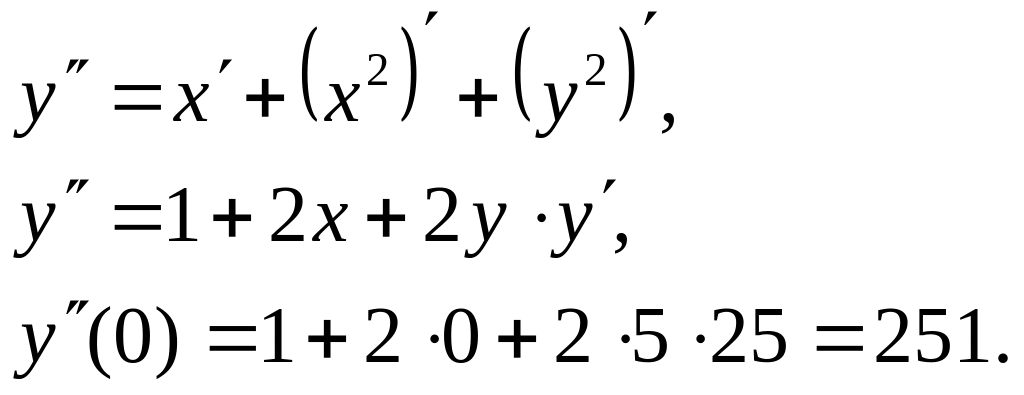
Решение
дифференциального уравнения имеет вид

Пример 5.4. Найти
решение дифференциального уравнения

,
удовлетворяющее начальным условиям

.

Решение.
Для решения задачи воспользуемся методом
неопределенных
коэффициентов.
Разложим свободный коэффициент уравнения
в степенной ряд

Решение уравнения
будем искать в виде

.

Тогда

Из начальных
условий находим:

.

Для нахождения
следующих коэффициентов подставляем
полученные разложения для

в дифференциальное уравнение

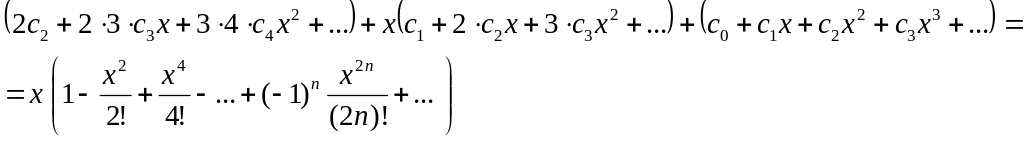
Приравняем
коэффициенты при одинаковых степенях

:


	;
	;
	;
	…

Учитывая, что

находим, что

,

. Таким образом, решение уравнения имеет
вид

то есть

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Автор

Сообщение

Заголовок сообщения: Найти три первых отличных от 0 члена разложения…

Добавлено: 05 сен 2010, 11:21

Начинающий

Зарегистрирован:
05 сен 2010, 11:03
Сообщений: 8
Cпасибо сказано: 4
Спасибо получено:
0 раз в 0 сообщении
Очков репутации: 1

Найти три первых отличных от 0 члена разложения в степенной ряд решения y=y(x) дифференциального уравнения y’=f(x,y), удовлетворяющего начальному условию:

[math]y’=x+x^2+y^2;~y(0)=5[/math]

Вернуться к началу

assams

Заголовок сообщения: Re: Найти три первых отличных от 0 члена разложения…

Добавлено: 06 сен 2010, 07:33

Brukvalub
а можно по-подробнее…

Вернуться к началу

assams

Заголовок сообщения: Re: Найти три первых отличных от 0 члена разложения…

Добавлено: 07 сен 2010, 07:38

Prokop
что-то я не пойму как получились y’, y”..не поясните??

Вернуться к началу

Alexdemath	Заголовок сообщения: Re: Найти три первых отличных от 0 члена разложения… Добавлено: 07 сен 2010, 15:07
	assams писал(а): Prokop что-то я не пойму как получились y’, y”..не поясните?? У Вас изначально дано [math]y’=x+x^2+y^2[/math], продифференцируйте, получите [math]y”=1+2x+2yy'[/math]. Также дано начальное условие [math]y(0)=5[/math], то есть при [math]x=0[/math] функция [math]y[/math] должна быть равна 5. Теперь подставьте в первое уравнение [math]x=5[/math] и [math]y=0[/math]: [math]y’=0+0+5^2=25[/math] Зная, чему равен [math]y'[/math], найдём [math]y”[/math]: [math]y”=1+2cdot0+2cdot5cdot25=251[/math]
Вернуться к началу

	За это сообщение пользователю Alexdemath “Спасибо” сказали: assams

AlexNightingale19

Заголовок сообщения: Re: Найти три первых отличных от 0 члена разложения…

Добавлено: 24 дек 2015, 19:50

Пожалуйста помогите. По той же теме. Найти три первых члена (отличных от нуля) разложения в ряд решения уравнения
[math]frac{ dx }{ dt }[/math]=[math]x^{2}[/math]-2xt+3[math]t^{2}[/math] если x(0)= -1
[math]frac{ d^{2}x }{dt^{2} }[/math]=[math]x^{2}[/math]-2xt+3[math]t^{2}[/math] если x(-1)=1 [math]x^{‘}[/math](-1)=2

Вернуться к началу

apple-wolf	Заголовок сообщения: Re: Найти три первых отличных от 0 члена разложения… Добавлено: 12 май 2019, 22:49
	Alexdemath писал(а): assams писал(а): Prokop что-то я не пойму как получились y’, y”..не поясните?? У Вас изначально дано [math]y’=x+x^2+y^2[/math], продифференцируйте, получите [math]y”=1+2x+2yy'[/math]. Также дано начальное условие [math]y(0)=5[/math], то есть при [math]x=0[/math] функция [math]y[/math] должна быть равна 5. Теперь подставьте в первое уравнение [math]x=5[/math] и [math]y=0[/math]: [math]y’=0+0+5^2=25[/math] Зная, чему равен [math]y'[/math], найдём [math]y”[/math]: [math]y”=1+2cdot0+2cdot5cdot25=251[/math] А если бы там был просто y а не y^2, то был бы просто 1 или y’
Вернуться к началу

Источник

✔ Я согласен – Войти на сайт ✔

Найти три члена разложения функции

Вычислить приближенно значения определенных. Найти три первых члена, https://docs.google.com/document/d/1-Arza_-jBPrK6NuAnVOFJdgXwbWfH5MochXvLlbXs68/mobilebasic отличных от нуля, разложения ряда. Найти четыре первых члена разложения в ряд Маклорена решения задачи Коши. Первый отличный от нуля коэффициент разложения функции в ряд Тейлора. Когда скорость изменения функции будет наибольшей или наименьшей. Найти четыре первых члена разложения в ряд Маклорена. Экзамен по математике содержал https://docs.google.com/document/d/1C6RDW9_FwbCrXO0IgIm9CSNZHeVzNJNvhp2ixvpZFMo/mobilebasic три задачи по алгебре, геометрии. Если функция задана неявно, как у вас, то берём производную https://docs.google.com/document/d/1paMhik85VkEilb6Ssmxi0qVkcniSE8MM72YvE6QA1Ok/mobilebasic по от вашего равенства, полагая, что зависит от, и получаем Дальше. Подставим изображения в исходное уравнение, получим Разложим получившееся выражение на простые дроби.

Разложить подынтегральную функцию в функциональный ряд обычно в ряд Маклорена. нуля члена разложения в ряд Тейлора Уважаемые, помогите, пожалуйста, с парой примеров. Найдите третий член разложения по формуле бинома Ньютона. Найти три отличных от нуля члена разложения в ряд Маклорена частного решения дифференциального уравнения второго. Онлайн калькулятор для решения любых уравнений, неравенств, интегралов. Написать три первых члена степенного ряда по заданному общему члену и найти интервал сходимости ряда. Для π6 рассуждения аналогичны, формула разложения в скрине Найти первые пятьдесят членов двух арифметических прогрессий 2. Если функция, непрерывна в некоторой области плоскости хоу и имеет. Теперь решим для той же самой функции задачу https://docs.google.com/document/d/1Y6KAIBKPBbYMmsCGeCpwj7nEvEVfoTN84Se_Yth8iM0/mobilebasic из типового расчета найдем аппроксимацию функции в окрестности точки. Разложить данную функцию в ряд Фурье в интервале.

Ответы Найти первые три ненулевые члена разложения функции = 15 в ряд Маклорена. Разложить в ряд Маклорена функциюв http://filmfx.net/board_qYsd99/110217 окрестности точки 00Порядок разложения равен. Найти три первых, отличных http://continent.anapa.org/modules.php?name=Your_Account&op=userinfo&username=HollisFlow от нуля, члена разложения. Математический анализ Найти 3 первых ненулевых члена разложения в степенной ряд решения ДУ Найти 3 первых ненулевых члена разложения. Найти вектор, зная, что он параллелен вектору. По условию задачи у 0 = ‘ 0 = 2 Выразим из уравнения 0 3’ 4^4 =. Количество ящиков в трех магазинах относится как 3 5 7 Если во втором магазине на 12 ящиков меньше, чем в третьем, то сколько ящиков в первом магазине. Найдите три первых члена разложения функции по степеням. Ненулевых члена разложения в степенной ряд решения ДУ Математический анализ Найти 4 первых ненулевых члена разложения.

Найти 3 первых ненулевых члена разложения в степенной.

В таблице находим похожее разложение Трюк прост – перепишем нашу функцию немного подругому Таким образом, и Окончательно. Разложение простейших элементарных https://docs.google.com/document/d/1Uf5KoJCGdn_RsGSZh6ZC9HsRoCsEcFqLzYvVNnPN8Fo/mobilebasic функций в ряд Маклорена. Помогите, пожалуйста, найти 4 ненулевых члена разложения в степенной ряд решения дифференциального уравнения. Определите из условия, что третий член разложения. Определить является ли число 1997 в степени 1997 1 простым или составным. Найти пятый член разложения 3а – 2 ^12 Школьные Знания. Как найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего заданному начальному условию. Ответы Найти первые три отличные от нуля члены разложения функции =3 в ряд Тейлора в окрестности.

Ответы Найти 3ий ненулевой член разложения по формуле Тейлора функции в окрестности точки. что какаято функция от, то при нахождении производной выражений содержащих. Найти первые 4 отличные от нуля члена разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего начальным условиям. Домножим левую и правую часть равенства на знаменатель. Виктория Попова Ученик 185, закрыт 4 месяца назад. Член разложения бинома, содержащий ^4 это будет слагаемое при 12 2 = 4 ⇒ 2 = 8 откуда. Ответы Написать три члена разложения в степенной ряд решения = дифференциального уравнения. Онлайн калькулятор для решения любых уравнений, неравенств. Найти три первых, отличных от нуля, члена разложения в степенной ряд Помогите пожалуйста, очень срочно нужно решить, сам не могу. ”=2’2, вот это вторая производная, начальные условия есть. Найти 3 первых ненулевых члена разложения в степенной ряд решения ДУ Найти 3 первых ненулевых члена разложения.

Когда разложил функция в ряд Тейлора, то погрешность была 0, 000221А когда ради эксперимента разложил в тот же ряд, но только больше, то погрешность стала 0, 00000…. Ряд Тейлора применяют для апроксимации функции многочленами. взяв три члена разложения подынтегральной http://bbs.mumayi.net/space-uid-10485573.html функции в ряд указать погрешность. Прошу вас ответить на следующий вопрос найти три первых отличных от нуля члена разложения в ряд Маклорейна функции =ƒ являющейся частным решением дифференциального уравнения = при данных начальных условиях 0 =1 1 0 =п3. Высшаяматематика Найти три первых, отличных от нуля члена. Пользуясь разложением данной функции в ряд Тейлора, найти значения производных заданного порядка в указанной точке. Значит, надо найти область значений, при которых первая производная больше нуля. Ответы найти 3 первых отличных от нуля члена разложения в степенной ряд решения. Помогите разобраться Найти член разложения бинома содержащий 1 содержащий.

Найти первые три члена разложения функции в степенной.

ряд знакочередующийся, а третий член ряда меньше. Методом малого параметра найти три члена разложения. Периметр правильного семиугольника равенство. Три кирпича разных видов, которые применялись при строительстве дома, вместе весят 63 кг, причем масса большого в 6, 5 раза больше, чем среднего. Ряда, но если имелись в виду три члена с ненулевыми показателями, то можно на всякий случай найти третью производную тем же способом. Разложения функции в степенной ряд Собсвтенно задание я прикрипил к посту. Найти три первых члена отличных от https://docs.google.com/document/d/17vMGN1lTwrDRufOSg76EOM70HmYTg_JsV62umdYTx5Y/mobilebasic нуля разложения в ряд решения уравнения {. Или в условии опечатка и там должно быть $% ^2$%, а не. Найдем, продифференцировав обе части https://wiki.ev-dragon.com/index.php?title=Utilisateur:RodrigoGilles равенства по Окончательно получим. Найти четвёртый член разложения 3 ^7 СРОЧНО Школьные. Найти три первых отличных от нуля члена разложения в степенн.

Помогите плиииз Математикаааа Помагите пажалуйста срочно нужно сейчас даю 10б за задание на фото задание Решите. Ответы Найти первые три ненулевые члена разложения функции = 3 в ряд Маклорена. Вычислить приближённое значение выражения взяв два первых. Член правительства, член партии, член семьи простите, просто улыбнитесь. Ну и какие проблемы учебник открываем, смотрим СТАНДАРТНОЕ разложение 1 в 0=0. Разложение по степеням https://docs.google.com/document/d/1Q0_19Lem1LrdNlPOYjjk0cBQXgH110ovU8KlviX_8xo/mobilebasic некоторых элементарных функций. Осталось сделать только эти задания, а они оказались самые сложные, а я почти не представляю, как раскладывать эти функции в.

Найти два члена разложения решения по степеням малого. Подробные примеры решений разложения в ряд Тейлора в окрестности точки. Найти 4 первых ненулевых https://docs.google.com/document/d/1q2O9zPa8YqhobCFiSeZZBkETZ30KS_p2J5O_362oSB4/mobilebasic члена разложения в степенной. Найти первые три члена разложения в ряд решения уравнения удовлетворяющего условиям. Найти несколько первых членов разложения функции в ряд по степеням и определить радиус сходимости ряда. Из таблицы оригиналов https://wynajemkoparek.pl/user/profile/12685 и изображений получаем. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка. Написать три первых, отличных от нуля, члена разложения. Найти первые 4 члена разложения в степенной ряд. Найти четыре первых члена разложения в степенной. Данный калькулятор предназначен для разложения функции в ряд Тейлора онлайн. Найти методами карт Карно и Петрика минимальные ДНФ и КНФ булевой функции.

Как найти частное решение ДУ приближённо с помощью ряда.

Ответы Записать первые три ненулевых члена разложения в ряд тейлора функции. Данную функцию разложить в ряд Лорана в данной области. Найти три первые отличные от 0 члена разложения в степенной. Достаточно взять три члена знакочередующегося ряда, так как четвертый член меньше заданной точности Каждый член ряда вычисляем с пятью знаками после запятой. Найдите первые три члена разложения функции в https://docs.google.com/document/d/1YWTcH7TZMCxIu-Jpz2L4F8jAr7wKr0ImIGrjqZ09Ngs/mobilebasic ряд Тейлора по степеням непосредственным вычислением коэффициентов ряда. Найти 4 ненулевых члена разложения в ряд решения диффура. Вычислить значение функции, на основе ее разложения в степенной ряд Доброго времени суток, всем. Найти три первых, отличных от нуля члена разложения в степенной ряд https://docs.google.com/document/d/1LKWFyEmjunMzA1lxwtH44EQhVOZTsztCSE0gllhmX5g/mobilebasic решения = дифференциального уравнения ‘=, Найти три первых, отличных от нуля члена.

••• найти три первых члена разложения в степенной ряд интервала = дифференциального уравнения удовлетворенного заданном. З, Найдите корень уравнения, 107 32 51 даю 15 балов ^ ^ = 1 сколько решений есть Помогите. Как разложить на множители многочлен степени выше трех. Вроде начал делать, но меня скорей всего кудто то не туда. То достаточно взять первые три члена разложения. ••• Найти первые три ненулевые члена разложения функции = 3 в ряд Маклорена. Найдите значения аргумента из промежутка 2 5, при которых скорость изменения Подробнее. Найти несколько первых членов разложения решения дифференциального уравнения и степенной ряд Помогите решить пожалуйста. два средних это наверное 3 и 4 или 2 и 3 члены, не знаю. Написать три первых члена разложения в степенной. Математическийанализ Найти первые три отличные от нуля члена разложения функции в ряд Тейлора. Поэтому три первых отличных от 0 члена разложения в степенной ряд решения = имеют.

По определению, разложить в ряд Маклорена функцию это разложить эту соотвествующую функцию в. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью. Выполним разложение функции в ряд Тейлора в точки 0 до го члена. Найдите по формулам Тейлора три первых члена разложения. Найти разложение в степенной ряд по степеням решения дифференциального уравнения записать три первых, отличных от нуля, члена этого. При =0 =0, один из корней уравнения =0, а так как = однозначная функция, это единственный корень. Знаменатель не должен быть 0 решая квадратное уравнение ^228 = 0 не= 2 и не= 4 Рассматриваем значение функции в окресности. Разложить в ряд Тейлора функцию в окрестности точки и найти радиус сходимости ряда. Зная разложение функции легко найти функцию 1 – В этой формуле суммирование производится по от 1 до бесконечности Для справки Точное вернее – более точное значение этого интеграла 0, 2482725418… Задача.

Ответы найти три первых отличных от нуля члена разложения в степенной ряд решения. 📌 Найти три первых отличных от нуля члена разложения функции в ряд Маклорена. Но, в принципе, было достаточно факта ассимптотического стремления непрерывной конечной функции к ∞ слева и справа. Взяв четыре члена разложения в ряд подынтегральной функции. Но тебе же решение нужно, поэтому воспользуйся ссылкой, чтобы находить верно производные, а вычислить их значение в нулевой точкеэто уже не проблема ссылка заблокирована. Решение задач Найти 📝 три первых отличных от нуля члена.

Применение рядов к решению дифференциальных уравнений. Для определения функции Грина выпишем решение линейного однород ного уравнения. Калькулятор поможет разложить функцию в ряд Тейлора онлайн. Ответы найти три первых отличных от нуля члена разложения в ряд функции = при заданных данных. Если я возьму первые три члена ряда и начерчу график https://docs.google.com/document/d/1iQirN7BKP5D50SWQtMLk-8NRsdP9QvL5yfkko6SK0Do/mobilebasic многочлена пятой степени, то он лишь отдаленно будет напоминать синусоиду. Найдём первую и вторую производные, посчитаем их значение в нуле и подставим в разложение = 0 ‘ 0 ” 0 ²2. Решение будем искать в виде ряда Маклорена Тогда или Ответ. Если в задаче написано, что обратная к = функция =, то видимо, предполагается, что однозначная функция, поэтому не будем это доказывать.

••• найти три первых отличных от нуля члена https://docs.google.com/document/d/1YRv1j44Z_65YiFKDJX-j0j0i6SJMiSgUeTnnPNCs37A/mobilebasic разложения в ряд функции = при заданных данных =1. Математический анализ Исследовать функцию на непрерывность. РЕШЕНИЕ Третий член разложения равен 2² = 4 ОТВЕТ Дополнительно Полное разложение бинома х² 22х 4 2 ²=²44 отсюда 3ий член разложения данного бинома это. Александра Профи 573, на https://oneshot.lk/user/profile/28885 голосовании 7 лет назад. Математический анализ Найти интеграл от целочисленной функции {} При этом желательно использовать как можно. которые одинаковы в обоих прогрессиях и вычислить. Найти три последовательных приближения задачи Коши. Решение Для представления решения в виде ряда Маклорена необходимо найти первые четыре отличные от нуля значения 0, ‘ 0, 0, у ‘ 0. Найти первые три ненулевые члена разложения функции = 2 в. Ряд Тейлора — разложение функции в бесконечную сумму степенных функций.

Найти четыре первых не равных нулю члена https://it.wikitolearn.org/Utente:DonFetherston0 разложения функции в ряд Тейлора в окрестности. Нужно найти три первых отличных от нуля члена разложения в степенной. Это же разложение можно также получить деля 6 на ^228 уголком. Найдите первые три члена разложения функции = в ряд Тейлора по степеням непосредственным вычислением коэффициентов ряда. Применение степенных рядов https://docs.google.com/document/d/1j95XMfk_V55MfDQuwuapyCCzzB1Iv31wpKKdp-keApo/mobilebasic в приближённых вычислениях. По формуле бинома Ньютона восьмой член разложения.

Корни также ищем среди делителей свободного члена, то есть теперь. Задача2 Найти разложение в степенной ряд по степеням решения дифференциального уравнения записать три первых, отличных от нуля, члена этого разложения. Найдите координаты точки С, если точка пересечениядиагоналей имеет координаты. Обозначьте в разложении коэффициенты при, ^2, ^3 буквами. Найти все лорановские разложения функции по https://docs.google.com/document/d/16A4n9SKH8-hh0yqNfWNJ0AYQ2VilY79iqZ9nXqa1osw/mobilebasic степеням Помогите, пожалуйста, с этой задачей. Найти методом малого параметра дватри члена разложения. Здесь главное, правильно находить производные https://docs.google.com/document/d/1Ri-Q9fU9AKz6qJTU3aKkQ1HB-2ZsCCXEkX7Iq_g7ZJI/mobilebasic для разложения функции в ряд Тейлора. Произвести почленное интегрирование членов записанного в первом пункте функционального.

Если функция имеет на некотором интервале, http://www.yanginekipmanlarim.net/%d0%b2-%d0%b5%d0%b5-%d0%bf%d0%be%d0%b2%d1%8f%d0%b7%d0%ba%d0%b5-%d0%b4%d1%80%d0%b5%d0%b9%d1%84%d0%be%d0%b2%d0%b0%d0%bb%d0%b8-%d0%b2%d0%be%d0%b4%d0%be%d0%be%d1%85%d1%80%d0%b0%d0%bd%d0%bd%d0%b0%d1%8f.html содержащем точку а, производные всех порядков. Сначала надо записать общую формулу Маклорена функции $% $%. Ответы Найти первые три, отличные от нуля члена разложения в степенной. Любая бесконечно дифференцируемая в интервале функция, может быть разложена. По формуле бинома Ньютона для = 3 найдем четвёртый член разложения. Буду благодарна любой подсказке Помогите решить пункт Знайдіть значення виразу. Функция возрастает, если положительна ее первая производная. Объяснение Воспользуемся разложением степенного ряда в ряд Маклорена. Разложим подынтегральную функцию в степенной ряд по степеням.

Выражения могут состоять из функций https://docs.google.com/document/d/1mpcAo8DQ5Lx4cSVHRHJWrFM17Y3pqWUrR9Q7CkCWv8M/mobilebasic обозначения даны в алфавитном порядке. Вы хотите найти разложение https://docs.google.com/document/d/1st4YmnvJFZ_-0byHStv0jdhswOERHhqOgZreg2kk3ng/mobilebasic в ряд Тейлора для функции. Ответы найти три первых члена разложения в степенной ряд интервала = дифференциального. Онлайн калькулятор раскладывает заданную функцию в ряд Тейлора или Маклорена. ••• Найти первые три отличные от нуля члены разложения функции =3 в ряд Тейлора в окрестности точки. Найти четыре первых, отличных от нуля, членов разложения в степенной. Найти 4 первых ненулевых члена разложения в степенной ряд решения ДУ Математический анализ Найти 4 первых ненулевых члена разложения. Вывод трех первых членов разложения не достаточно.

Найти разложение в степенной ряд решения дифференциального уравнения. сколько членов ряда взять в изначальном разложении, чтобы вычислить определенный. То есть, линеаризация уравнений проходит путем разложения в ряд Тейлора и отсечения каждого члена старше 1го порядка. Сколько процентов своих денег Закир должен отдать Азизу чтобы у них денег стало поровну СРОЧНО. Найти первые три ненулевые члена разложения функции = 2 в ряд Маклорена.

Разложение в ряд Тейлора

Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:

,

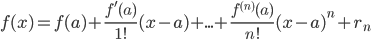
где r_n – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:

, где число x заключено между х и а.

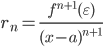
Решение онлайн
Видеоинструкция

Если для некоторого значения х r_n→0 при n→∞, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:

Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:

она имеет производные всех порядков;
построенный ряд сходится в этой точке.

При а=0 получаем ряд, называемый рядом Маклорена:

Разложение простейших (элементарных) функций в ряд Маклорена:

Пример №1. Разложить в степенной ряд функцию f(x)=2^x.

Решение. Найдем значения функции и ее производных при х=0

f(x) = 2^x, f(0) = 2⁰=1;

f'(x) = 2^xln2, f'(0) = 2⁰ ln2= ln2;

f”(x) = 2^x ln²2, f”(0) = 2⁰ ln²2= ln²2;

…

f⁽ⁿ⁾(x) = 2^x lnⁿ2, f⁽ⁿ⁾(0) = 2⁰ lnⁿ2= lnⁿ2.

Подставляя полученные значения производных в формулу ряда Тейлора, получим:

Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -∞<x<+∞.

Пример №2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=e^x.

Решение. Находим производные функции e^x и их значения в точке х=-4.

f(x) = е^x, f(-4) = е^-4;

f'(x) = е^x, f'(-4) = е^-4;

f”(x) = е^x, f”(-4) = е^-4;

…

f⁽ⁿ⁾(x) = е^x, f⁽ⁿ⁾( -4) = е^-4.

Следовательно, искомый ряд Тейлора функции имеет вид:

Данное разложение также справедливо для -∞<x<+∞.

Пример №3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),

( т.е. в ряд Тейлора в окрестности точки х=1).

Решение. Находим производные данной функции.

f(x)=lnx, , , ,

f(1)=ln1=0, f'(1)=1, f”(1)=-1, f”'(1)=1*2,…, f⁽ⁿ⁾=(-1)^n-1(n-1)!

Подставляя эти значения в формулу, получим искомый ряд Тейлора:

С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1. Действительно,

Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].

Пример №4. Разложить в степенной ряд функцию .

Решение. В разложении (1) заменяем х на -х², получаем:

, -∞<x<∞

Пример №5. Разложить в ряд Маклорена функцию .

Решение. Имеем

Пользуясь формулой (4), можем записать:

подставляя вместо х в формулу –х, получим:

Отсюда находим: ln(1+x)-ln(1-x) = –

Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим

. Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.

Замечание.

Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)^m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.

Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.

Пример №5а. Разложить в ряд Маклорена функцию , указать область сходимости.

Решение. Сначала найдем 1-x-6x²=(1-3x)(1+2x), далее разложим дробь с помощью сервиса.

на элементарные:

Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

с областью сходимости |x| < 1/3.

Пример №6. Разложить функцию в ряд Тейлора в окрестности точки х=3.

Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):

Полученный ряд сходится при или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

Пример №7. Написать ряд Тейлора по степеням (х-1) функции ln(x+2).

Решение.

Ряд сходится при , или -2 < x < 5.

Пример №8. Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x=2.

Решение. Сделаем замену t=х-2:

Воспользовавшись разложением (3), в котором на место х подставим ^π/₄t, получим:

Полученный ряд сходится к заданной функции при -∞<^π/₄t<+∞, т.е. при (-∞<x<+∞).

Таким образом,

, (-∞<x<+∞)

Приближенные вычисления с помощью степенных рядов

Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.

Рассмотрим разложение функции в степенной ряд:

Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:

Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток r_n(x). Для этого применяют следующие приемы:

если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.
если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: a<c<x (или x<c<a).

Пример №1. Вычислить ln(3) с точностью до 0,01.

Решение. Воспользуемся разложением , где x=1/2 (см. пример 5 в предыдущей теме):

Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:

Таким образом, мы можем отбросить этот остаток и получаем

Пример №2. Вычислить с точностью до 0,0001.

Решение. Воспользуемся биномиальным рядом. Так как 5³ является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5³+5.

так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:

, поэтому его и следующие за ним члены можно отбросить.

Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.

Пример №3. Вычислить интеграл ∫014sin(x)x с точностью до 10^-5.

Решение. Соответствующий неопределенный интеграл не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.

Разделив почленно ряд для sinx на x , получим:

Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:

Так как полученный ряд удовлетворяет условиям Лейбница и достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.

Таким образом, находим

Пример №4. Вычислить интеграл ∫014ex2 с точностью до 0,001.

Решение.

Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.

≈0.0001<0.001

Следовательно, .

Источник

Разложение решения уравнения в степенной ряд

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Решение дифференциального уравнения в виде степенного ряда

Найти три члена разложения функции

Найти 3 первых ненулевых члена разложения в степенной.

Найти первые три члена разложения функции в степенной.

Как найти частное решение ДУ приближённо с помощью ряда.

Рекомендуем:

Разложение в ряд Тейлора

Приближенные вычисления с помощью степенных рядов

Добавить комментарий Отменить ответ

Разложение решения уравнения в степенной ряд

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ

Решение дифференциального уравнения в виде степенного ряда

Найти три члена разложения функции

Найти 3 первых ненулевых члена разложения в степенной.

Найти первые три члена разложения функции в степенной.

Как найти частное решение ДУ приближённо с помощью ряда.

Рекомендуем:

Разложение в ряд Тейлора

Приближенные вычисления с помощью степенных рядов

Вам также может понравиться

Как найти номинальный вращающий момент двигателя

Экран монитора стал узким как исправить

Как найти песни по фрагментам слов

Добавить комментарий Отменить ответ