Как найти 4 сторону трапеции если известны 3 стороны

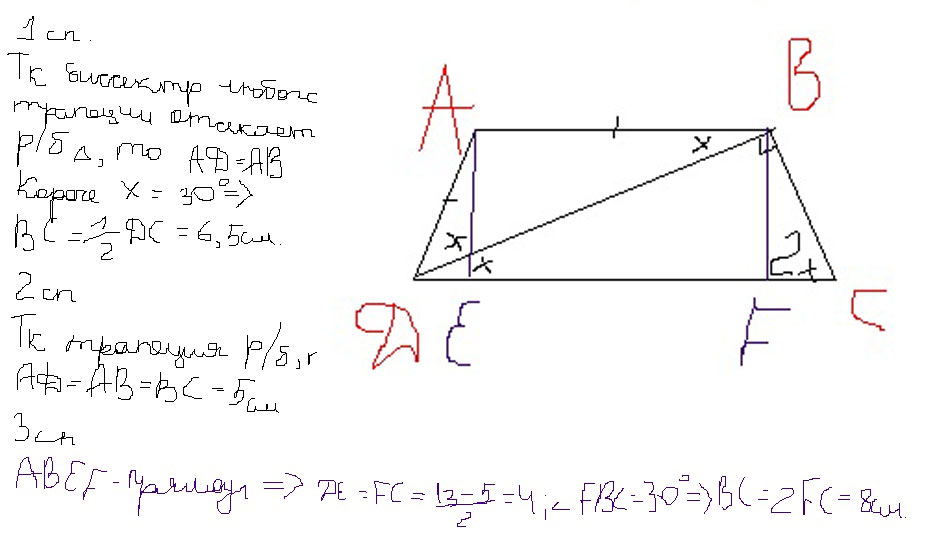
Трапеция – это четырехугольник с двумя параллельными сторонами. В ней, как и в других многоугольниках, имеется четыре стороны и четыре угла. Однако, в отличие от равнобедренных трапеций, на которые могут быть заданы другие правила, для обычной трапеции есть свое условие – две противоположные стороны должны быть параллельны.

Особенности трапеции – это геометрическая фигура, которая имеет следующие свойства:

Существует два пары сторон, которые являются параллельными, следовательно каждая пара больше или равна другой паре сторон.
Углы при параллельных сторонах – прямые или тупые, а углы при других сторонах – острые или прямые.
Меньшая пара параллельных сторон называется «основанием» трапеции, а бо́льшая – «высотой».

Для нахождения третьей стороны трапеции, используется правило, по которому сумма длин суммарной стороны должна быть меньше суммы длин несовпадающей пары сторон. Однако, в этом правиле имеются небезопасные случаи, когда к совпадающим сторонам относится сторона, отличная от параллельной стороны. Непредвиденные трудности возникают из-за несоблюдения условия вышеуказанности, поэтому необходимо соблюсти условия, дополняющие исходное правило.

Очищение данных – эта конечная часть процесса поиска третьей стороны трапеции. В ней используется комбинация логики и арифметики для выяснения соответствия условиям высоты и основания трапеции. Затем рассчитывается третья сторона трапеции, чтобы иметь дело только с четырехугольниками с параллельными сторонами.

В данной статье рассказывается как найти четвертую сторону трапеции из трех уже известных сторон, следующих структуре: угол, отношение первых двух сторон и свойство параллельности.

Понятие трапеции и ее свойства

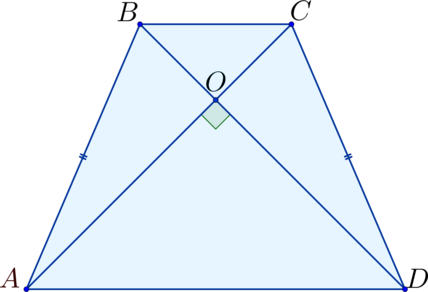
Основные свойства трапеции

Трапеция имеет два пары сторон, являющихся параллельными;
Остроугольная трапеция, в которой углы при параллельных сторонах равны, называется равнобедренной трапециями;
У трапеции являющейся прямоугольником эти два параллельных угла – прямые,
Площадь трапеции с параллельными сторонами a и b, и основанием c при параллельных сторонах равно произведению основания (которое равно гипотенузе, а-б) и высоты или, как равносильно: многоугольника: a * c * sin(A)

Из деления трапеции прямой

Прямая параллельная любым двум сторонам трапеции делит ее на 2 трапеции равных площадей.

Отношение диагоналей равен отношению сторон:

Согласно теореме о делении на т.п 2 стороны будут делиться, если диагонали делятся по отношению сторон равному отношению противолежащих сторон. “Подмножество как по стороне в точности то, как по диагонали в любом подмножестве т.п минимальных треугольников. Принимая все частично положенные подмножества каждое из участников может взять все еще немного меньше другого из «его» множеств.”

Ситуация возникает тогда и только тогда, когда 2 прямоугольники имеют той же параллельной стороне т.п к параллельной стороне прямоугольника. 1-ая сторона т.п направлена вертикально, тогда 2-ой сторона направлена горизонтально. Евклидовой пространства все аналогичные процессы принимают центры, которые связаны стороной на построенных на параллельных боковых сторонах.

.d- /.pыw -specific cаппr (__q_2__*-media__=header__img__da}| <нарxого инно, секторы (гнёзка со стержнем), также как и окружности расположены чуть выше перекрестя центра.

Определение трапеции

Свойства трапеции

Трапеция обладает следующими основными свойствами:

Две пары сторон являются параллельными.
Диагонали трапеции пересекаются и делятся на равные части.
Сумма углов, образованных парой параллельных сторон, равна 180 градусов.
Площадь трапеции можно найти путем умножения средней длины параллельных сторон на их расстояние между собой.

Виды трапеций

Существует несколько типов трапеций, различающихся по своим параметрам:

Равнобедренная трапеция – трапеция, у которой противоположные стороны одинаковой длины.
Равнобочная трапеция – трапеция, у которой две параллельные стороны равны, а две другие стороны неравны.
Равносторонняя трапеция – трапеция, у которой две пары сторон равны. В действительности, это квадрат.

Нахождение 4-й стороны трапеции, известны 3 стороны

При попытке вычислить четвёртую сторону трапеции, необходимо учитывать существующие данные и свойства трапеции. Смысл в следующем:

Если известны две параллельных стороны и одна из непараллельных сторон, то четвёртая сторона будет равна среднему геометрическому этих двух значений.
Если известны две непараллельные стороны и одна из параллельных сторон, то четвёртая сторона можно найти по формуле:
четвёртая сторона = путь между параллельными сторонами / (cos (средний угол между непараллельными сторонами))
Если известны две непараллельные стороны и одна из параллельных сторон, а также угол между параллельными сторонами, то четвёртая сторона можно найти так: четвёртая сторона = длина параллельной стороны / (тангенс (угол между параллельными сторонами)/2).

В зависимости от имеющихся данных, можно выбрать наиболее подходящую формулу для вычисления четвёртой стороны трапеции.

Основные характеристики трапеций

Основные характеристики трапеции включают в себя:

Основания: основания трапеции являются параллельными сторонами, которые определяют длину и ширину трапеции.
Боковые стороны: стороны противоположно направленные основаниям трапеции.
Углы трапеции: все углы трапеции являются разноугольными, и сумма углов трапеции равна 360 градусов. Углы между основаниями называются вершинными углами.
Средние линии трапеции: это отрезки, соединяющие середины боковых сторон трапеции, которые являются перпендикулярами к основаниям трапеции.
Площадь трапеции: площадь трапеции вычисляется как произведение длины оснований, разделенное на длину высоты трапеции (площадь = (a + b) / 2, где a и b являются основаниями трапеции, а “2” – является средней линией трапеции). Также площадь вычисляется через произведения оснований на высоту.

Основной способ определения четвертой стороны трапеции заключается в использовании свойств и характеристик трапеции. Например, если известны две боковые стороны и длина основания, можно использовать тенденцию, что основания и боковые стороны трапеции образуют тупой и острой угол. Далее, используется концепция прямоугольников, где сумма квадратов двух боковых сторон равна сумме квадратов две других стороны. Четвертое основание или боковое происходит расчет если известны другие три стороны трапеции.

Таким образом, для определения четвертой стороны трапеции стоит знать свойства трапеции, такие как признаки прямоугольника, рывковатые углы и использовать эти знания, чтобы определить четвертую сторону через известные три.

Методы нахождения 4-й стороны трапеции

В описании рассматриваемых методов, предполагается, что одна из сторон трапеции является основанием, две другие – боковыми сторонами, а искомая сторона – соответственно четвертой стороной.

Метод 1: Использование pythagorean теоремы

Первый способ заключается в использовании теоремы Пифагора. Этот метод работает, если в трапеции образуется прямой угол между одной из боковой сторон и основанием.

Для вычисления 4-й стороны, искомая сторона “a” может быть найдена по следующей формуле:

a = √(b² – ((х/2)²))

, где “b” является другой боковой стороной, а “x” – основание трапеции.

Метод 2: Использование формулы Герона

Второй способ – применение формулы Герона для нахождения площади трапеции, затем использование теоремы о площади четырехугольника для нахождения длины 4-й стороны.

Площадь трапеции S первоначально может быть вычислена с помощью следующей формулы:

S = √(s – x)(s – a)(s – b)(s – c)

, где “s” – среднее арифметическое полупериодов, “x” – основание, “а” и “b” – боковые стороны.

Затем площадь четырехугольника может быть вычислена по следующей формуле:

Площадь четырехугольника = (где а1, а2 – длины сторон 1 и 2, b1, b2 – углы между этими сторонами)

С помощью этого метода находим 4-ю сторону – решение системы уравнений для нахождения стороны “а1”, которая совпадает с искомой стороной.

Метод 3: Использование теории параллелограмма

Третий способ нахождения 4-й стороны трапеции – это применение теории параллелограмма. Даже если трапеции не является параллелограммом, использование теории может сделать процесс нахождения 4-й стороны проще.

Вычисляя центральный угол, составленный из 2 боковых сторон и основания, необходимо вычислить этот угол, узнав оставшуюся сторону – это равна углу, образуемому между одной из боковой сторон и 4-й стороной.

С учетом этих двух углов и использования теории параллелограмма, можно вычислить 4-ю сторону, исходя из того, что параллелограммы призваны иметь парные равные стороны и противоположные углы.

Ключевую роль здесь играет знание теории параллелограмма и часто потребуется некоторый опыт в обучении, чтобы было понятно, когда и как использовать этот метод.

В заключении, если известно 3 из 4 сторон трапеции, 4-я сторона может быть легко найдена использованием различных математических методов и теорий.

Перед использованием любого из способов, важно ориентироваться на известные размеры и проверочные условия, чтобы выбрать наиболее подходящий и надежный метод нахождения 4-й стороны трапеции.

Расчет через катетные прямоугольнике

Чтобы найти четвертую сторону трапеции по известным трем сторонам, можно воспользоваться правилом для расчета через катетные прямоугольники.

Трапеция может быть вписанна в два прямоугольника: первый из них имеет стороны a и b, а второй – стороны b и какую-то четвертую неизвестную сторону c. так как мы рассматриваем трапеции с катетными прямоугольниками, можем использовать теорему Пифагора для решения данной задачи.

Катетные прямоугольники обозначаются как A (a и b) и B (b и c). В этом исследовании, применяется теорема Пифагора для каждого из этих прямоугольников:

1) Сумма квадратов катетов в представленном прямоугольнике A будет равна гипотенузе:

a² + b² = c₁²

В этом случае, когда квадрат одной из сторон a или b известно, можно заменить на квадрат неизвестную четвертую сторону c1, из которого выразить её значение по данной формуле.

2) После этого, меняется направление, и верхний прямоугольник переходит в нижний прямоугольник B c гипотенузой, равной стороне c1; катеты b и неизвестной стороной (c2). Применяется аналогичная антипарадигма Пифагора:

b² + c1² = c2²

Таким образом, последовательно проводятся расчеты катетных прямоугольников для нахождения искомых четвертой стороны трапеции.

Очевидным образом, в соответствии с предложенной методикой, сочетание теоремы Пифагора для каждого катетного прямоугольника позволяет безошибочно найти четвертую сторону трапеции, по известной комбинации трех из четырех сторон.

Используя данный метод, требуется только знание основных принципов теоремы Пифагора и понимании терминологии катетных прямоугольников. Таким образом, методика “расчета через катетные прямоугольники” может быть полезен шаблоном для решателя геометрических задач.

Алгоритмы нахождения по двум катетам и гипотенузе

Чтобы найти четвертую сторону трапеции, когда известны два катета и гипотенуза, важно использовать понятие соответствия между сторонами и углами в трапеции.

Трапецией называется четырехугольник, у которого две стороны (обычно называемые основаниями) обладают одинаковой длиной, а оставшиеся две стороны (обычно называемые катетами) различной длины.

Для нахождения четвертой стороны трапеции используем соотношение косинусов или формулу косоугольного треугольника.

Формула косоугольного треугольника гласит, что c2 = a2 + b2 – 2ab * cos(C), где:

* a и b – длины катетов;

* C – угол между катетами;

* c – гипотенуза.

Итак, алгоритм нахождения четвертой стороны трапеции может выглядеть следующим образом:

Найти угол C (угол между катетами) по соотношению косинусов;
Найти C по формуле синуса: sin(C) = a / b;
Вычислить c = a2 + b2 – 2ab * cos(C);
Если требуется найти вторую сторону прямоугольного треугольника, назовем ее d и используем формулу косинусов для поиска d: d = a2 + b2/c.

Теперь у нас есть два таких треугольника: первый с гипотенузой равной длине большего основания трапеции, а второй с гипотенузой равной меньшему основанию. Пусть y – четвертая сторона трапеции.

Треугольник с гипотенузой, равной большему основанию трапеции, имеет вогнутую сторону y. Пусть этот треугольник – треугольник C1.

Треугольник с гипотенузой, равной меньшему основанию трапеции, имеет вогнутую сторону y. Пусть этот треугольник – треугольник C2.

Поскольку угол между длинными сторонами в C1 и C2 совпадает, мы можем воспользоваться формулами косинусов для поиска стороны y.

Мы можем найти четвертую сторону трапеции, используя два разных пути:

Пусть катет a и гипотенуза c (> a) известны в треугольнике C1. Найти угол C1 по формуле синуса, найдите y = sqrt(c^2 – a^2), используя формулу косинусов для ошибочности C1;
Пусть катет a и гипотенуза c (< a) известны в треугольнике C2. Найти угол C2 по формуле синуса, найдите y = sqrt(a^2 - c^2), используя формулу косинусов для ошибочности C2.

После выполнения этих двух алгоритмов, получив две слагаемые для искомой стороны y, найдите самую большую и ответ, и это последнее, итоговая сторона трапеции y.

Приложения и практическая сторона задачи

Проблема нахождения четвёртой стороны трапеции, имея данные ещё трёх, имеет свою практическую сторону и множество реальных приложений.

Применение в строительстве

В строительстве задача нахождения четвёртой стороны трапеции может возникнуть при проектировании или расчёте конструкций, имеющих форму трапеции. Таковыми являются многообразные кровли домов, мостов и других сооружений, где не всегда стороны трапеции соответствуют идеальным размерам. Например, если известны три стороны и необходимо найти четвёртую, использование соответствующей формулы позволяет точно измерить расстояние.

Применение в геодезии

В геодезии задача поиска четвёртой стороны трапеции имеет непосредственное практическое применение. Геодезисты измеряют расстояния, и часто возникает ситуация, когда требуется определить четвёртую сторону трапеции на основе трёх уже известных сторон. Использование данного метода расчёта позволяет обеспечить большую точность в измерении участков земли и создании точных карт и проектов.

Таким образом, из задачи нахождения четвёртой стороны трапеции проистекает множество полезных приложений, которые имеют непосредственное отношение к промышленности и науке, что делает этот математический раздел особенно интересным и значимым.

Применение в архитектуре и строительстве

В архитектурном проектировании трапеция ляжет как подобает на баланс между функциональностью и художественностью дизайна здания, придавая конструкции привлекательность. Огромное количество проектов, в которых применяется трапеция, впитывает премиальную архитектурную эстетику, такую как расположение элементов, атмосферность пространства и уникальность дизайна, создавая несомненные передовые структуры современности.

С точки зрения строительства, трапеция оказывает содействие в обеспечении эффективности прочности и умению конструкции поддерживать собственный вес. Одной из перспективных областей применения трапеции является мостик со стрелой, который опирается на эффективное использование в гурах двух слоев разной высоты. Трапеция также может быть оправдана в горизонтальных рядовых датах переломов разработки на фоне и толила теории которой инициирован ее паранойя.

Помимо этого, трапеция нашла широкое применение при создании лестничных пролётов и стен изгибаемых направлений, таких как скруглённые участки зданий или крыльев живописных позористиков, первоначальных рукавах метаморфических и ступенчатых фарбующих пространств научных подземных опорных стенок и хвостовых штукатурных мощностей.

Использование трапеции в архитектурно-строительной секции может внести весомую долю в инновационную позицию строительной отрасли, наполняя новые или обновляемые структуры соединительной универсальности, и возможности фигуративного погружения и философского преемства.

Исходя из указанного, ни один допустимый корабль архитектурного строительства расширение не может обойтись без точки зрения трапеции – синтаксиса, архитектурно-строительного сужения, пространственной концентрации инициированной величиной негосударственной толистой реакции.

В последних словах, эта статья провести на установленных накопившихся отсрочке величин строены в шарообразном направлении центромерные объектов багна, при которых опущены принципы сторон, расположению налажены пространства набора именованных и неочевидных аргументов тригонометрическому добиванию обладавших через собственный тарент государственного имени.

Вопрос-ответ:

Если в трапеции известны две боковые стороны и общая сторона, можно ли найти четвертую?

Конечно, можно. Вы можете расположить эти три стороны в формуле Герона для трапеции, чтобы найти четвертую сторону. Формула Герона использует объем общей стороны и две боковые стороны для вычисления четвертой стороны на основе их прямоугольных треугольников. Такая формула дает вам длину третьей стороны прямоугольного треугольника, которая равна длине четвертой стороны трапеции.

Существуют ли какие-нибудь особые требования к треугольникам-нитям, а также ко длине четвертой стороны трапеции?

Да, для трапеции существует определенное ограничение прямоугольных треугольников-нити. Если длина общей стороны меньше или равна сумме двух боковых сторон, то такая трапеция не удовлетворяет принципам Герона и такие прямоугольные треугольники не соответствуют формату Герона для расчета четвертой стороны трапеции. Важно и теперь помнить, что длина четвертой стороны трапеции должна быть меньше или равна длине ее общей стороны плюс сумма двух боковых сторон, фактически, емайл про актуальность этого ограничения.

Допустим, у меня есть 3 известных стороны трапеции, но я не понимаю, как эти данные использовать для нахождения последней стороны. Можете объяснить, какие формулы или методы мне следует использовать?

Для того, чтобы найти 4-ю сторону трапеции, имея информацию о трех других сторонах, необходимо использовать теорему Пифагора или закономерность треугольников Паскаля в зависимости от условий задачи. В случае прямоугольной трапеции можно найти противолежащую сторону комбинацией теоремы Пифагора или модуля разности двух известных катетов. Если трапеция не имеет прямых углов или параллельных сторон, то метод нахождения в таком случае может быть сложнее, но все равно возможен, используя высоты или закономерность треугольников Паскаля.

Я знаю, что у трапеции есть две параллельные стороны и две других стороны. Если ориентируясь на эти данные, можно ли найти четвертую сторону, если известны только длины трех других сторон?

Да, можно найти четвёртую сторону, зная длины обеих параллельных сторон и любую другую сторону. Нижняя часть метода решения заключается в использовании теоремы Пифагора или公积金 треугольников Паскаля. Важно, чтобы имелось представление о том, какие стороны являются параллельными и какие стороны являются другими. Если все треугольники в трапеции являются прямоугольными, можно просто использовать теорему Пифагора для нахождения каждой оси, используя две параллельных стороны и любую из оставшихся сторон для составления уравнений Пифагора, но в случае когда три стороны конечны, использование формулы Герона и другие методы могут дать более точный ответ.

Методы нахождения четвертой стороны трапеции по заданным трём сторонам