Как найти 4 точку если знаю 3

Как найти 4 точку если знаю 3

Мозг

Просветленный

(45393)


11 лет назад

Достаточно просто, если прямоугольник расположен на экране, а не под каким-нибудь углом в 47 градусов. Для этого, находим координаты по x и y у всех точек. Каждое значение должно повторяться дважды. Какие значения повторятся лишь один раз, те и есть у неизвестной точки.
Поясню на примере. Выше вам нарисовали прямоугольник ABDC
Допустим, неизвестна точка B (координаты) .
Возьмём для простоты такие значения для точек:
A (1, 3)
C (1, 7)
D (4, 7)
7 это координата игрек и она повторяется дважды: у точек C и D, которые находятся на одной вертикальной прямой.
точка 1 по икс есть у точек A и C, они расположены на одной прямой по оси икс.
Точка 3 по игрек есть только у A. Соответственно, раз она лишь однажды повторяется по оси игрек, то второй раз она повторится у точки B. Тогда координата по игрек у B равна 3.
Точка 4 по иксу есть лишь у точки D. Значит, второй раз она будет у B.
Соответственно, точка B имеет координаты B (4, 3)
Это справедливо лишь для прямоугольников, не имеющих сдвига относительно экрана.
Для сдвинутых на определённый угол, скажем на 53 градуса, нужно вычислить вначале, какая именно точка неизвестна (через сравнение координат) , а потом по относительному смещению (разница между координатами на параллельных сторонах) найти нужные координаты.
Приведу простой пример:
Имеет прямоугольник ABCD

Сверяем известные координаты по иксу, имеем значения -5, 1 и 7 и по игреку 8, 3 и 11 соответственно. Находим длины отрезков AB, BD, DA через сумму квадратов разницы их координат
AD ^ 2 (в квадрате) = (1 – (-5)) ^ 2 + (3 – 8) ^ 2 = (6 ^ 2 + (-5) ^ 2) = 36 + 25 = 61
Значит AB = корень квадратный из 61 или просто 61 ^ 0.5
Также находим длину AB ^ 2= (1 – 7) ^ 2 + (3 – 11) ^ 2 = 36 + 64 = 100
AB = 100 ^ 0.5 = 10
DB ^ 2 = (-5 -7) ^ 2 + (8 – 11) ^ 2 = (-12) ^ 2 + (-3) ^ 2 = 144 + 9 = 153
DB = 153 ^ 0.5
Так как мы знаем координаты трёх точек, то они в любом случае (в прямоугольнике) составляют прямоугольный треугольник. Нам важно выяснить, какая из сторон самая длинная (она будет гипотенузой, а значит, точка, не участвующая в границах отрезка гипотенузы, будет противоположна той, что неизвестна. В нашем случае мы получили отрезки длиной
153 ^ 0.5, 61 ^ 0.5 и 100 ^ 0.5.
При проверке на равенство оно не выполняется (ошибка) 100 + 61 != 153. Но это потому что я от балды нарисовал прямоугольник. В действительности, просто у прямоугольника, с точками A (1, 3) и D(-5, 8) точка B не может иметь координат (7, 11) . Хотя бы одна из координат будет немного отличаться.
Ну да ладно – это ведь просто наглядный пример, и мне некогда тут высчитывать точное равенство.
Тогда мы узнали, что самая длинная сторона, получающаяся из известных точек, это сторона DB. А значит, раз точка А не является концом этой стороны, то мы можем утверждать, что абсцисса (координата X) неизвестной точки C находится по неравенству Ax – Dx = Bx – Cx
Тогда Cx = Bx – Ax + Dx
Подставим известные абсциссы, получим
Cx = 7 – 1 + (-5) = 1
А ордината C (координата по Y) находится из неравенства:
Ay – Dy = By – Cy
Cy = By – Ay + Dy
Cy = 11 – 3 + 8 = 16
Итого, получили координаты точки C (1, 16), что является верным ответом.
Можно вычислить координаты C немного по-другому:
Ax – Bx = Dx – Cx
Cx = Dx – Ax + Bx
Cx = -5 – 1 + 7 = 1
Ay – By = Dy – Cy
Cy = Dy – Ay + By
Cy = 8 – 3 + 11 = 16
То есть, для получения неизвестной точки мы складываем координаты точек гипотенузы треугольника, составленного из известных точек, и вычитаем точку, объединяющую катеты.
Ничего сложного, элементарная геометрия за 7 класс. Прочитайте ещё раз внимательно.

Источник: Тут всё очень просто.

Источник

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.

Примеры.

1)

najti-koordinaty-vershiny-parallelogramma Дано: ABCD — параллелограмм,

A(-3;11), B(12;-4), C(1;-7)

Найти: D.

Решение:

najti-4-vershinu-parallelogramma1) Найдём координаты точки O — середины диагонали AC.

По формуле координат середины отрезка

    [x_O = frac{{x_A + x_C }}{2} = frac{{ - 3 + 1}}{2} = - 1;]

    [y_O = frac{{y_A + y_C }}{2} = frac{{11 + ( - 7)}}{2} = 2.]

То есть O(-1;2).

2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

    [x_O = frac{{x_B + x_D }}{2}; - 1 = frac{{12 + x_D }}{2};x_D = - 14;]

    [y_O = frac{{y_B + y_D }}{2};2 = frac{{ - 4 + y_D }}{2};y_D = 8.]

Ответ: D (-14; 8).

2)

Дано: ABCD — параллелограмм,

B(7;4), C(-5;10), D(-1;-2)

Найти: A.

Решение:

1) Ищем координаты точки O — середины отрезка BD:

    [x_O = frac{{x_B + x_D }}{2};x_O = frac{{7 + ( - 1)}}{2} = 3;]

    [y_O = frac{{y_B + y_D }}{2};x_O = frac{{4 + ( - 2)}}{2} = 1.]

Итак, O (3;1).

2) Точка O также является серединой AC:

    [x_O = frac{{x_A + x_C }}{2};3 = frac{{x_A + ( - 5)}}{2};x_A = 11;]

    [y_O = frac{{y_A + y_C }}{2};1 = frac{{y_A + 10}}{2};y_A = - 8.]

Ответ: A (11;-8).

Источник

$begingroup$

Lets say you have three points in $2D$, which are non-collinear: $a$, $b$ and $c$.

How can you find a $4$th point, when you have the distance from the $4$th point to $a$, $b$ and $c$ ?

Harish Chandra Rajpoot's user avatar

asked Dec 22, 2011 at 22:31

user1112570's user avatar

$endgroup$

2

$begingroup$

For each point a,b,c, draw a circle with center at that point, having a radius equal to its distance to 4th point. The 4th point is where all circles intersect.

answered Dec 22, 2011 at 22:43

$endgroup$

0

You must log in to answer this question.

Not the answer you’re looking for? Browse other questions tagged

.

Источник

Возможно ли найти 4ую сторону прямоугольника?

Доброго времени суток, друзья!
Прошу Вашей помощи в вопросе геометрии, по большому счету…натуральная житейская ситуация.
Можно ли математически найти 4ую сторону прямоугольника, если известно 3 его стороны, ширина и площадь?
Если это реально, то могли бы Вы кратко расписать с обоснованием, как это можно сделать?
Суть в том, что я с помощью фемиды пытаюсь решить спор по границе земельного участка. У участка сложились 3 стороны. (границы), а вот с 4ой проблема 🙁 «Эксперт» говорит, что это невозможно… но после его экспертизы, доверия к нему нет.
Спасите!

UPD: Простите пожалуйста, ввёл Вас в заблуждение. Это действительно не прямоугольник, а 4х угольник. Извините за не точность.

  • Вопрос задан более трёх лет назад
  • 2518 просмотров

Оценить 7 комментариев

Во-первых: ваш участок имеет форму выпуклого четырехугольника, не называйте его прямоугольником.
Во-вторых: есть три варианта:

  1. Можно однозначно определить одну сторону произвольного выпуклого четырехугольника, зная три другие стороны, площадь и два противолежащих угла (любую из двух пар):

    где p — полупериметр и

  2. Можно однозначно определить одну сторону произвольного выпуклого четырехугольника, зная три другие стороны, площадь и обе диагонали:

    где p — полупериметр, e и f -диагонали.

  3. Невозможно однозначно определить одну сторону произвольного выпуклого четырехугольника, зная только три другие стороны и площадь. То есть существует бесконечное множество значений длины искомой стороны, удовлетворяющих заданным условиям.

Короче: Меряйте или диагонали, или углы (любую пару противоположных углов).

Четырехугольники

теория по математике 📈 планиметрия

Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.

Выпуклый четырехугольник

Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Определение

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.

Виды и свойства выпуклых четырехугольников

Сумма углов выпуклого четырехугольника равна 360 градусов.

Прямоугольник

Прямоугольник – это четырехугольник, у которого все углы прямые.

На рисунке видно, что углы А, В, C и D прямые, то есть равны 90 градусов. Свойства прямоугольника, его периметр и площадь

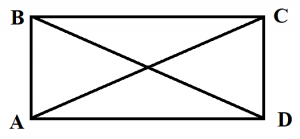
  1. Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
  2. Диагонали прямоугольника равны (АС=ВD).
  3. Диагонали пересекаются и точкой пересечения делятся пополам.
  4. Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
  5. Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:

S=ab, где a и b соседние стороны прямоугольника.

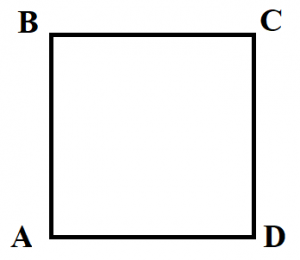
Квадрат

Квадрат – это прямоугольник, у которого все стороны равны.

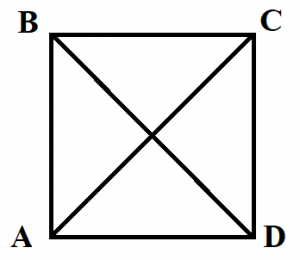
Свойства квадрата

  1. Диагонали квадрата равны (BD=AC).
  2. Диагонали квадрата пересекаются под углом 90 градусов.
  3. Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
  4. Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
  5. Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.

Параллелограмм

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Ромб – это параллелограмм, у которого все стороны равны.

Трапеция

Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.

Виды трапеций

Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.

углы А и С равны по 90 градусов

Средняя линия трапеции

Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.

Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.

По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17

Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).

Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .

Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула

S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63

pазбирался: Даниил Романович | обсудить разбор | оценить

Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .

Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:

с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88

pазбирался: Даниил Романович | обсудить разбор | оценить

Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8

Для выполнения данного задания надо подставить все известные данные в формулу:

12,8= d 1 × 16 × 2 5 . . 2 . .

В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .

Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2

Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4

pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.

Задание №1

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.

Объекты яблони теплица сарай жилой дом
Цифры

Решение

Для решения 1 задачи работаем с текстом и планом одновременно:

при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.

Итак, получили следующее:

1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.

Заполняем нашу таблицу:

Объекты яблони теплица сарай жилой дом
Цифры 3 5 1 7

Записываем ответ: 3517

Задание №2

Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?

Решение

Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».

Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.

Задание №3

Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение

Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4

Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.

Решение

Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м

Задание №5

Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.

Номер магазина Расход краски Масса краски в одной банке Стоимость одной банки краски Стоимость доставки заказа
1 0,25 кг/кв.м 6 кг 3000 руб. 500 руб.
2 0,4 кг/кв.м 5 кг 1900 руб. 800 руб.

Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?

Решение

Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:

1 магазин: 232х0,25=58 кг

2 магазин: 232х0,4=92,8 кг

Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:

1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)

2 магазин: 92,8:5=18,56; значит надо 19 банок.

Вычислим стоимость краски в каждом магазине плюс доставка:

1 магазин: 10х3000+500=30500 руб.

2 магазин: 19х1900+800=36900 руб.

Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.

Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

[spoiler title=”источники:”]

Четырехугольники

[/spoiler]

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

На главную страницу
На главную страницу

на главную

Как найти координаты точки

Поддержать сайтспасибо

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Найти координаты точки

Рассмотрим как в системе координат (на координатной плоскости):

  • находить координаты точки;
  • найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.

Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Координаты точки плоскости

Обозначают координаты точки, как указано выше (·) A (2; 3).

Пример (·) A (2; 3) и (·) B (3; 2).

Точки с разными координатами

Запомните!
!

На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.

Особые случаи расположения точек

  1. Если точка лежит на оси «Oy»,
    то её абсцисса равна 0. Например,
    точка С (0, 2).
  2. Если точка лежит на оси «Ox», то её ордината равна 0.
    Например,
    точка F (3, 0).
  3. Начало координат — точка O имеет координаты, равные нулю O (0,0).
    Точки на координатный осях
  4. Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
    Точки на прямой перпендикулярной оси абсцисс
  5. Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
    Точка на оси абсцисс
  6. Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
    Точка на оси абсцисс
  7. Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
    Точка на оси ординат

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:

  1. Отметить на оси «Ox», точку с координатой
    «−4», и провести через неё прямую перпендикулярную оси «Ox».
  2. Отметить на оси «Oy»,
    точку с координатой 2, и провести через неё прямую перпендикулярную
    оси «Oy».
  3. Точка пересечения перпендикуляров (·) D — искомая точка.
    У неё абсцисса равна «−4», а ордината равна 2.

    Как найти точку в системе координат

Второй способ

Чтобы найти точку D (−4 , 2) надо:

  1. Сместиться по оси «x» влево на
    4 единицы, так как у нас
    перед 4
    стоит «−».
  2. Подняться из этой точки параллельно оси y вверх на 2 единицы, так
    как у нас перед 2 стоит «+».
    Как найти точку на координатной плоскости

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.

Ваши комментарии

Важно!
Галка

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Пришелец пожимает плечами

Оставить комментарий:

Источник

Добавить комментарий