Как найти 4пи на окружности

Как обозначать числа с пи на числовой окружности?

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.

Обозначаем числа (2π), (π), (frac<π><2>), (-frac<π><2>), (frac<3π><2>)

Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки – это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac<π><2>) . (frac<π><2>) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-) (frac<π><2>) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac<3π><2>) . Для этого дробь (frac<3><2>) переведем в смешанный вид (frac<3><2>) (=1) (frac<1><2>) , т.е. (frac<3π><2>) (=π+) (frac<π><2>) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac<3π><2>) .

Обозначаем числа (frac<π><4>), (frac<π><3>), (frac<π><6>)

Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac<π><4>) , (frac<π><3>) и (frac<π><6>) .
(frac<π><4>) – это половина от (frac<π><2>) (то есть, (frac<π><4>) (=) (frac<π><2>) (:2)) , поэтому расстояние (frac<π><4>) – это половина четверти окружности.

(frac<π><4>) – это треть от (π) (иначе говоря, (frac<π><3>) (=π:3)), поэтому расстояние (frac<π><3>) – это треть от полукруга.

(frac<π><6>) – это половина (frac<π><3>) (ведь (frac<π><6>) (=) (frac<π><3>) (:2)) поэтому расстояние (frac<π><6>) – это половина от расстояния (frac<π><3>) .

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac<π><2>) ,(π), (frac<3π><2>) , (frac<π><4>) , (frac<π><3>) , (frac<π><6>) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

Обозначаем числа (frac<7π><6>), (-frac<4π><3>), (frac<7π><4>)

Обозначим на окружности точку (frac<7π><6>) , для этого выполним следующие преобразования: (frac<7π><6>) (=) (frac<6π + π><6>) (=) (frac<6π><6>) (+) (frac<π><6>) (=π+) (frac<π><6>) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac<π><6>) .

Отметим на окружности точку (-) (frac<4π><3>) . Преобразовываем: (-) (frac<4π><3>) (=-) (frac<3π><3>) (-) (frac<π><3>) (=-π-) (frac<π><3>) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac<π><3>) .

Нанесем точку (frac<7π><4>) , для этого преобразуем (frac<7π><4>) (=) (frac<8π-π><4>) (=) (frac<8π><4>) (-) (frac<π><4>) (=2π-) (frac<π><4>) . Значит, чтобы поставить точку со значением (frac<7π><4>) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac<π><4>) .

Обозначаем числа (10π), (-3π), (frac<7π><2>) ,(frac<16π><3>), (-frac<21π><2>), (-frac<29π><6>)

Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:

Числам с разницей в (2πn), где (n∈Z) (то есть (n) – любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).

Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).

Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).

Сейчас обозначим число (frac<7π><2>) . Как обычно, преобразовываем: (frac<7π><2>) (=) (frac<6π><2>) (+) (frac<π><2>) (=3π+) (frac<π><2>) (=2π+π+) (frac<π><2>) . Два пи – отбрасываем, и получается что, для обозначения числа (frac<7π><2>) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac<π><2>) (т.е. половину окружности и еще четверть).

Отметим (frac<16π><3>) . Вновь преобразования: (frac<16π><3>) (=) (frac<15π + π><3>) (=) (frac<15π><3>) (+) (frac<π><3>) (=5π+) (frac<π><3>) (=4π+π+) (frac<π><3>) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac<π><3>) – и мы найдем место точки (frac<16π><3>) .

Нанесем на окружность число (-) (frac<21π><2>) .
(-) (frac<21π><2>) (= -) (frac<20π><2>) (-) (frac<π><2>) (=-10π-) (frac<π><2>) . Значит, место (-) (frac<21π><2>) совпадает с местом числа (-) (frac<π><2>) .

Обозначим (-) (frac<29π><6>) .
(-) (frac<29π><6>) (=-) (frac<30π><6>) (+) (frac<π><6>) (=-5π+) (frac<π><6>) (=-4π-π+) (frac<π><6>) . Для обозначение (-) (frac<29π><6>) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac<π><6>) .

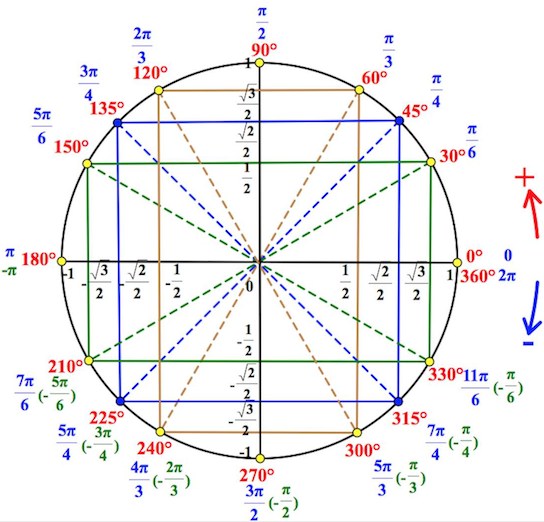
Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

• 

Вот что мы видим на этом рисунке:

Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.

Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .

И синус, и косинус принимают значения от до .

Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.

Знаки синуса, косинуса, тангенса и котангенса.

Синус — функция нечётная, косинус — чётная.

Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

• Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
• Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
• В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
• В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

• 2π радиан = 360°
• 1 радиан = (360/2π) градусов
• 1 радиан = (180/π) градусов
• 360° = 2π радиан
• 1° = (2π/360) радиан
• 1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

[spoiler title=”источники:”]

http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/

http://skysmart.ru/articles/mathematic/edinichnaya-okruzhnost

[/spoiler]