Угловые размеры
Угловые размеры на чертеже
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Наиболее распространенный способ измерения угловых величин – градусная мера.
Градус – «gradus», в переводе с латинского языка, означает – шаг, ступень.
При обозначении угловых размеров используется единицы измерения – градусы, минуты и секунды. После числового значения угловых размеров ставится специальные знаки:
- Градус – «
°» - Минута – «
′» - Секунда – «
″»
Размерные числа наносят над размерными линиями в зоне расположенной выше горизонтальной осевой линии со стороны их выпуклости, а в зоне расположенной ниже со стороны вогнутости размерных линий.В тех местах, где нанесена штриховка, размерные числа указывать не рекомендуется. В таких случаях размерные числа указывают на горизонтально нанесенных полках.
Нанесение угловых размеров на чертеже
Нанесение угловых размеров
Градусы минуты секунды – n° n′ n″
Окружность, разделённая на 360°, включает в свой состав помимо градусов, минуты и секунды n° n′ n″.
1° = 1/360 – один градус равен одной тристашестидесятой полного оборота.
1° = 60′ – один градус равен шестьдесят минут.
60′ = 60″ – шестьдесят минут ровны шестидесяти секундам.
Градусная мера полного оборота равна 360° = 21600′ = 1296000″.
360°– один оборот90°– прямой угол180°– развёрнутый угол
Углы – это геометрические фигуры, образованные двумя лучами, которые выходят из одной точки. Обозначения углов регламентированы ГОСТ 2.307-2011 «Нанесение размеров и предельных отклонений».
Как обозначается угол на чертеже
Угол на чертеже обозначается с помощью универсального и общепринятого символа, на котором показаны два луча, выходящие из одной точки. За символом указывается размер угла в градусах, минутах и секундах. Острый угол символа направлен в сторону уклона.
Обозначение углов на чертеже по ГОСТу
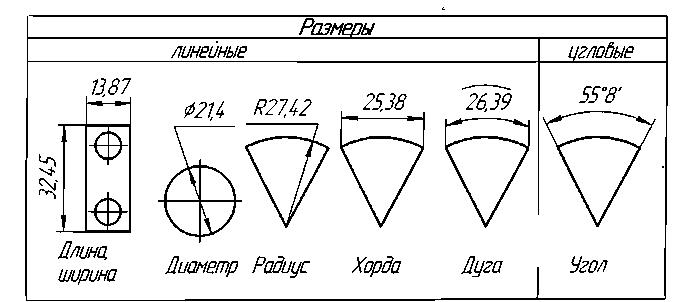
Согласно ГОСТ 2.307 размеры делятся на линейные и угловые. И если в линейных размерах не ставят единицы измерения, т. к. всегда подразумевается, что значения приведены в миллиметрах, то для угловых размеров обязательно указывается значок градуса, минуты и секунды, в зависимости от того, в каких величинах измеряется угол.
Рисунок 1. Линейные и угловые размеры
Как показать угол на чертеже
Чтобы показать размер используются сплошные тонкие линии, они могут быть выносные или размерные. Любой угол имеет вершину и две стороны. Градусами или минутами обычно обозначается внутренняя сторона угла. В качестве условного обозначения используется символ в виде острого угла, далее указывается числовое значение и единицы измерения. Следует помнить о том, что минута — это одна шестидесятая часть градуса, а секунда одна шестидесятая часть минуты. Градусы обозначаются с помощью маленького круга в верхнем правом углу возле значения, минуты обозначаются одной надстрочной запятой, а секунды двумя надстрочными запятыми.
Допуск угла
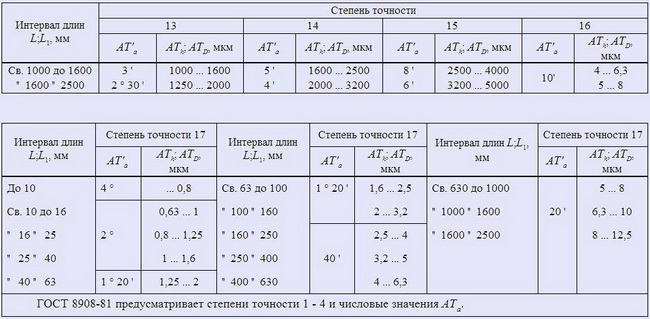
В ГОСТ 8908-81 приведены стандарты на допуски углов, применяемые в машиностроении, при меньшей стороне угла до 2,5 м. Значения уклона и угла уклона приведены в таблице (рис. 1). Стандартом установлено 17 степеней точности допусков, которые зависят от длин сторон и размера угла.
Рисунок 2. Степень точности допуска угла
Виды углов на чертеже
На чертежах могут быть обозначены следующие виды углов:
- острый – менее 90 градусов;
- прямой – равен 90 градусам;
- тупой – более 90 и менее 180 градусов;
- развернутый – равен 180 градусам.
Обозначение у прямого и развернутого угла ставится при необходимости.
Углы наклона
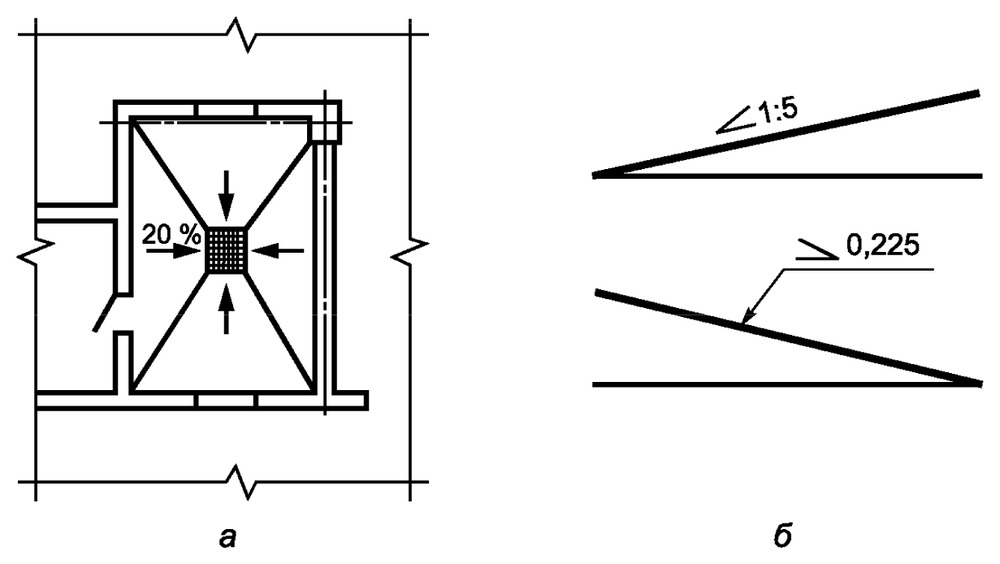
Угол уклона часто встречается как на машиностроительных, так и на строительных чертежах. Он показывает, под каким углом к базовой линии расположен наклонный элемент. Для обозначения наклона используется универсальный символ, который ставится перед размерным числом. К примеру, на строительном чертеже отмостка всегда имеет уклон, для обозначения этого уклона ставится символ и значение в 5 промилле.
Рисунок 3. Обозначение уклона на плане кровли
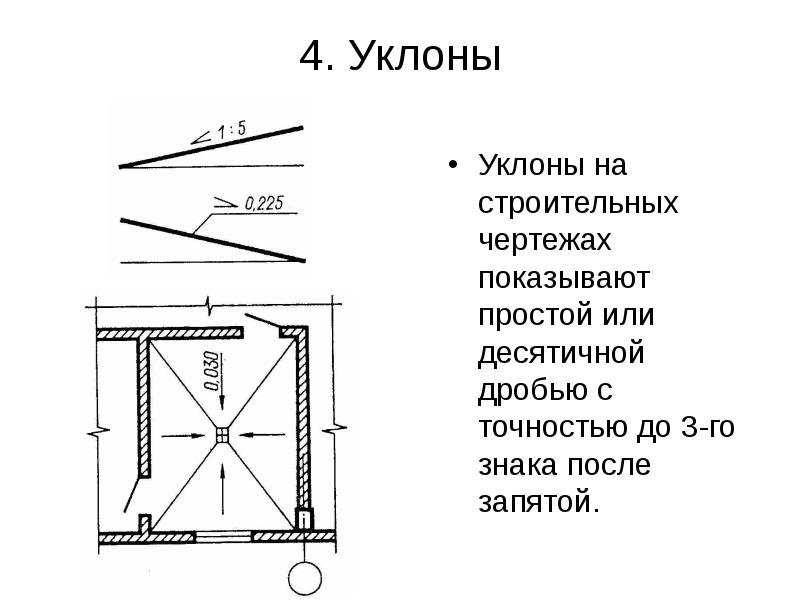
Промилле — это одна тысячная или десятая часть процента, поэтому к знаку промилле добавлен еще один нолик. Через промилле в строительных чертежах указывается уклон пандусов и других наклонных поверхностей.
Рисунок 4. Уклон на чертеже
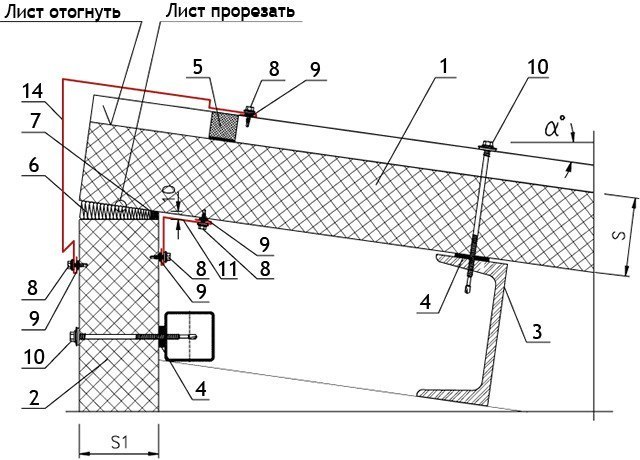
Рисунок 5. На узле сопряжения сендвич панелей указывается угол под которым конструкции крпятся друг к другу
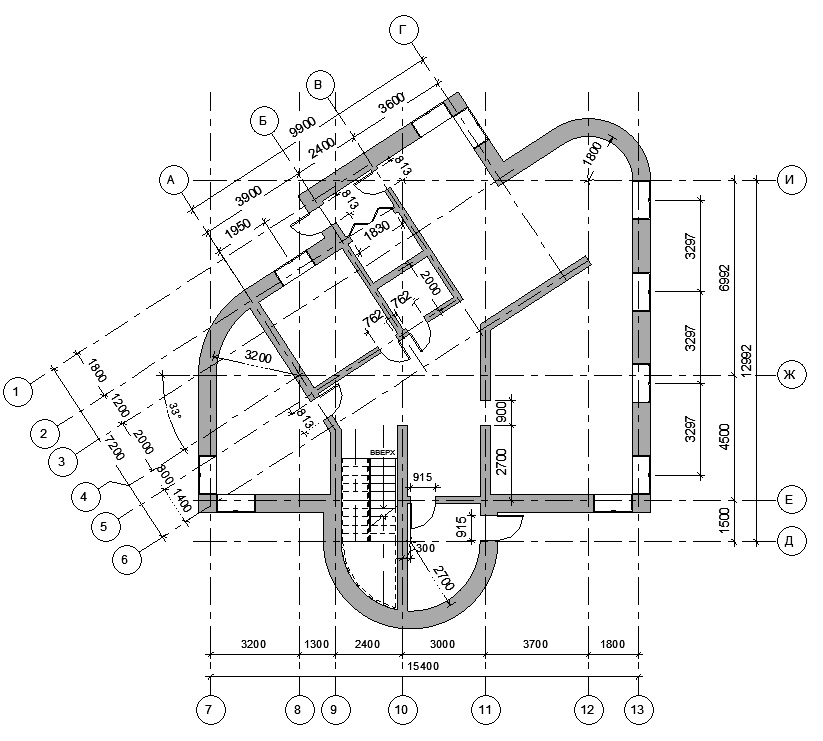
Рисунок 6. Углы. На строительном чертеже обозначен угол в 33 градуса
Угол преломления
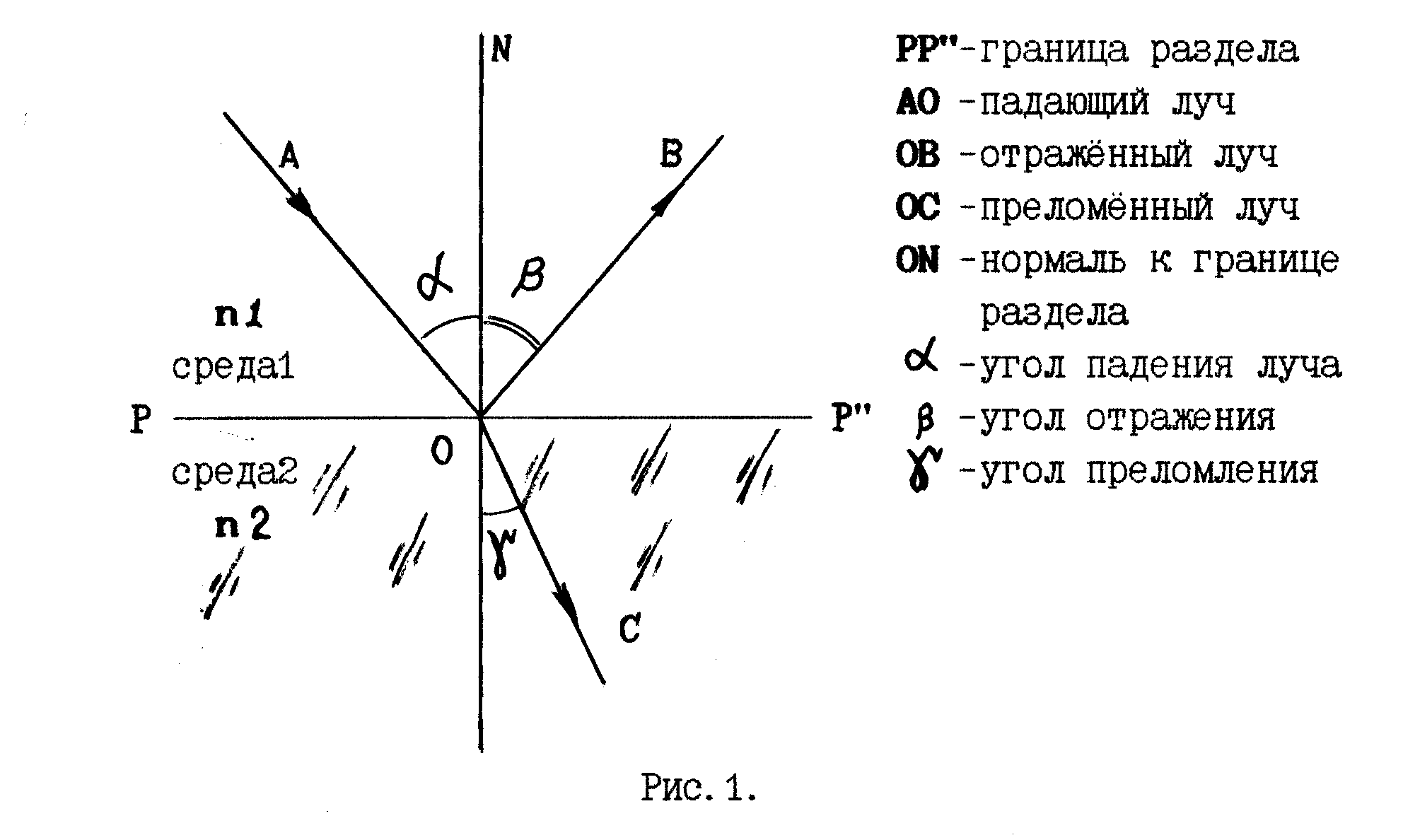
Преломление возникает на границе двух сред, при этом угол падения равен углу отражения. Падающий и отраженный лучи показывают на чертеже, а значение угла наносят относительно вертикали, прямого угла.
Рисунок 7. Угол преломления
Вертикальные углы
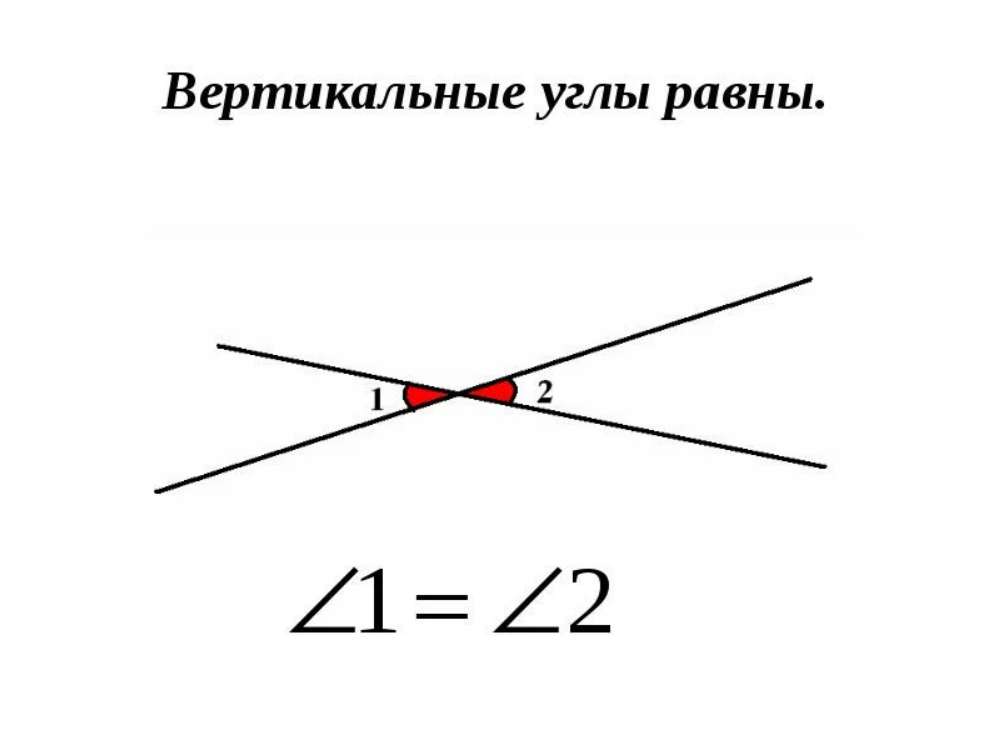
Согласно определению вертикальными называют два угла, в том случае, если стороны одного угла являются продолжением сторон другого. Такие углы будут попарно равны. Обычно на чертеже их обозначают с помощью полукруга или двойного полукруга.
Рисунок 8. Вертикальные углы, пример обозначения
Многогранные углы
Понятие многогранного угла относится к трехмерному пространству, такой угол состоит из плоских углов, которые его образуют, имея общую точку. При этом они не должны лежать в одной плоскости.
У многогранного угла есть два свойства:
- сумма плоских углов многогранного угла превышает 360 градусов;
- существует плоскость, пересекающая все ребра многогранного угла.
По количеству граней многогранные углы делят на трехгранные, четырехгранные, пятигранные и так далее.
Самым показательным примером многогранного угла является вершина четырехугольной пирамида. Многогранный угол может быть невыпуклым и выпуклым.
Смежные углы
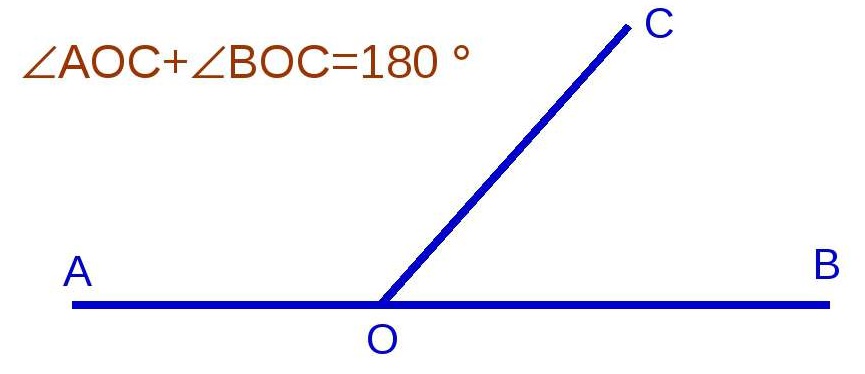
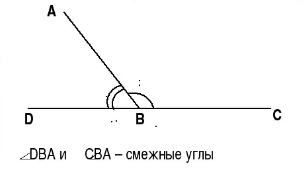
Смежными называются углы, которые имеют одну общую сторону, а две другие их стороны являются продолжением друг друга. Сумма смежных углов равна 180 градусам. Поэтому, если известно значение одного угла, то найти значение второго не составляет труда.
Рисунок 9. Пример смежных углов
Углы фаски
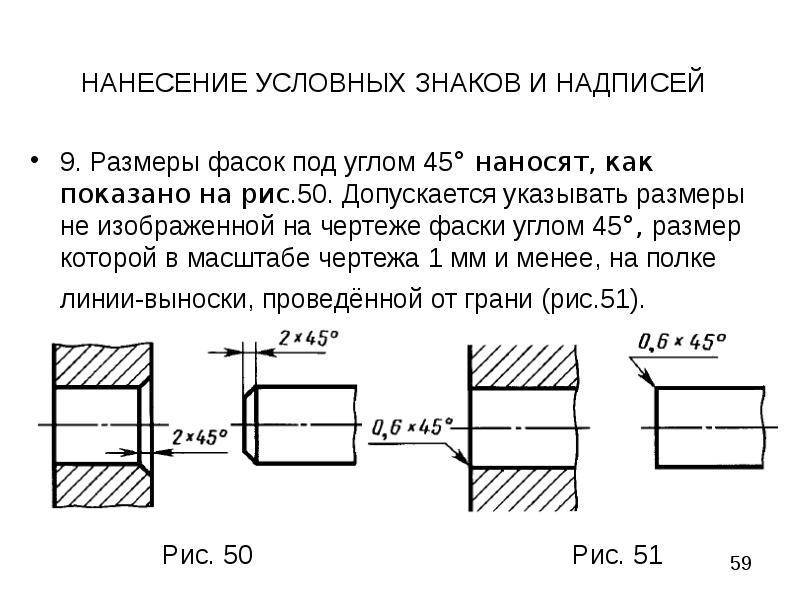
Деталь может иметь скос или скругление, которое называется фаской. Обозначение фаски установлено в ГОСТ 2.307-2011, обычно ее показывают размерными линиями. Запрещено использовать осевые и контурные линии для обозначения фаски. На чертеже обязательно указывают ширину, размер скоса и угол относительно главной оси элемента или механизма. Если на чертеже показана фаска, но не указан угол, то подразумевается ее стандартное значение 45 градусов. Обозначение выполняется с помощью выносной линии или с помощью линейных размеров.
Рисунок 10. Обозначение фаски по ГОСТ
Внешние углы на чертеже
На чертежах может потребоваться указать внешний угол треугольника, это угол смежный с любым из внутренних углов. Следовательно, у каждой вершины можно построить два равных внешних угла. Также существует теорема, доказывающая что внешний угол равен сумме двух внутренних углов, которые не смежны с ним.
Центральные углы на чертеже
Центральным называется угол, который равен градусной мере дуги, на которую он опирается. Центральный угол отличается от вписанного тем, что вершин вписанного угла лежит на окружности, и он равен половине дуги, на которую опирается. Вписанные и центральные углы имеют зависимость, например, если нарисовать их на одной окружности, то вписанный угол будет равен половине центрального, если они опираются на одну дугу. Таким образом, зная один угол, можно определить другой.
Ответы на вопросы
Как обозначается радиус окружности на чертеже?
Для обозначения радиуса используется значок R, после которого указывается значение в миллиметрах и сплошная тонкая линия со стрелкой на конце. Радиус проводят от центра окружности к обозначаемому отрезку. Обычно указывают только радиус, диаметр при необходимости можно найти путем удвоения радиуса.
Как указать прямой угол?
При обозначении острого или тупого угла в основании между лучами проводят полукруг, если угол прямой в его основании рисуют квадрат.
Как отсчитывают угол на чертеже?
Угол образовывается двумя лучами, чтобы найти его значение используют транспортир.
daybit
Высший разум
(146207)
7 лет назад
а = 360 – (180-108) – (180-72) – 64 = 116 градусов
Источник: 2015-05-20 16:36 (utc3)
dima sexУченик (137)
7 лет назад
спасибо! )
daybit
Высший разум
(146207)
пожалуйста
ну блин у тебя и ник. долго думал пока выбирал?
dima sexУченик (137)
7 лет назад
помоги остальные !
Определение
Геометрия — это раздел математики, который занимается изучением форм и их измерений. Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.
Все геометрические фигуры состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется углом. В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.
Определение угла в математике
Определение
Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.
Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.
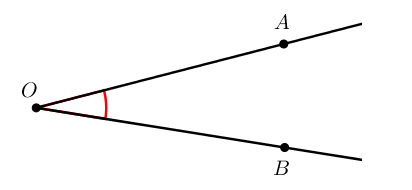
Стороны угла – лучи, которые образуют угол (А, В).
Вершина угла – точка, из которой выходят лучи (О).
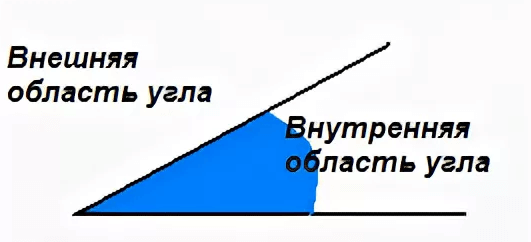
Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.
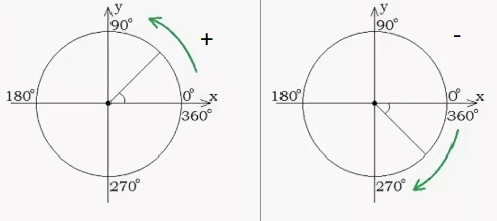
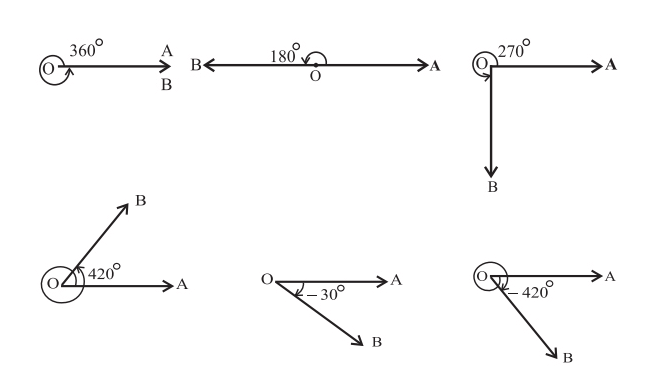
Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
- Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
- Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.
Интересно
Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».
Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.
Как обозначить углы?
Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:
- Способ 1:
Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д. - Способ 2:
Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).
Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.
Типы углов
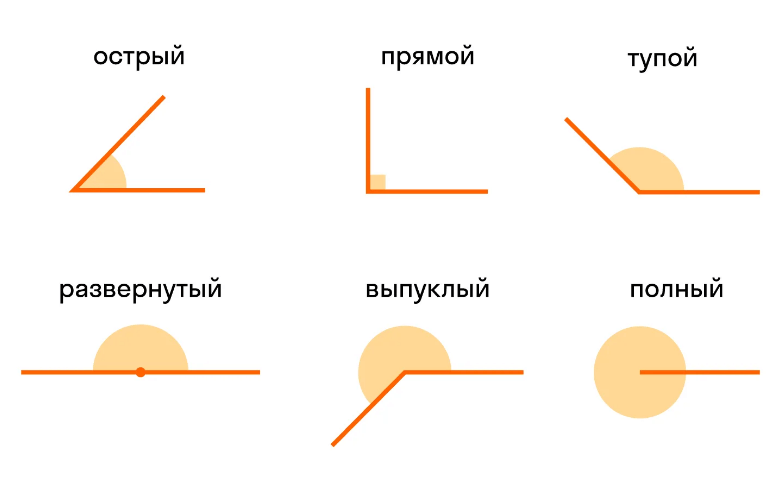
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
- Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
- Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
Прямой угол можно легко наблюдать, так как он образует форму буквы L. - Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
это тупой угол. - Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
половина полного оборота круга. Размер прямого угла равен 180°. - Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
- Полный угол — когда измерение угла равно 360 градусам, это полный угол.
Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.
Углы образованные при пересечении двух прямых
При пересечении двух прямых образуются два вида углов:
- смежные;
- вертикальные.
Смежные углы
Определение
Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.
Свойства смежных углов
- Сумма смежных углов равна 180°
- Если оба смежных угла равны между собой, то они являются прямыми.
- В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
- Синусы смежных углов равны.
- Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.
Вертикальные углы
Определение
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
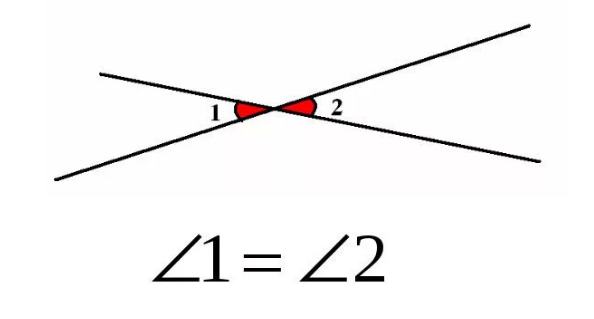
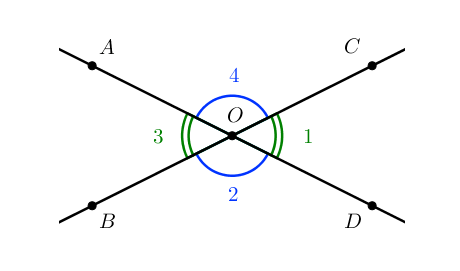
Пример:
Пары углов 1 и 3; 2 и 4 – являются вертикальными
По свойству вертикальных углов:
[angle C O D=angle A O B]
[angle B O D=angle A O C]
Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными
По свойству смежных углов:
[angle C O D+angle D O B=180^{circ}]
[angle D O B+angle B O A=180^{circ}]
[angle B O A+angle A O C=180^{circ}]
[angle A O C+angle C O D=180^{circ}]
| Смежные углы | Вертикальные углы |
| Два угла с общей стороной и вершиной называются смежными. | Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами. |
| Имеют общую сторону и общую вершину. | Имеют общую вершину, но не имеют общую сторону |
| Смежные углы не всегда равны по величине | Вертикально противоположные углы равны по величине |
Сравнение углов
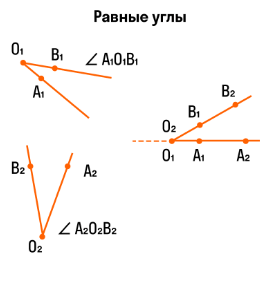
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
[angle A_{1} O_{1} B_{1}] и [angle A_{2} O_{2} B_{2}] полностью совмещаются при наложении следовательно: [angle A_{1} O_{1} B_{1}=angle A_{2} O_{2} B_{2}]
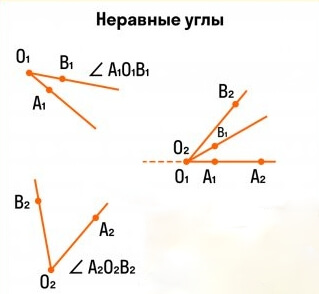
[angle A_{1} O_{1} B_{1}] и [ angle A_{2} O_{2} B_{2}] не совмещаются при наложении: [angle A_{1} O_{1} B_{1} neq angle A_{2} O_{2} B_{2}]
Причем: [angle A_{1} O_{1} B_{1}<angle A_{2} O_{2} B_{2}]
При этом развернутые углы всегда являются равными.
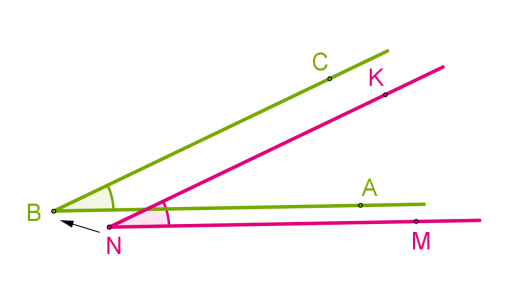
Совмещение углов [angle A B C] и [angle M N K] происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
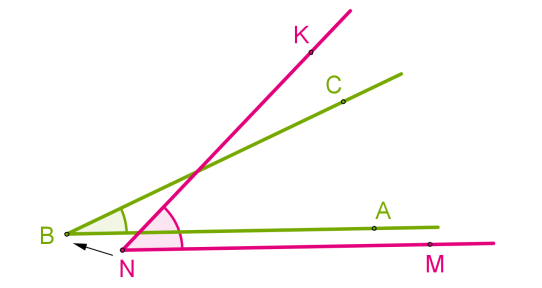
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.
Измерение углов
Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:
Градусная мера
Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет [left(frac{1}{360}right)] оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.
Мы измеряем время в часах, минутах и секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов
- 1 градус = 60 минут, обозначаемый как 1° = 60′.
- 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.
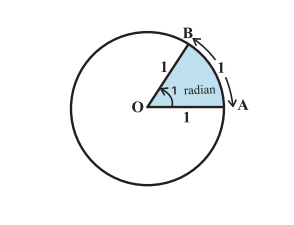
Радианная мера
Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица. Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
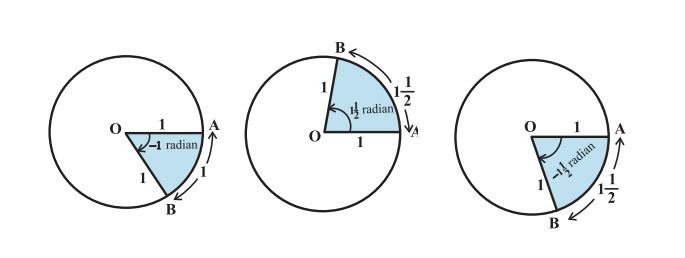
Вот еще несколько примеров углов: -1 радиан, радиан, [1 frac{1}{2}] радиан, [-1 frac{1}{2}] радиан.
Длина окружности = [2 pi r ldots] где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна [2 pi]. Следовательно, один полный оборот начальной стороны образует в центре угол [2 pi] радиан. Обобщая это, имеем:
В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = [frac{l}{r}] радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:
[theta=frac{l}{r}]
[l=r theta]
Связь между степенью и радианными мерами
По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:
- 360° – по градусной мере
- [2 pi] радиан — в радианах
Следовательно, [2 pi] радиан = 360° ⇒ [pi] радиан = 180°. Теперь подставим приблизительное значение [pi] как [frac{22}{7}] в уравнении выше и получить, 1 радиан [frac{180^{circ}}{pi}=57^{circ} 16^{prime}]. Кроме того, [1^{0}=frac{pi}{180^{circ}}] радиан = 0,01746 радиан примерно. Ниже таблица, изображающая соотношение между градусами и радианами некоторых распространенных углов:
| Градусы | [30^{circ}] | [45^{circ}] | [60^{circ}] | [90^{circ}] | [180^{circ}] | [270^{circ}] | [360^{circ}] |
| Радианы | [frac{pi}{6}] | [frac{pi}{4}] | [frac{pi}{3}] | [frac{pi}{2}] | [pi] | [frac{3pi}{2}] | [2pi] |
Пример
Преобразуйте 40° 20′ в радианы.
Решение: мы знаем, что 1° = 60′, следовательно, 20′ = [frac{1^{0}}{3}].
Следовательно,
[40^{circ} 20^{prime}=40 frac{1}{3}=frac{121}{3}];
Кроме того, мы знаем, что
радианная мера = [frac{pi}{180^{0}} x] градусную меру
Следовательно, радианная мера [40^{circ} 20^{prime}=frac{pi}{180} times frac{121}{3}=frac{121 pi}{540}] радиан.
Нет времени решать самому?
Наши эксперты помогут!
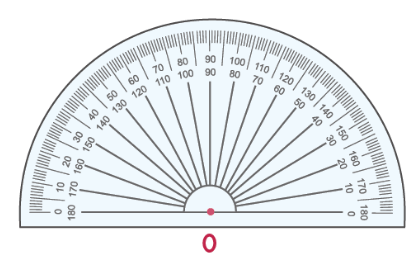
Как измерить угол
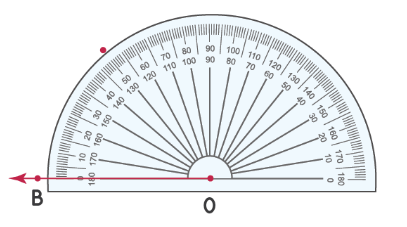
Для измерения углов используется транспортир:
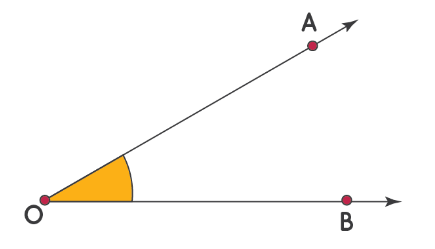
Попробуем измерить угол [angle A O B]
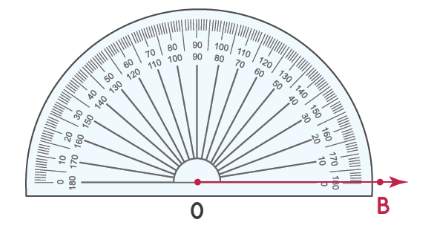
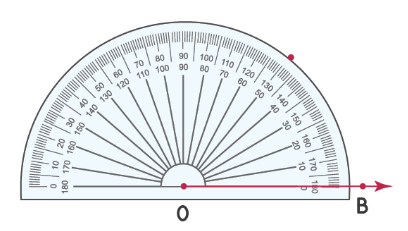
Шаги для измерения угла [angle mathrm{AOB}].
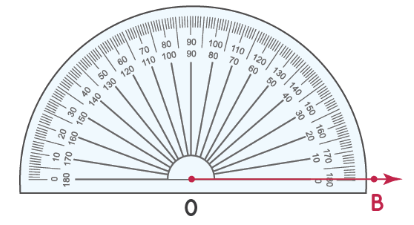
Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
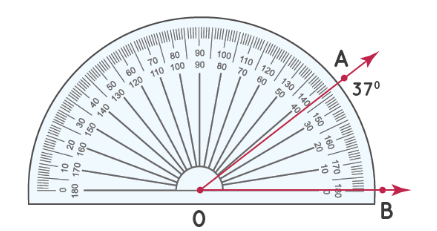
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°
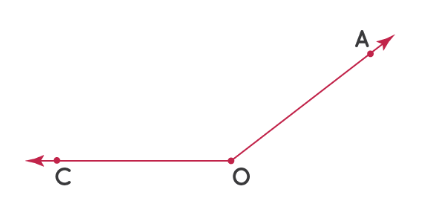
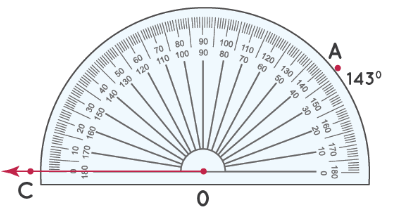
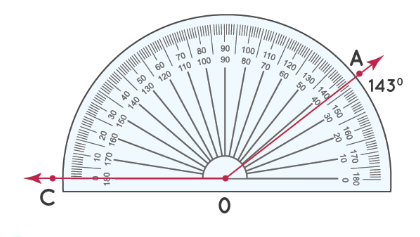
Далее попробуем измерить этот ∠AOC:
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°
Как построить углы
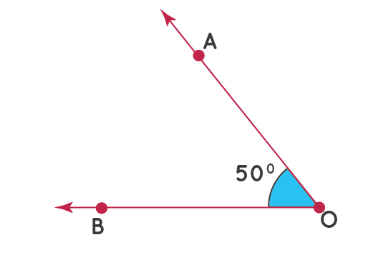
Используем транспортир для построения углов. Нарисуем угол 50°.
Шаг 1: сначала нарисуйте луч OB и совместите транспортир с OB, как показано.
Шаг 2: поместите точку над отметкой на транспортире, которая соответствует 50°.
Шаг 3: Уберите транспортир и нарисуйте луч, начинающийся в точке О и проходящий через эту точку. Таким образом, ∠AOB – искомый угол, т.е. ∠AOB = 50°.
Примечание. Если луч идет в другом направлении, мы измеряем угол от отметки 0° в левом нижнем углу.
На изображении ниже показано, как нарисовать угол 50°, когда луч указывает в другом направлении.
Обозначение углов на чертеже
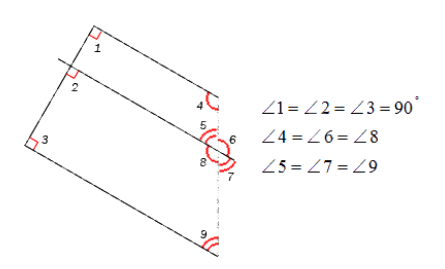
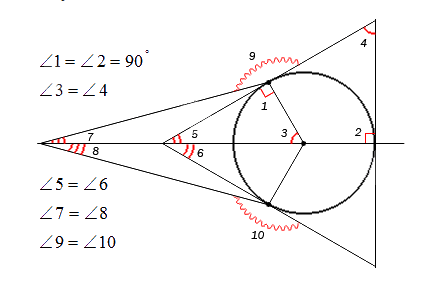
Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.
На чертеже запечатлено корректное обозначение острых, равных и неравных углов.
Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.
Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.
Угол уклона в процентах и промилле
Угол уклона – показатель наклона какой либо поверхности (дороги, крыши, пандуса, лестничного марша и пр.) относительно уровня горизонта.
Угловые размеры указывают на чертежах в градусах, минутах и секундах с обозначением единицы измерения (ГОСТ 2.307-2011 “Единая система конструкторской документации (ЕСКД). Нанесение размеров и предельных отклонений“).

В соответствии с ГОСТ Р 21.1101-2013 “Система проектной документации для строительства (СПДС). Основные требования к проектной и рабочей документации”, на планах направление уклона плоскостей указывают стрелкой, над которой при необходимости проставляют числовое значение уклона в процентах или в виде отношения единицы высоты плоскости к соответствующей горизонтальной проекции. Допускается числовое значение уклона указывать в промилле или в виде десятичной дроби с точностью до третьего знака.

На разрезах, сечениях и схемах перед размерным числом, определяющим числовое значение уклона, наносят знак,
острый угол которого должен быть направлен в сторону уклона (кроме крутизны откосов насыпей и выемок). Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.

Также вместо знака угла, на чертежах встречается и буквенное обозначение уклона ( i ).
В процентах обычно обозначают углы уклонов крыш, пандусов, лестничных маршей и т.п.

В промилле обозначают углы уклонов плоскостных сооружений – спортивные игровые площадки, поля, беговые дорожки, а также линейные сооружения – автомобильные и железные дороги.

Процент ( % ) – одна сотая доля.
Промилле ( ‰ ) – одна тысячная доля.
Например: уклон при высоте 0,2 метра и протяженностью по горизонтали 4 метра будет равен 5 % (читается как – пять сотых) или 50 ‰ (читается как – пятьдесят тысячных), это значение также будет соответствовать приблизительно – 3 о.
Чертеж 1

Часто спрашивают, что означает уклон, на пример 0,05 – это соотношение высоты к длине горизонтального участка (0,2 м / 4 м = 0,05 – см. чертеж 1), которое при необходимости можно перевести в проценты или промилле, смотря что требуется.
Для определение угла уклона в процентах (%) (см. чертеж 1) необходимо: 0,2 м / 4 м х 100 = 5 %.
Для определение угла уклона в промилле (‰) необходимо: 0,2 м / 4 м х 1000 = 50 ‰.
Ту же величину уклона можно обозначить и как соотношение высоты к длине горизонтального участка – 1:20 (4 / 0,2 = 20).
Если требуется определить протяженность горизонтального участка, зная величину уклона в процентах и его высоту из чертежей, необходимо – 0,2 м / (5 % / 100) = 4 м.
Чтобы определить высоту уклона, зная величину уклона в процентах и протяженность участка из чертежей, необходимо – 5 % / 100 х 4 м = 0,2 м.
Аналогичным образом вычисляются размеры для угла уклона выраженного в промилле, только вместо деления на 100, выполняется деление на 1000.
Примечание: для того чтобы ввести на компьютере символ промилле (‰), необходимо включить NumLock, нажать клавишу Alt и удерживая ее набрать на цифровом блоке клавиатуры 0137, отпустить клавишу Alt после чего появится символ ‰.
Если требуется определить уклон с точностью до 1 градуса, нужно: 0,2 м / 4 м = 0,05. Полученное число – 0,05 необходимо найти в таблице tg (тангенсов) для углов. Приближенное значение в таблице – 0,0524, будет соответствовать углу 3 о (см. таблицу).
Полная таблица тангенсов для углов от 0о до 360о