N -й процентиль набора данных — это значение, которое отсекает первые n процентов значений данных, когда все значения отсортированы от наименьшего к наибольшему.
Например, 90-й процентиль набора данных — это значение, которое отсекает нижние 90 % значений данных от верхних 10 % значений данных.
Одним из наиболее часто используемых процентилей является 50-й процентиль, который представляет собой медианное значение набора данных: это значение, ниже которого 50% всех значений данных.
Процентили можно использовать для ответа на такие вопросы, как:
- Какой балл должен набрать учащийся по конкретному тесту, чтобы попасть в 10% лучших? Чтобы ответить на этот вопрос, мы должны найти 90-й процентиль всех оценок, то есть значение, которое отделяет нижние 90% значений от верхних 10%.
- Какой рост охватывает средние 50% роста учащихся в конкретной школе? Чтобы ответить на этот вопрос, мы должны найти 75-й процентиль роста и 25-й процентиль роста, которые являются двумя значениями, определяющими верхнюю и нижнюю границы для средних 50% роста.
Как рассчитать процентили в R
Мы можем легко вычислить процентили в R, используя функцию quantile() , которая использует следующий синтаксис:
квантиль (x, probs = seq(0, 1, 0,25))
- x: числовой вектор, процентили которого мы хотим найти
- probs: числовой вектор вероятностей в [0,1], который представляет процентили, которые мы хотим найти
Нахождение процентилей вектора
Следующий код иллюстрирует, как найти различные процентили для заданного вектора в R:
#create vector of 100 random values uniformly distributed between 0 and 500
data <- runif(100, 0, 500)
#Find the quartiles (25th, 50th, and 75th percentiles) of the vector
quantile (data, probs = c(.25, .5, .75))
# 25% 50% 75%
# 97.78961 225.07593 356.47943
#Find the deciles (10th, 20th, 30th, ..., 90th percentiles) of the vector
quantile (data, probs = seq(.1, .9, by = .1))
# 10% 20% 30% 40% 50% 60% 70% 80%
# 45.92510 87.16659 129.49574 178.27989 225.07593 300.79690 337.84393 386.36108
# 90%
#423.28070
#Find the 37th, 53rd, and 87th percentiles
quantile (data, probs = c(.37, .53, .87))
# 37% 53% 87%
#159.9561 239.8420 418.4787
Поиск процентилей столбца фрейма данных
Чтобы проиллюстрировать, как найти процентили определенного столбца фрейма данных, мы будем использовать встроенный набор данных iris :
#view first six rows of *iris* dataset
head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
В следующем коде показано, как найти значение 90-го процентиля для столбца Sepal.Length :
quantile (iris$Sepal.Length, probs = 0.9)
#90%
#6.9
Нахождение процентилей нескольких столбцов фрейма данных
Мы также можем найти процентили сразу для нескольких столбцов с помощью функции apply() :
#define columns we want to find percentiles for
small_iris<- iris[ , c('Sepal.Length', 'Sepal.Width', 'Petal.Length', 'Petal.Width')]
#use *apply()* function to find 90th percentile for every column
apply (small_iris, 2, function(x) quantile(x, probs = .9))
#Sepal.Length Sepal.Width Petal.Length Petal.Width
# 6.90 3.61 5.80 2.20
Поиск процентилей по группам
Мы также можем найти процентили по группам в R, используя функцию group_by() из библиотеки dplyr .
В следующем коде показано, как найти 90-й процентиль Sepal.Length для каждого из
три вида в наборе данных ириса:
#load *dplyr* library
library(dplyr)
#find 90th percentile of *Sepal.Length* for each of the three species
iris %>%
group_by(Species) %>%
summarise (percent90 = quantile(Sepal.Length, probs = .9))
# A tibble: 3 x 2
# Species percent90
#
#1 setosa 5.41
#2 versicolor 6.7
#3 virginica 7.61
В следующем коде показано, как найти 90-й процентиль для всех переменных по видам:
iris %>%
group_by(Species) %>%
summarise (percent90_SL = quantile(Sepal.Length, probs = .9),
percent90_SW = quantile(Sepal.Width, probs = .9),
percent90_PL = quantile(Petal.Length, probs = .9),
percent90_PW = quantile(Petal.Width, probs = .9))
# A tibble: 3 x 5
# Species percent90_SL percent90_SW percent90_PL percent90_PW
#
#1 setosa 5.41 3.9 1.7 0.4
#2 versicolor 6.7 3.11 4.8 1.51
#3 virginica 7.61 3.31 6.31 2.4
Визуализация процентилей
В R нет встроенной функции для визуализации процентилей набора данных, но мы можем относительно легко создать график для визуализации процентилей.
В следующем коде показано, как создать график процентилей для значений данных Sepal.Length из набора данных радужной оболочки :
n = length(iris$Sepal.Length)
plot((1:n - 1)/(n - 1), sort(iris$Sepal.Length), type="l",
main = "Visualizing Percentiles",
xlab = "Percentile",
ylab = "Value")
Дополнительные ресурсы
Руководство по apply(), lapply(), sapply() и tapply() в R
Создайте новые переменные в R с помощью mutate() и case_when()
В статистике процентили используются для понимания и интерпретации данных. n -ый процентиль набора данных – это значение, при котором n процентов данных находится ниже него. В повседневной жизни процентили используются для понимания таких значений, как результаты тестов, показатели здоровья и другие измерения. Например, 18-летний мужчина ростом шесть с половиной футов находится в 99-м процентиле своего роста. Это означает, что 99 процентов всех 18-летних мужчин имеют рост не более шести с половиной футов. С другой стороны, 18-летний мужчина ростом всего пять с половиной футов находится в 16-м процентиле для своего роста, то есть только 16 процентов мужчин его возраста имеют такой же рост или ниже.
Содержание
- Ключевые факты: процентили
- Что означает процентиль
- Формула процентиля
- Децили и общие процентили
- Применение процентилей
Ключевые факты: процентили
• Процентили используются для понимания и интерпретации данных. Они указывают значения, ниже которых находится определенный процент данных в наборе данных.
• Процентили можно рассчитать по формуле n = (P/100) x N, где P = процентиль , N = количество значений в наборе данных (отсортированных от наименьшего к наибольшему) и n = порядковый номер данного значения.
• Процентили часто используются для понимания результатов тестов и биометрических измерений.
Что означает процентиль
Не следует путать процентили с процентами. Последний используется для выражения долей от целого, а процентили – это значения, ниже которых находится определенный процент данных в наборе данных. На практике между ними есть существенная разница. Например, студент, сдающий сложный экзамен, может получить 75 процентов. Это означает, что он правильно ответил на каждые три из четырех вопросов. Однако ученик, набравший 75-й процентиль, получил другой результат. Этот процентиль означает, что учащийся получил более высокий балл, чем 75% других учащихся, сдавших экзамен. Другими словами, процентная оценка отражает, насколько хорошо студент сдал экзамен; оценка в процентиле отражает его успеваемость по сравнению с другими учениками.
Формула процентиля
Процентили для значений в данном задании набор данных можно рассчитать по формуле:
n = (P/100) x N
где N = количество значений в наборе данных, P = процентиль и n = порядковый ранг данного значения (со значениями в наборе данных, отсортированными от наименьшего к наибольшему). Например, возьмем класс из 20 учеников, набравших следующие баллы на последнем тесте: 75, 77, 78, 78, 80, 81, 81, 82, 83, 84, 84, 84, 85, 87, 87, 88, 88, 88, 89, 90. Эти оценки могут быть представлены в виде набора данных с 20 значениями: {75, 77, 78, 78, 80, 81, 81, 82, 83, 84, 84, 84, 85, 87, 87, 88, 88, 88, 89, 90}.
Мы можем найти результат 20-го процентиля, подставив известные значения в формулу и решив для n :
n = (20/100) x 20
n = 4
Четвертое значение в наборе данных – это балл 78. Это означает, что 78 обозначает 20-й процентиль; 20 процентов учащихся в классе получили 78 баллов или ниже.
Децили и общие процентили
Учитывая Набор данных, который был упорядочен по возрастающей величине, можно использовать медиана, первый квартиль и третий квартиль, разделив данные на четыре части. Первый квартиль – это точка, в которой одна четвертая данных находится ниже нее. Медиана расположена точно в середине набора данных, а половина всех данных находится под ним. Третий квартиль – это место, где три четверти данных находятся ниже него.
Медиана, первый квартиль и третий квартиль могут быть указаны в терминах. процентилей. Поскольку половина данных меньше медианы, а половина равна 50 процентам, медиана отмечает 50-й процентиль. Одна четвертая равна 25 процентам, поэтому первый квартиль отмечает 25-й процентиль. Третий квартиль отмечает 75-й процентиль.
Помимо квартилей, довольно распространенным способом упорядочения набора данных является дециль. Каждый дециль включает 10 процентов набора данных. Это означает, что первый дециль – это 10-й процентиль, второй дециль – это 20-й процентиль и т. Д. Децили позволяют разделить набор данных на большее количество частей, чем на квартили, без разделения набора на 100 частей, как в случае с процентилями.
Применение процентилей
Показатели процентилей имеют множество применений. В любое время, когда необходимо разбить набор данных на удобоваримые части, полезны процентили. Они часто используются для интерпретации результатов тестов, таких как результаты SAT, чтобы тестируемые могли сравнивать свои результаты с результатами других учащихся. Например, студент может получить на экзамене 90% баллов. Звучит довольно впечатляюще; однако этого становится меньше, когда результат 90 процентов соответствует 20-му процентилю, то есть только 20 процентов класса получили оценку 90 процентов или ниже.
Другой пример процентилей – графики роста детей. Помимо измерения физического роста или веса, педиатры обычно указывают эту информацию в виде процентилей. Процентиль используется для сравнения роста или веса ребенка с другими детьми того же возраста. Это позволяет использовать эффективные средства сравнения, чтобы родители могли знать, является ли рост их ребенка типичным или необычным..
Процентильная шкала определяет позицию определенного значения среди других данных в базе. Процентили в первую очередь используются для описания стандартных результатов тестов. Если же результат в стандартном тесте находится в 90-ом процентиле – это значит, что данный результат является выше чем 90% результатов показателей которые принимают участие в тесте. Другими словами, результат находится среди 10% самых высоких показателей, использованных в тесте.
Пример вычисления формулы процентиля в Excel
Перцентили (они же процентили или персентили) часто применяются в анализе данных. Они являются инструментом для оценки результатов на фоне целой группы данных. С их помощью можно, например, определить персентильную классификацию работника по его годовому обороту.
В программе Excel персентильную классификацию можно легко определить при использовании функции ПЕРСЕНТИЛЬ. Данная функция имеет 2 аргументы:
- Массив – диапазон исходных данных.
- К – значение найденного процентиля (чаще всего число в десятичной дроби диапазоном от 0 и до 1).
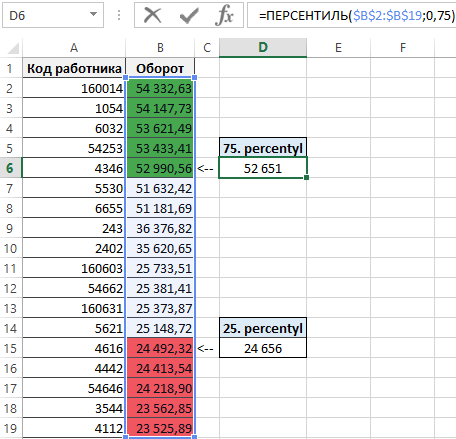
В примере, изображенном ниже на рисунке ячейка D6 содержит значение, которое является результатом вычисления ниже указанной формулы – число 0,75 процентиля данных диапазоне ячеек $B$2:$B$19:
Результат выше приведенной формулы указывает на то, что каждый работник, для которого годовые обороты превышают 52651 работает лучше, чем 75% всех остальных сотрудников.
Ячейка D15 содержит результат вычисления формулы, которая возвращает число 25 процентиля данных в диапазоне ячеек $B$2:$B$19.
Результат выше приведенной формулы указывает на то, что каждый работник, для которого годовой оборот не превышает 24656 находится среди 25% самых слабых сотрудников.
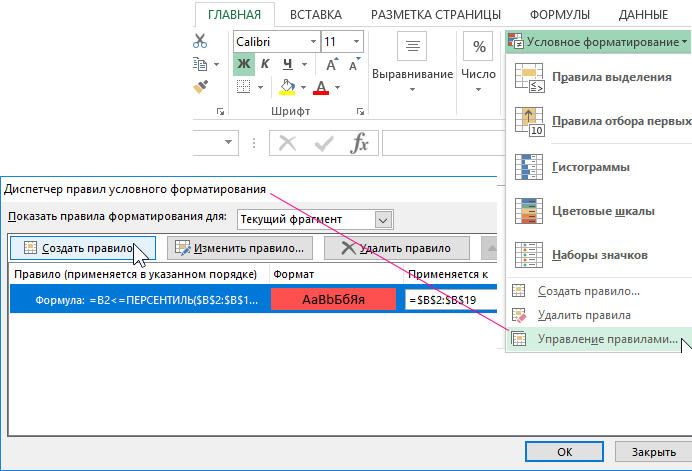
В данном примере используется условное форматирование использующие выше приведенные значения перцентилей. Значения больше чем 75 перцентиля выделены зеленым цветом, а значения меньше чем 25 перцентиля выделены красным цветом.
Два правила условного форматирования для одного диапазона ячеек в Excel
Чтобы создать описанную схему автоматического выделения ячеек по условию пользователя, выполните целый ряд следующих действий шаг за шагом:
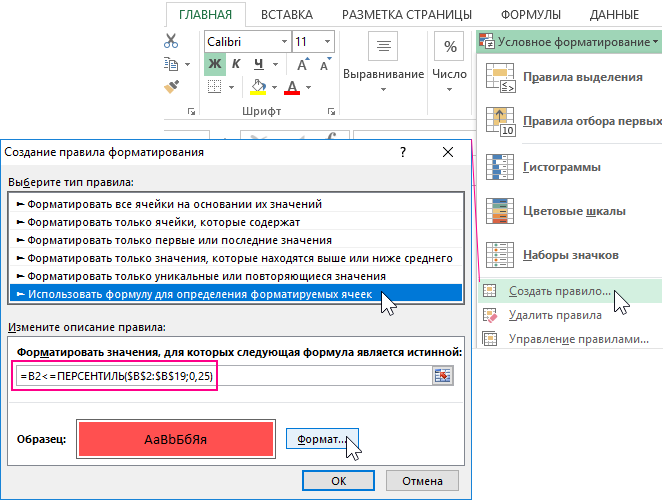
- Выделите диапазон ячеек B2:B19, которые будут автоматически выделятся цветом по условию формулы и выберите инструмент: «ГЛАВНАЯ»-«Условное форматирование»-«Создать правило». В результате чего высветится окно как ниже на рисунке:
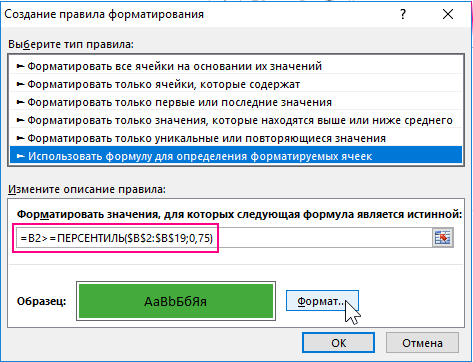
- В верхней части окна находится список опций. Выберите из него опцию «Использовать формулу для определения форматируемых ячеек». Данная опция служит для преобразования формата в ячейках в зависимости от их значений с помощью определенной формулы с логическим выражением. Если в результате вычисления формулы будет возвращено логическое значение ИСТИНА, тогда к текущей ячейке будет применено условное форматирование.
- В полю ввода введите формулу с логическим выражением, которая представлена ниже в этом разделе. Данная формула проверяет: если значение в целевой ячейке B2 меньше чем значение 25 перцентиля, тогда ей присваивается новый формат красного цвета фона для экспонирования.
=B2<=ПЕРСЕНТИЛЬ($B$2:$B$19;0,25)
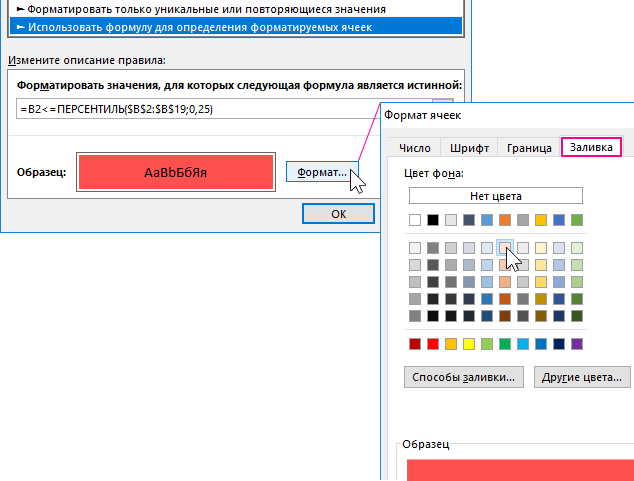
- Нажмите на кнопку «Формат». Появится окно «Формат ячеек», в котором находятся все опции для форматирования шрифта, границы и фона ячеек. Главное укажите красный фон заливки. После указания своих пользовательских опций форматирования нажмите на кнопки ОК на все открытых окнах чтобы подтвердить и применить все изменения.
- Снова выделите диапазон ячеек B2:B19 и на этот раз уже выберите инструмент «ГЛАВНАЯ»-«Условное форматирование»-«Управление правилами». В результате появится окно «Диспетчер правил условного форматирования», где находится наше первое правило. Для создания второго правила в этом же окне нажмите на кнопку «Создать правило».
- И снова в появившемся окне «Создание правила форматирования» выберите опцию «Использовать формулу для определения форматируемых ячеек».
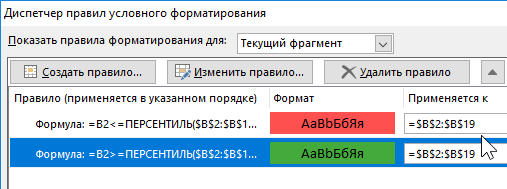
- В полю ввода формул на этот раз введите другую формул представленную на этом шаге. Данная формула проверяет: если значение в целевой ячейке B2 больше чем 75 персентиля, тогда применить для нее новый формат (зеленый фон).
- Снова нажмите на кнопку «Формат» где на этот раз следует указать зеленый фон заливки для ячеек. После чего нажмите на кнопку ОК для всех открытых окон.
В результате к одному и тому же диапазону ячеек одновременно применяется 2 правила условного форматирования. В следствии чего одна группа значений выделена красным цветом значение которых меньше 25% показателей, а вторая группа – зеленым >75%.
Random converter
- Калькуляторы
- Математика
Калькулятор для расчета процентилей
Этот калькулятор определяет P-й процентиль для исходного набора данных.
Пример: рассчитать 95-й процентиль для следующего набора данных: 3,77; 3,96; 4,26; 3,99; 3,79; 3,90; 4,30; 4,28; 4,16; 4,13; 4,03; 4,55; 4,56; 4,64; 4,85; 4,69; 4,47; 4,99; 5,14; 4,68; 4,91; 5,03; 4,71; 4,57; 4,94; 4,96; 4,97; 5,25; 4,72; 5,06; 4,78; 4,36; 5,00; 4,87; 4,53; 4,06; 4,00; 4,39.
Набор данных
Введите числа, разделенные символом «;». Максимальное число символов: 1000
Процентиль
P %
0 ≤ P ≤ 100
Поделиться ссылкой на этот калькулятор, включая входные параметры
Выходные данные
Определение 1
Определение 2
Определение 3
Введите набор данных и процентиль и нажмите кнопку Рассчитать.
Описание и примеры
Процентиль (в разных источниках и версиях программ называется также перцентиль, персентиль и центиль) — статистическая мера, указывающая значение, которое заданная случайная величина не превышает с указанной вероятностью. Например, фраза «95-й процентиль равен 7» означает, что 95% всех измеренных величин не достигает значения 7 и только 5% всех измеренных величин превышает это значение.
Когда провайдер услуг по размещению оборудования клиента в дата-центре, подключению его к электропитанию и каналам связи (колокации) выставляет ежемесячный счет на оплату услуг на основании 95-го процентиля (англ. bustable billing), это означает, что провайдер отсекает 5% пиковых значений трафика за месяц. Данный метод расчета позволяет пользователям иметь короткие периоды с очень высоким трафиком, возможно в десятки раз выше, чем «обычный» трафик, без дополнительной оплаты. Если счет выставляется ежемесячно, то пользователи могут иметь очень большой трафик (в пределах выделенной пропускной способности канала) в течение 24 × 30 × 0.05 = 36 часов без дополнительной оплаты. Пример такого трафика приводится ниже на рисунке.
Процентили также часто используются педиатрами для оценки роста детей по сравнению со статистическими данными Всемирной организации здравоохранения (ВОЗ) по весу, росту и окружности головы. Значение в процентилях позволяет сопоставить окружность головы, вес и рост ребенка с данными других детей. Например, 60-й процентиль роста означает, что девочка выше, чем 60% других девочек и ниже, чем 40% других девочек.
Определения
Интересно отметить, что, несмотря на то что мы часто используем процентили, универсального определения этого термина не существует. Здесь мы дадим три определения процентиля, одно простое и два не таких простых, так как в них используется линейная интерполяция. В литературе можно найти и другие определения процентиля. Вычисления по всем определениям дают похоже результаты, если количество величин в данных наблюдений велико. Если же количество величин невелико, то результаты могут довольно сильно отличаться.
Определение 1
В соответствии с первым определением, P-й процентиль списка из N упорядоченных по величине чисел (от меньших к большим) является наименьшее в списке число, которое больше, чем N процентов всех чисел исследуемого ряда. Например, для приведенного выше примера с ростом детей, 60-й процентиль означает рост, который больше, чем рост 60% других детей. В этом определении используется метод ближайшего ранга (англ. nearest rank method). Отметим, что любое значение, вычисленное по данному методу, будет всегда присутствовать в исходном наборе данных. Для расчета процентиля необходимо расположить значения в наборе данных по порядку от меньшего к большему и каждому значению из набора данных присвоить порядковый номер (ранг). Затем рассчитывается порядковый номер n для заданного процентиля по формуле:
Обозначение ⌈x⌉ означает, что результат округляется до ближайшего целого числа в бóльшую сторону. Такое округление называется также потолком (англ. ceiling). Например, результаты 2,2 и 2,7 будут округлены до 3. После этого значение процентиля v берется из отсортированных по порядку значений по порядковому номеру n.
100-й процентиль определяется как самое большое значение в исходном наборе данных.
Определение 2
В этом и следующем определениях для повышения точности используется линейная интерполяция между соседними значениями в наборе данных. Это делается вместо округления до целого значения в соответствии с первым определением. Имеется несколько вариантов этого метода. Здесь мы рассмотрим только два из них, которые используются в MS Excel, начиная с версии 2010, и в некоторых других программах. Дробный порядковый номер x рассчитывается по следующей формуле:
В версиях Excel старше 2010 эта формула используется в функции PERCENTILE.INC() (англ. версия), которая называется ПРОЦЕНТИЛЬ.ВКЛ() в русской версии. Эта функция, возвращающая результаты для всего диапазона значений 0 ≤ P ≤ 1. Если P = 1, PERCENTILE.INC() возвращает старшее значение набора данных, и если P = 0, то функция PERCENTILE.INC() возвращает младшее значение набора данных.
Для получения порядкового номера n результат вычисления по приведенной выше формуле округляется до ближайшего целого числа в меньшую сторону, то есть до числа, которое не превышает округляемую величину. Например, результаты 2,2 и 2,7 будут округлены до порядкового номера значения из входного набора данных n = 2.
Дробная часть {x} результата вычисления дробного порядкового номера x затем используется для дальнейшего расчета величины процентиля v по двум смежным значениям из исходного набора данных: значения с рассчитанным порядковым номером vn и следующего за ним большего значения vn+1:
где по определению дробной части
Ниже представлен пример расчетов по определению 2.
Определение 3
В соответствии с этим определением, для расчета the дробного порядкового номера x используется формула, отличающаяся от той, что использовалась по определению 2:
В версиях Excel старше 2010 эта формула используется в функции PERCENTILE.EXC() (англ. версия) и ПРОЦЕНТИЛЬ.ИСКЛ() (русская версия). Эта функция выдает ошибку, если P находится за пределами действительного диапазона для данного исходного набора данных. Это означает, что PERCENTILE.EXC() выполняет интерполяцию только в том случае, если значение указанного процентиля находится между двумя значениями в исходном наборе данных. Если функция не может выполнить интерполяцию, она возвращает ошибку. Например, если набор данных содержит 10 значений, нельзя получить результат для величины процентиля менее 10% и более 90%. В то же время, функция PERCENTILE.INC() по второму определению выдаст в этой ситуации действительный результат.
Как и в определении 2, результат округляется до ближайшего целого числа в меньшую сторону, то есть до числа, которое не превышает округляемую величину. Например, результаты 2,2 и 2,7 будут округлены до порядкового номера значения из входного набора данных n = 2.
Как и в определении 2, дробная часть {x} результата вычисления дробного порядкового номера x затем также используется для дальнейшего расчета величины процентиля v по двум смежным значениям из исходного набора данных: значения с рассчитанным порядковым номером vn и следующего за ним большего значения vn+1:
где по определению дробной части
Примеры вычисления процентилей
Рассмотрим для примера набор данных из N = 12 значений, представленный ниже в таблице 1. Для этого набора данных мы рассчитаем 40-й процентиль с помощью всех трех описанных выше методов. Значения набора данных упорядочены по величине от меньших к большим и каждому из них присвоен ранг от 1 до 12. Мы выполним расчет по трем определениям и сравним результаты наших расчетов.
Таблица 1. Набор данных для примера расчетов
| Значение | Ранг |
|---|---|
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 9 | 4 |
| 11 | 5 |
| 13 | 6 |
| 15 | 7 |
| 17 | 8 |
| 20 | 9 |
| 24 | 10 |
| 29 | 11 |
| 30 | 12 |
Расчет по методу 1
Определяем порядковый ранг n по определению 1 для 40-го процентиля:
Поскольку порядковый ранг n не является целым числом, мы округляем его до n = 5. По таблице 1, значение 40-го процентиля для n = 5 равно 11.
Расчет по методу 2
Этот метод является альтернативой методу ближайшего ранга. В нем используется линейная интерполяция между соседними значениями в наборе данных. Дробный порядковый номер x рассчитывается по следующей формуле:
Порядковый ранг n = 5. Дробная часть {x} = 0,4 результата вычисления дробного порядкового номера x затем используется для дальнейшего расчета величины процентиля v по двум смежным значениям из исходного набора данных: значения с рассчитанным порядковым номером vn и следующего за ним большего значения vn+1:
Расчет по методу 3
Этот метод является еще одной альтернативой методу ближайшего ранга. В нем используется линейная интерполяция между соседними значениями в наборе данных. Определяем дробный порядковый номер x:
Порядковый ранг n = 5. Дробная часть {x} = 0,2 результата вычисления дробного порядкового номера x затем используется для дальнейшего расчета величины процентиля v по двум смежным значениям из исходного набора данных: значения с рассчитанным порядковым номером vn и следующего за ним большего значения vn+1:
Просмотреть эти примеры в калькуляторе.
Метод оплаты по 95-му процентилю является стандартным промышленным методом измерения ширины полосы пропускания (пропускной способности) канала, используемым интернет-провайдерами и дата-центрами.
Использование процентилей
Метод оплаты трафика по 95-му процентилю
Метод оплаты по 95-му процентилю является стандартным промышленным методом измерения ширины полосы пропускания (пропускной способности) канала, используемым интернет-провайдерами и дата-центрами. Метод позволяет пользователям резко увеличивать трафик в течение 5% времени без увеличения стоимости оплаты услуг дата-центра. Метод основан на учете пиковой нагрузки и обычно используется для выставления счетов на оплату трафика для оборудования, установленного в дата-центрах.
На этом графике показана статистика загрузки канала провайдера, измеренная в течение 32 часов.
1. Средний исходящий трафик 2,9 мегабит в секунду (Мбит/с).
2. 95-й процентиль исходящего трафика 4,1 Мбит/с.
3. Максимальный исходящий трафик 5,7 Мбит/с.
4. Отфильтрованные пики трафика в расчете оплаты не учитываются.
В связи с тем, что 95-й процентиль равен 4,1 Мбит/с, в этом примере провайдер выставляет счет на 5 Мбит/с, так как у него принят шаг инкрементирования 1 Мбит/с. Это следует учитывать при определении стоимости услуг. Если бы 95-й процентиль был 3,9 Мбит/с, данный провайдер бы выставил счет на 4 Мбит/с.
Большинство Интернет-провайдеров используют пятиминутный интервал выборки для записи трафика, а затем рассчитывают использование по 95-му процентилю. Иногда провайдеры предлагают расчет по 90-му процентилю, чтобы привлечь больше клиентов. Средняя ширина канала во время интервала выборки представляет значение набора данных, которое рассчитывается как количество мегабит, переданное через порт связи и деленное на длину пятиминутного интервала выборки (300 секунд). В течение месячного периода, за который клиенту выписывается счет, таких значений в наборе данных для расчета будет около 9 тысяч. Затем этот набор данных сортируется, как описано выше, и 5% данных с самым большим трафиком отбрасываются. Значение 95-го процентиля и указывается в счете, но только в том случае, если оно превышает гарантированную пропускную способность канала, указанную в контракте и оплачиваемую клиентом в любом случае, даже если реальный трафик меньше этой пропускной способности, так как гарантированная пропускная способность обычно включена в стоимость эксплуатации арендованного или собственного сервера в дата-центре.
На основании этой модели в месячном счете не учитывается высокий трафик в течение 24 часа × 30 дней × 0.05 = 36 часов. Для определения 95-го процентиля обычно учитывают как исходящий, так и входящий трафик.
Клиенты дата-центра, оплачивающие его услуги по 95-му процентилю, могут платить за мегабит регулярно используемой пропускной способности и в то же время при необходимости могут резко увеличить трафик в течение коротких промежутков времени без финансовых последствий.
В этом примере месячного трафика клиент дата-центра оплачивает 95-й процентиль, что составляет всего около 4,5 Мбит/с. В то же время пиковый трафик равен 95 Мбит/с и он не учитывается при расчете оплаты, так как эти периоды короткие.
Индекс массы тела, вес и рост детей
Индекс массы тела (ИМТ) определяется как отношение массы тела в килограммах к квадрату роста в метрах и обычно выражается в кг/м² даже в тех нескольких странах, где все еще используют традиционные единицы измерения. Индекс массы тела позволяет характеризовать людей на группы с недостаточной массой (до 18,5 кг/м²), с нормальной массой (8,5–25 кг/м²), с избыточной массой (25–30 кг/м²) и ожирением (более 30 кг/м²).
Дети, у которых вес находится между 5-м и 85-м процентилем, относятся к группе с нормальным весом
У детей и подростков индекс массы тела определяется иначе. Для вычисления используется та же формула, что и для взрослых, но разделение на категории иное: вместо сравнения с несколькими фиксированными пороговыми значениями (недостаточная масса, нормальная масса, избыточная масса и ожирение), ИМТ сравнивают с величиной процентиля для детей того же пола, возраста и живущих в той же стране. Например, фраза «у девочки индекс массы тела равен 40-му процентилю» означает, что 40% девочек того же возраста имеют более низкий индекс массы тела. Считается, что дети с ИМТ ниже 5-го процентиля имеют недостаточную для их возраста массу тела, а те, у кого ИМТ находится между 5-м и 85-м процентилем имеют нормальную массу тела. Те, у кого ИМТ находится между 85-м и 94-м процентилем считаются имеющими избыточный вес и более 94-го процентиля — имеющими ожирение.
В педиатрии часто используют вес и рост ребенка для оценки его физического развития по сравнению с картами роста, в которых приводятся средние значения и процентили для детей различного возраста и пола для данной страны.
Конечно, индекс массы тела трудно назвать идеальным показателем. Он не учитывает множество факторов физического развития, таких как масса жировой ткани и мышц и тип телосложения. ИМТ может неправильно интерпретировать спортсмена с большой мышечной массой как имеющего избыточную массу тела и в то же время не отметить недостаток человека с излишней массой жировой ткани, который, несмотря на нормальный индекс массы тела относится к группе людей с повышенным риском сердечно-сосудистых заболеваний, диабета 2-го типа и преждевременной смерти.
Показатели в процентилях в образовании
Еще один привычный в западной системе образования пример — рейтинг выполнения тестов в форме процентиля, которые представляют собой процент результатов ниже заданного. Результаты выполнения контрольных работ в форме процентилей часто можно найти в отчетах, которые школы предоставляют родителям. Например, если ученик имеет ранг 60-го процентиля, это означает, что ученик учился лучше, чем 60% других учеников. Иными словами, этот результат лучше среднего и означает, что ученик учился неплохо. Результаты в процентилях для учеников или студентов, которые выполняют контрольную работу или сдают экзамен, позволяют сравнить успехи отдельного ученика с другими учениками в группе, для которой выполняется сравнение.
Результаты выполнения контрольных работ в форме процентилей часто можно найти в отчетах, которые школы предоставляют родителям.
Что такое процентиль?
Термин ″процентиль″ (percentile) часто встречается в зарубежной литературе про инвестиции и вообще в статистических исследованиях – одно из таких исследований я упоминал в этой статье. Другими вариантами русских названий являются ″персентиль″ и ″перцентиль″. Думаю, что небольшая известность термина в России не вполне заслужена, поскольку нередко именно в процентилях удобно выразить полученные результаты.
Процентиль это определенная часть выборки данных
Возьмем простой пример. Группа студентов из 200 человек пишет тест, состоящий из 100 вопросов. Проходной порог, когда тест считается сданным, составляет 2/3 правильных ответов, т.е. не менее 66. Что получается с точки зрения отдельного студента?
Допустим, Иван правильно ответил на 70 вопросов. Задачу он выполнил — тест засчитан. Результат каждого участника теста также сравнивается с числом 66: если правильных ответов больше, тест сдан. В результате формируется список сдавших и не сдавших: каждый студент проходил через это. Пока ничего нового.
Но задачу можно поставить и по-другому: нужно сравнить результаты студентов не с проходным баллом в 66 пунктов, а между собой. Зачем это нужно? В данном случае, например, для объективной оценки сложность теста, что достигается группировкой результатов.
Вернемся к Ивану, который получил 70 правильных ответов. Много это или мало по сравнению с остальными? Это и покажет процентиль.
Процентили делят всю выборку на определенные части. Например, пятый процентиль охватывает 5% объема выборки. Предположим, показатель Ивана равен пятому процентилю. Это означает, что Иван написал тест лучше, чем 5% студентов (10 человек из 200 получили от нуля до 70 баллов). Не густо, поскольку в этом случае остальные 190 человек набрали больше, чем 70. Значит, тест был очень легкий и порог в 66 баллов можно и повысить.
Но в том же самом тесте может быть и обратная ситуация: результат Ивана равен 90-ому процентилю. Это значит, что Иван написал тест лучше, чем 90% студентов. Или по другому: только 10% (20 человек) набрали более 70 правильных ответов. Следовательно, тест был весьма трудным. Преимущество метода еще и в том, что разбивкой на процентили можно сравнивать тесты с разным числом участников.
Функция Гаусса
Процентиль можно пояснить и на примере симметричного распределения Гаусса, которое часто встречается в статистике для оценки веса, роста и т.п. На рисунке выше показаны 25, 50, 75 и 100 процентили. Случаи 25 и 75-ого процентиля, включающие четверть и три четверти выборки соответственно, называются квартилями.
Чем более высок процентиль, тем больше данных он включает
Расчет процентиля в Excel
Процентиль несложно вычислить по формуле:
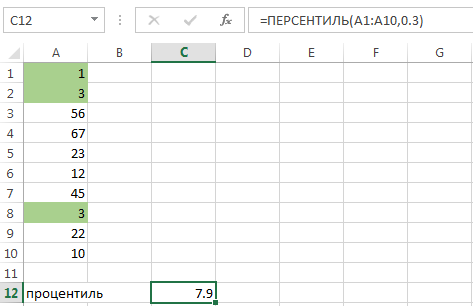
но проще обрабатывать массив данных одноименной функцией Excel. Для примера возьмем произвольную выборку полученных баллов и рассчитаем в ней процентили:
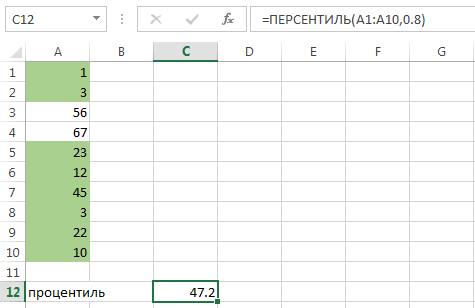
Функция PERCENTILE (ПЕРСЕНТИЛЬ) включает в себя ввод диапазона ячеек данных (А1:А10) и значения процентиля К, деленного на 100%. Т.е. в данном случае ввод 0.3 означает нахождение тридцатого процентиля. Смысл расчета: к 30-му процентилю будут относиться все результаты, меньше или равные 7.9.
Если мы хотим узнать процентиль участника, получившего 10 баллов, то это несложно сделать, варьируя значение К до тех пор, пока значение в ячейке С12 не станет близким 10. Получится примерно 34-ый процентиль. При увеличении процентиля в выборку попадает больше табличных значений:
Итого, в 80-ый процентиль попадает уже 8 табличных значений из 10, которые меньше или равны 47.2. При этом подчеркнуть результат можно диапазоном процентилей — например, между восьмидесятым и сотым. В этом случае значения будут лежать между 47.2 и 67 (максимальным числом выборки).