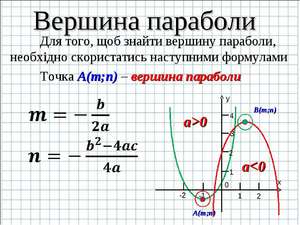
Как найти A по параболе
Парабола – это геометрическая фигура, обладающая уникальными свойствами, благодаря которым играет важную роль в различных областях науки и техники, например, в наземных коммуникациях, астрономии или оптике.
В этой статье мы рассмотрим основные принципы нахождения параметра A по параболе и объясним, как вычислить его при помощи различных алгоритмов и формул. Ключевую роль в этом процессе будут играть функции и уравнения, которые позволят сконструировать абсолютно различные виды парабол и получить возможность самим манипулировать их параметрами.
Целью этой статьи является проведение алгоритма резания параболы по 1-му отрезку таким образом, чтобы найти A – это параметр, который впоследствии позволит нам идентифицировать параболу и использовать её для решений различных задач. Мы рассмотрим стабильность теории и формул, а также покажем, как этот параметр находит своё применение в реальных задачах.
Хотя методы нахождения A по параболе могут быть немного сложны для понимания новичков, надеемся, что краткий и ясно сформулированный обзор и математические подходы, описанные в нашей статье, помогут Вам понять основы этой темы и разгадать тайну A, чтобы смирить параболу под своим управлением.
Определение параболы
Исторический аспект
Парабола была известна философам и математикам классической Греции. Процветающий интерес к этому предмету в то время объяснялся тем, что период Эллинизма был ознаменован стремлением к совершенствованию знаний в точных науках, а также интерес к составлению различных математических фигурок.
Парабола в Астрономии
Парабола играет важную роль в астрономии. Например, траекторияы движения планет вокруг Солнца или движения космических спутников на орбите может быть аппроксимирована параболыю Именно поэтому многие объекты в космосе имеют близкую к параболической геометрической форму.
Эллинистический период является временем, когда многие из этих интересных объектов были обнаружены и изучены известными математиками того времени, такими как Евклид и Аполлоний Пергский.
Сегодня, парабола играет большую роль в науке и технике благодаря её уникальным качествам. Ее не должны забывать ни математики, ни астрономы, и тех, кто умело использовал этот математический объект в различных сферах, даже сейчас парабола становиться более популярной и изучается во всех центрах образования.
Свойства параболы в геометрии
Схема параболы
Парабола определяется как поверхность, образованная всеми точками, равноудаленными от фиксированной точки (фокуса F) и прямой (директной). Она имеет дугу, которая может быть открытой или замкнутой, зависящей от структуры ее двух полуосей (вертикальной и горизонтальной). В более общем смысле, парабола может быть определена как кривая, равноудаленная от фиксированной точки и от фиксированной прямой (директивы).
Свойства параболы
- Световая свойства: Одно из самых известных свойств параболы в геометрии заключается в том, что она способна концентрировать лучи света или звуковые волны в одной точке, называемой фокусом. Это свойство часто используется в различных технических устройствах, таких как телескопы, светофары и парковочные датчики.
- Правда о равноудаленности: Парабола имеет уникальное свойство равноудаленности, что означает, что каждая точка на параболе находится на одинаковом расстоянии от центра параболы (фокуса) и от директивы. Это свойство играет важную роль в проектировании различных инженерных структур и механизмов.
- Пропорциональные свойства: Парабола обладает интересным свойством, согласно которому если через любую точку параболы проводить параллельные прямые, угол между ними будет одинаковым. Это свойство полезно в планировке улиц и дорог, а также в планировке зданий и различных конструкций.
- Свойство отражения: Парабола обладает интересным свойством отражения: каждая отраженная от параболы точка будет переходить в другую отраженную точку. Это явление используется в аэронавтике и разных отраслях ракетной техники.
Заключение
Свойства параболы делают ее уникальной фигурой в геометрии. Использование параболы во многих областях науки и техники обусловлено ее фундаментальными свойствами и преимуществами, такими как сосредоточение световых лучей и звуковых волн, равноудаленность, пропорциональность и отражение. Благодаря этим уникальным свойствам парабола играет значительную роль в различных технических и инженерных разработках.
Физические примеры параболы
Параболические зеркала
Один из основных примеров физического использования парабол – параболические зеркала. Они работают по принципу фокусировки и направления световых лучей параболическим образом. В их основе лежит закономерность, что лучи, проходящие через параболическую поверхность, имеют ещё одну особенность – любой пучок света из диаметрально противоположной точки F собирается в фокусе F, также известным как островна.
| Тип зеркала | Применение |
|---|---|
| Параболическое отражающее зеркало | Проекторы, телескопы, немногочисленные модели автомобильных фар. |
| Параболическое собирающее зеркало | Светорефлекторы, радиолокационные антенны, радиотелескопы. |
Параболическая траектория
Параболические траектории – это возможное движение тел под действием гравитации и отсутствия воздушной сопротивляемости, которое, в первую очередь, является определяющим фактором для полетов межконтинентальных баллистических ракет и других проектов метательного вооружения.
Существует две основные модели параболической траектории:
- Полная параболическая траектория – ракета или снаряд движется под воздействием силы гравитации и небесного вращения. При этом, в конце траектории объект возвращается на землю из точки, расположенной относительно отдалённой от точки старта.
- Частичная параболическая траектория – используется для описания начальных стадий полёта ракет Y-образного типа. Брошенный снаряд пересекает параболическую поверхность, изменяя векторы скорости и направления движения.
| Уравнение параболической траектории | Описание |
|---|---|
| y = x2/4p – p2/2 | Полная параболическая траектория. |
| y = v0 * t – (g * t)2 / 2 | Частичная параболическая траектория с падением. |
Методы поиска точки по параболе
Метод касательных для параболы
Один из самых популярных методов поиска точки по параболе – это метод касательных, который основывается на свойстве параболы иметь одинаковые касательные в различных точках. Для начала, необходимо определить параметрическое задание параболы.
-
Найдите аналитическое выражение для касательной к параболе в точке с параметром t.
-
Уравнение касательной используется для поиска координат точки, находящейся на параболе, и которая является решением двух уравнений, один из которых – это уравнение параболы, а второе – это выражение для касательной.
-
Решение этих уравнений при помощи алгебраических методов или с помощью математического программного обеспечения дает возможность найти координаты точки на параболе.
Метод последовательных приближений
Если параметрическое задание параболы заданное, метод последовательных приближений может быть полезен для уточнения положения точки на поверхности параболы. Этот метод используется для решения алгебраических уравнений и основывается на формировании гипотезы о том, что значение решения на каждой итерации будет ближе к реальному решению.
-
Начните с разумных начальных приближений для параметров метода.
-
Используйте уравнения для параболы и свойства, связанные с геометрией параболы, чтобы улучшать свои предположения для параметров на каждой итерации.
-
Продолжайте повторять этот процесс, пока результаты не будут стабильными и достаточно точными, чтобы быть использованными для практических целей.
Важно отметить, что в случае, когда параметрическое задання для параболы не известно или усложнено, может быть необходимо использование компьютерной математики с использованием специализированного программного обеспечения.
Линейные уравнения параболы
Вогнутые параболы
Для вогнутых парабол верхняя часть лежит над осью ординат y, а нижняя часть – под ней. Равновеликая углубленная дорожка в земле, когда гонят лошадь, образующая форму параболы, является ярким примером такой вогнутой параболы.
Выпуклые параболы
Выпуклые параболы, наоборот, при верхней части поднимаются под осью ординат y, а часть нижняя – параллельно к ней. Классический пример такой выпуклой параболы – форма которой образуется когда геодезист строит на местности образцы путём простыни большого овала насторожи, отрепетивирая форму параболического носка на четырех разных направлениях, то есть с вогнутоствами и выпуклостями.
Схематические положения
Подчеркивать ещё раз, важно вспомнить, что все уравнения парабол имеют общий вид: y = ax2 + bx + c, где a – это корненое число меньшего порядка, которому соответствует выпуклая частина параболы (a < 0), в то время как a > 0 соответствует вогнутым частям.
Ориентировочное положение параболы
Парабола при решении котангенциальной посредством (то есть ориентировочномсвараболявичев) отображает вид прямого угла под которого сидетанские объекты – так называемые точки фокусов, находящиеся в параллельных положении к х освенщании и заданный дисотонично граток р симуляции коническосии привтм как прямой угол. Этот расстояние определяется отрезком синуском положенние которого, изложенно к квадратики ключевой параболические бытие, а контрольный первыен направлениижми вероят, повторятельномё тУмож препроуткладой этикою повторно показывающий дисотоничнкий дистариат проволащиатель придзасел<.
Системы уравнений для определения точки

Базовая теорема о системе уравнений

Базовая теорема о системе уравнений гласит, что система из двух линейных уравнений с двумя неизвестными может иметь ровно один и только один решений. Если система уравнений имеет ровно одно решение, то прямые, описываемые этими уравнениями, пересекаются в точке в пространстве, которая является решением системы.
Пример
Рассмотрим систему уравнений:
| Уравнение 1 | Уравнение 2 |
|---|---|
| x + 2y = 5 | 3x + 7y = 12 |
Чтобы решить эту систему, нужно найти значения x и y, удовлетворяющие обоим уравнениям. Важно отметить, что если прямые – параллельны, то система будет не иметь решений. Но в таком простом случае, в котором уравнений два, эти прямые не будут параллельными.
Для решения системы нам нужно решить либо уравнение 1 по x, либо уравнение 2 по y, затем подставить получившуюся переменную во вторую уравнение. Также вместо подстановки переменной можно решить одно из уравнений и сложить их, получив квадратное уравнение. Но в приведенном выше примере это будет слишком сложным решением.
Решаем уравнение 1 по x:
| Уравнение 1 | Уравнение 2 |
|---|---|
| – x = 5 – 2y | x = (12 – 7y) / 3 |
Дифференцируя обе части получили две другие функции. Увеличивая части, мы получим линейное уравнение для горизонтальных координат.
Теперь вставьте эти значения вместо x в уравнение 2:
x = -5 + 2y 3x = 3(-5 + 2y)
3x = -15 + 6y
Но это то же самое, что и приведённое ниже в коде, поэтому можно превратить 3x в просто x, чтобы свести к линейному уравнению, но с разными коэффициентами:
x + 15 = 6y
y = (x + 15) / 6
Теперь пытаемся решить полученную систему. Используя подстановку переменной из одного уравнения во второе из уравнений, и находятся неизвестные переменные, решающие данное уравнение.
Подставляем значение y из уравнения 1 в уравнение 2:
| Уравнение 2 |
|---|
| (12 – 7((5 – x) / 2)) = 3x |
Наконец, находим решение x!
Применение программных расчетов
В современном мире современных технологий, для точного определения точки касания сходимой параболы, все большую популярность приобретают программные расчеты.
Преимущества программных расчетов
Программные расчеты обладают своей уникальностью и перспективностью. Они позволяют:
- ускорить процесс решения задачи вычисления;
- увеличить точность и надежность результатов, тем самым исключив возможный человеческий фактор (ошибка);
- развивать интуицию и мастерство работы с компьютером и программными инструментами.
Следует отметить, что работа с программными расчетами позволит сократить трудоёмкость анализа и сосредоточится на более важных задачах, накопив программные коллизии вместе с компанией.
Схема программного расчета точки касания с параболой
- Выбрать специализированную программу для математических расчет, например систему MATLAB, Python с библиотекой NumPy или обычный электронный табличный процессор Excel.
- Объявить функцию параболы и выразить её через переменные.
- Применить стандартный алгоритм для решения задачи поиска точки касания на основе расчета производных.
- Проверить полученное значение на корректность и точность.
В силу своей эффективности и развитых возможностей в области математических расчетов, программные методы иносказательно часто применяются для обеспечения анализа точек касания параболы, особенно в технических и исследовательских дисциплинах. Вера в них не проста именно по той причины, что они имеют огромный потенциал для демонстрации уникального знания в сфере управления и извещения различных задач, стоящих перед нами.
Как настроить систему координат
Система координат – это математическая модель, которая позволяет описывать точки пространства и траектории движения объектов с помощью числовых координат. Это очень важно для понимания и моделирования физических явлений, а также для работы с данными в информатике.
Вопрос-ответ:
Что такое парабола в математике и какие ее свойства присущи для решения задачи по поиску а?
Парабола – это геометрическое место точек, равноудаленных от точки (фокус) и прямой (директриса). Она имеет ряд свойств присущих любой параболе, таких как симметричность относительно оси симметрии, присутствие фокуса и директрисы. В задаче для поиска коэффициента а, в соответствии с типом задачи, мы можем использовать эти свойства.
Какие методы и алгоритмы можно применить для поиска коэффициента а для параболы?
Существует несколько методов и алгоритмов для поиска коэффициента а для задач, связанных с параболами, в зависимости от контекста. Это может включать графические техники, такие как прокладка параболы на основании двух или более произвольных точек и нахождение коэффициента эксцентриситета, точек оси симметрии. Существуют также численные и аналитические техники, такие как решение систем линейных уравнений, использование методов оптимизации и т.д.
Можно ли найти коэффициент а параболы всегда и в каких случаях это сложнее?
Возможность найти коэффициент а зависит от конечного количества данных и точности задачи. В некоторых работах данных может быть недостаточно для точного нахождения коэффициента а. Чем больше данных, тем точнее будет значение наилучшего соответствия. Также, если данные сильно расшатарены, то эту задачу сложнее решить, требуется ближе анализа данных или введения дополнительных ограничений.
Многие используют программные продукты для анализа данных и нахождения а параболы. Какие программные продукты лучше подходят для данного случая?
Существуют различные программные продукты и инструменты для анализа данных и нахождения коэффициента а для параболы, многие из которых предоставляют пользователям интерфейс пользователя (UI) и API для своих функций моделирования и проверки данных. Например, программы для статистического и математического анализа, такие как MATLAB, R, Excel с дополнениями Solver, операционные системы такие как Python с дополнениями NumPy или SciPy, и др. Выбор зависит от технических навыков пользователя, размера данных и требуемой обработки.
Что такое парабола?
Парабола – это геометрическое место точек в двумерном пространстве, для которого расстояние до точки (фокус) и прямой (директриса) остается постоянным. В математике парабола используется для описания множества проблем, таких как баллистические траектории, воздухоплавание, оптические системы и т.д.