Как найти абциссу точки в которой касательная - Сайт, где вы сможете решить свои вопросы

Всего: 23 1–20 | 21–23

Добавить в вариант

Прямая параллельна касательной к графику функции Найдите абсциссу точки касания.

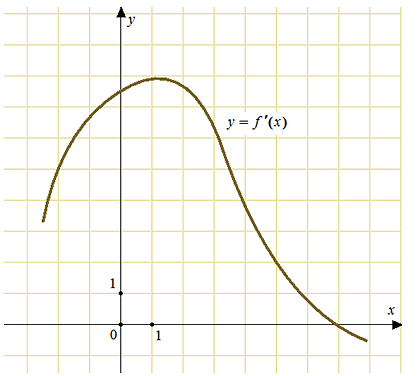
На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y  =  f(x) параллельна прямой y  =  6x или совпадает с ней.

Прямая параллельна касательной к графику функции Найдите абсциссу точки касания.

На рисунке изображён график y  =  f‘(x)  — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику функции y  =  f(x) параллельна прямой y  =  6 − 2x или совпадает с ней.

Прямая y  =  −5x + 2 параллельна касательной к графику функции y  =  x² + 5x + 3. Найдите абсциссу точки касания.

Всего: 23 1–20 | 21–23

Источник

Абсцисса точки касания. Задание В8 (2014)

Задание B9 (№ 27485) из Открытого банка заданий для подготовки к ЕГЭ по математике.

Прямая y=7x-5 параллельна касательной к графику функции y=x 2 +8x+6. Найдите абсциссу точки касания.

Чтобы выполнить это задание, нам нужно вспомнить теорию.

1. Прямая y=k₁x+b₁ параллельна прямой y=k₂x+b₂, если k₁=k₂. k₁ и k₂ – коэффициенты наклона прямых. Коэффициент наклона прямой равен тангенсу угла между этой прямой и положительным направлением оси ОХ: tg(a)=AB/OA

2. Геометрический смысл производной: значение производной функции у=f(x) в точке x₀ равнo угловому коэффициенту касательной, проведенной к графику функции у=f(x) в точке x₀, то есть tg(a)=k=f'(x₀), где k — угловой коэффициент касательной: Решение.
Так как касательная параллельна прямой y=7x-5, следовательно коэффициент наклона касательной, а, значит, производная функции в точке касания равны 7.
Найдем производную функции y=x 2 +8x+6:

Приравняем производную к 7:

В этом уравнении x₀ – абсцисса точки касания.
Решим уравнение:
2x₀+8=7
x₀=-0,5
Ответ: -0,5

Задание №6. Производная. Поведение функции. Первообразная — профильный ЕГЭ по Математике

Необходимая теория:

Задание 6 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих встречаются вопросы о первообразной.

Геометрический смысл производной

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .

Достроив до прямоугольного треугольника АВС, получим:

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой в точке

При значения выражений и равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

Из второго уравнения находим или Первому уравнению удовлетворяет только .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени получим:

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция возрастает.

Если , то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

возрастает	точка максимума	убывает	точка минимума	возрастает
0	0

5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.

Производная функции в точках максимума и минимума функции Таких точек на графике 5.

6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке производная функции положительна.

Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой

Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это

9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.

Значит, является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Функция для которой является производной, называется первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» – в этой статье

Решение задачи 6. Вариант 370

На рисунке изображен график функции y=f'(x) производной функции f(x). Найдите целочисленную абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой y=2x+12 или совпадает с ней.

По геометрическому смыслу производной

Значит мы ищем точку, где производная равна 2. Таких точек две, но т.к просят целочисленную, то это ( x=1 )

[spoiler title=”источники:”]

http://ege-study.ru/ru/ege/materialy/matematika/zadanie-7-profilnogo-ege-po-matematike-proizvodnaya-povedenie-funkcii-pervoobraznaya/

Решение задачи 6. Вариант 370

[/spoiler]

Источник

В этой статье мы разберем все типы задач на нахождение уравнения касательной.

Вспомним геометрический смысл производной: если к графику функции y=f(x) в точке x_0 проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке x_0 .

$k=tg{alpha}=f^{prime}(x_0)$

Возьмем на касательной произвольную точку с координатами ( x;y) :

И рассмотрим прямоугольный треугольник 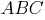ABC :

В этом треугольнике $tg{alpha}={BC}/{AB}={y-f(x_0)}/{x-x_0}=f{prime}(x_0)$

Отсюда ${y-f(x_0)}= f{prime}(x_0)(x-x_0)$

Или

$y=f(x_0)+ f{prime}(x_0)(x-x_0)$

Это и есть уравнение касательной, проведенной к графику функции y=f(x) в точке x_0 .

Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти f(x_0) и $f{prime}(x_0)$ .

Есть три основных типа задач на составление уравнения касательной.

1. Дана точка касания x_0

2. Дан коэффициент наклона касательной, то есть значение производной функции y=f(x) в точке x_0 .

3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.

Рассмотрим каждый тип задач.

1. Написать уравнение касательной к графику функции в точке x_0=1 .

а) Найдем значение функции в точке x_0=1 .

б) Найдем значение производной в точке x_0=1 . Сначала найдем производную функции y=f(x)

$f{prime}(x)=3x^2-4x$

$f{prime}(1)=3*1^2-4*1=-1$

Подставим найденные значения в уравнение касательной:

Раскроем скобки в правой части уравнения. Получим: y=-x+3

Ответ: y=-x+3 .

2. Найти абсциссы точек, в которых касательные к графику функции $y={1/4}x^4-{8/3}x^3 +{{15}/2}x^2$ параллельны оси абсцисс.

Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции $y={1/4}x^4-{8/3}x^3 +{{15}/2}x^2$ в точках касания равно нулю.

а) Найдем производную функции $y={1/4}x^4-{8/3}x^3 +{{15}/2}x^2$ .

$y{prime}=x^3-8x^2+15x$

б) Приравняем производную к нулю и найдем значения , в которых касательная параллельна оси :

Приравняем каждый множитель к нулю, получим:

Ответ: 0;3;5

3. Написать уравнения касательных к графику функции , параллельных прямой y=-x+3 .

Касательная параллельна прямой y=-x+3 . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.

Это второй тип задач на нахождение уравнения касательной.

Итак, у нас дана функция и значение производной в точке касания.

а) Найдем точки, в которых производная функции равна -1.

Сначала найдем уравнение производной.

Нам нужно найти производную дроби.

$({u/v})^{prime}={u{prime}v-v{prime}u}/{v^2}$

$y{prime}={(3x-4){prime}(2x-3)-(2x-3){prime}(3x-4)}/{(2x-3)^2}={3(2x-3)-2(3x-4)}/{(2x-3)^2}={-1}/{(2x-3)^2}$

Приравняем производную к числу -1.

${-1}/{(2x-3)^2}=-1$

2x-3=1 или 2x-3=-1

x_0=2 или x_0=1

б) Найдем уравнение касательной к графику функции в точке x_0=2 .

Найдем значение функции в точке x_0=2 .

(по условию)

Подставим эти значения в уравнение касательной:

б) Найдем уравнение касательной к графику функции в точке x_0=1 .

Найдем значение функции в точке x_0=1 .

(по условию).

Подставим эти значения в уравнение касательной:

Ответ:

4. Написать уравнение касательной к кривой $y=sqrt{8-x^2}$ , проходящей через точку A(3,1)

Сначала проверим, не является ли точка A(3,1) точкой касания. Если точка является точкой касания, то она принадлежит графику функции, и её координаты должны удовлетворять уравнению функции. Подставим координаты точки A(3,1) в уравнение функции.

$1<>sqrt{8-3^2}$ . Мы получили под корнем отрицательное число, равенство не верно, и точка A(3,1) не принадлежит графику функции и не является точкой касания.

Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания.

Найдем значение x_0 .

Пусть x_0 – точка касания. Точка A(3,1) принадлежит касательной к графику функции $y=sqrt{8-x^2}$ . Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:

$1=f(x_0)+ f{prime}(x_0)(3-x_0)$ .

Значение функции $y=sqrt{8-x^2}$ в точке x_0 равно $f(x_0)= sqrt{8-{x_0}^2}$ .

Найдем значение производной функции $y=sqrt{8-x^2}$ в точке x_0 .

Сначала найдем производную функции $y=sqrt{8-x^2}$ . Это сложная функция.

$f{prime}(x)={1/{2sqrt{8-x^2}}}*(8-x^2){prime}={{-2x}/{2sqrt{8-x^2}}}$

Производная в точке x_0 равна $f{prime}(x_0)={-2{x_0}}/{2sqrt{8-{x_0}^2}}$ .

Подставим выражения для f(x_0) и $f{prime}(x_0)$ в уравнение касательной. Получим уравнение относительно x_0 :

$1=sqrt{8-{x_0}^2}+{-2{x_0}}/{2sqrt{8-{x_0}^2}}(3-x_0)$

Решим это уравнение.

Сократим числитель и знаменатель дроби на 2:

$1=sqrt{8-{x_0}^2}+{-{x_0}}/{sqrt{8-{x_0}^2}}(3-x_0)$

Приведем правую часть уравнения к общему знаменателю. Получим:

$1={8-{x_0}^2-{x_0}(3-x_0)}/{sqrt{8-{x_0}^2}}$

Упростим числитель дроби и умножим обе части на ${sqrt{8-{x_0}^2}}$ – это выражение строго больше нуля.

Получим уравнение

${8-3x_0}={sqrt{8-{x_0}^2}}$

Это иррациональное уравнение.

Решим его. Для этого возведем обе части в квадрат и перейдем к системе.

$delim{lbrace}{matrix{2}{1}{{64-48{x_0}+9{x_0}^2=8-{x_0}^2} {8-3x_0>=0} }}{ }$

Решим первое уравнение.

$10{x_0}^2-48x_0+56=0$

$5{x_0}^2-24x_0+28=0$

Решим квадратное уравнение, получим

x_0=2 или x_0=2,8

Второй корень не удовлетворяет условию , следовательно, у нас только одна точка касания и её абсцисса равна .

Напишем уравнение касательной к кривой $y=sqrt{8-x^2}$ в точке x_0=2 . Для этого подставим значение x_0=2 в уравнение $y=sqrt{8-{x_0}^2}+{-2{x_0}}/{2sqrt{8-{x_0}^2}}(x-x_0)$ – мы его уже записывали.

Получим:

$y=sqrt{8-{2}^2}-{2*{2}}/{2sqrt{8-{(2)}^2}}(x-2)$

Ответ: y=-x+4
И.В. Фельдман, репетитор по математике.

Источник

Найдите абсциссу точки, в которой касательная

Дата: 2015-07-30

18215

Категория: Производная

Метка: ЕГЭ-№7

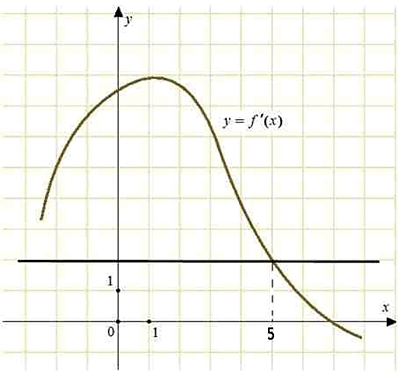
40130. На рисунке изображен график у=f′(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику у=f(x) параллельна прямой у = 2х–2 или совпадает с ней.

Значение производной в точке касания равно угловому коэффициенту касательной. Так как касательная параллельна прямой у = 2х–2 или совпадает с ней, она имеет такой же угловой коэффициент равный 2 и значит f′(x₀) = 2.

Осталось найти, при каких x производная принимает значение 2. Графически это точка пересечения графика производной с прямой f′(x₀) = 2

Искомая точка x₀ = 5

Ответ: 5

Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.

Источник

Тема 7.

Взаимосвязь функции и ее производной

Расчет касания двух графиков

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами – ЛЕГКО!

Подтемы раздела

взаимосвязь функции и ее производной

Решаем задачи

Прямая параллельна касательной к графику функции
. Найдите абсциссу точки касания.

Показать ответ и решение

Поскольку касательная параллельна прямой , то уравнение
касательной имеет вид , где . Поскольку прямая является
касательной, то это может быть только, если функции совпадают, но при этом
решение может быть только одно, то есть должно получиться уравнение,
дискриминант которого равен 0:

pict

Однако если квадратное уравнение имеет D = 0 , то его корень равен
x = − b-= − −-11-= 5,5
2a 2 , что и будет являться абсциссой точки касания.

Прямая параллельна касательной к графику функции 2
y = x + 7x− 6. Найдите абциссу точки
касания.

Показать ответ и решение

Пусть — абцисса точки касания. Тогда угловой коэффициент касательной в точке равен значению производной в этой
точке. Найдём производную функции f(x) в точке x0 :

Если прямые параллельны, то их угловые коэффициенты равны, значит,

Показать ответ и решение

Способ 1

Прямая и парабола касаются, если их функции совпадают только в одной
точке. Нужно приравнять функции, тогда получится квадратное уравнение,
которое будет иметь один корень при нулевом дискриминанте:

pict

Способ 2

В точке касания значения функций и их производных равны:

pict

Чтобы найти , подставим в квадратное уравнение:

pict

Прямая параллельна касательной к графику функции

2
f(x) = 3x + 7x+ 5

Найдите абсциссу точки касания.

Показать ответ и решение

Так как параллельные прямые имеют равные угловые коэффициенты и прямая имеет вид , то уравнение
касательной будет выглядеть как

где — некоторое число. Так как значение производной в точке касания равно угловому коэффициенту
касательной, то

Показать ответ и решение

Графики функций и касаются в точке (x0;y0) тогда и только тогда,
когда

{
f(x0) = g(x0) = y0
f′(x0) = g′(x0)

Тогда график функции и прямая y = x касаются в точке (x0;y0) тогда и только тогда,
когда

{ {
x02 + c = x0 = y0 0,25 + c = 0,5 = y0
2x = 1 ⇔ x = 0,5,
0 0

то есть ответ: 0, 5 .

Прямая параллельна касательной к графику функции . Найдите абсциссу
точки касания.

Найдите ординату точки касания графика функции и прямой π
y = x + 0, 5 − --
4 .

Показать ответ и решение

Если указанные графики касаются в точке (x0;y0) , то производные соответствующих функций равны в
точке :

π-
2sinx0 ⋅ cos x0 = 1 ⇔ sin2x0 = 1 ⇔ x0 = 4 + πk, k ∈ ℤ

При этом необходимо, чтобы при x = x0 значения соответствующих функций совпадали:

2 π-
sin x0 = x0 + 0,5 − 4 ,

но при π
x0 = --+ πk, k ∈ ℤ
4 имеем: , тогда

0,5 = x0 + 0,5 − π,
4

куда
подходит только π-
x0 = 4 .

Таким образом, для касания указанных графиков в точке (x0;y0) необходимо, чтобы было
выполнено π-
x0 = 4 . Но этого и достаточно, ведь при совпадают значения функций и их
производных.