Как найти абсциссу точки пересечения прямых
На чтение 2 мин Просмотров 822 Опубликовано 07.05.2019
Содержание
- Ответ или решение 1
- Другие вопросы из категории
- Читайте также
Ответ или решение 1
![]()
Точка пересечения графиков имеет координаты одинаковые для обоих графиков, значит функции в этой точке будут равны и следует их приравнять и решить полученное уравнение относительно переменной х, так как стоит задача найти абсциссу точки пересечения. Для этого второе уравнение приведем в стандартный вид (у выразим через х):
у = (4 * х — 12) / 2 = 2 * х — 6;
Ответ: абсциссой точки пересечения является х = 2.
![]()
Выражаем из первого уравнения у:у=(6-х)÷3 Второе уравнение у=0 приравниваем: (6-х)÷3=0 х=6

Если ответ по предмету Математика отсутствует или он оказался неправильным, то попробуй воспользоваться поиском других ответов во всей базе сайта.
![]()
![]()
Надо составить систему уравнений:
выражаем отсюда х, он равен х=3у+5
подставляем во второе выражение:
теперь подставляем найдённое значение у в первое выражение
Другие вопросы из категории
Помогите Маржан с помощью двух вёдер вместимостью 5 литров и 9 литров набрать из реки 6 литров воды
влито 75% раствора серной кислоты?
больше.Чему ровна расстояние между пристаней?
Читайте также
прямых MN и KL; б) прямой MN с осью координат; в) прямой KL с осью абцисс.
Помогите, пожалуйста. Срочно надо)
принадлежит большей дуге окружности? Ответ дайте в градусах.
2.найдите значение выражения
3. Прямая y=2x+5 является касательной к графику функции y=c-2x-x2
найдите абсциссу точки касания.
4.на столе лежат цветные ручки : три синие,две красные,шесть черных и четыре зеленых. В школе разрешают писать либо синей,либо черной ручкой. Коля случайно берет со стола ручку. С какой вероятностью выбранная ручка подойдет для школы?
2) Даны уравнения сторон треугольника. Найдите координаты вершин этих точек.
Найдите уравнение прямой, проходящей через точку пересечения прямых. 3x-2y-7 = 0 и x + 3y-6 = 0 и отсекает на оси абсцисс отрезок, равный 3
В статье покажем, как найти точку пересечения отрезков. Это совсем не тривиальная задача, хотя на первый взгляд она кажется именно такой. Поиск пересечения двух отрезков имеет множество полезных приложений. Например, с помощью него можно определить пересекаются ли фигуры на плоскости или нет.
Начальные условия
На протяжении всей статьи мы будем писать метод, который ищет пересечение двух отрезков на плоскости и даёт ответ: пересекаются они или нет.
Входными параметрами метода являются 4 точки — точки начала и конца двух отрезков.
Точка — это экземпляр класса Point. Она имеет два параметра: значение абсциссы (x) и значение ординаты (y). Класс Point:
|
public class Point { double x, y; public Point (double newX, double newY) { x = newX; y = newY; } } |
Поиск пересечения двух отрезков
Метод, который будет искать пересечение двух отрезков, назовём: checkIntersectionOfTwoLineSegments. Он возвращает true, если отрезки пересекаются и false в противном случае.
|
private boolean checkIntersectionOfTwoLineSegments(Point p1, Point p2, Point p3, Point p4) { |
Его аргументы — это четыре точки. p1 и p2 — начало и конец первого отрезка, а p3 и p4 — соответственно начало и конец второго отрезка.
Мы подразумеваем, что начальная точка находится левее конечной относительно оси абсцисс (оси X). Также возможен вариант, когда точки имеют одинаковую абсциссу, то есть отрезок является вертикальным.
В общем случае должно выполняться условие: p1.x <= p2.x и p3.x <= p4.x.
Но если вдруг программист задал точки отрезка не по порядку, мы расставим их, как следует:
|
if (p2.x < p1.x) { Point tmp = p1; p1 = p2; p2 = tmp; } if (p4.x < p3.x) { Point tmp = p3; p3 = p4; p4 = tmp; } |
После того, как точки отрезков расставлены по порядку, мы можем сразу проверить наличие потенциального интервала, на котором отрезки могут пересекаться.
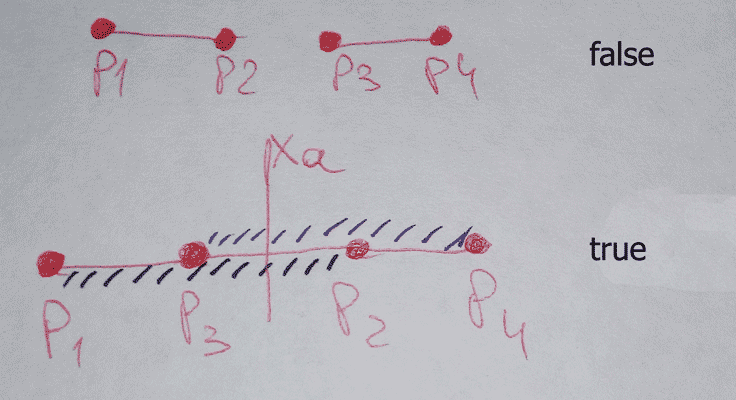
Если конец первого отрезка находится левее начала правого отрезка (по оси X), то отрезки точно не имеют точки пересечения.
|
if (p2.x < p3.x) { return false; } |
Потенциальный интервал пересечения имеется. Идём далее.
Оба отрезка вертикальные (частный случай)
Мы отдельно от общего решения будем рассматривать вертикальные отрезки, поскольку тангенс 90 градусов не определён, и, тем самым, мы в общем решении избежим деления на ноль.
Сначала обсудим такой частный случай, когда оба отрезка являются вертикальными.
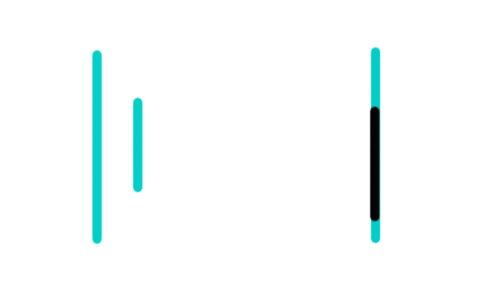
Непересекающиеся (слева) и пересекающиеся (справа) вертикальные отрезки
Отрезок вертикальный, тогда и только тогда, когда абсциссы его обеих точек равны.
В случае проверки условия вертикальности обоих отрезков, выражение (p1.x — p2.x == 0) && (p3.x — p4.x == 0) должно быть истинным.
Два отрезка будут иметь точку пересечения в том случае, когда их абсцисса одинакова (для этого достаточно условия p1.x == p3.x) и они имеют общую часть по оси ординат (общий Y); в противном случае делаем вывод, что они не пересекаются.
Составить условие для проверки существования общего Y мысленно довольно сложно. Поэтому мы поступим проще: составим условие для проверки того, что отрезки не имеют общего Y и возьмём от него отрицание.
Напишем код на Java для всего вышесказанного:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
//если оба отрезка вертикальные if((p1.x – p2.x == 0) && (p3.x – p4.x == 0)) { //если они лежат на одном X if(p1.x == p3.x) { //проверим пересекаются ли они, т.е. есть ли у них общий Y //для этого возьмём отрицание от случая, когда они НЕ пересекаются if (!((Math.max(p1.y, p2.y) < Math.min(p3.y, p4.y)) || (Math.min(p1.y, p2.y) > Math.max(p3.y, p4.y)))) { return true; } } return false; } |
Решаем систему уравнений и находим точку пересечения отрезков
Каждый отрезок — это часть прямой. Уравнение прямой в общем случае имеет всем нам знакомый вид:
A * x + b = y (1)
Для случая с двумя прямыми получаем систему уравнений (2):
A1 * x + b1 = y
A2 * x + b2 = y
Решив её, мы получим координаты точки (x, y) пересечения двух прямых. Но у нас нет значений параметров A1, A2, b1 и b2. Найдём их.
Параметр A — это тангенс угла между прямой и осью X. Вычислим его по определению: тангенс — это отношение противолежащего катета к прилежащему.
A1 = (p1.y — p2.y) / (p1.x — p2.x) (3)
A2 = (p3.y — p4.y) / (p3.x — p4.x) (4)
Параметр b найдём для каждой прямой, выразив его из уравнений (2):
b1 = p1.y — A1 * p1.x = p2.y — A1 * p2.x (5)
b2 = p3.y — A2 * p3.x = p4.y — A2 * p4.x (6)
Теперь, зная все параметры, решим систему уравнений (2). Найдём абсциссу точки пересечения прямых (обозначим её Xa):
Xa = (b2 — b1) / (A1 — A2) (7)
Как практически в любом решении и, к сожалению, здесь тоже есть частные случаи, о которых следует поговорить отдельно.
При нахождении параметров A1 и A2 (уравнения 3, 4) может возникнуть исключительная ситуация деления на ноль. Такое возможно, когда один из отрезков вертикальный.
Один из отрезков вертикальный (частный случай)
Сначала рассмотрим ситуацию, когда первый отрезок вертикальный.
Предположим, что x вертикального отрезка является абсциссой точки пересечения отрезков: Xa = p1.x. Параметры A2 и b2 найдём, как это было описано выше. Также вычислим ординату предполагаемой точки пересечения (используя формулу 1):
Ya = A2 * Xa + b2
Найденная точка (Xa, Ya) будет являться точкой пересечения двух отрезков только в том случае, если p3.x <= Xa <= p4.x и Ya входит в интервал вертикального отрезка по Y. В противном случае — отрезки не пересекаются.
Оформим всё вышесказанное в этом подпункте в виде кода:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
//если первый отрезок вертикальный if (p1.x – p2.x == 0) { //найдём Xa, Ya – точки пересечения двух прямых double Xa = p1.x; double A2 = (p3.y – p4.y) / (p3.x – p4.x); double b2 = p3.y – A2 * p3.x; double Ya = A2 * Xa + b2; if (p3.x <= Xa && p4.x >= Xa && Math.min(p1.y, p2.y) <= Ya && Math.max(p1.y, p2.y) >= Ya) { return true; } return false; } |
Когда второй отрезок является вертикальным — это тоже частный случай, который должен быть рассмотрен. Аналогично:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
//если второй отрезок вертикальный if (p3.x – p4.x == 0) { //найдём Xa, Ya – точки пересечения двух прямых double Xa = p3.x; double A1 = (p1.y – p2.y) / (p1.x – p2.x); double b1 = p1.y – A1 * p1.x; double Ya = A1 * Xa + b1; if (p1.x <= Xa && p2.x >= Xa && Math.min(p3.y, p4.y) <= Ya && Math.max(p3.y, p4.y) >= Ya) { return true; } return false; } |
Оба отрезка невертикальные (общий случай)
Сначала найдём параметры A1, A2, b1 и b2 по формулам 3, 4, 5, 6.
Затем проверим равенство A1 == A2. Если оно верно, то значит отрезки параллельны, а следовательно не пересекаются — возвращаем false. Кроме того, данная проверка позволяет избежать деления на ноль при нахождении Xa в выражении 7.
Далее вычисляем Xa (по формуле 7).
После необходимо проверить входит ли Xa в пересечение проекций обоих отрезков на ось X. Входит — возвращаем true, не входит — false.
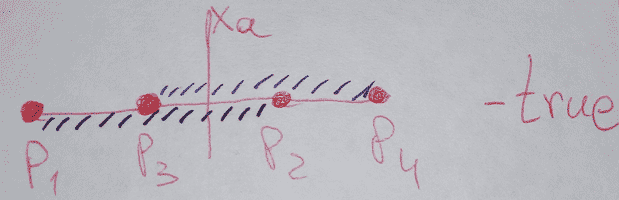
Код на Java:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
//оба отрезка невертикальные double A1 = (p1.y – p2.y) / (p1.x – p2.x); double A2 = (p3.y – p4.y) / (p3.x – p4.x); double b1 = p1.y – A1 * p1.x; double b2 = p3.y – A2 * p3.x; if (A1 == A2) { return false; //отрезки параллельны } //Xa – абсцисса точки пересечения двух прямых double Xa = (b2 – b1) / (A1 – A2); if ((Xa < Math.max(p1.x, p3.x)) || (Xa > Math.min( p2.x, p4.x))) { return false; //точка Xa находится вне пересечения проекций отрезков на ось X } else { return true; } |
Написание метода для нахождения точки пересечения двух отрезков завершено.
Скачать его полностью в текстовом файле:
Скачать код метода
Приложения
Написанный в статье метод можно использовать для определения пересечения плоских фигур. Фигуры должны состоять из замкнутой ломаной линии, то есть состоять из отрезков. Это могут быть треугольники, прямоугольники, либо другие произвольные фигуры.
Чтобы определить пересечение двух фигур, нужно проверить пересечение каждой стороны одной фигуры с каждой стороной другой фигуры. Если хотя бы одна сторона с чем-то пересекается — значит и фигуры пересекаются.
Например, если нужно определить пересекаются ли прямоугольники, то необходимо будет выполнить 16 проверок.
Спасибо за прочтение статьи!
Ответы Mail.ru
Домашние задания
Русский язык
Литература
Математика
Алгебра
Геометрия
Иностранные языки
Химия
Физика
Биология
История
Обществознание
География
Информатика
Экономика
Другие предметы
Вопросы – лидеры.
Помогите с впр!
1 ставка
Помагите с математикой
1 ставка
При каких значениях n, 7n + 5 кратно 8?
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Найдите абсциссу точки пересечения отрезков ав и сд.
AKIKAT OMIRZAK
Ученик
(101),
на голосовании
2 года назад
Найдите абсциссу точки пересечения отрезков ав и сд.
ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО ЗАРАНИЕ СПАСИБО

Голосование за лучший ответ
Петрович
Гуру
(4652)
3 года назад
(-3,-2)
Похожие вопросы
Абсцисса – точка – пересечение – график
Cтраница 1
Абсцисса точки пересечения графиков является решением уравнения.
[1]
Ордината и абсцисса точки пересечения графиков х, иг и лг, д u ( r – t, ) / 2 дают время и координату точки соударения частиц: f ( 2д – иг, ) / и, л 2а – vtl.
[2]
Очевидно, что абсциссы точек пересечения графиков этих функций и будут действительными корнями уравнения.
[3]
Частотам стационарных движений соответствуют абсциссы точек пересечения графиков характеристики двигателя L ( Я) и момента S ( Q) сил сопротивления вращению ротора. Из рассмотрения графиков следует, что при квазистатическом увеличении мощности не реализуется участок TRH, а при уменьшении – участок RTP. Срывы колебаний при прямом и обратном прохождении через резонанс показаны стрелками.
[4]
Найдите с точностью до 10 – 3 абсциссу точки пересечения графиков функций ycosx и у 1х, определив интервал, которому принадлежит точка пересечения графиков функций.
[5]
Очевидно, что такие значения аргумента х являются абсциссами точек пересечения графиков этих двух функций.
[6]
Действительные корни уравнения можно также определить графически, как абсциссы точек пересечения графика функции yf ( x) с осью Ох. Если уравнение не имеет близких между собой корней, то этим способом его корни легко отделяются.
[7]
На рис. 188 видно, что пределами интегрирования являются абсциссы точек пересечения графиков данных функций.
[8]
V) 0 строят график функции v f ( х); абсциссы точек пересечения графика с осью х или абсциссы точек касания графика с осью х дают вещественные корни уравнения.
[9]
Для графического решения уравнения / ( дс) 0 строят график функции / (); абсциссы точек пересечения графика с осью х или абсциссы точек касания графика с осью х дают вещественные корни уравнения.
[10]
Для графического решения уравнения / ( jc) 0 строят график функции у / ( х); абсциссы точек пересечения графика с осью х и абсциссы точек касания графика с осью х дают вещественные корни уравнения.
[11]
При графическом приближенном решении уравнений корни получаются довольно грубо, так как невозможно осуществить с высокой точностью измерение абсцисс точек пересечения графика с осью абсцисс.
[12]
Один из способов решения уравнения ( 1), когда функция f ( х) – многочлен выше второй степени – это графический: корнями уравнения ( 1) будут абсциссы точек пересечения графика функции с осью Ох.
[13]
Согласно формуле (15.6), уравнение касательной записывается в виде у – уо / ( о) ( – хц), где ( хо; у0) – точка касания. Абсцисса дго точки пересечения графика с осью Оу равна 0, а ордината у / ( 0) – 2; значит, ( 0; – 2) – точка касания.
[14]
Значит, даннсе уравнение имеет бес-конечное множество корней. Этот корень является абсциссой точки пересечения графиков.
[15]
Страницы:
1
2
Как найти точку пересечения отрезков
Простейшие геометрические примитивы, такие как точки, прямые, плоскости, фигурируют в большинстве научных и инженерных задач, связанных с проектированием, графическими построениями, визуализацией и машинной графикой. Подобные задачи, как правило, решаются путем применения принципа декомпозиции и сведения их к последовательностям элементарных действий с геометрическими примитивами. Так, сложные трехмерные объекты в машинной графике аппроксимируются полигонами, а те в свою очередь – треугольниками, треугольники задаются отрезками ребер, которые определяются их конечными точками. Именно поэтому понимание того, как решить простейшие геометрические задачи, например того, как найти точки пересечения отрезков, весьма важно для любого технического специалиста.
Вам понадобится
- Лист бумаги, ручка.
Инструкция
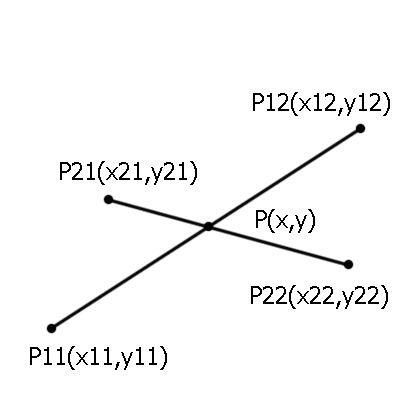
Подготовьте исходные данные. В качестве исходных данных удобно принять отрезки, заданные координатами точек их концов в декартовой системе координат. В данной системе координатные оси ортогональны и имеют одинаковый линейный масштаб. Допустим, имеются отрезки O1 и O2. Отрезок O1 задан точками с координатами P11(x11, y11) и P12(x12, y12), а отрезок O2 задан точками с координатами P21(x21, y21) и P22(x22, y22).
Составьте уравнения прямых, к которым принадлежат отрезки O1 и O2. Уравнение прямой отрезка O1 будет иметь вид: K1*x+d1-y=0. Уравнение прямой отрезка O2 будет иметь вид: K2*x+d2-y=0. Здесь K1=(y12-y11)/(x12-x11), d1=(x12*y11-x11*y12)/(x12-x11), K2=(y22-y21)/(x22-x21), d2=(x22*y21-x21*y22)/(x22-x21).
Решите систему уравнений, состоящую из уравнений прямых, составленных на предыдущем шаге. Вычтя из первого уравнения второе, можно получить: K1*x-K2*x+d1-d2=0. Откуда x=(d2-d1)/(K1-K2). Подставив x в первое уравнение, получим: y=K1*(d2-d1)/(K1-K2)+d1. Значения K1, K2, d1, d2 известны. Точка P(x, y) является пересечением прямых, на которых лежат исходные отрезки.
Проверьте, является ли точка с найденными координатами точкой пересечения именно отрезков, а не прямых, на которых они лежат. Для этого убедитесь, что координата точки x принадлежит одновременно диапазонам значений [x11,x12] и [x21,x22], а координата y принадлежит одновременно диапазонам [y11,y12] и [y21,y22].
Видео по теме
Источники:
- как пересекаются два отрезка
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
