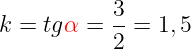Как найти абсциссу точки пересечения прямых
На чтение 2 мин Просмотров 832 Опубликовано 07.05.2019
Содержание
- Ответ или решение 1
- Другие вопросы из категории
- Читайте также
Ответ или решение 1
Точка пересечения графиков имеет координаты одинаковые для обоих графиков, значит функции в этой точке будут равны и следует их приравнять и решить полученное уравнение относительно переменной х, так как стоит задача найти абсциссу точки пересечения. Для этого второе уравнение приведем в стандартный вид (у выразим через х):
у = (4 * х — 12) / 2 = 2 * х — 6;
Ответ: абсциссой точки пересечения является х = 2.
Выражаем из первого уравнения у:у=(6-х)÷3 Второе уравнение у=0 приравниваем: (6-х)÷3=0 х=6
Если ответ по предмету Математика отсутствует или он оказался неправильным, то попробуй воспользоваться поиском других ответов во всей базе сайта.
Надо составить систему уравнений:
выражаем отсюда х, он равен х=3у+5
подставляем во второе выражение:
теперь подставляем найдённое значение у в первое выражение
Другие вопросы из категории
Помогите Маржан с помощью двух вёдер вместимостью 5 литров и 9 литров набрать из реки 6 литров воды
влито 75% раствора серной кислоты?
больше.Чему ровна расстояние между пристаней?
Читайте также
прямых MN и KL; б) прямой MN с осью координат; в) прямой KL с осью абцисс.
Помогите, пожалуйста. Срочно надо)
принадлежит большей дуге окружности? Ответ дайте в градусах.
2.найдите значение выражения
3. Прямая y=2x+5 является касательной к графику функции y=c-2x-x2
найдите абсциссу точки касания.
4.на столе лежат цветные ручки : три синие,две красные,шесть черных и четыре зеленых. В школе разрешают писать либо синей,либо черной ручкой. Коля случайно берет со стола ручку. С какой вероятностью выбранная ручка подойдет для школы?
2) Даны уравнения сторон треугольника. Найдите координаты вершин этих точек.
Найдите уравнение прямой, проходящей через точку пересечения прямых. 3x-2y-7 = 0 и x + 3y-6 = 0 и отсекает на оси абсцисс отрезок, равный 3
Тема 10.
Задачи на свойства графиков функций
10
.
09
Комбинации нескольких графиков
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
задачи на свойства графиков функций
Решаем задачи
На рисунке изображены графики двух линейных функций, пересекающиеся в точке Найдите абсциссу точки
Показать ответ и решение
Найдем уравнения прямых.
Определим коэффициенты и
для нижней прямой. Найдём
как тангенс угла наклона прямой:
Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом
Подставим точку
Значит, первая функция имеет вид
Теперь определим коэффициенты и
для верхней прямой. Найдём
как тангенс угла наклона прямой:
Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом
Подставим точку
Значит, вторая функция имеет вид
Теперь найдем абсциссу точки пересечения двух прямых.
На рисунке изображены графики двух линейных функций, пересекающиеся в точке Найдите абсциссу точки
Показать ответ и решение
Найдем уравнения прямых.
Определим коэффициенты и
для нижней прямой. Найдём
как тангенс угла наклона прямой:
Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом
Подставим точку
Значит, первая функция имеет вид
Теперь определим коэффициенты и
для верхней прямой. Найдём
как тангенс угла наклона прямой:
Чтобы найти подставим одну из точек на прямой в уравнение с уже расcчитанным коэффициентом
Подставим точку
Значит, вторая функция имеет вид
Теперь найдем абсциссу точки пересечения двух прямых.
На рисунке изображены графики двух линейных функций. Найдите ординату
точки пересечения графиков.
Показать ответ и решение
Способ 1
Найдём уравнение функции график которой из себя представляет убывающую прямую, на которой отмечены
точки
Найдём угловой коэффициент:
Получим уравнение функции
Найдём значение подставив в уравнение точку
Получится уравнение
Найдём уравнение функции график которой из себя представляет возрастающую прямую, на которой
отмечены точки
Найдём угловой коэффициент:
Получим уравнение функции
Найдём значение подставив в уравнение точку
Получится уравнение
Теперь решим уравнение
Тогда ордината точки пересечения прямых равна
Способ 2
По картинке видим, что целые точки и
принадлежат графику первой прямой
поэтому можем
составить систему из двух уравнений:
Также целые точки и
принадлежат графику второй прямой
поэтому можем составить
систему из двух уравнений:
Значит, функции имеют вид и
Аналогично первому способу решаем уравнение
и получаем ответ.
На рисунке изображены графики двух функций вида которые
пересекаются в точке Найдите
Показать ответ и решение
Первый способ.
Пусть — уравнение первой прямой,
— уравнение второй прямой.
Заметим, что первая прямая проходит через точки и
Если прямая проходит через точку на плоскости, то
координаты этой точки обращают уравнение этой прямой в верное равенство. Тогда мы получаем систему из двух
уравнений:
Значит, — уравнение первой прямой. Вторая прямая проходит через точки
и
Следовательно, мы
можем получить следующую систему:
Значит, — уравнение второй прямой. Обе прямые проходят через точку
по условию, тогда мы имеем
систему:
Второй способ.
Если прямая на плоскости проходит через две точки
и
то мы можем составить ее каноническое
уравнение:
На рисунке видно, что одна из прямых проходит через точки и
Тогда мы можем записать ее каноническое
уравнение:
Другая прямая проходит через точки и
. Аналогично запишем ее каноническое уравнение:
Если прямая проходит через точку на плоскости, то координаты этой точки обращают уравнение прямой в верное равенство.
Обе прямые проходят через точку по условию, тогда имеем систему:
Друзья, поздравляем вас с Новым годом! Этот новогодний пробный вариант ЕГЭ подготовлен специально для вас, и, прорешав все задачи правильно, вы можете получить секретный код. Числу, составленному из цифр каждого ответа, соответствует буква в русском алфавите. Тогда правильные ответы ко всем задачам помогут вам составить фразу, которую мы загадали. Введите ее в поле ответа к заданию 19 без пробелов с маленькой буквы.
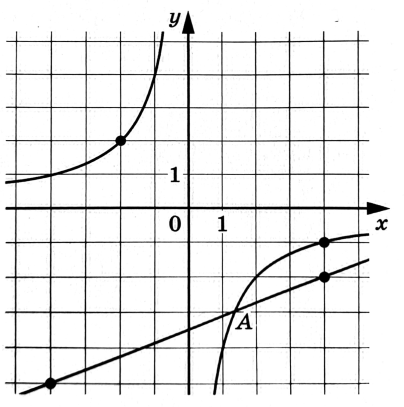
На рисунке изображены графики функций и
которые
пересекаются в точке Найдите абсциссу точки
Показать ответ и решение
По картинке видим, что точка принадлежит графику функции
следовательно,
Посмотрим теперь на график функции Это прямая, которой принадлежат
точки и
Найдем угловой коэффициент:
Найдем подставив в уравнение
точку
и
Найдем абсциссу точки приравняв
и
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите
Показать ответ и решение
Для начала разберемся, какой из графиков какой функции соответствует.
Координата по вершины параболы
равна
что
соответствует правой параболе.
Любую параболу вида можно представить в виде
Здесь — координаты ее вершины. По картинке несложно видеть, что
вершина левой параболы имеет координаты
значит функция имеет
вид
Также по картинке видно, что в точке -4 функция равна 1. Это условие
можно записать следующим образом:
Теперь мы полностью восстановили функцию она имеет вид
Найдем точки пересечения и
Пересечение, соответствующее это точка
Тогда координата
точки равна 3.
На рисунке изображены графики функций и
которые пересекаются в точках и
Найдите абсциссу точки
Показать ответ и решение
Восстановим уравнение функции По картинке видно, что её график проходит через три целые точки:
и
Так как график проходит через точку
то имеем уравнение:
Так как график проходит через точку
то имеем уравнение:
Так как график проходит через точку
то имеем уравнение:
Решим систему из двух уравнений:
Таким образом, мы полностью восстановили уравнение функции
Восстановим уравнение функции По картинке видно, что её график проходит через целые точки
и
Значит, можем составить систему из двух уравнений:
Таким образом, мы полностью восстановили уравнение функции
Найдем координаты второй точки пересечения графиков этих функций:
Значит, абсцисса точки равна 2,5.
На рисунке изображены графики функций и
которые пересекаются в точках и
Найдите ординату точки
Показать ответ и решение
По картинке видно, что график функции проходит через точки
и
Если график функции проходит
через определенную точку, то ее координаты обращают уравнение функции в верное равенство. Значит, мы можем составить
систему из трех уравнений:
Из первого уравнения следует, что Тогда, подставив этот результат во второе уравнение, получим:
Подставив и
в третье уравнение, получим:
Тогда можем найти
Значит, мы нашли уравнение функции
По условию функции и
пересекаются в точках
и
Тогда координаты точки
обращают
уравнения функций и
в верные равенства:
Тогда ордината точки
равна
На рисунке изображены графики функций
которые пересекаются в точках и
Найдите
Показать ответ и решение
Заметим, что любую квадратичную функцию можно представить в виде
где — координаты вершины параболы. По графику видно, что
Найдём подставив точку
в уравнение параболы:
Получим уравнение параболы
Найдём уравнение линейной функции
график которой проходит через точки и
Найдём значение углового коэффициента
Значение коэффициента равно 3, поскольку прямая пересекает ось ординат в точке
Получим уравнение функции
Чтобы найти координаты точки надо решить уравнение
Первое значение соответствует абсциссе точки
тогда второе — абсциссе точки
Найдём её ординату, подставив
в уравнение любой из функций. Подставим в
На рисунке изображены графики функций и
которые пересекаются в точках и
Найдите ординату точки
Показать ответ и решение
Определим какой из графиков («верхний» или «нижний») принадлежит функции Заметим, что
значит, график функции проходит через точку
то есть функции
соответствует «верхний»
график.
Восстановим уравнение функции Заметим, что «нижний» график проходит через точку
следовательно
справедливо равенство
Также график функции проходит через целые точки
и
, значит, можем составить систему
уравнений:
Таким образом, мы полностью восстановили уравнение функции
Теперь найдем абциссу второй точки пересечения графиков функций и
Значит, абсцисса точки равна 7. Тогда ордината точки
равна
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите
Показать ответ и решение
Найдём уравнение функции По графику видно, что
поскольку функция увеличивается на 1 при увеличении
аргумента на 1. Также прямая пересекает ось ординат в точке откуда
Тогда уравнение прямой имеет
вид
Найдём уравнение функции Подставим точку
на графике в уравнение функции:
Тогда уравнение корня имеет вид
Найдём координаты точек пересечения графиков, приравняв функции:
Сделаем замену и получим квадратное уравнение:
Сделаем обратную замену и получим совокупность
Точке соответствует координата
Подставим её в
и получим
На рисунке изображены графики функций и
которые пересекаются в точках и
Найдите абсциссу точки
Показать ответ и решение
Заметим, что область определения функции совпадает с
областью определения функции и равна
Из графика видно, что определена на
откуда получаем
Тогда функция примет вид
По графику то есть
По графику то есть
Найдем отличную от точку пересечения графиков функций
и
Из последней системы получаем Тогда абсцисса точки
пересечения
графиков равна 8.
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите
Показать ответ и решение
Поскольку — квадратичная функция, абсцисса вершины ее графика равна
Тогда по рисунку график функции — это правая парабола.
Найдём уравнение левой параболы в виде
где — ее вершина. Подставим точку
в уравнение
Получим
Чтобы найти координаты точки решим уравнение
Значение — это абсцисса точки
тогда
— это абсцисса
точки
На рисунке изображены графики функций
которые пересекаются в точке Найдите абсциссу точки
Показать ответ и решение
По картинке видим, что точка принадлежит графику функции
следовательно,
Посмотрим теперь на график функции По картинке видим, что ему принадлежат точки
и
Найдем угол
наклона
Найдем подставив точку
Найдем абсциссу точки приравняв
и
На рисунке изображены графики двух функций: одна из них линейная, другая — вида
Найдите абсциссу точки пересечения графиков этих функций. Если таких точек несколько, в ответе укажите наименьшую
абсциссу.
Показать ответ и решение
Для решения найдём уравнения обеих функций, после чего решим уравнение, приравняв эти функции, что и будет означать
пересечение графиков функций.
Найдём уравнение линейной функции. Заметим, что прямая проходит через точки и
Тогда угловой
коэффициент можно найти по формуле
Получим уравнение прямой
Для нахождения свободного коэффициента подставим произвольную точку на прямой в это уравнение. Подставим точку
Получаем уравнение прямой
Найдём уравнение второй функции. Заметим, что график имеет вершину из чего можно сделать вывод, что
Чтобы найти
подставим в полученную функцию
координаты точки
которая находится на
графике.
Получаем уравнение второй функции
Приравняем полученные функции:
Возведём в квадрат обе части уравнения, отметив, что правая чать должна быть неотрицательной, то есть
Поскольку решение уравнения существует при , получим единственное решение
На рисунке изображены графики функций и
которые пересекаются в точках и
Найдите
Показать ответ и решение
Восстановим график функции Он проходит через точку
Значит, можем составить уравнение:
Значит,
Восстановим график функции Он проходит через точку
следовательно,
Также график проходит через точку
следовательно,
Значит,
Найдем абсциссу точки
На рисунке изображены графики функций
которые пересекаются в точках и
Найдите ординату точки
Показать ответ и решение
Подставим точку расположенную на графике гиперболы, в функцию
Найдём коэффициент по точкам на графике линейной функции
Найдём подставив точку
Найдём точки пересечения, приравняв и
Решим данное уравнение методом переброски коэффициента. Решим уравнение
По теореме Виета легко находятся корни и
Тогда у исходного уравнения корни равны
Видно, что точке соответствует координата
тогда точке
— координата
Найдём ординату, подставив
в
На рисунке изображены графики функций и
которые пересекаются в точках
и
Найдите абсциссу точки
На рисунке изображены графики функций и
, которые пересекаются в точках
и
.
Найдите ординату точки .
На рисунке изображены графики функций
которые пересекаются в точках
и
Найдите
Показать ответ и решение
Найдем уравнения каждой функции. Пусть
— функции, задающие второе уравнение условия. Тогда график проходит
через точки и
, следовательно,
Следовательно,
График проходит через точки
Следовательно,
Найдем четвертую точку пересечения, то есть корень уравнения
По картинке можно предположить, что точка
— общая для
графиков и
Тогда имеем:
Корни последнего уравнения Мы ищем корень
Тогда
Как найти абсциссу точки пересечения графиков двух линейных уравнений
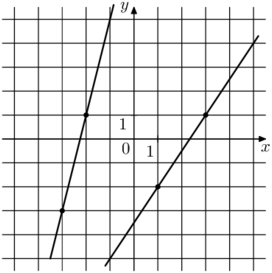
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Заметим, что на рисунке изображены графики линейных функций. Найдём их уравнения y = kx + b. Первая прямая проходит через точки (−1; 0) и (0; 1), следовательно
Значит, уравнение первой прямой — y = x + 1.
Вторая прямая проходит через точки (−4; 1) и (−2; 4), следовательно,
Значит, уравнение второй прямой —
Теперь найдём абсциссу точки пересечения графиков:
Решение на Номер 12.26 из ГДЗ по алгебре за 7 класс: Мордкович А.Г.
Условие
Решение 1
Решение 2
Поиск в решебнике
Популярные решебники
Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013г.
Издатель: А.Г. Мордкович, 2013г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015г.
Решение №2132 На рисунке изображён графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
На рисунке изображён графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
На рисунке изображены прямые, линейных функции их вид имеет вид:
Найдём k и b функции справа .
k – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на –3,5 .
b = –3,5
Функции справа имеет вид:
Найдём k и b функции слева .
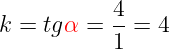
b = 9
Функции слева имеет вид:
y = 4x + 9
В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:
1,5x – 3,5 = 4x + 9
1,5x – 4x = 9 + 3,5
–2,5x = 12,5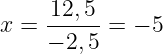
[spoiler title=”источники:”]
http://vipgdz.com/7-klass/algebra/mordkovich/nomer-12-26
[/spoiler]
Решение:
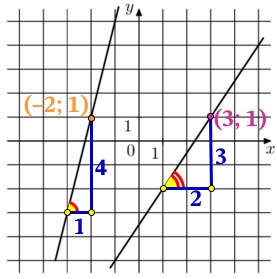
На рисунке изображены прямые, линейных функции их вид имеет вид:
y = kx + b
Найдём k и b функции справа.
k – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
k=tg{color{Red}alpha}=frac{color{Blue} 3}{color{Blue} 2}=1,5
Подставим в общий вид функции значение k и координаты точки (3; 1) найдём b:
y = kx + b
1 = 1,5·3 + b
1 = 4,5 + b
1 – 4,5 = b
–3,5 = b
Функции справа имеет вид:
y = 1,5x – 3,5
Найдём k и b функции слева.
k=tg{color{Red}alpha}=frac{color{Blue} 4}{color{Blue} 1}=4
Подставим в общий вид функции значение k и координаты точки (–2; 1) найдём b:
y = kx + b
1 = 4·(–2) + b
1 = –8 + b
1 + 8 = b
9 = b
Функции слева имеет вид:
y = 4x + 9
В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:
1,5x – 3,5 = 4x + 9
1,5x – 4x = 9 + 3,5
–2,5x = 12,5
x=frac{12,5}{–2,5}=-5
Ответ: –5.
Lara Kroft
Знаток
(280)
10 лет назад
чтобы найти точку пересечения данных прямых необходимо составить систему из этих уравнений
3х+2у=6
у=х
подставляем второе уравнение в первое и получаем:
3х+2х=6
5х=6
х=6/5 – абсцисса (тогда и у=6/5- ордината)
ответ: х=6/5=1,2
Альберт Романов
Ученик
(178)
10 лет назад
вы где этот ответ откопали такое не может быть посудите сами если подставить если икс равно игрек тогда получится в первом уравнении 3+2=6 абсурд или 6+4=10 также абсурд притом данные уравнения не могут иметь две точки пересечения а могут только одну равную6/5