Как найти абсциссу точки графика параболы

• Решение

•   Видеорешение

Абсцисса точки касания. Задание В8 (2014)

Задание B9 (№ 27485) из Открытого банка заданий для подготовки к ЕГЭ по математике.

Прямая y=7x-5 параллельна касательной к графику функции y=x 2 +8x+6. Найдите абсциссу точки касания.

Чтобы выполнить это задание, нам нужно вспомнить теорию.

1. Прямая y=k₁x+b₁ параллельна прямой y=k₂x+b₂, если k₁=k₂. k₁ и k₂ – коэффициенты наклона прямых. Коэффициент наклона прямой равен тангенсу угла между этой прямой и положительным направлением оси ОХ: tg(a)=AB/OA

2. Геометрический смысл производной: значение производной функции у=f(x) в точке x₀ равнo угловому коэффициенту касательной, проведенной к графику функции у=f(x) в точке x₀, то есть tg(a)=k=f'(x₀), где k — угловой коэффициент касательной: Решение.
Так как касательная параллельна прямой y=7x-5, следовательно коэффициент наклона касательной, а, значит, производная функции в точке касания равны 7.
Найдем производную функции y=x 2 +8x+6:

Приравняем производную к 7:

В этом уравнении x₀ – абсцисса точки касания.
Решим уравнение:
2x₀+8=7
x₀=-0,5
Ответ: -0,5

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Определения и понятия

Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

• Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
• Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
• Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
• Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α – красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f ( x B ) – f x A x B – x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) – это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) – f ( x A ) x B – x A или k = f ( x A ) – f ( x B ) x A – x B , причем уравнение необходимо записать как y = f ( x B ) – f ( x A ) x B – x A · x – x A + f ( x A ) или
y = f ( x A ) – f ( x B ) x A – x B · x – x B + f ( x B ) .

Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.

Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) – f ( ∆ x ) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) .

Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 – 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 – 0 f ‘ ( x ) .

Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у – k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = – 1 , f ( x 0 ) = – 3 .

Необходимо найти производную в точке со значением – 1 . Получаем, что

y ‘ = e x + 1 + x 3 3 – 6 – 3 3 x – 17 – 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ – 6 – 3 3 x ‘ – 17 – 3 3 ‘ = e x + 1 + x 2 – 6 – 3 3 y ‘ ( x 0 ) = y ‘ ( – 1 ) = e – 1 + 1 + – 1 2 – 6 – 3 3 = 3 3

Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f ‘ ( x 0 ) · x – x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) – 3 y = 3 3 x – 9 – 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x – 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y ‘ = 3 · x – 1 5 + 1 ‘ = 3 · 1 5 · ( x – 1 ) 1 5 – 1 = 3 5 · 1 ( x – 1 ) 4 5

Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 – 0 3 5 · 1 ( x – 1 ) 4 5 = 3 5 · 1 ( – 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

Найти точки графика функции y = 1 15 x + 2 3 – 4 5 x 2 – 16 5 x – 26 5 + 3 x + 2 , где

1. Касательная не существует;
2. Касательная располагается параллельно о х ;
3. Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ – ∞ ; 2 и [ – 2 ; + ∞ ) . Получаем, что

y = – 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 , x ∈ [ – 2 ; + ∞ )

Необходимо продифференцировать функцию. Имеем, что

y ‘ = – 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ – ∞ ; – 2 1 15 x 3 – 6 x 2 + 9 x + 12 ‘ , x ∈ [ – 2 ; + ∞ ) ⇔ y ‘ = – 1 5 ( x 2 + 12 x + 35 ) , x ∈ – ∞ ; – 2 1 5 x 2 – 4 x + 3 , x ∈ [ – 2 ; + ∞ )

Когда х = – 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → – 2 – 0 y ‘ ( x ) = lim x → – 2 – 0 – 1 5 ( x 2 + 12 x + 35 = – 1 5 ( – 2 ) 2 + 12 ( – 2 ) + 35 = – 3 lim x → – 2 + 0 y ‘ ( x ) = lim x → – 2 + 0 1 5 ( x 2 – 4 x + 3 ) = 1 5 – 2 2 – 4 – 2 + 3 = 3

Вычисляем значение функции в точке х = – 2 , где получаем, что

1. y ( – 2 ) = 1 15 – 2 + 2 3 – 4 5 ( – 2 ) 2 – 16 5 ( – 2 ) – 26 5 + 3 – 2 + 2 = – 2 , то есть касательная в точке ( – 2 ; – 2 ) не будет существовать.
2. Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .

Когда x ∈ – ∞ ; – 2 , тогда – 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( – 2 ; + ∞ ) получаем 1 5 ( x 2 – 4 x + 3 ) = 0 .

– 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 – 4 · 35 = 144 – 140 = 4 x 1 = – 12 + 4 2 = – 5 ∈ – ∞ ; – 2 x 2 = – 12 – 4 2 = – 7 ∈ – ∞ ; – 2 1 5 ( x 2 – 4 x + 3 ) = 0 D = 4 2 – 4 · 3 = 4 x 3 = 4 – 4 2 = 1 ∈ – 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ – 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y – 5 = 1 15 – 5 + 2 3 – 4 5 – 5 2 – 16 5 – 5 – 26 5 + 3 – 5 + 2 = 8 5 y 2 = y ( – 7 ) = 1 15 – 7 + 2 3 – 4 5 ( – 7 ) 2 – 16 5 – 7 – 26 5 + 3 – 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 – 4 5 · 1 2 – 16 5 · 1 – 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 – 4 5 · 3 2 – 16 5 · 3 – 26 5 + 3 3 + 2 = 4 3

Отсюда – 5 ; 8 5 , – 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

1. Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ – ∞ ; – 2 , получаем, что – 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( – 2 ; + ∞ ) , тогда 1 5 ( x 2 – 4 x + 3 ) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

– 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 – 4 · 43 = – 28 0

Другое уравнение имеет два действительных корня, тогда

1 5 ( x 2 – 4 x + 3 ) = 8 5 x 2 – 4 x – 5 = 0 D = 4 2 – 4 · ( – 5 ) = 36 x 1 = 4 – 36 2 = – 1 ∈ – 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ – 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y ( – 1 ) = 1 15 – 1 + 2 3 – 4 5 ( – 1 ) 2 – 16 5 ( – 1 ) – 26 5 + 3 – 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 – 4 5 · 5 2 – 16 5 · 5 – 26 5 + 3 5 + 2 = 8 3

Точки со значениями – 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках – 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x – π 4 – 1 3 , которые располагаются перпендикулярно прямой y = – 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется – 1 , то есть записывается как k x · k ⊥ = – 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = – 2 , тогда k x = – 1 k ⊥ = – 1 – 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.

y ‘ ( x 0 ) = 3 cos 3 2 x 0 – π 4 – 1 3 ‘ = 3 · – sin 3 2 x 0 – π 4 · 3 2 x 0 – π 4 ‘ = = – 3 · sin 3 2 x 0 – π 4 · 3 2 = – 9 2 · sin 3 2 x 0 – π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ – 9 2 · sin 3 2 x 0 – π 4 = 1 2 ⇒ sin 3 2 x 0 – π 4 = – 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 – π 4 = a r c sin – 1 9 + 2 πk или 3 2 x 0 – π 4 = π – a r c sin – 1 9 + 2 πk

3 2 x 0 – π 4 = – a r c sin 1 9 + 2 πk или 3 2 x 0 – π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 – a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z – множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у :

y 0 = 3 cos 3 2 x 0 – π 4 – 1 3

y 0 = 3 · 1 – sin 2 3 2 x 0 – π 4 – 1 3 или y 0 = 3 · – 1 – sin 2 3 2 x 0 – π 4 – 1 3

y 0 = 3 · 1 – – 1 9 2 – 1 3 или y 0 = 3 · – 1 – – 1 9 2 – 1 3

y 0 = 4 5 – 1 3 или y 0 = – 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 – a r c sin 1 9 + 2 πk ; 4 5 – 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; – 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x – 2 3 π 4 – a r c sin 1 9 + 2 πk + 4 5 – 1 3 , y = 1 2 x – 2 3 5 π 4 + a r c sin 1 9 + 2 πk – 4 5 + 1 3 , k ∈ Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ – 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = – 2 x + 1 2 . Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x – x c e n t e r 2 + y – y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 – x – x c e n t e r 2 + y c e n t e r y = – R 2 – x – x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 – x – x c e n t e r 2 + y c e n t e r или y = – R 2 – x – x c e n t e r 2 + y c e n t e r в указанной точке.

Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r – R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r – R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r – R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r – R .

Касательная к эллипсу

Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x – x c e n t e r 2 a 2 + y – y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y = b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r y = – b a · a 2 – ( x – x c e n t e r ) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.

Написать уравнение касательной к эллипсу x – 3 2 4 + y – 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x – 3 2 4 x = 2 + y – 5 2 25 = 1 1 4 + y – 5 2 25 = 1 ⇒ y – 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; – 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x – 3 2 4 + y – 5 2 25 = 1 y – 5 2 25 = 1 – x – 3 2 4 ( y – 5 ) 2 = 25 · 1 – x – 3 2 4 y – 5 = ± 5 · 1 – x – 3 2 4 y = 5 ± 5 2 4 – x – 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 – x – 3 2 , а нижний y = 5 – 5 2 4 – x – 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y ‘ = 5 + 5 2 4 – x – 3 2 ‘ = 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = – 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = – 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = 5 2 3 ( x – 2 ) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; – 5 3 2 + 5 принимает вид

y ‘ = 5 – 5 2 4 – ( x – 3 ) 2 ‘ = – 5 2 · 1 2 4 – ( x – 3 ) 2 · 4 – ( x – 3 ) 2 ‘ = = 5 2 · x – 3 4 – ( x – 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 – 3 4 – ( 2 – 3 ) 2 = – 5 2 3 ⇒ y = y ‘ ( x 0 ) · x – x 0 + y 0 ⇔ y = – 5 2 3 ( x – 2 ) – 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r – α ; y c e n t e r , имеет место задание неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r – b , тогда задается при помощи неравенства x – x c e n t e r 2 α 2 – y – y c e n t e r 2 b 2 = – 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 – a 2 + y c e n t e r или y = b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r y = – b a · ( x – x c e n t e r ) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Составить уравнение касательной к гиперболе x – 3 2 4 – y + 3 2 9 = 1 в точке 7 ; – 3 3 – 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x – 3 2 4 – y + 3 2 9 = 1 ⇒ y + 3 2 9 = x – 3 2 4 – 1 ⇒ y + 3 2 = 9 · x – 3 2 4 – 1 ⇒ y + 3 = 3 2 · x – 3 2 – 4 и л и y + 3 = – 3 2 · x – 3 2 – 4 ⇒ y = 3 2 · x – 3 2 – 4 – 3 y = – 3 2 · x – 3 2 – 4 – 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; – 3 3 – 3 .

Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 – 3 ) 2 – 4 – 3 = 3 3 – 3 ≠ – 3 3 – 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y ( 7 ) = – 3 2 · ( 7 – 3 ) 2 – 4 – 3 = – 3 3 – 3 ≠ – 3 3 – 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

y ‘ = – 3 2 · ( x – 3 ) 2 – 4 – 3 ‘ = – 3 2 · x – 3 ( x – 3 ) 2 – 4 ⇒ k x = y ‘ ( x 0 ) = – 3 2 · x 0 – 3 x 0 – 3 2 – 4 x 0 = 7 = – 3 2 · 7 – 3 7 – 3 2 – 4 = – 3

Ответ: уравнение касательной можно представить как

y = – 3 · x – 7 – 3 3 – 3 = – 3 · x + 4 3 – 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x – x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .

Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c – x = 0 D = b 2 – 4 a ( c – x ) y = – b + b 2 – 4 a ( c – x ) 2 a y = – b – b 2 – 4 a ( c – x ) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Написать уравнение касательной к графику x – 2 y 2 – 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

– 2 y 2 – 5 y + 3 – x = 0 D = ( – 5 ) 2 – 4 · ( – 2 ) · ( 3 – x ) = 49 – 8 x y = 5 + 49 – 8 x – 4 y = 5 – 49 – 8 x – 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = – 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y ‘ = 5 + 49 – 8 x – 4 ‘ = 1 49 – 8 x ⇒ y ‘ ( x 0 ) = 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y ‘ = 5 – 49 – 8 x – 4 ‘ = – 1 49 – 8 x ⇒ y ‘ ( x 0 ) = – 1 49 – 8 x 0 = – 1 3 ⇔ 49 – 8 x 0 = – 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 – 49 – 8 · 23 4 – 4 = – 5 + 3 4

Имеем, что точки касания – 23 4 ; – 5 + 3 4 .

Ответ: уравнение касательной принимает вид

Уравнение касательной к графику функции

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace_<=k>x+underbrace_ <=b>$$

п.2. Алгоритм построения касательной

На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)

Пусть (f(x)=x^2+3). Найдем касательную к этой параболе в точке (x_0=1).

(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)

п.3. Вертикальная касательная

Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).

Вертикальные касательные характерны для радикалов вида (y=sqrt[n]).

Пусть (f(x)=sqrt[5]+1). Найдем касательную к этой кривой в точке (x_0=1).

(f(x_0)=sqrt[5]<1-1>+1=1)
(f'(x)=frac15(x-1)^<frac15-1>+0=frac15(x-1)^<-frac45>=frac<1><5(x-1)^<frac45>> )
(f'(x_0)=frac<1><5(1-1)^<frac45>>=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin x=0\ x=-2 end right. $$ Две точки на оси: (0;0) и (-2;0). Касательная в точке (x_0=0): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end Касательная в точке (x_0=-2): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

Общее уравнение касательной: (f'(x)=4x+4) По условию (f'(x_0)=tgalpha=tg45^circ=1) Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac<15> <8>end Уравнение касательной: begin y=1cdotleft(x+frac34right)-frac<15><8>=x-frac98 end

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2). Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end Точка касания (x_0=-frac32) begin f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end Уравнение касательной: begin y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end Или, в каноническом виде: begin 2x+y+frac92=0 end

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

У горизонтальной прямой (k=0). Получаем уравнение: (f'(x_0)=0). begin 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end Точка касания (x_0=-1) begin f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end Уравнение касательной: begin y=0cdot(x+1)-2=-2 end

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.

Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac<1>=-frac<1><11>) begin f'(x)=left(fracright)’-x’=frac<2x(x+3)-(x^2+2)cdot 1><(x+3)^2>-1=frac<2x^2+6x-x^2-2-(x+3)^2><(x+3)^2>=\ =frac<(x+3)^2>=- frac<11> <(x+3)^2>end В точке касания: begin f'(x_0)=k_2Rightarrow=-frac<11><(x+3)^2>=-frac<1><11>Rightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin x=-14\ x=8 end right. end
Уравнение касательной при (x_0=-14) begin f(x_0)=frac<(-14)^2+2><-14+3>+14=frac<198><-11>+14=-18+14=-4\ y=-frac<1><11>(x+14)-4=-frac <11>end Уравнение касательной при (x_0=8) begin f(x_0)=frac<8^2+2><8+3>-8=frac<66><11>-8=-2\ y=-frac<1><11>(x-8)-2=-frac <11>end
Ответ: точка касания (-14;-4), уравнение (y=-frac<11>)
и точка касания (8;-2), уравнение (-frac<11>)

Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.

Найдем производные функций: begin f_1′(x)=2x-5, f_2′(x)=2x+1 end Пусть a – абсцисса точки касания для первой параболы, b – для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin begin 2a-5=2b+1\ 6-a^2=1-b^2 end Rightarrow begin 2(a-b)=6\ a^2-b^2=5 end Rightarrow begin a-b=3\ (a-b)(a+b)=5 end Rightarrow begin a-b=3\ a+b=frac53 end Rightarrow \ Rightarrow begin 2a=3+frac53\ 2b=frac53-3 end Rightarrow begin a=frac73\ b=-frac23 end end Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac<49><9>=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac<49><9>-frac<35><3>+6=frac<49-105+54><9>=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac<4-6+9><9>=frac79 end
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))

Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.

Решим уравнение: (x^4+3x^2+2x=2x-1) begin x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac<-3pmsqrt<5>> <2>end Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) – решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.

Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin x=0\ 2x^2+3=0 end right. Rightarrow left[ begin x=0\ x^2=-frac32 end right. Rightarrow left[ begin x=0\ xinvarnothing end right. Rightarrow x=0 end Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)

Ищем расстояние между двумя параллельными прямыми: (y=2x) и (y=2x-1). Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0).

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac<0,4><2>=-0,2 end Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt<0,4^2+(-0,2)^2>=0,2sqrt<2^2+1^2>=frac<sqrt<5>><5>)
Ответ: (frac<sqrt<5>><5>)

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/proizvodnye/kasatelnaja-k-grafiku-funktsii-v-tochke/

http://reshator.com/sprav/algebra/10-11-klass/uravnenie-kasatelnoj-k-grafiku-funkcii/

[/spoiler]

Формула нахождения вершины параболы

Вы будете перенаправлены на Автор24

Парабола – это геометрическое множество точек, равноудалённых от точки F, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.

Что значит вершина параболы

Вершина параболы – это точка, ближайшая к директрисе параболы. Она является центром отрезка, ограниченного точкой фокуса параболы $F$ и директрисой $d$.

Производная в вершине квадратичной параболы равна нулю.

Каноническое уравнение параболы $y^2 = 2px$ справедливо для параболы, вершина которой находится в центре осей.

Для того, чтобы определить, принадлежит ли точка графику заданной параболы, необходимо подставить её координаты в формулу $y = ax^2 + bx + c$.

Если равенство выполняется — точка принадлежит графику.

Как найти вершины параболы, задающейся квадратичной функцией

Рисунок 1. Пример уравнения и графика квадратичной параболы

Довольно часто парабола задаётся квадратичной функцией вида $y = ax^2 + bx + c$, вершина такой параболы находится в произвольной точке.

Какой-то единой формулы для нахождения сразу обеих координат вершины параболы нет, но при этом определить координаты вершины параболы по уравнению довольно просто.

Алгоритм для нахождения вершины параболы такой:

1. Запишите коэффициенты $a, b, c$ из уравнения. Если коэффициент $a$ при $y$ положительный, то ветви параболы будут смотреть вверх, а если отрицательный, то вниз.
2. Найдите абсциссу вершины параболы ($x$ вершины) по формуле $x = — frac<2a>$, для этого воспользуйтесь коэффициентами $a, b, c$ из уравнения.
3. Подставьте найденный $x$ в уравнение параболы и вычислите ординату вершины параболы $y$.
4. Запишите полученные координаты x и y вершины параболы в форме точки $(x; y)$.

Рассмотрим уравнение параболы $y = x^2 – 5x + 7$

1. Коэффициенты этой параболы $a = 1$, $b = -5$, $c = 7$.
2. Для вычисления x вершины параболы подставьте $a = 1$ и $b = -5$ в формулу $x = — frac<2a>= frac<5><2>=2.5$
3. Подставьте найденный $x$ в исходное уравнение:
4. $y = 2,5^2 – 5 cdot 2.5 + 7$
5. $y = 0,75$
6. Координаты вершины этой параболы $(2.5;0.75)$.

Вершина кубической параболы

Чтобы найти вершины (точки локальных минимумов и максимумов) кубической параболы, необходимо найти её производную, приравнять её к нулю и затем вычислить $x$ и $y$.

Если же необходимо найти точку перегиба кубической параболы, необходимо найти вторую производную и также приравнять её к нулю.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 12 2021

Как найти вершину параболы: три формулы

Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.

Нахождение вершины параболы: способы, примеры, советы

График функции y = ax 2 + bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.

У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.

Первый способ

Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.

Например, y =x 2 –8 x +15;

находим первый, второй коэффициенты и свободный член;

подставляем значения a и b в формулу;

вычисляем значения y;

Значит, вершина находится в точке (4;-1).

Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.

Рассмотрим на примере y =x 2 –6x+5

1) Приравниваем к нулю:

2) Находим дискриминант, используя формулу: D = b 2 –4 ac:

3) Находим корни уравнения по формуле (-b±√ D)/2a:

• 1 — первый корень;
• 5 — второй корень.

Второй способ

Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.

1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.

2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.

У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:

3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.

4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).

Третий способ

Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:

1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.

2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.

Рассмотрим этот способ подробнее.

Дана функция y = 4x²+16x-17;

• Записываем производную и приравниваем к нулю.

f'(x) = (4x²+16x-17)’ = 8x+16 =0

Построение параболы

Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

2) Заполняем таблицу

Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Советы

Правильно находите коэффициенты.

Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.

Делайте всё поэтапно. Следуйте алгоритму.

Обратите ваше внимание на то, что:

• Нужно проверять правильно ли ваше решение.
• Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.

Видео

Это видео поможет вам научиться находить вершину параболы

Как найти вершину параболы — методы, формулы и примеры вычислений

Общие сведения

Парабола — кривая, состоящая из равноудаленных точек от заданной точки (вершина) и прямой. Последняя называется директрисой. График функции имеет ось симметрии, которая проходит по определенной траектории и зависит от функции кривой (рис. 1). Ее вершина находится в центре координат.

Рисунок 1. График квадратичной функции с вершиной в начале координат.

Однако существуют и другие случаи прохождения кривой. Она может пересекать оси абсцисс или ординат. В некоторых случаях ее ветви направлены вниз. При вращении вокруг оси симметрии получается поверхность, которая используется в различных устройствах. По этому принципу изготовлены фары автомобиля, зеркала в телескопах и т. д. Кроме того, парабола — это квадратичная зависимость переменных друг от друга. Парабола имеет некоторые свойства:

1. Парабола — кривая второго порядка.
2. Ось симметрии перпендикулярна директрисе и проходит через фокус и вершины.
3. Оптическое свойство отражения.
4. Отрезок, который соединяет середину любой хорды параболы и точку пересечения касательных прямых, является перпендикуляром относительно директрисы.
5. Подобность всех парабол.
6. Траектория фокуса, которая катится по произвольной прямой — цепная молния.

Следует отметить, что оптическое свойство — это способность отражать свет от источника. Если пучок лучей, которые являются параллельными ее оси, отражаются в параболе, то они собираются в фокусе кривой. При нахождении источника света в фокусе происходит отражение параллельного пучка лучей относительно ее оси.

Уравнения квадратичной функции

Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:

В первой форме она имеет следующий вид: y 2 = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x 2 = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).

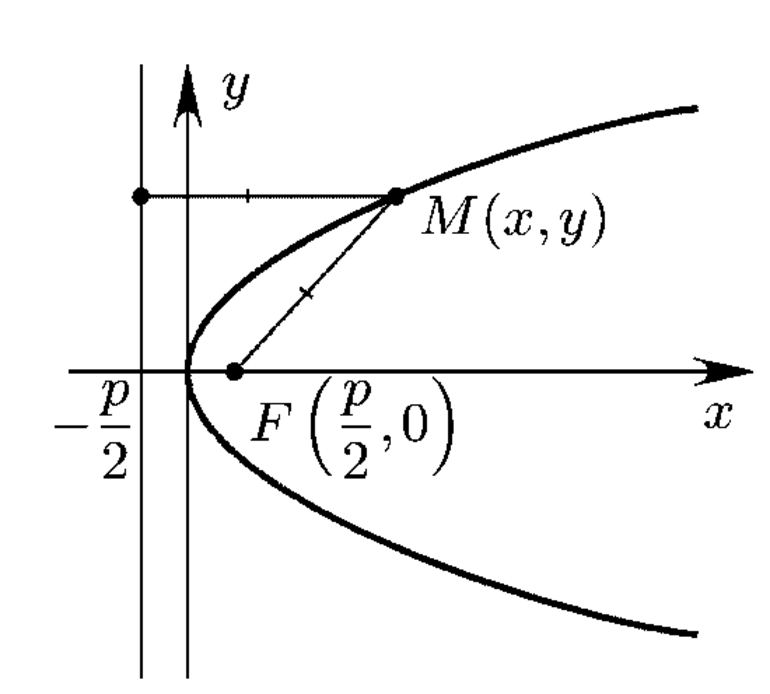
Рисунок 2. Директриса и фокус.

Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y 2 ]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y 2 ]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y 2 = 2px).

Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax 2 + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax 2 . В этом случае формула нахождения вершины параболы выглядит таким образом:

1. Абсцисса вершины параболы: xa = -b / 2a.
2. Координата «игрек» по оси ординат: yb = — D / 2a.

В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b 2 — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а 2 + Bxy + Cy 2 + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).

В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.

Методы нахождения вершины

В математике есть три способа нахождения координат точки вершины кривой: по формуле, выделением полного квадрата и нахождением производной. Следует отметить, что первый способ не подойдет в том случае, когда функция отличается от вида y = ax 2 + bx + c. Первый способ — расчет по формуле вершины параболы квадратичной функции. Координата x0 вычисляется таким образом: x0 = -b / 2a. Для нахождения координаты y0 следует подставить в функцию найденное значение x0.

Когда функция представлена неполным квадратом, нужно прибавить или отнять одинаковое число к двум частям уравнения. Если воспользоваться этим методом, то можно вычислить сразу значения х и у. Алгоритм нахождения вершины для функции у = x 2 + 4x + 2 имеет такой вид:

1. Приравнять многочлен к нулю, и перенести свободный член в правую сторону с противоположным знаком: x 2 + 4x = -2.
2. Дополнить до полного квадрата. Необходимо вычислить свободный член по такому соотношению: с = (b/2)^2 = (4/2)^2 = 4.
3. Записать полный квадрат, отняв и прибавив свободный член: x 2 + 4x + 4 — 4 = -2.
4. Выделить квадрат: (x 2 + 2x + 4) — 4 = -2.
5. Перенести свободное число в правую сторону с противоположным знаком: (x 2 + 2x + 4) = 4 — 2.
6. Уравнение принимает следующий вид: (x + 2)^2 = 2.
7. Для того чтобы вычислить x0, нужно решить уравнение (x + 2)^2 = 0. Следовательно, x = -2.
8. Ординату точки определить очень просто, поскольку ее значение соответствует числу (нужно брать с противоположным знаком), которое находится в правой части уравнения, т. е. у = -2.

При изображении графика вершину нужно сместить в точку (-2;2). Третий способ позволяет узнать координаты вершины с помощью определения производной. Находить ее следует от заданной функции. Для вычисления координат вершины нужно действовать по следующему алгоритму:

1. Найти производную и приравнять ее к нулю: f'(x) = (ax 2 + bx + c)’ = 2ax + b.
2. Выразить х: х = -b / (2a).
3. Подставить в функцию для вычисления y.
4. Записать координаты точки.

Однако эти все три метода относятся к ручному вычислению. Автоматизация действий осуществляется с помощью специализированного программного обеспечения. Для этой цели подойдет онлайн-калькулятор, поддерживающий функцию нахождения точек вершины квадратичной кривой. Программы рекомендуется применять только для проверки решения, поскольку очень важно знать методы нахождения этой точки.

Алгоритм построения

В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:

1. Если вершина не задана, то нужно найти ее любым из методов.
2. Определить точки пересечения с осями декартовой системы координат.
3. Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
4. Выполнить построение, соединив точки.

Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x 2 + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.

Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.

Примеры решений

В математике существует определенная классификация заданий на простые и сложные типы. Все они считаются однотипными, но отличаются только объемами вычислений и необходимостью построения графиков. Для решения нужно воспользоваться рекомендуемыми алгоритмами, которые существенно оптимизируют вычисления.

«Корень» трудностей при расчете — отсутствие систематизации вычислений. Не все ими пользуются. В результате простая задача становится очень сложной, поскольку в ней присутствует много ненужных вычислений. Кроме того, как отмечалось выше, рекомендуется «набить руку» на ручных вычислениях, ведь не всегда можно будет воспользоваться программами.

Упрощенная задача

Простым примером задания является следующий: необходимо вычислить координаты вершины точки параболы y = x 2 + 3x — 18. Следует продемонстрировать решение тремя способами. Решение первым методом:

1. Координата по оси абсцисс: х0 = -3 / (2 * 1) = -1,5.
2. По ординате: (-1,5)^2 + 3 * (-1,5) — 18 — y= 0. Отсюда, y = -20,25.

Следовательно, вершина находится в точке (-1,5;20,25). Второй способ решения данной задачи имеет такой вид:

1. Составить уравнение и перенести свободный член: x 2 + 3x = 18.
2. Вычислить свободный член: с = (b/2)^2 = 2,25.
3. Записать выражение: x 2 + 3x + 2,25 — 2,25 = 18.
4. Выделить квадрат: (x 2 + 3x + 2,25) = 20,25.
5. Определить координаты: (x + 1,5)^2 = 20,25.
6. Искомая точка: (-1,5;20,25).

Для решения третьим методом следует найти производную: y’ = (x 2 + 3x — 18)’ = 2x + 3. Затем нужно приравнять ее к нулю: 2х + 3 = 0. Уравнение является простым, а его переменная легко находится: x = -3 / 2 = -1,5. После этого необходимо подставить абсциссу в функцию, приравняв ее к 0: y = 20,25.

Повышенная сложность

Задания повышенной сложности сводятся к вычислению нескольких значений. Кроме того, в некоторых случаях следует построить график параболы y = x 2 — 7x +10. Необходимо выполнить такие действия:

1. Пересечение с осями.
2. Вычислить экстремум (вершину) всеми методами.
3. Выполнить графический эскиз (график).

Точек пересечения по ОУ нет. Они есть по оси абсцисс. Следует приравнять функцию к 0. Нахождение корней выполняется по теореме Виета: x1 = 2 и x2 = 5.

Для нахождения вершины необходимо воспользоваться тремя методами. При решении первым способом находится координата x0 = 7 / (2 * 1) = 3,5. Ордината определяется таким образом: y0 = (3,5)^2 — (7 * 3,5) + 10 = -2,25. Точка экстремума имеет координаты (3,5;-2,25). Находить вершину параболы необходимо по такому алгоритму:

1. Записать уравнение, и выполнить перенос свободного члена: x 2 — 7x = -10.
2. Найти свободный член: с = (7/2)^2 = 12,25.
3. Составить уравнение: x 2 — 7x + 12,25 — 12,25 = -10.
4. Выделить квадрат: (x — 3,5)^2 = 2,25.
5. Экстремум: (3,5;-2,25).

Для следующего метода нужно найти производную: y’ = (x 2 — 7x +10)’ = 2x — 7. Далее нужно приравнять y’ к нулю: 2x — 7 = 0. Значение по оси абсцисс равно х0 = 3,5, а y0 = -2,25. Далее нужно заполнить таблицу зависимостей ординаты от переменной.

y	4	0	-2	-2,25	-2	0	4
x	1	2	3	3,5	4	5	6

Таблица 1. Зависимость y от x.

После заполнения таблицы следует построить график искомой функции (рис. 3). Таблица состоит из следующих элементов: вершины, точек пересечения с осью абсцисс и 4 произвольных значений.

Рисунок 3. График функции.

Математики рекомендуют использовать для построения графика полученные значения при расчетах, поскольку подстановка и вычисление произвольных х существенно снижает скорость вычислений.

Таким образом, нахождение координат вершины параболы является довольно простой задачей, поскольку существует несколько методов. Из них можно выбрать оптимальный, который подходит в конкретной ситуации.

источники:

http://liveposts.ru/articles/education-articles/matematika/kak-najti-vershinu-paraboly-tri-formuly

http://nauka.club/matematika/algebra/vershin%D0%B0-paraboly.html

Как найти абсциссу точки касания

При составлении уравнения касательной к графику функции используется понятие «абсцисса точки касания». Данная величина может задаваться изначально в условиях задачи или же ее необходимо определять самостоятельно.

Инструкция

Начертите на листе в клеточку оси координат х и у. Изучите заданное уравнение для графика функции. Если оно является линейным, то достаточно узнать два значения для параметра у при любых х, после чего построить найденные точки на оси координат и соединить их прямой линией. Если же график нелинейный, то составьте таблицу зависимости у от х и подберите как минимум пять точек для построения графика.

Постройте график функции и поставьте на оси координат заданную точку касательной. Если она совпадает с функцией, то ее координата х приравнивается к букве «а», которой обозначается абсцисса точки касания.

Определите значение абсциссы точки касания для случая, когда заданная точка касательной не совпадает с графиком функции. Задаем третий параметр буквой «а».

Запишите уравнение функции f(a). Для этого в исходное уравнение вместо х подставьте а. Найдите производную функции f(x) и f(a). Подставьте необходимые данные в общее уравнение касательной, которое имеет вид: y = f(a) + f ‘(a)(x – a). В результате получить уравнение, которое состоит из трех неизвестных параметров.

Подставьте в него вместо х и у координаты заданной точки, через которую проходит касательная. После этого найдите решение полученного уравнения для всех а. Если оно является квадратным, то будет два значения абсциссы точки касания. Это значит, что касательная проходит два раза возле графика функции.

Нарисуйте график заданной функции и параллельной прямой, которые заданы по условию задачи. В этом случае необходимо также задать неизвестный параметр а и подставить его в уравнение f(a). Приравняйте производную f(a) к производной уравнения параллельной прямой. Данное действие выходит из условия параллельности двух функций. Найдите корни полученного уравнения, которые будут являться абсциссами точки касания.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?