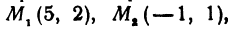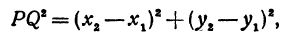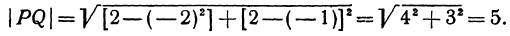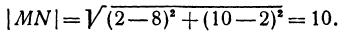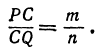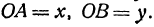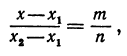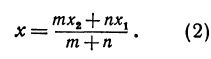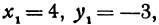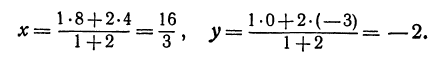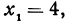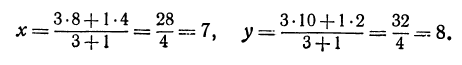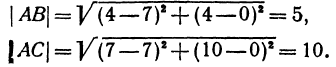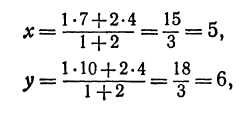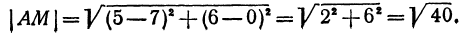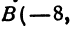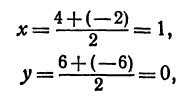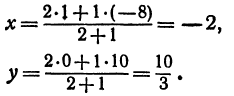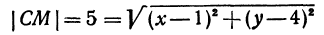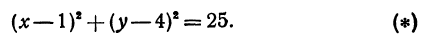1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Как найти координаты точки?
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Примеры решений по аналитической геометрии на плоскости
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.
Решения задач о треугольнике онлайн
Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.
Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.
Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.
Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.
Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.
Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.
Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/kak-najti-koordinaty-tochki
http://www.matburo.ru/ex_ag.php?p1=agtr
[/spoiler]
Координаты на плоскости:
Возьмем на плоскости две взаимно перпендикулярные прямые, пересекающиеся в точке
Определение: Координатными осями на плоскости называются две взаимно перпендикулярные прямые, на которых установлены: 1) направления, 2) масштаб и 3) общая точка отсчета.
Назовем одну из осей осью 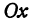
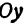
Возьмем произвольную точку 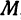
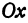
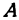
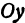
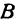
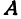
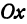
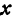
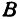
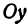
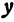
Определение. Абсциссой точки называется координата ее проекции на ось 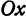
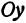
Абсциссу точки обычно обозначают буквой 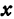
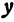
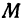
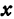
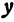
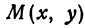
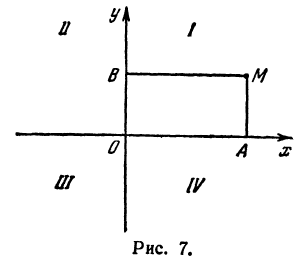
Координатные оси разделяют плоскость на четыре части, которые называют четвертями.
Первой четвертью называется та часть плоскости, в которой абсцисса и ордината положительны.
Второй четвертью — та часть, в которой абсцисса отрицательна, а ордината положительна.
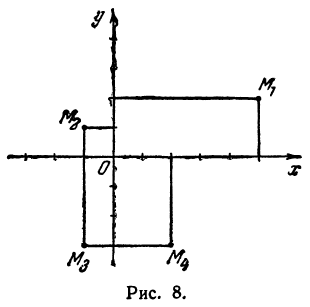
Третьей четвертью—та часть, в которой абсцисса и ордината отрицательны, и, наконец, четвертой,—та часть, в которой абсцисса положительна, а ордината отрицательна (рис. 7). На рис. 8 указаны 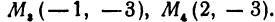
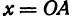
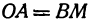
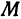
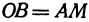
Пример:
Найти точку 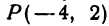
Решение:
Возьмем на оси 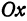
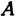
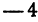
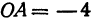
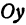
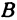
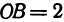
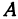
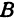
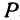
Пример:
Найти расстояние между точками 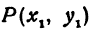
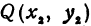
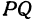
Решение:
Обозначим проекцию точки 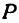
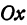
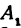
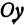
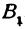
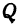
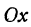
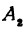
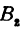
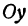
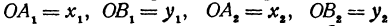
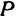
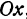
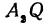
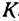
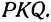
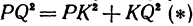
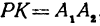
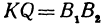
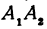
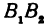
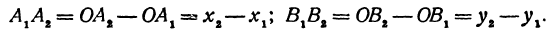
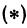
откуда
т. е. расстояние между двумя точками равно корню квадратному из суммы квадратов разностей, координат.
Примечание. Расстояние между двумя точками, так же как длина отрезка, всегда положительно, поэтому в формуле (1) перед квадратным корнем берут только знак плюс.
Пример:
Найти расстояние между точками 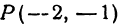
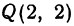
Решение:
Применяя формулу (1), получим
Пример:
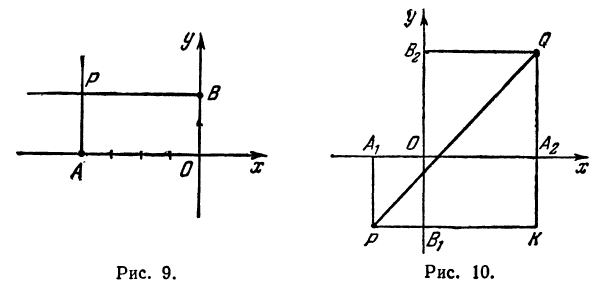
Найти длину отрезка 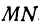
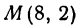
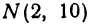
Решение:
Применяя формулу (1), получим
Пример:
Найти точку 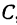
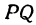
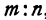
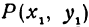
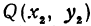
Решение:
По условию задачи надо найти такую точку 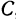
Обозначим, как и выше, проекции точки 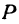
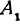
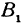
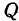
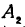
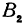
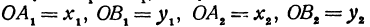
Кроме того, обозначим координаты искомой точки 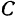
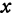
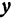
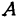
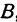
Так как прямые 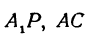
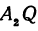
Но 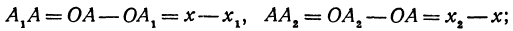
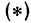
решая которое найдем абсциссу точки 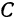
Рассуждая аналогично о проекциях на оси 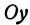
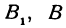
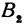
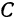
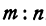
Итак, искомая точка 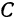
Пример:
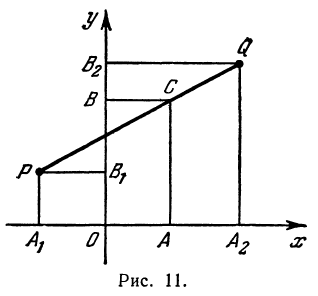
Найти точку, делящую в отношении 1:2 отрезок 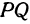
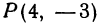
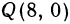
Здесь 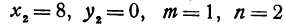
Решение:
Применяя формулы (2) и (3), получим:
- Заказать решение задач по высшей математике
Пример:
Найти точку, делящую расстояние между точками 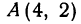
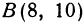
Здесь 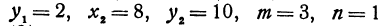
Решение:
По формулам (2) и (3) находим:
Следствие (из формул (2) и (3)). Если точка 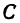
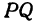
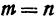
т. е. абсцисса середины отрезка равна средней арифметической абсцисс его начала и конца; ордината середины отрезка равна средней арифметической ординат его начала и конца.
Пример:
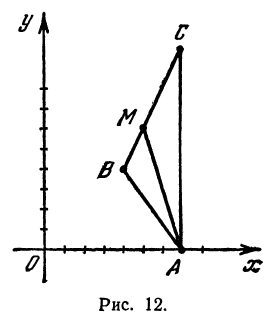
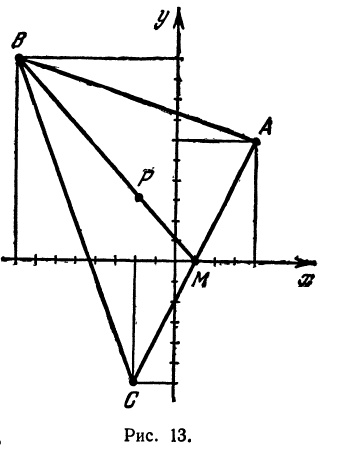
Даны три вершины треугольника: 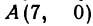
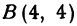
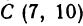
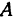
Решение:
Найдем длины сторон 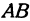
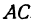
Обозначим точку пересечения биссектрисы угла 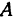
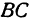
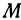
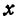
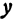
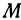
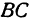
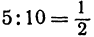
т.е. 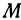
Теперь вычисляем длину биссектрисы как расстояние между точками 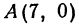
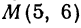
Пример:
Найти точку пересечения медиан треугольника, вершинами которого являются точки 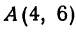

Решение:
Точка пересечения медиан делит каждую из медиан в отношении 2:1, считая от вершины треугольника. Обозначим через 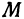
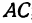
т. е. 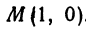
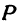
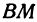
Итак, искомая точка 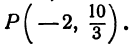
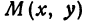
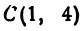
или, возводя обе части равенства в квадрат, получим
Это равенство есть уравнение с двумя неизвестными 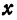
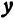
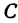
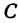
Следовательно, можно сказать, что уравнение 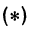
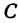
В следующих главах будут рассмотрены уравнения с двумя неизвестными 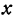
- Линейная функция
- Квадратичная функция
- Тригонометрические функции
- Производные тригонометрических функции
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 251 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …
Добавить в вариант
Вектор 
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
На рисунке изображён график функции
и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Из точки А(6; 8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку А(6; 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.
Найдите расстояние от точки A с координатами (6; 8) до оси абсцисс.
Найдите расстояние от точки A с координатами (6; 8) до оси ординат.
Найдите абсциссу точки, симметричной точке A(6; 8) относительно оси Oy.
Найдите ординату точки, симметричной точке A(6; 8) относительно оси Ox.
Найдите абсциссу точки, симметричной точке A(6; 8) относительно начала координат.
Найдите ординату точки, симметричной точке A(6; 8) относительно начала координат.
Найдите абсциссу середины отрезка, соединяющего точки O(0; 0) и A(6; 8).
Найдите абсциссу середины отрезка, соединяющего точки A(6; 8) и B(−2; 2).
Найдите синус угла наклона отрезка, соединяющего точки O(0; 0) и A(6; 8), с осью абсцисс.
Найдите косинус угла наклона отрезка, соединяющего точки O(0; 0) и A(6; 8), с осью абсцисс.
Всего: 251 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …
Помогите как найти абсциссу точки?
Андрей Барыбин
Профи
(506),
закрыт
14 лет назад

Olya
Мастер
(1607)
14 лет назад
Всё просто: точка А -точка пересечения двух прямых АС и АВ.
Уравнение прямой AC (просто переносим 2х в правую часть, выразив таким образом y): y = 3 – 2x
Уравнение прямой АВ: y = 7 + 2x
Чтобы найти абсциссу точки А, нужно эти уравнения приравнять (есть такое правило для нахождения абсциссы точки пересечения прямых) :
3 – 2х = 7 + 2х
-4х = 4
х = 4 : (-4)
х = -1
Ответ: -1
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Как найти координаты точки
Поддержать сайт
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.
Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».
Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).
Запомните!
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий: