Погрешность произведения
Пусть в результате измерений получено:
$$ x = x_0 pm Delta x, quad y = y_0 pm Delta y, quad x, y gt 0 $$
Найдём границы для произведения этих величин: z = xy
$$ {left{ begin{array}{c} x_0- Delta x le x le x_0+ Delta x \ y_0- Delta y le y le y_0+ Delta y end{array} right.} Rightarrow (x_0- Delta x)(y_0-Delta y) le xy le (x_0+ Delta x)(y_0+ Delta y) Rightarrow $$
$$ Rightarrow x_0 y_0-( Delta xy_0+x_0 Delta y- Delta x Delta y) le xy le x_0 y_0-( Delta xy_0+x_0 Delta y+ Delta x Delta y) $$
(О правилах умножения двух неравенств, см. §36 данного справочника).
Абсолютные погрешности $Delta x ≪ x_0, Delta y≪y_0$ заметно меньше $x_0$ и $ y_0$, поэтому будем считать, что произведение $Delta x Delta y approx 0$, и им можно пренебречь. Получаем:
$$ x_0 y_0-( Delta xy_0+x_0 Delta y) le xy le x_0 y_0-( Delta xy_0+x_0 Delta y) $$
$$ z = z_0 pm Delta z: z_0 = x_0 y_0, quad Delta z = Delta xy_0+x_0 Delta y $$
$$ δ_z = frac{Delta z}{z_0} = frac{Delta xy_0+x_0 Delta y}{x_0 y_0} = frac{Delta x}{x_0} + frac{Delta y}{y_0} = δ_x+δ_y $$
$$ δ_{xy} = δ_x+δ_y $$
При умножении приближенных величин их относительные погрешности складываются.
Погрешность степени
Пусть в результате измерений получено: $x = x_0 pm Delta x, x gt 0$
Тогда, для квадрата x из выражения для относительной погрешности произведения получаем: $δ_{x^2} = δ_x+δ_x = 2δ_x$.
Для куба: $δ_{x^3 } = δ_{x^2}+δ_x = 2δ_x+δ_x = 3δ_x$.
Для произвольной степени n:
$$ δ_{x^n} = n δ_x $$
При возведении приближенной величины в натуральную степень n, её относительная погрешность увеличивается в n раз.
Погрешность частного
Пусть в результате измерений получено:
$$x = x_0 pm Delta x, quad y = y_0 pm Delta y, quad x,y gt 0 $$
Найдём границы для частного этих величин: $z = frac{x}{y}$
$$ {left{ begin{array}{c} x_0- Delta x le x le x_0 + Delta x \ y_0- Delta y le y le y_0+ Delta y end{array} right.} Rightarrow {left{ begin{array}{c}x_0- Delta x le x le x_0+ Delta x \ frac{1}{y_0-Delta y} ge frac{1}{y} ge frac{1}{y_0+ Delta y} end{array} right.} Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} x_0- Delta x le x le x_0+ Delta x \ frac{1}{y_0+ Delta y} le frac{1}{y} le frac{1}{y_0- Delta y} end{array} right.} Rightarrow frac{x_0- Delta x}{y_0+ Delta y} le frac{x}{y} le frac{x_0+ Delta x}{y_0- Delta y} Rightarrow $$
$$ Rightarrow frac{ (x_0- Delta x)(y_0- Delta y)}{(y_0+ Delta y)(y_0- Delta y)} le frac{x}{y} le frac{(x_0+ Delta x)(y_0+ Delta y)}{(y_0- Delta y)(y_0+ Delta y)} Rightarrow $$
$$ Rightarrow frac{x_0 y_0-( Delta xy_0+x_0 Delta y- Delta x Delta y)}{y_0^2- Delta y^2} le frac{x}{y} le frac{x_0 y_0+( Delta xy_0+x_0 Delta y+ Delta x Delta y)}{y_0^2- Delta y^2} $$
О правилах умножения двух неравенств и обращения положительных сторон, см. §36 данного справочника.
Считаем произведения и квадраты абсолютных погрешностей малыми величинами $Delta x Delta y approx 0, quad Delta y^2 approx 0$, которыми можно пренебречь. Получаем:
$$ frac{x_0 y_0-( Delta xy_0+x_0 Delta y)}{y_0^2} le frac{x}{y} le frac{x_0 y_0+( Delta xy_0+x_0 Delta y)}{y_0^2} $$
$$frac{x_0}{y_0} – left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2} right) le frac{x}{y} le frac{x_0}{y_0} + left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2} right) $$
$$ z = z_0 pm Delta z: z_0 = frac{x_0}{y_0}, Delta z = frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}$$
$$ δ_z = frac{Delta z}{z_0} = left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}right) : frac{x_0}{y_0} = left( frac{Delta x}{y_0} + frac{x_0 Delta y}{y_0^2}right) cdot frac{y_0}{x_0} = frac{Delta x}{x_0} + frac{Delta y}{y_0} = δ_x+δ_y $$
$$ δ_{frac{x}{y}} = δ_x+δ_y $$
При делении приближенных величин их относительные погрешности складываются.
Внимание!
Как при умножении, так и при делении приближённых величин, их относительные погрешности складываются.
Точность произведения или частного всегда меньше точности исходных величин.
Примеры
Пример 1. Точное значение выражения:
$$5,31 cdot 4,16+2,19 cdot 1,51 = 22,0896+3,3069 = 25,3965 $$
Считая все величины, входящие в выражение, приближёнными с абсолютной погрешностью $Delta$ x = 0,01, выясните, нужно ли округлять ответ.
Во сколько раз абсолютная погрешность результата больше абсолютной погрешности исходных данных? Во сколько раз относительная погрешность результата больше относительной погрешности сомножителя 5,31?
Обозначим a = 5,31, b = 4,16, c = 2,19, d = 1,51.
Относительные погрешности (округление с избытком):
$$δ_a = frac{0,01}{5,31} cdot 100 text{%} = 0,19 text{%}, quad δ_b = frac{0,01}{4,16} cdot 100 text{%} = 0,25 text{%} $$
$$δ_c = frac{0,01}{2,19} cdot 100 text{%} = 0,46 text{%}, quad δ_d = frac{0,01}{1,51} cdot 100 text{%} = 0,67 text{%} $$
Относительные погрешности произведений:
$$ δ_{ab} = δ_a+δ_b = 0,19 text{%} + 0,25 text{%} = 0,44 text{%} $$
$$ δ_{cd} = δ_c+δ_d = 0,46 text{%} +0,67 text{%} = 1,13 text{%} approx ↑ 1,2 text{%} $$
Абсолютные погрешности произведений:
$$ Delta_{ab} = δ_{ab} cdot ab = 0,0044 cdot 22,0896 approx 0,09719 approx ↑ 0,098 $$
$$ Delta_{cd} = δ_{cd} cdot cd = 0,012 cdot 3,3069 approx 0,03968 approx 0,040 $$
Оставляем в промежуточных оценках 2 значащие цифры для последующего округления. Абсолютная погрешность выражения:
$$ Delta_{ab+cd} = Delta_{ab} + Delta_{cd} = 0,098+0,040 = 0,138 approx ↑ 0,2 $$
Таким образом, ответ нужно округлить до десятых:
$$ 5,31 cdot 4,16+2,19 cdot 1,51 approx 25,4 ± 0,2 $$
Отношение абсолютной погрешности результата к погрешности исходных данных:
$ frac{0,2}{0,01} = 20$ – абсолютная погрешность увеличилась в 20 раз.
Относительная погрешность результата: $δ = frac{0,2}{25,4} cdot 100 text{%} approx 0,79 text{%} $
По отношению к $δ_a: frac{δ}{δ_a} = frac{0,79}{0,19} approx 4,2$ – относительная погрешность результата в 4,2 раза больше.
Пример 2. а) Границы приближенных величин $5 le x le 6,6 le y le 7$. Оцените сумму, разность, произведение и частное этих величин.
б) Считая x и y точными величинами, принимающими значения на заданных отрезках, найдите границы суммы, разности и произведения этих величин.
а) По условию:
$$ {left{ begin{array}{c} x_0-Delta x = 5 \ x_0+Delta x = 6 end{array} right.} Rightarrow {left{ begin{array}{c} 2x_0 = 5+6 = 11 \ 2 Delta x = 6-5 = 1 end{array} right.} Rightarrow {left{ begin{array}{c} x_0 = 5,5 \ Delta x = 0,5 end{array} right.} Rightarrow δ_x = frac{0,5}{5,5} cdot 100 text{%} approx 9,1 text{%} $$
$$ {left{ begin{array}{c} y_0- Delta y = 6 \ y_0+ Delta y = 7 end{array} right.} Rightarrow {left{ begin{array}{c} 2y_0 = 6+7 = 13 \ 2 Delta y = 7-6 = 1 end{array} right.} Rightarrow {left{ begin{array}{c} y_0 = 6,5 \ Delta y = 0,5 end{array} right.} Rightarrow δ_y = frac{0,5}{6,5} cdot 100 text{%} approx 7,7 text{%} $$
Абсолютная погрешность суммы: $Delta_{x+y} = Delta_x+Delta_y = 0,5+0,5 = 1$
$$ x+y = (5,5+6,5) pm 1 = 12 pm 1 $$
Границы суммы: $ 11 le x+y le 13$
Абсолютная погрешность разности: $Delta _{x-y} = Delta _x + Delta _y = 0,5+0,5 = 1$
$$ x-y = (5,5-6,5) pm 1 = -1 pm 1 $$
Границы разности: $-2 le x-y le 0$
Относительная погрешность произведения:
$$δ_{xy} = δ_x+δ_y = 9,1 text{%} +7,7 text{%} = 16,8 text{%} approx 17 text{%}$$
Абсолютная погрешность произведения:
$$ Delta_{xy} = δ_{xy} cdot x_0 y_0 = 0,17 cdot 5,5 cdot 6,5 = 6,0775 approx ↑ 7 $$
$$ xy = (5,5 cdot 6,5) pm 7 approx 36 pm 7 $$
Границы произведения: $29 le xy le 43$
Относительная погрешность частного:
$$ δ_{x/y} = δ_x+δ_y = 9,1 text{%} +7,7 text{%} = 16,8 text{%} approx 17 text{%} $$
Абсолютная погрешность частного:
$$ Delta_{frac{x}{y}} = δ_{frac{x}{y}} cdot frac{x_0}{y_0} = 0,17 cdot frac{5,5}{6,5} approx 0,14 approx ↑ 0,2 $$
$$ frac{x}{y} = left( frac{5,5}{6,5} right) pm 0,2 approx 0,8 pm 0,2 $$
Границы частного: $0,6 le frac{x}{y} le 1,0$
б) Для точных величин получаем следующие границы:
Границы суммы:
$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow 5+6 le x+y le 6+7 Rightarrow 11 le x+y le 13 $$
Границы разности:
$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow {left{ begin{array}{c} 5 le x le 6 \ -7 le -y le -6 end{array} right.} Rightarrow 5-7 le x-y le 6-6 Rightarrow -2 le x-y le 0 $$
Границы произведения:
$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow 5 cdot 6 le xy le 6 cdot 7 Rightarrow 30 le xy le 42 $$
Границы частного:
$$ {left{ begin{array}{c} 5 le x le 6 \ 6 le y le 7 end{array} right.} Rightarrow {left{ begin{array}{c} 5 le x le 6 \ frac{1}{7} le frac{1}{y} le frac{1}{6} end{array} right.} Rightarrow frac{5}{7} le frac{x}{y} le 1 $$
Пример 3. В эксперименте по определению плотности вещества получен объём V = 9, 7 $pm$ 0,05 мл и масса m = 107 $pm$ 2 г. Найдите плотность.
Это свинец или железо?
Плотность:
$$ ρ = frac{m}{V}, ρ_0 = frac{m_0}{V_0} = frac{107 cdot 10^{-3} кг}{9,7 cdot 10^{-6} м^3} approx 11031 frac{кг}{м^3} $$
Относительные погрешности (округление с избытком):
$$ δ_V = frac{0,05}{9,7} cdot 100 text{%} approx 5,2 text{%}, δ_m = frac{2}{107} cdot 100 text{%} approx 1,9 text{%} $$
$$ δ_ρ = δ_V+δ_m = 5,2 text{%} +1,9 text{%} = 7,1 text{%} $$
Абсолютная погрешность для плотности (округление с избытком):
$$ Δ_ρ = δ_ρ cdot ρ_0 = 0,071 cdot 11031 approx 800 frac{кг}{м^3} $$
$$ ρ = 11000 pm 800 frac{кг}{м^3} $$
Это – свинец (табличное значение $ρ_{таб} = 11340 frac{кг}{м^3}$ ).
Погрешности произведения
Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел. Докажем данное утверждение.
|
f = x1 x2 xn , |
xi > 0 , i =1, ,n . |
||||||||||||||||
|
n |
|||||||||||||||||
|
Прологарифмируем данное выражение: ln f = ∑ln xi . |
|||||||||||||||||
|
i=1 |
|||||||||||||||||
|
∆ln f ≈ d(ln x)= (ln x)′∆x = ∆x . Тогда ∆f |
n |
∆xi |
. |
Используя свойства модуля |
|||||||||||||
|
= ∑ |
|||||||||||||||||
|
x |
f |
i=1 |
xi |
||||||||||||||
|
суммы, получаем |
|||||||||||||||||
|
∆f |
n |
∆x |
i |
, а |
∆x |
i |
≈δi . |
(1.9) |
|||||||||
|
f |
≤ ∑ |
xi |
xi |
||||||||||||||
|
i=1 |
|||||||||||||||||
|
n |
|||||||||||||||||
|
Тогда (1.9) можно |
записать |
в |
виде |
δ ≤ ∑δi . В доказательстве |
было |
||||||||||||
|
i=1 |
|||||||||||||||||
|
использовано условие, что xi |
> 0 . Однако данная формула справедлива для |
||||||||||||||||
|
любых xi ≠ 0 . |
|||||||||||||||||
|
Предельная относительная |
погрешность |
произведения равна |
сумме |
n
предельных относительных погрешностей сомножителей δ f = ∑δi .
i=1
Предельная абсолютная погрешность произведения вычисляется по формуле
|
∆ f = |
f |
δ f . |
(1.10) |
||
|
В частном случае, если f = kx ( k = const , k ≠ 0), то δ f = δx , ∆ f |
= |
k |
∆x . |
||
Правила округления при умножении
1.Выбрать число с наименьшим количеством значащих цифр (n).
2.Округлить остальные приближенные числа так, чтобы каждое из них содержало на одну или две значащие цифры больше, чем у числа из пункта 1
(n+1 или n+2).
– 14 –
3.Провести операцию умножения.
4.Если дальнейшие вычисления не требуются, то округлить произведение до n значащих цифр. Если проводятся дальнейшие преобразования, то произведение округляется до n+1 или n+2 значащих цифр.
5.Провести дальнейшие вычисления и окончательно округлить результат до n значащих цифр.
Пример. Вычислить произведение двух приближенных чисел x1 = 27,12 ,
x2 =14,721 и найти погрешность данной операции.
|
Произведение |
f |
= x1 x2 = 399,23352 ≈ 399,234 . Так |
как |
x1 имеет четыре |
|
значащие цифры, |
а |
x2 имеет пять значащих цифр, |
то |
при округлении |
произведения оставляются шесть значащих цифр, из которых две – запасные. Вычисляем погрешности: ∆x1 = 0,005, ∆x2 = 0,0005.
|
δ f |
= |
∆x1 |
+ |
∆x2 |
= |
0,005 |
+ 0,0005 = 2,1 10−4 . |
|||||||||||
|
x2 |
27,12 |
|||||||||||||||||
|
x1 |
14,721 |
|||||||||||||||||
|
∆ f |
= |
f |
δ f |
= 399,234 2,1 10−4 = 0,084 . |
||||||||||||||
|
Проводим окончательное округление: f |
= 399,2 ± 0,08. |
|||||||||||||||||
|
Ответ: |
f = 399,2 ± 0,08. |
|||||||||||||||||
Число верных знаков произведения |
||||||||||||||||||
|
Пусть |
f |
= x1 x2 xn , причем n ≤10 , |
а α1,α2 , ,α n – первые ненулевые |
|||||||||||||||
|
значащие |
цифры |
у |
соответствующих переменных x1, x2 , , xn . Любую |
|||||||||||||||
|
переменную |
xi |
можно |
представить |
в |
следующем |
виде: |
||||||||||||
|
xi =αi 10mi |
+ βi 10mi−1 + , где i=1,2,…,n. Тогда предельную относительную |
|||||||||||||||||
|
погрешность |
xi |
можно вычислить по формуле |
δxi = |
1 |
101−Ni , где |
Ni – |
||||||||||||
|
2 αi |
||||||||||||||||||
|
количество |
верных |
цифр |
в |
переменной |
xi . |
Следовательно, предельная |
||||||||||||
|
относительная |
погрешность |
произведения |
будет |
иметь |
вид |
|||||||||||||
|
– 15 – |
|
δ f |
= |
1 |
( |
1 |
+ |
1 |
+ + |
1 |
) 101−N , где N – наименьшее количество верных цифр |
|||||
|
2 |
||||||||||||||
|
α1 |
α2 |
αn |
||||||||||||
|
в переменных x , x |
2 |
, , x |
n |
. Оценив сумму |
1 |
+ |
1 |
+ + |
1 |
≤10 с учетом того, |
||||
|
1 |
α1 |
α2 |
αn |
|||||||||||
что n ≤10 , получаем значение предельной относительной погрешности
δ f ≤ 12 102−N . Таким образом, число верных знаков произведения будет не
менее N-2. При благоприятных обстоятельствах количество верных знаков произведения будет только на один меньше, чем у сомножителей. Поэтому при выполнении операции умножения достаточно взять сомножители с одной или двумя запасными знаками. Далее рассмотрим два примера, которые покажут, какой случай считать благоприятным, а какой – нет.
Пример 1. Вычислить количество верных цифр произведения двух приближенных чисел x1 = 87,34, x2 = 64,721.
Так как x1 имеет четыре значащие цифры, а x2 имеет пять значащих цифр, то наименьшее количество верных цифр равно четырем. Вычисляем
|
предельную |
относительную |
погрешность |
||||||||||||
|
δ f |
= |
1 |
( |
1 |
+ |
1) 101−4 |
= |
7 |
10 |
−3 ≤ |
1 |
10−3 . В данном случае |
получаем, что |
|
|
2 |
8 |
48 |
2 |
|||||||||||
|
6 |
произведение имеет на одну верную цифру меньше, чем сомножители. Ответ: данное произведение имеет три верных знака.
Пример 2. Вычислить количество верных цифр произведения двух приближенных чисел x1 =17,34, x2 =14,721. Хотя внешне этот пример похож на пример 1, он имеет определенные особенности. Как и в предыдущем случае, x1 имеет четыре значащие цифры, а x2 имеет пять значащих цифр, и наименьшее количество верных цифр равно четырем. Вычисляем предельную
|
относительную погрешность δ f |
= |
1 |
(1 |
+ |
1) 101−4 |
=10−3 ≤ |
1 |
10−2 . В этом |
|
2 |
1 |
1 |
2 |
– 16 –
случае количество верных цифр у произведения будет равно двум, и произведение имеет на две верные цифры меньше, чем сомножители.
Ответ: данное произведение имеет два верных знака.
Погрешности частного
Относительная погрешность частного двух приближенных чисел не превышает суммы относительных погрешностей делимого и делителя. Доказательство данного утверждения аналогично доказательству относительной погрешности произведения.
|
Дано: f |
= |
x1 |
, x2 ≠ 0. |
|||||||||||||||||
|
x2 |
||||||||||||||||||||
|
Прологарифмируем данное |
выражение: |
ln f |
= ln x1 −ln x2 . |
Используя |
||||||||||||||||
|
свойство: ∆ln f ≈ d(ln x)= (ln x)′∆x = ∆xx , получаем |
||||||||||||||||||||
|
∆f |
= ∆x1 |
− ∆x2 . |
||||||||||||||||||
|
f |
x |
x |
2 |
|||||||||||||||||
|
1 |
||||||||||||||||||||
|
Используя свойства модуля суммы, получаем |
||||||||||||||||||||
|
∆f |
≤ |
∆x1 |
+ |
∆x2 |
, а |
∆xi |
≈δi . |
(1.11) |
||||||||||||
|
f |
x1 |
x2 |
xi |
|||||||||||||||||
|
Тогда (1.11) |
можно записать в виде δ ≤ δx1 +δx2 . Следовательно, предельная |
относительная погрешность частного равна сумме предельных относительных погрешностей делимого и делителя δ f = δx1 +δx2 .
Предельная абсолютная погрешность частного вычисляется по формуле
|
∆ f = |
f |
δ f . |
(1.12) |
||
|
Правила округления при делении аналогичны правилам округления при |
|||||
|
умножении. |
|||||
|
Пример. Вычислить частное двух |
приближенных чисел |
x1 = 27,12 , |
x2 =14,721 и найти погрешность данной операции.
– 17 –
Лабораторная работа №1
Методы оценки погрешностей
I. Описание работы
Тема: Методы оценки погрешностей приближенных величин.
Задание 1. Округляя точные числа ![]() до трех значащих цифр, определить абсолютную
до трех значащих цифр, определить абсолютную ![]() и относительную
и относительную ![]() погрешности полученных приближенных чисел.
погрешности полученных приближенных чисел.
Дано: ![]()
![]()
Найти: ![]()
Решение:
![]() – приближенное значение числа A
– приближенное значение числа A
Абсолютная погрешность: ![]()
Относительная погрешность: ![]()
Ответ: ![]() ;
; ![]()
Задание 2. Определить абсолютную погрешность приближенных чисел ![]() по их относительной погрешности
по их относительной погрешности ![]() .
.
Дано: ![]()
![]()
Найти: ![]()
Решение:
Абсолютная погрешность: ![]()
Ответ: ![]()
Задание 3. Решить задачу.
При измерении длины с точностью до 5 м получено ![]() км, а при определении другой длины с точностью до 0.5 см, получено
км, а при определении другой длины с точностью до 0.5 см, получено ![]() метров. Какое измерение по своему качеству лучше?
метров. Какое измерение по своему качеству лучше?
Дано: ![]() Км,
Км, ![]() М,
М, ![]() М,
М, ![]() См
См
Сравнить: ![]() и
и ![]()
Решение: Итак, по 1-му измерению, результат ![]() Км =
Км = ![]() М с точностью до
М с точностью до ![]() М (
М (![]() – абсолютная погрешность величины
– абсолютная погрешность величины ![]() ).
).
Тогда относительная погрешность: ![]() %
%
По 2-му измерению, результат ![]() Км с точностью до
Км с точностью до ![]() См =
См =![]() М (
М (![]() – абсолютная погрешность величины
– абсолютная погрешность величины ![]() ).
).
Тогда относительная погрешность: ![]() %
%
Так как ![]() , то измерение
, то измерение ![]() можно считать по качеству лучше, чем
можно считать по качеству лучше, чем ![]() .
.
Ответ: измерение ![]() по качеству лучше, чем
по качеству лучше, чем ![]() .
.
Задание 4. а) Определить количество верных знаков в числе ![]() , если известна его предельная абсолютная погрешность
, если известна его предельная абсолютная погрешность ![]()
Дано: ![]()
![]()
Найти: ![]()
Решение:
По определению, n первые значащие цифры являются верными в узком смысле, если абсолютная погрешность этого числа не превышает половины единицы разряда младшей цифры, считая слева направо.
Абсолютная погрешность: ![]() , поэтому значащие цифры 8 и 4 числа 0,00842 верны в узком смысле.
, поэтому значащие цифры 8 и 4 числа 0,00842 верны в узком смысле.
Ответ: число X имеет две верных цифры в узком смысле (8 и 4), то есть ![]()
Б) Определить количество верных знаков в числе ![]() , если известна его предельная относительная погрешность
, если известна его предельная относительная погрешность ![]() .
.
Дано: ![]()
![]() %
%
Найти: ![]()
Решение:
Предельная абсолютная погрешность:
![]()
Только первая значащая цифра 1 числа A верна в узком смысле.
Ответ: число A имеет одну верную цифру в узком смысле (1), то есть ![]()
Задание 5. Найти предельные относительные погрешности, допускаемые при взятии вместо ![]() чисел 3.1, 3.14, 3.1416:
чисел 3.1, 3.14, 3.1416:
А) считая, что у них все записанные знаки являются верными;
Б) зная, что ![]()
Провести сравнения погрешностей и сделать необходимые выводы.
Дано: ![]() ,
, ![]() ,
, ![]()
Найти: ![]()
Решение:
А) ![]() :
:
Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:
![]()
Предельная абсолютная погрешность: ![]()
Тогда предельная относительная погрешность:
![]() %
%
![]() :
:
Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:
![]()
Предельная абсолютная погрешность: ![]()
Тогда предельная относительная погрешность:
![]() %
%
![]() :
:
Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:
![]()
Предельная абсолютная погрешность: ![]()
Тогда предельная относительная погрешность:
![]() %
%
Б) Пусть ![]() (прервем запись числа
(прервем запись числа ![]() на 7-м знаке после запятой и считаем полученное число точным значением числа
на 7-м знаке после запятой и считаем полученное число точным значением числа ![]() ).
).
Тогда абсолютная погрешность первого представления числа ![]() :
: ![]() .
.
Относительная погрешность: ![]() %
%
Абсолютная погрешность второго представления числа ![]() :
: ![]() .
.
Относительная погрешность: ![]() %
%
Абсолютная погрешность третьего представления числа ![]() :
: ![]() %.
%.
Относительная погрешность: ![]() %
%
Выводы:
1) Можно заметить, что ![]() , то есть
, то есть ![]() ;
;
![]() , то есть
, то есть ![]() ;
;
![]() , то есть
, то есть ![]()
Иными словами, для трех чисел ![]() их «истинная» относительная погрешность ограничена предельной относительной погрешностью, определенной из условия верности знаков чисел. Причем, для каждого числа две оценки отличаются меньше, чем на порядок. Значит, предположение о верности всех знаков чисел
их «истинная» относительная погрешность ограничена предельной относительной погрешностью, определенной из условия верности знаков чисел. Причем, для каждого числа две оценки отличаются меньше, чем на порядок. Значит, предположение о верности всех знаков чисел ![]() Обосновано.
Обосновано.
2) Сравнение относительных погрешностей чисел ![]() :
:
![]() показывает,
показывает,
Что числа ![]() Перечислены
Перечислены
В порядке увеличения точности представления числа ![]() ,
,
То есть ![]() точнее
точнее ![]() ,
, ![]() точнее
точнее ![]() .
.
Ответ: а) ![]()
б) ![]()
Задание 6. Найти сумму приближенных чисел ![]() ,
, ![]() , считая в них все знаки верными, т. е. что абсолютная погрешность каждого слагаемого не превосходит половины единицы младшего разряда этого слагаемого. Определить абсолютную и относительную погрешности суммы.
, считая в них все знаки верными, т. е. что абсолютная погрешность каждого слагаемого не превосходит половины единицы младшего разряда этого слагаемого. Определить абсолютную и относительную погрешности суммы.
Дано: ![]() ,
, ![]() ,
, ![]()
Найти: ![]()
Решение:
1) Считаем, что в числах ![]() ,
, ![]() ,
, ![]() все знаки верны в узком смысле, то есть
все знаки верны в узком смысле, то есть
![]()
![]()
![]()
Число с наибольшей абсолютной погрешностью ![]() .
.
2) Остальные числа округлим, сохраняя один запасный десятичный знак по сравнению с ранее выделенным наименее точным слагаемым ![]() :
:
![]() , абсолютная погрешность округления
, абсолютная погрешность округления ![]()
![]() , абсолютная погрешность округления
, абсолютная погрешность округления ![]()
3) Сложим все эти числа, учитывая все сохраненные знаки:
![]()
4) Полученный результат округлим на один знак (формально):
![]() , абсолютная погрешность округления
, абсолютная погрешность округления ![]()
5) Полную абсолютную погрешность суммы будем складывать из трех компонентов:
A) суммы предельных абсолютных погрешностей исходных чисел;
B) абсолютной величины суммы ошибок округления слагаемых;
C) заключительной погрешности округления результата.
![]()
![]()
![]()
![]() – абсолютная погрешность суммы.
– абсолютная погрешность суммы.
![]() % – относительная погрешность суммы.
% – относительная погрешность суммы.
Ответ: ![]() ;
; ![]() %.
%.
Задание 7. Найти предельную абсолютную и относительную погрешности при вычислении объема прямого кругового цилиндра, если значения его высоты ![]() и радиуса основания
и радиуса основания ![]() имеют все верные знаки.
имеют все верные знаки.
Дано: ![]() ,
, ![]()
Найти: ![]()
Решение:
![]() ,
, ![]()
Примем ![]()
1) Так как в числах ![]() и
и ![]() все числа верны, то их абсолютные погрешности:
все числа верны, то их абсолютные погрешности:
![]()
![]()
Число с наибольшей абсолютной погрешностью ![]() .
.
Число R округлим, сохраняя один запасный десятичный знак по сравнению с ранее выделенным наименее точным слагаемым ![]() :
:
![]() , абсолютная погрешность округления
, абсолютная погрешность округления ![]() (округления не требуется)
(округления не требуется)
2) перемножим числа, учитывая все сохраненные знаки:
![]()
3) Полученный результат округляем, сохраняя столько значащих цифр, сколько верных цифр имеется в числе H, то есть 2 значащих цифры:
![]() ;
;
Абсолютная погрешность округления ![]()
4) Полную абсолютную погрешность произведения будем складывать из двух слагаемых:
A) предельной абсолютной погрешности произведения до его округления;
B) заключительной погрешности округления произведения.
Абсолютную погрешность произведения до округления вычислим на основе предварительно найденной относительной погрешности произведения округленных сомножителей:
![]() %.
%.
![]()
Полная абсолютная погрешность ![]()
Теперь перейдем к искомому объему.
![]() (Здесь полученный результат округляем до трех значащих цифр).
(Здесь полученный результат округляем до трех значащих цифр).
![]() – предельная абсолютная погрешность объема.
– предельная абсолютная погрешность объема.
![]() % – предельная относительная погрешность объема.
% – предельная относительная погрешность объема.
Ответ: ![]() ,
, ![]() ,
, ![]() %
%
Задание 8. Привести пример потери точности при вычитании двух близких чисел.
Решение:
Пусть ![]() и
и ![]() – два близких числа; примем, что у них одинаковое число знаков после запятой.
– два близких числа; примем, что у них одинаковое число знаков после запятой.
Считаем, что все знаки в числах ![]() и
и ![]() верны в узком смысле. Тогда абсолютные погрешности:
верны в узком смысле. Тогда абсолютные погрешности:
![]()
![]()
Относительные погрешности:
![]() %
%
![]() %
%
Так как ![]() , то
, то ![]()
![]()
Абсолютная погрешность результата: ![]()
Относительная погрешность результата: ![]() %
%
При вычитании двух близких чисел ![]() и
и ![]() относительная погрешность возросла на 3 порядка!
относительная погрешность возросла на 3 порядка!
Лабораторная работа №2
Метод Гаусса
I. Описание работы
Тема: Решение системы линейных неоднородных алгебраических уравнений методом Гаусса (схема единственного деления).
Задание. Решить систему трех уравнений с тремя неизвестными с точностью искомых неизвестных до ![]() .
.
Промежуточные вычисления вести с двумя запасными знаками.
 ,
, 
Решение:
Исходные данные и все результаты вычислений запишем в таблицу 1.
Прямой ход
1. Записываем коэффициенты данной системы в трех строках и четырех столбцах раздела 1 таблицы 1.
2. Суммируем все коэффициенты по строке и записываем сумму в столбце ![]() (столбец контроля), например
(столбец контроля), например ![]() .
.
3. Делим все числа, стоящие в первой строке, на ![]() и результаты
и результаты ![]() записываем в 4-й строке раздела 1.
записываем в 4-й строке раздела 1.
4. Вычисляем ![]() и делаем проверку, если вычисления ведутся с 6 и более знаками после запятой, то числа
и делаем проверку, если вычисления ведутся с 6 и более знаками после запятой, то числа ![]() и
и ![]() не должны отличаться более, чем на единицу последнего разряда:
не должны отличаться более, чем на единицу последнего разряда:
![]()

5. По формулам ![]() вычисляем коэффициенты
вычисляем коэффициенты ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Результаты записываем в первые две строки раздела:
6. Делаем проверку. Сумма элементов каждой строки  не должна отличаться от
не должна отличаться от ![]() более, чем на 1-2 единицы последнего разряда. Заметим, что
более, чем на 1-2 единицы последнего разряда. Заметим, что ![]() ,
, ![]()
 ,
, ![]()
 ,
, ![]()
7. Делим все элементы 1 строки раздела 2 на ![]() и результаты записываем в 3 строке раздела 2.
и результаты записываем в 3 строке раздела 2.
8. Делаем проверку:

![]()
9. По формулам ![]() вычисляем
вычисляем ![]() :
:
![]()
![]()
![]()
Результаты записываем в 1 строку раздела 3.
10. Делаем проверку:
 ,
, ![]()
11. Делим все элементы 1 строки раздела 3 на ![]() и результаты записываем в следующей (второй) строке этого раздела.
и результаты записываем в следующей (второй) строке этого раздела.
12. Делаем проверку:

![]()
Обратный ход
1. В разделе 4 записываем единицы
2. Записываем ![]() .
.
3. Для вычисления ![]() и
и ![]() используем лишь строки разделов, содержащие 1.
используем лишь строки разделов, содержащие 1.
4. Вычислим ![]() по формуле:
по формуле: ![]() .
.
5. Вычислим ![]() по формуле:
по формуле:
![]() .
.
6. Аналогично проводим обратный ход в контрольной системе. Записываем ![]() ,
,
вычисляем ![]() и
и ![]() с заменой
с заменой ![]() и
и ![]() на
на ![]() и
и ![]() соответственно:
соответственно:
![]()
![]()
Делаем обычную проверку по строкам – должно быть ![]() , с точностью до 1-2 единиц последнего разряда.
, с точностью до 1-2 единиц последнего разряда.
Действительно:
![]()
![]()
![]()
Заполним таблицу 1 результатами вычислений:
Таблица 1
|
Раз Дел |
|
|
|
|
|
|
|
1 |
1 2 3 |
|
|
|
|
|
|
2 |
2 3 |
|
|
|
|
|
|
3 |
3 |
|
|
|
||
|
4 |
1 1 1 |
1 |
1 |
|
|
Округлим полученное решение до ![]() , по требованию задачи:
, по требованию задачи:
![]()
![]()
![]()
Окончательную проверку точности полученного решения системы выполним подстановкой этого решения в систему. Должно получиться приближенное тождество с точностью до ![]() .
.

Ответ: ![]()
![]()
![]()
| < Предыдущая | Следующая > |
|---|
Действия с приближенными числами.
На практике пользуются более простыми правилами, которые называются
Правила подсчета цифр:
Задача:
Решение:
Задача:
Решение:
Задача:
Найдите произведение двух приближенных чисел: 0,3862 * 0,85
Решение:
Задача:
Решение:
Задача:
Решение:
Задача:
Решение:
(Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие))
При решении некоторых задач возникает необходимость указать верные цифры результата,
т.е. найти границу абсолютной погрешности результата вычислений.
На практике сначала находят относительную погрешность результата, а затем, используют формулу:
Формулы для вычисления границ абсолютной и относительной погрешностей некоторых функций приведены в таблице.
Задача:
Решение:
Так как a=0,3862 то ∆a=0,00005 , b = 0,8 значит ∆b=0,05
Находим границу абсолютной погрешности произведения по формуле
(Н.В. Богомолов Практические занятия по математике)
Загрузить PDF
Загрузить PDF
Абсолютная погрешность – это фактическая ошибка, допущенная при измерении какой-либо величины. Относительная погрешность сравнивает абсолютную погрешность со значением измеряемой величины. Чтобы вычислить относительную погрешность, следует найти и абсолютную погрешность. Если вы измеряете предмет, длина которого равна 12 см, и вы допустили ошибку в 6 см, то относительная погрешность будет огромной. Но если длина измеряемого предмета равна 12 м, а ошибка – 6 см, то относительная погрешность будет значительно меньше, даже с учетом того, что абсолютная погрешность (6 см) не изменилась.[1]
-

1
Если вам дано ожидаемое значение, вычтите из него полученное вами значение, чтобы вычислить абсолютную погрешность. Как правило, ожидаемое значение находится в ходе тестовых или лабораторных испытаний. Ожидаемое значение является наиболее точным значением некоторой величины, которое используется при различных вычислениях. Чтобы получить абсолютную погрешность, сравните результаты ваших измерений с ожидаемым значением – так вы узнаете, насколько ваши результаты отличаются от ожидаемого значения. Для этого просто вычтите полученное вами значение из ожидаемого. Если разность отрицательная, превратите ее в положительную, проигнорировав знак «минус». Вы получите абсолютную погрешность.[2]
- Например, вы хотите узнать точность измерения расстояния при помощи шагов. Вы идете от одного дерева к другому, считаете шаги и выясняете, что деревья расположены на расстоянии 5,4 м друг от друга. Это экспериментальное значение. Потом вы берете рулетку и измеряете точное расстояние между деревьями, которое равно 6 м. Это действительное значение. Абсолютная погрешность равна: 6 – 5,4 = 0,6 м = 60 см.[3]
- Например, вы хотите узнать точность измерения расстояния при помощи шагов. Вы идете от одного дерева к другому, считаете шаги и выясняете, что деревья расположены на расстоянии 5,4 м друг от друга. Это экспериментальное значение. Потом вы берете рулетку и измеряете точное расстояние между деревьями, которое равно 6 м. Это действительное значение. Абсолютная погрешность равна: 6 – 5,4 = 0,6 м = 60 см.[3]
-

2
Теперь допустим, что абсолютная погрешность – это наименьшая единица измерения. Например, рулетка имеет миллиметровые деления, то есть ее наименьшей единицей является 1 мм. Таким образом, вы можете измерить расстояние с точностью до ± 1 мм; в этом случае абсолютная погрешность составляет 1 мм.
- Это верно для любых измерительных инструментов или систем. Например, на корпус многих научных инструментов, таких как прецизионные весы и измерительные приборы, наносят маркировку об абсолютной погрешности в виде «± ____».
-

3
Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Используйте те же единицы измерения, которыми вы пользовались в ваших измерениях.[4]
-

4
Попрактикуйтесь на нескольких примерах. Это наилучший способ научиться вычислять погрешность. Решите следующие задачи (ответы приведены в конце каждой задачи).
- На уроке химии в результате реакции ученик получил вещество массой 32 г. Известно, что действительное значение выхода этой реакции равно 34 г. Абсолютная погрешность равна ± 2 г.
- На уроке химии ученику необходимо 10 мл воды, чтобы вызвать реакцию; при этом погрешность капельницы составляет «± 0,5 мл». В этом случае абсолютная погрешность измерений равна ± 0,5 мл.
-

5
Уясните, что приводит к появлению погрешности и как ее устранить. Всякое научное исследование подразумевает наличие ошибок – даже в научных работах, за которые вручаются Нобелевские премии, сообщается о допущениях или погрешностях. Но если вы определите причину появления погрешности, вы, возможно, сможете устранить ее.[5]
- Человеческий фактор – наиболее распространенная причина появления ошибок. Сюда относятся неподобающие условия для проведения измерений и плохо продуманные эксперименты.
- Одной из причин появления ошибок может являться внезапное отключение энергии, недостаточное количество рабочего материала или изменение других условий, например, нехватка воды в результате ее испарения, внезапное изменение температуры окружающей среды и так далее.
- Еще одной причиной является несовершенство оборудования, используемого для измерений или исследований, например, прецизионных инструментов или горелок, которые обеспечивают неравномерное распределение тепла.[6]
Реклама
-

1
Разделите абсолютную погрешность на действительное значение исследуемой величины. Так вы вычислите относительную погрешность. Эта формула позволит вам выяснить, насколько полученное вами значение отличается от действительного значения изучаемой величины. Конечно, прекрасно, если относительная погрешность мала. Продолжим рассматривать пример с измерением расстояния между двумя деревьями.
- Абсолютная погрешность равна 0,6 м, а действительное значение равно 6 м.
- 0,6 м / 6 м
- Относительная погрешность равна 0,1 м.[7]
-

2
Полученный результат умножьте на 100, чтобы выразить относительную погрешность в процентах. Вы можете представить относительную погрешность в виде обыкновенной дроби, десятичной дроби или в процентах – в этом случае умножьте десятичную дробь на 100. Так вы узнаете, какой процент от полученного вами значения составляет погрешность. Если вы измеряете длину 60 м лодки, а погрешность составляет 0,6 м, то процент ошибки будет значительно меньше, чем при вычислении расстояния между деревьями (6 м) с погрешностью 0,6 м. Погрешность представляет собой небольшой процент от экспериментального значения. [8]
- 0,6 м / 6 м = 0,1 м
- 0,1 * 100 = 10% – относительная погрешность.
-

3
Вычислите относительную погрешность без нахождения абсолютной погрешности. Для этого выражение для вычисления абсолютной погрешности запишите в числителе выражения для нахождения относительной погрешности. Уяснив разницу между абсолютной и относительной погрешностями, нет необходимости отдельно вычислять абсолютную погрешность. Просто замените значение абсолютной погрешности на выражение для ее вычисления. Обратите внимание, что вертикальные черты обозначают абсолютную величину, то есть любое полученное значение нужно превратить в положительное.
- Относительная погрешность:
, где Е — экспериментальное значение, D — действительное значение.
- Умножьте это выражение на 100, чтобы выразить относительную погрешность в процентах.[9]
- Относительная погрешность:
-

4
Не забудьте приписать соответствующие единицы измерения. Предположим, что абсолютная погрешность равна 2 м. Такая информация позволит наглядно представить величину ошибки. Но если вы записываете, что погрешность равна 2, то эта цифра ничего не значит. Также не имеет смысла указывать погрешность в виде процентов от ошибки (10% от 0,6 м) – следует писать, например, так: относительная погрешность равна 10%.[10]
Реклама
Советы
- Удостоверьтесь, что экспериментальное значение и действительное значение измеряются в одних единицах измерения. Например, если экспериментальное значение измеряется в сантиметрах, а действительное значение – в миллиметрах, преобразуйте одну из этих единиц измерения в другую.
Реклама
Предупреждения
- Убедитесь, что вы правильно округляете числа.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 166 879 раз.
Была ли эта статья полезной?
Определение относительной погрешности измерений
Относительная погрешность измерений – это отношение абсолютной погрешности измерений к истинному значению измеряемой величины, в долях или процентах:
$ δ = frac{Delta x}{x_{ист}}$ или $ δ = frac{Delta x}{x_{ист}} cdot 100 text{%} $
Правила округления
На практике относительную погрешность округляют до двух значащих цифр, выполняя округление с избытком, т.е. всегда увеличивая последнюю значащую цифру на единицу.
Например:
Для x = 1, $7 pm 0,2$ относительная погрешность измерений
$δ = frac{0,2}{1,7} cdot 100 text{%} approx 11,8 text{%} approx 12 text{%}$ — погрешность достаточно велика.
Внимание!
Чем меньше относительная погрешность измерения, тем оно точнее.
Примеры
Пример 1. Согласно данным эксперимента, проведенного в 1975 году, скорость света равна $c = 299 792 458 pm 1,2 м/с$. Найдите относительную погрешность измерений в этом эксперименте в долях и процентах.
$$ δ = frac{1,2}{299 792 458} approx 4,0 cdot 10^{-9} $$
$$δ = 4,0 cdot 10^{-9} cdot 100 text{%} approx (4,0 cdot 10^{-7} ) text{%} $$
Пример 2. В результате школьного эксперимента ускорение свободного падения оказалось равным $g = 10,0 pm 0,1 м/с^2$. Определите относительную погрешность для данного эксперимента, а также относительную погрешность по отношению к табличной величине $g_0 = 9,81 м/с^2$. Что вы можете сказать о систематической ошибке эксперимента?
Для данного эксперимента $δ = frac{0,1}{10,0} cdot 100 text{%} = 1,0 text{%} $
Относительная погрешность по отношению к табличной величине:
$$ δ_{таб} = frac{|g-g_0 |}{g_0} cdot 100 text{%}, δ_{таб} = frac{|10,0-9,81|}{9,81} cdot 100 text{%} approx 1,9 text{%} $$
Согласно полученным результатам $9,9 le g le 10,1$, табличное значение в этот отрезок не входит. В эксперименте присутствует систематическая ошибка: результаты систематически завышены.
Пример 3. При взвешивании масса слона оказалась равной $M = 3,63 pm 0,01$ т, а масса муравья $m = 41,2 pm 0,5$ мг. Какое измерение точнее?
Найдем относительные погрешности измерений:
$$ δ_M = frac{0,01}{3,63} cdot 100 text{%} approx 0,28 text{%} $$
$$ δ_m = frac{0,5}{41,2} cdot 100 text{%} approx 1,21 text{%} approx ↑1,3 text{%} $$
Таким образом, масса слона определена точнее.
Пример 4. Вольтметр измеряет напряжение с относительной погрешностью 0,5%. Найдите границы точного значения величины, если при измерении получено $V_0$ = 5 В.
Абсолютная погрешность измерений данным вольтметром:
$$ Delta V = V_0 cdot δ, Delta V = 5 cdot 0,005 = 0,025 (В) approx 0,03(В) $$
Границы точного значения:
$$ V = 5,00 pm 0,03 (В) или 4,97 le V le 5,03 (В) $$
Вычисление абсолютной и относительной погрешностей измерений при прямых измерениях
1. Абсолютная погрешность
Оценить отклонение
каждого из результатов измерения от
истинной величины можно лишь при наличии
данных большого числа измерений с
использованием теории вероятности.
Однако на практике, в лабораторных
условиях проводят 3-5 измерений. В этом
случае абсолютная погрешность отдельного
i-го
измерения будет следующей:
|DАi|
= |АСР
— Аi|,
где
АСР
— средняя величина размера А. Средняя
арифметическая величина всех ½DАi½
значений
![]()
называется
абсолютной погрешностью опыта.
Окончательный результат измерения
может быть записан в виде
А = АСР
±
DАСР,
где
А — искомая величина, которая лежит
внутри интервала
АСР
±
DАСР.
Н
14
апример, если сделаем несколько
измерений длины заготовки в столярной
мастерской и получим среднее значение
lСР
= 75.5 см, а среднее
арифметическое абсолютной погрешности
lСР
= 0.3 см, то результат
запишется в виде
l
= (75.5 ± 0.3) см.
Это
означает, что истинное значение длины
заготовки лежит в интервале от 75.2 см до
75.8 см. При этом не имеет смысла вычислять
среднее значение с большим числом знаков
после запятой, так как от этого точность
не увеличивается.
2. Относительная погрешность
Абсолютная
погрешность измерения не характеризует
точности проведенных измерений. Поэтому
для того, чтобы сравнить точность
различных измерений и величин разной
размерности, находят среднюю относительную
погрешность результата (ЕА).
Относительная погрешность определяется
отношением абсолютной погрешности к
среднему арифметическому значению
измеряемой величины, которая определяется
в процентах:
ЕА= 100%.
100%.
Относительная
погрешность показывает, какая часть
абсолютной погрешности приходится на
каждую единицу измеренной величины.
Это дает возможность оценить точность
проведенных измерений, качество работы.
Так,
например, пусть при измерении бруска
длиной l
= 1.51 см была допущена абсолютная
погрешность 0.03 мм, а при измерении
расстояния от Земли до Луны L
= 3.64.105
км абсолютная погрешность составила
100 км. Может показаться, что первое
измерение выполнено намного точнее
второго. Однако о точности измерения
можно судить по относительной погрешности,
а она показывает, что второе измерение
было выполнено в семь раз точнее первого:
El
=
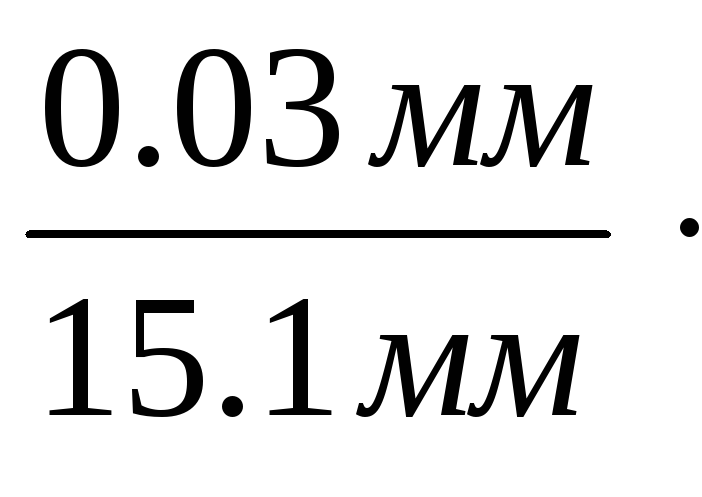
100% = 0.2%
и
ЕL
=
 100%
100%
= 0.03%.
Вычисление абсолютных и относительных погрешностей при косвенных2 измерениях
В
большинстве случаев при выполнении
физических экспериментов исследуемая
величина не может быть измерена
непосредственно, а является функцией
одной или нескольких переменных,
измеренных непосредственно. При косвенных
измерениях абсолютная и относительная
погрешности результатов измерений
находятся вычислением через абсолютные
и относительные погрешности непосредственно
измеренных величин.
Использование формул дифференцирования
Для
определения абсолютных и относительных
погрешностей искомой величины при
косвенных измерениях можно воспользоваться
формулами дифференцирования, потому
что абсолютная ошибка функции равна
абсолютной ошибке аргумента, умноженной
на производную этой функции, то есть
полному дифференциалу функции.
Рассмотрим
это более подробно. Допустим, что
физическая величина А является функцией
многих переменных:
A
= f
(x,
y,
z
…).
Правило
I. Вначале
находят абсолютную погрешность величины
А, а затем относительную погрешность.
Для этого необходимо:
1) Найти полный
дифференциал функции
![]()
.
2
16
) Заменить бесконечно малые dx, dу,
dz, … соответствующими абсолютными
ошибками аргументовDx,
Dy,
Dz,
… (при этом знаки «минус» в абсолютных
ошибках аргументов заменяют знаками
«плюс», так чтобы величина ошибки
была максимальной):
![]()
.
Применяя
это правило к частным случаям, получим:
—
абсолютная погрешность суммы равна
сумме абсолютных погрешностей слагаемых.
Если X
= a
+ b,
то DX
= Da
+ Db;
—
абсолютная погрешность разности равна
сумме абсолютных погрешностей
уменьшаемого и вычитаемого. Если X
= a
— b,
то DX
= Da
+ Db;
—
абсолютная погрешность произведения
двух сомножителей равна сумме произведений
среднего значения первого множителя
(aCP)
на абсолютную погрешность второго и
среднего значения второго множителя
(bCP)
на абсолютную погрешность первого. Если
X
= а
b,
то DX
= aCP
Db
+ bCP
Dа.
Если X
= a n
, то DX
= n
аCPn-1
Dа;
—
абсолютная погрешность дроби равна
сумме произведения знаменателя на
абсолютную погрешность числителя и
числителя на абсолютную погрешность
знаменателя, деленной на квадрат
знаменателя. Если X
=![]() ,
,
то DX=![]() .
.
3) По определению
найдем относительную погрешность
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
12.02.2015183.3 Кб27Пример работы по теме ПЕРЕСКАЗ.doc
- #
Абсолютная и относительная погрешность


4.2
Средняя оценка: 4.2
Всего получено оценок: 2108.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2108.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-

Светлана Лобанова-Асямолова
10/10
-

Валерий Соломин
10/10
-

Анастасия Юшкова
10/10
-

Ксюша Пономарева
7/10
-

Паша Кривов
10/10
-

Евгений Холопик
9/10
-

Guzel Murtazina
10/10
-

Максим Аполонов
10/10
-

Olga Bimbirene
9/10
-

Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2108.
А какая ваша оценка?

Чтобы оценить степень отклонения, используется показатель абсолютной и относительной погрешности.
В математике, физике и метрологии этот коэффициент может быть использован для округления полученных результатов.
Показатель бывает нескольких видов. Для его определения применяют разные методы.
Понятие и классификация
Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.
Существует несколько разновидностей погрешности:

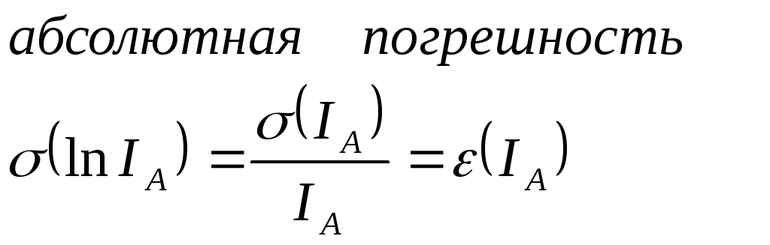
- Абсолютная — оценка ошибки в абсолютных единицах. Величина ее может быть разной в зависимости от способа расчета.
- Относительная — отношение абсолютной величины к тому значению, которое принято считать истинным. Измеряется в процентах.
- Приведенная — разновидность относительной. Ее вычисляют отношением абсолютной и условной постоянной величины, определяется в процентах.
- Приборная или инструментальная — погрешность, которую дают технические средства измерений. Она обусловлена неточной цифровой градуировкой приборов или недостаточной наглядностью. Класс точности приборов будет равен максимальной приведенной погрешности и выражается в процентах. К примеру, класс точности вольтметра ΔU = ±0,75 В.
- Методическая — связанная с несовершенством метода измерения или его чрезмерным упрощением.
- Субъективная или операторная — погрешность, связанная с личными свойствами оператора — невнимательностью, утомлением, профессиональной подготовленностью.
- Случайная. Погрешность, которая может изменяться при разных измерениях. Изменения возможны по знаку или величине отклонения. Причиной может быть техническое несовершенство приборов отсчета или объекта измерения, неблагоприятные для работы условия или особенности измеряемых единиц.
- Систематическая. Погрешность, изменения которой имеют некоторую закономерность во времени. В качестве частного случая допускают постоянное отклонение, которое не изменяется во времени.
- Прогрессирующая или дрейфовая — медленно изменяется во времени и не может быть предсказана. Такое отклонение относится к случайным.
- Грубая или промах. Значительное отклонение от принятой нормы. Возникает в результате неисправности аппаратуры или ошибки экспериментатора.
Выделяют также отклонения прямых или косвенных измерений. Вторая разновидность учитывается в тех случаях, когда измерить величину напрямую невозможно и ее можно посчитать по формулам исходя из других данных.
Абсолютная и относительная погрешности
Абсолютная погрешность величины — это разница между ней и принятым точным значением. Чтобы определить этот показатель, из большего числа вычитают меньшее. Единицы обозначения такие же, как и для основной величины. В формулах обозначается греческой буквой дельта и исследуемой величиной.
Пример: В пакете находится 478 граммов сахара. Это число можно округлить до 500. В этом случае абсолютная погрешность приближения будет 500 — 478 =22 г

Для вычислений разработана специальная формула: Δа=А-а,
где А — это точная величина,
а — приближенная, это число, которое немного отличается от точного.
Результаты вычисления записывают со знаком ±. Например, длина бумажного рулона составляет 25 м ± 5 см. Наибольшее значение абсолютной погрешности принято называть ее пределом.
Чтобы получить измерения высокой точности, рассчитать абсолютную погрешность недостаточно. Если измерять предмет длиной 30 см и допустить неточность в 1 см, ее величина будет значительной. При измерении 30-метрового участка дороги то же самое отклонение в 1 см допускается, такое измерение будет наиболее точным. При вычислении ускорения свободного падения с помощью маятника неточность не превышает 10 -5 м/с. 2
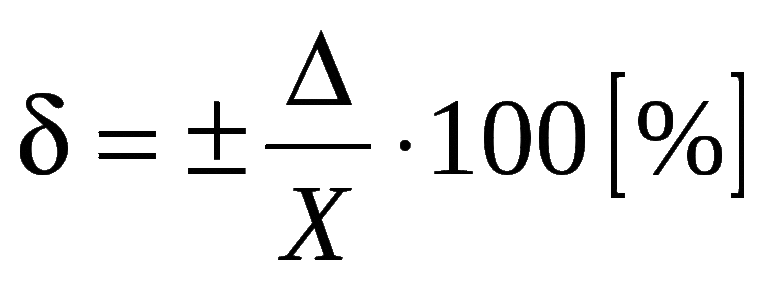
Относительная погрешность — условная величина, равная отношению абсолютной к самому числу.
Пример: количество сахара в пакете равно 478 граммов, абсолютная погрешность составляет 22 грамма, относительная равняется 22: 478 = 0, 046. Если перевести в проценты, получается 4,6%. Для отрезка длиной 10 см погрешность в 1 см будет составлять 10%, а для отрезка в 1 м такая же абсолютная величина составит всего 1%. Относительная оценка считается наиболее точной.
Относительная погрешность может быть случайной, возникающей под действием внешних факторов. Ее размер зависит от способа нахождения.
Методики расчета
Существует несколько методов определения отклонения. Наиболее простой и доступный способ:

- Необходимые измерения проводят не менее 5 раз. Это дает возможность вычислить наиболее точное значение параметра. Результаты вносят в таблицу excel.
- Полученные величины складывают и делят на количество замеров. В результате получится действительное значение. Его обычно применяют вместо истинного, так как нет возможности вычислить последнее.
- Следующий шаг — определение абсолютной погрешности. Ее считают для каждого измерения. Чтобы узнать величину этого показателя, из результата каждого замера вычитают действительное значение. Для обработки данных неважно, положительная или отрицательная получилась цифра. Используют модули полученных чисел, пренебрегая знаками.
- Чтобы определить относительную погрешность измерения, нужно разделить абсолютную на действительное значение. Полученное число умножают на 100%.
Для определения предельного отклонения выбирают наибольшее значение из всех полученных.
Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:
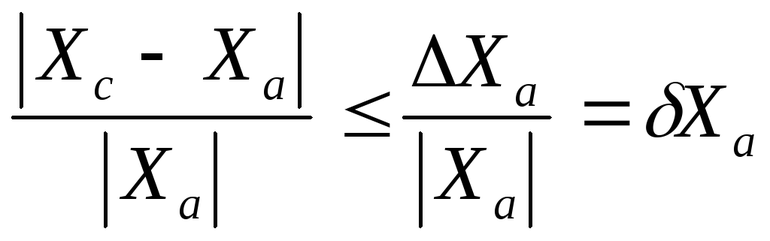
- Каждый показатель абсолютной погрешности возводят в квадрат и записывают.
- Полученные результаты складывают между собой.
- Сумму всех квадратов делят на число, которое на единицу меньше количества измерений.
- Из результата вычислений извлекают квадратный корень — это и будет среднее квадратическое отклонение.
Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения. Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.
Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение. При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.
При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.
Произвести необходимые расчеты можно с помощью онлайн-калькулятора. В окошки вносятся необходимые данные, после чего программа выдает результат.
Методы Корнфельда и Стьюдента
Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.
Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:

- Предполагается, что имеется ряд результатов измерений от Х1 до Хn.
- Из этих величин выбирают минимальную и максимальную.
- Вычисляют среднее значение Х.
- В пределах от наименьшего до наибольшего показателя выбирают доверительный интервал.
- Чтобы найти абсолютное отклонение, необходимо вычесть из максимального результата измерения величину минимального. Полученную разность делят пополам.
Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.
Эти показатели вычисляются на основе доверительной вероятности и большого количества измерений.
Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».
Сначала надо вспомнить основные понятия теории погрешности.
Абсолютная погрешность физической величины ΔА — это
разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:
ΔА = А — Апр .
Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной
погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.
Относительная погрешность измерения
εА равна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из
множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.
Зная относительную погрешность, найти абсолютную погрешность измерений можно так:
ΔА = εA· А.
«Правило ничтожных погрешностей»
при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟4 от другого.
Запись результата с указанием погрешности.
Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.
Пример:

Результат записывается в виде:
А = Аизм ± ΔА, например: ℓ = (13 ± 2) мм.
При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении
погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения). Значение величины и погрешность следует
выражать в одних и тех же единицах!
Пример:

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения
Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?
Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за
топливо?
Статья обновлена 10.07.2022
Что такое погрешность измерения
Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.
- Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
- Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.
Математическая погрешность: формула для каждого типа
Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?
Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.
Формулы погрешностей вычисляются следующим образом.
Абсолютная погрешность измерений: формула
Формула дает разницу между измеренным и реальным значением.

Относительная погрешность: формула
Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.

Приведенная погрешность: формула
Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Классификация оценочной погрешности
Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.
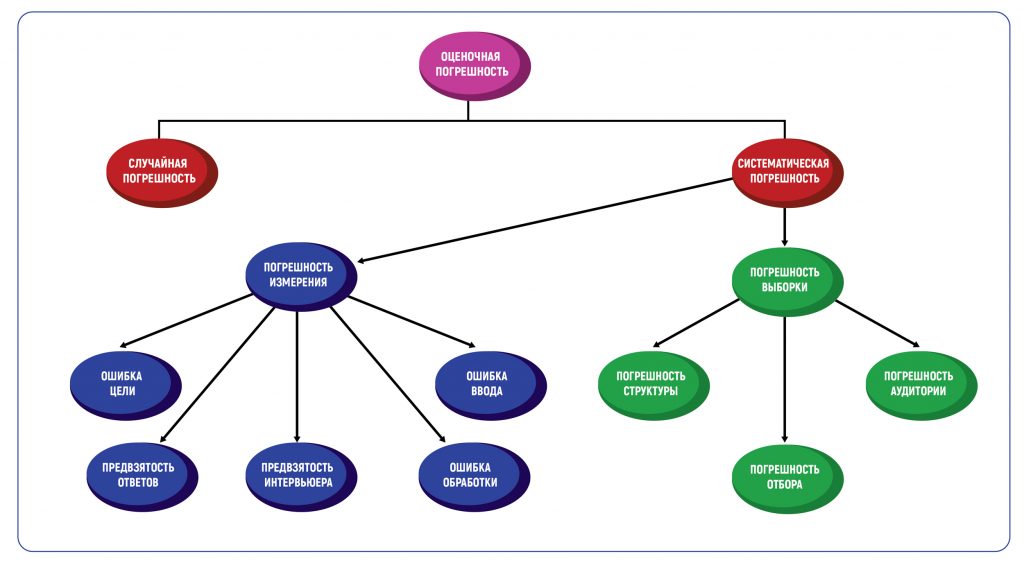
Что такое случайная погрешность
Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.
Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.
Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.
Что такое систематическая погрешность
Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.
В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.
Погрешность выборки
Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.
Погрешность структуры
Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.
Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.
Погрешность аудитории
Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.
Погрешность отбора
Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.
Как минимизировать погрешность выборки
- Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам. - Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию. - Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.
Погрешность измерения
Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.
К погрешностям измерения приводят следующие виды ошибок.
Ошибка цели
Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.
Предвзятость ответов
Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.
Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.
Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.
Предвзятость интервьюера
Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.
Ошибка обработки
Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.
Ошибка ввода
Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.
Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.
Как минимизировать погрешность измерения
- Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью. - Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка. - Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования. - Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.
Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.
Download Article
Download Article
Absolute error is the actual amount you were off, or mistaken by, when measuring something. Relative error compares the absolute error against the size of the thing you were measuring. In order to calculate relative error, you must calculate the absolute error as well. If you tried to measure something that was 12 inches long and your measurement was off by 6 inches, the relative error would be very large. But, if you tried to measure something that was 120 feet long and only missed by 6 inches, the relative error would be much smaller — even though the value of the absolute error, 6 inches, has not changed.
-

1
When given an expected value, subtract the value you got from the expected value to get the Absolute Error. An expected value is usually found on tests and school labs. Basically, this is the most precise, common measurement to come up with, usually for common equations or reactions. You can compare your own results to get Absolute Error, which measures how far off you were from the expected results. To do so, simply subtract the measured value from the expected one. Even if the result is negative, make it positive. This is your absolute error![1]
- Example: You want to know how accurately you estimate distances by pacing them off. You pace from one tree to another and estimate that they’re 18 feet apart. This is the experimental value. Then you come back with a long measuring tape to measure the exact distance, finding out that the trees are in fact 20 feet (6 meters) apart. That is the «real» value. Your absolute error is 20 — 18 = 2 feet (60.96 centimeters).
-

2
Alternatively, when measuring something, assume the absolute error to be the smallest unit of measurement at your disposal. For example, if you’re measuring something with a meter stick, the smallest unit marked on the meter stick is 1 millimeter (mm). So you know that your measurement is accurate to within + or — 1 mm; your absolute error is 1 mm.
- This works for any measurement system. Many scientific tools, like precision droppers and measurement equipment, often has absolute error labeled on the sides as «+/- ____ «
Advertisement
-

3
Always add the appropriate units. Say your Absolute Error was «2 meters.» This tells your viewers exactly how far off your error was. But if you write that your error was simply «2,» this doesn’t tell your audience anything. Use the same unites as the ones in your measurements.
-

4
Practice with several examples. The best way to learn how to calculate error is to go ahead and calculate it. Take a stab at the following problems, then highlight the space after the colon (:) to see your answer.
- Jill is studying chemical reactions. After mixing and matching, her test tube contains 32 grams of substrate. The accepted value for her experiment was 34 grams. Her Absolute Error is: +/- 2 grams
- Clive is testing reactions in chemistry. It takes 10ml drops of water to cause a reaction, but his dropper claims it is «+/- .5ml.» The Absolute Error in his measurements must be: +/- .5ml
-

5
Understand what causes error, and how you can work to eliminate it. No scientific study is ever perfectly error free — even Nobel Prize winning papers and discoveries have a margin or error attached. Still, understanding where error comes from is essential to help try and prevent it:[2]
- Human error is the most common. This is from bad measurements, faulty premises, or mistakes in the lab.
- Incidental energy/material loss, such as the little fluid left in the beaker after pouring, changes in temperature due to the environment, etc.
- Imperfect equipment used either for measurement or studies, such as very small, precise measurements or burners that provide uneven heat.[3]
Advertisement
-

1
Divide the Absolute Error by the Actual Value of the item in question to get Relative Error. The result is the relative error.[4]
-

2
Multiply the answer by 100 to get an easier to understand percentage. Leave the relative error in fraction form, complete the division to render it in decimal form, or multiply the resulting decimal form by 100 to render your answer as a percentage. This tells you what percentage of the final measurement you messed up by. If you are measuring a 200 foot boat, and miss the measurement by 2 feet, your percentage error will be much lower than missing the 20 foot tree measurement by 2 feet. The error is a smaller percentage of the total measurement.[5]
-

3
Calculate Relative Error all at once by turning the numerator (top of fraction) into your Absolute Error equation. Once you understand the difference between Absolute and Relative Error, there is really no reason to do everything all by itself. Simply substitute the equation for Absolute Error in for the actual number. Note that the vertical bars are absolute value signs, meaning anything within them must be positive.[6]
- Relative Error
- Multiply the whole thing by 100 to get Relative Error Percentage all at once.[7]
- Relative Error
-

4
Always provide units as context. Let the audience know the units you’re using for measurement. However, the relative error does not employ units of measurement. It is expressed as a fraction or a percentage, such as a relative error of 10%.[8]
Advertisement
Add New Question
-
Question
What does the +/- sign tell about the relative percentage error?

It means the reported or estimated amount could be higher or lower than the true amount.
-
Question
What is the difference between systematic and random errors?

Systematic errors are those which occur according to a certain pattern or system; these errors are due to known reasons. Random errors have no set pattern or cause.
-
Question
If the absolute error was 0.94, then what will the relative error be?

Aditya Kannan
Community Answer
Relative error, as mentioned in the answer, equals (Absolute Error)/(Actual Value). Hence, it isn’t possible to calculate relative error just by knowing the absolute error.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Make sure that your experimental value and real value are all expressed in the same unit of measurement. For example, if your experimental value is in inches but your real value is in feet, you must convert one of them to the other unit of measurement.
Thanks for submitting a tip for review!
Advertisement
-
If taking the regents exam, make sure you round correctly
Advertisement
References
About This Article
Article SummaryX
Before you can calculate relative error, you must calculate the absolute error in your calculations. To do this, subtract your answer from the expected value, or the correct answer. Write the answer as a positive number, even if it’s negative, and add the appropriate units. To get the relative error, divide the absolute error by the actual value of the item in question. If you’d like, you can multiply the answer by 100 to display it as a percentage. To understand when you would need to use relative error, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 467,629 times.
Reader Success Stories
-

Aditya Kannan
Jul 11, 2017
«I’ve got this messed up exam tomorrow. Heck, if wikiHow didn’t exist, Relative Errors would’ve pulled the carpet…» more
Did this article help you?
Download Article
Download Article
Absolute error is the actual amount you were off, or mistaken by, when measuring something. Relative error compares the absolute error against the size of the thing you were measuring. In order to calculate relative error, you must calculate the absolute error as well. If you tried to measure something that was 12 inches long and your measurement was off by 6 inches, the relative error would be very large. But, if you tried to measure something that was 120 feet long and only missed by 6 inches, the relative error would be much smaller — even though the value of the absolute error, 6 inches, has not changed.
-

1
When given an expected value, subtract the value you got from the expected value to get the Absolute Error. An expected value is usually found on tests and school labs. Basically, this is the most precise, common measurement to come up with, usually for common equations or reactions. You can compare your own results to get Absolute Error, which measures how far off you were from the expected results. To do so, simply subtract the measured value from the expected one. Even if the result is negative, make it positive. This is your absolute error![1]
- Example: You want to know how accurately you estimate distances by pacing them off. You pace from one tree to another and estimate that they’re 18 feet apart. This is the experimental value. Then you come back with a long measuring tape to measure the exact distance, finding out that the trees are in fact 20 feet (6 meters) apart. That is the «real» value. Your absolute error is 20 — 18 = 2 feet (60.96 centimeters).
-

2
Alternatively, when measuring something, assume the absolute error to be the smallest unit of measurement at your disposal. For example, if you’re measuring something with a meter stick, the smallest unit marked on the meter stick is 1 millimeter (mm). So you know that your measurement is accurate to within + or — 1 mm; your absolute error is 1 mm.
- This works for any measurement system. Many scientific tools, like precision droppers and measurement equipment, often has absolute error labeled on the sides as «+/- ____ «
Advertisement
-

3
Always add the appropriate units. Say your Absolute Error was «2 meters.» This tells your viewers exactly how far off your error was. But if you write that your error was simply «2,» this doesn’t tell your audience anything. Use the same unites as the ones in your measurements.
-

4
Practice with several examples. The best way to learn how to calculate error is to go ahead and calculate it. Take a stab at the following problems, then highlight the space after the colon (:) to see your answer.
- Jill is studying chemical reactions. After mixing and matching, her test tube contains 32 grams of substrate. The accepted value for her experiment was 34 grams. Her Absolute Error is: +/- 2 grams
- Clive is testing reactions in chemistry. It takes 10ml drops of water to cause a reaction, but his dropper claims it is «+/- .5ml.» The Absolute Error in his measurements must be: +/- .5ml
-

5
Understand what causes error, and how you can work to eliminate it. No scientific study is ever perfectly error free — even Nobel Prize winning papers and discoveries have a margin or error attached. Still, understanding where error comes from is essential to help try and prevent it:[2]
- Human error is the most common. This is from bad measurements, faulty premises, or mistakes in the lab.
- Incidental energy/material loss, such as the little fluid left in the beaker after pouring, changes in temperature due to the environment, etc.
- Imperfect equipment used either for measurement or studies, such as very small, precise measurements or burners that provide uneven heat.[3]
Advertisement
-

1
Divide the Absolute Error by the Actual Value of the item in question to get Relative Error. The result is the relative error.[4]
-

2
Multiply the answer by 100 to get an easier to understand percentage. Leave the relative error in fraction form, complete the division to render it in decimal form, or multiply the resulting decimal form by 100 to render your answer as a percentage. This tells you what percentage of the final measurement you messed up by. If you are measuring a 200 foot boat, and miss the measurement by 2 feet, your percentage error will be much lower than missing the 20 foot tree measurement by 2 feet. The error is a smaller percentage of the total measurement.[5]
-

3
Calculate Relative Error all at once by turning the numerator (top of fraction) into your Absolute Error equation. Once you understand the difference between Absolute and Relative Error, there is really no reason to do everything all by itself. Simply substitute the equation for Absolute Error in for the actual number. Note that the vertical bars are absolute value signs, meaning anything within them must be positive.[6]
- Relative Error
- Multiply the whole thing by 100 to get Relative Error Percentage all at once.[7]
- Relative Error
-

4
Always provide units as context. Let the audience know the units you’re using for measurement. However, the relative error does not employ units of measurement. It is expressed as a fraction or a percentage, such as a relative error of 10%.[8]
Advertisement
Add New Question
-
Question
What does the +/- sign tell about the relative percentage error?

It means the reported or estimated amount could be higher or lower than the true amount.
-
Question
What is the difference between systematic and random errors?

Systematic errors are those which occur according to a certain pattern or system; these errors are due to known reasons. Random errors have no set pattern or cause.
-
Question
If the absolute error was 0.94, then what will the relative error be?

Aditya Kannan
Community Answer
Relative error, as mentioned in the answer, equals (Absolute Error)/(Actual Value). Hence, it isn’t possible to calculate relative error just by knowing the absolute error.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Make sure that your experimental value and real value are all expressed in the same unit of measurement. For example, if your experimental value is in inches but your real value is in feet, you must convert one of them to the other unit of measurement.
Thanks for submitting a tip for review!
Advertisement
-
If taking the regents exam, make sure you round correctly
Advertisement
References
About This Article
Article SummaryX
Before you can calculate relative error, you must calculate the absolute error in your calculations. To do this, subtract your answer from the expected value, or the correct answer. Write the answer as a positive number, even if it’s negative, and add the appropriate units. To get the relative error, divide the absolute error by the actual value of the item in question. If you’d like, you can multiply the answer by 100 to display it as a percentage. To understand when you would need to use relative error, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 467,629 times.
Reader Success Stories
-

Aditya Kannan
Jul 11, 2017
«I’ve got this messed up exam tomorrow. Heck, if wikiHow didn’t exist, Relative Errors would’ve pulled the carpet…» more


