Как найти абсолютно случайное число

И так, человеку крайне сложно получить случайное число, тем более если нужно сгенерировать более 1 000, а то и 1 000 000 чисел. Поэтому мы придумали алгоритмы генерации чисел. Случайное число можно получить 2-мя видами либо с помощью физики, либо математике.

Но есть одна проблема, любой алгоритм можно предугадать и он начнет зацикливаться, так в 1983г на шоу “Поймай свою удачу”, водитель грузовика Майкл Ларсон он выиграл просто блять сумасшедшие деньги просчитав алгоритм случайных числе этой передачи. После этого случая появился сайт random.org, который генерирует по настоящему рандомное число.

Давайте разберем, как он их получает. Получает этот сайт благодаря матушки природы, да-да наша природа которую мы порой блять недооцениваем, потому-что только матушка природа способна получить хаос который мы не можем предугадать, точнее можем, но это будет пиздец как не скоро, т.к. надо будет рассчитать движение каждого атома во вселенной. Сайт random.org генерирует свои основываясь на данных атмосферных шумов.

Окей, нахуя я тут распинался и рассказывал про этот сайт рандом орг?

Благодаря природе, наш цифровой мир находиться под защитой. Случайные коды которые приходят при платежах ваших банков, основаны на подобных алгоритмах, то есть ни один хакер в мире не сможет предугадать код и спиздить ваши 300р на последний дошик, в военной промышленности тоже эта хрень используется, поэтому, что вы сейчас прочитали, не так уж и не нужно.

Спасибо за то, что вы с нами.
С любовью, Рителлинг favorite

Краеугольный камень псевдослучайности: с чего начинается поиск чисел

(с)

Случайные числа постоянно генерируются каждой машиной, которая может обмениваться данными. И даже если она не обменивается данными, каждый компьютер нуждается в случайности для распределения программ в памяти. При этом, конечно, компьютер, как детерминированная система, не может создавать истинные случайные числа.

Когда речь заходит о генераторах случайных (или псевдослучайных) чисел, рассказ всегда строится вокруг поиска истинной случайности. Пока серьезные математики десятилетиями ведут дискуссии о том, что считать случайностью, в практическом отношении мы давно научились использовать «правильную» энтропию. Впрочем, «шум» — это лишь вершина айсберга.

С чего начать, если мы хотим распутать клубок самых сильных алгоритмов PRNG и TRNG? На самом деле, с какими бы алгоритмами вы не имели дело, все сводится к трем китам: seed, таблица предопределенных констант и математические формулы.

Каким бы ни был seed, еще есть алгоритмы, участвующие в генераторах истинных случайных чисел, и такие алгоритмы никогда не бывают случайными.

Что такое случайность

Первое подходящее определение случайной последовательности дал в 1966 году шведский статистик Пер Мартин-Лёф, ученик одного из крупнейших математиков XX века Андрея Колмогорова. Ранее исследователи пытались определить случайную последовательность как последовательность, которая проходила все тесты на случайность.

Основная идея Мартина-Лёфа заключалась в том, чтобы использовать теорию вычислимости для формального определения понятия теста случайности. Это контрастирует с идеей случайности в вероятности; в этой теории ни один конкретный элемент пространства выборки не может быть назван случайным.

«Случайная последовательность» в представлениях Мартина-Лёфа должна быть типичной, т.е. не должна обладать индивидуальными отличительными особенностями.

Было показано, что случайность Мартина-Лёфа допускает много эквивалентных характеристик, каждая из которых удовлетворяет нашему интуитивному представлению о свойствах, которые должны иметь случайные последовательности:

• несжимаемость;
• прохождение статистических тестов для случайности;
• сложность создания прогнозов.

Существование множественных определений рандомизации Мартина-Лёфа и устойчивость этих определений при разных моделях вычислений свидетельствуют о том, что случайность Мартина-Лёфа является фундаментальным свойством математики.

Seed: основа псевдослучайных алгоритмов

Первые алгоритмы формирования случайных чисел выполняли ряд основных арифметических действий: умножить, разделить, добавить, вычесть, взять средние числа и т.д. Сегодня такие мощные алгоритмы, как Fortuna и Yarrow (используется в FreeBSD, AIX, Mac OS X, NetBSD) выглядят как генераторы случайных чисел для параноиков. Fortuna, например, это криптографический генератор, в котором для защиты от дискредитации после выполнения каждого запроса на случайные данные в размере 220 байт генерируются еще 256 бит псевдослучайных данных и используются в качестве нового ключа шифрования — старый ключ при этом каждый раз уничтожается.

Прошли годы, прежде чем простейшие алгоритмы эволюционировали до криптографически стойких генераторов псевдослучайных чисел. Частично этот процесс можно проследить на примере работы одной математической функции в языке С.

Функция rand () является простейшей из функций генерации случайных чисел в C.

#include <stdio.h>
#include <stdlib.h>

int main()
{
int r,a,b;

     puts("100 Random Numbers");
     for(a=0;a<20;a++)
     {
         for(b=0;b<5;b++)
         {
             r=rand();
             printf("%dt",r);
          }
          putchar('n');
      }
      return(0);
}

В этом примере рандома используется вложенный цикл для отображения 100 случайных значений. Функция rand () хороша при создании множества случайных значений, но они являются предсказуемыми. Чтобы сделать вывод менее предсказуемым, вам нужно добавить seed в генератор случайных чисел — это делается с помощью функции srand ().

Seed — это стартовое число, точка, с которой начинается последовательность псевдослучайных чисел. Генератор псевдослучайных чисел использует единственное начальное значение, откуда и следует его псевдослучайность. Генератор истинных случайных чисел всегда имеет в начале высококачественную случайную величину, предоставленную различными источниками энтропии.

#include <stdio.h>
#include <stdlib.h>

int main()
{
    unsigned seed;
    int r,a,b;

    printf("Input a random number seed: ");
    scanf("%u",&seed);
    srand(seed);
    for(a=0;a<20;a++)
    {
        for(b=0;b<5;b++)
        {
            r=rand();
            printf("%dt",r);
         }
         putchar('n');
     }  
     return(0);
}

srand() принимает число и ставит его в качестве отправной точки. Если seed не выставить, то при каждом запуске программы мы будем получать одинаковые случайные числа.

Вот пример простой формулы случайного числа из «классики» — книги «Язык программирования C» Кернигана и Ричи, первое издание которой вышло аж в 1978 году:

int rand() { random_seed = random_seed * 1103515245 +12345;  
return (unsigned int)(random_seed / 65536) % 32768; }

Эта формула предполагает существование переменной, называемой random_seed, изначально заданной некоторым числом. Переменная random_seed умножается на 1 103 535 245, а затем 12 345 добавляется к результату; random_seed затем заменяется этим новым значением. Это на самом деле довольно хороший генератор псевдослучайных чисел. Если вы используете его для создания случайных чисел от 0 до 9, то первые 20 значений, которые он вернет при seed = 10, будут такими:

44607423505664567674

Если у вас есть 10 000 значений от 0 до 9, то распределение будет следующим:

0 — 10151 — 10242 — 10483 — 9964 — 9885 — 10016 — 9967 — 10068 — 9659 — 961

Любая формула псевдослучайных чисел зависит от начального значения. Если вы предоставите функции rand() seed 10 на одном компьютере, и посмотрите на поток чисел, которые она производит, то результат будет идентичен «случайной последовательности», созданной на любом другом компьютере с seed 10.

К сожалению, у генератора случайных чисел есть и другая слабость: вы всегда можете предсказать, что будет дальше, основываясь на том, что было раньше. Чтобы получить следующее число в последовательности, мы должны всегда помнить последнее внутреннее состояние генератора — так называемый state. Без state мы будем снова делать одну и ту же математическую операцию с одинаковыми числами, чтобы получить тот же ответ.

Как сделать seed уникальным для каждого случая? Самое очевидное решение — добавить в вычисления текущее системное время. Сделать это можно с помощью функции time().

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main()
{
    int r,a,b;

    srand((unsigned)time(NULL));
    for(a=0;a<20;a++)
    {
        for(b=0;b<5;b++)
        {
            r=rand();
            printf("%dt",r);
         }
         putchar('n');
     }
     return(0);
}

Функция time() возвращает информацию о текущем времени суток, значение, которое постоянно изменяется. При этом метод typecasting гарантирует, что значение, возвращаемое функцией time(), является целым числом.

Итак, в результате добавления «случайного» системного времени функция rand() генерирует значения, которые являются более случайными, чем мы получили в первом примере.

Однако в этом случае seed можно угадать, зная системное время или время запуска приложения. Как правило, для приложений, где случайные числа являются абсолютно критичными, лучше всего найти альтернативное решение.

В .net framework есть функция System.Security.Cryptography.RandomNumberGenerator, где в расчетах учитываются следующие факторы:

• ID текущего процесса;
• текущий ID потока;
• количество отсчетов с момента загрузки;
• текущее время;
• различные высокоточные счетчики производительности процессора;
• MD4-хэш среды пользователя (имя пользователя, имя компьютера и т.д.).

Но опять же, все эти числа не случайны.

Лучшее, что вы можете сделать с детерминированными генераторами псевдослучайных чисел — добавить энтропию физических явлений.

Период (цикл) генератора

Одними из наиболее часто используемых методов генерации псевдослучайных чисел являются различные модификации линейного конгруэнтного метода, схема которого была предложена Дерриком Лемером еще в 1949 году:

X_n+1 = (aX_n + c) mod m, где m — модуль, a — множитель, c — приращение, mod — операция взятия остатка от деления. Причем m > 0, 0 < a ≤ m, 0 < c ≤ m, также задается начальное значение X₀: 0 < X₀ ≤ m.

Линейный конгруэнтный метод дает нам повторяющиеся последовательности — конгруэнтная последовательность всегда образует «петли». Этот цикл (период), повторяющийся бесконечное число раз — свойство всех последовательностей вида X_n+1 = f(n).

В языке С линейно-конгруэнтный метод реализован в уже знакомой вам функции rand():

#define RAND_MAX 32767 
unsigned long next=1; 
int rand(void) 
{ next=next*1103515245+12345; 
return((unsigned int)(next/65536)%RAND_MAX);} 
void srand(unsigned int seed) 
{ next=seed; } 

Что вообще такое цикл с точки зрения случайных чисел? Период — это количество чисел, которое генерируется до того, как они вернутся в той же последовательности. Для примера число периодов в шифре А5 в среднем составляет 2²³, а сложность атаки 240, что позволяет взломать его на любом персональном компьютере.

Рассмотрим случай, когда seed равен 1, а период — 100 (на языке Haskell):

random i = (j, ans)
    where j   = 7 * i  `mod` 101
          ans = (j — 1) `mod` 10 + 1 — just the ones place, but 0 means 10

В результате мы получим следующий ответ:

random 1 —> ( 7, 7)
random 7 —> (49, 9)
random 49 —> (40, 10)
random 40 —> (78, 8)
random 78 —> (41, 1)
random 41 —> (85, 5)
random 85 —> (90, 10)
random 90 —> (24, 4)
random 24 —> (67, 7)
random 67 —> (65, 5)
random 65 —> (51, 1)

Это лишь пример и подобную структуру в реальной жизни не используют. В Haskell, если вы хотите построить случайную последовательность, можно воспользоваться следующим кодом:

random :: StdGen —> (Int, StdGen)

Выбор случайного Int дает вам обратно Int и новый StdGen, который вы можете использовать для получения более псевдослучайных чисел. Многие языки программирования, включая Haskell, имеют генераторы случайных чисел, которые автоматически запоминают свое состояние (в Haskell это randomIO).

Чем больше величина периода, тем выше надежность создания хороших случайных значений, однако даже с миллиардами циклов крайне важно использовать надежный seed. Реальные генераторы случайных чисел обычно используют атмосферный шум (поставьте сюда любое физическое явление — от движения мыши пользователя до радиоактивного распада), но мы можем и схитрить программным методом, добавив в seed асинхронные потоки различного мусора, будь то длины интервалов между последними heartbeat потоками или временем ожидания mutual exclusion (а лучше добавить все вместе).

Истинная случайность бит

Итак, получив seed с примесью данных от реальных физических явлений (либо максимально усложнив жизнь будущему взломщику самым большим набором потоков программного мусора, который только сможем придумать), установив state для защиты от ошибки повтора значений и добавив криптографических алгоритмов (или сложных математических задач), мы получим некоторый набор данных, который будем считать случайной последовательностью. Что дальше?

Дальше мы возвращаемся к самому началу, к одному из фундаментальных требований — тестам.

Национальный институт стандартов и технологий США вложил в «Пакет статистических тестов для случайных и псевдослучайных генераторов чисел для криптографических приложений» 15 базовых проверок. Ими можно и ограничиться, но этот пакет вовсе не является «вершиной» проверки случайности.

Одни из самых строгих статистических тестов предложил профессор Джордж Марсалья из Университета штата Флорида. «Тесты diehard» включают 17 различных проверок, некоторые из них требуют очень длинных последовательностей: минимум 268 мегабайт.

Случайность можно проверить с помощью библиотеки TestU01, представленной Пьером Л’Экуйе и Ричардом Симардом из Монреальского университета, включающей классические тесты и некоторые оригинальные, а также посредством общедоступной библиотеки SPRNG.

Еще один полезный сервис для количественного измерения случайности.

Для работы проектов iXBT.com нужны файлы cookie и сервисы аналитики.
Продолжая посещать сайты проектов вы соглашаетесь с нашей
Политикой в отношении файлов cookie

Подбрасывая монетку, можно быть уверенным, что шансы выпадения орла и решки одинаковы. Но можно зайти на сайт с генерацией рандомных чисел или скачать приложение на телефон, в котором будет возможность имитировать бросок монетки. Однако будет ли в таком случае результат действительно случайным, или же программа подберет число/результат, который заранее был известен?

В большинстве случаев результат не будет действительно случайным, он будет получен алгоритмом, выдающим последовательность чисел близкую к случайной. Подобных алгоритмов очень много, и все они используют различные формулы, однако они все зацикливаются и могут выдать ограниченное количество цепочек “случайных” чисел.

Хорошим и простым примером будет один из самых ранних алгоритмов для генерации псевдослучайных чисел. Например, трехзначное число возводится в квадрат, затем из середины квадрата числа берётся трехзначное число, которое и становится результатом. А производя подобные вычисления несколько раз подряд, получается цепочка псевдослучайных чисел. Выглядит это так: допустим начальное значение 111, в таком случае 111² = 12321, получаем результат 232, после чего повторяем процедуру — 232² = 53824 и результатом становится 382. Чтобы подбор чисел не был постоянно одинаковым, важно чтобы начальное значение было разным при запуске алгоритма. Так, например, программы могут брать начальное значение исходя из даты и времени, когда был запущен алгоритм/приложение.

Большинство игр, приложений и сайтов используют именно генераторы псевдослучайных чисел, поскольку это значительно проще в реализации, а результат может быть получен мгновенно и без подключения к сети. Однако предсказуемость подобного генератора совершенно не подходит для использования его в целях шифрования данных. Тут на помощь приходит генератор истинно случайных чисел.

Простейшим истинным генератором случайных чисел является игральный кубик. Однако создать большой массив данных кидая кубик едва ли получится, а чтобы узнать результат даже одного броска, требуется время. Поэтому современные генераторы случайных чисел используют данные, полученные измерением различных физических процессов. Например, используют шум в электрических цепях, атмосферный шум, космическое излучение, колебания электромагнитного поля вакуума или шум радиоактивного распада атомов. Полученные данные являются абсолютно случайными и никак не могут быть предсказаны.

Недостатком подобноных генераторов является относительно медленная скорость выдачи результата, все же передача данных занимает больше времени, чем получение результата путем расчета по алгоритму. Однако уверенность в получении случайного числа важна во многих сферах. Но несмотря на сложность генераторов случайных чисел ими может воспользоваться каждый. Есть большое количество сайтов предоставляющих такую возможность (обычно, если сайт использует генератор истинно случайных чисел, то об этом есть информация).

Сейчас на главной

Новости

Публикации

Библиографическое описание:

Гончарук, В. С. Методы генерации случайных чисел / В. С. Гончарук, Ю. С. Атаманов, С. Н. Гордеев. — Текст : непосредственный // Молодой ученый. — 2017. — № 8 (142). — С. 20-23. — URL: https://moluch.ru/archive/142/40025/ (дата обращения: 18.05.2023).



Случайные числа играют довольно важную роль для программистов разной направленности. Чаще всего случайные числа требуются в задачах моделирования, численного анализа, тестирования, криптографии и теории игр, но существует и множество других весьма специфических задач.

Но для начала давайте разберемся с понятием случайных чисел. Само понятие «случайное число» пришло из такого раздела математики, как теория вероятности, и всегда рассматривается в контексте какой-то последовательности, которая характеризуется тем, что каждое число последовательности не зависит от всех остальных чисел последовательности, то есть случайное число непредсказуемо, никогда нельзя с полной уверенностью предугадать, какое будет следующее число в случайной последовательности. Кроме того, случайные числа должны подчиняться равномерному распределению, то есть вероятность появления каждого числа равновероятна.

Теперь, когда у нас есть понимание, что такое случайные числа и для каких целей они необходимы, стоит вопрос получения какой-то случайной последовательности. Человек очень плох в качестве генератора случайных чисел. Это связано с нашим неверным интуитивным пониманием теории вероятностей. Компьютер справляется с задачей построения последовательности случайных чисел гораздо лучше.

Все генераторы случайных чисел делятся на два вида:

‒ True random number generator (ГНСЧ, генератор настоящих случайных чисел)

‒ Pseudo random number generator (ГПСЧ, генератор псевдослучайных чисел)

Эти два генератора задания случайной последовательности отличаются способом получения случайного числа.

ГНСЧ использует в качестве механизма получения случайного числа некий физический процесс, который сам по себе является непредсказуемым. Если оцифровать такой процесс (например, шумы атмосферы), то можно использовать его для генератора случайных чисел. ГПСЧ в свою очередь использует математические алгоритмы (полностью производимые компьютером) [2].

Рассмотрим сравнительную таблицу 1, которая показывает отличия между ГНСЧ и ГПСЧ.

Таблица 1

Отличия ГНСЧ иГПСЧ

	ГНСЧ	ГПСЧ
1) Механизм	Физический процесс	Математика
2) Равномерное распределение	✔	✔
3) Независимость	✔	✖
4) Скорость	✖	✔

Стоить отметить, что, используя ГПСЧ, мы вычисляем наши числа по какой-то формуле, то естественно они будут как-то связаны между собой, поэтому псевдо-генераторы не обладают свойством независимости, они всегда связаны между собой, но этот недостаток компенсирует высокая скорость вычисления, так как какой-то физический процесс получает эти числа гораздо медленнее нежели чем, если мы будем вычислять их на процессоре.

Далее рассмотрим один из распространённых методов генерации псевдослучайных чисел — линейный конгруэнтный метод. В большинстве языков программирования именно этот метод используется в стандартной функции получения случайных чисел.

В линейном конгруэнтным методе случайное число вычисляется по следующей рекуррентной формуле: , где — модуль (), — множитель (), — приращение (), — начальное значение, которое также иногда называют зерном (от англ. seed) ().

Рассмотрим работу данного алгоритма при следующих значениях: , , , при 50 итерациях. Результаты вычислений представлены в виде графика на рис. 1.

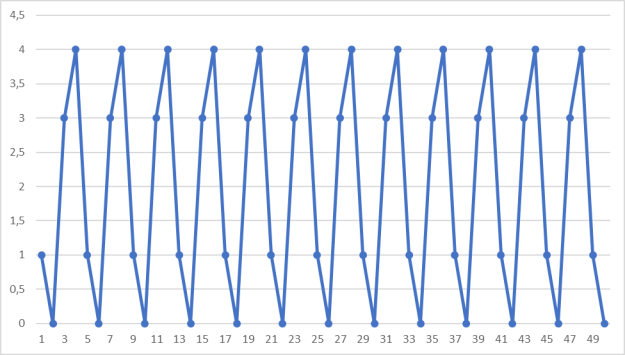
Рис. 1. Пример работы алгоритма при , , ,

Как видно из графика, данный метод даёт нам повторяющиеся последовательности, но задача состоит в том, чтобы максимально удлинить уникальную часть последовательности (граница длины уникальной части определяется величиной ).

Теперь пусть (рис. 2).

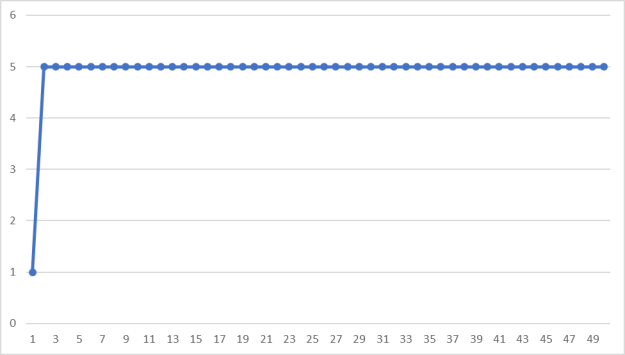
Рис. 2. Пример работы алгоритма при , , ,

Как видно, последовательность сразу же начинает повторяться. Это происходит потому, что должно быть простым числом, чтобы периоды были гораздо больше. Вообще говоря, все коэффициенты формулы не должны быть случайными, чтобы полученная в результате последовательность была более случайной.

Теперь в качестве возьмём большое простое число, пусть (рис. 3).

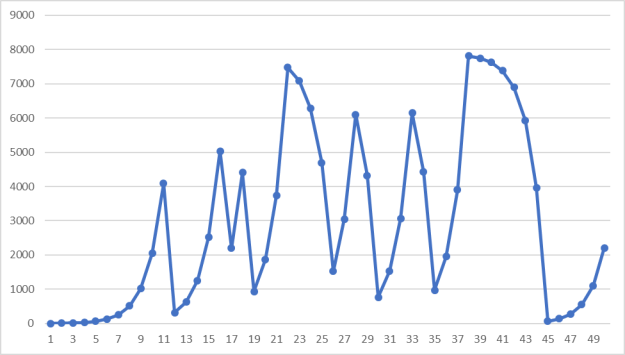
Рис. 3. Пример работы алгоритма при , , ,

Как видно, если является большим простым числом, то случайная последовательность ведёт себя вполне непредсказуемо. При удачно подобранных коэффициентах данный метод может давать достаточно случайные числа.

Однако применять данный метод стоит в достаточно простых случаях, так как он не обладает криптографической стойкостью, так как зная четыре подряд идущих числа, криптоаналитик может составить систему уравнений, из которой можно найти , и .

Также существуют более случайные и надёжные модифицированные варианты данного метода генерации последовательностей псевдослучайных чисел. Кроме данного алгоритма применяется и ряд других алгоритмов, которые основаны на другой математике.

Литература:

1. Генерация псевдослучайных чисел // habrahabr.ru. URL: https://habrahabr.ru/post/132217/ (дата обращения: 22.02.2017).
2. Pseudorandom number generator // en.wikipedia.org. URL: https://en.wikipedia.org/wiki/Pseudorandom_number_generator (дата обращения: 22.02.2017).
3. William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. — 2nd ed. — Cambridge University Press, 1992. — P. 277. — ISBN 0–521–43108–5.