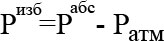2.В данной точке внутри жидкости давление по всем направлениям одина-
ково. Это означает, что давление в жидкости на определенном уровне
можно определять и сверху, и снизу, и слева, и справа.
3.На внешней поверхности жидкости давление направлено перпендикулярно к поверхности. В противном случае на жидкость действовали бы касательные силы и она бы двигалась.
4.При перемещении в жидкости сверху вниз давление увеличивается:
р3 > р2 > р1 > р0 .
Молекулы жидкости, стремясь освободиться от сжимающих напряжений, в свою очередь оказывают силовое воздействие на окружающие поверхности (3ий закон Ньютона – действие равно противодействию!). В результате и возникают силы давления на крышки в нашей задаче.
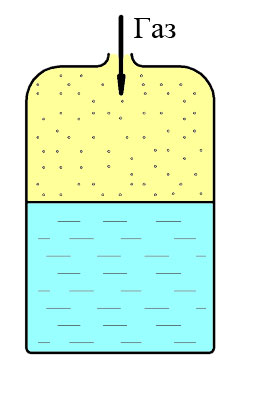
Давление в газе
В идеальном газе отсутствуют связи между молекулами, поэтому давление газа имеет совсем другой физический смысл, чем давление в жидкости. Молекулы газа совершают хаотическое (броуновское) движение. При этом они ударяются о поверхность жидкости и теряют свой импульс. Как известно из теоретической механики, при изменении импульса появляется сила, в данном случае это сила давления газа на поверхность жидкости. Единичная (на единицу площади) сила
давления и есть давление газа.
Состояние газа определяется тремя параметрами – абсолютным давлением р, плотностью ρ и абсолютной температурой T, которые связаны уравнением состояния (уравнением Клапейрона).
p V = m R T,
где R – газовая постоянная, R=287дж/кг°К для воздуха. Уравнение состояния можно записать в виде:
p/ρ =R T.
При увеличении температуры усиливается броуновское движение молекул
ичастота их ударов о поверхность. При этом давление газа увеличивается.
Вмалых объёмах давление газа одинаково во всех точках объёма. В больших объёмах давление газа уменьшается с высотой по экспотенциальному закону.
Абсолютное давление в жидкости можно вычислить по формуле (1), которая называется основным уравнением гидростатики, а также можно измерить с помощью приборов – мановакуумметров.
|
p = р0 + ρg h; |
(1) |
|
рвес. = ρg h, |
(2) |
-20-

где рвес – давление за счет веса жидкости (весовое давление или давление столба жидкости). Давление газа р0 передается через жидкость на глубину h по закону Паскаля.
Основное уравнение гидростатики (1) связывает давления на двух горизонтальных плоскостях в жидкости.
Закон Паскаля: Давление р0, созданное на жидкость любым путем, передается во все точки объёма жидкости без изменения.
Манометр – измеряет избыток абсолютного давления над атмосферным.
Вакуумметр – измеряет недостаток абсолютного давления до атмосферного.
Используя показания приборов, можно определить абсолютное давление по формулам пересчета (5) и (6).
|
р = рат + рм; |
(5) |
|
р = рат – рv. |
(6) |
Атмосферное давление рат определяется по барометру. Если рат не задано, оно принимается равным: рат=105Па=0,1МПа.
Возвращаемся к решению задачи.

вает рм0;
р = рат – рv0 – если давление газа меньше атмосферного и прибор показывает рv0.
2. Определяем абсолютное давление в жидкости на глубине H по уравне-
нию (1):
рH = р0 + ρg H = рат + рм0 + ρg H – если давление газа больше атмосферного;
рH = р0 + ρg H = рат – рv0 + ρg H – если давление газа больше атмосферного.
3. Определяем показание манометра рмH:
рмH = рH – рат = рат + рм0 + ρg H – рат = рм0 + ρg H- если давление газа больше атмосферного;
рмH = рH – рат = рат – рv0 + ρg H – рат = – рv0 + ρg H- если давление газа меньше атмосферного.
Как определяется сила, с которой жидкость давит на соприкасающуюся с ней поверхность?
Поверхности, с которыми соприкасается жидкость, бывают плоские и криволинейные (в большинстве случаев цилиндрические или сферические).
-21-

Сила давления – вектор. Необходимо определить модуль силы, её направление и точку приложения. Методика определения сил давления на криволинейные поверхности здесь не рассматривается.
Для плоских поверхностей сила давления всегда перпендикулярна по-
верхности (Рис.3, 3е свойство давления).
3.3. ОПРЕДЕЛЕНИЕ СИЛЫ ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКУЮ ПОВЕРХНОСТЬ
Рассмотрим простейший случай, когда сосуд открытый, и на свободную поверхность жидкости действует атмосферное давление (Рис.4).
Абсолютное давление в жидкости в данном случае на произвольной глубине h равно:
рh = рат + ρg h.
Атмосферное давление передается по закону Паскаля через жидкость и действует на крышку изнутри. Так как снаружи также действует атмосферное давление, то в результате оно уравновешивается и не влияет на крышку.
|
рат |
эпюра давления |
ось симметрии |
||
|
cмоченная жидкостью |
||||
|
площадь крышки (s) |
||||
|
h0 |
рат |
|||
|
H |
c |
ε |
k |
|
|
d |
||||
|
Fж |
||||
|
центр тяжести площади s (точка с) |
m |
|||
|
центр давления площади s (точка d) |
Рис. 4 Определение силы давления жидкости для открытого сосуда
Таким образом, в открытом сосуде соприкасающие с жидкостью поверхности находятся под воздействием только весового давления.
3.3.1. Графоаналитический способ определения силы и центра давления
На Рис.4 показано распределение весового давления по контуру стенки, которое называется эпюрой. Из теоретической механики известна связь между распределенной нагрузкой и сосредоточенной силой. Итак, графоаналитический способ:
Давление – распределенная нагрузка на поверхность. Сила давления равна объёму эпюры давления. Линия действия силы проходит через центр тяжести объёма эпюры. Точка пересечения линии действия силы давления и плоскости стенки – центр давления (точка d).
-22-

Суммарная сила давления на стенку в данном случае равна силе весового давления жидкости, так как силы атмосферного давления с обеих сторон стенки уравновещиваются.
F∑ = Fж .
На практике, если стенка переменной ширины (например, круглая как в данном случае), определить объём эпюры затруднительно. Поэтому используется аналитический способ.
3.3.2. Аналитический способ определения силы и центра давления
|
Этот способ описан в разделе 2.1.3 данного учебного пособия. |
|
|
Модуль (величина) силы весового давления определяется так: |
(7) |
|
Fж = рс s = ρg hc s ; |
|
|
рс = ρg hc,, |
(8) |
где рс– давление в центре тяжести площади s, s –площадь смоченной поверхности стенки;
hc – глубина погружения центра тяжести под уровень свободной поверхности (расстояние по вертикали от свободной поверхности до центра тяжести).
ВНИМАНИЕ!
Площадь крышки по форме и по величине отличается от площади s, смоченной жидкостью. При определении силы давления в формулу следует подставлять смоченную площадь, которая равна площади отверстия.
Направление силы: всегда перпендикулярно поверхности.
Координаты точки приложения силы (центра давления) – это координаты точки на плоскости.
Положение точки на плоскости определяется двумя координатами.
1.Центр давления точка d лежит на оси симметрии стенки.
2.Расстояние ε по оси симметрии от центра тяжести до центра давления (Рис.4) определяется так:
|
Ic |
(9) |
|||||
|
ε = cd = |
, |
|||||
|
s lc |
||||||
где Ic –момент инерции площади s относительно горизонтальной оси (справочная величина, Приложение 1).
Вданном случае Ic = mk3/12; lc –расстояние по контуру стенки от центра тяжести площади s до свободной поверхности жидкости.
Внашей задаче lc = h0.
ВНИМАНИЕ!
|
Если стенка не является вертикальной, |
lc ≠ h0 ! В нашей задаче: |
||||
|
ε = |
mk 3 |
= |
k 2 |
. |
|
|
12km h |
12 h |
||||
|
0 |
0 |
Что изменится, если резервуар закрыт и на свободной поверхности жидкости давление не равно атмосферному (как в нашей задаче,
Рис.1)?
-23-

Величина силы давления будет определяться по формуле :
|
F = рс ω ; |
(10) |
|
|
рс = р0 + |
ρ |
(11) |
|
g h – рат , |
где рс – результирующее давление в центре тяжести площади s (с учетом противодействующего атмосферного давления с другой стороны).
Но в этом случае величину ε нельзя определять по формуле (9).
ε = cd ≠ sIclc !
Формула (9) выведена для случая р0= рат.
Точка приложения равнодействующей силы для закрытого сосуда определяется по правилам сложения параллельных сил.
3.3.3. Определение суммарной силы давления как равнодействующей системы параллельных сил
Сила давления жидкости на стенку слева (изнутри) Fлев разбивается на две параллельные силы – силу внешнего давления F0 и силу весового давления жидкости Fж.
Fлев. = рс s = (р0 + ρg h) s = р0 s + ρg h s = F0 + Fж.
С внешней стороны стенки действует сила атмосферного давления. Определяются по отдельности эти силы и точки их приложения. Далее находится суммарная сила как равнодействующая системы параллельных сил (Рис. 7).
|
рм0 |
ось симметрии отверстия |
||||
|
р0>pат |
|||||
|
смоченная жидкостью площадь |
|||||
|
крышки s = k × m |
|||||
|
h0 |
F0 |
k |
ε – расстояние по оси симмет- |
||
|
ε |
|||||
|
Fж |
Fат |
рии от центра тяжести до цен- |
|||
|
тра весового давления |
|||||
|
m |
|||||
|
центр тяжести площади s – |
центр весового давления площади s – |
||||
|
точка приложения сил F0 и Fат |
точка приложения силы Fж |
Рис. 7 Схема к определению равнодействующей системы параллельных сил
-24-
Абсолю́тное давле́ние ─ это истинное давление сплошных масс (жидкостей, паров и газов), отсчитываемое от абсолютного нуля давления ─ абсолютного вакуума. Абсолютный нуль давления макроскопических объёмов вещества практически недостижим, так как любое твёрдое тело образует пары, да и космическое пространство также не представляет собой абсолютную пустоту, лишённую вещества, поскольку содержит водород в количестве нескольких молекул на кубический сантиметр.
Различают также избыточное или манометрическое (приборное) давление и давление окружающей среды (в земных условиях ─ атмосферное давление). Избыточное давление представляет собой разность абсолютного давления и давления окружающей среды. [1]. Эта разность может быть как положительной, так и отрицательной. В последнем случае её называют разрежением или вакуумом, а избыточное давление – остаточным. Измерение абсолютного давления в земных условиях связано с определёнными трудностями. Практически измеряют атмосферное давление приборами барометрического типа, избыточное давление ─ приборами манометрического типа, а абсолютное давление вычисляют по формуле:

где: 


(В приближённых технических расчётах вместо реального атмосферного давления используют его величину, измеренную на уровне моря).
В уравнения термодинамики, газовых законов, входят только абсолютные давления 
Примечания[править | править код]
- ↑ Вукалович М. П., Техническая термодинамика, 1968, с. 12.
- ↑ Кириллин В. А., Техническая термодинамика, 1983, с. 5.
- ↑ Нащокин В. В., Техническая термодинамика и теплопередача, 1975, с. 11—12.
Литература[править | править код]
- Вукалович М. П.,. Техническая термодинамика. — Энергия, 1968. — 496 с.
- Кириллин В. А. Техническая термодинамика. — Энергоатомиздат, 1983. — 416 с..
- Нащокин В. В. Техническая термодинамика и теплопередача. — Высшая школа, 1975. — 496 с.
На чтение 7 мин Просмотров 5.3к.
В гидравлике есть несколько ключевых понятий. Центральное место отводится понятию гидростатического давления жидкости. Оно тесно связано с понятием напора жидкости, о котором будет сказано чуть позже.
Содержание
- Что такое
- В чем измеряется
- Шкала и виды давлений
- Формула расчета давления в открытом сосуде
- Давление жидкости в трубах и его нормативы
- Распределение давления жидкости в тубах
Что такое
Одно из широко распространенных определений гидростатического давления звучит так: «Гидростатическое давление в точке жидкости – это нормальное сжимающее напряжение, возникающее в покоящейся жидкости под действием поверхностных и массовых сил».
Напряжение – это понятие, широко используемое в курсе сопротивления материалов. Идея в следующем. В физике, мы знаем, есть понятие силы. Сила – векторная величина, характеризующая воздействие. Векторная – это значит, что представляется в виде вектора, т.е. стрелки в трехмерном пространстве. Эта сила может быть приложена в отдельной точке (сосредоточенная сила), или к поверхности (поверхностная), или ко всему телу (говорят, массовая / объемная). Поверхностные и массовые силы являются распределенными. Только такие и могут действовать на жидкость, так как она обладает функцией текучести (легко деформируется от любого воздействия).
Сила приложена к поверхности с какой-то конкретной площадью. В каждой точке этой поверхности возникнет напряжение, равное отношению силы к площади, это и есть понятие давления в физике.
В чем измеряется
В системе СИ единица измерения силы – Ньютон [Н], площади – квадратный метр [м2].
Отношение силы к площади: 1 Н / 1 м2 = 1 Па (Паскаль).
Паскаль является основной единицей измерения давления, но далеко не единственной. Ниже представлен пересчет единиц измерения давлений из одной в другую
100 000 Па = 0,1 МПа = 100 кПа ≈ 1 атм = 1 бар = 1 кгс/см2 = 14,5 psi ≈ 750 мм.рт.ст ≡ 750 Торр ≈ 10 м.вод.ст (м)
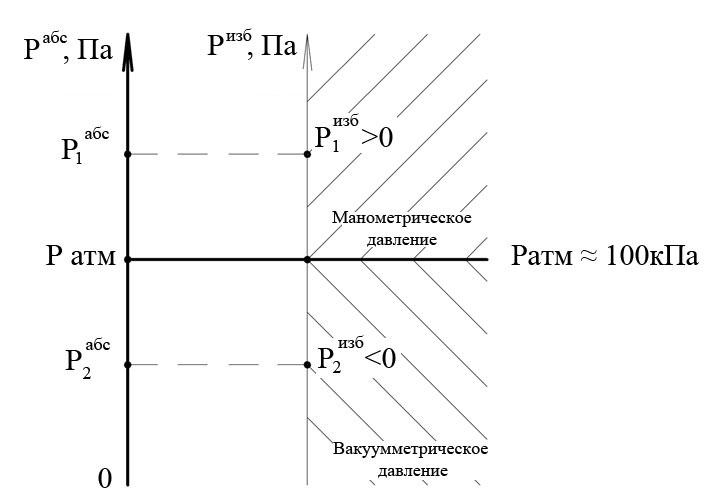
Шкала и виды давлений
Далее, принципиально важным моментом является так называемая шкала давлений или виды давлений. На рисунке ниже представлено, как взаимоувязаны такие понятия как абсолютное давление, абсолютный вакуум, частичный вакуум, избыточное или манометрическое давление.
Абсолютное давление – давление, отсчитываемое от нуля.
Абсолютный вакуум – ситуация, при которой на рассматриваемую точку ничего не действует, т.е. давление, равное 0 Па.
Атмосферное давление – давление, равное 1 атмосфере. Отношение веса (mg) вышележащего столба воздуха к площади его поперечного сечения. Атмосферное давление зависит от места, времени суток. Это один из параметров погоды. В прикладных инженерных дисциплинах обычно все отсчитывают именно от атмосферного давления, а не от абсолютного вакуума.
Частичный вакуум (или еще часто говорят – «величина вакуума», « разрежение» или «отрицательное избыточное давление» ). Частичный вакуум – недостаток давления до атмосферного. Максимально возможная на Земле величина вакуума как раз равняется одной атмосфере (~10 м.вод.ст.). Это означает, что у вас не получится попить воду через трубочку с расстояния 11 м при всем желании.
* на самом деле при нормальном для трубочек для напитков диаметре (~5-6 мм) эта величина будет гораздо меньше из-за гидравлических сопротивлений. Но даже через толстый шланг вы не сможете попить воду с глубины 11 м.
Если заменить вас на насос, а трубочку – на его всасывающий трубопровод, то ситуация принципиально не изменится. Поэтому воду из скважин добывают как правило именно скважинными насосами, которые опускаются непосредственно в воду, а не пытаются засасывать воду с поверхности земли.
Избыточное давление (или также еще называемое манометрическим)– превышение давления над атмосферным.
Приведем следующий пример. На данной фотографии показано измерение давления в автомобильной шине при помощи прибора манометра.
Манометр показывает именно избыточное давление. На этой фотографии видно, что избыточное давление в данной шине приблизительно 1,9 бар, т.е. 1,9 атм, т.е. 190 000 Па. Тогда абсолютное давление в этой шине – 290 000 Па. Если мы шину проткнем, то воздух начнет под разницей давлений выходить наружу до тех пор, пока давление внутри и снаружи шины не станет одинаковым, атмосферным. Тогда избыточное давление в шине будет равно 0.
Формула расчета давления в открытом сосуде
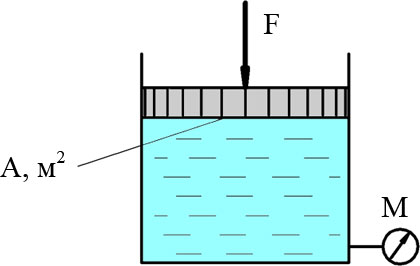
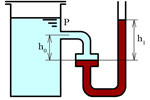
Теперь посмотрим, как определить гидростатическое давление в жидкости, находящейся в определенном объеме. Допустим, мы рассматриваем открытую бочку с водой.
На поверхности воды в бочке устанавливается атмосферное давление (обозначено маленькой буквой p с индексом «атм»). Соответственно, избыточное давление жидкости на поверхности равняется 0 Па. Теперь рассмотрим гидростатическое давление в точке X. Эта точка заглублена относительно поверхности воды на расстояние h, и за счет столба жидкости, гидростатическое давление в ней будет больше, чем на поверхности.
Давление в точке X (px) будет определяться, как давление на поверхности + давление, создаваемое столбом жидкости. Это называется основным уравнением гидростатики.
Для приблизительных расчетов можно принимать g = 10 м/с2. Плотность воды зависит от температуры, но для приблизительных расчетов может приниматься 1000 кг/м3.
При глубине h 2 м, абсолютное гидростатическое давление составит:
100 000 Па + 1000·10·2 Па = 100 000 Па +20 000 Па = 120 000 Па = 1,2 атм.
Избыточное давление жидкости – это значит за вычетом атмосферного: 120 000 – 100 000 = 20000 Па = 0,2 атм.
Таким образом, в избыточное давление в точке X определяется высотой столба жидкости. Форма емкости при этом никак не влияет. Если мы рассмотрим гигантский бассейн с глубиной 2 м, и трубку высотой 3 м, то гидростатическое давление на дне трубки будет больше, нежели на дне бассейна.
(Абсолютное гидростатическое давление на дне бассейна: 100000 + 1000*9,81*2 =
Абсолютное
Высота столба жидкости определяет давление, создаваемое этим столбом жидкости.pизб = ρgh.
Таким образом, гидростатическое давление можно выражать единицами длины (высоты): h = p / ρg
Например, рассмотрим, какое давление создает столб ртути высотой 750 мм:
p = ρgh = 13600 · 10 · 0,75 = 102 000 Па ≈ 100 000 Па, что отсылает нас к единицам измерения давления, рассмотренным ранее.
Т.е. 750 мм.рт.ст. = 100 000 Па.
По тому же принципу получается, что давление в 10 метров водяного столба равняется 100 000 Па:
1000 · 10 · 10 = 100 000 Па.
Выражение гидростатического давления в метрах водяного столба принципиально важно для водоснабжения, водоотведения, а также гидравлических расчетов отопления, гидротехнических расчетов и т. д.
Давление жидкости в трубах и его нормативы
Теперь посмотрим гидростатическое давление жидкости в трубопроводах. Что физически означает замеренное мастером давление в определенной точке (X) трубопровода? Манометр в данном случае показывает 2 кгс/см² (2 атм). Это избыточное давление в трубопроводе, оно эквивалентно 20 метрам водяного столба. Иными словами, если подсоединить к трубе вертикальную трубку, то вода в ней поднимется на величину избыточного давления, т.е. на высоту 20 м. Вертикальная трубка, которая сообщается с атмосферой (т.е. открытая) называются пьезометром.
Основная задача системы водоснабжения заключается в том, чтобы в требуемой точке вода имела необходимое избыточное давление. Например, согласно нормативному документу:
[ Постановление Правительства РФ от 06.05.2011 N 354 (ред. от 13.07.2019) «О предоставлении коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов» (вместе с «Правилами предоставления коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов») ] >>> давление в точке водоразбора должно быть не менее 3 м.вод.ст (0,03 МПа)
Под точкой водоразбора можно понимать место подключения смесителя (1). Эта точка находится приблизительно на расстоянии 1 м от пола, там же, где и подключение к стояку самой квартиры (2) . То есть давление примерно одинаково при закрытых кранах (вода не движется!). Давление регламентируется именно в этих точках, и, как указано выше, должно быть не меньше 3 — 6 м.вод.ст.
Однако необходимо отметить, что нормативно допустимая величина в 3 м.вод.ст – это совсем не много, так как современное сантехническое оборудование может требовать гидростатическое давление жидкости до 13 м.вод.ст в месте подключения для нормальной работы (подачи достаточного количества воды). Например, даже в старом СНиП по внутреннему водопроводу (СНиП 2.04.01-85*), указано, что при использовании аэратора на смесителе (сеточка, перекрывающая выходное отверстие), в точке подключения смесителя необходимо давление 5 м.вод.ст.
Распределение давления жидкости в тубах
2017-04-01
Давление и силы действующие на жидкость
Содержание:
- Массовые и поверхностные силы действующие на жидкость
- Давление
- Абсолютное и избыточное давление
- Манометрическое и вакуумметрическое давление
Массовые и поверхностные силы действующие на жидкость
Из-за легкоподвижности на жидкость не могут действовать сосредоточенные нагрузки, а возможно лишь действие сил непрерывно распределенных либо по массе либо по поверхности жидкости. Все многообразие сил делят на массовые и поверхностные.
Массовые силы распределены по массе жидкого тела, и при их непрерывном распределении пропорционально этой массе.
В гидравлических расчетах используют единичные массовые силы, приходящиеся на единицу массы твердого тела.
Поверхностные силы – непрерывно распределены по поверхности жидкого тела и при их непрерывном распределении пропорционально площади этой поверхности. Это силы с которыми данные тела взаимодействую с жидким телом, воздействуют на него через поверхность соприкосновения.
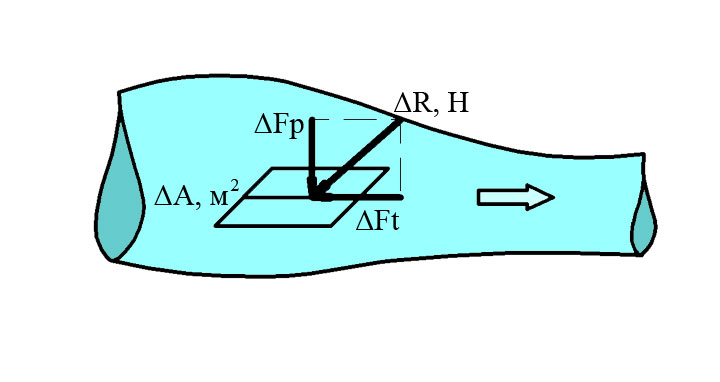
Поверхностная сила ΔR, с которой выше лежащие потоки действуют на нижележащие.
ΔFр направленная перпендикулярно площадке нормально сжимающая сила или сила давления
ΔFt – сила трения в плоскости площадки
В механике жидкости и газа используют единичные поверхностные силы, то есть напряжения. Единица измерения напряжения Н/м2 = Па (Паскаль).
Средняя величина нормально вжимающего напряжения в площадке ΔA определяется по формуле:
Fср = ΔFр/ΔA
Истинное давление в данной точке жидкого тела.
Давление
При равновесии ньютоновской жидкости в ней возможен только один вид напряжений – нормальные сжимающие напряжения, которые называют гидростатическим давлением.
Давление – нормальное напряжение сжатия в жидкости или газе.
P=F/A
Измеряется давление в системе СИ Н/м2 или Па (Паскалях), также существует множество других единиц измерения давления.
Давление, приложенное к внешней поверхности жидкости передается вем точкам и во сех направлениях одинаково, это положение называют законом Паскаля.
В обычных условиях (медленное текущих) жидкость на растяжение не работает, а значит давление положительно.
Если жидкость очень чистая (дегазированная), а процесс проходит очень быстро, знакопеременно, то в жидкости возможны кратковременные растягивающие напряжения, то есть давление может быть отрицательным.
Давление в газе всегда положительно.
Абсолютное и избыточное давление
Давление может измеряться по избыточный или абсолютной шкалам.
В избыточной шкале за 0 принято давление атмосферы, давление ниже атмосферного записывается со знаком минус.
Истинное давление называют абсолютным.
Таким образом, можно записать зависимости:
- 1 атм. абс = 0 атм. изб
- P изб.= P абс. – 1 Атм.
Манометрическое и вакуумметрическое давление
Положительное избыточное давление называют манометрическим, его измеряют с помощью манометра.
Отрицательное избыточное давление называют вакуумметрическим, его измеряют с помощью вакуумметра.
Читайте также:
Все новости
Существует множество способов, позволяющих экспериментально измерить давление жидкости. При создании вычислительных моделей гидродинамических процессов важно использовать корректное значение давления для постановки граничных условий и определения свойств материалов. В данной статье мы рассмотрим отличия между относительным и абсолютным давлением, объясним, почему в программном пакете COMSOL Multiphysics® для решения задач гидродинамики используется относительное давление, и покажем, в каких случаях следует применять эти способы определения давления.
В чем различие между абсолютным и относительным давлениями?
В механике жидкостей давление определяется как отношение силы к площади поверхности, к которой приложена эта сила. COMSOL Multiphysics позволяет решать уравнения Навье — Стокса, описывающие течение жидкости, и находить поля скорости и давления движущейся среды.
В задачах вычислительной гидродинамики давление можно задавать двумя способами, используя либо абсолютное, либо относительное давление.
Абсолютное давление
Абсолютным давлением называют истинное давление жидкости относительно вакуума. Например, если измерить давление окружающего воздуха барометром в обычный день, то мы увидим, что абсолютное давление составляет около 1 атм или 101,325 кПа — это значение соответствует атмосферному давлению на уровне моря. Нулевое абсолютное давление соответствует вакууму.
Барометр позволяет измерять давление воздуха от 950 до 1050 мбар (1 мбар = 100 Па). Изображение, предоставленное Langspeed. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.
Относительное давление
Относительное давление — это давление жидкости относительно базового значения, которое используется в качестве уровня отсчета давления. Манометрическое давление — это давление, измеренное относительно давления окружающей среды, то есть это относительное давление при условии, что давление окружающей среды принято за начало отсчета. Обычно относительное давление используется для характеристики закрытых систем. Его можно измерить манометром — прибором, который позволяет соотнести внутреннее давление с давлением внешней среды.
Манометры, используемые для измерения относительного давления на станции регулирования давления. Обратите внимание, что шкалы начинаются с нуля, который соответствует базовому значению давления в системе. Изображение предоставлено Holmium — собственное произведение. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.
Абсолютное давление и относительное давление связаны следующим образом:
рА = р + рref.
В случае, когда в качестве базового давления используется давление вакуума, значения абсолютного и относительного давлений совпадают. Во многих случаях базовое значение давления соответствует атмосферному давлению или давлению окружающей среды.
Давайте соотнесем указанные способы определения давления с тем, что мы видим в COMSOL Multiphysics. При решении задач гидродинамики программное обеспечение COMSOL® рассчитывает значения компонент скорости (u,v,w) и относительного давления (р). Далее мы поясним, как использование относительного давления вместо абсолютного в качестве зависимой переменной позволяет точнее рассчитать давление в нашей модели. Мы можем использовать значения относительного давления при задании начальных и граничных условий, как показано в следующем примере.
Как задается давление жидкости в COMSOL Multiphysics®
Рассмотрим пример, показывающий, как правильно использовать переменные для относительного и абсолютного давлений в модели COMSOL Multiphysics. Для этого воспользуемся простой моделью течения воздуха, который поступает в канал со скоростью 1 м/с при абсолютном давлении в выходном сечении 1 атм. На верхней и нижней границах используются условия нулевой скорости за исключением короткого входного участка, на котором заданы условия симметрии. Специальные условия на коротком входном участке позволяют избежать несогласованности граничных условий, возникающей при задании равномерного распределения скорости на входе, которое не может быть удовлетворено на твердых стенках.
Схематическое изображение канала и проходящего через него потока воздуха.
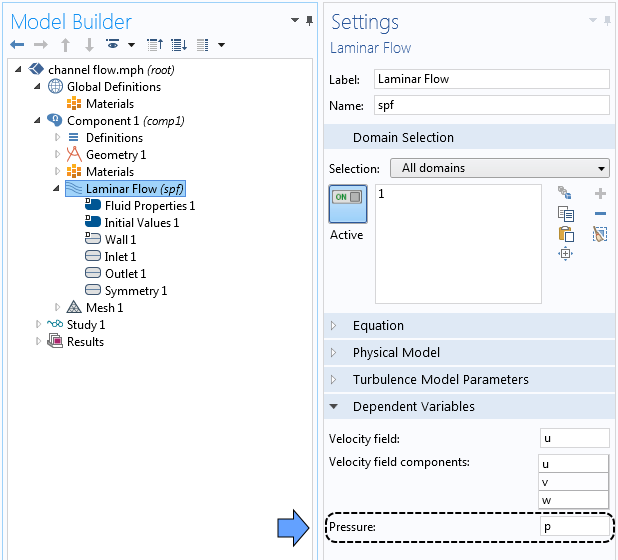
В рассматриваемой модели переменные для относительного и абсолютного давлений обозначены соответственно р и spf.pA. В настройках интерфейса Laminar Flow (Ламинарное течение) видно, что искомые зависимые переменные представляют собой компоненты скорости (u,v,w) и относительное давление (р).
Окно Settings (Настройки) со списком зависимых переменных.
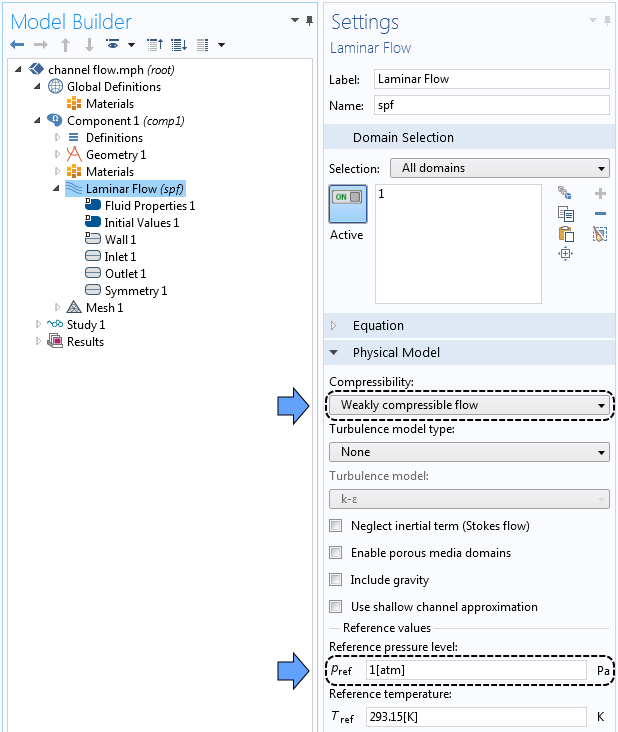
Как видно из рисунка ниже, базовое давление по умолчанию составляет 1 атм. Это значение используется при расчетах абсолютного давления: spf.pA = p + spf.pref.
Для сжимаемости выберем параметр Weakly compressible flow (Слабо сжимаемая среда), который означает, что плотность среды зависит только от температуры и рассчитывается для базового значения давления. Узнать больше о различных настройках сжимаемости можно в предыдущей статье блога.
Настройки сжимаемости и базового давления.
Теперь зададим граничные условия. Для нормальной компоненты скорости на входе зададим значение 1 м/с. При задании граничного условия в выходном сечении и начальных значений искомых переменных нужно вводить значение относительного давления с учетом заданного базового значения, поскольку мы используем настройки по умолчанию. При добавлении условия на выходе мы видим, что значение относительного давления по умолчанию р = 0, то есть абсолютное давление равно 1 атм при использовании заданного по умолчанию базового значения давления.
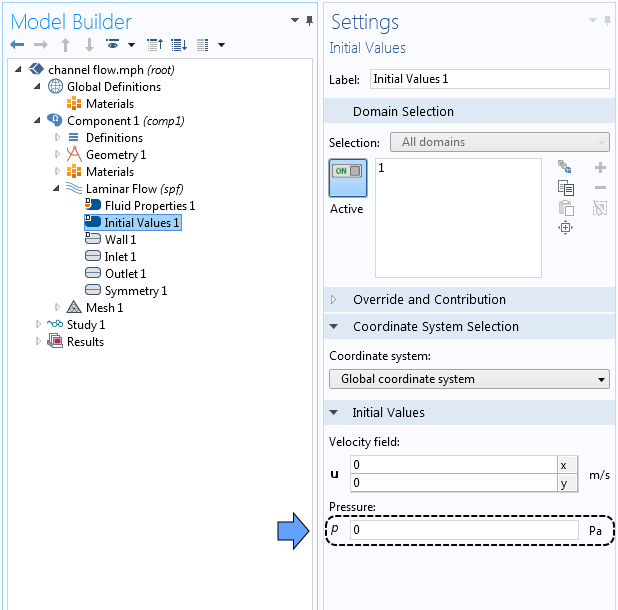
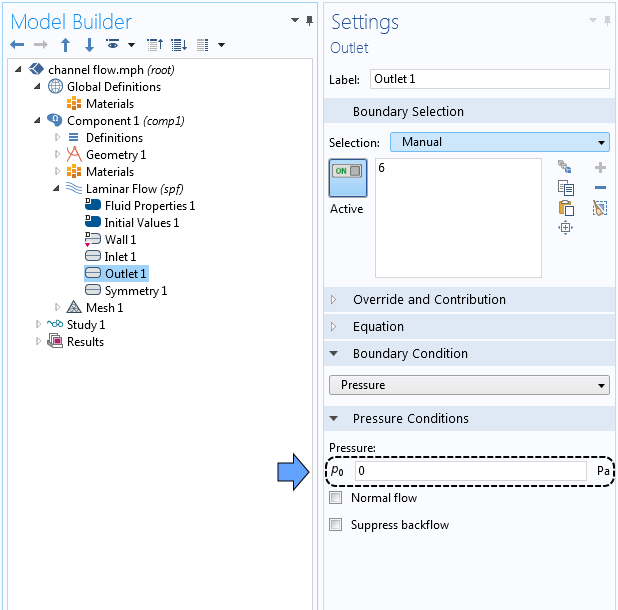
Окна настроек для граничных условий, в которых заданы значения относительного давления в качестве начальных (слева) и граничных (справа) условий.
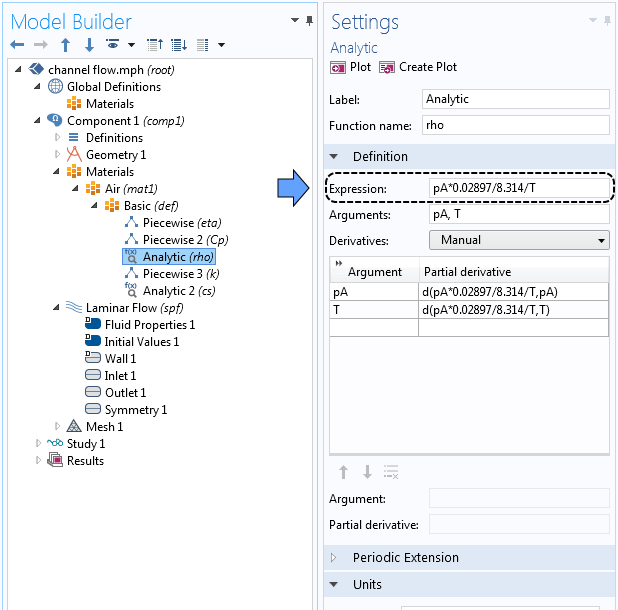
Возможно, у вас возник вопрос, для чего в COMSOL® выполняется расчет переменной для абсолютного давления spf.pA. Абсолютное давление используется при расчете плотности сжимаемой жидкости. К примеру, если перейти к описанию свойств воздуха в канале, мы увидим, что плотность рассчитывается по уравнению состояния идеального газа, где рА — абсолютное давление, Т — температура. Поскольку в уравнение состояния идеального газа входит абсолютное давление, при расчете плотности нужно прибавить к уровню отсчета давления относительное давление р. Тем не менее вклад относительного давления в полное давление здесь настолько мал (0,00025%, см. ниже), что при расчете плотности можно использовать базовое значение давления — именно так и выполняется расчет плотности при выборе параметра Weakly compressible flow (Слабо сжимаемая среда). В системах с большим изменением давления в потоке можно выбрать вариант Compressible flow (Сжимаемая среда).
Расчет плотности по уравнению состояния идеального газа.
Теперь, задав граничные условия для нашей задачи, можно получить ее решение и визуализировать поле течения с помощью линий тока. 
Поле течения в канале, показанное с помощью линий тока и векторного поля скорости.
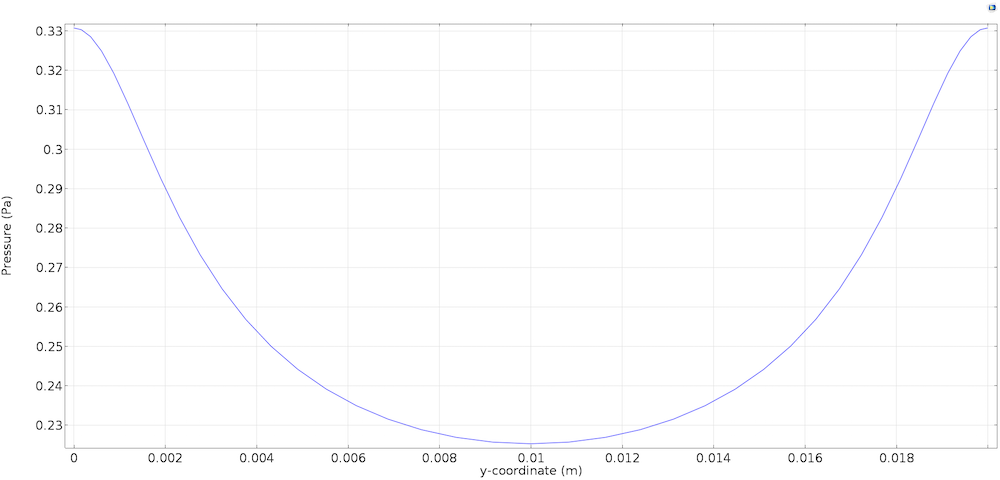
Кроме того, мы можем построить распределение давления во входном сечении канала (по оси у на левой вертикальной границе). Из графика ниже видно, что изменение давления в пределах входного сечения составляет примерно 0,1 Па при базовом давлении 105 Па. Это означает, что базовое давление примерно в миллион раз превышает изменение давления во входном сечении!
Распределение относительного давления вдоль вертикальной входной границы.
Решение гидродинамических задач с помощью относительного давления
По умолчанию при решении задач гидродинамики в COMSOL Multiphysics в качестве зависимой переменной используется относительное давление, а когда требуется получить значение абсолютного давления, например, для расчета плотности жидкости, к относительному просто прибавляется базовое давление. Это повышает точность расчета флуктуаций поля давления вокруг базового значения, а также расчета градиентов давления.
Теперь вернемся к нашему примеру и вычислим перепад давления. С помощью операции Line Average (Осреднение по линии) мы можем определить, что значение относительного давления на входе равно pinlet = 0,26 Па.
Представим теперь, что мы решили задачу, используя абсолютное давление. В этом случае значения давления на входе и на выходе оказались бы равны соответственно 101 325,26 Па и 101 325,00 Па. Относительное изменение давления между входным и выходным сечениями канала составляет 0,000253814%. Как показано на графике распределения давления, на входе изменения еще более незначительны: давление меняется в пределах одной миллионной от значения абсолютного давления. Столь малое относительное изменение очень сложно точно рассчитать при решении уравнений.
Так как мы решаем задачу численным методом, мы получаем лишь приближенные значения реального поля давления. Давление определено в каждой точке, тогда как численное решение позволяет найти значения давления в относительно малом числе точек. За счет погрешности округления и интерполяции появляется числовая погрешность. Кроме того, численное решение уравнений может быть получено только с некоторой ограниченной, заданной точностью. Погрешность найденных численными методами значений давления сопоставима с относительно малыми изменениями давления, которые мы ищем. С помощью разложение давления на базовое и относительное, мы можем более эффективно, чем при использовании абсолютного давления, рассчитывать градиенты давления и колебания давления относительно атмосферного при приемлемых значениях относительной погрешности.
Как задать базовое давление
Теперь, когда мы понимаем, для чего используется относительное давление при решении гидродинамических задач в COMSOL Multiphysics, становится ясно, насколько важно правильно задавать базовое давление. Очевидно, что значение базового давления 1 атм подходит для систем, работающих при давлении, близком к атмосферному. В системах с очень высоким либо низким давлением следует использовать базовое значение давления, которое соответствует уровню давления в потоке.
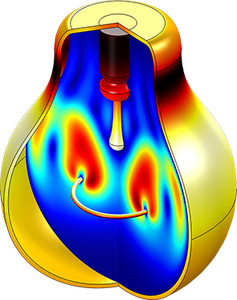
Например, в колбе обычной лампы накаливания находится разреженный аргон, предотвращающий окисление нити. В учебной модели из Галереи приложений значение базового давления задано в соответствии с давлением газа, заполняющего колбу (50 кПа). В разделе Initial Values (Исходные значения) относительное давление задано как р = 0, что соответствует абсолютному давлению 50 кПа при заданном уровне базового давления.
Моделирование свободной конвекции аргона в лампе накаливания.
При моделировании систем с очень низким давлением важно убедиться, что среду все еще можно считать сплошной. Чтобы узнать, не потребуется ли для моделирования течения использование методов молекулярной физики, можно рассчитать число Кнудсена, которое равно отношению средней длины свободного пробега частицы к характерному размеру системы.
Особенности задания давления жидкости в COMSOL Multiphysics®: краткий обзор
Итак, в этой публикации мы постарались объяснить, что абсолютное давление является результатом прямого измерения, а относительное отсчитывается от базового значения давления.
В COMSOL Multiphysics для решения задач гидродинамики используется относительное давление, что позволяет повысить точность расчета поля давления. Это означает, что начальные и граничные условия необходимо задавать с помощью значений относительного давления. Вместе с тем для расчета плотности газа используется абсолютное давление, которое вычисляется путем сложения базового и относительного давлений. Для систем высокого или низкого давления базовое давление необходимо задавать в соответствии со средним значением давления в системе.