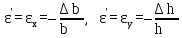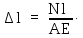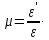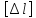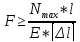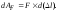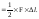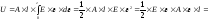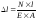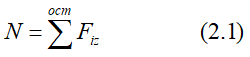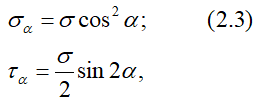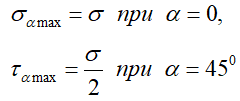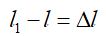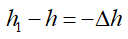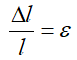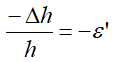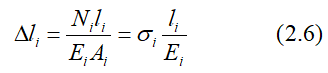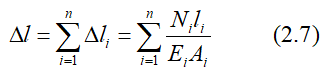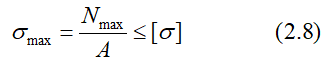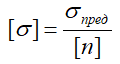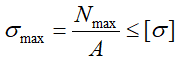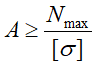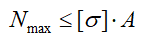Выделим
из стержня на участке, где действует
постоянная продольная
сила N,
некоторую его часть длиной l
и шириной b
(см. рис. 4.3, а). Опыты показывают,
что при растяжении резинового стержня
его длина увеличивается, а ширина
уменьшается. Пусть
l1
и b1 –
длина и ширина стержня после деформации
соответственно.
Изменение
длины стержня при растяжении (сжатии)
называется абсолютной продольной
деформацией и определяется по формуле
∆l
= l1
– l2.
Отношение
абсолютной продольной деформации к
первоначальной длине стержня называется
относительной продольной деформацией
и определяется по формуле
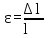
По
аналогии с продольными деформациями
имеем:
∆b
= b1
– b,
∆h
= h1
– h
– абсолютные
поперечные деформации;
– относительные
поперечные деформации.
При
растяжении: N
0, ∆l
0, ε
0, ∆b
< 0, ε‘
<
0; при сжатии:
N
< 0, ∆l
< 0, ε
<
0, ∆b
0, ε‘
0.
Закон
Гука –
относительная продольная деформация
прямо пропорциональна нормальному
напряжению, а именно:
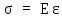
где
Е
– модуль
Юнга или модуль упругости первого рода
(кН/см2,
МПа).
Используя
зависимости
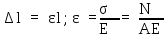
получим
Абсолютная
продольная деформация прямо пропорциональна
продольной силе в пределах участка
длиной l
при
постоянных N
и
EА,
где EА
– жесткость поперечного сечения при
растяжении (сжатии).
Коэффициент
Пуассона
– безразмерная величина, характеризующая
упругие свойства и способность материала
деформироваться в поперечном направлении
при его растяжении или сжатии в продольном
направлении.
Для
реальных материалов коэффициент Пуассона
изменяется в очень узких пределах:
= 0…0,5.
Значение
для некоторых
материалов:
–
пробка –
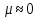
–
резина –
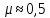
–
сталь –
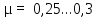
–
свинец –
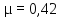
–
бетон –
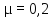
–
каучук –
0,5.
Значение
коэффициента Пуассона определяется
опытным путем в результате специальных
испытаний материала.
4.4. Условия прочности и жесткости
Условие
прочности элементов конструкций и
сооружений рассмотрено в главе 3.
В
некоторых случаях для обеспечения
нормальной работы машин, конструкций
и сооружений требуется проектировать
размеры деталей и элементов таким
образом, чтобы обеспечивалось условие
жесткости:
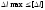
где
– допускаемое удлинение, задается
техническими условиями.
Удлинение
ступенчатых стержней, а также когда
внешние силы приложены в разных точках
продольной оси стержня, определяется
суммированием удлинений отдельных
участков.
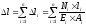
где
Ni,
li,
Ei,
Аi
– нормальная сила, длина, модуль упругости
и площадь поперечного сечения і–го
участка соответственно.
Условие
жесткости позволяет выполнять три вида
расчетов:
1)
проверочный:
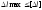
2)
проектировочный: 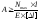
постоянного сечения);
3)
расчет грузоподъемности или несущей
способности:
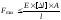
4.5. Потенциальная энергия упругой деформации
Внешние
силы, приложенные к упругому телу и
вызывающие изменение его геометрии,
совершают работу АF
на соответствующих перемещениях. В
упругом теле накапливается потенциальная
энергия деформации U.
При действии динамических нагрузок
часть работы внешних сил превращается
в кинетическую энергию движения частиц
тела К.
Уравнение
баланса энергии можно записать в
следующем виде:
АF = U + K.
При
статическом нагружении упругого тела
работа внешних сил полностью преобразуется
в потенциальную энергию деформации,
следовательно, АF = U.
При разгрузке тела производится работа
за счет потенциальной энергии деформации,
накопленной телом. При этом упругое
тело является аккумулятором энергии.
Это свойство упругого тела широко
используется в заводных пружинах часовых
механизмов, в конструкции лука и т. д.
Для вывода необходимых расчетных
зависимостей потенциальной энергии
деформации рассмотрим простейший случай
– растяжение стержня.
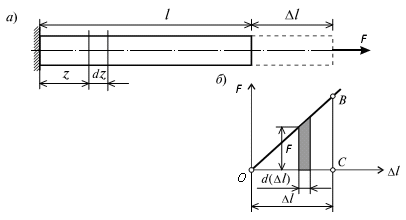
На
рис. 4.5, а изображен стержень,
растягиваемый силой F,
удлинение которого соответствует l.
График изменения величины удлинения
стержня l
в зависимости от силы F
показан на рис. 4.5, б.
В соответствии
с законом Гука этот график носит линейный
характер.
Рис.
4.5. а
– схема растягиваемого стержня; б
– график зависимости F
– ∆l
Пусть
некоторому значению силы F соответствует
удлинение стержня l.
Дадим некоторое приращение силе
F соответствующее
приращение удлинения составит d (l ).
Элементарная работа на этом приращении
удлинения составит:
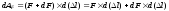
Вторым
слагаемым, в силу его малости, можно
пренебречь, и тогда
Полная
работа равна сумме элементарных работ,
тогда при линейной зависимости работа
внешней силы F
на перемещении l
будет равна площади треугольника ОСВ
(рис. 4.5, б), т. е.
Если
напряжения
и деформации
распределены по объему тела V
равномерно, то потенциальную энергию
деформации стержня можно записать в
следующем виде:
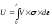
где
V = А l,
F =
A,
= Е ;
А
– площадь поперечного сечения стержня.
Тогда
окончательно
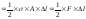
С
учетом
для
однородного стержня с постоянным
поперечным сечением при F = const
получим:
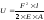
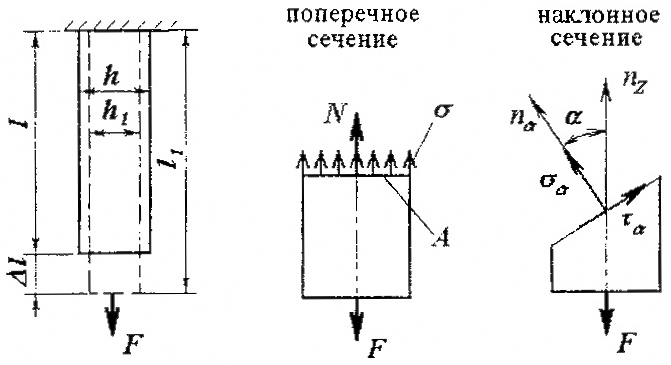
Растяжением и сжатием называют такой вид деформации бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N.
Брус при растяжении-сжатии называют стержнем.
Для определения продольной силы используется метод сечений:
В сечениях бруса, удаленных более чем на величину h (рис. 2.1) от торцов (мест нагружения), усилие N на основании принципа Сен-Венана равномерно распределяется по площади поперечного сечения, вызывая нормальные напряжения:
В наклонном сечении возникают нормальные σα и касательные τα напряжения:
причем
Рис. 2.1
При растяжении (сжатии) имеют место только линейные деформации:
— абсолютная продольная деформация (удлинение/укорочение)
— абсолютная продольная деформация (сужение/утолщение)
— относительная продольная деформация
— относительная поперечная деформация
Отношение
называется коэффициентом поперечной деформации (коэффициентом Пуассона).
Напряжения и деформации взаимосвязаны законом Гука
где:
E – модуль упругости I рода (модуль Юнга), является постоянной величиной для данного материала и характеризует его жесткость, для стали E=200ГПа.
Изменение длины участка бруса постоянного сечения вычисляется по формуле
Величина EiAi называется жесткостью поперечного сечения бруса при растяжении (сжатии).
Полное удлинение (укорочение) бруса с несколькими силовыми участками:
Условие прочности при растяжении/сжатии выражается неравенством:
Здесь
— допускаемое напряжение;
σпред — предельное (опасное) для данного материала напряжение, равное пределу текучести (σТ или σ0,2) для пластичных материалов или пределу прочности σпч для хрупких материалов;
[n] – нормативный коэффициент запаса прочности.
Условие прочности позволяет решать три типа задач:
1. Проверка прочности (проверочный расчет)
2. Подбор сечения (проектировочный расчет)
3. Определение грузоподъемности (допускаемой нагрузки)
При расчете на жесткость растянутого (сжатого) бруса обычно определяют величину продольной деформации, которая не должна превышать допустимых значений, т.е.
Примеры решения задач >
Лекции по сопромату >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Сопротивление материалов
Деформации при растяжении и сжатии
Продольные деформации при растяжении и сжатии
Характер деформаций, которым подвергается прямой брус при растяжении или сжатии мы определили, проведя опыт с резиновым брусом, на котором была нанесена сетка линий.
Теперь представим себе брус постоянного сечения имеющий длину l, один из концов которого защемлен, а к свободному концу приложена растягивающая сила F. Под действием этой силы брус удлинится на некоторую величину Δl, которую назовем абсолютным удлинением бруса.
Отношение абсолютного удлинения Δl к первоначальной длине бруса l назовем относительным удлинением и обозначим ε:
ε = Δl / l
Относительное удлинение – величина безразмерная, иногда его выражают в процентах.
Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.
***
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой линейной зависимостью, которая называется законом Гука, по имени английского физика Р. Гука (1653-1703 г.г.), установившего этот закон.
Сформулировать закон Гука можно так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.
Математически эта зависимость записывается так:
σ = E ε.
Здесь Е – коэффициент пропорциональности, который характеризует жесткость материала бруса, т. е. его способность сопротивляться деформации; его называют модулем продольной упругости, или модулем упругости первого рода.
Модуль упругости, как и напряжение, выражаются в паскалях (Па).
Значения Е для различных материалов устанавливаются экспериментально-опытным путем, и их величину можно найти в соответствующих справочниках.
Так, для стали Е = (1,96.…2,16) х 105 МПа, для меди Е = (1,00…1,30) х 105 МПа и т. д.
Следует оговориться, что закон Гука справедлив лишь в определенных пределах нагружения.
Если в формулу закона Гука подставить полученные ранее значения относительного удлинения и напряжения: ε = Δl / l , σ = N / А, то можно получить следующую зависимость:
Δl = Nl / (EА).
Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.
Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение ЕА / l называют жесткостью бруса при растяжении и сжатии.
Приведенные выше формулы закона Гука справедливы лишь для брусьев и их участков, имеющих постоянное поперечное сечение, изготовленных из одного материала и при постоянной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами сечения, продольной силой, изменение длины всего бруса определяется, как алгебраическая сумма удлинений или укорочений отдельных участков:
Δl = Σ (Δli)
***
Поперечные деформации при растяжении и сжатии
Описанный ранее опыт с резиновым брусом, на котором нанесена сетка линий, показал, что при растяжении поперечные размеры бруса уменьшаются, а при сжатии – увеличиваются, т. е. брус становится либо тоньше, либо толще. Это явление характерно для брусьев, изготовленных из всех материалов.
Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций для данного материала – величина постоянная.
Впервые на эту зависимость указал французский ученый С. Пуассон (1781-1840 г.г.) и математически она записывается так:
|ε1| = ν |ε|,
где ν – коэффициент поперечной деформации, называемый коэффициентом Пуассона.
Коэффициент Пуассона является безразмерной величиной, и характеризует упругие свойства материала. При растяжении и сжатии этот коэффициент принимается одинаковым.
Значения коэффициента Пуассона для разных материалов установлены опытным путем и их величины можно найти в соответствующих справочниках.
***
Потенциальная энергия деформации при растяжении
При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W.
Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что W = U.
Путем изучения диаграмм растяжения образцов, установлено, что потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна:
U = W = F Δl / 2 = N2 l / (2E А)
Сопротивление материалов оперирует, также, таким понятием, как удельная потенциальная энергия деформации, которая подсчитывается, как потенциальная энергия, приходящаяся на единицу объема бруса.
При одновременном действии растягивающих и сжимающих нагрузок или ступенчатом изменении размеров поперечного сечения бруса, его разбивают на однородные участки и для каждого подсчитывают потенциальную энергию деформации. Потенциальную энергию деформации всего бруса определяют, как сумму потенциальных энергий отдельных участков.
Анализируя формулу потенциальной энергии деформации можно сделать вывод, что эта величина всегда положительная, поскольку в ее выражения входят квадраты линейных и силовых величин. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (поскольку квадрат суммы не равен сумме квадратов слагаемых).
Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж).
***
Материалы раздела “Растяжение и сжатие”:
- Основные понятия о деформации растяжения и сжатия.
- Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.
Смятие
Правильные ответы на вопросы Теста № 5
|
№ вопроса |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Правильный вариант ответа |
3 |
3 |
1 |
2 |
1 |
3 |
2 |
2 |
1 |
1 |
Вывод закона Гука при растяжении – сжатии. В ходе многочисленных экспериментов установлена зависимость между нагрузкой, приложенной к стержню, и перемещениями сечений, к которым эта нагрузка приложена:

Произведение ЕА – называется жесткостью сечения стержня при растяжении – сжатии.
Учитывая, что F/А = σ, выражение (1) можно записать так:

Тогда:
Этот закон был предложен в 1660 г. английским физиком Гуком (закон был опубликован только в 1678 г.). В 1680 г. этот же закон независимо от Гука открыл французский ученый Мариотт.