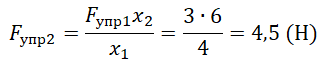Абсолютное удлинение — показывает на сколько изменилась длина тела (увеличилась или уменьшилась).
Δl=l-l0
Единица измерения абсолютного удлинения метр – [м]
Для того, чтобы было более понятно, что же такое абсолютное удлинение, давайте рассмотрим такой пример. У нас есть металлическая труба длиной 8 метров. К трубе приложили некую силу (сжали ее) и длина трубы стала 7 метров. Тогда абсолютное удлинение будет рассчитываться как: 8м-7м=1м. То есть, длина тела изменилась на 1 метр.
Обозначения:
Δl — абсолютное удлинение тела
l0 — начальная длина тела
l — конечная длина тела, после приложения к нему силы
Абсолютное удлинение — Показывает на сколько изменилась длина тела (увеличилась или уменьшилась).
[Метр]
Для того, чтобы было более понятно, что же такое абсолютное удлинение, давайте рассмотрим такой пример. У нас есть металлическая труба длиной 10 метров. К трубе приложили некую силу (сжали ее) и длина трубы стала 2 метра. Тогда абсолютное удлинение будет рассчитываться как:
То есть, длина тела изменилась на 8 метров.
В Формуле мы использовали :
— Абсолютное удлинение тела
— Начальная длинна тела
— Длина тела, после приложения на него силы
-
Как вычисляется абсолютное удлинение стержня?
Из
формул (2.2), (2.3) и (2.4), легко получить
зависимость для абсолютного удлинения
стержня:
.
(2.5)
Выражение
(2.5) иногда также называют законом Гука,
но уже не для материала,
а для всего стержня.
Произведение
,
стоящее в знаменателе (2.5), характеризуетжесткость стержня
при растяжении (сжатии).
-
Какие напряжения возникают в наклонных сечениях стержня, то есть в сечениях, которые не являются поперечными?
Начнем
ответ со следующих рассуждений. Да, мы
уже умеем определять нормальные
напряжения, которые возникают в опасном
поперечном сечении стержня. Но можем
ли мы утверждать, что эти нормальные
напряжения являются наибольшими и
именно их значения следует использовать
для оценки прочности стержня? Нам уже
известно, что касательные напряжения
в поперечном сечении стержня при
растяжении (сжатии) не возникают. Но
возникают ли они в наклонных
сечениях?
Таким
образом,
нам необходимо научиться определять
напряжения на любых
площадках, проходящих через некоторую
точку К тела и находить именно те
площадки, на которых нормальные и
касательные напряжения достигают
наибольших значений.
А
теперь ответим на поставленный вопрос.
Разрежемстержень,
растягиваемый силами P,
плоскостью, проходящей через точку К
и наклоненной под углом
к поперечному сечению (рис. 2.2, а).
Отбросимправую
часть стержня.
Внешняя
нормаль
к этомунаклонному
сечению будет составлять с осью
такой же угол
.
Действие отброшенной нами правой части
стержня на левую часть заменим
внутренними усилиями (рис. 2.2, б).
Чтобы левая часть стержня находилась
в
равновесии,
в каждой точке наклонного сечения
стержня должно возникнуть продольное
противодействующее усилие. Очевидно,
что равнодействующая всех
этих внутренних усилий N
равна внешней силе P.
Будем
считать, что внутренние усилия равномерно
распределены по всей площади наклонного
сечения
.
Тогдаполное
напряжение в каждой
точке наклонного сечения будет равно:
,
(2.6)
где
– нормальное напряжение, возникающее
в этих же точках (в том числе и в точкеК), но в
поперечном
сечении стержня (рис. 2.1, в).
Разложим
полное напряжение p,
возникающее в некоторой точке К
наклонного
сечения, на две составляющие – нормальное
икасательное
напряжения (рис. 2.2,г).
Они будут равны:
.
(2.7)
Проследим,
как будет меняться каждое из этих
напряжений с изменением угла наклона
сечения
от нуля до
.
При
увеличении угла
нормальное напряжение в точкеК
будет постепенно уменьшаться от своего
максимального значения до нуля.
Касательное напряжение при этом будет
сначала возрастать от нулевого до
максимального значения
при
,
а затем убывать. При угле
касательное напряжение снова станет
равным нулю.
Следовательно,
наибольшеенормальноенапряжение
действительно возникает в точкахпоперечногосечения стержня. Впродольномсечении оно равнонулю.
Отсюда следует, что продольные волокна
стержня не давят друг на друга.
Наибольшие
касательныенапряжения возникают
в сечениях, расположенных под углом
к оси стержня. В поперечном и в продольном
сечениях они равны нулю.
Сила упругости — сила, которая возникает при деформациях тел в качестве ответной реакции на внешнее воздействие. Сила упругости имеет электромагнитную природу.
Деформация — изменение формы или объема тела.
Виды деформаций
- сжатие;
- растяжение;
- изгиб (сжатие и растяжение в комбинации);
- сдвиг;
- кручение (частный случай сдвига).
Сила упругости обозначается как Fупр. Единица измерения — Ньютон (Н). Сила упругости направлена противоположно перемещению частиц при деформации.
Если после окончания действия внешних сил тело возвращает прежние форму и объем, то деформацию и само тело называю упругими. Если после окончания действия внешних сил тело остается деформированным, то деформацию и само тело называют пластическими, или неупругими.
Примеры упругой деформации:
- Сжатый воздушный шарик распрямляется после того, как его отпустят.
- Если согнуть ластик, а затем отпустить, он распрямится.
- Мостик из доски, перекинутой через ручей, прогибается под пешеходом. Но когда пешеход ступает на землю, доска распрямляется.
Примеры пластической деформации:
- Скомканная бумага остается скомканной и после того, как ее отпустили.
- Пластилин сохраняет форму вылепленной из него фигуры.
- Согнутая металлическая пластина остается согнутой.
Закон Гука
При упругой деформации есть взаимосвязь между силой упругости, возникающей в результате деформации, и удлинением деформируемого тела. Эту взаимосвязь первым обнаружил английский ученый Роберт Гук.
Закон Гука
Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению.
x — абсолютное удлинение (деформация), k — коэффициент жесткости тела.
Абсолютное удлинение определяется формулой:
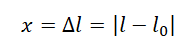
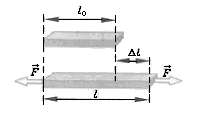
l0 — начальная длина тела, l — длина деформированного тела, ∆l — изменение длины тела.
Коэффициент жесткости тела определяется формулой:
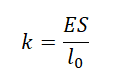
E — модуль упругости (модуль Юнга). Каждое вещество обладает своим модулем упругости. S — площадь сечения тела.
Важно! Закон Гука не работает в случае, если деформация была пластической.
Пример №1. Под действием силы 3Н пружина удлинилась на 4 см. Найти модуль силы, под действием которой удлинение пружины составит 6 см.
Согласно третьему закону Ньютона модуль силы упругости будет равен модулю приложенной к пружине силе. В обоих случаях постоянной величиной окажется только жесткость пружины. Выразим ее из закона Гука и применим к каждому из случаев:
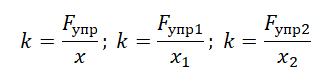
Приравняем правые части формул:
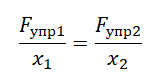
Выразим и вычислим силу упругости, возникающую, когда удлинение пружины составит 6 см:
Полезные факты
Если пружину растягивают две противоположные силы, то модули силы упругости и модули этих сил равны между собой:
F1 = F2 = Fупр
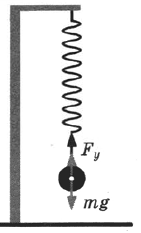
Если груз подвешен к пружине, сила упругости будет равна силе тяжести, действующей на это тело:
Fупр = Fтяж = mg.
Если пружины соединены параллельно, их суммарный коэффициент жесткости будет равен сумме коэффициентов жесткости каждой из этих пружин:
Если пружины соединены последовательно, их обратное значение суммарного коэффициента жесткости будет равен сумме обратных коэффициентов жесткости для каждой из пружин:
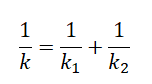
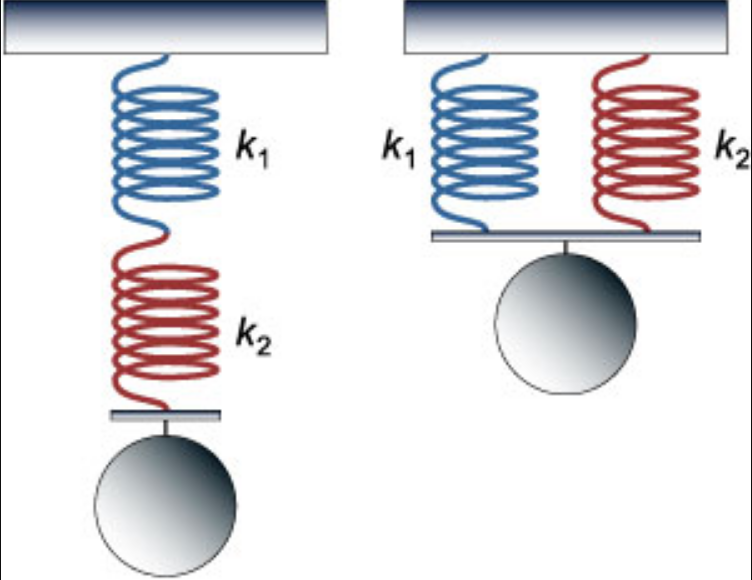
Пример №2. Две пружины соединены параллельно. Жесткость одной из пружин равна 1000 Нм, второй — 4000 Нм. Когда к пружинам подвесили груз, они удлинились на 5 см. Найти силу тяжести груза.
Переведем сантиметры в метры: 5 см = 5∙10–2 м.
Запишем закон Гука с учетом параллельного соединения пружин:
Модуль силы тяжести согласно третьему закону Ньютона равен модулю силы упругости. Отсюда:
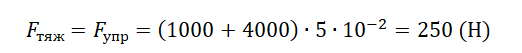
Задание E17590
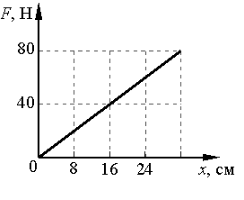На рисунке представлен график зависимости модуля силы упругости от удлинения пружины. Какова жёсткость пружины?
а) 250 Н/м
б) 160 Н/м
в) 2,5 Н/м
г) 1,6 Н/м
Алгоритм решения
2.Выразить из закона Гука формулу для вычисления коэффициента упругости.
3.Выбрать любую точку графика и извлечь из нее исходные данные.
4.Перевести единицы измерения в СИ.
5.Вычислить коэффициент упругости, используя извлеченные из графика данные.
Решение
Запишем закон Гука:
Fупр = kx
Отсюда коэффициент упругости пружины равен:
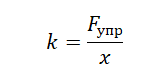
Возьмем на графике точку, соответствующую удлинению пружины 16 см. Ей соответствует модуль силы упругости, равный 40 Н. Переведем сантиметры в метры: 16 см = 0,16 м.
Вычислим жесткость пружины:
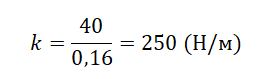
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18489
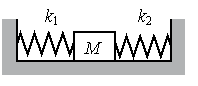Кубик массой 1 кг покоится на гладком горизонтальном столе, сжатый с боков пружинами (см. рисунок). Первая пружина сжата на 4 см, а вторая сжата на 3 см. Жёсткость второй пружины k2 = 600 Н/м. Чему равна жёсткость первой пружины k1?
Алгоритм решения
- Записать исходные данные.
- Записать закон Гука.
- Применить закон Гука к обеим пружинам.
- Применить третий закон Ньютона.
- Выразить жесткость первой пружины.
- Вычислить искомую величину.
Решение
Запишем исходные данные:
- Сжатие первой пружины x1 — 4 см.
- Сжатие второй пружины x2 — 3 см.
- Жесткость второй пружины k2 — 600 Н/м.
Запишем закон Гука:
Fупр = kx
Применим этот закон к обеим пружинам:
Fупр1 = k1x1
Fупр2 = k2x2
Силы упругости обеих пружин уравновешены, так как тело между ними покоится. Согласно третьему закону Ньютона:
Fупр1 = Fупр2
Отсюда:
k1x1 = k2x2
Выразим отсюда жесткость первой пружины:
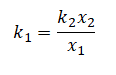
Подставим известные данные и вычислим:
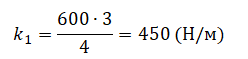
Внимание! В данном случае переводить единицы измерения в СИ не нужно. Отношение длин постоянно независимо от выбранной единицы измерения.
Ответ: 450
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17520
Две упругие пружины растягиваются силами одной и той же величины F. Удлинение второй пружины Δl2 в 2 раза меньше, чем удлинение первой пружины Δl1. Жёсткость первой пружины равна k1, а жёсткость второй k2 равна…
а) 0,25k1
б) 2k1
в) 0,5k1
г) 4k1
Алгоритм решения
- Записать исходные данные.
- Записать закон Гука.
- Применить закон Гука к обеим пружинам.
- Выразить величину жесткости второй пружины.
Решение
Записываем исходные данные:
- Первая и вторая пружины растягиваются под действием одной и той же силы. Поэтому: F1 = F2 = F.
- Удлинение первой пружины равно: Δl1 = 2l.
- Удлинение второй пружины вдвое меньше удлинения первой. Поэтому: Δl2 = l.
Закон Гука выглядит следующим образом:
F = k Δl
Применим закон Гука для обеих пружин:
F1 = k1 Δl1
F2 = k2 Δl2
Так как первая и вторая силы равны, можем приравнять правые части выражений. Получим:
k1 Δl1 = k2 Δl2
Перепишем выражение с учетом значения удлинений первой и второй пружин:
k1 2l = k2 l
«l» в левой и правой частях выражения взаимоуничтожаются, отсюда жесткость второй пружины равна:
k2 = 2k1
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.9k
Абсолютное удлинение стержня формула
Формула абсолютного удлинения стержня, связывающая продольную силу, длину стержня и жесткость, имеет вид:
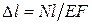
Формулу абсолютного удлинения стержня иногда называют законом Гука, но не для материала, а для всего стержня, а стоящее в знаменателе произведение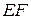 
– жесткостью стержня при растяжении (сжатии).
