Напомним теорему сложения скоростей
при сложном движении точки:
абсолютная скорость точки равна
геометрической сумме относительной и
переносной скоростей:
![]()
Теорема сложения ускорений при сложном
движении точки имеет вид:
![]() ,
,
где вектор
![]()
называется ускорением Кориолиса.
Таким образом,
абсолютное ускорение точки равно
геометрической сумме относительного,
переносного и кориолисова ускорений.
Пример 3.3
Круглая трубка радиуса
![]() вращается вокруг горизонтальной оси
вращается вокруг горизонтальной оси![]() по часовой стрелке с постоянной угловой
по часовой стрелке с постоянной угловой
скоростью![]() .
.
Внутри трубки около ее точки![]() колеблется шарик
колеблется шарик![]() ,
,
причем так, что![]() (Рис. 3.5). Определить скорость, касательное
(Рис. 3.5). Определить скорость, касательное
и нормальное ускорения в абсолютном
движении шарика в любой момент времени.
|
|
|
Рис.3.5 |
Относительное движение шарика
представляет собой движение по окружности
радиуса![]() с центром в точке
с центром в точке![]() по закону
по закону![]() .
.
Определим закон изменения дуговой
координаты шарика в относительном
движении:
![]()
Вычислим относительную скорость и
относительное ускорение шарика:
![]()
![]()
![]()
Трубка сообщает шарику переносную
скорость
![]()
и переносное ускорение
![]()
Угол между осью вращения трубки,
вдоль которой направлен вектор ее
угловой скорости, и вектором относительной
скорости шарика равен
![]() ,
,
так что
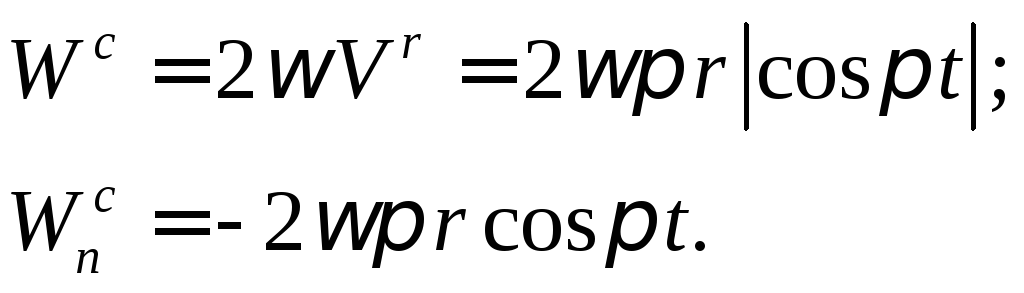
Для определения направления ускорения
Кориолиса удобнее всего воспользоваться
правилом Жуковского.
Абсолютная траектория шарика в
данном случае очевидна – это все та же
окружность с центром
![]() радиуса
радиуса![]() .
.
Используя теорему сложения скоростей,
получаем:
![]()
Используя теорему Кориолиса (3.12),
получаем:
![]()
![]()
Направления векторов указаны на Рис.
3.5. Ускорение Кориолиса и относительная
скорость представлены на рисунке для
случая
![]()
Пример 3.4
Лопатка
![]() рабочего колеса турбины, вращающегося
рабочего колеса турбины, вращающегося
против хода часовой стрелки замедленно
с угловым ускорением![]() ,
,
имеет радиус кривизны 0.2 м и центр
кривизны в точке![]() ,
,
причем![]() м. Частица воды
м. Частица воды![]() ,
,
отстоящая от оси![]() турбины на расстоянии 0.2 м, движется по
турбины на расстоянии 0.2 м, движется по
лопатке наружу и имеет скорость 0.25 м/с
и касательное ускорение 0.5 м![]() по отношению к лопатке. Определить
по отношению к лопатке. Определить
абсолютное ускорение частицы![]() в тот момент времени, когда угловая
в тот момент времени, когда угловая
скорость турбины равна 2 рад/с.
Подвижную систему координат свяжем
с рабочим колесом турбины (Рис. 3.6).
Относительной траекторией частицы воды
является кривая
![]() – лопатка турбины. Определим нормальное
– лопатка турбины. Определим нормальное
ускорение точки![]() в относительном движении
в относительном движении
![]()
Точка
![]() турбины описывает окружность с центром
турбины описывает окружность с центром![]() радиуса
радиуса![]() .
.
Определим переносное ускорение точки:
![]()
Направление ускорения Кориолиса
определяем по правилу Жуковского. Модуль
ускорения Кориолиса равен
![]()
Используя теорему Кориолиса, найдем
проекции абсолютного ускорения частицы
![]() на оси подвижной системы координат
на оси подвижной системы координат
(Рис. 3.6):
![]()
![]()
|
|
|
|
|
Рис. 3.6 |
Рис. 3.7 |
Остается определить
![]() и
и![]() .
.
Для этого используем теорему косинусов
(Рис. 3.7):
![]()
Отсюда
![]()
Таким образом,
![]()
Окончательно получаем:
![]()
Пример 3.5
Диск радиуса
![]() вращается вокруг неподвижной оси
вращается вокруг неподвижной оси![]() с постоянной угловой скоростью
с постоянной угловой скоростью![]() .
.
По ободу диска движется точка![]() ,
,
имея относительно диска постоянную по
модулю скорость![]() .
.
Определить абсолютную скорость и
абсолютное ускорение точки![]() .
.
Подвижную систему отсчета связываем
с диском (Рис. 3.8). По отношению к диску,
т.е. в относительном движении, точка
![]() движется равномерно со скоростью
движется равномерно со скоростью![]() ,
,
описывая окружность радиуса![]() с центром в точке
с центром в точке![]() .
.
Определяем относительное ускорение
точки:
![]()
Рассмотрим переносное движение –
его совершает диск. Точка
![]() диска описывает окружность с центром
диска описывает окружность с центром![]() ,
,
плоскость которой параллельна координатной
плоскости![]() .
.
Переносная скорость
![]()
направлена по касательной к этой
окружности в сторону вращения диска,
т.е. перпендикулярно плоскости диска в
отрицательном направлении координатной
оси
![]() .
.
Поскольку вращение диска по условию
равномерное, отличным от нуля оказывается
только осестремительное ускорение:
![]()
Вектор ускорения Кориолиса точки
![]() направлен перпендикулярно плоскости
направлен перпендикулярно плоскости
чертежа, в которой расположены векторы![]() и
и![]() ,
,
причем, в ту сторону, откуда кратчайшее
совмещение направления вектора![]() с направлением вектора
с направлением вектора![]() видно против хода часовой стрелки. В
видно против хода часовой стрелки. В
указанном на Рис. 3.9 положении точки![]() вектор ускорения Кориолиса направлен
вектор ускорения Кориолиса направлен
на нас, т.е. параллелен координатной
оси![]() в положительную сторону этой оси. На
в положительную сторону этой оси. На
Рис. 3.9 это направление условно обозначено
острием стрелки, заключенным в кружок.
Модуль ускорения Кориолиса вычисляется
по формуле:
![]() .
.
|
|
|
|
|
Рис.3.8 |
Рис.3.9 |
При перемещении точки
![]() по диску направление ускорения Кориолиса
по диску направление ускорения Кориолиса
не будет изменяться до тех пор, пока![]() ,
,
т.е. пока![]() (точка
(точка![]() ).
).
При пересечении точкой![]() координатной оси
координатной оси![]() ускорение Кориолиса обращается в нуль.
ускорение Кориолиса обращается в нуль.
При движении точки в нижней части диска,
т.е. при![]() ,
,
проекция ускорения Кориолиса на
направление оси![]() становится отрицательной и вектор
становится отрицательной и вектор![]() направлен от нас (точки
направлен от нас (точки![]() и
и![]() ).
).
Таким образом,
![]()
Используя теорему сложения скоростей
![]()
находим проекции вектора абсолютной
скорости на оси подвижной системы
координат:
![]()
![]()
![]()
Используя теорему Кориолиса
![]()
находим проекции абсолютного ускорения
точки на оси подвижной системы координат:
![]()
![]()
![]()
![]()
Примечание.
Последняя задача позволяет
проиллюстрировать некоторые явления,
связанные с вращением Земли, в частности,
размыв берегов рек. Как видно, вращение
Земли приводит к возникновению у частиц
воды кориолисова ускорения, направленного
перпендикулярно линии берегов. Наличие
такого ускорения приводит к тому, что
в северном полушарии дополнительно
подмывается правый берег, который на
прямолинейных участках рек заметно
выше левого берега. В южном полушарии
более высокий левый берег. Это явление
в географии отражено в законе Бэра.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 22.10;
22.14; 22.17; 22.26; 23.1; 23.9; 23.13; 23.18; 23.19;
23.27; 23.29; 23.34; 23.47; 23.48; 23.49; 23.56.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-23;
СР-24; СР-25.
КОНТРОЛЬНЫЕ
МЕРОПРИЯТИЯ:
-
После
практического занятия №7(15) проводится
тест «МОДУЛЬ КБ».
ЛИТЕРАТУРА:
-
Антонов В.И., Белов В.А., Егорычев О.О.,
Степанов Р.Н.//Курс теоретической
механики (теория и практика) – М.:
Архитектура – С, 2011 г. -
Мещерский И.В.//Сборник задач по
теоретической механике. – Спб.: Лань,
2010 г.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2015560.03 Кб15PSY – recommendation.pdf
- #
- #
Пример решения задачи по определению в заданный момент времени при сложном движении, абсолютной скорости и абсолютного ускорения точки, которая движется по ободу диска вращающегося вокруг оси.
Задача
Диск радиуса R=0,5 м вращается вокруг оси, лежащей в его плоскости и касающейся диска, с угловой скоростью ω=πt2 c-1 (рисунок 3.5). По ободу диска движется точка M по закону: ∪OM=πRt2/6 м.
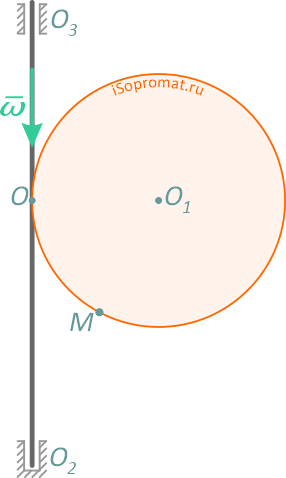
Рисунок 3.5
Требуется, в момент времени t=2c определить абсолютные скорость и ускорение точки M.
Другие примеры решений >
Помощь с решением задач >
Решение
Точка M в данном примере совершает сложное движение, которое может быть разложено на два движения: относительное движение — движение точки M по движущемуся диску (именно с ним может быть скреплена подвижная система отсчета) и переносное движение — вращение диска вместе с находящейся на нем точкой.
Поскольку переносное движение по определению это движение той точки диска, в которой находится в данный момент точка M, то сначала необходимо определить положение точки M на диске в момент времени t=2 c:
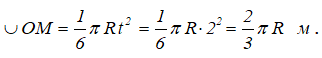
Центральный угол составит
![]()
Расчет скорости
В относительном движении закон движения задан естественным способом, поэтому скорость определяется как производная его дуговой координаты и направлена по касательной к траектории относительного движения в плоскости диска:
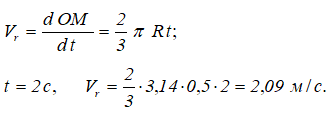
Переносное движение в данном случае — вращение вокруг неподвижной оси O2O3, расстояние до которой от точки M равно KM.
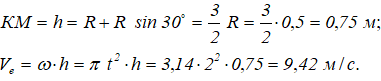
По направлению вектора угловой скорости ω определяем, что при вращении вокруг оси O2O3 точка M движется к нам, то есть вектор Ve перпендикулярен плоскости диска и для выбранной системы отсчета Mxyz, скрепленной с диском, направлен по оси Mx.
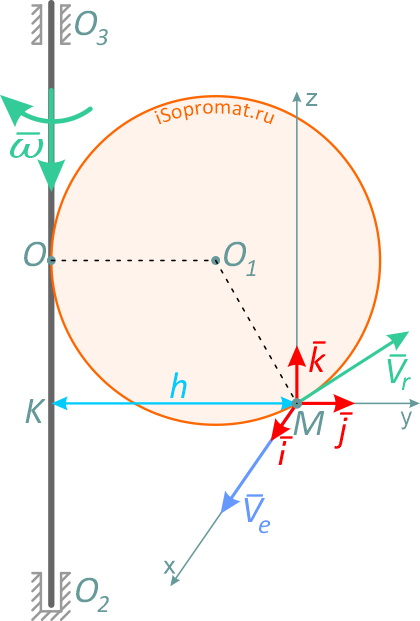
Рисунок 3.6
Абсолютная скорость точки в нашем примере определяется как геометрическая сумма векторов:
![]()
численная величина:
![]()
Спроецировав векторную сумму на выбранные оси координат, получим проекции абсолютной скорости на эти оси:
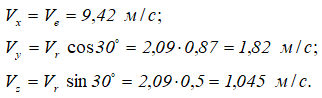
Направление вектора скорости определяют направляющие косинусы, то есть углы, которые вектор скорости составляет с выбранными осями:
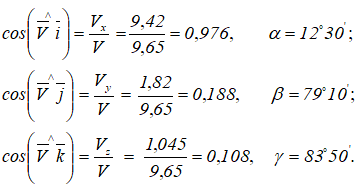
Расчет ускорения
В данном примере и переносные и относительные движения точки M — криволинейные, поэтому абсолютное ускорение определяется по формуле:
![]()
Составляющие ускорения определяются независимо друг от друга. В переносном движении точка M вращается вокруг оси O2O3 и движется по окружности радиуса h (рисунок 3.7).
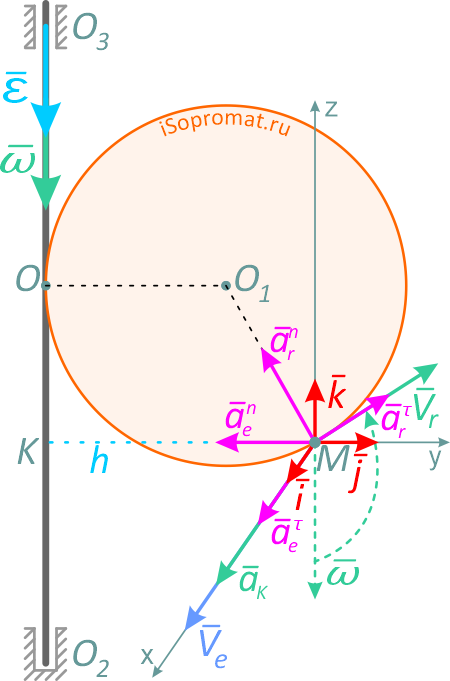
Рисунок 3.7
Нормальное ускорение в этом движении:
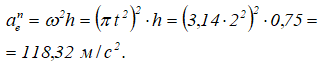
Этот вектор направлен от точки M к точке K (к оси вращения).
Касательное ускорение в переносном движении определится по формуле
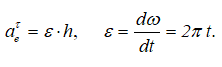
Знак производной положителен, то есть вращение ускоренное и направления векторов Ve и aeτ совпадают:
![]()
В относительном движении точка M движется по окружности радиуса R. Нормальное ускорение:
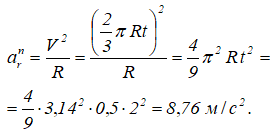
Этот вектор направлен от точки M к центру окружности — точке O1.
Касательное ускорение в относительном движении:
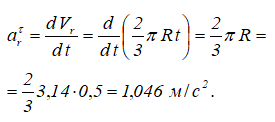
Производная от относительной скорости получена со знаком плюс, поэтому aeτ совпадает по направлению с Vr.
Кориолисово ускорение определяется по формуле
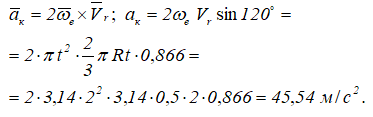
Вектор кориолисова ускорения должен быть перпендикулярен векторам ωe и Vr (в нашем случае перпендикулярен плоскости чертежа). Если смотреть навстречу вектору ak, то мы должны видеть поворот вектора ωe (мысленно перенесенного в точку) на кратчайший угол до совмещения с вектором Vr, происходящий против хода часовой стрелки. То есть в этом примере вектор ak направлен по оси Mx к нам.
Направление кориолисова ускорения может быть определено и по правилу Жуковского. Проецируем вектор V на плоскость, перпендикулярную вектору ωe (на плоскость Mxy; в данном примере эта проекция совпадает с осью My), и поворачиваем проекцию Vr на 90o в сторону вращения, то есть вектор ak направлен к нам по оси Mx.
Для определения абсолютного ускорения проецируем векторное равенство (3.6) на оси координат:
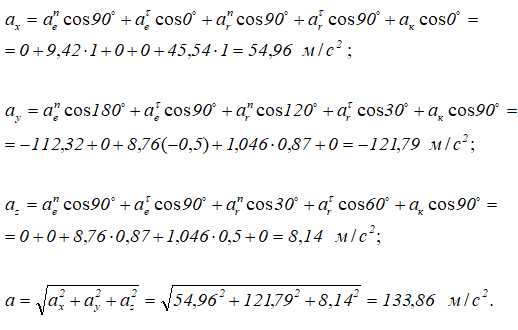
Направление вектора ускорения определяется с помощью направляющих косинусов (см. формулы (3.7)):
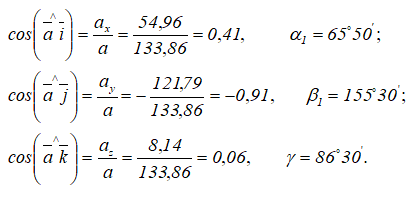
Другие примеры решения задач >
| Ускорение | |
|---|---|
 |
|
| Размерность | LT−2 |
| Единицы измерения | |
| СИ | м/с² |
| СГС | см/с² |
| Примечания | |
| векторная величина |

Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.
Ускоре́ние (обычно обозначается латинскими буквами a (от лат. acceleratio) или w) — физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости 
Например, тела, свободно падающие вблизи поверхности Земли вдоль вертикали, в случаях, когда испытываемое ими сопротивление воздуха мало, увеличивают свою скорость примерно на 9,8 м/с за секунду, то есть их ускорение примерно равно 9,8 м/с². При непрямолинейном движении учитывается изменение не только величины скорости, но и её направления: скажем, ускорение тела, движущегося по окружности с постоянной по модулю скоростью, не равно нулю: имеется постоянное по модулю (и переменное по направлению) ускорение, направленное к центру окружности.
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (русское обозначение: м/с2; международное: m/s2).
Ускорение в кинематике точки[править | править код]
Наиболее общий случай[править | править код]
Ускорение и связанные величины[править | править код]
Вектор ускорения материальной точки в любой момент времени находится путём однократного дифференцирования по времени вектора скорости материальной точки (или двукратного дифференцирования радиус-вектора):
Если на траектории точки известны координаты 


Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
где
— вектор рывка.
Анализ движения по кривой[править | править код]

Траекторию движения материальной точки на малом участке можно считать плоской. Вектор ускорения 

где
— величина скорости,
— единичный касательный к траектории вектор, направленный вдоль скорости (касательный орт),
— орт главной нормали к траектории, который можно определить как единичный вектор в направлении
— орт бинормали к траектории, перпендикулярный одновременно ортам
и
(то есть ортогональный к мгновенной плоскости траектории),
— радиус кривизны траектории.
Слагаемое 

Векторы 

Итак, учитывая сказанное выше, вектор ускорения при движении по любой траектории можно записать как:
Важные частные случаи[править | править код]
Равноускоренное движение[править | править код]
Если вектор 
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). Обратное, вообще говоря, неверно.
Равноускоренное движение при переходе в другую инерциальную систему отсчёта остаётся равноускоренным.
Случай равноускоренного движения, когда ускорение (постоянное) и скорость направлены по одной прямой, но в разных направлениях, называется равнозамедленным движением. Равнозамедленное движение всегда одномерно. Движение можно рассматривать как равнозамедленное лишь до того момента, пока скорость не станет равной нулю. Кроме того, всегда существуют инерциальные системы отсчёта, в которых движение не является равнозамедленным.
Прямолинейное движение[править | править код]
Важным частным случаем движения с ускорением является прямолинейное движение, когда ускорение в любой момент времени коллинеарно скорости (например, случай падения тела с вертикальной начальной скоростью). В случае прямолинейного движения можно выбрать одну из координатных осей вдоль направления движения и заменить радиус-вектор и векторы ускорения и скорости на скаляры. При этом, при постоянном ускорении из приведённых выше формул вытекает, что
Здесь v0 и v — начальная и конечная скорость тела, a — его ускорение, s — пройденный телом путь.
Ряд практически важных формул связывают затраченное время, пройденный путь, достигнутую скорость и ускорение при равноускоренном прямолинейном движении с нулевой (
так что любые две из этих величин определяют две другие (здесь предполагается, что время отсчитывается от начала движения: t0 = 0).
Движение по окружности[править | править код]

Равномерное движение по окружности. Ускорение всегда перпендикулярно скорости и направлено к центру.

Пример неравномерного движения по окружности (математический маятник). Ускорение, складывающееся из тангенциальной и центростремительной компонент, в разные моменты изменяется от полностью касательного до полностью нормального к траектории.
Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное или касательное ускорение 


Центростремительное или нормальное ускорение 


а модуль равен
где ω — угловая скорость относительно центра вращения, а r — радиус окружности.
Кроме этих двух компонент, используется также понятие угловое ускорение, показывающее, на сколько изменилась угловая скорость за единицу времени, и, аналогично линейному ускорению, вычисляемое следующим образом:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и угловой скорости сонаправлены (или хотя бы их скалярное произведение положительно), значение скорости растёт, и наоборот.
В частном случае равномерного движения по окружности векторы углового ускорения и тангенциального ускорения равны нулю, а центростремительное ускорение постоянно по модулю.
Ускорение при сложном движении[править | править код]
Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой, «лабораторной», системы отсчёта. Тогда абсолютное ускорение тела в лабораторной системе равно сумме относительного, переносного и кориолисова ускорений:
Последний член содержит векторное произведение угловой скорости вращения движущейся системы отсчёта и скорости материальной точки в этой движущейся системе.
Ускорения в кинематике твёрдого тела[править | править код]
Связь ускорений двух точек абсолютно твёрдого тела A и B можно получить из формулы Эйлера для скоростей этих точек:
где 
где 
Второе слагаемое называется осестремительным ускорением, а третье — вращательным ускорением[1].
Создание ускорения. Динамика точки[править | править код]
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие[4].
Классическая механика[править | править код]
Второй закон Ньютона применительно к нерелятивистскому движению (то есть к движению со скоростями, много меньшими скорости света) утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется инертной массой материальной точки):
Если известны масса материальной точки и (как функция времени) сила, действующая на неё, то из второго закона Ньютона известно и её ускорение: 
Релятивистская механика[править | править код]
В релятивистской физике второй закон Ньютона записывается в форме
что делает нахождение ускорения более сложной задачей, чем в классическом случае. В частности, длительное движение с постоянным ускорением принципиально невозможно (иначе скорость точки в конце концов превысит скорость света), а неизменность силы не означает неизменности ускорения: оно будет стремиться к нулю при нарастании скорости. Тем не менее, если зависимость 


Ускорение в теории относительности[править | править код]
В теории относительности движение тела с переменной скоростью вдоль мировой линии в 4-мерном пространстве-времени характеризуется определённой величиной, аналогичной ускорению. В отличие от обычного (трёхмерного) вектора ускорения, 4-вектор ускорения (называемый 4-ускорением) ai является второй производной от 4-вектора координат xi не по времени, а по пространственно-временному интервалу τ (или, что то же самое, по собственному времени) вдоль мировой линии тела:
В любой точке мировой линии 4-вектор ускорения всегда ортогонален к 4-скорости:
Это означает, в частности, что 4-скорости меняются не по модулю, а лишь по направлению: независимо от направления в пространстве-времени 4-скорость любого тела равна по модулю скорости света. Геометрически, 4-ускорение совпадает с кривизной мировой линии и является аналогом нормального ускорения в классической кинематике.
В классической механике значение ускорения не изменяется при переходе от одной инерциальной системы отсчета к другой, то есть ускорение инвариантно относительно преобразований Галилея. В релятивистской механике 4-ускорение является 4-вектором, то есть при преобразованиях Лоренца изменяется аналогично пространственно-временным координатам.
“Обычный” трёхмерный вектор ускорения 





Измерения ускорений[править | править код]
Используемые единицы[править | править код]
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ;
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС, имеет также собственное наименование гал, или галилео (применяется преимущественно в гравиметрии);
- g (произносится «же»), стандартное ускорение свободного падения на поверхности Земли, равное по определению 9,80665 м/с². В технических расчётах, не требующих точности выше 2 %, часто используется приближение g ≈ 10 м/с².
| м/с2 | фут/с2 | g | см/с2 | |
|---|---|---|---|---|
| 1 м/с² = | 1 | 3,28084 | 0,101972 | 100 |
| 1 фут/с² = | 0,304800 | 1 | 0,0310810 | 30,4800 |
| 1 g = | 9,80665 | 32,1740 | 1 | 980,665 |
| 1 см/с² = | 0,01 | 0,0328084 | 0,00101972 | 1 |
Технические средства[править | править код]
Приборы для измерения ускорения называются акселерометрами. Они не «детектируют» ускорение непосредственно, а измеряют силу реакции (укр.) (рус. опоры, возникающую при ускоренном движении. Поскольку аналогичные силы сопротивления возникают в поле тяготения, с помощью акселерометров можно измерять также гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Значения ускорения в некоторых случаях[править | править код]
Значения ускорений различных движений:[5]
| Вид движения | Ускорение, м/с2 |
|---|---|
| Центростремительное ускорение Солнечной системы при орбитальном движении в Галактике | 2,2⋅10−10 |
| Центростремительное ускорение Земли при орбитальном движении вокруг Солнца | 0,0060 |
| Центростремительное ускорение Луны при орбитальном движении вокруг Земли | 0,0027 |
| Пассажирский лифт | 0,9—1,6 |
| Поезд метро | 1 |
| Автомобиль «Жигули» | 1,5 |
| Бегун на коротких дистанциях | 1,5 |
| Велосипедист | 1,7 |
| Конькобежец | 1,9 |
| Мотоцикл | 3—6 |
| Аварийное торможение автомобиля | 4—6 |
| Усэйн Болт, максимальное ускорение | 8[6] |
| Гоночный автомобиль | 8—9 |
| Торможение при открытии парашюта | 30 (3 g) |
| Запуск и торможение космического корабля | 40—60 (4—6 g) |
| Манёвр реактивного самолёта | до 100 (до 10 g) |
| Свая после удара копром | 300 (30 g) |
| Поршень двигателя внутреннего сгорания | 3×103 |
| Пуля в стволе винтовки | 2,5×105 |
| Микрочастицы в ускорителе | (2—50)×1014 |
| Электроны между катодом и анодом трубки цветного телевизора (20 кВ, 0,5 м) | ≈7×1015 |
| Электроны при соударении с люминофором трубки цветного телевизора (20 кВ) | ≈1022 |
| Альфа-частицы в атомном ядре | ≈1027 |
Примечание: здесь g ≈ 10 м/с2.
Понятие “обобщённое ускорение”[править | править код]
Если динамика механической системы описывается не в декартовых, а в обобщённых координатах 


См. также[править | править код]
- Ускорение свободного падения
- Собственное ускорение
- Релятивистски равноускоренное движение
- Приливное ускорение
- Кориолисово ускорение
- Рывок (кинематика)
Примечания[править | править код]
- ↑ 1 2 Маркеев А. П. Теоретическая механика. — М.: ЧеРо, 1999. — С. 59. — 572 с.
- ↑ Обзор результатов Ривальса: Appendice au Mémoire de M. Bresse // Journal de l’École polytechnique. — 1853. — Т. 20. — С. 109—115. Архивировано 9 марта 2016 года.
- ↑ Joulin L. Notice biographique sur M. le commandant Rivals // Mémoires de l’Académie royale des sciences, inscriptions et belles-lettres de Toulouse. — 1891. — Т. 3, вып. 9. — С. 535—539. Архивировано 8 марта 2016 года.
- ↑ Для того, чтобы использовать уравнение движения в форме, совпадающей с формой уравнения второго закона Ньютона, применительно к ускорениям, возникающим в неинерциальных системах отсчёта даже в отсутствие каких-либо воздействий на тело, вводят фиктивные силы инерции. Например, пусть тело массой m покоится в инерциальной системе отсчёта на некотором расстоянии R от оси. Если привести систему отсчёта во вращение с угловой скоростью ω вокруг этой оси, то система становится неинерциальной, а тело будет совершать видимое вращательное движение с линейной скоростью v=ωR по окружности вокруг оси. Для его описания во вращающейся системе отсчёта необходимо ввести центростремительное ускорение, которое можно формально считать результатом действия одной из сил инерции — силы Кориолиса, равной по модулю 2mvω и направленной к оси, перпендикулярно оси и скорости тела; при этом она наполовину компенсируется действием другой силы инерции — центробежной силы, равной по модулю mvω и направленной от оси вращения.
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9.
- ↑ График зависимости ускорения У. Болта от времени Архивная копия от 10 мая 2013 на Wayback Machine — забег на 100 м на летних Олимпийских играх 2008 года в Пекине
Ссылки[править | править код]
- Ландау Л. Д., Лифшиц Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6.
- David C. Cassidy, Gerald James Holton, and F. James Rutherford. Understanding physics. — Birkhäuser (англ.) (рус., 2002. — ISBN 978-0-387-98756-9.
- Pauli W. Theory of Relativity. — Dover, 1981. — ISBN 978-0-486-64152-2.
В физике, при рассмотрении нескольких систем отсчёта (СО) возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух СО.
Обычно выбирают одну из СО за базовую («абсолютную»), другую называют «подвижной» и вводят следующие термины:
- абсолютное движение — это движение точки/тела в базовой СО.
- относительное движение — это движение точки/тела относительно подвижной системы отсчёта.
- переносное движение — это движение второй СО относительно первой.
Также вводятся понятия соответствующих скоростей и ускорений. Например, переносная скорость — это скорость точки, обусловленная движением подвижной системы отсчёта относительно абсолютной. Другими словами, это скорость точки подвижной системы отсчёта, в данный момент времени совпадающей с материальной точкой.
Оказывается, что при получении связи ускорений в разных системах отсчёта возникает необходимость ввести ещё одно ускорение, обусловленное вращением подвижной системы отсчёта:
- ускорение Кориолиса.
В дальнейшем рассмотрении, базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Содержание
- 1 Классическая механика
- 1.1 Кинематика сложного движения точки
- 1.1.1 Скорость
- 1.1.2 Ускорение
- 1.2 Кинематика сложного движения тела
- 1.3 Динамика сложного движения точки
- 1.1 Кинематика сложного движения точки
- 2 Релятивистская механика
- 2.1 Скорость
- 2.2 Неинерциальные СО
- 3 Литература
- 4 См. также
- 5 Ссылки
Классическая механика
Кинематика сложного движения точки
Скорость
-
.
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть
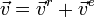 .
.
Ускорение
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что координатные векторы подвижной системы координат также могут зависеть от времени.
Абсолютное ускорение точки равно геометрической сумме трёх ускорений — относительного, переносного и кориолисова, то есть
![vec w^a=vec {w}^r + vec {w}^e + 2left[vec omega times vec {v}^r right]](https://dic.academic.ru/pictures/wiki/files/53/56737bf083652f5ae3275fda7739ab3e.png) .
.
Кинематика сложного движения тела
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. Если же составными движениями тела являются и поступательные, и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки
При рассмотрении движения в неинерциальной СО нарушаются первые 2 закона Ньютона. Чтобы обеспечить формальное их выполнение, обычно вводятся дополнительные, фиктивные (не существующие на самом деле), силы инерции: центробежная сила и сила Кориолиса. Выражения для этих сил получаются из связи ускорений (предыдущий раздел).
Релятивистская механика
Скорость
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей: 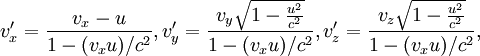
в предположении, что скорость  направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Литература
- Н. Г. Четаев. «Теоретическая механика». М.: Наука. 1987. 368 с.
См. также
- Относительность
Ссылки
Wikimedia Foundation.
2010.
Содержание:
Абсолютная и относительная производные от вектора:
При рассмотрении сложного движения точки в общем случае переносного движения приходится рассматривать изменение векторных величин с течением времени по отношению к системам отсчета, движущимся друг относительно друга. Одно изменение имеет векторная величина относительно подвижной системы отсчета, движущейся относительно другой, неподвижной, и другое — относительно неподвижной системы отсчета. Неподвижной системой отсчета считается система, движение которой относительно других систем отсчета не рассматривается.
Введем обозначения производных от векторных величин при рассмотрении их изменения относительно различных систем отсчета, движущихся друг относительно друга. Для любого вектора 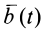
Установим зависимость между полной и относительной производными по времени вектора 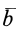 и величинами, характеризующими движение подвижной системы отсчета относительно неподвижной. Для этого разложим вектор
и величинами, характеризующими движение подвижной системы отсчета относительно неподвижной. Для этого разложим вектор 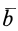 на составляющие, параллельные осям подвижной системы координат. Имеем
на составляющие, параллельные осям подвижной системы координат. Имеем
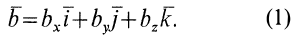
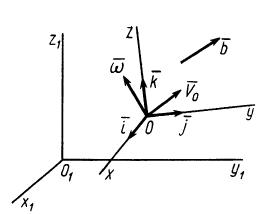
Рис. 87
Изменение вектора 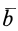 относительно неподвижной системы координат
относительно неподвижной системы координат 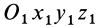 . в зависимости от времени состоит из изменения его проекций
. в зависимости от времени состоит из изменения его проекций 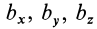 на подвижные оси координат и изменения единичных векторов
на подвижные оси координат и изменения единичных векторов 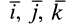 подвижных осей вследствие движения подвижной системы координат относительно неподвижной. Вычислим полную производную по времени от вектора
подвижных осей вследствие движения подвижной системы координат относительно неподвижной. Вычислим полную производную по времени от вектора 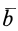 , используя формулу (1). Получим
, используя формулу (1). Получим
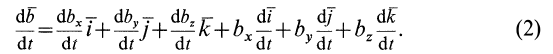
Первые три слагаемых учитывают изменение вектора 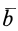 при неизменных
при неизменных 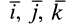 и поэтому составляют относительную производную, т. е.
и поэтому составляют относительную производную, т. е.
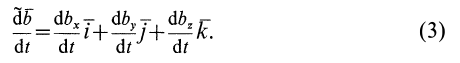
Производные по времени единичных векторов определим по формулам Пуассона
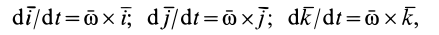
так как эти векторы не изменяются от поступательного движения со скоростью 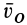 вместе с подвижной системой отсчета (рис. 87). Вектор
вместе с подвижной системой отсчета (рис. 87). Вектор 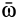 есть угловая скорость вращательной части движения вокруг точки
есть угловая скорость вращательной части движения вокруг точки 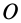 подвижной системы координат относительно неподвижной. Подставляя эти значения производных единичных векторов в (2) и вынося
подвижной системы координат относительно неподвижной. Подставляя эти значения производных единичных векторов в (2) и вынося 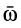 за скобки, получим
за скобки, получим
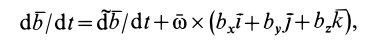
или, учитывая (1),
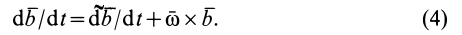
Получена формула зависимости производных векторов 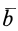 в двух системах отсчета, движущихся друг относительно друга. Формула (4) называется формулой Бура.
в двух системах отсчета, движущихся друг относительно друга. Формула (4) называется формулой Бура.
Известно, что произвольное движение системы координат как свободного твердого тела можно представить как поступательное движение вместе с полюсом, например с точкой 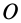 , и вращение вокруг этой точки. Из формулы Бура следует, что поступательная часть движения вместе с полюсом не влияет на зависимость между производными, а влияет только вращательная часть движения.
, и вращение вокруг этой точки. Из формулы Бура следует, что поступательная часть движения вместе с полюсом не влияет на зависимость между производными, а влияет только вращательная часть движения.
Рассмотрим частные случаи.
1. Если вектор 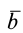 не изменяется относительно подвижной системы координат, то его относительная производная
не изменяется относительно подвижной системы координат, то его относительная производная 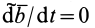 и по формуле (4) получаем
и по формуле (4) получаем
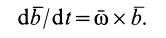
Это формула для производной от вектора постоянного модуля, доказанная ранее для радиуса-вектора при вращении вокруг неподвижной оси. Она справедлива для любого вектора при произвольном движении подвижной системы осей координат. В рассматриваемом случае 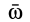 не только угловая скорость вращения подвижной системы координат, но и угловая скорость вращения вектора
не только угловая скорость вращения подвижной системы координат, но и угловая скорость вращения вектора 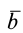 , так как вектор
, так как вектор 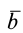 можно при этом считать скрепленным с подвижной системой координат.
можно при этом считать скрепленным с подвижной системой координат.
2. Если вектор 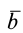 не изменяется относительно основной системы координат, то полная производная
не изменяется относительно основной системы координат, то полная производная 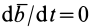 и, согласно (4), его относительная производная
и, согласно (4), его относительная производная
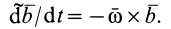
3. Если 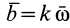 , т. е. вектор
, т. е. вектор 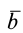 все время параллелен вектору угловой скорости
все время параллелен вектору угловой скорости 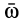 , то
, то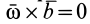 и
и
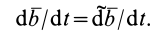
В частности, если 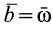 , то
, то
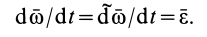
Полная и локальная производные также равны друг другу в те моменты времени, в которые вектор 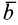 параллелен вектору угловой скорости
параллелен вектору угловой скорости 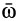 .
.
Сложение скоростей
Если 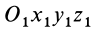 —неподвижная система осей координат, а
—неподвижная система осей координат, а 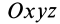 — подвижная (рис. 88), то, как известно, абсолютным движением точки называют ее движение относительно неподвижной системы осей координат, а относительным — ее движение относительно подвижной. Переносным движением точки называют ее движение в рассматриваемый момент времени вместе с подвижной системой осей относительно неподвижных. Относительные скорость и ускорение обозначают
— подвижная (рис. 88), то, как известно, абсолютным движением точки называют ее движение относительно неподвижной системы осей координат, а относительным — ее движение относительно подвижной. Переносным движением точки называют ее движение в рассматриваемый момент времени вместе с подвижной системой осей относительно неподвижных. Относительные скорость и ускорение обозначают 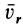 и
и 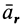 , переносные —
, переносные — 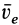 и
и 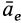 , а абсолютные —
, а абсолютные — 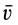 и
и 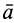 . Другие характеристики этих движений снабжаются соответствующими значками.
. Другие характеристики этих движений снабжаются соответствующими значками.
Движение подвижной системы осей координат относительно неподвижной можно охарактеризовать скоростью ее поступательного движения 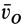 , например вместе с точкой
, например вместе с точкой 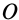 и вектором угловой скорости
и вектором угловой скорости 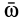 ее вращения вокруг
ее вращения вокруг 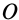 . Пусть точка
. Пусть точка 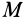 движется относительно подвижной системы координат. Получим теорему сложения скоростей. Для этого проведем векторы
движется относительно подвижной системы координат. Получим теорему сложения скоростей. Для этого проведем векторы 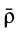 и
и 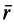 , характеризующие положение точки
, характеризующие положение точки 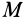 относительно неподвижной и подвижной систем осей координат, и вектор
относительно неподвижной и подвижной систем осей координат, и вектор 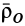 точки
точки 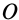 . Для любого момента времени
. Для любого момента времени
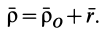
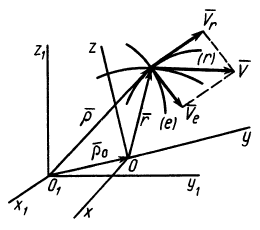
Рис. 88
Продифференцируем по времени это векторное тождество, учитывая изменения векторов относительно неподвижных осей координат, т. е. вычислим полные производные. Получим
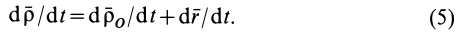
По определению, 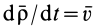 является абсолютной скоростью точки
является абсолютной скоростью точки 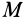 ,
, 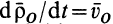 — абсолютной скоростью точки
— абсолютной скоростью точки 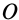 . Для вычисления
. Для вычисления 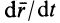 применим формулу Бура. Имеем
применим формулу Бура. Имеем
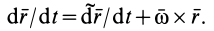
Относительная производная 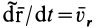 является относительной скоростью точки
является относительной скоростью точки 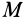 по отношению к подвижной системе отсчета, а
по отношению к подвижной системе отсчета, а 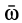 — угловая скорость вращения подвижной системы отсчета и, следовательно, радиуса-вектора
— угловая скорость вращения подвижной системы отсчета и, следовательно, радиуса-вектора 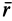 , если бы он в рассматриваемый момент времени был скреплен с подвижной системой осей координат. Таким образом, из (5) получаем
, если бы он в рассматриваемый момент времени был скреплен с подвижной системой осей координат. Таким образом, из (5) получаем

Скорость
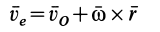
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка 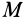 в движении тела относительно неподвижной системы осей координат. Это есть переносная скорость точки
в движении тела относительно неподвижной системы осей координат. Это есть переносная скорость точки 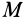 . Из (6) получаем следующую теорему сложения скоростей для точки:
. Из (6) получаем следующую теорему сложения скоростей для точки:

т. е. скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей.
Сложение ускорений точки в общем случае переносного движения
Абсолютное ускорение точки определим вычислением полной производной по времени от абсолютной скорости (6). Имеем
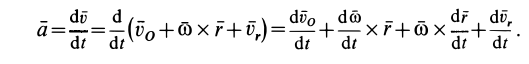
Для полных производных от векторов 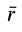 и
и 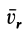 применим формулу Бура. Получим
применим формулу Бура. Получим
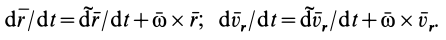
Учитывая, что
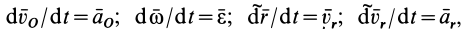
получим для абсолютного ускорения
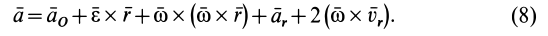
В этой формуле первые три слагаемых составляют ускорение точки свободного твердого тела в общем случае его движения вместе с подвижной системой осей координат относительно неподвижной. Первое слагаемое 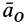 — ускорение точки
— ускорение точки 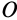 ,
, 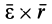 и
и 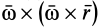 — соответственно вращательное и осестремительное ускорения точки
— соответственно вращательное и осестремительное ускорения точки 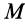 , если бы она двигалась только вместе с подвижной системой осей координат, не имея в рассматриваемый момент времени относительного движения. После этого (8) примет вид
, если бы она двигалась только вместе с подвижной системой осей координат, не имея в рассматриваемый момент времени относительного движения. После этого (8) примет вид

где

Ускорение 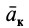 называется ускорением Кориолиса. Иногда его также называют добавочным (или поворотным) ускорением.
называется ускорением Кориолиса. Иногда его также называют добавочным (или поворотным) ускорением.
Формула (9) выражает теорему сложения ускорений точки, или кинематическую теорему Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений — переносного, относительного и Кориолиса.
Переносное ускорение рассматривалось при изучении движения свободного твердого тела. Относительное ускорение изучалось в кинематике точки. Его можно выразить в двух формах в зависимости от способа задания относительного движения. При координатном способе задания в декартовых координатах
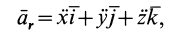
где 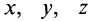 — координаты движущейся_ точки относительно подвижной системы осей координат;
— координаты движущейся_ точки относительно подвижной системы осей координат;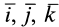 — единичные векторы этих осей. При естественном способе задания движения
— единичные векторы этих осей. При естественном способе задания движения
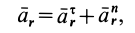
причем
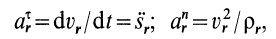
где 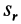 — расстояние от начала отсчета до точки по траектории относительного движения;
— расстояние от начала отсчета до точки по траектории относительного движения; 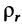 — радиус кривизны этой траектории. В частном случае, когда переносное движение есть вращение вокруг неподвижной оси, переносное ускорение
— радиус кривизны этой траектории. В частном случае, когда переносное движение есть вращение вокруг неподвижной оси, переносное ускорение
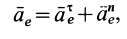
где касательное переносное ускорение
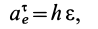
причем 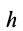 есть кратчайшее расстояние от движущейся точки до оси вращения. Нормальное переносное ускорение
есть кратчайшее расстояние от движущейся точки до оси вращения. Нормальное переносное ускорение
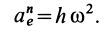
Абсолютное ускорение в этом случае
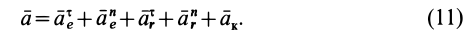
Ускорение Кориолиса
Рассмотрим ускорение Кориолиса и его свойства. Оно определяется формулой (10)
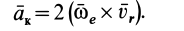
Угловую скорость вращательной части движения подвижной системы отсчета, т. е. угловую скорость переносного движения, заменили на 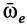 .
.
Ускорение Кориолиса является результатом взаимного влияния двух движений: переносного и относительного. Часть его 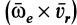 получается вследствие изменения переносной скорости точки из-за относительного движения. Другая его часть, тоже
получается вследствие изменения переносной скорости точки из-за относительного движения. Другая его часть, тоже 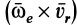 , есть результат изменения относительной скорости вследствие переносного движения. Это следует из анализа формул при выводе абсолютного ускорения.
, есть результат изменения относительной скорости вследствие переносного движения. Это следует из анализа формул при выводе абсолютного ускорения.
Модуль ускорения Кориолиса в соответствии с (10) определяется выражением
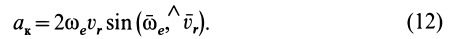
Для определения ускорения Кориолиса очень удобно правило Н. Е. Жуковского. Оно основано на формуле (10). Пусть имеем точку 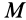 , движущуюся с относительной скоростью
, движущуюся с относительной скоростью 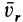 (рис. 89). Построим плоскость
(рис. 89). Построим плоскость 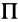 , перпендикулярную угловой скорости переносного вращения и спроецируем
, перпендикулярную угловой скорости переносного вращения и спроецируем 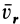 на эту плоскость. Проекцию обозначим
на эту плоскость. Проекцию обозначим 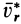 . Она является вектором; ее модуль
. Она является вектором; ее модуль
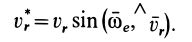
Ускорение Кориолиса выразится в форме

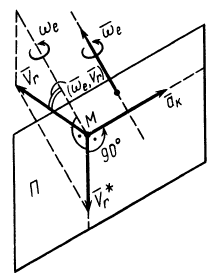
Рис. 89
Учитывая (10) и (12′), получаем правило Жуковского: модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направление ускорения Кориолиса, следует вектор проекции относительной скорости 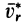 повернуть на
повернуть на 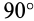 вокруг оси, параллельной оси переносного вращения, в направлении этого вращения.
вокруг оси, параллельной оси переносного вращения, в направлении этого вращения.
Рассмотрим случаи обращения в нуль ускорения Кориолиса. Из (12) следует, что 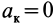 , если:
, если:
-
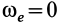 , т. е. переносное движение является поступательным;
, т. е. переносное движение является поступательным; -
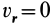 , т. е. в те моменты времени, в которые происходит изменение направления относительного движения;
, т. е. в те моменты времени, в которые происходит изменение направления относительного движения; -
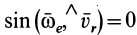 , т. е. когда скорость относительного движения
, т. е. когда скорость относительного движения 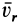 параллельна угловой скорости переносного вращения
параллельна угловой скорости переносного вращения 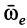 .
.
Следует отметить, что при различном разложении одного и того же абсолютного движения точки на переносное и относительное получим разные ускорения Кориолиса.
Пример №1
Шар радиусом 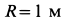 вращается вокруг вертикальной оси
вращается вокруг вертикальной оси 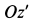 по закону
по закону 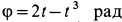 . По меридиану шара движется точка
. По меридиану шара движется точка 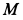 по закону
по закону 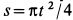 (рис. 90,а). Расстояние
(рис. 90,а). Расстояние 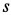 отсчитывается от точки
отсчитывается от точки 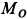 меридиана.
меридиана.
Определить абсолютные скорость и ускорение точки 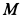 в момент времени
в момент времени 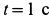 .
.
Решение. За переносное движение точки примем вращение ее вместе с шаром вокруг оси 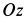 (рис. 90, б). Тогда относительным движением точки будет ее движение по меридиану шара.
(рис. 90, б). Тогда относительным движением точки будет ее движение по меридиану шара.
Определим положение точки 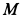 на меридиане в момент времени
на меридиане в момент времени 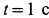 . Имеем
. Имеем 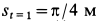 . Так как
. Так как 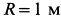 , то положение точки определяется углом широты
, то положение точки определяется углом широты 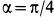 .
.
Вычислим угловые скорость и ускорение переносного движения. Получаем 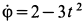 ; при
; при 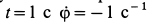 . Угловая скорость
. Угловая скорость 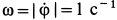 . Знак минус у
. Знак минус у 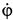 показывает, что вращение шара происходит в отрицательную сторону угла
показывает, что вращение шара происходит в отрицательную сторону угла 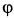 , т. е. по часовой стрелке.
, т. е. по часовой стрелке.
Так как 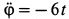 и при
и при 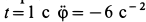 , то угловое ускорение переносного движения
, то угловое ускорение переносного движения 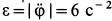 . Знак минус у
. Знак минус у 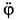 указывает, что оно направлено по часовой стрелке, против положительного направления угла ф. Так как знаки у
указывает, что оно направлено по часовой стрелке, против положительного направления угла ф. Так как знаки у 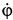 и
и 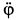 одинаковы, то вращение шара в рассматриваемый момент времени является ускоренным.
одинаковы, то вращение шара в рассматриваемый момент времени является ускоренным.
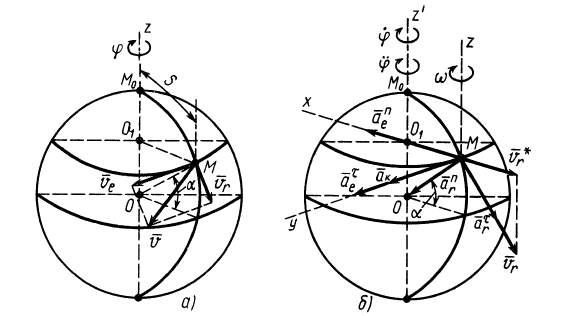
Рис. 90
Абсолютную скорость точки определяем по формуле
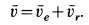
Скорость переносного движения при 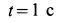
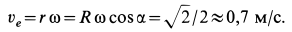
Скорость относительного движения точки 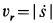 , где
, где 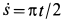 . При
. При 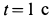
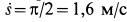 . Следовательно,
. Следовательно, 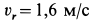 . Знак плюс у
. Знак плюс у 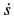 указывает, что
указывает, что 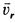 направлено в сторону возрастания
направлено в сторону возрастания 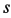 .
.
В рассматриваемом случае 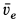 направлена по касательной к параллели шара и перпендикулярна
направлена по касательной к параллели шара и перпендикулярна 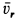 , которая направлена по касательной к меридиану. Следовательно,
, которая направлена по касательной к меридиану. Следовательно,
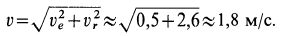
Так как переносное движение является вращением шара вокруг неподвижной оси, то абсолютное ускорение точки определяем по формуле

Переносное нормальное ускорение
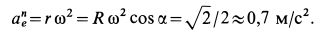
Ускорение 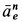 направлено по кратчайшему расстоянию от точки до оси, т. е. по
направлено по кратчайшему расстоянию от точки до оси, т. е. по 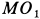 . Переносное касательное ускорение
. Переносное касательное ускорение 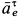 перпендикулярно
перпендикулярно 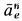 и направлено в соответствии с направлением углового ускорения по скорости
и направлено в соответствии с направлением углового ускорения по скорости 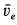 . Числовое значение этого ускорения
. Числовое значение этого ускорения
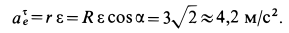
Относительное нормальное ускорение
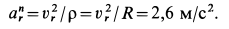
Ускорение 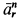 направлено к центру кривизны траектории относительною движения, т. е. к центру шара
направлено к центру кривизны траектории относительною движения, т. е. к центру шара  . Относительное касательное ускорение
. Относительное касательное ускорение 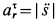 , где
, где 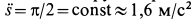 . Следовательно,
. Следовательно, 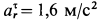 . Так как
. Так как 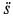 положительно, то
положительно, то 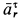 направлено в сторону возрастающих значений
направлено в сторону возрастающих значений 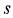 по касательной к траектории относительного движения. Относительное движение оказалось ускоренным в рассматриваемый момент времени.
по касательной к траектории относительного движения. Относительное движение оказалось ускоренным в рассматриваемый момент времени.
Ускорение Кориолиса определяем по правилу Жуковского. Его модуль 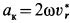 , где
, где 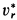 —проекция
—проекция 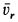 на плоскость, перпендикулярную оси переносного вращения
на плоскость, перпендикулярную оси переносного вращения 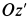 . Имеем
. Имеем
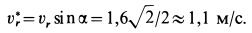
После этого находим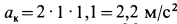 . Чтобы определить направление
. Чтобы определить направление 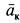 , следует
, следует 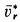 повернуть вокруг оси
повернуть вокруг оси 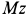 , параллельной
, параллельной 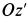 , на
, на 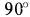 в сторону переносного вращения, т. е. в рассматриваемом случае по часовой стрелке. Получаем, что ускорение направлено по ускорению
в сторону переносного вращения, т. е. в рассматриваемом случае по часовой стрелке. Получаем, что ускорение направлено по ускорению 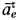 .
.
Для определения абсолютного ускорения выбираем прямоугольные оси координат 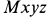 и проецируем обе части векторного равенства (а) на эти оси, учитывая направление составляющих ускорений (рис. 90, б). Получаем:
и проецируем обе части векторного равенства (а) на эти оси, учитывая направление составляющих ускорений (рис. 90, б). Получаем:
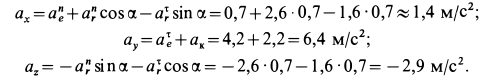
Числовое значение абсолютного значения
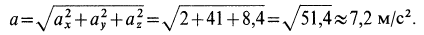
Пример №2
Колечко 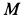 (рис. 91), надетое на стержень, движется в плоскости
(рис. 91), надетое на стержень, движется в плоскости 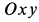 согласно уравнениям
согласно уравнениям
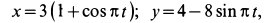
где 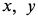 —в см;
—в см; 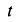 — в с. Стержень может вращаться вокруг оси
— в с. Стержень может вращаться вокруг оси 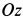 .
.
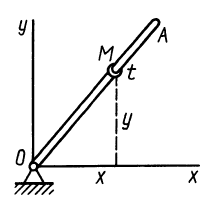
Рис.91
Определить в момент 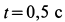 угловую скорость и угловое ускорение стержня, а также скорость и ускорение движения колечка по стержню.
угловую скорость и угловое ускорение стержня, а также скорость и ускорение движения колечка по стержню.
Решение. Положение колечка в момент времени 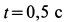 определяется координатами
определяется координатами
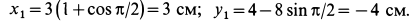
Примем движение колечка вместе с вращающимся стержнем за переносное. Тогда его движение по стержню будет относительным движением.
Вычислим проекции на оси координат абсолютных скорости и ускорения колечка для произвольного момента времени. Имеем:
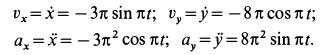
Для момента времени 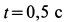 получаем:
получаем:
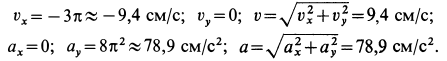
По проекциям изображаем векторы абсолютных скорости и ускорения в рассматриваемый момент времени (рис. 92). По теореме сложения скоростей для колечка,
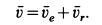
Скорость переносного движения 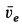 перпендикулярна стержню
перпендикулярна стержню 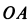 , а скорость относительного движения
, а скорость относительного движения 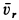 направлена по стержню. Разлагая абсолютную скорость
направлена по стержню. Разлагая абсолютную скорость 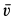 по этим двум направлениям, получаем
по этим двум направлениям, получаем
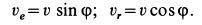
Но
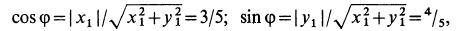
поэтому
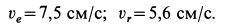
Угловая скорость вращения стержня определяется по формуле
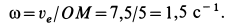
В соответствии с направлением 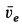 изображаем на рисунке дуговую стрелку для угловой скорости.
изображаем на рисунке дуговую стрелку для угловой скорости.
В частном случае переносного вращательного движения по теореме сложения ускорений для абсолютного ускорения имеем
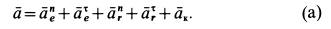
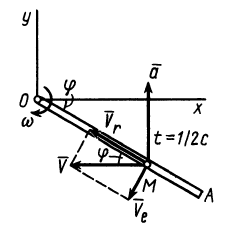
Рис. 92
Вычисляем отдельные составляющие абсолютного ускорения 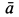 и изображаем их на рис. 93. Для модуля нормального переносного ускорения
и изображаем их на рис. 93. Для модуля нормального переносного ускорения 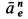 получаем
получаем
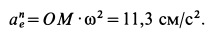
Ускорение 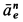 направлено к оси переносного вращения, т. е. к точке
направлено к оси переносного вращения, т. е. к точке 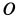 . Составляющая переносного ускорения
. Составляющая переносного ускорения 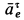 направлена перпендикулярно
направлена перпендикулярно 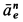 а” и по величине неизвестна. Предполагая, что дуговая стрелка для
а” и по величине неизвестна. Предполагая, что дуговая стрелка для 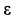 направлена против часовой стрелки, изображаем на рисунке ускорения
направлена против часовой стрелки, изображаем на рисунке ускорения 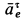 .
.
Нормальная составляющая относительного ускорения 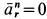 , так как относительное движение колечка по стержню является прямолинейным. Касательная составляющая относительного ускорения в этом случае равна полному относительному ускорению, т. е.
, так как относительное движение колечка по стержню является прямолинейным. Касательная составляющая относительного ускорения в этом случае равна полному относительному ускорению, т. е. 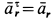 . Предположим, что
. Предположим, что 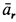 направлено от точки
направлено от точки 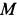 к
к 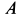 .
.
Ускорение Кориолиса 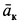 определяем по правилу Жуковского. Для его модуля имеем
определяем по правилу Жуковского. Для его модуля имеем 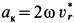 , где
, где 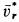 — проекция относительной скорости
— проекция относительной скорости 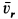 на плоскость, перпендикулярную оси переносного вращения
на плоскость, перпендикулярную оси переносного вращения 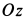 . В рассматриваемом случае
. В рассматриваемом случае 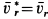 , поэтому
, поэтому 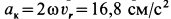 . Направление ускорения
. Направление ускорения 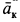 получаем поворотом на
получаем поворотом на 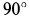 вектора
вектора 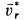 по направлению дуговой стрелки
по направлению дуговой стрелки 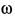 вокруг оси, проходящей через точку
вокруг оси, проходящей через точку 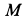 параллельно оси вращения стержня
параллельно оси вращения стержня 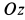 .
.
Выбираем оси координат 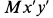 и проецируем векторы, входящие в уравнение (а) на эти оси. Имеем:
и проецируем векторы, входящие в уравнение (а) на эти оси. Имеем:
- для
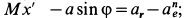
- для
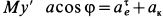 .
.
Из этих уравнений определяем неизвестные ускорения:
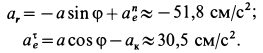
Ускорение 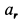 получилось отрицательным. Следовательно, предположение о направлении его оказалось неверным. В действительности
получилось отрицательным. Следовательно, предположение о направлении его оказалось неверным. В действительности 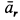 направлено против ранее принятого направления. Ускорение
направлено против ранее принятого направления. Ускорение 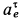 оказалось положительным. Предположение о направлении дуговой стрелки для
оказалось положительным. Предположение о направлении дуговой стрелки для 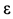 подтвердилось. Угловое ускорение стержня определяем по формуле
подтвердилось. Угловое ускорение стержня определяем по формуле
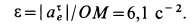
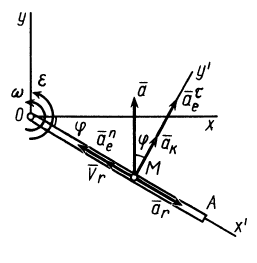
Рис. 93
Составное (сложное) движение. Относительное и переносное движения
Абсолютным движением называют движение точки или системы точек по отношению к основной системе отсчета.
Абсолютное движение
Механическое движение выражается в изменении с течением времени взаимных положений тел (или частей тела). Такое изменение можно отметить только относительно других тел. Так, река течет вдоль берегов, биллиардный шар катится по биллиардному столу, пароход пересекает экватор. Реальные или условные тела (берега, биллиардный стол, экватор), по отношению к которым мы определяем положения других движущихся тел (воды, шара, парохода) и которые мы принимаем за системы отсчета, тоже не неподвижны. Так, системы отсчета, только что приведенные нами в виде примера, находятся на поверхности нашей планеты и вместе с ней вращаются вокруг земной оси, движутся вокруг Солнца и совершают множество других движений. Но и предметы, не связанные непосредственно с Землей, тоже не неподвижны—Солнце движется относительно звезд, которые движутся относительно друг друга.
Однако для целей механики далеко не всегда нужно иметь неподвижную систему отсчета. Так, например, если мы передвигаем какой-либо груз с носа корабля на корму, то нас может интересовать движение груза по палубе независимо от движения корабля. В подобных случаях в кинематике можно условно принять за неподвижную любую систему отсчета и назвать ее основной системой отсчета. Движение же точки (или системы точек) по отношению к основной системе отсчета называют абсолютным движением.
Относительным движением называют движение точки или системы точек по отношению к подвижной системе отсчета
Относительное движение
Встречаются случаи, когда приходится изучать движение (точки или тела) по отношению к системе отсчета, которая сама передвигается относительно другой системы, принятой за основную. При рассмотрении движения точки или тела по отношению к двум системам отсчета ту из этих систем, которая движется относительно основной системы отсчета, называют подвижной системой отсчета.
Так, например, перемещение корабля в море, измеренное при помощи лага, не учитывает снос корабля морским течением. Лагом измеряют движение корабля относительно воды. Можно представить себе подвижную систему координат, плывущую вместе с водой по течению, т. е. передвигающуюся относительно другой системы отсчета, принятой за основную. Движения корабля можно рассматривать по отношению к двум системам отсчета: по отношению к подвижной системе (связанной с водой) и к основной (связанной с материками, принимаемыми за неподвижные). Движение корабля по отношению к подвижной системе координат, измеряемое лагом, будем называть относительным движением корабля. Вообще относительным движением будем называть движение (точки, тела или системы точек) по отношению к подвижной системе отсчета. Относительное движение изучают обычно в тех случаях, когда приходится учитывать не только движение данного объекта по отношению к подвижной системе отсчета, но и движение самой системы отсчета.
Переносным движением называют движение подвижной системы отсчета по отношению к основной системе отсчета
Переносное движение
Так, в данном примере, чтобы знать движение корабля относительно берегов, надо кроме движения корабля относительно воды знать также и движение самой воды, т. е. движение подвижной системы отсчета относительно основной. Движение подвижной системы отсчета по отношению к основной системе отсчета называют переносным движением.
Во многих задачах кинематики переносным бывает движение среды, в которой находится тот объект, движение которого нужно изучить. В только что рассмотренном примере течение воды действительно переносит корабль. Еще один пример: человек идет по поезду. Движение поезда является переносным движением для человека, а движение человека относительно вагонов является относительным. Поезд переносит (в буквальном смысле слова) человека. Но иногда переносное движение не является движением среды, которая увлекает с собой данный объект. Например, рассматривая движение Земли вокруг ее оси и вокруг Солнца, мы можем первое из этих движений считать относительным, а второе — переносным, хотя нет такой среды, которая вращалась бы вокруг Солнца, увлекая с собой и Землю.
Составным движением называют абсолютное движение точки или системы точек, составляемое из их относительного и переносного движений
Составное движение
В первых двух примерах движение объекта (корабля, человека) состоит из двух движений, которые мы назвали относительным и переносным. В третьем примере Земля совершает движение, которое мы искусственно разложили на относительное и переносное. Часто, чтобы упростить изучение какого-либо сложного движения, это движение искусственно раскладывают на более простые, называя одно из них относительный!, другое—переносным. Независимо от того, состоит ли движение в действительности из относительного и переносного или же мы искусственно, для упрощения расчетов, считаем его состоящим из двух движений, мы будем называть сложным или составным движением абсолютное движение точки или системы точек, состоящее (или составляемое) из относительного движения по отношению к подвижной системе отсчета и переносного движения вместе с подвижной системой отсчета.
Если в cocтавном движении мы мысленно прекратим одно из составляющих движений, то получим второе составляющее движение. При решении некоторых задач бывает удобно пользоваться таким приемом:
- чтобы определить относительное движение, мысленно остановим переносное;
- чтобы определить переносное движение, мысленно остановим относительное.
Возвращаясь к первому из только что разобранных примеров, мысленно остановим морское течение; корабль будет двигаться относительно воды, но не будет относиться течением; останется только одно движение — относительное. Остановим теперь собственный ходкорабля, но предоставим воде продолжать свое течение, и корабль поплывет по течению; останется только одно движение корабля —переносное.
Также легко выделить относительное и переносное движения во втором примере. Остановим мысленно поезд, но предоставим человеку идги по вагону, и получим относительное движение человека; остановим мысленно человека в его движении по поезду, но не будем останавливать поезд, и найдем переносное движение человека.
Движение точки, тела или системы точек часто рассматривают как составное, мысленно раскладывая его на два или несколько движений более простых
Несколько сложнее третий пример (движение Земли)
Здесь нет движения среды, переносящей Землю, подобно морскому течению, переносящему корабль. Мы лишь мысленно приняли движение Земли за составное, искусственно разложили его на переносное и относительное, чтобы упростить его, чтобы более наглядно себе его представить и легче понять. Мы можем вообразить подвижную систему координат, связанную с Землей и движущуюся относительно основной системы, связанной с Солнцем и звездами, и считать, что движение Земли состоит из переносного и относительного. Поскольку движение земного шара (движение по отношению к основной системе) мы искусственно рас: сматриваем как составное, постольку от нас самих зависит, как разложить это движение на переносное и относительное. Мы можем считать, что подвижная система отсчета движется поступательно или вращательно. В зависимости от этого, конечно, изменится и относительное движение. Земля совершает 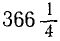 оборота в год относительно поступательно движущихся осей (рис. 114, а) и на один оборот меньше относительно осей, вращающихся вокруг Солнца (рис. 114, б) и совершающих один оборот в год.
оборота в год относительно поступательно движущихся осей (рис. 114, а) и на один оборот меньше относительно осей, вращающихся вокруг Солнца (рис. 114, б) и совершающих один оборот в год.
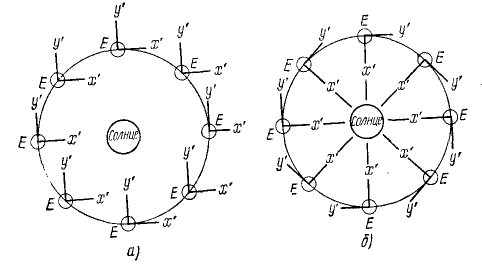
Рис. 114
Такой искусственный метод разложения движения на относительное и переносное широко применяют в различных областях механики. Л. Пуансо в предисловии ко второму изданию своей книги «Элементы статики» (1824) писал даже о невозможности представить наглядно движение тел иначе, как в виде одновременного перемещения и вращения.
Очень часто движение раскладывают не на два, а на большее число составляющих движений. Напомним, что мы уже так поступали, изучая движение точки как составное из трех прямолинейных движений, параллельных осям координат.
Теоремы параллелограмма скоростей и параллелограмма ускорений
Относительными скоростью и ускорением точки называют ее скорость и ускорение по отношению к подвижной системе отсчета
Относительные скорость и ускорение
Пусть некоторая точка M (рис. 115) движется относительно системы координат.x’Ey’z’. Если бы эту систему координат мы считали неподвижной, то движение, скорость и ускорение точки по отношению к этим координатам мы называли бы абсолютными. Но пусть система координатных осей x’Ey’z’ по условиям задачи движется относительно основной системы отсчета xОyz. В таком случае скорость и ускорение точки M относительно системы координат x’Ey’z’ называют относительными.
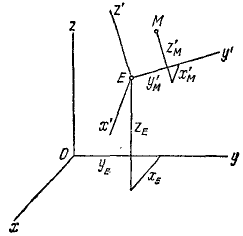
Рис. 115
Итак:
- относительной скоростью точки называют скорость точки по отношению к подвижной системе отсчета1;
- относительным ускорением точки называют ускорение точки по отношению к подвижной системе отсчета.
Мы будем обозначать относительную скорость буквой υ с индексом r (от латинского слова relativus—относительный). Относительное ускорение будем обозначать буквой а с тем же индексом r.
Для обозначения проекций относительных скорости и ускорения будем ставить рядом с индексом r второй индекс. Так, υrx есть проекция относительной скорости на ось Ox; arN—относительное нормальное ускорение.
Переносными скоростью и ускорением точки называют абсолютные скорость и ускорение той точки подвижной системы отсчета, с которой в данное мгновение совпадает движущаяся точка
Переносные скорость и ускорение
Чтобы определить переносное движение точки М, прекратим мысленно ее относительное движение, закрепив ее относительно координатных осей х’Еу’z’ в том положении, которое она занимает в данное мгновение. Таким образом, мы будем считать, что точка M неизменно скреплена с осями х’Еу’z’ , но оси продолжают двигаться относительно основной системы координат xOyz вместе с точкой М. Тогда скорость и ускорение точки M относительно основных осей координат явятся скоростью и ускорением точки M в ее переносном движении.
Итак:
- переносной скоростью точки M называют абсолютную скорость той точки подвижной системы отсчета, с которой в данное мгновение совпадает движущаяся точка М;
- переносным ускорением точки M называют абсолютное ускорение той точки подвижной системы отсчета, с которой в данное мгновение совпадает движущаяся точка М.
Мы будем обозначать переносную скорость точки буквой υ с индексом е (от французского слова entrainer—увлекать за собой), а переносное ускорение—буквой а с тем же индексом. Для обозначения проекций переносных скорости и ускорения на какую-либо ось будем ставить рядом с индексом е индекс, соответствующий оси.
Вектор абсолютной скорости равен сумме векторов относительной и переносной скоростей:
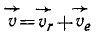
Параллелограмм скоростей
Ознакомившись с понятиями относительной и переносной скоростей точки, найдем зависимость между этими скоростями и абсолютной скоростью, т. е. скоростью точки по отношению к основной системе отсчета.
Пусть подвижная система координат x’Ey’z’ (рис. 116) движется поступательно. В таком случае оси Ex’, Ey’ и Ez’ будут оставаться параллельными своему начальному направлению. Для простоты выкладок пусть эти оси направлены параллельно осям основной системы координат. Тогда во все время движения будем иметь:
Ex’ ||Ox; Ey’||Oy; Ez’||Oz.
Рассмотрим сначала относительное движение точки M и для этого остановим мысленно движение подвижной системы отсчета.
Напишем уравнения движения точки M относительно подвижной системы отсчета:
x’ = x'(t). y’=y'(t), z’ = z'(t). (102)
Продифференцировав по времени и обозначая, как обычно, точкой производные по времени, найдем проекции относительной скорости на подвижные оси координат:
υrx’=x’; υry’=y’; υrz’ = r’.
Так как оси подвижной системы координат параллельны соответствующим осям основной системы, то проекции относительной скорости на оси Ex’, Ey’ и Ez’ соответственно равны проекциям на параллельные им оси Ox, Oy и Oz основной системы отсчета:
υrx=x’; υry = y’; υrz=z’.
Зная проекции относительной скорости, легко найдем по формулам (64) и (62) величину и направление полной относительной скорости.
Чтобы определить переносное движение, мысленно остановим движение точки относительно подвижной системы координат, но предоставим самой подвижной системе x’Ey’z’ продолжать движение.
Напишем по (77) уравнения переносного поступательного движения:
xЕ=x (t); yЕ = y(t), zЕ=z(t).
Продифференцировав равенства (77), получим проекции переносной скорости точки М, которые при поступательном движении системы равны проекциям скорости точки Е:
υex =xE; υey = yE, υez = zE.
Величину и направление вектора полной переносной скорости точки M легко найти по формулам (64) и (62).
Для определения абсолютной скорости точки M найдем сначала ее координаты х, у и г. Применив формулу преобразования начала координатных осей при сохранении направления осей, получим
х-=х’ + хE, y = y’ + yE, z = z, + zE.
Точка M находится в составном движении, следовательно, х, у и г изменяются с течением времени, причем первые члены правых частей этих равенств изменяются согласно (102), а вторые—согласно (77). Продифференцировав по времени, получим проекции абсолютной скорости точки М:
υx = x’+’xE, υy=y’ + yE, υz = z,+ zE
или
υx =υrχ+υeχ, υy =υry+ υey, υz = υrz +υez. (103)
Эти равенства показывают, что проекция абсолютной скорости на какую-либо ось равна сумме проекций относительной и переносной скоростей на ту же ось. Следовательно, вектор абсолютной скорости точки равен сумме векторов относительной скорости и переносной скорости той же точки:
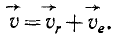 (103‘ )
(103‘ )
Поэтому доказанную теорему называют теоремой параллелограмма скоростей.
Равенства (103) и (103′) выражают связь между тремя скоростями (абсолютной, относительной и переносной) одной и той же точки и позволяют определить любую из этих скоростей, если известны две другие,Они доказаны в предположении, что переносное движение поступательное, но справедливы при всяком переносном движении, как это будет показано в § 31.
Из равенств (103) непосредственно получаем:
- проекция относительной скорости точки на какую-либо ось равна разности проекций абсолютной и переносной скоростей той же точки на ту же ось;
- проекция переносной скорости точки на какую-либо ось равна разности проекций абсолютной и относительной скоростей той же точки на ту же ось.
Из векторного равенства (103) получаем
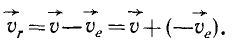
Отсюда вытекает следующее правило: чтобы найти относительную скорость точки, надо сложить вектор абсолютной скорости точки с вектором, равным по модулю, но обратным по направлению вектору ее переносной скорости. Аналогично, чтобы найти переносную скорость точки, надо сложить вектор абсолютной скорости точки с вектором, равным по модулю, но обратным по направлению вектору ее относительной скорости.
Пример №3
Вертикально падают дождевые капли со скоростью 2 м/сек. Пешеход идет справа налево со скоростью 1,5 м/сек. Найти скорость дождя по отношению к пешеходу (рис. 117, а).
Решение. В данной задаче за основную систему отсчета примем Землю. Подвижная система отсчета связана с пешеходом. Вертикальная скорость дождя является абсолютной скоростью (υ = 2 м/сек); переносной скоростью υe является скорость подвижной системы отсчета, т. е. скорость человека, направленная влево и равная 1,5 м/сек. Чтобы найти вектор относительной скорости, сложим вектор абсолютной скорости (рис. 117,6) с вектором, который по величине равен переносной скорости, а по направлению противоположен ей, т. е. направлен слева направо:
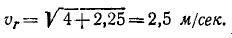
Вектор относительной скорости составляет с вертикалью угол а, тангенс которого равен
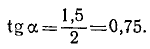
Ответ. υr = 2,5 м/сек, α = 37°.
Пример №4
Корабль плывет на юг со скоростью 42,3 км/ч. Второй корабль идет курсом на юго-восток со скоростью 30 км/ч. Найти величину и направление скорости второго корабля, определяемую наблюдателем, находящимся на палубе первого корабля. При вычислении принять 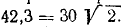 .
.
Решение. Задача аналогична предыдущей, но решать ее будем не в векторной, а в координатной форме, для чего перепишем (103) в следующем виде:
υrx=υx – υex, υry = υy– υey∙
Построим основную систему координат, связанную с Землей, направив ось Ox на юг, а ось Оу— на восток, (рис. 118). Подвижную систему отсчета свяжем с первым кораблем, так как относительно первого корабля надо определить скорость второго. Проекции абсолютной скорости второго корабля на оси основной системы таковы:
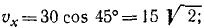
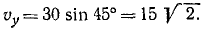
Переносным движением мы называем движение подвижной системы отсчета по отношению к основной. Поэтому в данной задаче переносной скоростью является скорость первого корабля. Ее проекции следующие:
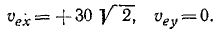
Подставляя эти значения в написанные выше уравнения, найдем проекции относительной скорости:
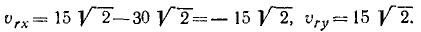
По проекциям находим модуль:
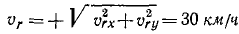
и направляющие косинусы относительной скорости:
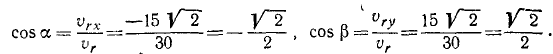
Следовательно, относительная скорость второго корабля составляет углы по 45о C положительным направлением оси Oy и с отрицательным направлением оси Ох, т. е. направлена на северо-восток.
Ответ, υr = 30 км/ч н направлена на северо-восток.
Пример №5
Ширина АВ реки (рис. 119,а) равна 900 м, и берега ее параллельны. Моторная лодка, выйдя из пункта В, держала курс перпендикулярно берегам и достигла противоположного берега через 5 мин, но не в пункте А, находящемся против В, а в пункте С, лежащем на 300 м ниже по течению. Во втором рейсе та же моторная лодка, выйдя из того же пункта В, взяла курс под углом О к BA (начальное направление на пункт D, лежащий на 300 м выше пункта А по течению) и сохраняла свое направление (угол δ), но подошла к правому берегу в пункте Е, лежащем ниже А.
Считая скорость лодки относительно воды постоянной и пренебрегая изменением течения воды у берегов, определить расстояние AE, скорость течения, скорость лодки относительно воды и скорости υ1 и υ2 лодки относительно беретов в обоих рейсах.
Решение. Возьмем начало основной системы координат в точке В, направив ось абсцисс перпендикулярно к берегу по BA, а ось ординат — вниз по течению реки (для решения задачи пользуемся формулами 103). Скорость лодки относительно этой системы является абсолютной. Подвижная система координат движется поступательно вместе с водой и скорость течения реки является переносной скоростью лодки.
Тогда, имея в виду, что АC = 300 м = DA, для первого рейса (рис. 119,6)
υ1 cos δ = υr, υ1 sin δ = υe
и для второго рейса (рис. 119, в)
υ2 cos δ’ =υr cos δ, υ2 sin δ, =υe—vr sin δ.
В первом рейсе лодка держала курс перпендикулярно берегам и в относительном движении проплыла 900 я за 5 мин = 300 сек. Следовательно, υr=3 м/сек.
За то же время ее снесло течением на 300 м, а потому υe=l м/сек.
Подставляя эти значения в уравнения, составленные для первого рейса, и деля второе из этих уравнений на первое, найдем
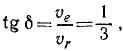 откуда
откуда 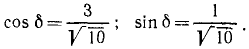
Из тех же уравнений найдем скорость лодки относительно берегов (т. е. абсолютную скорость) в первом рейсе:
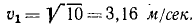
Величина относительной скорости лодки, определенная по ‘данным первого рейса, не изменится и во втором, так как по условию задачи скорость лодки относительно воды постоянна. Также не изменится и переносная скорость лодки — скорость течения реки. Подставляя найденные значения в уравнения, составленные для второго рейса, получим
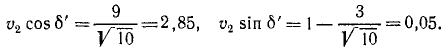
Из этих уравнении найдем: υ2 = 2,85 м/сек и sin δ’ = 0,018.
Умножая АB = 900 м на tg δ’, найдем AE.
Ответ. υe=l м/сек-, υr=3 м/сек-, υ1 = 3,16 м/сек;
v2 = 2,85 м/сек, АЕ=16 м.
Если переносное движение поступательное, то вектор абсолютного ускорения точки равен сумме векторов ее относительного и переносного ускорений
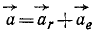
Параллелограмм ускорений
В отличие от теоремы параллелограмма скоростей, применимой при всяком переносном движении, аналогичная теорема параллелограмма ускорений справедлива только в том случае, если переносное движение поступательное.
Пусть точка совершает составное движение, причем подвижная система отсчета x’Ey’z’ движется поступательно по отношению к основной системе хОуz. Пусть соответствующие оси обеих координатных систем параллельны друг другу, это упростит доказательство.
Проекции относительной скорости точки нами уже определены. Продифференцировав эти равенства по времени, найдем проекции относительного ускорения точки:
arx = χ’; ary=y,; arz=z’.
Величину и направление полного относительного ускорения можно определить по формулам (66) и (67).
Продифференцировав по времени равенства (78), найдем проекции ускорения точки в переносном поступательном движении:
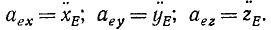
Величину и направление полного переносного ускорения можно определить по формулам (66) и (67), применимым для всякого ускорения точки, независимо от того, является это ускорение абсолютным, относительным или переносным.
Чтобы определить проекции абсолютного ускорения точки (в рассматриваемом случае переносного поступательного движения), надо продифференцировать по времени равенства (103). Получим
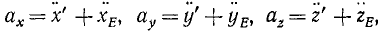
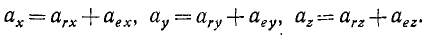 (104)
(104)
Из этих равенств видно, что если переносное движение поступательное, то проекция абсолютного ускорения точки на ось состоит из суммы проекций на ту же ось относительного и переносного ускорений точки. Следовательно, вектор абсолютного ускорения точки в этом случае равен геометрической сумме двух векторов—относительного и переносного ускорений:
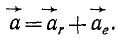 (104′)
(104′)
В этом заключается теорема параллелограмма ускорений.
Равенства (104) и (104′) выражают связь между абсолютным, относительным и переносным ускорениями точки в случае, если переносное движение поступательное, и позволяют определить какое-либо одно из этих ускорений по двум другим.
Если относительное и переносное движения заданы в естественной форме, то для определения ускорений приходится сначала определять их нормальную и касательную составляющие. Так, для определения относительного ускорения надо определить относительное касательное и относительное нормальное ускорения, а уж потом по формулам (75) и (76)—полное относительное ускорение. Аналогично для определения переносного ускорения определяют переносные касательное и нормальное ускорения, а затем полное переносное ускорение. Для получения полного абсолютного ускорения нужно взять геометрическую сумму полного относительного и полного переносного ускорений, которые составляют между собой, вообще говоря, угол, отличный от прямого.
Приводим схему разложения полного абсолютного ускорения точки для случая переносного поступательного движения. При решении задач на параллелограмм ускорений бывает полезно написать эту схему и заполнять ее справа налево:
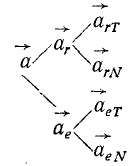
Часто определяют абсолютное ускорение по его проекциям ах, ay, az на оси основной системы координат и, получив проекции результирующего вектора 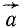 как алгебраические суммы проекций составляющих
как алгебраические суммы проекций составляющих 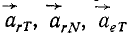 и
и 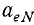 , на те же оси:
, на те же оси:
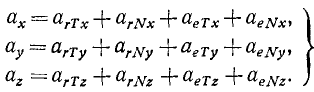 (106)
(106)
Эти равенства являются лишь некоторым видоизменением равенств (104).
Если переносное движение не поступательное, то абсолютное ускорение точки состоит из суммы трех векторов: относительного ускорения, переносного ускорения и ускорения Кориолиса. Доказательство теоремы Кориолиса дано в § 31.
Пример №6
Кривошипио-кулнсный механизм приводного молота (рис. 120, а) состоит из прямолинейной поступательно движущейся кулисы АВ, в прорези которой скользит звено C (камень), соединенный шарнирно с кривошипом ОС длины e, вращающимся с постоянной угловой скоростью ω. Найти скорость и ускорение кулисы как функции угла поворота кривошипа.
Решение. Будем рассматривать движение камня C как составное, состоящее из относительного движения по прорези кулисы и переносного движения вместе с кулисой. Для решения воспользуемся формулами (103) и (104). Примем неподвижный шарнир О за начало основной системы координат, направив ось Ox вправо и ось Oy вверх (рис. 120,6). Подвижную систему координат неизменно соединим с кулисой, взяв начало в точке E и направив ось Ex’ по прорези вправо, a Ey’- вверх. Движение подвижной системы координат, как и движение кулисы, поступательное. Ось Ex’ передвигается к неподвижной оси Ох, а ось Ey’ скользит по оси Оу.
Абсолютное движение камня есть круговое поступательное движение по отношению к основной системе координат. Для определения абсолютных скорости и ускорения обратим внимание на то, что точка C (шарнир) принадлежит не только камню, но и кривошипу, а потому абсолютная скорость точки C равна ωr. (см. рис. 120, б), а ее проекции:
υx = ωr cos ωt и υy= ωr sin ωt.
Абсолютное ускорение точки C равно ω2r, а его проекции (рис. 120, в):
ах = — ω2r sin ωt и ay = ω2r cos ωt.
Эти равенства можно было бы получить, продифференцировав предыдущие.
Относительное движение камня — это возвратно-поступательное движение по прорези вправо и влево. Такое движение камня мы видели бы, если бы сами двигались вместе с кулисой, не замечая ее движения. Камень движется по горизонтальной оси Ex’, а потому
υrx= ± υr, υry = 0.
Проекции относительного ускорения:
αrx=±ar, αry = 0.
Переносное движение камня (движение подвижной системы отсчета относительно основной) —возвратно-поступательное движение кулисы вверх и вниз. Поэтому проекции переносных скорости и ускорения на вертикальную ось Oy равны модулям скорости и ускорения со знаком «-(-» или «—», а на горизонтальную ось Ох—равны нулю. Имеем
υex = 0, υey= ± υe и αex = 0, αey=± αe.
Из трех движений камня нас интересует переносное движение (движение кулисы). Определив проекции переносной скорости
υex = υx – υrx , υey= υy – υry
и подставив найденные значения, получим переносную скорость из уравнений
0 = ωr cos ωt — υr, υe = ωr sin ωt.
Таким образом, переносная скорость камня (скорость кулисы) определена.
Для определения переносного ускорения мы могли бы продифференцировать по времени выражение, полученное для переносной скорости (так как переносное движение прямолинейно-поступательное). Но мы применим более общий метод — определим из (104) проекции переносного ускорения:
αex = ax—arx, aey=ay – ary
подставим в эти уравнения найденные нами значения проекций переносного и абсолютного ускорений камня:
0 = — ω2r sin ωt-ar, ae = ω2r cos ωt.
Таким образом, переносное ускорение ае камня равно ω2r cos ωt. Оно же является ускорением кулисы.
Ответ. υ = ωr sιnωt; a = ω2r cos ωt.
Теорема сложения ускорений точки при переносном вращательном движении (теорема Кориолиса)
При составном движении точки в случае непоступательиого переносного движения возникает добавочное ускорение, называемое ускорением Кориолиса:
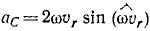
Величина ускорения Кориолиса
Теорема параллелограмма ускорений пригодна только в частном случае, если подвижная система отсчета движется поступательно. Если же переносное движение не поступательное, то у абсолютного ускорения появляется еще одна составляющая, называемая ускорением Кориолиса, или поворотным ускорением. Выведем формулы, позволяющие определить абсолютное ускорение при всяком составном движении точки.
Пусть точка M (рис. 121) движется относительно подвижной системы x’0y’z’ и это движение определяется какими-либо уравнениями
x’=x'(t), y’=y'(t), z’ = z’ (t).
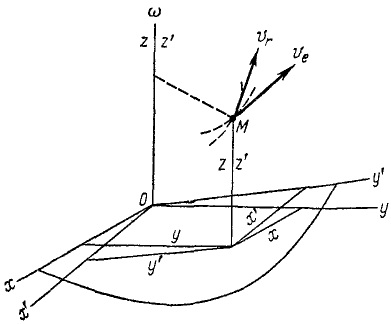
Рис. 121
Пусть подвижная система отсчета вращается вокруг оси Oz основной системы согласно уравнению T==T (О-
Сохраним и в этом параграфе расположение осей координат (см. рис. 101, стр. 165), при котором оси Oz’ и Oz подвижной и неподвижной систем совпадают между собой и с осью вращения, а плоскость х’Оу’ находится в плоскости хОу. Тогда координаты точки M в основной системе определятся соотношениями
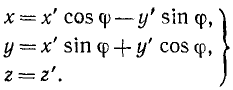 (107)
(107)
Эти равенства (107) отличаются от уже известных нам равенств (88) тем, что здесь координаты х’, у’ и z’ переменны, тогда как в равенствах (88) они были постоянны.
Если мы мысленно остановим точку M в ее относительном движении, т. е. будем считать ее координаты х’, у’ и z’ постоянными, но сохраним переносное вращение, то, дифференцируя равенства (88) по времени, найдем знакомые нам выражения (89) проекций вращательной скорости, которая в данном случае явится переносной скоростью точки М:
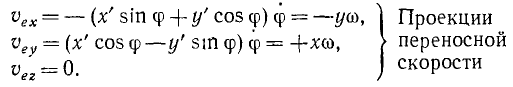
Дифференцируя вторично, найдем проекции переносного ускорения, которые выражаются также известными нам формулами (95):
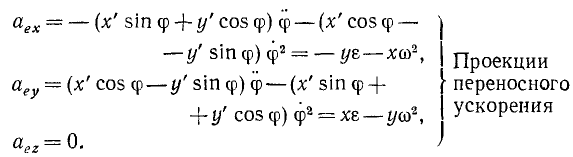
Чтобы определить относительное движение, мысленно остановим переносное, т. е. будем считать 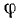 постоянной, a’, x’, у’ и z’ — переменными. Дифференцируя при таких условиях (107) по времени, определим проекции относительной скорости:
постоянной, a’, x’, у’ и z’ — переменными. Дифференцируя при таких условиях (107) по времени, определим проекции относительной скорости:
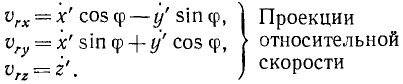
Заметим попутно, что, возводя каждое из этих равенств в квадрат, складывая и извлекая квадратный корень, мы определили бы величину относительной скорости (рис. 122). Если же мы возведем в квадрат и сложим лишь два первых равенства, то, извлекая корень, мы получим, очевидно, величину проекции относительной скорости на плоскость хОу:
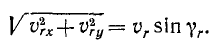
Напомним, что вектор угловой скорости 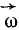 направлен по оси вращения, а потому угол γr есть угол между векторами относительной и угловой скоростей, и последнее равенство можно записать так:
направлен по оси вращения, а потому угол γr есть угол между векторами относительной и угловой скоростей, и последнее равенство можно записать так:
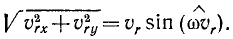
Это соотношение скоро нам понадобится.
Чтобы получить проекции относительного ускорения, надо продифференцировать по времени выражения, полученные для проекций относительной скорости, по-прежнему считая φ постоянной. Имеем
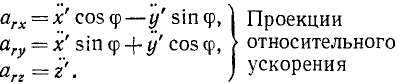
Чтобы определить проекции абсолютной скорости точки М, надо продифференцировать уравнения (107) по времени, считая все величины переменными. Имеем
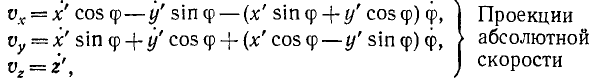
или
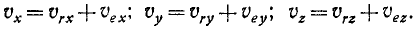 (103)
(103)
Мы получили теорему параллелограмма скоростей, которая, следовательно, остается в силе и при вращательном переносном движении.
Чтобы определить проекции абсолютного ускорения, возьмем вторые производные, опять-таки считая все величины переменными. Имеем:
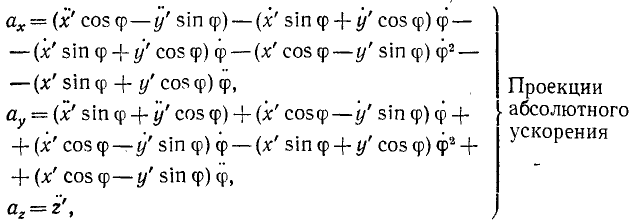
или
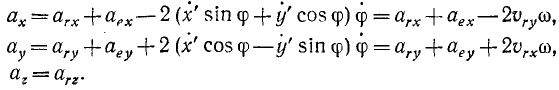
Таким образом, в выражениях проекций абсолютного ускорения, вдобавок к проекциям относительного и переносного ускорений, появляется еще одно слагаемое, выражающее проекции добавочного ускорения ac:
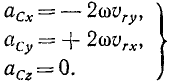 (108)
(108)
Это добавочное ускорение называют ускорением Кориолиса.
Определим величину ускорения Кориолиса:
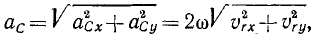
или, заменив корень полученным выше значением, находим окончательно
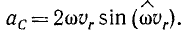 (109)
(109)
Мы вывели формулу (109) в предположении, что переносное движение вращательное. Она остается без изменений и при всяком ином непоступательном переносном движении.
Итак, если переносное движение не поступательное, то абсолютное ускорение точки равно геометрической сумме трех составляющих: относительного ускорения, переносного ускорения и ускорения Кориолиса:
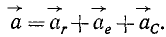 (110)
(110)
В случае, если переносное движение непоступательное, необходимо дополнить ускорением Кориолиса и схему (105), которая принимает следующий вид:
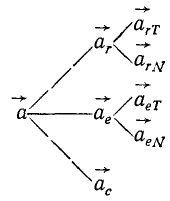 (110/)
(110/)
Пользоваться этой схемой при решении задач надо так же, как и схемой (105), заполняя ее справа и геометрически складывая составляющие.
Ускорение Кориолиса существует только при составном движении, если переносное движение непоступательное
При каком движении бывает ускорение Кориолиса
В выражение (109) ускорения Кориолиса входят множителями относительная скорость точки, угловая скорость подвижной системы отсчета и синус угла между векторами этих скоростей. Но относительная скорость бывает только при составном движении. Поэтому и ускорение Кориолиса может быть только при составном движении. Если нет относительной скорости точки, т. е. если υr = 0, то не может быть и ускорения Кориолиса. Однако ускорение Кориолиса бывает не при всяком составном движении точки. Так, если переносное движение поступательное и ω = 0, то нет и ускорения Кориолиса. Из формулы (109) видно, что и в составном движении точки, и при переносном вращательном движении ускорение Кориолиса равно нулю, если относительная скорость параллельна оси вращения. Так, например, корабль, плывущий по меридиану, имеет ускорение Кориолиса, если рассматривать его движение как составное из относительного движения корабля и переносного движения Земли. Это ускорение равно удвоенному произведению скорости корабля на угловую скорость Земли и на синус географической широты (рис. 123) и равнялось нулю в то время, когда корабль пересекал экватор и его относительная скорость была параллельна вектору угловой скорости Земли.
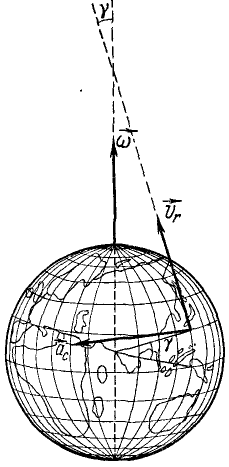
Рис. 123
Физическая причина ускорения Кориолиса заключается в изменении вектора переносной скорости от относительного движения и вектора относительной скорости от переносного движения
Физическая причина ускорения Кориолиса
Постараемся уяснить физические причины, вызывающие ускорение Кориолиса, для чего представим себе два прямолинейных отрезка O1A1 и O2A2 (рис. 124), рис. 123 по которым движутся точки B1 и B2. Штрихами отмечены положения этих отрезков и точек через промежуток времени Δ t. Первый из отрезков движется поступательно, второй вращается вокруг O2.
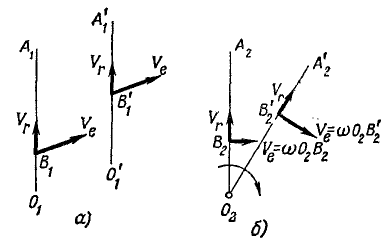
Рис. 124
Существуют две физические причины ускорения Кориолиса:
1. Переносная скорость точки B1 не зависит от положения ее на отрезке O1A1, так как, по свойству поступательного движения, скорости всех точек прямой O1X1 между собой равны. Напротив, величина переносной скорости точки B2 равна ω.O2B2 и всецело зависит от ее положения. Переносная скорость точки B2 меняется от ее относительного движения. Чем быстрее движется точка B2 по прямой O2A2 и чем быстрее вращается эта прямая, тем значительнее изменяется переносная скорость точки B2. Таким образом, изменение скорости точки в данное мгновение (т. е. ускорение точки), вызванное указанной причиной, пропорционально величине агносительной и угловой скоростей. В этом заключается один из факторов, порождающих ускорение Кориолиса.
2. Направление относительной скорости точки B1 не меняется, так как, по свойству поступательного движения, прямая O1A1 передвигается параллельно самой себе. Напротив, направление относительной скорости точки B2 непрерывно изменяется по мере вращения O2А2. Даже при прямолинейном относительном движении направление относительной скорости изменяется (вследствие переносного вращения). Изменение вектора скорости точки в данное мгновение (ускорение), вызванное этой причиной, тоже пропорционально величине относительной и угловой скоростей, В этом заключается другой фактор, порождающий ускорение Кориолиса. Ускорение Кориолиса как бы поворачивает вектор относительной скорости в направлении переносного вращения. По этой причине его иногда называют поворотным ускорением.
Вектор ускорения Кориолиса перпендикулярен векторам угловой и относительной скоростей
Направление ускорения Кориолиса
При выводе формулы ускорения Кориолиса мы убедились, что проекция этого ускорения на Oz равна нулю. Отсюда следует, что вектор ускорения Кориолиса лежит в плоскости, перпендикулярной к оси вращения, или, иными словами, к вектору угловой скорости, который направлен по оси вращения Oz.
Уточним теперь направление ускорения Кориолиса в плоскости, перпендикулярной к осп вращения, и обозначим углы, составляемые им с осью Ox и Оу, через αc и βc. Направляющими косинусами являются:
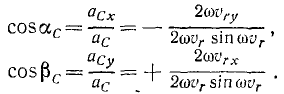
Углы, составляемые относительной скоростью точки с теми же осями, обозначим через ar и βr:
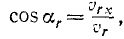
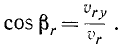
Сравнивая направляющие косинусы ускорения Кориолиса с направляющими косинусами относительной скорости, находим, что удовлетворяется известное из аналитической геометрии условие перпендикулярности двух направлений—сумма произведений соответствующих направляющих косинусов равна нулю:
cos ac cos ar + cos βc cos βr = 0,
следовательно, ускорение Кориолиса перпендикулярно не только к угловой, но и к относительной скорости точки М.
Отсюда вытекает следующее правило: для определения направления ускорения Кориолиса надо спроецировать вектор относительной скорости на плоскость, перпендикулярную Oz (оси вращения), и затем повернуть эту проекцию вокруг оси вращения на 90° в сторону переносного вращения. Следовательно, если переносное вращение происходит в положительном направлении, то проекцию υrxy относительной скорости надо повернуть на 90° против хода стрелки часов, а если переносное вращение происходит в отрицательном направлении, то по ходу стрелки. Это определяется самой сущностью поворотного ускорения, поворачивающего вектор относительной скорости в направлении переносного вращения. К тому же результату мы пришли бы, сравнивая знаки направляющих косинусов ускорения Кориолиса и относительной скорости.
Таким образом, ускорение Кориолиса по величине и направлению можно выразить удвоенным векторным произведением угловой скорости и относительной скорости:
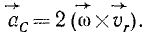 (109/)
(109/)
Если относительное движение точки происходит в плоскости, перпендикулярной оси переносного вращения, то угол между векторами угловой и относительной скоростей равен 90°, его синус равен единице и выражение ускорения Кориолиса упрощается:
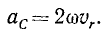 (109//)
(109//)
В этом частном, но очень распространенном в технике случае для определения направления ускорения Кориолиса не нужно проецировать вектор относительной скорости точки, а достаточно повернуть его на 90° в плоскости движения точки в сторону переносного вращения. Поясним это следующей задачей.
Пример №7
Стержень OA вращается вокруг оси, перпендикулярной к плоскости чертежа (рис. 125) в точке О. Вдоль стержня движется ползун В. Указать направление ускорения Кориолиса.
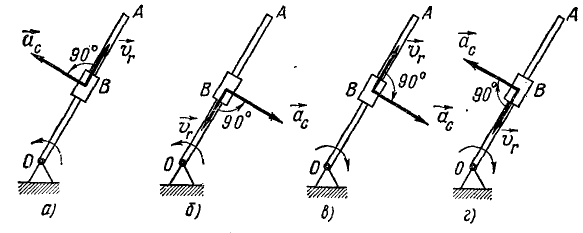
Рис. 125
Решение. Ускорение Кориолиса всегда перпендикулярно к угловой скорости к оси вращения и к относительной скорости. Следовательно, ускорение Кориолиса лежит в плоскости чертежа и перпендикулярно к стержню. Четыре возможных случая изображены на рис. 125, а, б, в, г.
Пример №8
Прямая трубка (рис. 126) равномерно вращается с угловой скоростью ω = π рад/сек вокруг осн Oz, перпендикулярной к плоскости чертежа в точке О. Шарик M совершает гармонические колебания вдоль трубки по закону x’ = ОM = A sin πt. Определить ускорение шарика при t=4 сек.
Решение. Будем рассматривать движение шарика как составное, состоящее из движения относительно трубки и движения вместе с трубкой (рис. 126, а). Для решения задачи воспользуемся схемой (110′) (см. стр. 206).
Чтобы определить относительное движение, мысленно остановим переносное вращение трубки. Уравнение относительного движения шарика есть
x’=A sin πt.
Относительная скорость
υr =x’= Aπ2 cos πt.
В относительном движении шарик имеет касательное ускорение
arT =x’=- Aπ2 sin πt.
Относительное движение в данном случае прямолинейное, поэтому относительное нормальное ускорение αrN=0.
Переносное движение обусловлено вращением трубки. Мысленно остановим шарик, предоставив трубке вращаться. Напишем уравнение равномерного вращения трубки, положив φo = 0:
φ=πt.
Переносной скоростью шарика является вращательная скорость той точки среды (трубки), в которой в это мгновение находится шарик:
υe = ωr = Aπ sin πt,
причем в этом выражении время t соответствует тому мгновению, в которое мысленно остановлен шарик, а потому t здесь нельзя рассматривать как переменную величину.
Переносное вращение равномерное, и переносное касательное ускорение равно нулю:
aeT = εr = 0.
Переносное центростремительное ускорение
aeN = ω2r — Aπ2 sin πt,
где t имеет заданное значение, соответствующее данному мгновению, в которое мысленно остановлено относительное движение.
Кроме этих составляющих абсолютного ускорения, имеется ускорение Кориолиса, так как переносное движение вращательное:
ас = 2ωυr = 2Aπ2 cos πt.
Эти составляющие абсолютного ускорения вносим в схему (110′):
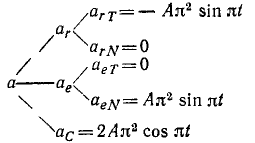
В мгновение t = 4 сек имеем:
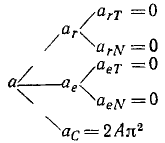
Таким образом, абсолютное ускорение в это мгновение состоит из ускорения Кориолиса a = ac = 2Aπ2.
При t = 4 сек точка M совпадала с точкой О (x’ = A sin 4π = 0) и имела относительную скорость + Аπ, направленную в положительном направлении Ox’. Чтобы определить направление ускорения Кориолиса, надо повернуть вектор относительной скорости на 90° в сторону вращения трубки, т. е. против хода часовой стрелки.
При t = 4 сек угол поворота трубки φ = 4π и ось Ox’ совпадала с осью Ох. Следовательно, в это мгновение ускорение Кориолиса направлено по положительной оси Оу.
Если мы не станем рассматривать движение шарика как составное, а изучим его непосредственно по отношению к основной системе отсчета, то получим, разумеется, тот же результат.
Составим уравнения движения шарика в основной системе координат (рис. 126, б):
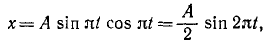
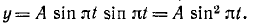
Дифференцируя эти уравнения по времени, найдем проекции скорости:
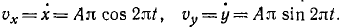
Дифференцируя по времени второй раз, найдем проекции ускорения:
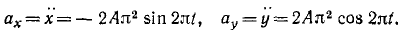
При t = 4 сек
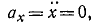
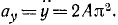
Мы получили те же значения ускорения точки, не пользуясь ускорением Кориолиса. Из этого примера видно, что ускорение Кориолиса бывает лишь при составном движении точки.
Для определения траектории шарика в основной системе отсчета исключим время из уравнений движения. Из второго уравнения находим 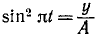 , подставляем в первое уравнение и возводим в квадрат (рис. 126, в):
, подставляем в первое уравнение и возводим в квадрат (рис. 126, в):
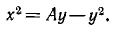
Это уравнение окружности с центром в точке x = 0, 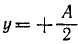 . Чтобы убедиться, достаточно перенести в эту точку начало основной системы , положив
. Чтобы убедиться, достаточно перенести в эту точку начало основной системы , положив 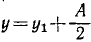 , тогда уравнение траектории примет вид:
, тогда уравнение траектории примет вид:
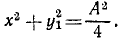
Найдем уравнение движения шарика M по этой окружности:
dx = Аπ cos 2πt dt; dy = Аπ sin 2πt dt;
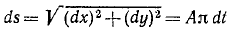
и, интегрируя,
s = Аπt + С = Аπt .
Следовательно, шарик движется по своей траектории равномерно со скоростью υ= Аπ; при t = 4 сек он находится в наинизшей точке окружности, а нормальное ускорение 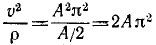 направлено вертикально вверх.
направлено вертикально вверх.
Резюмируя, убеждаемся, что движение шарика (как и движение всякого тела) можно представить различными способами и ускорение шарика в заданное мгновение (t = 4 сек) можно выразить различными формулами.
Можно представить его как составное, состоящее из колебаний шарика вдоль трубки и одновременного вращения трубки. Тогда ускорение 2Аπt2 шарика в заданное мгновение является ускорением Кориолиса.
Можно представить то же движение шарика уравнениями в декартовых координатах, а ускорение 2Аπt2— проекциями на оси координат.
Можно, наконец, это движение шарика определить как равномерное движение со скоростью υ = Аπ по окружности радиуса 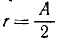 и ускорение 2Аπt2 представить как нормальное ускорение
и ускорение 2Аπt2 представить как нормальное ускорение 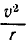 .
.
Различные способы лишь выражают объективно существующее движение и позволяют определить его характеристики.
Ответ. a = 2Аπt2.
Задача №1
Окружность радиуса г равномерно вращается по ходу стрелки часов с угловой скоростью ω вокруг оси, перпендикулярной к ней в одной из ее точек C (рис. 127, а). По окружности движется точка M со скоростью υr = ωr, обходя окружность против вращения часовой стрелки. Определить ускорение точки М.
Решение. Движение точки будем рассматривать как составное, состоящее из относительного равномерного движения по окружности и переносного равномерного вращения самой окружности.
Напишем схему (110′) и будем заполнять ее справа (см. стр. 208).
Чтобы определить относительное движение точки М, мысленно остановим вращение окружности. Относительная скорость равна υr = ωr и направлена по касательной к окружности. Относительное касательное ускорение αrT = 0, а относительное нормальное направлено к центру О окружности и равно
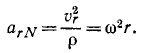
Чтобы определить переносное движение, мысленно закрепим точку M на окружности. Проведем хорду MC (рис. 127, б) и обозначим через δ угол, составляемый ею с диаметром, проходящим через С. Так как окружность вращается равномерно, то αeT = 0 и
αeN = ω2CM = ω22r cos δ
и направлено по хорде MC к точке С.
Величина ускорения Кориолиса в нашем случае равна
ac = 2ωυr-2ω2r.
Переносное вращение происходит по ходу стрелки часов, следовательно, для определения направления ускорения Кориолиса повернем вектор относительной скорости на 90° по ходу стрелки часов.
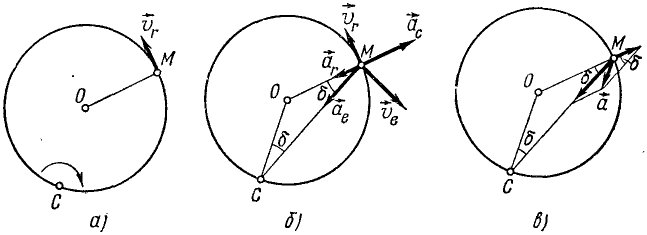
Рис. 127
Скорости и ускорения точки изображены на рис. 127, б, а ускорения записаны по схеме (110′):
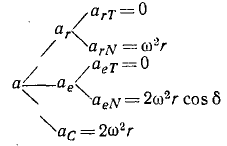
Чтобы определить абсолютное ускорение точки М, надо сложить его составляющие. Сложив ускорение Кориолиса с противоположным ему по направлению нормальным относительным ускорением, найдем, что результирующий вектор этих двух ускорений равен ω2r и направлен в сторону ускорения Кориолиса:
2ω2r-ω2r = ω2r.
Чтобы сложить этот результирующий вектор с вектором переносного ускорения, воспользуемся теоремой косинусов (рис. 127, в). Имеем
a2 = (ω2r)2+ (2ω2r cos δ)2 — 2 (ω2r) (2ω2r cos δ) cos δ = (ω2r)2.
Как видно из чертежа (рис. 127, в), абсолютное ускорение направлено параллельно ОС независимо от угла δ, т. е. независимо от положения точки M на окружности. Иными словами, независимо от положения точки M на окружности вектор ее абсолютного ускорения равен вектору ускорения центра окружности в его движении вокруг оси С.
Ответ. a = ω2r.
Задача №2
В ручке молочного сепаратора по ее длине просверлен цилиндрический канал, закрытый с одной стороны металлической пластинкой (звонком) (рис. 128). В канале помещен металлический шарик. Если вращать ручку с недостаточной скоростью (менее 45 об/мин), то шарик ударится о звонок и даст соответствующий сигнал. Определить ускорение Кориолиса сигнального шарика, если ручка сепаратора наклонена к своей оси вращения под углом 75°, рабочий вращает ручку, делая 45 об/мин, а шарик движется по каналу по закону х’= 220 sin φ + 357e-φ мм.
Решение. Вектор угловой скорости ручки направлен по оси вращения, а относительная скорость шарика —вдоль канала, составляя с ним угол 75°. Ускорение Кориолиса определяем по формуле (105). Угловая скорость 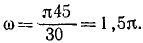 Синус 75° берем из таблиц или подсчитываем как sin (45°+30°) = 0,966.
Синус 75° берем из таблиц или подсчитываем как sin (45°+30°) = 0,966.
Чтобы определить относительную скорость, надо продифференцировать по времени уравнение движения, в котором φ=ωt=1,5πt.
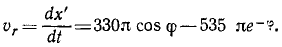
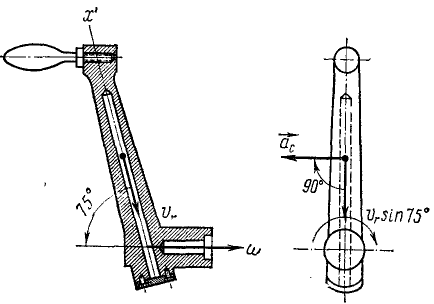
Рис. 128
Таким образом, имеем
αс = 2 • 1, 5π (330π cos φ—535πe – φ) 0,966.
Ответ. Ускорение Кориолиса равно 9420 cos φ—15300e-φ мм/сек2 и направлено перпендикулярно к ручке и к ее оси.
Сложное движение точки и тела
При решении задач, в которых рассматривается сложное движение точки или тела, необходимо уметь правильно расчленить сложное (составное), или так называемое абсолютное движение, на переносное и относительное.
При расчленении сложного движения рекомендуется учитывать следующее. Абсолютное (составное) движение происходит относительно неподвижной системы координат. Обычно эту систему координат связывают с Землей или с неподвижными относительно Земли предметами: зданием, деревом, полотном дороги и т. д.
Переносное движение точки или тела происходит вместе с некоторой материальной средой (телом), внутри или на поверхности которой находится рассматриваемое в задаче тело или рассматриваемая точка. Таким образом, переносное движение — это движение
материальной среды вместе с точкой также относительно неподвижной системы координат.
Относительное движение точки или тела — это перемещение их внутри материальной среды, или по ее поверхности, независящее от движения самой материальной среды.
В тех случаях когда заданы движения двух (или более) тел (точек) относительно неподвижной системы координат и необходимо определить движение одного из этих тел относительно другого, удобно пользоваться теми же приведенными выше соображениями.
Тело, относительно которого требуется рассмотреть движение, мысленно остановим, а неподвижную систему координат заставим двигаться по его закону, но в обратном направлении. Тогда для второго тела это движение станет переносным, а движение второго тела — относительным. После этого очень просто понять, как будет двигаться второе тело по отношению к первому.
Этот последний прием использован при решении задач 177-36 и 184-37 и обычно его используют при рассмотрении планетарных механизмов (см. ниже § 40-9).
Решение всех задач на сложное движение необходимо иллюстрировать рисунком.
Сложение движений точки, когда переносное и относительное движения направлены вдоль одной прямой
При изучении сложного движения точки будем рассматривать только перемещение и скорость.
Если переносное и относительное движения направлены вдоль одной прямой, то:
- перемещение точки в абсолютном движении равно алгебраической сумме перемещений в переносном и относительном движениях;
- скорость точки в абсолютном движении равна алгебраической сумме переносной и относительной скоростей.
Условимся направление переносного перемещения и соответственно направление переносной скорости считать положительными. Тогда относительное перемещение и соответственно относительная скорость будут также положительными, если они направлены в ту же сторону, что и переносное. Если же относительное перемещение (и скорость) имеют направление, противоположное переносному, то будем считать их отрицательными.
Таким образом, при совпадении направлений переносного и относительного движений
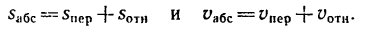
При противоположных друг другу направлениях переносного и относительного движений
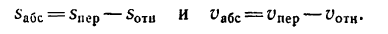
Задача №3
Вниз по течению реки равномерно плывет лодка, приводимая в движение гребным винтом от мотора. Скорость течения реки 4 км/ч, скорость лодки, сообщаемая ей гребным винтом по отношению к воде, составляет 8 км/ч. Определить скорость лодки относительно берегов и расстояние, которое проходит лодка вдоль берегов за 20 мин.
Решение иллюстрировать рисунком, считая берега реки на данном участке прямолинейными и параллельными.
Решение.
1. Лодку принимаем за материальную точку, а водную массу реки —за материальную среду.
Движение лодки относительно берегов или, иначе говоря, движение лодки, наблюдаемое с берега, — это абсолютное движение.
Переносное движение лодки—ее перемещение вместе с рекой; скорость 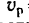 = 4 км/ч, которую сообщает лодке река, — ее переносная скорость.
= 4 км/ч, которую сообщает лодке река, — ее переносная скорость.
Относительное движение— перемещение лодки по поверхности воды, создаваемое гребным винтом; скорость относительного движения 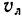 = 8 км/ч.
= 8 км/ч.
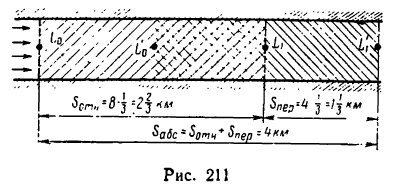
2. Так как в данном случае переносное и относительное движения направлены в одну и ту же сторону, то скорость лодки относительно берегов (абсолютная скорость)
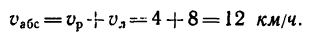
3. За время 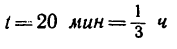 лодка вдоль берегов проходит расстояние
лодка вдоль берегов проходит расстояние
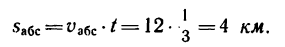
4. Иллюстрируем решение задачи следующим образом (рис. 211).
Изобразим на рисунке тот участок водного пространства, который проходит лодка независимо от того, перемещается этот участок воды или нет. За 20 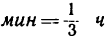 лодка успевает пройти по этому пространству из положения
лодка успевает пройти по этому пространству из положения 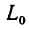 в положение
в положение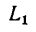 расстояние
расстояние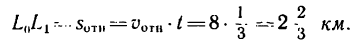
За эти же 20 мин, или
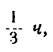 показанное водное пространство
показанное водное пространство
переместится на расстояние
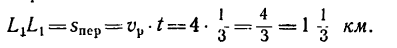
Таким образом, лодка, находившаяся в начале рассматриваемого движения относительно берегов в точке 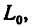 через 20 сек оказывается в точке
через 20 сек оказывается в точке 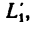 т. е. проходит расстояние
т. е. проходит расстояние
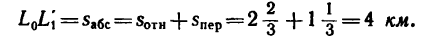
Следовательно, скорость абсолютного движения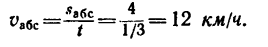
Задача №4
Два автомобиля 1 и 2 движутся параллельно друг другу в одну и ту же сторону со скоростями 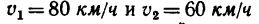 (рис. 212, а). С какой скоростью второй автомобиль двигается относительно первого? Решение.
(рис. 212, а). С какой скоростью второй автомобиль двигается относительно первого? Решение.
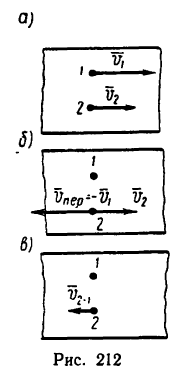
1. Ответ «по соображению» получается мгновенно: 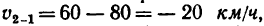 т. е. относительно первого второй автомобиль двигается со скоростью 20 км/ч, но в обратную сторону.
т. е. относительно первого второй автомобиль двигается со скоростью 20 км/ч, но в обратную сторону.
2. Объясним это решение с точки зрения теории сложного движения точки. Условно остановим первый автомобиль. Но тогда, чтобы не изменились условия движения, необходимо мысленно представить, что полотно дороги под вторым автомобилем и вместе с ним получает движение в обратную сторону со скоростью 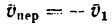 (рис. 212, б).
(рис. 212, б).
Находясь в условном переносном движении со скоростью 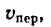 второй автомобиль относительно дороги движется со скоростью
второй автомобиль относительно дороги движется со скоростью 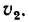
Поэтому результирующая обеих скоростей 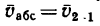 численно равна их разности:
численно равна их разности:
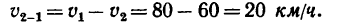
Как видно на рис. 212, а, результирующая направлена в сторону, противоположную скорости 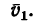
Задача №5
Расстояние s = 90 км между двумя пристанями, расположенными на роке, теплоход проходит без остановки в одном направлении (по течению) за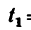 = 3 ч и в обратном направлении (против течения) за
= 3 ч и в обратном направлении (против течения) за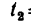 = 5 ч. Определить скорость течения реки и собственную скорость теплохода.
= 5 ч. Определить скорость течения реки и собственную скорость теплохода.
Решение.
1. Теплоход, который принимаем за материальную точку, двигаясь по течению, имеет абсолютную скорость (скорость относительно берегов):
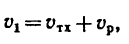
где 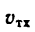 — искомая собственная скорость теплохода (относительная скорость);
— искомая собственная скорость теплохода (относительная скорость);
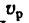 — скорость течения реки (переносная скорость).
— скорость течения реки (переносная скорость).
При движении против течения абсолютная скорость теплохода
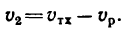
2. Движение теплохода по течению описывается уравнением (рис. 213, а)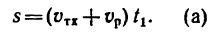
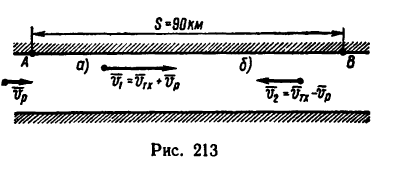
Движение теплохода против течения происходит по уравнению (рис. 213, б)
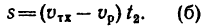
2. Решаем полученную систему уравнения. Из (а) и (б)
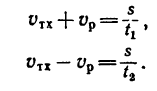
Сложим правые и левые части этих уравнений:
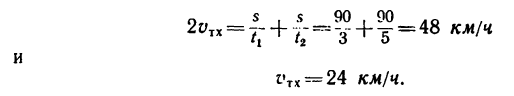
Вычитаем из верхнего равенства нижнее:
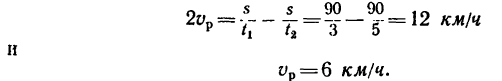
Таким образом, собственная скорость теплохода составляет 24 км/ч и скорость течения реки равна 6 км/ч.
Следующую задачу рекомендуется решить самостоятельно.
Задача №6
Расстояние между двумя пристанями, расположенными на реке, теплоход, двигаясь равномерно без остановки, проходит по течению реки за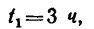 а против течения (двигаясь в обратном направлении) —
а против течения (двигаясь в обратном направлении) —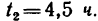 За какое время
За какое время 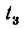 проплывает это же расстояние плот, передвигаемый только течением реки?
проплывает это же расстояние плот, передвигаемый только течением реки?
Задачу надо решить в общем виде, а потом подставить числовые значения.
Ответ.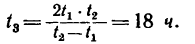
Сложение движений точки, когда переносное и относительное движения направлены под углом друг к другу
Когда переносное и относительное движения направлены под углом друг к другу, то перемещения и скорости складываются геометрически.
Таким образом, абсолютная скорость точки 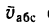 определяется как геометрическая сумма переносной
определяется как геометрическая сумма переносной 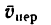 и относительной оог„ скоростей;
и относительной оог„ скоростей;

т. е. либо как диагональ параллелограмма, построенного на переносной и относительной скоростях (рис. 214, а), либо как замыкающий вектор треугольника скоростей (рис. 214, б).
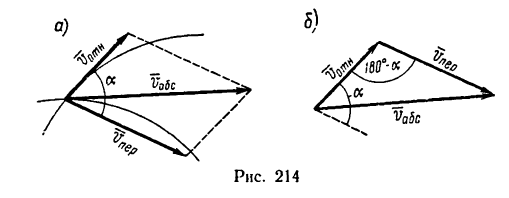
При решении задач на определение скоростей наиболее удобно применять графо-аналитический способ (см. § 3-1 настоящего пособия).
Если применяется правило параллелограмма, то модуль абсолютной скорости определяется по формуле, выведенной из теоремы косинусов
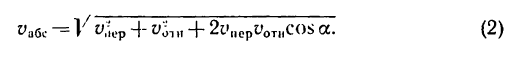
Если применяется правило треугольника, то модуль абсолютной скорости определяется по теореме синусов.
Направление абсолютной скорости по отношению к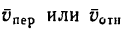 можно найти также при помощи теоремы синусов.
можно найти также при помощи теоремы синусов.
В частном случае, когда параллелограмм скоростей превра шается в прямоугольник или когда треугольник скоростей получается прямоугольным, для решения задачи используются тригонометрические функции и теорема Пифагора (см. ниже задачи 181-37, 182-37, 185-37).
Бели в частном случае 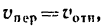 то при геометрическом сложении таких скоростей образуется ромб (рис. 215, а) или равнобедренный треугольник (рис. 215, б), тогда
то при геометрическом сложении таких скоростей образуется ромб (рис. 215, а) или равнобедренный треугольник (рис. 215, б), тогда
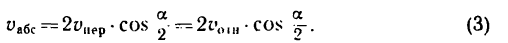
Задача №7
Вертикально падающие капли дождя оставляют на боковых стеклах автомобиля полосы под углом 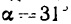 к вертикали. Скорость движения автомобиля 40 км’ч. Определить, с какой скоростью надают капли дождя.
к вертикали. Скорость движения автомобиля 40 км’ч. Определить, с какой скоростью надают капли дождя.
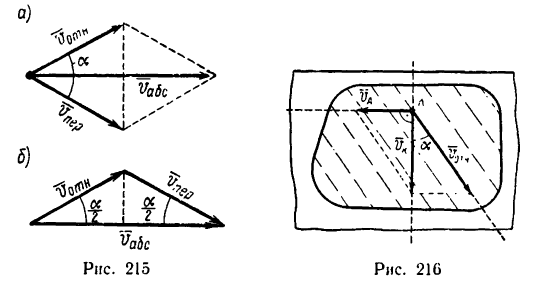
Решение.
1. Изобразим движение капли дождя на рисунке (рис. 216). Капли падают вертикально, следовательно, скорость ик какой-либо капли К относительно Земли является скоростью абсолютного (составного) движения. И эту скорость 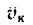 можно представить в виде геометрической суммы горизонтально направленной переносной скорости автомобиля
можно представить в виде геометрической суммы горизонтально направленной переносной скорости автомобиля 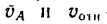 — относительно скорости капли при ее движении по стеклу автомобиля.
— относительно скорости капли при ее движении по стеклу автомобиля.
2. Получившийся параллелограмм скоростей диагональ делит на два прямоугольных треугольника. Рассмотрев любой из этих треугольников, найдем
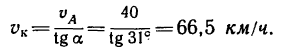
Переводим полученную скорость падения капель в м/сек:
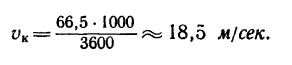
Задача №8
От одного берега реки к другому плывет лодка, держа курс перпендикулярно к берегам. Ширина реки 800 м лодка достигает противоположного берега через 12 мин после начала переправы. За это время лодку сносит вниз по течению на расстояние 600 м. Определить скорость течения реки; собственную скорость лодки: скорость лодки относительно берегов. Скорость течения у берегов и на середине реки считать одинаковой.
Решение.
1. Изобразим на рисунке движение лодки (рис. 217). Представим, что лодка отплывает из точки А на правом берегу. Если бы
не было течения, она достигла бы противоположного берега в точке В; известно, что ширина реки 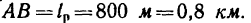 Но лодку сносит вниз по течению (переносное движение) на расстояние
Но лодку сносит вниз по течению (переносное движение) на расстояние 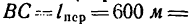 0,6 км и поэтому движение лодки относительно берегов (абсолютное движение) происходит но прямой АС.
0,6 км и поэтому движение лодки относительно берегов (абсолютное движение) происходит но прямой АС.
Обозначим точкой L положение лодки через некоторое время после начала движения. Скорость лодки относительно берегов — абсолютная скорость 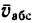 — направлена вдоль прямой АС и складывается из собственной скорости
— направлена вдоль прямой АС и складывается из собственной скорости 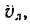 сообщаемой гребным винтом или веслами, и из переносной скорости течения реки
сообщаемой гребным винтом или веслами, и из переносной скорости течения реки 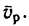
2. Допустим, что нет течения реки, тогда лодка будет перемещаться относительно берегов так же, как и относительно воды, по прямой АВ и ее движение опишется уравнением
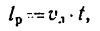
где t — время переправы (t=12 мин =0,2 ч).
Отсюда находим собственную скорость лодки (скорость лодки относительно воды — относительную скорость)
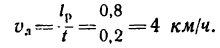
3. Если лодка будет плыть, подчиняясь только течению реки, ее движение опишется уравнением
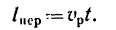
Из этого уравнения найдем скорость течения реки:
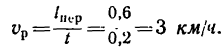
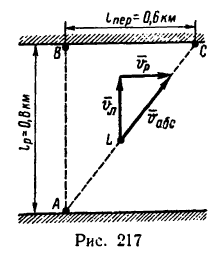
4. Теперь из прямоугольного треугольника скоростей (см. рис. 217) легко найти скорость лодки относительно берегов — абсолютную скорость:
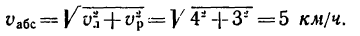
Задача №9
Трассы двух воздушных лайнеров пересекаются над поселком А. Первый лайнер летит точно на север, второй лайнер — на юго-восток. Скорости 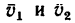 обоих лайнеров численно равны (
обоих лайнеров численно равны (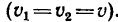 ). Определить, чему равна и как направлена в этот момент скорость второго лайнера относительно первого.
). Определить, чему равна и как направлена в этот момент скорость второго лайнера относительно первого.
Решение 1—методом «остановки» одного из тел.
1. Обозначим точкой А поселок, над которым” в определенный момент находятся оба лайнера. Покажем страны света: С —север, Ю — юг, В —восток и 3 —запад. Изобразим скорости лайнеров относительно Земли: 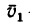 —скорость первого лайнера и
—скорость первого лайнера и 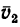 — скорость второго (рис. 218, а).
— скорость второго (рис. 218, а).
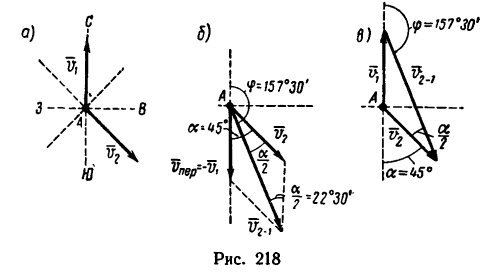
2. Так как нужно определить скорость второго лайнера относительно первого, то мысленно первый лайнер остановим над пунктом А, а воздушной среде вместе со вторым лайнером сообщим скорость 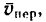 но в обратную сторону по отношению к скорости
но в обратную сторону по отношению к скорости 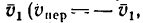 рис. 218, б). Тогда скорость
рис. 218, б). Тогда скорость 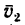 второго лайнера приобретет значение относительной скорости (скорости относительно перемещающейся воздушной среды).
второго лайнера приобретет значение относительной скорости (скорости относительно перемещающейся воздушной среды).
3. Сложив по правилу параллелограмма скорости 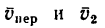 (см. рис. 218, б), получим скорость
(см. рис. 218, б), получим скорость 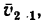 ( изображающую скорость второго лайнера по отношению к первому.
( изображающую скорость второго лайнера по отношению к первому.
4. Так как скорости лайнеров 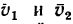 численно равны
численно равны 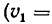
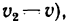 то параллелограмм скоростей на рис. 218, б — ромб и, следовательно [см. формулу (3) в начале этого параграфа], числовое значение
то параллелограмм скоростей на рис. 218, б — ромб и, следовательно [см. формулу (3) в начале этого параграфа], числовое значение 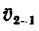 равно:
равно:
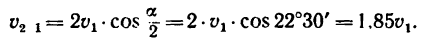
Таким образом, второй лайнер движется относительно первого со скоростью, численно равной и, как видно из рис. 218, б, удаляется от него на юго-юго-запад, т. е. под углом 157°30′ (903 + 45° + 22‘30′) к направлению скорости первого лайнера.
* Когда будет определен этот угол, его нужно сравнить с углом между векторами 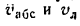 из предыдущей задачи.
из предыдущей задачи.
Решение 2 —методом разности скоростей.
1. Из выражения геометрической суммы скоростей
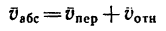
следует, что

2. Для определения скорости второго лайнера относительно первого примем за абсолютную скорость 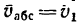 — скорость первого лайнера и за переносную скорость
— скорость первого лайнера и за переносную скорость 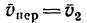 – скорость второго лайнера; тогда искомую относительную скорость
– скорость второго лайнера; тогда искомую относительную скорость 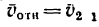 получим как разность (см. рис. 3)
получим как разность (см. рис. 3)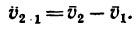
3. Чтобы произвести вычитания векторов, необходимо конец вычитаемого вектора  соединить с концом уменьшаемого вектора
соединить с концом уменьшаемого вектора 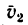 в направлении от первого ко второму искомым вектором
в направлении от первого ко второму искомым вектором 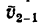 (рис. 218, в).
(рис. 218, в).
4. В результате построения имеем равнобедренный треугольник скоростей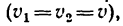 из которого легко найти, что числовое значение
из которого легко найти, что числовое значение
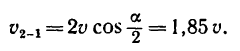
Угол 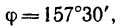 определяющий в данный момент направление вектора
определяющий в данный момент направление вектора 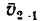 относительно
относительно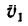 определяется непосредственно по рис. 218, в.
определяется непосредственно по рис. 218, в.
Задача №10
В кривошипно-кулисном механизме с поступательно движущейся кулисой ВС кривошип ОА (расположенный позади кулисы) длиной l= 400 мм вращается с постоянной угловой скоростью 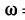 =10 рад/сек. Концом А, соединенным шарнирно с камнем, скользящим в прорези кулисы, кривошип сообщает кулисе ВС возвратно-поступательное движение. Определить скорость кулисы в момент, когда кривошип образует с осью кулисы угол
=10 рад/сек. Концом А, соединенным шарнирно с камнем, скользящим в прорези кулисы, кривошип сообщает кулисе ВС возвратно-поступательное движение. Определить скорость кулисы в момент, когда кривошип образует с осью кулисы угол 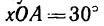 (рис. 219, а).
(рис. 219, а).
Решение.
1. В данном случае движение точки А вместе с кривошипом можно считать сложным, т. е. получающимся в результате сложения:
а) движения точки А вместе с кулисой в ее возвратно-поступательном (переносном) движении вдоль оси х;
б) относительного движения точки А вместе с камнем, движущимся возвратно-поступательно в прорези кулисы в направлении, перпендикулярном к оси х.
2. Абсолютная скорость точки А, модуль которой легко определяется по формуле 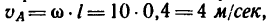 направлена перпендикулярно к кривошипу ОА. Переносная скорость точки А равна поступательной скорости кулисы
направлена перпендикулярно к кривошипу ОА. Переносная скорость точки А равна поступательной скорости кулисы  направлена по прямой АО (рис. 219, б). Относительная скорость
направлена по прямой АО (рис. 219, б). Относительная скорость  точки А, равная скорости камня в прорези кулисы, направлена по прямой Ас.
точки А, равная скорости камня в прорези кулисы, направлена по прямой Ас.
3. Изобразим скорость 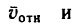
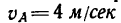 вектором, перпендикулярным к ОА. Разложим ее на составляющие уоти и
вектором, перпендикулярным к ОА. Разложим ее на составляющие уоти и 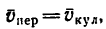 как показано на рис. 219, б. Вектор
как показано на рис. 219, б. Вектор 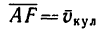 изображает искомую скорость кулисы.
изображает искомую скорость кулисы.
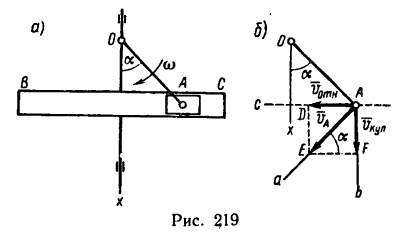
4. 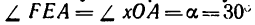 (как углы с взаимно перпендикулярными сторонами) и, следовательно,
(как углы с взаимно перпендикулярными сторонами) и, следовательно,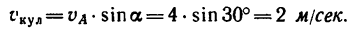
Таким образом, в данный момент кулиса перемещается вниз со скоростью 2 м,сек.
Чтобы лучше проанализировать движение кулисы, необходимо знать, когда кулиса двигается ускоренно, когда замедленно, при каких положениях кривошипа кулиса имеет максимальную скорость и чему равна эта скорость, при каких положениях кривошипа скорость кулисы равна нулю?
Следующие задачи рекомендуется решить самостоятельно.
Задача №11
Кривошип 0С=30 см вращается равномерно с угловой скоростью 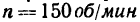 и приводит в возвратно-поступательное движение кулису АВ при помощи ползуна С, передвигающегося в прорези кулисы. Определить скорость
и приводит в возвратно-поступательное движение кулису АВ при помощи ползуна С, передвигающегося в прорези кулисы. Определить скорость 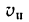 ползуна в прорези кулисы и скорость
ползуна в прорези кулисы и скорость 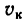 самой кулисы в тот момент, когда кривошип составляет с горизонталью угол а = 35° (рис. 220). Ответ.
самой кулисы в тот момент, когда кривошип составляет с горизонталью угол а = 35° (рис. 220). Ответ. 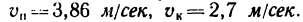
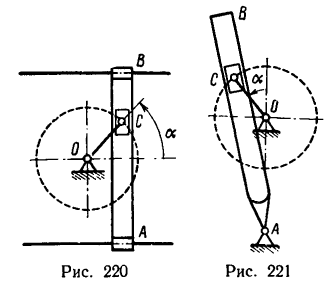
Задача 187-37. Кривошип ОС = 20 см вращается равномерно с угловой скоростью n = 180 об/мин и приводит в движение качающуюся кулису АВ при помощи ползуна С, двигающегося в прорези кулисы. Определить скорость 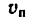 ползуна в прорези кулисы и угловую скорость
ползуна в прорези кулисы и угловую скорость  кулисы в тот момент, когда кривошип составляет с вертикалью угол а=40°. Расстояние /40 = 40 см (рис. 221).
кулисы в тот момент, когда кривошип составляет с вертикалью угол а=40°. Расстояние /40 = 40 см (рис. 221).
Ответ. 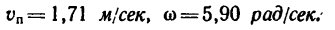
Сложное движение точки в плоскости
постановка задачи. Геометрическая фигура вращается вокруг оси, перпендикулярной ее плоскости по известному закону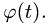 . В канале, расположенном на фигуре, движется точка М по закону
. В канале, расположенном на фигуре, движется точка М по закону 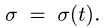 Найти абсолютную скорость и абсолютное ускорение точки в заданный момент времени
Найти абсолютную скорость и абсолютное ускорение точки в заданный момент времени 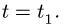
План решения:
Сложное движение точки М представляется в виде суммы относительного и переносного. Характерной особенностью этой задачи является то, что траектории относительного, переносного и абсолютного движения лежат в одной плоскости. Ось z, на которую проектируются векторы переносной угловой скорости и переносного углового ускорения, перпендикулярна этой плоскости и направлена на наблюдателя. Угол поворота считается положительным, если со стороны оси 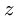 он виден против часовой стрелки.
он виден против часовой стрелки.
Искомые величины получаем из векторных равенств:
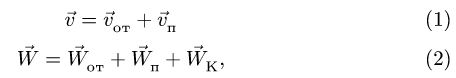
где 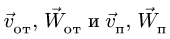 — соответственно относительные и переносные скорости и ускорения:
— соответственно относительные и переносные скорости и ускорения: 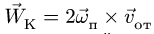 — ускорение Кориолиса .
— ускорение Кориолиса .
1. Вычисляем значение дуговой координаты 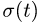 при
при 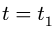 и определяем положение точки в подвижной системе координат.
и определяем положение точки в подвижной системе координат.
2. Дифференцируя 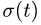 по времени, находим относительную скорость (скорость точки относительно фигуры):
по времени, находим относительную скорость (скорость точки относительно фигуры):
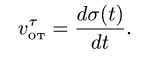
 Кориолис Гаспар Гюстав (1792-1843) французский механик и математик.
Кориолис Гаспар Гюстав (1792-1843) французский механик и математик.
Вектор 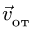 направляем по касательной к относительной траектории в сторону увеличения
направляем по касательной к относительной траектории в сторону увеличения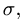 , если
, если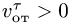 и в обратную сторону в противном случае;
и в обратную сторону в противном случае; 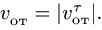
3. Вычисляем радиус траектории переносного движения 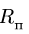 — расстояние от точки М в положении
— расстояние от точки М в положении 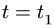 до оси переносного вращения.
до оси переносного вращения.
4. Находим переносную скорость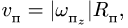 где переносная угловая скорость
где переносная угловая скорость
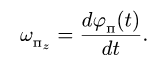
Вектор 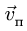 направляем перпендикулярно
направляем перпендикулярно 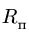 в сторону переносного вращения.
в сторону переносного вращения.
5. Определяем вектор абсолютной скорости, вычисляя компоненты 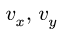 векторной суммы (1) на произвольно выбранные оси, и модуль
векторной суммы (1) на произвольно выбранные оси, и модуль
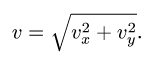
6. Вычисляем относительное ускорение. В случае криволинейной относительной траектории
где 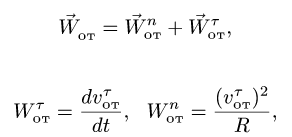
R — радиус кривизны относительной траектории в точке М. Для прямолинейной траектории относительного движения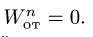 Вектор
Вектор 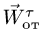 направляем по касательной к относительной траектории, вектор
направляем по касательной к относительной траектории, вектор 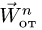 — к центру кривизны этой же кривой.
— к центру кривизны этой же кривой.
7. Вычисляем переносное ускорение:
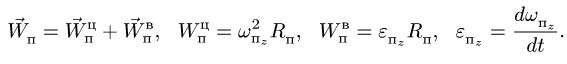
Вектор 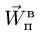 направляем перпендикулярно
направляем перпендикулярно 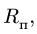 , вектор
, вектор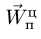 — к оси переносного вращения (вдоль
— к оси переносного вращения (вдоль 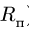 ).
).
8. Находим ускорение Кориолиса 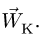 Так как в задачах этого типа вектор переносной угловой скорости перпендикулярен вектору относительной скорости, то
Так как в задачах этого типа вектор переносной угловой скорости перпендикулярен вектору относительной скорости, то 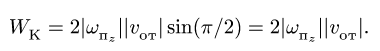
Направление вектора ускорения Кориолиса можно определить по правилу Жуковского 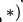 поворотом на 90° вектора относительной скорости по направлению переносного вращения. В результате вектор ускорения Кориолиса в таких задачах будет лежать на одной прямой с
поворотом на 90° вектора относительной скорости по направлению переносного вращения. В результате вектор ускорения Кориолиса в таких задачах будет лежать на одной прямой с 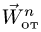 при криволинейном относительном движении, а в случае прямолинейного относительного движения
при криволинейном относительном движении, а в случае прямолинейного относительного движения 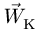 перпендикулярен относительной траектории.
перпендикулярен относительной траектории.
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат. Модуль абсолютного ускорения 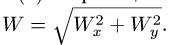
Задача №12
Прямоугольник ABCD вращается вокруг оси, проходящей через вершину А, по закон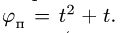 Ось вращения перпендикулярна плоскости прямоугольника (рис. 109). По круговому каналу радиуса R = 10 см с центром в точке С, расположенному на прямоугольнике, движется точка М. Дуговая координата точки меняется по закону
Ось вращения перпендикулярна плоскости прямоугольника (рис. 109). По круговому каналу радиуса R = 10 см с центром в точке С, расположенному на прямоугольнике, движется точка М. Дуговая координата точки меняется по закону 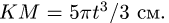 Дано: АВ = 12 см, ВС = 15
Дано: АВ = 12 см, ВС = 15 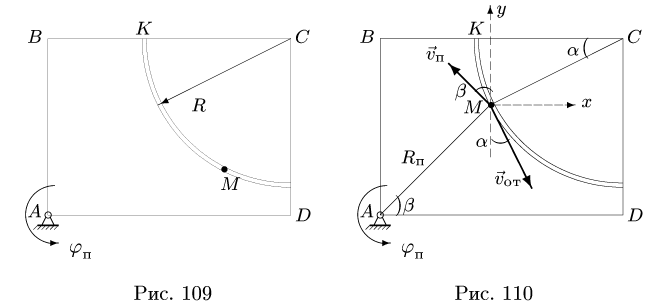
Найти абсолютную скорость и абсолютное ускорение точки М при 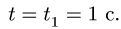
Решение
Движение точки М представим в виде относительного движения по круговому каналу и переносного движения вместе с вращающимся прямоугольником.
1. Вычисляем значение дуговой координаты 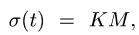 при
при
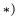 Жуковский Николай Егорович (1847-1921) русский ученый, основоположник гидроаэродинамики. Преподавал теоретическую механику в МГУ. Правило Жуковского для общего случая см. с. 204
Жуковский Николай Егорович (1847-1921) русский ученый, основоположник гидроаэродинамики. Преподавал теоретическую механику в МГУ. Правило Жуковского для общего случая см. с. 204
Гл.9.Сложное движение точки
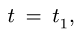 и определяем положение точки в подвижной системе координат. За время
и определяем положение точки в подвижной системе координат. За время 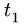 точка проходит по дуге окружности путь
точка проходит по дуге окружности путь 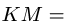
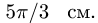 Центральный угол, соответствующий этой дуге,
Центральный угол, соответствующий этой дуге, 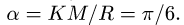 Изображаем точку в этом положении (рис.110).
Изображаем точку в этом положении (рис.110).
2. Дифференцируя 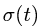 по времени, находим относительную скорость. Находим ее значение при t = 1с:
по времени, находим относительную скорость. Находим ее значение при t = 1с:
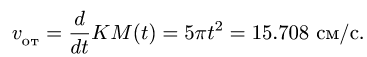
Вектор  направлен по касательной к окружности.
направлен по касательной к окружности.
3. Вычисляем радиус траектории переносного движения 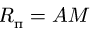
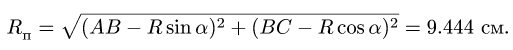
4. Находим переносную скорость 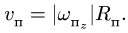 Переносной скоростью точки является скорость точки прямоугольника, совпадающей в данный момент с М
Переносной скоростью точки является скорость точки прямоугольника, совпадающей в данный момент с М  .Угловая скорость фигуры, при t =1с,
.Угловая скорость фигуры, при t =1с,
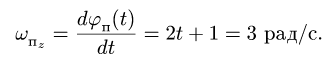
Отсюда 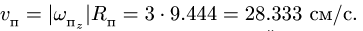
5. Определяем вектор абсолютной скорости по формуле (1). Модуль абсолютной скорости 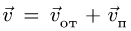 находим, проецируя
находим, проецируя
это равенство на неподвижные оси координат х, у (можно воспользоваться также теоремой косинусов):
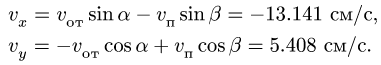
Тригонометрические функции угла 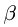 вычисляем по формулам
вычисляем по формулам
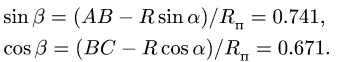
Модуль абсолютной скорости 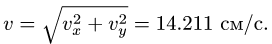
 Иногда переносная скорость обозначается
Иногда переносная скорость обозначается 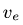 (от французского слова emporter), реже
(от французского слова emporter), реже 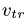 (от английского слова transport), а относительная —
(от английского слова transport), а относительная — 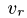 (от английского слова relativ). Эти же индексы используются и для других компонентов сложного движения.
(от английского слова relativ). Эти же индексы используются и для других компонентов сложного движения.
6. Вычисляем относительное ускорение. Ускорение точки, движущейся относительно прямоугольника по окружности, имеет нормальную и тангенциальную составляющую:
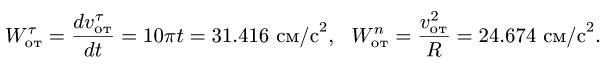
Модуль относительного ускорения
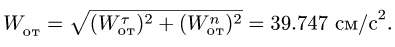
Вектор ускорения 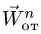 направляем по радиусу окружности к точке
направляем по радиусу окружности к точке 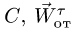 — по касательной, в сторону увеличения дуги КМ, так как
— по касательной, в сторону увеличения дуги КМ, так как 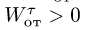 (рис.11)
(рис.11)
7. Вычисляем переносное ускорение 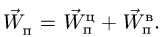 Траектория переносного движения точки — окружность радиуса
Траектория переносного движения точки — окружность радиуса 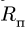 с центром А. Прямоугольник вращается с угловой скоростью
с центром А. Прямоугольник вращается с угловой скоростью 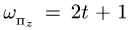 и угловым ускорением
и угловым ускорением
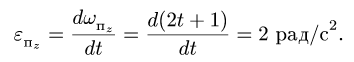
Отсюда получаем
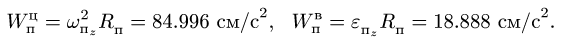
Вектор 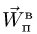 направлен против часовой стрелки перпендикулярно радиусу
направлен против часовой стрелки перпендикулярно радиусу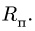 Вектор
Вектор 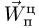 — к центру А. Модуль переносного ускорения
— к центру А. Модуль переносного ускорения
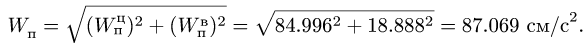
8. Находим ускорение Кориолиса 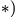 . Модуль вектора ускорения
. Модуль вектора ускорения 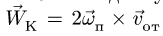 определяем по формуле
определяем по формуле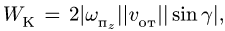 где
где 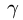 — угол между
— угол между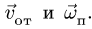 Вектор
Вектор 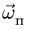 перпендикулярен плоскости чертежа, следовательно, угол
перпендикулярен плоскости чертежа, следовательно, угол 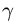 равен 90°. Имеем
равен 90°. Имеем
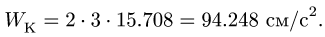
Направление вектора ускорения Кориолиса получаем по правилу Жуковского — поворотом на 90° вектора относительной скорости
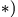 Это ускорение называют иногда поворотным, а в англоязычной литературе — supplementary (дополнительным).
Это ускорение называют иногда поворотным, а в англоязычной литературе — supplementary (дополнительным).
по направлению переносного вращения, т.е. против часовой стрелки (рис. 112).
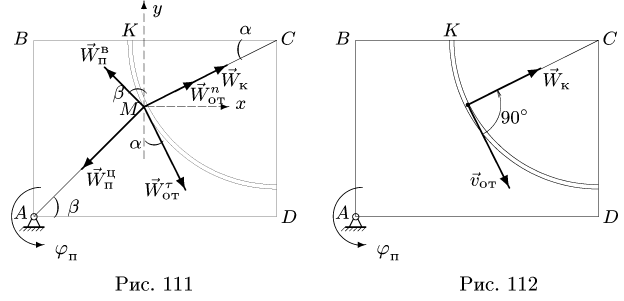
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат (рис. 111):
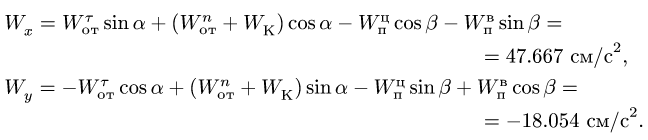
Находим модуль ускорения: 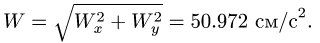
Ответы заносим в таблицу. Радиус траектории переносного движения — в см, скорости — в см/с, ускорения — в 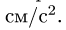

Сложное движение точки в пространстве
Постановка Задачи. Геометрическая фигура вращается по заданному закону вокруг неподвижной оси, лежащей в ее плоскости. По каналу, расположенному на фигуре, движется точка М по известному закону 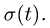 Найти абсолютную скорость и абсолютное ускорение точки.
Найти абсолютную скорость и абсолютное ускорение точки.
План решения:
Искомые величины получаем из векторных равенств
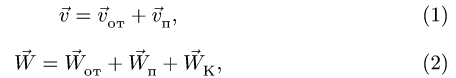
где 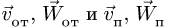 — соответственно относительные и переносные скорости и ускорения;
— соответственно относительные и переносные скорости и ускорения; 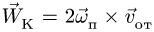 — ускорение Кориолиса. Решение задачи о сложном движении точки в пространстве отличается от аналогичной задачи, где точка движется в плоскости (с. 195) тем, что векторные суммы для абсолютных величин вычисляются по трем компонентам, а ускорение Кориолиса содержит синус угла между вектором переносной угловой скорости и относительной скоростью. Относительная скорость в этих задачах всегда перпендикулярна переносной, что упрощает вычисление модуля их суммы.
— ускорение Кориолиса. Решение задачи о сложном движении точки в пространстве отличается от аналогичной задачи, где точка движется в плоскости (с. 195) тем, что векторные суммы для абсолютных величин вычисляются по трем компонентам, а ускорение Кориолиса содержит синус угла между вектором переносной угловой скорости и относительной скоростью. Относительная скорость в этих задачах всегда перпендикулярна переносной, что упрощает вычисление модуля их суммы.
1. Вычисляем значение дуговой координаты 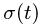 при
при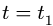 и определяем положение точки в подвижной системе координат.
и определяем положение точки в подвижной системе координат.
2. Дифференцируя 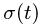 по времени, находим величину относительной скорости
по времени, находим величину относительной скорости 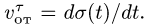 Вектор
Вектор 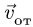 направляем по касательной к относительной траектории в сторону увеличения
направляем по касательной к относительной траектории в сторону увеличения 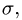 если
если 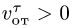 и в обратную сторону в противном случае;
и в обратную сторону в противном случае; 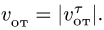
3. Вычисляем радиус траектории переносного движения 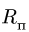 — расстояние от точки М в расчетном положении до оси переносного вращения.
— расстояние от точки М в расчетном положении до оси переносного вращения.
4. Находим модуль переносной скорости 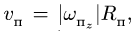 где переносная угловая скорость
где переносная угловая скорость 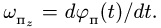 Вектор
Вектор 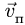 располагается в плоскости перпендикулярной оси вращения и направлен перпендикулярно
располагается в плоскости перпендикулярной оси вращения и направлен перпендикулярно 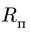 в сторону переносного вращения.
в сторону переносного вращения.
5. Определяем величину абсолютной скорости 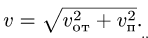
6. Вычисляем относительное ускорение. В случае криволинейной относительной траектории
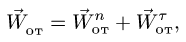
где 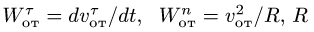 — радиус кривизны относительной траектории в точке М. Для прямолинейной траектории относительного движения
— радиус кривизны относительной траектории в точке М. Для прямолинейной траектории относительного движения 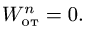 Вектор
Вектор 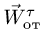 направляем по касательной к относительной траектории, вектор
направляем по касательной к относительной траектории, вектор 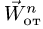 — к центру кривизны этой же кривой.
— к центру кривизны этой же кривой.
7. Вычисляем переносное ускорение:
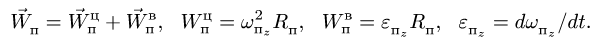
Вектор 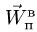 направляем перпендикулярно
направляем перпендикулярно 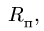 вектор
вектор 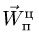 — к оси переносного вращения (вдоль
— к оси переносного вращения (вдоль 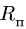 ).
).
8. Величину вектора ускорения Кориолиса определяем по формуле
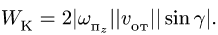
Направление вектора ускорения Кориолиса можно определить по правилу Н.Е. Жуковского поворотом на 90° проекции вектора относительной скорости на плоскость, перпендикулярную 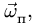 по направлению переносного вращения.
по направлению переносного вращения.
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат. Ось 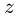 направляем по оси вращения. Модуль абсолютного ускорения
направляем по оси вращения. Модуль абсолютного ускорения
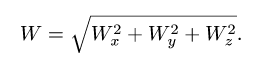
- Заказать решение задач по теоретической механике
Задача №13
Прямоугольник ABCD вращается вокруг неподвижной оси, проходящей по стороне DC (рис. 113). По круговому каналу радиуса R = 12 см с центром в точке О, расположенному на прямоугольнике, движется точка М по закону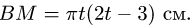 Найти абсолютную скорость и абсолютное ускорение точки при
Найти абсолютную скорость и абсолютное ускорение точки при 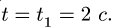
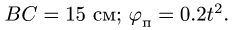
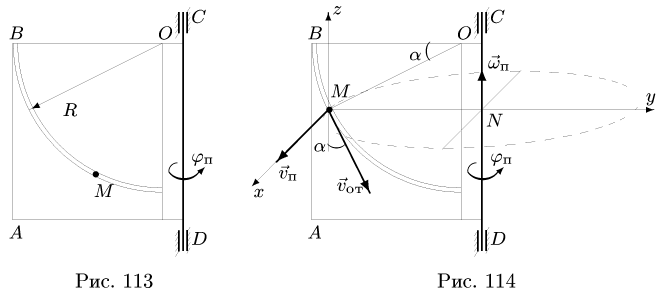
Решение
1. Вычисляем значение дуговой координаты 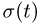 при
при 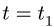 и определяем положение точки в подвижной системе координат:
и определяем положение точки в подвижной системе координат:
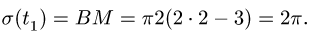
Находим центральный угол, соответствующий дуге ВМ:
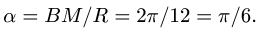
Изображаем точку в этом положении (рис. 114).
9.2.Сложное движение точки в пространстве
2. Дифференцируя 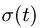 по времени, находим относительную скорость:
по времени, находим относительную скорость:
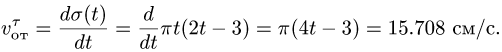
3. Траекторией переносного движения является окружность с центром N. Относительна скорость точки М направлена по касательной к этой окружности. Траектория лежит в плоскости ху, перпендикулярной к оси вращения 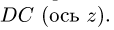 Находим радиус окружности:
Находим радиус окружности:
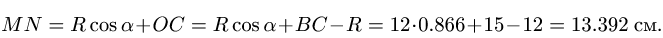
4. Находим переносную скорость. Вычисляем угловую скорость вращения прямоугольника ABCD:
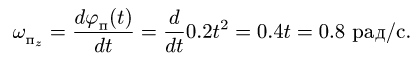
Вычисляем переносную скорость
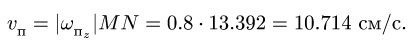
5. Определяем величину абсолютной скорости. Вектор 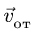 лежит в плоскости
лежит в плоскости 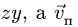 направлен по оси х, следовательно, они перпендикулярны. Модуль скорости
направлен по оси х, следовательно, они перпендикулярны. Модуль скорости
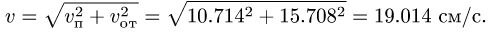
6. Вычисляем относительное ускорение. Находим нормальную составляющую ускорения точки, движущейся по окружности радиуса R:
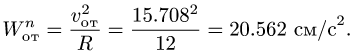
Тангенциальная составляющая
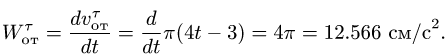
Оба вектора лежат в плоскости 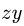 (рис.115.),
(рис.115.),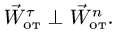
7. Вычисляем компоненты переносного ускорения. Прямоугольник вращается с угловой скоростью 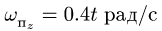 и угловым ускорением
и угловым ускорением
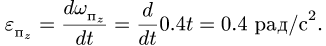
Получаем

Вектор 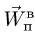 направлен по оси х, вектор
направлен по оси х, вектор 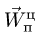 — к оси вращения вдоль оси у.
— к оси вращения вдоль оси у.
8. Величину вектора ускорения Кориолиса определяем по формуле 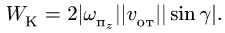 Вектор
Вектор 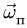 всегда направлен по оси вращения в ту сторону, откуда вращение видно против часовой стрелки. В нашем случае — вверх.
всегда направлен по оси вращения в ту сторону, откуда вращение видно против часовой стрелки. В нашем случае — вверх.
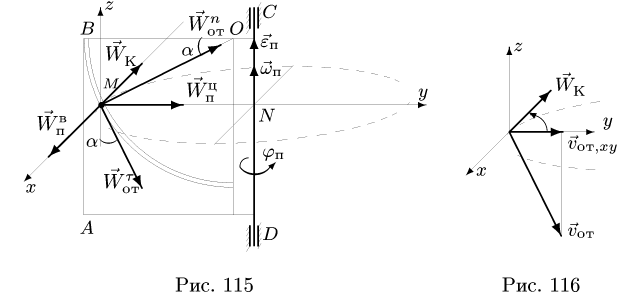
Угол 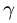 между
между 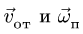 равен 150°. Определяем
равен 150°. Определяем
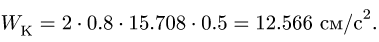
Для того, чтобы найти направление вектора ускорения Кориолиса, воспользуемся правилом Жуковского (рис. 116). Проецируем вектор относительной скорости 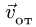 на плоскость перпендикулярную оси вращения, т.е. на плоскость ху. Повернув проекцию
на плоскость перпендикулярную оси вращения, т.е. на плоскость ху. Повернув проекцию 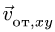 по направлению переносного вращения на 90°, получаем направление вектора ускорения Кориолиса. Вектор
по направлению переносного вращения на 90°, получаем направление вектора ускорения Кориолиса. Вектор 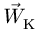 лежит на оси х и направлен в сторону отрицательных значений.
лежит на оси х и направлен в сторону отрицательных значений.
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат:
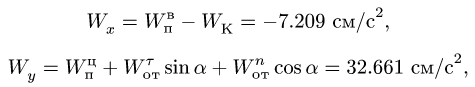
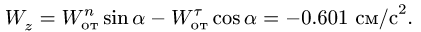
Окончательно, абсолютное ускорение точки М
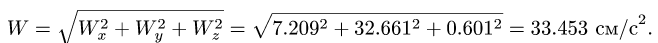
Ответы заносим в таблицу. Радиус траектории переносного движения — в см, скорости — в см/с, ускорения — в 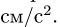

Движение точки по звену механизма
Постановка Задачи. Плоский шарнирно-стержневой механизм приводится в движение кривошипом, который вращается с заданной угловой скоростью. Вдоль одного из стержней по известному закону движется тючка М. Найти абсолютную скорость и абсолютное ускорение точки М.
План решения:
Представляем движение точки в виде суммы относительного движения по звену механизма и переносного движения вместе со звеном.
1. Вводим неподвижную систему координат ху, совмещая се начало с положением одного из шарниров механизма в заданный момент времени. Вдоль стержня, по которому движется точка, располагаем подвижную ось 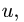 направляя ее в сторону движения точки. Зная закон относительного движения
направляя ее в сторону движения точки. Зная закон относительного движения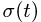 (он задан в условии), определяем положение точки относительно звена и неподвижных осей ху в расчетный момент. Определяем координаты х и у шарниров.
(он задан в условии), определяем положение точки относительно звена и неподвижных осей ху в расчетный момент. Определяем координаты х и у шарниров.
2. Дифференцируя 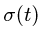 по времени, находим проекции относительной скорости и относительного ускорения на ось и:
по времени, находим проекции относительной скорости и относительного ускорения на ось и:
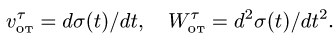
Зная угол между осями 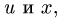 находим проекции векторов
находим проекции векторов 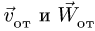 на оси ху.
на оси ху.
3. Решаем задачу о скоростях точек многозвенного механизма, используя аналитические методы (§ 8.3, с. 179, § 8.5, с. 188). Вычисляем вектор скорости той точки механизма, в которой в данный момент находится подвижная точка М. Эта скорость является переносной скоростью для точки М.
4. Определяем вектор абсолютной скорости, 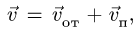 и его модуль,
и его модуль,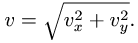
5. Решаем задачу об ускорениях точек многозвенного механизма, используя аналитические методы (§ 8.4, с. 183, § 8.5, с. 188). Вычисляем вектор ускорения той точки механизма, в которой в данный момент находится подвижная точка М. Это ускорение является переносным для точки М.
6. Находим ускорение Кориолиса:
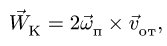
где 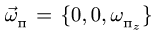 — вектор угловой скорости звена, по которому движется точка.
— вектор угловой скорости звена, по которому движется точка.
7. Находим абсолютное ускорение, 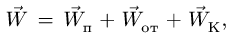 и его модуль:
и его модуль: 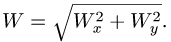
Задача №14
Плоский шарнирно-стержневой механизм ОABC приводится в движение кривошипом OA =60 см, который вращается с постоянной угловой скоростью 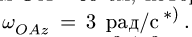 Вдоль стержня АВ движется точка М по закону
Вдоль стержня АВ движется точка М по закону 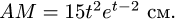
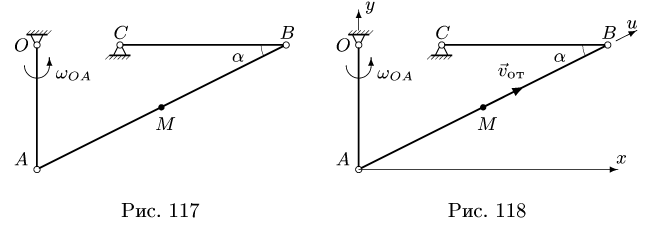
Положение механизма при 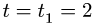 с указано на рис. 117; АВ =120 см, ВС =80 см,
с указано на рис. 117; АВ =120 см, ВС =80 см, 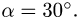 Найти абсолютную скорость и абсолютное ускорение точки М в этот момент.
Найти абсолютную скорость и абсолютное ускорение точки М в этот момент.
Решение
Абсолютное движение точки представляем в виде суммы относительного движения по звену АВ и переносного движения вместе с ним. Переносные скорость и ускорение являются соответственно скоростью и ускорением той точки звена, в которой в данный момент располагается точка М.
1. Вводим неподвижную систему координат ху, совмещая ее начало с положением шарнира А механизма в заданный момент времени. Вдоль стержня АВ, по которому движется точка, располагаем подвижную ось 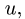 направляя ее в сторону движения точки (рис. 118). Зная закон относительного движения
направляя ее в сторону движения точки (рис. 118). Зная закон относительного движения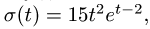 определяем положение точки относительно звена при t = 2 с:
определяем положение точки относительно звена при t = 2 с: 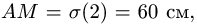 т.е. точка находится в центре звена АВ. Определяем координаты шарниров в неподвижных осях координат:
т.е. точка находится в центре звена АВ. Определяем координаты шарниров в неподвижных осях координат:
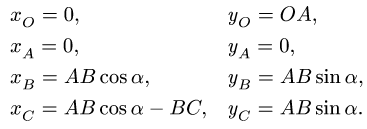
 Проекция угловой скорости на ось
Проекция угловой скорости на ось 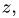 перпендикулярную плоскости чертежа,
перпендикулярную плоскости чертежа, 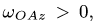 следовательно, кривошип вращается против часовой стрелки.
следовательно, кривошип вращается против часовой стрелки.
2. Дифференцируя 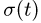 по времени, находим проекции относительной скорости и относительного ускорения на ось
по времени, находим проекции относительной скорости и относительного ускорения на ось 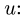
Угол между осями  равен
равен 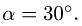 Находим проекции:
Находим проекции:
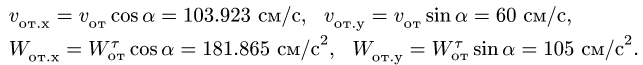
3. Решаем задачу о скоростях точек многозвенного механизма, используя уравнения трех угловых скоростей (§ 8.3, с. 179):
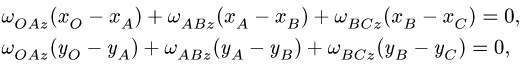
где по условию 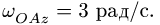 Решаем систему двух уравнений относительно
Решаем систему двух уравнений относительно 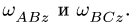 Подставляя численные значения, получаем
Подставляя численные значения, получаем 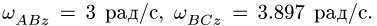 Скорость
Скорость 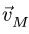 определяем из
определяем из
равенства 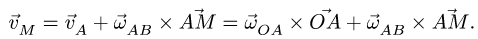
Переписываем это равенство в виде
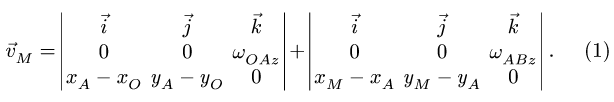
Получаем
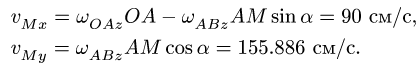
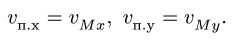
Модуль переносной скорости 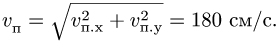
4. Определяем проекции.
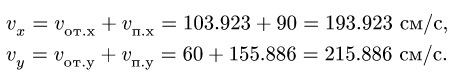
и модуль абсолютной скорости: 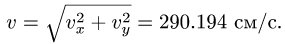
5. Решаем задачу об ускорениях точек многозвенного механизма, используя уравнения трех угловых ускорений (уравнение (2), с. 184), где 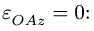
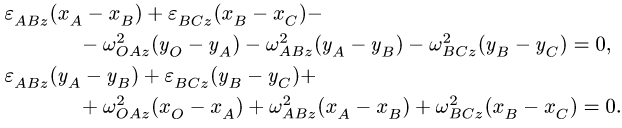
Находим 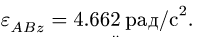 Вычисляем вектор ускорения той точки механизма, в которой в данный момент находится подвижная точка М. Это ускорение является переносным для точки М. Учитывая, что
Вычисляем вектор ускорения той точки механизма, в которой в данный момент находится подвижная точка М. Это ускорение является переносным для точки М. Учитывая, что 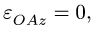 записываем векторное равенство
записываем векторное равенство
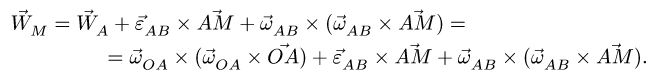
Раскрывая векторные произведения по аналогии с (1), вычисляем
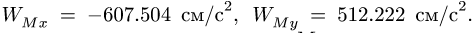 Это ускорение является переносным для точки М:
Это ускорение является переносным для точки М:
Модуль переносного ускорения 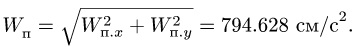
6. Находим ускорение Кориолиса 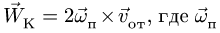 — вектор угловой скорости звена АВ, по которому движется точка:
— вектор угловой скорости звена АВ, по которому движется точка:
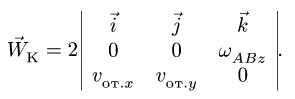
Вычисляем
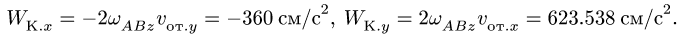
Модуль ускорения Кориолиса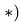
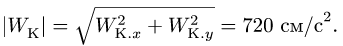
7. Вычисляем абсолютное ускорение 
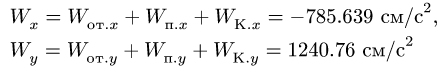
и его модуль 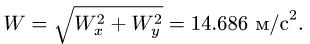
Результаты заносим в таблицу. Скорости в м/с, ускорения — в 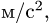 угловая скорость — в рад/с, угловое ускорение — в
угловая скорость — в рад/с, угловое ускорение — в 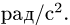

Механизм с муфтой
Постановка Задами. Плоский механизм с одной степенью свободы состоит из шарнирно соединенных стержней и муфты, скользящей по направляющему стержню и шарнирно закрепленной на другом стержне или на неподвижном шарнире. Задана угловая скорость ведущего звена механизма. Найти скорость муфты относительно направляющего стержня.
План решения:
1. Представляем движение муфты М в виде суммы относительного движения по направляющему стержню механизма и переносного движения вместе с этим стержнем. Траекторией относительного движения муфты является прямая. Задачу решаем, используя координатную запись векторных соотношений для скоростей при плоском движении. Выбираем систему координат и определяем координаты всех шарниров механизма и муфты.
2. Мысленно снимаем муфту с механизма и находим скорости шарниров и угловые скорости звеньев получившегося механизма (§ 8.1, с. 158, § 8.3, с. 179, § 8.5, с. 188).
3. Записываем уравнение сложения скоростей: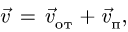 где абсолютная скорость
где абсолютная скорость 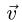 или относительная скорость
или относительная скорость 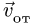 выражается через скорости шарниров механизма. Составляем уравнение
выражается через скорости шарниров механизма. Составляем уравнение
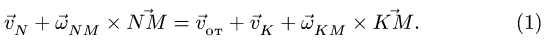
Это векторное уравнение содержит две неизвестные величины. Одна из них — искомый модуль вектора относительной скорости 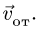 Направление этого вектора всегда известно и задается направлением стержня, по которому скользит муфта
Направление этого вектора всегда известно и задается направлением стержня, по которому скользит муфта 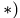 . В зависимости от варианта задачи второй неизвестной может быть угловая скорость
. В зависимости от варианта задачи второй неизвестной может быть угловая скорость 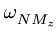 или
или 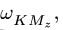 где N и К — точки механизма с известными скоростями.
где N и К — точки механизма с известными скоростями.
Если муфта скользит по стержню КМ, угловая скорость 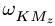 которого известна, то неизвестной величиной будет угловая скорость
которого известна, то неизвестной величиной будет угловая скорость 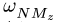 звена, шарнирно соединяющего муфту с неподвижной точкой
звена, шарнирно соединяющего муфту с неподвижной точкой 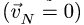 или с шарниром N механизма с известной скоростью.
или с шарниром N механизма с известной скоростью.
Если муфта шарнирно закреплена на стержне NM с известной угловой скоростью 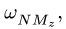 то неизвестной величиной будет угловая скорость
то неизвестной величиной будет угловая скорость 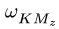 звена, по которому скользит муфта, где точка К неподвижна или является шарниром с известной скоростью.
звена, по которому скользит муфта, где точка К неподвижна или является шарниром с известной скоростью.
Если муфта закреплена на неподвижном шарнире, то абсолютная скорость равна нулю 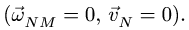
3. Решаем векторное уравнение (1). Определяем 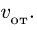
Задача №15
Плоский механизм с одной степенью свободы состоит из шарнирно соединенных стержней и муфты D, скользящей по направляющему стержню (кривошипу) OA. Муфта шарнирно закреплена на стержне BD. Кривошип вращается против часовой стрелки с постоянной угловой скоростью 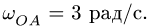 Даны длины: OA = 40 см, АВ = 111 см, ВС = 43 см, ОС = 62 см. Найти скорость муфты относительно направляющего стержня в тот момент, когда
Даны длины: OA = 40 см, АВ = 111 см, ВС = 43 см, ОС = 62 см. Найти скорость муфты относительно направляющего стержня в тот момент, когда 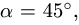 а муфта находится на середине кривошипа: OD = ОА/2 (рис. 119).
а муфта находится на середине кривошипа: OD = ОА/2 (рис. 119).
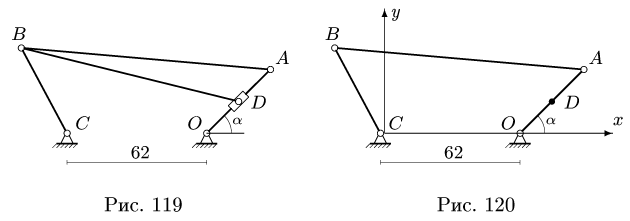
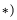 Направляющий стержень.
Направляющий стержень.
Решение
1. Представляем движение муфты М в виде суммы относительного движения по направляющему стержню OA и переносного движения вместе с .этим стержнем. Выбираем систему координат и определяем координаты всех шарниров механизма и муфты. Помещаем начато координат в точку С (рис. 120) и вычисляем координаты:
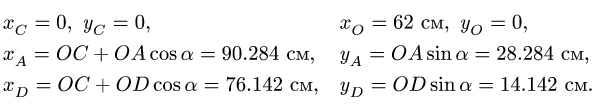
Координаты точки В найдем из системы уравнений
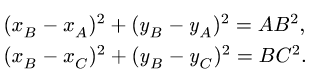
Система имеет два решения (задача о точках пересечения двух окружностей с радиусами АВ и ВС). Выбираем то решение, у которого 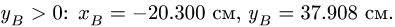
Нелинейную систему уравнений удобно решать на компьютере, например, в системе Maple V. Программа решения имеет вид

Числа заносятся в десятичной форме: АВ: =111.0 и т.д.
2. Мысленно снимаем муфту с механизма (рис. 120) и находим скорости шарниров и угловые скорости звеньев получившегося механизма. Записываем уравнения трех угловых скоростей четырехзвенника ОABC (§8.3, с. 179):
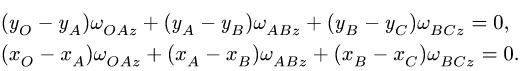
При 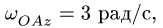
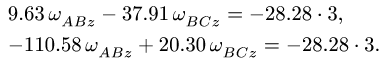
Получаем решение: 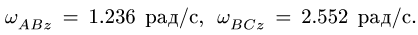 Зная
Зная 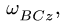 находим
находим
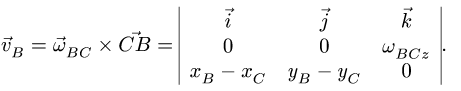
Компоненты скорости имеют следующие значения:
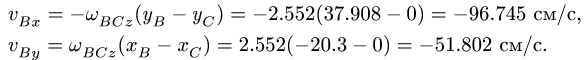
3. Записываем уравнение сложения скоростей 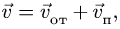 где абсолютная скорость
где абсолютная скорость 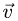 выражается через известную скорость шарнира В. Составляем векторное уравнение
выражается через известную скорость шарнира В. Составляем векторное уравнение
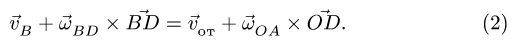
Это уравнение содержит две неизвестные величины. Одна из них — искомый модуль вектора относительной скорости 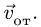 Направление этого вектора известно и задается направлением стержня OA, по которому скользит муфта. Вторая неизвестная — угловая скорость
Направление этого вектора известно и задается направлением стержня OA, по которому скользит муфта. Вторая неизвестная — угловая скорость 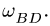 Подставляем численные значения. Уравнение (2) принимает вид
Подставляем численные значения. Уравнение (2) принимает вид

где 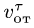 — проекция относительной скорости муфты на ось, направленную от О к А. Находим решение системы:
— проекция относительной скорости муфты на ось, направленную от О к А. Находим решение системы: 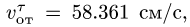
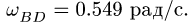 Таким образом, в указанный момент муфта движется по стержню OA вверх со скоростью
Таким образом, в указанный момент муфта движется по стержню OA вверх со скоростью 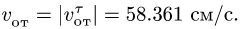
Замечание. Эту задачу можно решить по крайней мере ещё двумя способами. Во-первых, методами аналитической геометрии можно найти расстояние 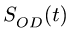 от шарнира О до муфты D как функцию времени. Дифференцируя
от шарнира О до муфты D как функцию времени. Дифференцируя 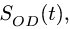 найдем относительную скорость. Во-вторых, можно найти скорость стержня OA относительно муфты. Подвижная система координат будет связана с муфтой. В этом случае абсолютная скорость точки стержня OA под муфтой — это скорость точки тела при вращательном движении с угловой скоростью
найдем относительную скорость. Во-вторых, можно найти скорость стержня OA относительно муфты. Подвижная система координат будет связана с муфтой. В этом случае абсолютная скорость точки стержня OA под муфтой — это скорость точки тела при вращательном движении с угловой скоростью 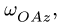 переносная — скорость муфты, выраженная через скорость шарнира В.
переносная — скорость муфты, выраженная через скорость шарнира В.
Замечание. В ответах, помимо искомой относительной скорости, даны промежуточные результаты — скорости точек А, Б и D. Причем в вариантах 1,2,7,8 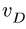 — это скорость той точки направляющего стержня, в которой в этот момент находится муфта.
— это скорость той точки направляющего стержня, в которой в этот момент находится муфта.
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
- Дифференциальные уравнения движения материальной точки
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Мгновенный центр вращения
- Вращение твердого тела вокруг неподвижной точки
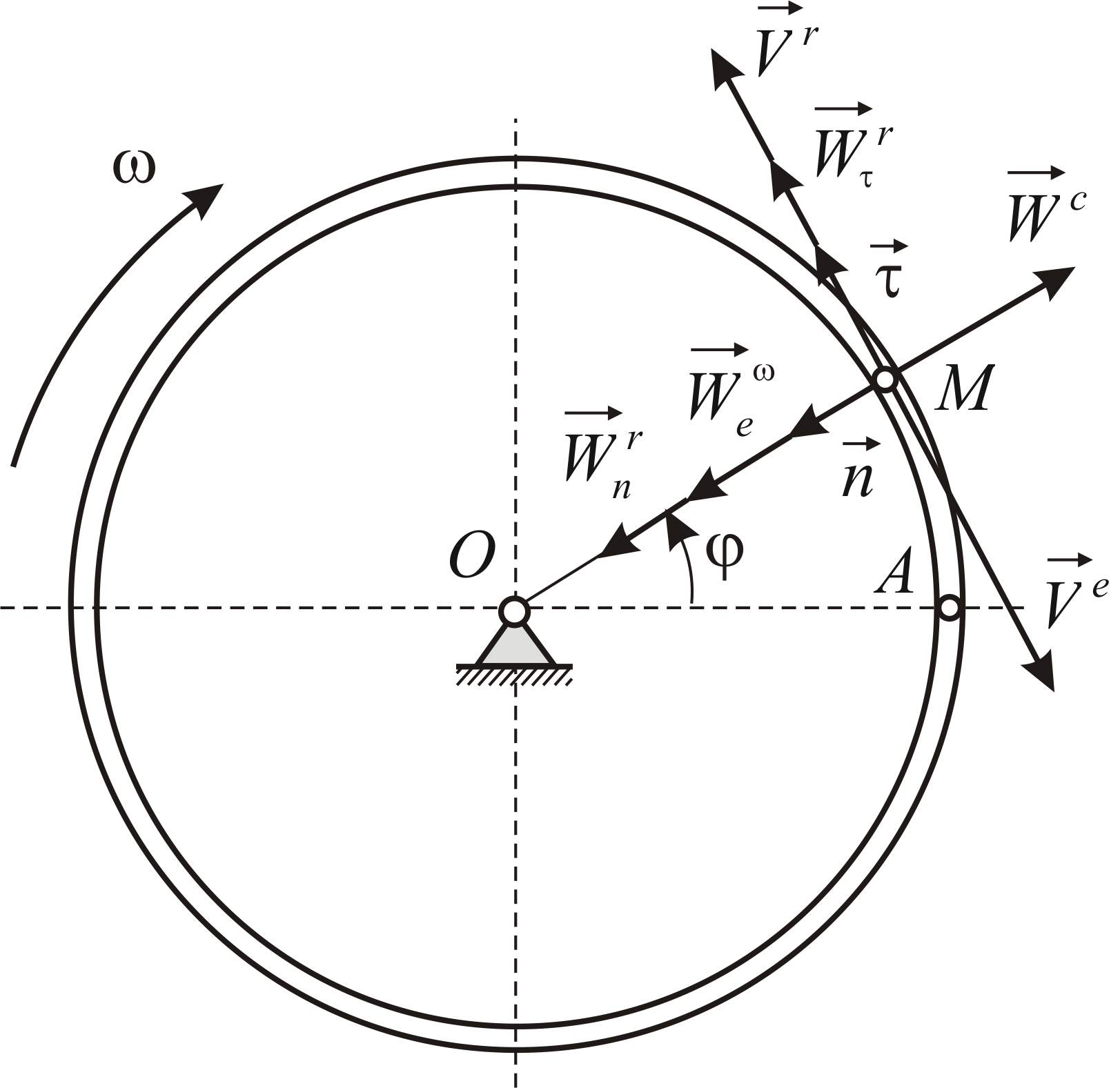



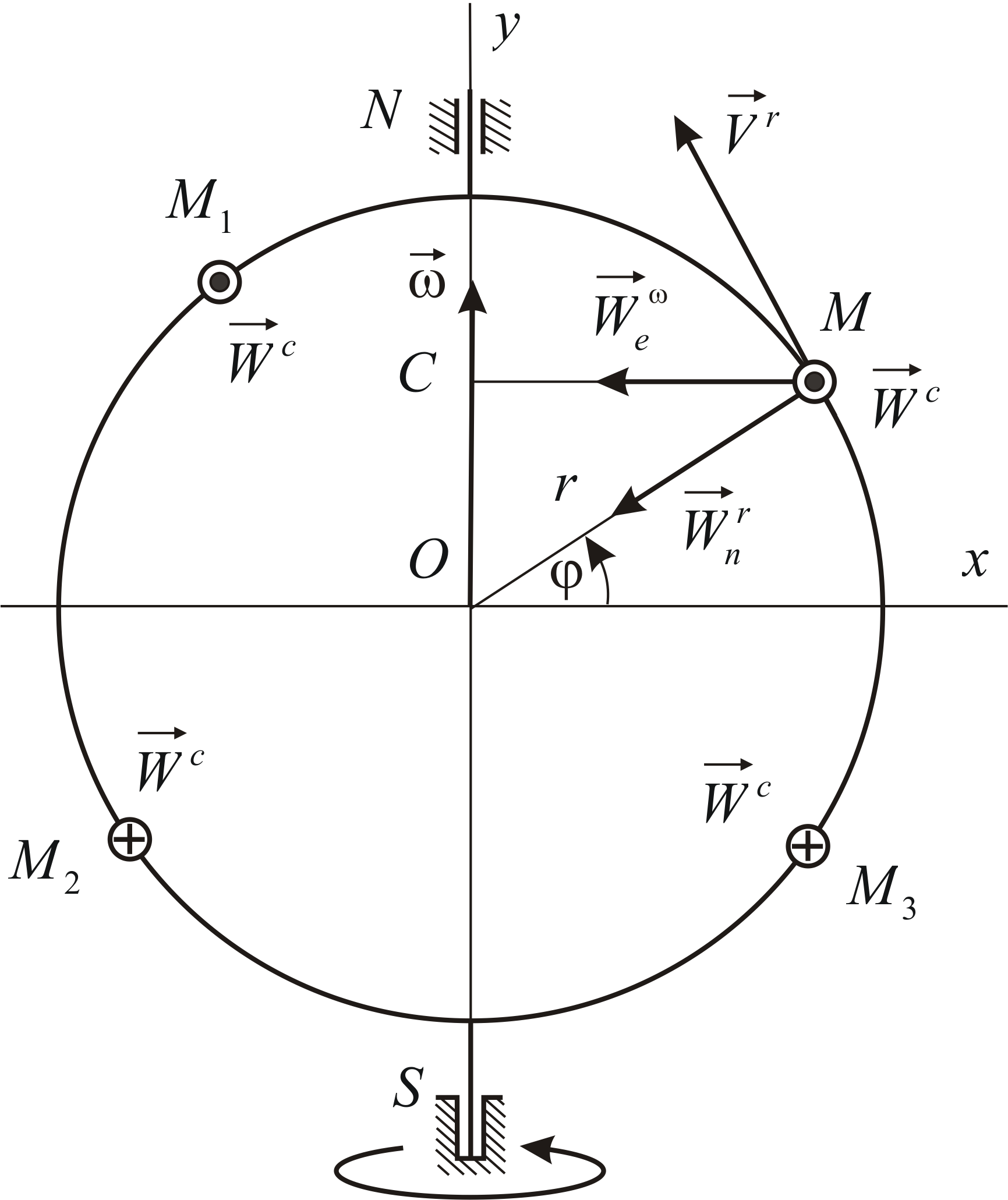


















![{displaystyle {vec {a}}={vec {a}}_{r'}+{vec {a}}_{e}+2left[{vec {omega }}times {vec {v}}_{r'}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14c94b28221af9efd57db669ebd5baabb5db5e85)
![vec{v}_B = vec{v}_A + left[vec{omega}timesvec{AB}right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/674393e427cf0812f2a78e9593820b0f5f0dd0a7)
![vec{a}_B = vec{a}_A + left[vec{omega}times left[ vec{omega}times vec{AB}right] right] + left[ vec{varepsilon}times vec{AB} right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/73ba130aeb13035b7b570db42daa1c2bf8bd55f0)




