Как найти абсолютную энтропию

Прикладное
значение постулата Планка состоит в
том, что он устанавливает
начало отсчета значений энтропии и
открывает путь определения абсолютной
величины этой термодинамической функции.

Если,
например, повышать температуру 1 моля
идеального кристалла вещества
от 0 до Т при р=1атм, то при отсутствии
полиморфных превращений и других
изменений фазовых состояний для
нахождения энтропии необходимо провести
интегрирование уравнения:

В общем же случае
приходится обращаться к более громоздкому
выражению:

*)
Поскольку, строго говоря, третий закон
термодинамики применим только к
ограниченному
классу веществ, а именно, к чистым
бездефектным кристаллам, некоторые
авторы
(А. Мюстер, Химическая термодинамика,
М.: Мир, 1971.—295 с.; с. 196-197,) полагают, что
третье начало должно быть сформулировано
не в виде закона, а в форме правила,
которое на практике “выполняется с
достаточной точностью”.

74

[p# 75]

где
sq
–
остаточная или нулевая энтропия;
а,р,.,8,… – символы, обозначающие полиморфные
модификации кристаллической фазы; Т_нтк
– нормальная температура
кипения.

Графической
иллюстрацией записанного выше
уравнения являются данные
об энтропиях воды и брома, показанные
на рис.11
.

Рис.
11. Температурная зависимость энтропии
воды и брома

Как
видно из рис.11,
зависимость
энтропии от температуры имеет сложный
характер. В области низких температур,
когда теплоемкость возрастает
пропорционально температуре в третьей
степени, вторая производная
энтропии по температуре

3. Критерии (энтропия)

75

[p# 76]

положительна,
т.е. кривая S
= f
(Т) является вогнутой. Выше 200
К теплоемкость слабо зависит от
температуры. В этих условиях

/V

вторая
производная отрицательна и наблюдаемая
зависимость будет выпуклой. Процедура
нахождения абсолютной энтропии веществ
основывается на обработке
экспериментальных данных о
температурной зависимости их
теплоемкости.
С этой целью массив экспериментальных
данных представляют в

Ср
координатах
—*- = f(T)
либо C_p=f(lnT)
В результате получают сложную

зависимость. В
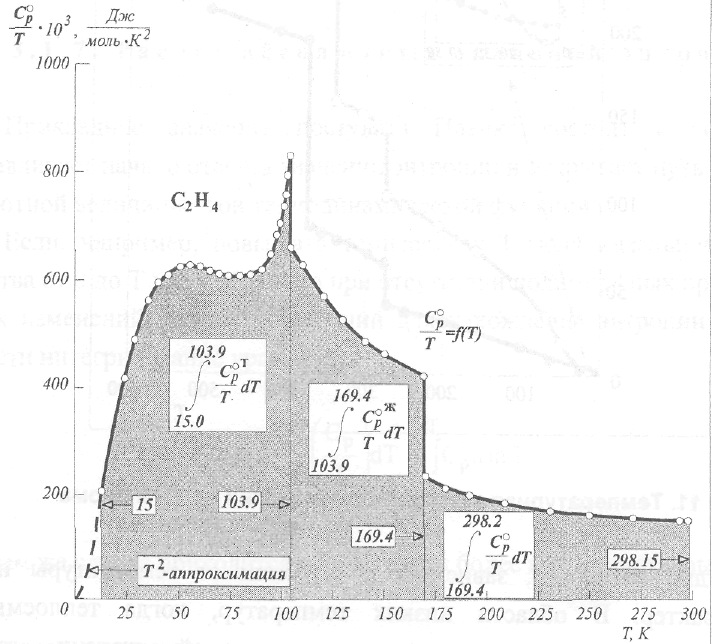
качестве примера на рис.12 приведены
данные для этилена.

Рис.
12. Интерирование зависимостис
целью нахождения величины

м.

Абсолютной энтропии

[p#
77]

76

[p# 78]

с°

V^.
rt

Как
видно, зависимость —~
= f
(Т) разделяется на несколько
участков,

характеризующих
поведение фаз, существующих в
рассматриваемом температурном
интервале. Суммируя интегралы, относящиеся
ко всем фазовым состояниям,
с учетом области экстраполяции к
абсолютному нулю температуры и
принимая во внимание энтропии всех
фазовых переходов, приходим к значению
S^gjs-

Современная
криогенная техника позволяет производить
измерения теплоемкости
при весьма низких, но все же отличных
от абсолютного нуля температурах.
Так как интегрирование должно быть
выполнено во всем интервале
температур, то всегда существует
необходимость экстраполировать данные
о теплоемкости к абсолютному нулю
температуры. С этой целью в случае
трехмерных кристаллических структур
используют Т³
– и для слоистых, т.е. двумерных структур
Т²
– экстраполяцию.

Если
при проведении экспериментов в качестве
хладоагента применяют жидкий
гелий, температура кипения которого
при атмосферном давлении составляет
4,22 К, то экстраполяция не является
далёкой и не вносит ощутимой ошибки
в значение энтропии.

За пределами
области экстраполяции для каждого из
участков проводят

С°

D

графическое
интегрирование зависимости — = f
(Т). Затем суммируют

значения
отдельных составляющих энтропии,
включают в сумму величины энтропии
всех фазовых переходов, имеющих место
в интервале температур О
– Т, и учитывают эффекты, связанные с
нагреванием газообразных веществ

В
качестве численной иллюстрации к
изложенному, ниже указаны величины,
суммирование которых приводит к значению
энтропии газообразного
азота при 298 К и давлении 1 атм. Слагаемыми
суммы, выраженными
в Дж/ (моль К), являются величины,
относящиеся к:

1) экстраполяции
экспериментальных данных от 10 К до О К
по

^

уравнению
Дебая (Т -экстраполяция) 1,92;

2) графическому
интегрированию от 10 К до 35.61 К, что
отвечает
нагреванию
твердого азота до температуры фазового
превращения

в
твердом состоянии 25,25

1. энтропии
   фазового перехода при 35.61 К 6,43;

2. графическому
   интегрированию от температуры

фазового
перехода до температуры плавления азота
при 63.14 К 23,38;

5) энтропии
плавления 11,42;

3.
Критерии (энтропия) 77

[p# 79]

6) графическому
интегрированию в интервале 63.14-77.32
К,
которое
относится к температурной области
существования жидкого

азота
при давлении 1 атм 11,41;

1. энтропии
   парообразования при нормальной
   температуре
   кипения 72,13;

2. изобарическому
   нагреванию азота как идеального газа
   в
   интервале
   77.32-298.15 К 39.20;

3. поправки
   на неидеальность поведения газа 0,92
   .

В
результате получаем S^g
⁼
192.06 Дж/(моль-К).

Измерения
низкотемпературной теплоёмкости очень
трудоемки, поэтому массив
справочных данных о величинах абсолютных
энтропии веществ значительно
меньше, чем по стандартным энтальпиям
образования.

В
некоторых справочных руководствах
наряду с данными о S^g
(будьте

внимательны:
это именно абсолютная энтропия, но не
AfS^g)
приводятся сведения
о высокотемпературных составляющих
энтропии Sj
– 8298 • Последнее
избавляет от необходимости интегрирования
в интервале температур 298
– Т и открывает возможность расчета Sj
по уравнению:

Если
требуется рассчитать величину мольной
энтропии при давлении, отличном
от стандартного, то вычисления проводят
по уравнению*):

•

*) Вывод уравнения
дан в разделе 3.2.8.

3.
Критерии (энтропия) 78

Как
уже отмечалось, для конденсированных
фаз влиянием давления на величину
энтропии можно пренебречь. В случае
идеальных газов расчет осуществляют
по уравнению:

[p# 80]

Для вычисления
энтропии реальных газов необходимо
знать

fdV]
соответствующее
уравнение состояния и, представив
— как функцию

давления, взять
интеграл, приведенный выше.

Так
как данные об абсолютных энтропиях
конденсированных фаз сравнительно
(с информацией о стандартных энтальпиях
образования) немногочисленны,
полезно принять во внимание эмпирическое
уравнение Веннера,
позволяющее оценить или уточнить
сомнительное по тем или иным причинам
значение энтропии. Это уравнение,
справедливое для ряда однотипных
неорганических веществ, имеет вид:

S
= AlgM
+ B,

где
М – – молярная масса соединения, А и В –
эмпирические константы, характеризующие
рассматриваемый ряд веществ.

Отметим
здесь же, что для газообразных веществ,
состояние которых близко
к идеальному, значения энтропии при
любых температурах и давлениях могут
быть вычислены методами статистической
термодинамики из данных о пространственном
строении молекулы и величинах ее
молекулярных постоянных.
Соответствующие уравнения будут выведены
при рассмотрении свойств
идеальных газов.

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Понятие энтропии

Абсолютная энтропия веществ и изменение энтропии в процессах

Стандартная энтропия

Стандартная энтропия образования

Энергия Гиббса

Стандартная энергия Гиббса образования

Энтальпийный, энтропийный фактор и направление процесса

Примеры решения задач

Задачи для самостоятельного решения

Понятие энтропии

Энтропия S – функция состояния системы. Энтропия характеризует меру неупорядоченности (хаотичности) состояния системы. Единицами измерения энтропии являются Дж/(моль·К).

Абсолютная энтропия веществ и изменение энтропии в процессах

При абсолютном нуле температур (Т = 0 К) энтропия идеального кристалла любого чистого простого вещества или соединения равна нулю. Равенство нулю S при 0 К позволяет вычислить абсолютные величины энтропий веществ на основе экспериментальных данных о температурной зависимости теплоемкости.

Изменение энтропии в процессе выражается уравнением:

ΔS = S_(прод.) – S_(исх.)

где S_(прод.) и S_(исх.) – соответственно абсолютные энтропии продуктов реакции и исходных веществ.

На качественном уровне знак S реакции можно оценить по изменению объема системы ΔV в результате процесса. Знак ΔV определяется по изменению количества вещества газообразных реагентов Δn_г. Так, для реакции

CaCO₃(к) = CaO(к) + CO₂(г)

(Δn_г = 1) ΔV > 0, значит, ΔS > 0.

Для реакции:

С(графит) + 2Н₂(г) = СН₄(г)

(Δn_г = -1) ΔV < 0, следовательно и ΔS < 0.

Стандартная энтропия

Величины энтропии принято относить к стандартному состоянию. Чаще всего значения S рассматриваются при Р = 101,325 кПа (1 атм) и температуре Т = 298,15 К (25^оС). Энтропия в этом случае обозначается S^о₂₉₈ и называется стандартной энтропией при Т = 298,15 К. Следует подчеркнуть, что энтропия вещества S (S^о) увеличивается при повышении температуры.

Стандартная энтропия образования

Стандартная энтропия образования ΔS^о_f,298 (или ΔS^о_обр,298) – это изменение энтропии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии.

Энергия Гиббса

Энергия Гиббса G – функция состояния системы. Энергия Гиббса равна:

G = Н – ТS.

Абсолютное значение энергии Гиббса определить невозможно, однако можно вычислить изменение δG в результате протекания процесса.

Критерий самопроизвольного протекания процесса: в системах, находящихся при Р, Т = const, самопроизвольно могут протекать только процессы, сопровождающиеся уменьшением энергии Гиббса (ΔG < 0). При достижении равновесия в системе ΔG = 0.

Стандартная энергия Гиббса образования

Стандартная энергия Гиббса образования δG^о_f,298 (или δG^о_обр,298) – это изменение энергии Гиббса в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества пристутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.

Для простых веществ, находящихся в термодинамически наиболее устойчивой форме, δG^о_f,298 = 0.

Энтальпийный, энтропийный фактор и направление процесса

Проанализируем уравнение ΔG^о_Т = ΔН^о_Т — ΔТS^о_Т. При низких температурах ТΔS^о_Т мало. Поэтому знак ΔG^о_Т определяется в основном значением ΔН^о_Т (энтальпийный фактор). При высоких температурах ТΔS^о_Т – большая величина, знак Δ G^о_Т определяется и энтропийным фактором. В зависимости от соотношения энтальпийного (ΔН^о_Т) и энтропийного (ТΔS^о_Т) факторов существует четыре варианта процессов.

• • 1. Если ΔН^о_Т < 0, ΔS^о_Т > 0, то ΔG^о_Т < 0 всегда (процесс может протекать самопроизвольно при любой температуре).
    2. Если ΔН^о_Т > 0, ΔS^о_Т < 0, то ΔG^о_Т > 0 всегда (процесс не протекает ни при какой температуре).
    3. Если ΔН^о_Т < 0, ΔS^о_Т < 0, то ΔG^о_Т < 0 при Т < ΔН^о/ΔS^о (процесс идет при низкой температуре за счет энтальпийного фактора).
    4. Если ΔН^о_Т > 0, ΔS^о_Т > 0, то ΔG^о_Т < 0 при Т > ΔН^о/ ΔS^о (процесс идет при высокой температуре за счет энтропийного фактора).

Примеры решения задач

Задача 1. Используя термодинамические справочные данные, вычислить при 298,15 К изменение энтропии в реакции:

4NH_3(г) + 5O_2(г) = 4NО_(г) + 6H₂O_(ж)

Объяснить знак и величину ΔS^о.

Решение. Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	NH3(г)	O2(г)	NО(г)	H2O(ж)
Sо298, Дж/(моль·К)	192,66	205,04	210,64	69,95

ΔS^о_х.р.,298 = 4S^о₂₉₈(NО_(г) ) + 6S^о₂₉₈(H₂O_(ж)) — 4S^о₂₉₈(NH_3(г)) — 5S^о₂₉₈(O_2(г)) = 4× 210,64 + 6× 69,95 — 4× 192,66 — 5× 205,04 = — 533,58 Дж/К

В данной реакции ΔV < 0 (Δn_г = — 5), следовательно и ΔS^o_х.р.,298 < 0, что и подтверждено расчетом.

Задача 2. Используя справочные термодинамические данные, рассчитать стандартную энтропию образования NH₄NO_3(к). Отличается ли стандартная энтропия образования NH₄NO_3(к) от стандартной энтропии этого соединения?

Решение. Стандартной энтропии образования NH₄NO₃ отвечает изменение энтропии в процессе:

N_(г) + 2H_2(г) + 3/2O_2(г) = NH₄NO_3(к); δS^о_f,298(NH₄NO_3(к)) = ?

Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2(г)	H2(г)	O2(г)	NH4NO3(к)
Sо298, Дж/(моль·К)	191,50	130,52	205,04	151,04

ΔS^о_х.р.,298 = ΔS^о_f,298(NH₄NO_3(к)) = S^о₂₉₈(NH₄NO_3(к)) — S^о₂₉₈(N_2(г)) — 2S^о₂₉₈(H_2(г)) – 3/2S^о₂₉₈(O_2(г)) = 151,04–191,50 —— 2× 130,52–3/2× 205,04 = — 609,06 Дж/(моль·К).

Стандартная энтропия образования NH₄NO₃(к), равная — 609,06 Дж/(моль·К), отличается от стандартной энтропии нитрата аммония S^о₂₉₈(NH₄NO_3(к)) = +151,04 Дж/(моль·К) и по величине, и по знаку. Следует помнить, что стандартные энтропии веществ S^о₂₉₈ всегда больше нуля, в то время как величины ΔS⁰_f,298, как правило, знакопеременны.

Задача 3. Изменение энергии Гиббса реакции:

2Н_2(г) + О_2(г) = 2 Н₂О_(ж)

равно δG^о₂₉₈= –474,46 кДж. Не проводя термодинамические расчеты, определить, за счет какого фактора (энтальпийного или энтропийного) протекает эта реакция при 298 К и как будет влиять повышение температуры на протекание этой реакции.

Решение. Поскольку протекание рассматриваемой реакции сопровождается существенным уменьшением объема (из 67,2 л (н.у.) исходных веществ образуется 36 мл жидкой воды), изменение энтропии реакции ΔS^о<0. Поскольку ΔG^о₂₉₈ реакции меньше нуля, то она может протекать при температуре 298 К только за счет энтальпийного фактора. Повышение температуры уменьшает равновесный выход воды, поскольку ТΔS^о<0.

Задача 4. Используя справочные термодинамические данные, определить может ли при 298,15 К самопроизвольно протекать реакция:

С₄Н_10(г) = 2С₂Н_4(г) + Н_2(г)

Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	С4Н10(г)	С2Н4(г)	Н2(г)
ΔGоf,298× , кДж/моль	— 17,19	68,14	0
Sо298, Дж/(моль·К)	310,12	219,45	130,52

ΔG^о_х.р.,298 = 2ΔG^о_f,298(С₂Н_4(г)) + ΔG^о_f,298(Н_2(г)) — ΔG^о_f,298(С₄Н_10(г)) = 2× 68,14 + 17,19 = 153,47 кДж.

ΔG^о_х.р.,298 > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет.

ΔS^о_х.р.,298 = 2S^о₂₉₈(С₂Н_4(г)) + S^о₂₉₈(Н_2(г)) — S^о₂₉₈(С₄Н_10(г)) = 2× 219,45 + 130,52 – 310,12 = +259,30 Дж/К.

Поскольку ΔS^о_х.р.,298 > 0, то при температуре Т>ΔН^о/ΔS^о величина ΔG^о_х.р.,298 станет величиной отрицательной и процесс сможет протекать самопроизвольно.

Задача 5. Пользуясь справочными данными по ΔG^о_f,298 и S^о₂₉₈, определите ΔH^о₂₉₈ реакции:

N₂O_(г) + 3H_2(г) = N₂H_4(г) + H₂O_(ж)

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2O(г)	H2(г)	N2H4(г)	H2O(ж)
ΔGоf,298, кДж/моль	104,12	0	159,10	-237,23
Sо298, Дж/(моль·К)	219,83	130,52	238,50	69,95

ΔG^о_х.р.,298 = ΔG^о_f,298(N₂H₄(г)) + ΔG^о_f,298(H₂O(ж)) – ΔG^о_f,298(N₂O(г)) – 3ΔG^о_f,298(H₂(г)) = 159,10 + (–237,23) – 104,12 – 0 = –182,25 кДж.

ΔS^о_х.р.,298 = S^о₂₉₈(N₂H₄(г)) + S^о₂₉₈(H₂O(ж)) – S^о₂₉₈(N₂O(г)) — 3S^о₂₉₈(H₂(г)) = 238,50 + 69,95 – 219,83 –3× 130,52 = –302,94 Дж/К.

ΔG^о₂₉₈ = ΔН^о₂₉₈ – ТΔS^о₂₉₈. Подставляя в это уравнение величины ΔН^о₂₉₈ и ТΔS^о₂₉₈, получаем:

ΔН^о₂₉₈ = –182,25× 10³ + 298·(–302,94) = –272526,12 Дж = – 272,53 кДж.

Следует подчеркнуть, что поскольку ΔS^о₂₉₈ выражена в Дж/(моль× К), то при проведении расчетов ΔG⁰₂₉₈ необходимо также выразить в Дж или величину ΔS⁰₂₉₈ представить в кДж/(мольK).

Задачи для самостоятельного решения

1. Используя справочные данные, определите стандартную энтропию образования ΔS^о_f,298 NaHCO_3(к).

2. Выберите процесс, изменение энергии Гиббса которого соответствует стандартной энергии Гиббса образования NO_2(г):

а) NO_(г) + 1/2O_2(г) = NO_2(г);

б) N_2(г) + 2O_2(г) = 2NO_2(г);

в) 1/2N_2(г) + O_2(г) = NO_2(г);

г) N_(г) + O_2(г) = NO_2(г).

3. Используя справочные данные, вычислите при 298,15 К изменение энтропии в реакции:

2NH₄NO_3(к) = 2N_2(г) + 4H₂O_(г) + О_2(г).

Объясните знак и величину  ΔSº реакции.

• .

δSох.р.,298 =1040,84 Дж/К. В данной реакции δV > 0 (D nг = 7), следовательно и δSох.р.,298 > 0, что и подтверждено расчетом.

4. Используя справочные данные, определите принципиальную возможность протекания реакции при 298,15 К:

NiO_(к) + C_{(графит)} = Ni_(к) + CO_(г)

Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.

ΔGох.р.,298 = 74,45 кДж > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет. Поскольку ΔSох.р.,298 = 183,69 Дж/К, то есть больше нуля, то при достаточно высоких температурах ΔGох.р.,298 изменит знак на обратный.

5. Рассчитайте стандартную энергию Гиббса образования ΔG^о_f,298 C₂H₅OH_(ж), используя справочные данные о величинах ΔН^о_f,298 и S^о₂₉₈.

6. Используя справочные данные, определите стандартную энтропию образования ΔS^о_f,298 K₂Cr₂O_7(к).

7. На основе расчетов термодинамических величин покажите, чем эффективнее восстанавливать при 298 К Cr₂O_3(к) до металла — алюминием или магнием:

1) Cr₂O_3(к) + 3Mg_(к) = 3MgO_(к) + 2Cr_(к); ΔG^о₁;
2) Cr₂O_3(к) + 2Al_(к) = Al₂O_3(к) + 2Cr_(к); ΔG^о₂.

ΔGо1=-648,9 кДж; ΔGо2=-523,3 кДж. Таким образом, самопроизвольно протекают два процесса. Так как значение ΔGо1 более отрицательное, то эффективнее при 298 К будет протекать процесс восстановления магнием.

8. Используя справочными данными по величинам S^о₂₉₈, определите возможность самопроизвольного протекания в изолированной системе при 298 К процесса:

KClO_3(к) = KCl_(к) + 3/2O_2(к)

ΔSо298=247,1 Дж/К. ΔSо298 больше 0, следовательно данный процесс будет протекать самопроизвольно в изолированной системе при 298 К.

9. Используя справочные данные, вычислите при 298 К изменение энтропии в процессе:

Н_2(г) + 1/2О_2(г) = Н₂О_(г)

10. На основе справочных данных оценить температуру восстановления WO_3(к) водородом:

WO_3(к) + 3H_2(г) = W_(к) + 3H₂O_(г).

Абсолютное значение – энтропия

Cтраница 2

Определение абсолютного значения энтропии различных веществ при тех или иных температурах возможно, если известны теплоемкости этих веществ при всех температурах от абсолютного нуля до интересующей нас температуры, а также тепловые эффекты и температуры всех фазовых переходов, если они имеют место в этом температурном интервале. В самом деле, пусть рас-с матриваемое вещество при интересующей нас температуре Т находится в кристаллическом состоянии и в той же модификации, что и при абсолютном нуле.
 [16]

Чтобы определить абсолютное значение энтропии для какого-либо состояния тела, необходимо фиксировать начало ее отсчета.
 [17]

Для вычисления абсолютных значений энтропии обычно необходимы экспериментальные значения теплоемкости в интервале от 0 К до исследуемой температуры. Поскольку измерение теплоемкости вблизи абсолютного нуля представляет значительные экспериментальные трудности, в литературе практически отсутствуют значения теплоемкостей ниже 4 – 10 К.
 [18]

Для вычисления абсолютного значения энтропии какого-либо вещества надо знать теплоемкости, определенные до возможно более низких температур, и теплоты фазовых переходов. Значения теплоемкости вблизи О К находят путем экстраполяции.
 [19]

Для вычисления абсолютных значений энтропии используют экспериментальные значения теплоемкости в интервале от О К до исследуемой температуры. Поскольку измерение теплоемкости вблизи абсолютного нуля представляет значительные экспериментальные трудности, в литературе практически отсутствуют значения теплоемкости ниже 4 – 10 К. Значение энтропии в этой области часто определяют методом экстраполяции, используя уравнение теплоемкости Дебая.
 [20]

Для вычисления абсолютных значений энтропии обычно необходимы экспериментальные значения теплоемкости в интервале от 0 К до исследуемой температуры. Поскольку измерение теплоемкости вблизи абсолютного нуля представляет значительные экспериментальные трудности, в литературе практически отсутствуют значения теплоемкостей ниже 4 – 10 К.
 [21]

Для вычисления абсолютных значений энтропии элементов и соединений в стандартных условиях существуют два способа. Первый способ основан на применении теоремы Нернста и использовании экспериментальных данных о теплоемкостях. Второй способ основан на статистических расчетах из спектральных данных.
 [22]

Для нахождения абсолютных значений энтропии углеродистых тел необходимо знать, кроме температурной зависимости теплоемкости, остаточную энтропию, о которой говорилось в предыдущем параграфе.
 [23]

Обычно определяют не абсолютное значение энтропии, а ее изменение ( 52 – Si) в том или ином процессе.
 [24]

Необходимые для расчета абсолютные значения энтропии участвующих в реакции веществ находят в стандартных таблицах или вычисляют с помощью одного из рассмотренных выше способов.
 [25]

Обычно определяют не абсолютное значение энтропии, а изменение ее в том или ином процессе. Увеличение энтропии свидетельствует об уменьшении работоспособности системы.
 [26]

В отношении определения абсолютных значений энтропии уместно сделать еще одно замечание.
 [27]

В технической термодинамике абсолютным значением энтропии не интересуются, а определяют только ее изменение в соответствующих процессах. Поэтому нулевое значение энтропии выбирают условно при / 0 С. Обычно значения s или As определяют расчетным путем и сводят их в таблицы или используют для построения диаграмм, которыми пользуются при практических расчетах.
 [28]

В справочных таблицах находим абсолютные значения энтропии для всех участников реакций.
 [29]

В отличие от энтальпии абсолютные значения энтропии могут быть определены экспериментально. Порядок значения энтропии S определяется величиной И, которая колоссальна. Обычно приходится иметь дело с объектами, содержащими 1023 частиц и более.
 [30]

Страницы:  

   1

   2

   3