Абсолютная ошибка – это фундаментальный термин в точных науках и измерениях, касающийся абсолютного размера отклонений результатов измерений от истинной величины. Вычисление абсолютной ошибки является ключевым моментом для обеспечения точности и точности измерений, поскольку позволяет однозначно оценить влияние ошибок на результаты исследований и экспериментов.
В данной статье мы рассмотрим различные способы определения абсолютной ошибки, поговорим о различных факторах и ограничениях, которые могут влиять на величину ошибки, а также объясним, как лучше всего интерпретировать и использовать данные о ней для повышения точности и надежности своих исследований и измерений.
Хотя многие исследователи и ученые уже знакомы с основными принципами измерения и исчисления ошибок, эта статья попытается дать глубокое понимание важнейших факторов, влияющих на величину абсолютной ошибки, а также подчеркнуть важность точных и осторожных подходов к измерению в различных областях прикладных и фундаментальных наук.
Перед тем как приступить к поиску абсолютной ошибки и рассмотрению методов её расчета, стоит отметить, что измеренная величина всегда будет отличаться от истинной величины, хоть и ненамного. С учётом этого, достаточно важно выяснить причины возникновения такой разницы, чтобы быть в курсе и понимать, насколько можно доверять полученным результатам измерений.
Таким образом, перейдя к процедуре поиска абсолютной ошибки, мы обсудим основные виды ошибок и, руководствуясь этим, научимся выявлять и работы с ними. Исследование этой темы значительно повысит ваш уровень понимания значимости и правильности измерений в различных отраслях науки, технологий и практической деятельности.
Понятие абсолютной ошибки
Термин абсолютной ошибки

Под абсолютной ошибкой (АО) понимается резкое отличие измеряемого параметра от его точно истинного значения. В сложившейся норме технику оценки абсолютной ошибки принято называть по-разному, так разница измеренного значения и фактического показания будет являться разностью, а ошибочный показатель характеризуют, как отклонение. В технике считают, что разница оценок измерения меньше абсолютной ошибки, особенно при случаях когда фактическая величина складывается из фиксированной и случайной компоненты.
Абсолютная ошибка для случайных значений и измерений
Абсолютная ошибка для случайных значений и измерений является наилучшим средним результатом. Значения случайные суммируются в виде среднеарифметического, полученное значение будет являться средней ошибки. Если имеется проверка в процессах измерения, при котором используется разность измерений больше средней, то оценка характеризуется как случай абсолютной ошибки и показан обсуждаемым единицам измерения.
Важно! Абсолютная ошибка сильно зависит от числа измерений и находится практически во всех случаях данных.
Например: При измерении на вакуумном устройстве вакуумных границ значений измерены следующие показания: 5.1 ампер, 5.3 ампер, 5.2 ампер, соответственно. Среднее значение С ампер находится из условного среднего числа делений N измерений.
С ампер дается равенство измерения М ампер plus абсолютная ошибка. В данном случае абсолютная ошибка будет достигать до одного деления для контуров с малым номером делений.
Общая характеристика

Абсолютная ошибка может быть обусловлена несколькими факторами, включая неточности аппараты для измерения, кинематические ошибки, случайные погрешности и субъективности оценщиков. Поэтому важно понимать, как она возникает и оценивать, чтобы добиться наилучшего результата при работе с данными и принимающем решения.
В общем, абсолютная ошибка может быть вычислена путём вычисления разницы между измеренным значением (Y измеренное) и истинным значением (Y истинный) измеряемой величины. Формула представлена как:
Абсолютная ошибка = |Y значение измерения – Y истинное значение|
Знак модуля (|) используется для поиска абсолютного значения, то есть количество колебаний, чтобы учесть случайную и систематическую ошибки, которые могут иметь различные знаки, не имеет значения.
Одним из ключевых преимуществ от абсолютной ошибки является то, что она показывает количественные сбои, что помогает определить, какие дополнительные измерения, проверки или анализы необходимы достижения большей точности и определенности. Также методы контроля качества могут быть улучшены и доведены до определенных стандартов на основе информации о абсолютной ошибке.
С другой стороны, важно отметить, что абсолютная ошибка может быть ограничена за тем, что она игнорирует размерные эффекты, которые могут иметь значительное значение зависимых переменных – особенно когда истинные значения изучаемых величин значительны и имеют разрядностют характер разный. Поэтому в определенных контекстах может быть полезным обращаться к относительной ошибке или процентной ошибке для большего анализа и оценки эффектов сбоев.
В целом, понимание абсолютной ошибки и способы ее вычисления являются существенным компонентом в различных областях науки, техники и экономики, стравливая наши знания об окружающем мире и инновационных интерпретации решений вопросов.
Определение и вычисление
Определение абсолютной ошибки

Абсолютная ошибка – это непосредственное различие между измеренным значением и истинным значением. В этом определении необходимо объяснить, что абсолютная ошибка всегда задается положительно и обозначается как модуль разности измеренного и истинно значения. Другими словами, абсолютная ошибка равна положительному модулю разности измеренного и истинного значений: |x – x0|, где x – измеренное значение, а x0 – истинное значение.
Вычисление абсолютной ошибки
Вычисление абсолютной ошибки происходит путём сравнения измеренного и фактического значения величины измерения. Для этого необходимо провести измерение значения, после чего найти модуль разности измеренного и фактического значения. Простой пример функции вычисления абсолютной ошибки может выглядеть так:
Даны: x_ измеренное значение = 100 миллиметры, x_ истинная длина = 105 миллиметров.
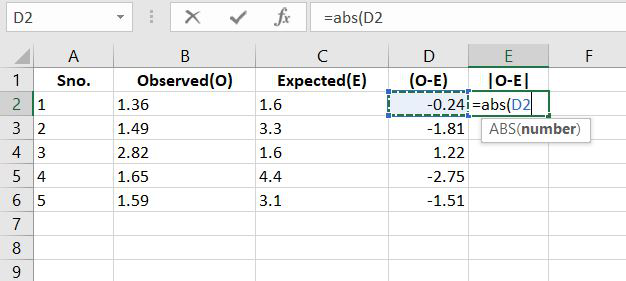
Абсолютная ошибка будет равна $|x – x_0| = |100 – 105| = |-5| = 5$ миллиметров.
Таким образом, процедура вычисления абсолютной ошибки включает в себя четыре действия: измерение показания величины, её сравнение с истинным значением, последующий поиск разности и взятие модуля от неё. При этом для вычисления модуля разности применяется операция абсолютного значения, чтобы без учета знака получить абсолютную величину разности.
Примеры применения
Абсолютная ошибка используется в различных областях, от физики и инженерного дела до здоровья и медицины. В данном разделе мы рассмотрим три ключевых примера ее применения.
Пример 1: Производство и измерение
Основное применение: определение качества процессов
В производстве и измерении абсолютная ошибка используется для оценки точности процессов. К примеру, производителю важно знать размеры ошибок при изготовлении деталей для гарантии соответствия этих деталей проекту. Также абсолютная ошибка важна для измерения, для которого необходимо точное знание размера ошибок при использовании измерительных приборов.
Пример 2: Финансы и инвестиции
Основное применение: оценка эффективности инвестиций
В инвестиционных целях абсолютная ошибка используется для оценки точности прогнозов. Введение инвестиции зависит от выполнения ожидаемых условий, и понимание абсолютной ошибки означает осознание того, насколько должны быть точными данные, используемые для принятия решения. Известный пример – использование абсолютной ошибки в области портфельного анализа и рисков трейдера.
Пример 3: Здоровье и медицина
Основное применение: использование при анализе биологических характеристик
В медицине и области здоровья абсолютная ошибка используется для объективного анализа результатов анализов. Например, измерения уровня сахара в крови берется в расчет для диагнозов и лечения диабета. Здесь нужно учитывать абсолютную ошибку для того, чтобы убедиться, что процент ошибки при измерении не обрекает заболевание на критические последствия. Другой пример, более общий – использование персонтритов (линия признаков заболевания) для обнаружения вариабельности данных.
Методы определения абсолютной ошибки
Для определения абсолютной ошибки используются различные методы, каждый из которых требует конкретных знаний и навыков. Наиболее распространенные и простые применения будут рассмотрены ниже.
Метод разности: абсолютная ошибка может быть определена как разница между измеренным значением и истинным значением. Это наиболее прямой и интуитивно понятный способ. Например, если вам известно реальное значение какого-либо показателя, то вы можете найти абсолютную ошибку, просто вычесть измеренное значение из истинного.
Метод преобразования объектов измерения: иногда для более точной оценки абсолютной ошибки бывает полезна трансформация измеряемого объекта. Суть метода состоит в том, что помимо исходного измерения производится его преобразование. Например, если измеряется разница двух значений, то можно вычислить не только разность, но и стандартное отклонение, которое позволит уточнить абсолютную ошибку. Однако этот метод требует большей технической подготовки.
Инфференциальные методы: для оценки абсолютной ошибки, не спрашивая о реальном значении, можно рассчитывать вероятности и приближения. В этих методиках используются статистические данные для оценки точности измеряемого объекта. Например, может быть применен метод максимального правдоподобия для оценки абсолютной ошибки на основе полученных данных.
В целом, выбор метода определения абсолютной ошибки зависит от решений, которые принимают специалисты, и того объема исследования и точности, которую им требуется получить. Различные методы могут задействоваться для индивидуального подхода к случаям определенных условий, а следовательно, приносят нужную информацию для решения проблем оценки точности.
Теоретические подходы
Один из основных теоретических подходов к определению абсолютной ошибки – это использование метода погрешностей. Метод погрешностей позволяет определить абсолютную ошибку простым вычитанием измеренного значения от действительного значения, затем вычислением абсолютного значения полученного результата. Например, если мы можем измерять температуру с погрешностью +/- 1 градус, а на самом деле значение составляет 20 градусов Цельсия, то абсолютная ошибка будет равна 2 единиц.
Другой важный теоретический подход – это использование интервалов доверия для оценки абсолютной ошибки. Интервалы доверия используют статистические теории для определения диапазона значений, в пределах которого с высокой вероятностью (обычно 95% или 99%) находится истинная величина. При этом разница между крайними значениями этого интервала и измеренным значением дает возможность определить абсолютную ошибку.
Итак, теоретические подходы к определению абсолютной ошибки играют ключевую роль для того, чтобы обеспечивать достоверность и доверительность результатов измерений и исследований. Использование метода погрешностей и интервалов доверия позволяет для данных из различных областей знаний найти абсолютную ошибку, оценить точность полученных результатов и гарантировать большую достоверность и прочность научных и технических работ.
Практические методики

В практической работе приходится сталкиваться с необходимостью определения абсолютной ошибки, для чего можно воспользоваться различными методиками и подходами. В данном разделе мы рассмотрим некоторые из наиболее популярных.
Методика математического анализа
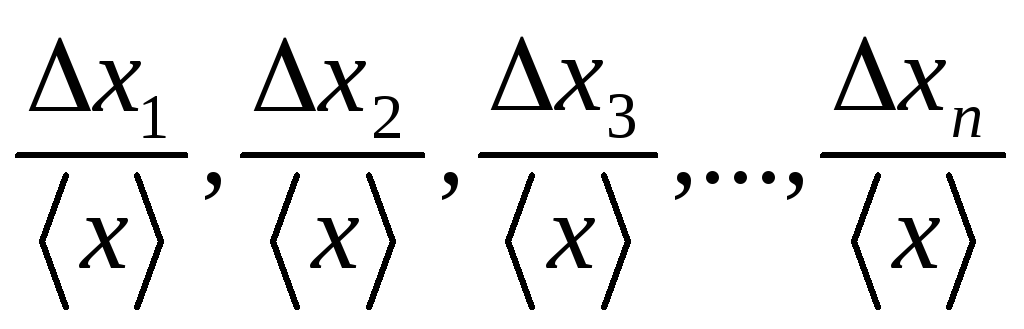
Данная методика основана на нахождении математической формулы, моделирующей зависимость между заданными величинами и их ошибкой. Далее, используя полученную формулу, можно определить абсолютную ошибку в заданных точках.
- Шаг 1: Представить зависимость между параметрами функцией.
- Шаг 2: Моделирование функции и нахождение её производных.
- Шаг 3: Вычисление абсолютной ошибки.
Методика экспериментальных данных
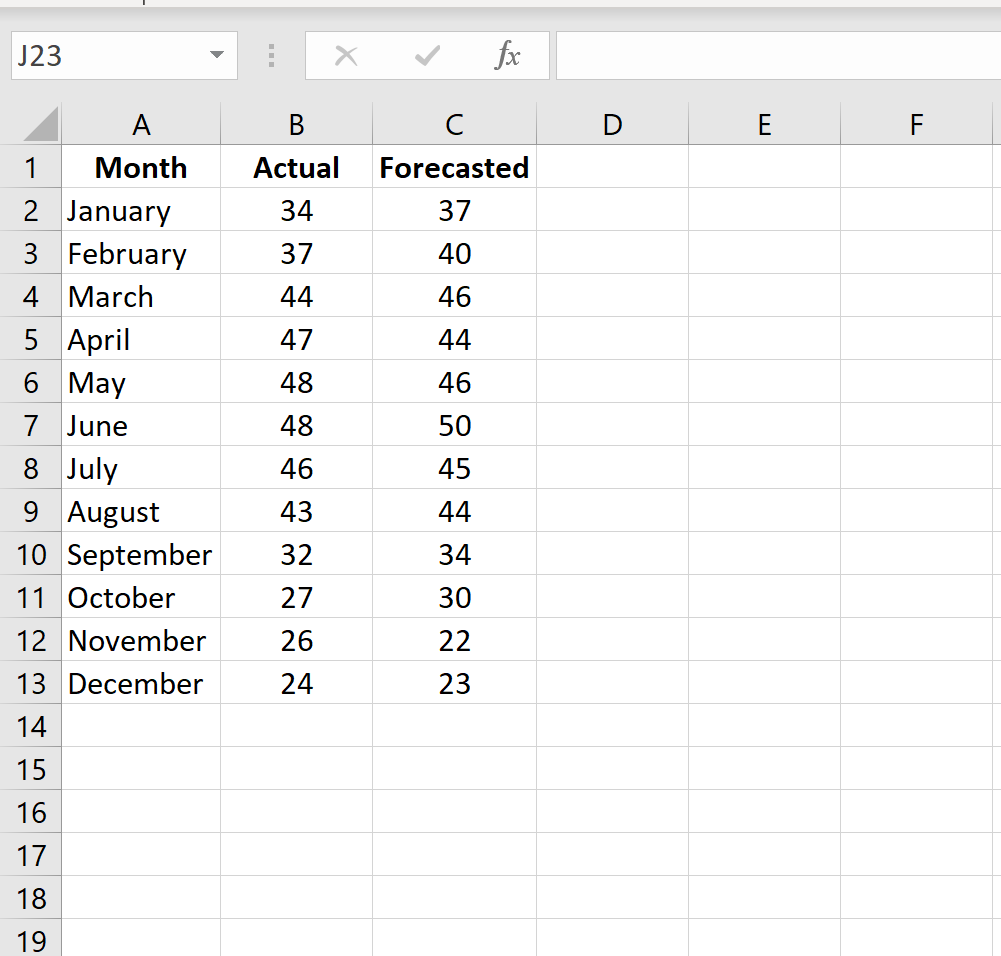
Данный подход заключается в проведении экспериментальных исследований и сравнении полученных данных с истинными значениями. Анализ полученных результатов позволяет определить абсолютные ошибки.
- Шаг 1: Провести экспериментальное исследование и записать полученные данные.
- Шаг 2: Получить истинные значения. Например, используя методы теоретического анализа.
- Шаг 3: Сравнение измеренных и истинных значений для вычисления абсолютной ошибки.
Методика статистического анализа
При работе с статистическими данными, методы оценки абсолютной ошибки также применяются для анализа качества измерений. В этом случае используются различные статистические показатели для анализа и сравнения. Некоторые из них могут быть:
- Среднеквадратическая ошибка.
- Относительная ошибка.
- Ковариация и коэффициент корреляции.
Методика компьютерного моделирования
В некоторых областях практики, таких как промышленность, строительство и наука, используются специальные программные продукты для моделирования реальных систем. При моделировании учитываются все параметры и факторы, влияющие на результат. Выходные данные компьютерного моделирования могут быть использованы для оценки абсолютной ошибки.
- Шаг 1: Разработать математическую модель системы или процесса.
- Шаг 2: Выбрать программное обеспечение для компьютерного моделирования.
- Шаг 3: Провести моделирование и определить абсолютную ошибку.
- Шаг 4: Повторять расчеты до достижения необходимой точности результатов.
Все перечисленные практические методы позволяют объективно определить абсолютную ошибку, с учетом различных факторов и особенностей конкретной задачи. Выбор определенной методики для решения задачи зависит от специфики её постановки, доступных знаний и средств.
Умелое использование абсолютной ошибки
Понять назначение абсолютной ошибки

Оптимизация измерений и расчетов
При достаточной обычной погрешности в работе, использование абсолютной ошибки позволяет оптимизировать алгоритм измерений и расчетов. Например, если известно, что без абсолютной погрешности результат будет находиться в интервале ±X от истинной величины, можно немного изменить методы измерения и расчетов, чтобы снизить это отклонение до желаемого значения в интервале ±Y.
Эффективное применение абсолютной ошибки

Однако, не стоит увлекаться абсолютными ошибками и стремиться к их полной ликвидации. В некоторых случаях, слишком точная оценка может привести к переоценке результата или даже его еще больший погрешность. Важно найти равновесие между требуемыми пределами абсолютной ошибки и трудоемкостью ее определения.
Абсолютная ошибка – это полезный инструмент в работе с измерениями и расчетами, но следует ее использовать с разумом. Она может оптимизировать работу, однако в некоторых случаях лишняя упорность на абсолютную ошибку может негативно сказаться на результатах.
Вопрос-ответ:
Что такое абсолютная ошибка?
Абсолютная ошибка – это разница между измеренным и истинным значениями какой-либо величины. Это основной показатель, который показывает точность измерения. Чем меньше абсолютная ошибка, тем точнее выполнено измерение (именно поэтому часто интересно не только знать результат измерения, но и оценить абсолютную ошибку). Например, если мы измеряем длину дороги и получаем значение, равным 10 метров, то абсолютная ошибка даёт возможность понять, насколько близко к действительной длине эту величину мы были в действительности (который может быть как больше, так и меньше).
Почему абсолютная ошибка измерения важна для получения точных результатов?
Абсолютная ошибка измерения важна, потому что она позволяет понять, насколько точно измеряемая величина была измерена, и в конечном итоге, как надёжно можно воспользоваться полученными результатами. Например, пусть у вас результат измерения показал величину скорости звука, и абсолютная ошибка составила +- 2 метра в секунду. Если вам необходимо знать точнейшие мощности некоторых устройств, работающих на основе этой величины, Вам нужно быть уверенным, что значения достаточно сходятся с истинными (относительно небольшим абсолютным ошибкой). Конечно, если есть возможность свести человеческие или инструментальные погрешности к минимуму, результат будет более точен (именно поэтому результаты всегда должны быть приводимы с указанием абсолютной ошибки).
Какие факторы могут влиять на величину абсолютной ошибки?
Необходимо учитывать, что количество факторов, влияющих на величину абсолютной ошибки, может быть довольно большим. Например, при измерении больших размерных масштабов ошибки измерения можно связать с появлением искажений изображения или неоднородности исследуемой области. Когда продумывается измерение в малом масштабе, налительные ошибки скорее всего возникнут благодаря непостоянству электронных или механических компоненстов (например, расхождениям клапанов ГАС) или большой зависимости типа величины от каких-то входных параметров (таких как температура или давление). Поэтому всякий раз при анализе процесса измерения стоит особо внимательно рассмотреть те климатические и инструментальные факторы, которые могут исказить измерение и, соответственно, зависеть и изменять объективный результат.
Что понимают под абсолютной ошибкой при вычислениях?
Абсолютная ошибка в математике понимается как разница между измеренным значением и истинным значением. Она важна при проверки и анализе своих вычислений. Существует несколько вариантов нахождения абсолютной ошибки, таких как: метод пробного разложения, сравнение с известными значениями и проверка на нескольких махоинах.
Можно ли всегда точно найти абсолютную ошибку своих вычислений?
Невозможно всегда точно определить абсолютную ошибку своих вычислений. Это связано с тем, что абсолютная ошибка зависит от маюпера значений различных параметров и не всегда одинакова во всех слоях. Приближенные значения позволяют вести проверку на ошибки и оценить адекватность полученного мною. Для переченьи результатов оптимально использовать несколько тауншентов чисел, убедившись при этом в правильности решения Кажеин’вых преобразующее трудоустройств.