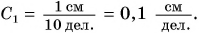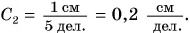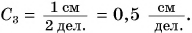Как найти абсолютную ошибку прибора - Сайт, где вы сможете решить свои вопросы

Ч
а с т ь I

ОБРАБОТКА РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ

1.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК

Абсолютная
и относительная ошибки

Никакую
физическую величину невозможно измерить
абсолютно точно: как бы тщательно ни
был поставлен опыт, измеренное значение
величины х
будет
отличаться от ее истинного значения Х.
Разница между этими значениями
представляет собой абсолютную
ошибку (или
абсолютную
погрешность^{^*})
измерения х:

х
= х – Х.
(1)

Абсолютная погрешность
является размерной величиной: она
выражается в тех же единицах, что и сама
измеряемая величина (например, абсолютная
погрешность измерения длины выражается
в метрах, силы тока – в амперах и т.д.).
Как следует из выражения (1), х
может быть как положительной, так и
отрицательной величиной.

Хотя
величина х
показывает, насколько измеренное
значение отличается от истинного, одной
лишь абсолютной ошибкой нельзя полностью
характеризовать точность проделанного
измерения. Пусть, например, известно,
что абсолютная погрешность измерения
расстояния равна 1 м.
Если измерялось расстояние между
географическими пунктами (порядка
нескольких километров), то точность
такого измерения следует признать
весьма высокой; если же измерялись
размеры помещения (не превышающие
десятка метров), то измерение является
грубым. Для характеристики точности
существует понятие относительной
ошибки
(или относительной
погрешности)
Е,
представляющей собой отношение модуля
абсолютной ошибки к измеряемой величине:

.
(2)

Очевидно, что
относительная погрешность – величина
безразмерная, чаще всего ее выражают в
процентах.

При
определении ошибок измерений важно
иметь в виду следующее. Выражения (1) и
(2) содержат истинное значение измеряемой
величины Х,
которое точно знать невозможно: поэтому
значения х
и Е
в принципе не могут быть рассчитаны
точно. Можно лишь оценить
эти значения, т.е. найти их приближенно
с той или иной степенью достоверности.
Поэтому все расчеты, связанные с
определением погрешностей, должны
носить приближенный (оценочный) характер.

Случайная
и приборная погрешности

Разнообразные ошибки,
возникающие при измерениях, можно
классифицировать как по их происхождению,
так и по характеру их проявления.

По происхождению
ошибки делятся на инструментальные и
методические.

Инструментальные
погрешности обусловлены несовершенством
применяемых измерительных приборов и
приспособлений. Эти погрешности могут
быть уменьшены за счет применения более
точных приборов. Так, размер детали
можно измерить линейкой или штанген-циркулем.
Очевидно, что во втором случае ошибка
измерения меньше, чем в первом.

Методические
погрешности возникают из-за того, что
реальные физические процессы всегда в
той или иной степени отличаются от их
теоретических моделей. Например, формула
для периода колебаний математического
маятника в точности верна лишь при
бесконечно малой амплитуде колебаний;
формула Стокса, определяющая силу трения
при движении шарика в вязкой жидкости,
справедлива только в случае идеально
сферической формы и т.д. Обнаружить и
учесть методическую погрешность можно
путем измерения той же величины совершенно
иным независимым методом.

По характеру проявления
ошибки бывают систематические и
случайные.

Систематическая
погрешность может быть обусловлена как
приборами, так и методикой измерения.
Она имеет две характерные особенности.
Во-первых, систематическая погрешность
всегда либо положительна, либо отрицательна
и не меняет своего знака от опыта к
опыту. Во-вторых, систематическую
погрешность нельзя уменьшить за счет
увеличения числа измерений. Например,
если при отсутствии внешних воздействий
стрелка измерительного прибора показывает
величину х₀, отличную от
нуля, то во всех дальнейших измерениях
будет присутствовать систематическая
ошибка, равная х₀.

Случайная
ошибка также может быть как инструментальной,
так и методической. Причину ее появления
установить трудно, а чаще всего –
невозможно (это могут быть различные
помехи, случайные толчки, вибрации,
неверно взятый отсчет по прибору и
т.д.). Случайная погрешность бывает и
положительной и отрицательной, причем
непредсказуемо изменяет свой знак от
опыта к опыту. Значение ее можно уменьшить
путем увеличения числа измерений.

Детальный
анализ погрешностей измерения представляет
собой сложную задачу, для решения которой
не существует единого рецепта. Поэтому
в каждом конкретном случае этот анализ
проводят по-разному. Однако, в первом
приближении, если исключена систематическая
ошибка, то остальные можно условно
свести к следующим двум видам: приборная
и случайная.

Приборной
погрешностью в дальнейшем будем
называть случайную ошибку, обусловленную
измерительными приборами и приспособлениями,
а случайной – ошибку, причина
появления которой неизвестна. Приборную
погрешность измерения величины х
будем обозначать как х,
случайную – как _sx.

Оценка
случайной погрешности. Доверительный
интервал

Методика оценки
случайной погрешности основана на
положениях теории вероятностей и
математической статистики. Оценить
случайную ошибку можно только в том
случае, когда проведено неоднократное
измерение одной и той же величины.

Пусть
в результате проделанных измерений
получено п
значений величины х:
х₁,
х₂,
…, х_п.
Обозначим через

среднеарифметическое значение

.
(3)

В
теории вероятностей доказано, что при
увеличении числа измерений п
среднеарифметическое значение измеряемой
величины приближается к истинному:

При
небольшом числе измерений (п  10)
среднее значение может существенно
отличаться от истинного. Для того, чтобы
знать, насколько точно значение

характеризует измеряемую величину,
необходимо определить так называемый
доверительный интервал полученного
результата.

Поскольку
абсолютно точное измерение невозможно,
то вероятность правильности утверждения
«величина х
имеет значение, в точности равное
»
равна нулю. Вероятность же утверждения
«величина х
имеет какое-либо значение»
равна единице (100%). Таким образом,
вероятность правильности любого
промежуточного утверждения лежит в
пределах от 0 до 1. Цель измерения – найти
такой интервал, в котором с наперед
заданной вероятностью 
(0 <  < 1)
находится истинное значение измеряемой
величины. Этот интервал называется
доверительным
интервалом,
а неразрывно связанная с ним величина

–
доверительной вероятностью
(или коэффициентом
надежности).
За середину интервала принимается
среднее значение, рассчитанное по
формуле (3). Половина ширины доверительного
интервала представляет собой случайную
погрешность _sx
(рис. 1).

Рис.1

Очевидно,
что
ширина доверительного интервала (а
следовательно, и ошибка _sx)
зависит от того, насколько сильно
отличаются отдельные измерения величины
х_i
от среднего
значения
.
«Разброс» результатов измерений
относительно среднего характеризуется
среднеквадратичной
ошибкой ,
которую находят по формуле

,
(4)

где
.

Ширина
искомого доверительного интервала
прямо пропорциональна среднеквадратичной
ошибке:

.
(5)

Коэффициент
пропорциональности t_n,_
называется
коэффициентом
Стьюдента;
он зависит от числа опытов п
и доверительной вероятности .

На
рис. 1, а, б
наглядно
показано, что при прочих равных условиях
для увеличения вероятности попадания
истинного значения в доверительный
интервал необходимо увеличить ширину
последнего (вероятность «накрывания»
значения Х
более широким интервалом выше).
Следовательно, величина t_n,_
должна быть тем больше, чем выше
доверительная вероятность
.

С
увеличением количества опытов среднее
значение приближается к истинному;
поэтому при той же вероятности 
доверительный интервал можно взять
более узким (см. рис. 1, а,в).
Таким образом, с ростом п
коэффициент Сьюдента должен
уменьшаться. Таблица значений коэффи-циента
Стьюдента в зависимости от п
и 
дана в приложениях к настоящему пособию.

Следует
отметить, что доверительная вероятность
никак не связана с точностью результата
измерений. Величиной 
задаются
заранее, исходя из требований к их
надежности. В большинстве технических
экспериментов и в лабораторном практикуме
значение 
принимается
равным 0,95.

Расчет
случайной погрешности измерения величины
х проводится
в следующем порядке:

1) вычисляется
сумма измеренных значений, а затем –
среднее значение величины

по формуле (3);

2) для
каждого i-го
опыта рассчитываются разность между
измеренным и средним значениями
,
а также квадрат этой разности (отклонения)
(х_i)²;

3) находится
сумма квадратов отклонений, а затем –
средне-квадратичная ошибка 
по формуле (4);

4) по
заданной доверительной вероятности 
и числу
проведенных опытов п
из таблицы на с. 149 приложений выбирается
соответствующее значение коэффициента
Стьюдента t_n,_
и определяется случайная погрешность
_sx
по формуле (5).

Для
удобства расчетов и проверки промежуточных
результатов данные заносятся в таблицу,
три последних столбца которой заполняются
по образцу табл.1.

Таблица
1

Номер опыта	…	х	х	(х)²
1	…
2	…
…	…
п	…
	 =		 =

В
каждом конкретном случае величина х
имеет определенный физический смысл и
соответствующие единицы измерения. Это
может быть, например, ускорение свободного
падения g
(м/с²),
коэффициент вязкости жидкости 
(Пас)
и т.д. Пропущенные столбцы табл. 1
могут содержать промежуточные измеряемые
величины, необходимые для расчета
соответствующих значений х.

Пример
1. Для
определения ускорения а
движения тела измерялось время t
прохождения им пути S
без начальной
скорости. Используя известное соотношение
,
получим расчетную формулу

.
(6)

Результаты
измерений пути S
и времени t
приведены во втором и третьем столбцах
табл. 2. Проведя вычисления по формуле
(6), заполним

четвертый
столбец значениями ускорения a_i
и найдем их сумму, которую запишем под
этим столбцом в ячейку « 
= ». Затем рассчитаем среднее значение

по формуле (3)

Таблица
2

Номер опыта	S, м	t, c	а, м/с²	а, м/с²	(а)², (м/с²)²
1	5	2,20	2,07	0,04	0,0016
2	7	2,68	1,95	-0,08	0,0064
3	9	2,91	2,13	0,10	0,0100
4	11	3,35	1,96	-0,07	0,0049
		 =	8,11	 =	0,0229

Вычитая
из каждого значения a_i
среднее, найдем разности a_i
и занесем их в пятый столбец таблицы.
Возводя эти разности в квадрат, заполним
последний столбец. Затем рассчитаем
сумму квадратов отклонений и запишем
ее во вторую ячейку « 
= ». По формуле (4) определим
среднеквадратичную погрешность:

Задавшись
величиной доверительной вероятности
 = 0,95,
для числа опытов п = 4
из таблицы в приложениях (с. 149) выбираем
значение коэффициента Стьюдента t_n,_
= 3,18; с помощью формулы (5) оценим
случайную погрешность измерения
ускорения

_sа
= 3,180,0437  0,139 (м/с²) .

Способы
определения приборных ошибок

Основными характеристиками
измерительных приборов являются предел
измерения и цена деления, а также –
главным образом для электро-измерительных
приборов – класс точности.

Предел
измерения П
– это максимальное значение величины,
которое может быть измерено с помощью
данной шкалы прибора. Если
предел измерения не указан отдельно,
то его определяют по оцифровке шкалы.
Так, если рис. 2
изображает шкалу миллиамперметра, то
его предел измерения равен 100 мА.

Р
ис.2

Цена
деления Ц –
значение измеряемой величины,
соответствующее самому малому делению
шкалы. Если шкала начинается с нуля, то

где
N
– общее количество делений (например,
на рис. 2
N = 50).
Если эта шкала принадлежит амперметру
с пределом измерения 5 А,
то цена деления равна 5/50 = 0,1 (А).
Если шкала принадлежит термометру и
проградуирована в С,
то цена деления Ц = 100/50 = 2 (С).
Многие электроизмерительные приборы
имеют несколько пределов измерения.
При переключении их с одного предела
на другой изменяется и цена деления
шкалы.

Класс
точности К
представляет собой отношение абсолютной
приборной погрешности к пределу измерения
шкалы, выраженное в процентах:

.
(7)

Значение класса
точности (без символа «%») указывается,
как правило, на электроизмерительных
приборах.

В зависимости от вида
измерительного устройства абсолютная
приборная погрешность определяется
одним из нижеперечисленных способов.

1. Погрешность
указана непосредственно на приборе.
Так, на микрометре есть надпись «0,01 мм».
Если с помощью этого прибора измеряется,
например, диаметр шарика D
(лабораторная работа 1.2), то погрешность
его измерения D = 0,01 мм.
Абсолютная ошибка указывается обычно
на жидкостных (ртутных, спиртовых)
термометрах, штангенциркулях и др.

2. На приборе указан
класс точности. Согласно определению
этой величины, из формулы (7) имеем

.
(8)

Например, для вольтметра
с классом точности 2,5 и пределом измерения
600 В абсолютная приборная ошибка
измерения напряжения

3. Если на приборе
не указаны ни абсолютная погрешность,
ни класс точности, то в зависимости от
характера работы прибора возможны два
способа определения величины х:

а) указатель
значения измеряемой величины может
занимать только определенные (дискретные)
положения, соответствующие делениям
шкалы (например, электронные часы,
секундомеры, счетчики импульсов и т.п.).
Такие приборы являются приборами
дискретного действия, и их абсолютная
погрешность равна цене деления шкалы:
х = Ц.
Так, при измерении промежутка времени
t секундомером с ценой
деления 0,2 с погрешность t = 0,2 с;

б) указатель
значения измеряемой величины может
занимать любое положение на шкале
(линейки, рулетки, стрелочные весы,
термометры и т.п.). В этом случае абсолютная
приборная погрешность равна половине
цены деления: х = Ц/2.
Точность снимаемых показаний прибора
не должна превышать его возможностей.
Например, при показанном на рис. 3
положении стрелки прибора следует
записать либо 62,5 либо 63,0 – в обоих
случаях ошибка не превысит половины
цены деления. Записи же типа 62,7 или 62,8
не имеют смысла.

Рис.3

4. Если какая-либо
величина не измеряется в данном оыте,
а была измерена независимо и известно
лишь ее значение, то она является заданным
параметром. Так, в работе 2.1 по
определению коэффициента вязкости
воздуха такими параметрами являются
размеры капилляра, в опыте Юнга по
интерференции света (работа 5.1) –
расстояние между щелями и т.д. Погрешность
заданного параметра принимается равной
половине единицы последнего разряда
числа, которым задано значение этого
параметра. Например, если радиус капилляра
r задан с точностью
до сотых долей миллиметра, то его
погрешность r = 0,005 мм.

Погрешности
косвенных измерений

В большинстве физических
экспериментов искомая величина и
не измеряется непосредственно каким-либо
одним прибором, а рассчитывается на
основе измерения ряда промежуточных
величин x, y, z,…
Расчет проводится по определенной
формуле, которую в общем виде можно
записать как

и = и(x, y, z,…).
(9)

В этом случае говорят,
что величина и представляет собой
результат косвенного измерения в
отличие от x, y, z,…,
являющихся результатами прямых
измерений. Например, в
работе 1.2 коэффициент вязкости жидкости

рассчитывается по формуле

,
(10)

где _ш
– плотность материала шарика; _ж
– плотность жидкости; g
– ускорение свободного падения; D
– диаметр шарика; t –
время его падения в жидкости; l
– расстояние между метками на сосуде.
В данном случае результатами прямых
измерений являются величины l,
D и t,
а коэффициент вязкости 
– результат косвенного
измерения. Величины _ш,
_ж
и g представляют
собой заданные параметры.

Абсолютная
погрешность косвенного измерения и
зависит от погрешностей прямых измерений
x,
y,
z…и
от вида функции (9). Как правило, величину
и
можно оценить по формуле
вида

,
(11)

где
коэффициенты k_x,
k_y,
k_z,…
определяются видом зависимостей величины
и от x,
y, z,…
Приведенная ниже табл. 3 позволяет
найти эти коэффициенты для наиболее
распространенных элементарных функций
(a, b, c, n
– заданные константы).

Таблица
3

и(х)	k_x

На
практике зависимость (9) чаще всего имеет
вид степенной функции

показатели степеней
которой k,
m, n,…
– вещественные (положительные или
отрицательные, целые или дробные) числа;
С – постоянный коэффициент. В этом
случае абсолютная приборная погрешность
и
оценивается по формуле

,
(12)

где

– среднее значение величины и;

– относительные приборные погрешности
прямых измерений величин x,
y, z,…
Для подстановки в формулу (12) выбираются
наиболее представительные, т.е.
близкие к средним значения x,
y, z,…

При расчетах по
формулам типа (12) необходимо помнить
следующее.

1. Измеряемые
величины и их абсолютные погрешности
(например, х и х)
должны быть выражены в одних и тех же
единицах.

2. Расчеты не требуют
высокой точности вычислений и должны
иметь оценочный характер. Так, входящие
в подкоренное выражение и возводимые
в квадрат величины (kE_x,
mE_y,
nE_z,…)
обычно округляются с точностью до
двух значащих цифр (напомним, что ноль
является значащей цифрой только тогда,
когда перед ним слева есть хотя бы одна
цифра, отличная от нуля). Далее, если
одна из этих величин (например, |kE_x|)по
модулю превышает наибольшую из остальных
(|mE_y|,
|nE_z|,…)
более чем в три раза, то можно, не прибегая
к вычислениям по формуле (12), принять
абсолютную ошибку равной
.
Если же одна из них более чем в три раза
меньше наименьшей из остальных, то при
расчете по формуле (12) ею можно пренебречь.

Пример 2.
Пусть при определении ускорения тела
(см. пример 1) путь S
измерялся рулеткой с ценой деления
1 мм, а время t
– электронным секундомером. Тогда, в
соответствии с изложенными в п.3, а, б
(с. 13) правилами, погрешности прямых
измерений будут равны

S = 0,5 мм = 0,0005 м;

t = 0,01 с.

Расчетную формулу
(6) можно записать в виде степенной
функции

a(S, t) = 2S¹t^– 2;

тогда на основании
(12) погрешность косвенного измерения
ускорения а
определится выражением

В
качестве наиболее представительных
значений измеренных величин возьмем
(см. табл. 2) S  8 м;
t  3 с
и оценим по модулю относительные
приборные ошибки прямых измерений с
учетом их весовых коэффициентов:

;

Очевидно,
что в данном случае величиной E_S
можно пренебречь и принять погрешность
а
равной

Пример 3.
Вернемся к определению коэффициента
вязкости жидкости (работа 1.2). Расчетную
формулу (10) можно представить в виде

Источник

Погрешности измерений, представление результатов эксперимента

Шкала измерительного прибора
Цена деления
Виды измерений
Погрешность измерений, абсолютная и относительная погрешность
Абсолютная погрешность серии измерений
Представление результатов эксперимента
Задачи

п.1. Шкала измерительного прибора

Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.

Примеры шкал различных приборов:

п.2. Цена деления

Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.

Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.

Пример определения цены деления:

Определим цену деления основной шкалы секундомера.
Два ближайших пронумерованных деления на основной шкале:a = 5 c
b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*}

п.3. Виды измерений

Вид измерений

Определение

Пример

Прямое измерение

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Косвенное измерение

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.

Составляющие погрешности измерений

Причины

Инструментальная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Погрешность метода

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Погрешность оператора

Определяется субъективным фактором, ошибками экспериментатора.

Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$

Если величина (a_0) – это истинное значение, а (triangle a) – погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).

Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$

Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$

Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.

Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

определение длины с помощью линейки или мерной ленты;
определение объема с помощью мензурки.

Пример получения результатов прямых измерений с помощью линейки:

Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями.
Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см})
Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$

Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями.
Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см})
Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

№ опыта	1	2	3	Сумма
Масса, г	99,8	101,2	100,3	301,3
Абсолютное отклонение, г	0,6	0,8	0,1	1,5

Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}

п.6. Представление результатов эксперимента

Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то

абсолютная погрешность их суммы равна сумме абсолютных погрешностей

$$ triangle (a+b)=triangle a+triangle b $$

абсолютная погрешность их разности также равна сумме абсолютных погрешностей

$$ triangle (a-b)=triangle a+triangle b $$

Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:

относительная погрешность их произведения равна сумме относительных погрешностей

$$ delta_{acdot b}=delta_a+delta_b $$

относительная погрешность их частного также равна сумме относительных погрешностей

$$ delta_{a/b}=delta_a+delta_b $$

Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:

относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности

$$ delta_{a^2}=2delta_a $$

относительная погрешность куба (a^3) равна утроенной относительной погрешности

$$ delta_{a^3}=3delta_a $$

относительная погрешность произвольной натуральной степени (a^n) равна

$$ delta_{a^n}=ndelta_a $$

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	(triangle=frac{b-a}{n+1}), мл
1	20	40	4	(frac{40-20}{4+1}=4)
2	100	200	4	(frac{200-100}{4+1}=20)
3	15	30	4	(frac{30-15}{4+1}=3)
4	200	400	4	(frac{400-200}{4+1}=40)

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем (V_0), мл	Абсолютная погрешность (triangle V=frac{triangle}{2}), мл	Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%})
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?

Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})

Источник

Загрузить PDF

Абсолютная ошибка – это разность между измеренным значением и фактическим значением.^[1] Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.^[2] Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.

1

Запишите формулу для вычисления абсолютной ошибки. Формула: $Delta x=x_{{0}}-x$ , где – абсолютная ошибка (разность между измеренным и фактическим значениями), $x_{{0}}$ – измеренное значение, – фактическое значение.^[3]
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо .
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м: $Delta x=x_{{0}}-105$ .
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо $x_{0}$ .
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м: .
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[4] Так вы вычислите абсолютную ошибку.
- В нашем примере: , то есть абсолютная ошибка измерения равна 1 м.
Реклама

1

Запишите формулу для вычисления относительной ошибки. Формула: $delta x={frac {x_{{0}}-x}{x}}$ , где – относительная ошибка (отношение абсолютной ошибки к фактическому значению), $x_{{0}}$ – измеренное значение, – фактическое значение.^[5]
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо .
- Например, если относительная ошибка равна 0,02, формула запишется так: $0,02={frac {x_{{0}}-x}{x}}$ .
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо .
- Например, если фактическое значение равно 105 м, формула запишется так: $0,02={frac {x_{{0}}-105}{105}}$ .
4

Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
5

Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете $x_{{0}}$ , то есть измеренное значение.
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[6] Так вы вычислите абсолютную ошибку.
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так: . Таким образом, абсолютная ошибка равна 2,1 м.
Реклама

1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.^[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
2
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.^[9] Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[10] Так вы вычислите абсолютную ошибку.
- Например, если измеренная длина поля равна м, то есть абсолютная ошибка равна 0,5 м.
Реклама

Советы

Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.

Об этой статье

Эту страницу просматривали 25 612 раз.

Была ли эта статья полезной?

Источник

Абсолютной
погрешностью
измерительного прибора называется
разность между его показанием и истинным
значением измеряемой величины. Так как
истинное значение измеряемой величины
установить невозможно, в измерительной
технике используется так называемое
действительное
значение,
полученное с помощью образцового прибора
[1-2].

Абсолютная
погрешность:
Δ = Х_п
— Q₀,

где
Х_п
— значение, полученное при измерении
величины рабочим измерительным прибором;
Q₀
— действительное значение измеряемой
величины.

Относительная
погрешность измерительного прибора
– это
отношение абсолютной погрешности к
действительному значению, выраженное
в %:

При
вычислении относительной погрешности
абсолютную погрешность можно также
относить к показанию рабочего прибора
X_п.

Если
прибор работает в условиях, отличных
от условий, оговоренных в паспорте, то
возникает дополнительная
погрешность, увеличивающая
общую погрешность прибора. К дополнительным
погрешностям относятся: температурная
погрешность, вызванная отклонением
температуры окружающей среды от
нормальной; инструментальная погрешность,
обусловленная отклонением положения
прибора от нормального рабочего положения
и т.п. За нормальную температуру
окружающего воздуха принимают 20° С, а
за нормальное атмосферное давление –
101325 Н/м²
(760 мм рт. ст.).

Приведённая
относительная погрешность
– это отношение абсолютной погрешности
к нормирующему значению:

где
Х_норм
– чаще всего диапазон шкалы измеряемого
прибора

Вариацией
измерительного
прибора N
называется
наибольшая экспериментально полученная
разность между показаниями измерительного
прибора при прямом и обратном ходе,
соответствующими одному и тому же
действительному значению измеряемой
величины при одинаковых условиях
измерения. Вариации вызываются трением
в механизме прибора, зазорами (люфтами)
в кинематических парах, гистерезисом
и упругим последействием чувствительных
элементов прибора. Таким образом, N
– это абсолютная вариация прибора.

Приведенная
вариация прибора :

где
ΔN
– абсолютная вариация прибора; N_max
и N_min
– соответственно верхнее и нижнее
предельные значения шкалы прибора.

1.8. Класс точности приборов

Обобщенной
характеристикой средств измерения
является класс точности, определяемый
предельными значениями допускаемых
основных и дополнительных погрешностей,
а также другими свойствами средств
измерения, влияющими на точность,
значение которых устанавливается в
стандартах на отдельные виды средств
измерений. Класс точности средств
измерений характеризует их точностные
свойства, но не является непосредственным
показателем точности измерений,
выполняемых с помощью этих средств.
Например, класс точности вольтметра
характеризует пределы допускаемой
основной погрешности и допускаемых
изменений показаний, вызываемых внешним
магнитным полем и отклонением от
нормальных значений температуры, частоты
переменного тока и некоторых других
влияющих факторов [1-2].

В
настоящее время в нашей стране используются
два вида классов точности: 1) по абсолютным
погрешностям (порядковые номера классов);
2) по относительным приведенным
погрешностям (отношение абсолютной
погрешности Δ к диапазону шкалы прибора,
выраженное в процентах).

Государственными
стандартами для разных приборов
установлены различные классы точности.
Класс точности обозначается на циферблате
прибора либо в паспорте прибора.

Согласно
ГОСТ 8.401-80 (взамен ГОСТ 13600-68) классы
точности выбираются из ряда:

К=(1;1.5;2.0;2.5;3.0;4.0;5.0;6.0)*10ⁿ,

где
n=1,0,-1,2….

Средства
измерений с двумя и более шкалами могут
иметь соответственно два и более классов
точности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: . То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):

(5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
Не вполне ровно установили рулетку.
Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины: и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

Для линейки 1:
Для линейки 2:
Для линейки 3:

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
Цена деления шкалы равна значению наименьшего деления шкалы.
Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

Заказать решение задач по физике

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.