Как найти абсолютную погрешность аргумента

Как найти абсолютную погрешность аргумента

Вычисление погрешности функций. Определение допустимой погрешности аргументов по допустимой погрешности функций

Страницы работы

Фрагмент текста работы

             б) 0,096835;   .                               б)
0,66385; .

        3) а)12,688 ;  б)
4,636.                                    3)   а) 6,743;   б) 0,543 .

18.4.
ВЫЧИСЛЕНИЕ ПОГРЕШНОСТИ ФУНКЦИЙ

18.4.1. Функции одной переменной. Абсолютная погрешность дифференцируемой
функции , вызываемая достаточно малой погрешностью
аргумента , оценивается величиной

                                                    
         ,                                         
(18.12)

          Если значения функции  положительны, то для относительной погрешности
имеет место оценка

                                                 
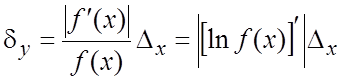.                             (18.13)

          Например, для
тригонометрических функций абсолютные погрешности синуса и косинуса не
превосходят абсолютных погрешностей аргумента:

                                         
,    .         (18.14)

18.4.2. Функции нескольких
переменных.   Пусть
задана некоторая функция , от п аргументов
 и пусть значения каждого из аргумен­тов , определены с некоторыми погрешностями , i = 1, 2,…, п.
Требуется найти погрешность данной функции.

Для
решения этой задачи будем предполагать, что функция  является
дифференцируемой в некоторой области D. Абсолютная погрешность  функции
y при заданных абсолютных погрешностях
 аргументов  равна

                      .             (18.15)

Предполагая, что величины , i = 1, 2,…, п  достаточно
малы, можно записать приближенные равенства

                                                  
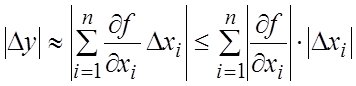                           (18.16)

Следовательно, предельная абсолютная
погрешность  функции y равна

                                                   
,                                             
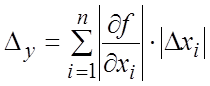(18.17)

где  предельная
абсолютная погрешность аргумента .

Оценка для относительной
погрешности функции получается путем деления обеих частей неравенства (18.15)
на

                                            
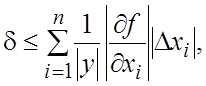                                          (18.18)

Из формулы (18.18) получаем выражение
для предельной отно­сительной погрешности функции у

                                                       
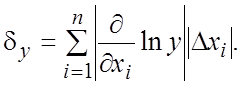                                     (18.19)

Рассмотрим
отдельные примеры на вычисление погрешностей различных функциональных
соотношений. Будем предполагать, что в каждом примере заданы те или иные
погрешности аргументов.

1. Пусть .
По формуле (18.17) предель­ная абсолютная погрешность суммы п слагаемых
равна

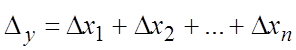                                          .                             (18.20)

2. Пусть . По
формуле (18.17) предельная абсолют­ная погрешность разности двух чисел равна

.

3. Пусть  , причем xi  (i=1, 2, …, п) положительны. В соответствии с формулой (18.19)
проведем  преобразования с целью получения выражения для предельной
относительной погрешности произведения п сомножителей

.

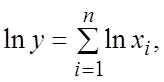
4. Пусть 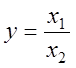. По
формуле (18.19) предельная относительная погрешность частного равна  

                                               
.

5. Пусть . Тогда .

.

6. Пусть .
Следовательно, .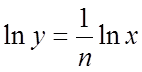

.

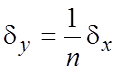18.5.    Определение допустимой погрешности аргументов по допустимой
погрешности функций

Задача определения какими должны быть
погрешности исходных приближений, чтобы полученный результат имел заданную
степень точности, имеет однозначное решение только для функции одной переменной
: если  эта функция дифференцируема и  , то

                                                      .                                              
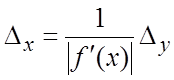(18.21)

          Для функций
нескольких переменных  эта задача решается
неоднозначно. Для ее решения необходимо наложить какие-либо условия на
погрешность исходных данных. Если использовать принцип равных влияний, считая что в формуле (18.17) все
слагаемые 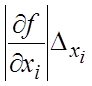 равны между собой, получим

                                             
  .                                            
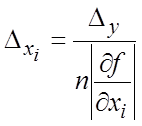
(18.22)

Пример
8. Даны числа ; . Тогда
. Причем последняя цифра сомнительная.

Пример
9. Найти сумму , где ; ; . Причем
все цифры верные.

 
Имеем . Предельная абсолютная погрешность суммы . Стало быть, 7.84 < y< 7.87. В результате верными будут
цифры 7.8. Последняя цифра 4 сомнительная. #

Похожие материалы

  • Вычисление приближенных значений
  • Вычисление тройного интеграла в декартовых координатах
  • Действительные функции одного переменного

Информация о работе

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Источник

Пусть
непрерывно
дифференцируемая функция,

–
приближенные значения ее аргументов,
для которых

–
известные абсолютные погрешности.

Для
погрешности приближенного значения
функции
по
формуле Лагранжа получаем

,
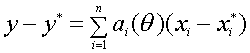где

Заменяя
, получаем

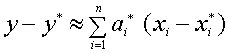
Оценка погрешности
соответственно:

,
где

Или
 ( 5) ,

 где
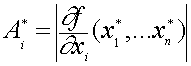 (6)

3.2.
Погрешность суммы

Пусть
задана функция

Тогда
из (5) , (6)
,.

Для абсолютной
погрешности получаем

.

Относительная
погрешность

.

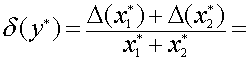
Пусть
,,
тогда,
т.е. при сложении приближенных величин
относительная погрешность не возрастает.

3.3.
Погрешность разности

Пусть
задана функция

Тогда аналогично
предыдущему абсолютная погрешность

.

Для относительной
погрешности имеем формулу

.

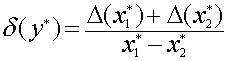Отсюда
следует, что если приближенные значения
иблизки
друг к другу, то относительная погрешность
их разностиможет оказаться намного большеи.

3.4.
Погрешность произведения

Пусть
задана функция 

Тогда абсолютная
погрешность

.

Относительная
погрешность

.

3.5.
Погрешность частного

Пусть
задана функция 

Тогда абсолютная
погрешность

.

Относительная
погрешность

3.6.
Обратная задача оценки погрешности

Иногда
возникает задача определения допустимой
погрешности аргументов, при которой
погрешность значений функции будет не
более заданной величины
.

Используем
ранее полученное неравенство ( 6 )

.

Должно
быть
.

При
n=1 вопрос
решается однозначно:

При
n>1
возможны разные подходы:

1. Считать погрешности
всех аргументов одинаковыми

Тогда
получаем 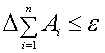, следовательно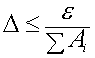

2.
Считать, что вклад погрешности каждого
аргумента в погрешность результата
одинаков.  ,
тогда

Если
для разных аргументов достижение
определенной точности их задания
существенно различается, то можно ввести
функцию стоимости
затрат
на задание точкис
заданными абсолютными погрешностямии
искать ее минимум в области

, 

4. Вычисление погрешности арифметических действий в среде Mathcad .

Настройка
среды MathCad
(системные
переменные ).

Изменение
значений системных переменных производят
во вкладке Встроенные
переменные
диалогового окна Math
Options
команды Математика
 Опции.

1)
Допустимая
погрешность – значение системной
переменной TOL
(по
умолчанию TOL =10-3).

Установить
TOL:=10–5.

2)
Изменение
количества цифр в результате после
разделяющей точки

производят
во вкладке Результат
диалогового
окна Количество
десятичных позиций команды
Формат
 Результат.

Установить
равным 6 (по
умолчанию равно 3) , что на 1 больше
порядка величины
TOL
– для возможности округления конечного
результата
.

Пример
4.1.Вычисление погрешности операций
сложения , вычитания , умножения и
деления.

Пусть
числа x и y заданы с абсолютными
погрешностями
x
иy

x
: = 2.5378   
x
: = 0.0001                 
y : = 2.536y
: = 0.001

Тогда относительные
погрешности чисел

,
,    ,
    

Найдем погрешности
суммы и разности чисел

S1
: = x + y      
S1
: =
x
+
y      
      

S1
= 1.1 x 10-3      

S2
: = x – y      
S2
: =
x
+
y      
      

S2
= 1.1 x 10-3
      

Относительная
погрешность разности в
раз больше относительной погрешности
суммы!

Пример
4.2. Погрешность
функции многих переменных.

Пусть
x : = -3.59       y : = 0.467     
z : = 563.2

По
приведенным начальным условиям считаем,
что абсолютные погрешности равны

x
: = 0.01    
y
: = 0.001z
: = 0.1

Значение
функции равно : f ( x, y, z ) = 6.64198865

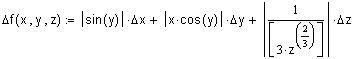
f
( x, y, z ) = 1.234 x 10
-3

f
( x, y, z ) = 8.196 x 10
-3    

Пример
4.3. Постановка
задачи:

Дан
ряд
.

Найти
сумму ряда S
аналитически.

Вычислить
значения частичных сумм ряда S=и найти величину погрешности при
значениях значениях=,,,,.

Построить
гистограмму зависимости верных цифр
результата от
.

Аналитическое
решение задачи:

S=


=

,

.

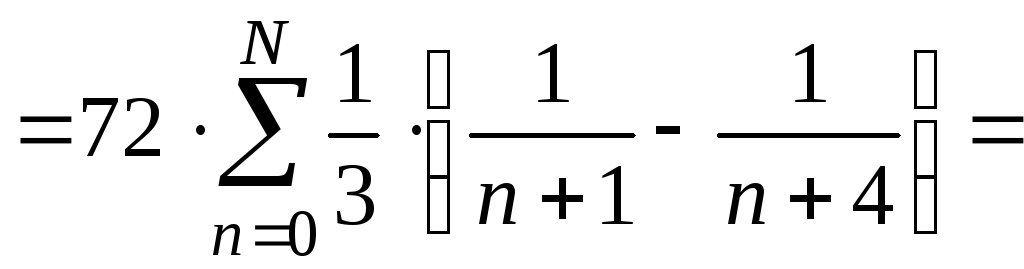
ОТВЕТ:
S
=
= 44.

Введем
функцию

S(N)=
.

Тогда
абсолютную погрешность можно определить
с помощью функции

d(S(N))
=.

Tексты
программ:

Гистограмма

Результаты
вычислительного эксперимента:

Значение
частичной Величина абсолютной
Количество

суммы
ряда погрешности
верных цифр

S(10)=38.439560439
d(10)=5.56

S(100)=43.3009269
d(100)=0.699

2

S(1000)=43.9282153
d(1000)=0.072

3

S(10000)=43.992802
d(10000)=0.0072

4

S(100000)=43.9992802159957
d(100000)=0.00072

5

Вывод:
Как
видно из приведенного вычислительного
эксперимента, увеличение числа членов
ряда в 10 раз по сравнению с предыдущим
случаем увеличивает число верных цифр
в ответе на 1.

Соседние файлы в папке MMM

  • #
  • #
  • #

    16.02.2016436.7 Кб50PZ-1 MathCAD.mcd

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Абсолютная и относительная погрешность


Абсолютная и относительная погрешность

4.2

Средняя оценка: 4.2

Всего получено оценок: 2180.

4.2

Средняя оценка: 4.2

Всего получено оценок: 2180.

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Опыт работы учителем математики – более 33 лет.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

  • при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
  • при делении и умножении чисел требуется сложить относительные погрешности;
  • при возведении в степень относительную погрешность умножают на показатель степени.

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Заключение

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Тест по теме

Доска почёта

Доска почёта

Чтобы попасть сюда – пройдите тест.

  • Светлана Лобанова-Асямолова

    10/10

  • Валерий Соломин

    10/10

  • Анастасия Юшкова

    10/10

  • Ксюша Пономарева

    7/10

  • Паша Кривов

    10/10

  • Евгений Холопик

    9/10

  • Guzel Murtazina

    10/10

  • Максим Аполонов

    10/10

  • Olga Bimbirene

    9/10

  • Света Колодий

    10/10

Оценка статьи

4.2

Средняя оценка: 4.2

Всего получено оценок: 2180.

А какая ваша оценка?

Источник

Абсолютная погрешность дифференцируемой функции y = f(x), вызываемая достаточно малой погрешностью аргу­мента Dx, оценивается величиной :.

Если значения функции f(x) положительны, то для относи­тельной погрешности имеет место оценка:

.

Пример 1

Абсолютные погрешности синуса и косинуса находится по формулам:

D sin x = |cos x|×Dx,

D cos x = |sin x|×Dx, где x изменяется в радианах.

Погрешность вычисления значения функции нескольких переменных (общая формула для погрешности)

Абсолютная погрешность дифференцируемой функции y = f(x1, x2, x3, …, xn), вызываемая достаточно малыми погрешно­стями Dx1, Dx2,…,Dxn­ аргументов x1, x2, x3,…,xn, оценивается вели­чиной:

.

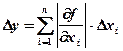Пример 2

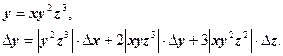
Если значения функции положительны, то для относитель­ной погрешности имеет место оценка:

.

Пример 3

Вычислить значение функции f, абсолютную и от­носительную погрешности вычисления f, если

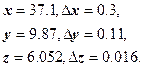
Сначала найдем относительную погрешность вычисления значения f, а затем абсолютную погрешность. Функция f положительна и дифференцируема, поэтому воспользуемся формулой:

;      ;

;

.

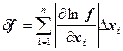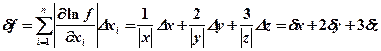Найдем относительные погрешности аргументов:

; .

Относительная погрешность является величиной порядка 1 %, следовательно, значение f содержит 2 верные значащие цифры. Следовательно, в записи f  нужно указать три значащие цифры, две из которых будут верными  и одна сомнительная. Вычислим xy2z3 = 801133.57, оставляя три значащие цифры, получим: f = 801*103. Зная значение f и её относительную погрешность, найдем абсолютную погрешность:

.

Источник

Добавить комментарий