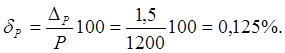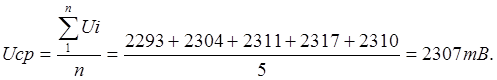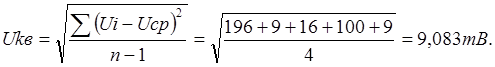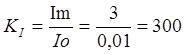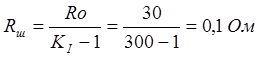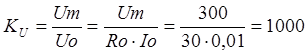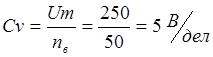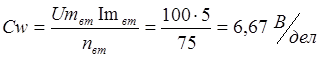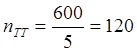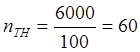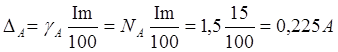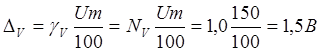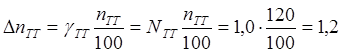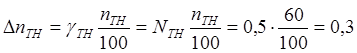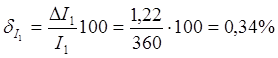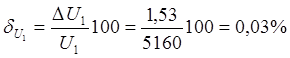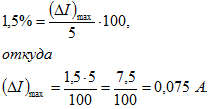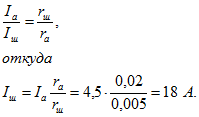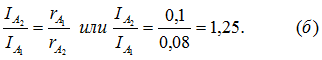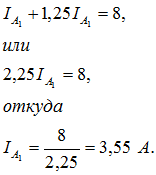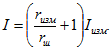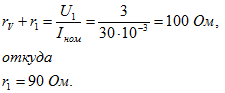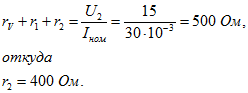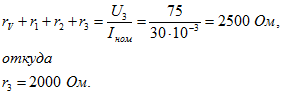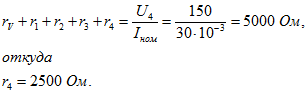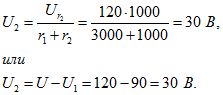Оценка погрешностей электрических измерений
Абсолютная
погрешность измерений, производимых
электроизмерительными приборами,
оценивается, исходя из класса точности
приборов. Обозначение класса точности
0,2; 0,5; 1,0 и т.д. не только характеризует
прибор в зависимости от системы,
конструкции, качества материалов,
точности градуировки и других факторов,
но и указывает, что погрешность показаний
прибора соответствующего класса в любом
месте шкалы не должна превышать 0,2%;
0,5%; 1%.
Если
обозначим через
максимально возможное показание прибора,
а через–
номер класса прибора, то получим
абсолютную погрешность прибора
.
Например,
вольтметр 0,2 класса (n
= 0,002),
шкала которого рассчитана на 50 В, имеет
абсолютную погрешность
,
а
амперметр класса 1,5, рассчитанный
на максимальное показание 5 А, имеет
абсолютную погрешность
.
Так
как абсолютная погрешность считается
одинаковой по всей шкале данного
электроизмерительного прибора, то
относительная погрешность
будет тем больше, чем меньше измеряемая
величина. Если, например, при помощи
указанного амперметра измерить ток
около 4А, то относительная погрешность
будет составлять 1,9%, а при измерении
силы тока около 1А – 7,5%.
При точных
измерениях следует пользоваться такими
приборами, чтобы предполагаемое значение
измеряемой величины составило 70-80% от
максимального (номинального) значения.
Поэтому применяют приборы, имеющие
несколько пределов измерений; при работе
с таким прибором его включают в цепь на
тот предел измерений, который достаточно
близок к предполагаемому значению
измеряемой величины.
Рассмотрим
вычисление погрешностей на следующем
примере.
Определить
погрешность измерения внутреннего
сопротивления элемента, электродвижущая
сила которого Е, напряжение на полюсах
U
и величина тока I.
Для измерения применены вольтметр
класса 0,5 ()
и
амперметр класса 1,0 ().Результаты
измерений следующие: Е = 2В, U
= 1,3 В,
I
= 1,2 А.
Абсолютные
погрешности измерений:
;
.
Вычисление
внутреннего сопротивления производим
по формуле
. (1)
Максимальная
относительная погрешность может быть
определена общеизвестным методом.
Логарифмируя выражение (1)
lnr
= ln(E-U)
– lnI,
находим относительную
погрешность
;
.
Эта
погрешность,
выраженная в процентах, составляет:
.
С
помощью формулы (1) находим внутренне
сопротивление r
и абсолютную погрешность
r:
Ом;
=
0,029 Ом =
0,03 Ом.
Следовательно,
внутреннее сопротивление
0,03)
Ом.
ЛАБОРАТОРНАЯ
РАБОТА № 2.1
Изучение электростатических полей методом электролитического моделирования
Цель
работы:
-
Ознакомиться
с одним из наиболее распространенных
способов изучения характеристик
электростатического поля с помощью
электролитической ванны. -
Практически
исследовать некоторые электростатические
поля.
Приборы и
принадлежности: электростатическая
ванна, набор электродов; индикатор нуля,
пантограф.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача 1
Для
определения мощности в цепи постоянного тока были измерены напряжение сети U вольтметром класса точности NB
с пределом измерений Um, ток I амперметром класса точности Na
с пределом измерений Im. Определить
мощность, потребляемую приёмником, а также относительную и абсолютную
погрешности её определения.
Дано:
Найти:
Решение:
1) Найдем
мощность, потребляемую приемником
2) Класс
точности определяет приведенную погрешность
3) Найдем
абсолютную погрешность измерения тока и напряжения
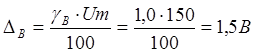
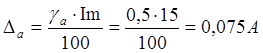
4) Найдем
абсолютную погрешность измерения мощности при косвенном измерении
5) Найдем
относительную погрешность измерения мощности
6) Доверительный
интервал результата измерения с вероятностью .
Задача 2
Проведено пять
независимых наблюдений одного и того же напряжения U.
Найти результат измерения и доверительную вероятность того, что абсолютная
погрешность измерения не превышает по модулю DU. Систематической погрешностью можно пренебречь.
Дано:
Найти:
Решение:
1) Определим
среднее арифметическое результатов измерения
2) Определяем
среднее квадратичное результатов измерения
3) Для
определения интервала и вероятности пользуются распределением Стьюдента, где
доверительный интервал равняется , где
– коэффициент Стьюдента,
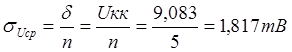
результата измерения.
4) Находим
доверительный интервал
5) Результат
измерения
Задача 3
Обмотка
магнитоэлектрического измерительного механизма имеет сопротивление RO и рассчитана на предельный длительный ток IO, при котором подвижная часть получает
наибольшее отклонение. Каким образом на базе указанного измерительного
механизма сделать амперметр с пределом измерений Im
и вольтметр с пределом измерений Um?
Дано:
Найти: ,
Решение:
1) Расчет
измерительной цепи амперметра
1.1
Определяем коэффициент расширения пределов измерения по току
1.2 Определяем сопротивление
шунта
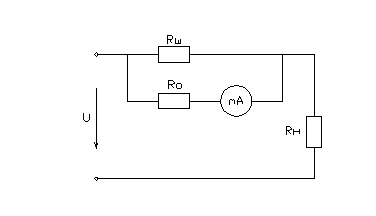
1.3
Схема измерительной цепи
2) Расчет
цепи вольтметра
2.1 Определяем коэффициент
расширения пределов измерения по напряжению
2.2 Определяем добавочное
сопротивление
2.3
Схема включения
Задача 4
Определить
цену деления измерительных приборов:
1) амперметра, имеющего на шкале na делений и предел измерения Im;
2)вольтметра, имеющего nв делений шкалы и предел измерения Um;
3) ваттметра, имеющего nВТ делений шкалы и пределы измерений по току Im ВТ и напряжению Um
ВТ.
Дано:
Найти:
Решение:
1) Цена деления
амперметра
2) Цена деления
вольтметра
3) Цена
деления ваттметра
Задача 5
У вольтметра и
амперметра с пределами измерений Um и Im, включенных соответственно через измерительные
трансформаторы напряжения 6000/100 и тока 600/5, отчёт по шкале составил U2 и I2.
Определить напряжение и ток в сети, а также предел допускаемой абсолютной и
относительной погрешностей измерения, если известны класс точности приборов Na и Nв и
измерительных трансформаторов Nтн и Nтт. Привести схему измерения.
Дано:
Найти:
Решение:
1) Определим
коэффициенты трансформации трансформатора напряжения и тока
2) Определим
ток и напряжение в сети
3) Определим
абсолютные погрешности амперметра и вольтметра
4) Определяем
абсолютные погрешности коэффициентов трансформации трансформатора тока и
напряжения
5) Результирующие
абсолютные погрешности измерения тока и напряжения равны
6)
Относительные погрешности измерения тока и напряжения
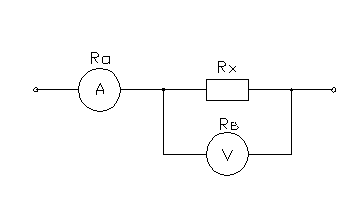
Задача 6
Определить
относительные погрешности измерения сопротивления Rx
в цепи постоянного тока с помощью амперметра и вольтметра при подключении их
двумя возможными способами. Сопротивление амперметра – Ra,
вольтметра – Rв. Сделать вывод о
целесообразности использования той или иной схемы.
Дано:
Найти: .
Решение:
Принципиальные
схемы
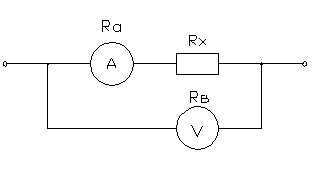
Схема
1 Схема 2
1) Для
схемы включения 1.
1.1.
Измеренное сопротивление.
1.2.
Определяем абсолютную погрешность.
1.3.
Определяем относительную погрешность.
Федеральное
Агентство по образованию
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И
РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра физики
ОТЧЕТ
Лабораторная
работа по курсу «Общая физика»
ИЗУЧЕНИЕ МАГНИТНОГО
ПОЛЯ КРУГОВОГО ТОКА
Преподаватель Студент
группы
___________ /____________.
/ __________ / /
___________201_
г. __________ 2011 г.
2011
Целью
настоящей работы является определение
величины удельного заряда электрона
методом магнетрона.
2. ОПИСАНИЕ УСТАНОВКИ
И МЕТОДИКИ ЭКСПЕРИМЕНТА
В качестве магнетрона
используется электронная лампа 3Ц22С,
которая имеет цилиндрические анод и
катод. Диаметр катода равен 1 мм.
Несоосность между осями катода и анода
порядка 1 мм. Поэтому для данной лампы
расстояние от катода до анода можно
принять R
= (8 ± 1) мм.
На лампу надевается
соленоид с большим числом витков на
единицу длины. Густота намотки соленоида
для разных блоков (вариантов) приведена
в Журнале измерений.
Погрешность густоты
намотки соленоида составляет 5 вит./см.
Для определения
зависимости анодного тока от тока
соленоида используется следующая схема
измерения (рис. 2.1).
Рисунок 2.1 – Схема
экспериментальной установки
Значение анодного
тока измеряется микроамперметром (μA),
который вмонтирован в основную панель
лабораторного макета. Значение тока
соленоида измеряется миллиамперметром
(mA),
который также вмонтирован в основную
панель. Регулировка тока соленоида
осуществляется с помощью ручки
потенциометра RP1,
выведенную на основную панель. Ручка
потенциометра RP2
для регулирования анодного напряжения
выведена на малую панель (блок питания
лабораторного макета). В эту же панель
вмонтирован вольтметр (V),
измеряющий анодное напряжение.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ
ФОРМУЛЫ
Для расчёта
удельного заряда электрона будем
использовать формулу:
, (3.1)
где e
– заряд электрона, m
– масса электрона
μ
– относительная магнитная проницаемость
среды (для вакуума μ
= 1);
μ0
– магнитная
постоянная (в СИ
μ0
= 4·π·10-7
Гн/м);
n –
число витков, приходящихся на единицу
длины соленоида;
Iкр
– значение
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения.
R
– расстояние от катода до анода
Ua
—
анодное напряжение лампы
Расчет погрешности:
Абсолютная
погрешность расчёта удельного заряда
электрона равна:
, (3.2)
где
— коэффициент Стьюдента,
(3.3)
Или
Относительная
погрешность расчёта удельного заряда
электрона
, (3.4)
где
— относительная погрешность измерения
анодного напряжения лампы ()
— относительная
погрешность расстояние от катода до
анода (
Относительная
погрешность квадрата расстояния от
катода до анода
(3.5)
— относительная
погрешность расчёта значения квадрата
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения ()
Относительная
погрешность расчёта значения силы тока
в соленоиде, при котором индукция
магнитного поля достигает критического
значения рассчитывается как:
, (3.6)
где
— абсолютная погрешность расчёта значения
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения, она вычисляется
по формуле
(3.7)
4. РЕЗУЛЬТАТЫ РАБОТЫ
И ИХ АНАЛИЗ.
Измеренные значения
и результаты их обработки приведены в
таблице.
Таблица 4.1
Зависимость
анодного тока Iа
от тока
соленоида Iс
при
различных значениях анодного напряжения
Uа
|
Номер опыта |
Uа |
Uа |
Uа |
Uа |
||||
|
Iс, mA |
Iа, μA |
Iс, MA |
Iа, μA |
Iс, mA |
Iа, μA |
Iс, mA |
Iа, μA |
|
|
1 |
50,286 |
500 |
49,615 |
500 |
50,016 |
500 |
50,061 |
500 |
|
2 |
54,486 |
500 |
73,173 |
500 |
87,873 |
500 |
98,231 |
500 |
|
3 |
64,4 |
486 |
75,172 |
475 |
89,233 |
475 |
101,89 |
486 |
|
4 |
64,629 |
438 |
75,882 |
327 |
89,848 |
373 |
103,19 |
299 |
|
5 |
64,559 |
450 |
76,42 |
228 |
91,117 |
167 |
103,44 |
260 |
|
6 |
65,322 |
276 |
76,633 |
192 |
91,479 |
111 |
104,0 |
185 |
|
7 |
66,011 |
131 |
77,199 |
82 |
91,652 |
82 |
104,54 |
116 |
|
8 |
71,368 |
34 |
77,944 |
55 |
99,23 |
9 |
105,43 |
55 |
|
9 |
75,093 |
10 |
86,133 |
17 |
102,77 |
11 |
113,01 |
32 |
|
10 |
78,522 |
10 |
89,103 |
10 |
106,09 |
10 |
120,82 |
10 |
|
Iкр,= |
Iкр,= |
Iкр,= |
Iкр,= |
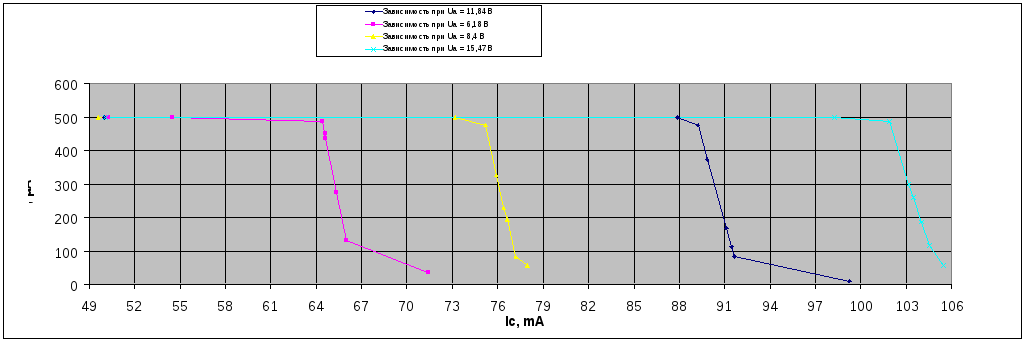
Рассчитаем удельный
заряд электрона по формуле (3.1),
густота намотки соленоида n
= 26000вит/м, расстояние от катода до анода
R
= 8 мм подробности
расчёта в таблице 2
Найдём значение
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения из графиков:
Рис 4.1 Зависимость
анодного тока от тока от тока в соленоиде
при Uа = 6.18В , Uа = 8.4В, Uа = 11,84В, Uа = 15,47В
Занесём данные
значение силы
тока в соленоиде, при котором индукция
магнитного поля достигает критического
значения от
анодного напряжение лампы в таблицу
4.2
Таблица 4.2
Зависимость силы
тока в соленоиде, при котором индукция
магнитного поля достигает критического
значения от
анодного напряжение лампы
|
Uа |
Iкр |
|
6,18 |
64,5 |
|
8,4 |
75 |
|
11,84 |
89 |
|
15,7 |
102 |
Найдём абсолютную
погрешность значения силы тока в
соленоиде, при котором индукция магнитного
поля достигает критического значения
по формуле (3.7).
Т.к. в нашем
эксперименте приборы цифровые, то их
приборная погрешность будет равняться
младшему разряду, значит
= 0.01 мА
=
0.001 мкА
Тогда
=1×10-5
А
Относительная
погрешность расчёта значения силы тока
в соленоиде, при котором индукция
магнитного поля достигает критического
значения рассчитывается по формуле
(3.3) подробности в таблице 2
Относительная
погрешность расчёта значения силы тока
в соленоиде, при котором индукция
магнитного поля достигает критического
значения рассчитывается по формуле
(3.6).
Относительная
погрешность расчёта значения квадрата
силы тока в соленоиде, при котором
индукция магнитного поля достигает
критического значения представлена в
таблице 2.
Абсолютная
погрешность расстояние
от катода до анода равна
1
мм, а само расстояние 8 мм, значит:
=0.125
Относительная
погрешность квадрата расстояние
от катода до анода рассчитывается по
формуле (3.5).
Т.к. измеритель
напряжения — цифровой прибор, то абсолютную
приборную погрешность можно принять
равной наименьшему разряду, значит
0.01
(В), тогда относительная погрешность
равна
,
расчет приведён в таблице 4.3.
Относительная
погрешность расчёта удельного заряда
электрона рассчитаем по формуле (3.4)
Таблица 4.3.
Погрешности расчёта удельного заряда
электрона
|
|
|
|
|
|
|
|
|
|
1 |
6,18 |
0,0645 |
0,0016 |
0.25 |
3E-05 |
0,25 |
4,346E+10 |
|
2 |
8,4 |
0,075 |
0,0012 |
0.25 |
3E-05 |
0,25 |
4,369E+10 |
|
3 |
11,84 |
0,089 |
0,0008 |
0.25 |
2E-05 |
0,25 |
4,373E+10 |
|
4 |
15,7 |
0,102 |
0,0006 |
0.25 |
2E-05 |
0,25 |
4,415E+10 |
По формуле (3.3)
находим стандартную ошибку
=
1×108
(Кл/кг), далее по формуле (3.2) находим
общую абсолютную ошибку (доверительную
вероятность возьмем равной ά=0.95, значение
Стьюдента равно t=
3.2)
5×108
(Кл/кг)
Итак, удельного
заряда электрона с учётом погрешности
равен:
=(
1,751+0.005)×1011
Кл/кг
Сравнивая с
табличным значением
=
1.7588×1011
Кл/кг, рассчитанное значение в данной
лабораторной работе в пределах погрешности
равно табличному значению.
5. ВЫВОДЫ
В данной лабораторной
работе была определена фундаментальная
константа удельный
заряд электрона
=(1,751+0.004)×1011
Кл/кг. Различия с табличными данными
можно объяснить тем, что недостаточно
точно определялся Iкр.
6. ОТВЕТЫ НА
КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1 Как устроена
магнетронная система?
Между анодом и
катодом приложено постоянное напряжение,
создающее радиальное электрическое
поле. На лампу надевают соленоид, по
которому протекает постоянный ток,
создающий постоянное магнитное поле,
направленное вдоль оси анода. Электроны,
испускаемые накалённым катодом, в
отсутствии магнитного поля движутся к
аноду так, что проекция их траектории
на плоскость YOX представляет собой
отрезки прямых.
При включении тока
в соленоиде, его магнитное поле будет
действовать на движущейся электрон с
силой Лоренца:
FЛ
= e[v,B],
где e
– заряд электрона;v
– скорость электрона;B
– индукция магнитного поля.
6.2 От чего зависит
радиус кривизны траектории электрона
в магнетроне?
Радиус кривизны
траектории электрона в магнетроне от
заряда частицы, индукции магнитного
поля, массы и скорости частицы.
6.3 Какая сила
называется силой Лоренца и как определяется
её направление?
Сила, действующая
на движущуюся заряженную частицу в
магнитном поле, называется силой Лоренца.
Сила Лоренца определяется по правилу
векторного произведения с учётом знака
заряда. Вектор силы всегда перпендикулярен
вектору скорости электрона
6.4 Почему сила
Лоренца не изменяет кинетической энергии
заряженной частицы?
Потому что, она
направлена перпендикулярно движению
и изменяет только траекторию движения.
6.5 По какому правилу
и как определяется направление вектора
магнитной индукции в соленоиде при
заданном направлении тока в нём?
Направление вектора
индукции магнитного поля В
определяется
по правилу буравчика
6.6 Что означают
величины, входящие в формулу для
определения магнитной индукции?
,
где e
– заряд электрона, m
– масса электрона, v
– скорость электрона, R
– радиус окружности, по которой движется
электрон.
6.7 Что происходит
с электронами, вылетевшими из катода,
если величина магнитной индукции В
≥ Вкр?
Увеличивая магнитную
индукцию В
до Вкр
электроны перестанут достигать анода.
6.8 Какие из
характеристик, измеренных и рассчитанных
в данной работе, зависят от величины
напряжения?
От величины
напряжения
зависит сила тока в соленоиде, при
котором индукция магнитного поля
достигает критического значения
6.9 В какой цепи
токи больше: в анодной цепи или в цепи
соленоида?
Ответ: С цепи
соленоида токи больше.
6.10 Каким способом
в данной работе определяется величина
критического тока Iкр?
Ответ: в данной
работе величина критического тока Iкр
определяется
из графиков.
6.11 Ток эмиссии
катода постоянен при постоянном токе
накала. Почему при увеличении тока в
соленоиде (I
>
Iкр)
наблюдается снижение анодного тока?
Потому что часть
электронов возвращается на катод.
6.12 Почему в
экспериментальной зависимости Iа=
f(Iс)
не наблюдается
резкого спада
анодного тока при величине магнитной
индукции B ≥
Bкр?
Ответ: Это
связано с тем, что в экспериментальной
установке катод установлен не точно по
оси анода. Кроме этого, радиус катода
отличен от нуля, т.е. катод не представляет
собой бесконечно тонкую нить. Он является
цилиндром малого диаметра. Так же
начальные скорости электронов, вылетевших
с поверхности катода, не равны нулю, а
имеют различные значения (согласно
распределению Максвелла).
6.13 Два электрона
с кинетическими энергиями Е1
и Е2
движутся в
магнитном поле, перпендикулярно
направлению поля. Найти отношение их
периодов обращения и радиусов траекторий.
Ответ: период
обращения электрона равен
Из формулы
найдем
отношение
=
— таким образом,
период обращения электрона не зависит
от кинетической скорости, и отношение
периодов равно 1.
6.14 Определить
частоту вращения (циклотронную частоту)
частицы массы m
и зарядом
q в магнитном
поле индукции
B.
Ответ: Период
обращения частицы равен
,
с одной стороны, и с другой
Из формулы
найдем
отношение
=
Тогда
6.15 Выполняется ли
принцип независимости движения для
заряженных частиц, движущихся одновременно
в электрическом и магнитном полях?
Нет, т.к. движущийся
заряд создает магнитное поле, а изменение
магнитного поля может создавать ток
(т.е. заряд в единицу времени).
6.16 Электрон,
обладающий скоростью v,
попадает в однородное магнитное поле,
индукция которого перпендикулярна
скорости v.
Окружность, какого радиуса описывает
электрон?
Ответ: Из формулы
вытекает, что
=
6.17 Заряженная
частица, пролетая некоторую область
пространства, не отклоняется от
первоначального направления движения.
Можно ли на основании этого факта
утверждать, что магнитное поле в этой
области отсутствует?
Нет, т.к. линии
магнитной индукции могут быть направлены
вдоль вектора скорости, тогда сила
Лоренса равна 0.
6.18 Пучок протонов,
попадая в некоторую область пространства,
отклоняется на некоторый угол. Можно
ли на основании этого факта определить,
каким полем вызвано отклонение,
электрическим или магнитным?
Нет, пучок протонов
мог отклониться как из-за сил Кулона,
так и из-за силы Лоренса, если априорно
нет данных, то нельзя сказать чем вызвано
отклонение пучка протонов.
6.19 Протон и электрон,
имеющие одинаковую скорость, попадают
в однородное магнитное поле, индукция
В
которого перпендикулярна скорости
частиц. Как будут различаться их
траектории?
В
— раз радиус
кривизны траектории протона будет
больше радиуса кривизны траектории
электрона и они будут вращаться в разные
стороны, т.к. у них разные знаки заряда
6.20 Протон и электрон,
ускоренные одинаковой разностью
потенциалов, влетают в однородное
магнитное поле. Во сколько раз радиус
кривизны траектории протона будет
больше радиуса кривизны траектории
электрона?
Ответ: Из формулы
определим радиуса
кривизны траектории электрона:
Для протона
Тогда
В
— раз радиус
кривизны траектории протона будет
больше радиуса кривизны траектории
электрона
6.21 Протон и электрон
влетают в однородное магнитное поле с
одинаковой скоростью. Во сколько раз
радиус кривизны траектории протона
будет больше радиуса кривизны траектории
электрона?
Ответ: Из формулы
определим радиуса
кривизны траектории электрона:
Для протона
Тогда
В
— раз радиус
кривизны траектории протона будет
больше радиуса кривизны траектории
электрона
6.22 Показать, что
какой бы скоростью
v ни обладал
электрон, влетающий в однородное
магнитное поле с индукцией В,
и каким бы ни был угол между векторами
v
и В,
время Т,
за которое он опишет виток винтовой
линии, будет одним и тем же.
Запишем силу
Лоренца
,
где e
– заряд электрона; v
– скорость электрона; B
– индукция магнитного поля.
Сила Лоренца
является центростремительной силой,
значит
Тогда
или
6.23 Показать, что
радиус кривизны траектории заряженной
частицы, движущейся в однородном
магнитном поле, перпендикулярном её
скорости, пропорционален импульсу
частицы.
Сила Лоренца
является центростремительной силой,
значит, скорость всегда будет направлена
по касательной и перпендикулярна радиусу
кривизны траектории заряженной частицы
7. ПРИЛОЖЕНИЕ
К работе прилагается
регистрационный файл (*.REG).
1. При измерении тока было получено значение , тогда как действительное его значение было I=25 A.
Определить абсолютную и относительную погрешности измерения.
Решение:
Абсолютной погрешностью измерения называют разность между полученными при измерении и действительным значениями измеряемой величины:
Относительная погрешность, оценивающая качество выполненного измерения, представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины (отношение, выраженное в процентах):
2. Чтобы измерить э. д. с. генератора, к его зажимам при холостом ходе присоединили вольтметр, сопротивление которого 1200 Ом. Внутреннее сопротивление генератора 0,6 Ом.
(Определить относительную погрешность, если показание вольтметра принимается равным э. д. с. генератора.
Решение:
На основании второго закона Кирхгофа для неразветвленного контура, состоящего из генератора и вольтметра, имеем
или, вынося I за скобку,
Если же приближенное показание вольтметра принять равным э. д. с. генератора, то
Абсолютная погрешность — это разность между найденным и действительным
значениями измеряемой величины:
Отношение абсолютной погрешности к действительному значению измеряемой величины
, выраженное в процентах, представляет собой относительную погрешность измерения:
Эта погрешность возникает от несовершенства метода измерения и относится к систематическим погрешностям, которые останутся при данном методе измерения и при повторных измерениях.
3. Номинальный ток амперметра равен 5 А. Класс точности его 1,5.
Определить наибольшую возможную абсолютную погрешность прибора.
Решение:
Число 1,5, указывающее класс точности амперметра, обозначает основную приведенную его погрешность, т. е. выраженное в процентах отношение наибольшей возможной абсолютной погрешности прибора , находящегося в нормальных условиях, к номинальной величине тока
:
Примечание. Условия нормальны, если прибор установлен в положении, указанном на его шкале, находится в среде с температурой 20°С и не подвержен действию внешних магнитных полей (кроме магнитного поля Земли).
Следовательно,
Подставив числовые значения, получим
4. Номинальный ток амперметра 5 А, сопротивление 0,02 Ом.
Какой ток проходит в цепи, если амперметр, зашунтированный сопротивлением 0,005 Ом, показывает 4,5 А?
Решение:
Шунт и амперметр соединены параллельно. Токи, проходящие в пассивных параллельных ветвях (не содержащих э. д. с), обратно пропорциональны сопротивлениям этих ветвей:
Ток I в цепи на основании первого закона Кирхгофа равен сумме токов в амперметре и в шунте
:
5. Через амперметр, номинальный ток которого 5 А и сопротивление 0,1 Ом, проходит ток 4 А; вольтметр, номинальное напряжение которого 150 В и сопротивление 5000 Ом, включен на напряжение 120 В.
Определить потери мощности в этих приборах.
Решение:
Потери мощности в амперметре
Потери мощности в вольтметре
Суммарные потери мощности в обоих электроизмерительных приборах
Анализируя формулы для можно сделать вывод, что при номинальных величинах потери мощности
будут тем меньше, чем меньше значение
, а потери мощности
— тем меньше, чем больше значение
. Кроме того, чем больше номинальный ток амперметра, тем меньше должно быть сопротивление амперметра. В свою очередь, чем больше номинальное напряжение вольтметра, тем больше должно быть сопротивление вольтметра. Тогда потери мощности в этих приборах не будут чрезмерно большими.
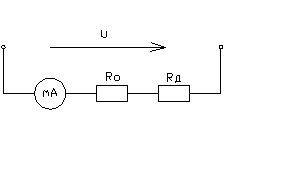
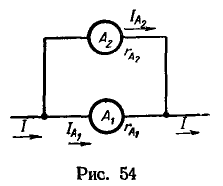
6. Ток в цепи по мере присоединения к ней приемников энергии стал больше номинального тока амперметра , внутреннее сопротивление которого
. Тогда было решено измерять ток в цепи двумя параллельно включенными амперметрами (рис. 54), причем номинальный ток второго амперметра
и внутреннее сопротивление
.
Определить показания амперметров при измерении суммарного тока I=8 А.
Решение:
Согласно первому закону Кирхгофа,
С другой стороны, отношение токов в параллельных пассивных ветвях равно обратному отношению сопротивлений этих ветвей:
Следовательно, вместо тока можно в уравнение (а) подставить, согласно уравнению (б), величину
:
Показание второго амперметра:
Отсюда видно неудобство рассматриваемой схемы параллельного включения двух амперметров с равными номинальными токами, но с различными внутренними сопротивлениями; суммарный ток цепи не разветвляется между амперметрами поровну: в то время как амперметр с меньшим сопротивлением будет нагружен предельно, другой амперметр останется нагружен неполностью.
7. Определить сопротивление шунта для магнитоэлектрического измерительного механизма, номинальный ток которого и сопротивление
, если шунтирующий множитель р = 6 (рис. 55).
Решение: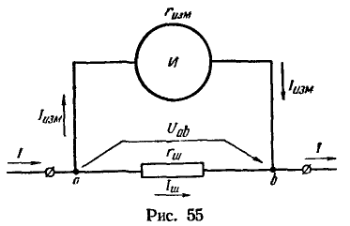
. Шунт включается в цепь измеряемого тока, а параллельно шунту присоединяется измерительный механизм (рис. 55). На основании закона Ома напряжение между точками а и b можно выразить через данные ветви измерительного механизма:
а также через ток в цепи I и эквивалентное сопротивление двух параллельных ветвей:
Разделив выражение (4) на (5), получим
откуда неразветвленный ток
Выражение в скобках обозначается буквой р и называется шунтирующим множителем:
который представляет собой число, показывающее, во сколько раз измеряемый ток больше тока в измерительном механизме.
Из последнего выражения следует, что сопротивление шунта
или, в рассматриваемом случае,
При шунте, имеющем эту величину сопротивления, номинальное значение измеряемого тока
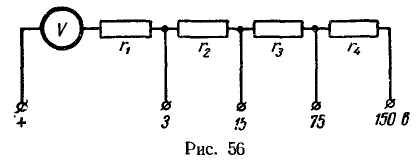
8. Многопредельный вольтметр имеет четыре предела измерения: 3, 15, 75 и 150 в (рис. 56). Наибольший допустимый (номинальный) ток прибора 30 мА.
Определить добавочные сопротивления , включенные последовательно с прибором, если сопротивление вольтметра без этих сопротивлений
.
Решение:
При пользовании вольтметром для измерения напряжений до трех вольт последовательно с прибором включается сопротивление . Сопротивление измерительной цепи на основании закона Ома
При использовании зажимов «+» и 15 В имеем увеличение сопротивления измерительной цепи на .На основании закона Ома
Если для измерения напряжения воспользоваться зажимами «+» и 75 В, то будем иметь в измерительной цепи четыре сопротивления, соединенных последовательно:
При включении вольтметра на напряжение до 150 В используются зажимы «+» и 150 В. Сопротивление неразветвленной цепи на основании закона Ома равно
9. Два пассивных приемника энергии, сопротивления которых , соединены последовательно и включены на напряжение 120 В.
Можно ли получить правильные значения напряжений на этих приемниках путем присоединения к их зажимам вольтметра, сопротивление которого равно 3000 Ом?
Решение:
Напряжение на приемниках можно определить расчетом на основании закона Ома. Действительно, напряжения относятся как сопротивления приемников:
Сумма напряжений приемников равна приложенному напряжению:
Напряжение на первом приемнике
Напряжение на втором приемнике
Присоединение вольтметра к зажимам первого приемника изменяет сопротивление на первом участке и делает его равным
Напряжение между зажимами этого участка
Это напряжение будет показанием вольтметра, относительная погрешность измерения
Если присоединить вольтметр к зажимам второго приемника, то изменится сопротивление на втором участке, которое станет равным
Напряжение между зажимами этого участка
Это напряжение будет показанием вольтметра. Относительная погрешность измерения
Характерно, что в обоих случаях относительная погрешность измерения отрицательна, т. е. присоединение вольтметра параллельно пассивному элементу цепи, сопротивление которого того же порядка, что и у вольтметра, заметно понижает напряжение на этом элементе.
Сопротивление вольтметра должно быть большим по сравнению с сопротивлением элемента цепи, напряжение на котором измеряется. Напротив, сопротивление амперметра, включенного в разрыв цепи так, что он оказывается соединенным последовательно с приемником энергии, должно быть мало по сравнению с сопротивлением приемника. В обоих случаях включение электроизмерительного прибора не должно изменять режима цени.
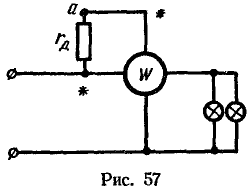
10. На рис. 57 приведена неправильная схема включения параллельной цепи ваттметра.
Определить разность потенциалов между генераторными зажимами обмоток (помечены звездочками), если номинальный ток параллельной цепи ваттметра 30 мА, сопротивление параллельной обмотки и сопротивление внутри прибора 1000 Ом, напряжение сети 220 В. Прибор рассчитан на напряжение 300 В.
Решение:
Сопротивление параллельной цепи ваттметра, обеспечивающее ток в цепи 30 мА при напряжении 300 В, равно
Добавочное сопротивление, включенное последовательно с параллельной обмоткой ваттметра,
Напряжение на параллельной обмотке, находящейся внутри прибора, при номинальном токе равно
Ток в параллельной цепи при напряжении сети меньше номинального тока:
Напряжение на добавочном сопротивлении при этом токе
Так как генераторный зажим последовательной обмотки ваттметра и один из зажимов добавочного сопротивления соединены в точке *, то потенциалы их равны. Следовательно, потенциал другого зажима на добавочном сопротивлении (точка а), соединенного с генераторным зажимом параллельной обмотки, отличается на от потенциала первого зажима, т. е. между генераторными зажимами параллельной и последовательной обмоток, помеченными звездочками, имеется разность потенциалов
. Она будет соответственно еще больше при большем напряжении сети. Так как обмотки находятся в непосредственной близости друг от друга, то при этом возможен пробой их изоляции.
В правильной схеме зажимы, помеченные звездочками, соединены непосредственно и имеют один и тот же потенциал.
11. Измерение мощности трехфазного электродвигателя при испытании было выполнено по схеме для равномерной нагрузки фаз и доступной нулевой точке. Показание однофазного ваттметра (типа ВИО) было при этом 500 Вт, показание амперметра 4,6 А, а показание вольтметра, включенного на линейное напряжение, 220 В.
Определить мощность электродвигателя в данном режиме и коэффициент мощности в месте потребления электрической энергии.
Решение:
Для рассматриваемой схемы включения ваттметр измеряет активную мощность одной фазы; следовательно, . Нагрузка в виде трехфазного электродвигателя равномерная. Поэтому активная мощность электродвигателя на входе
При равномерной нагрузке формуле мощности трехфазной цепи можно придать следующий вид:
где
Отсюда коэффициент мощности
Ни один прибор в мире не является точным. Величина, которую он измеряет, всегда будет отличаться от истины на ту величину, которую еще называют его погрешностью. Данная погрешность и будет определять класс точности амперметра. Задачей всех производителей измерительной техники, заключается в том, чтобы эта погрешность была, как можно ниже и стремилась к нулю.
Погрешность амперметра устанавливается в результате поверки и сравнении показаний замеров одних и тех же величин с эталонным или образцовым прибором, имеющий более высокий класс точности. При этом значение, полученное на образцовом приборе, считаются действительными.
Что такое амперметр и какие величины он измеряет
Амперметр — измерительный прибор, который служит для измерения силы тока [І] в электроцепях. Единицей [І] по системе СИ является ампер [А]. Электрические цепи могут проводить ток разной силы, поэтому градуируют приборную шкалу амперметра с различной градацией от микроампера равного 1 мкА = 1×0-6 ампер до килоампера равного: 1 кА = 1 000 ампер.
Важно! В электроцепь амперметр включают последовательно, а для повышения границы измерений, используют специальные устройства: трансформаторы, шунты м магнитные усилители.
Поскольку ток в цепи напрямую зависит от величины сопротивления [R] элементов электроцепи, то собственное сопротивление прибора [Rа] должно быть предельно низким, стремится к нулю. Это приведет к уменьшению влияния устройства в процессе замеров тока в цепи, тем самым будет повышена точность измерения.
Разновидности амперметров
Они могут быть электромеханическими или аналоговыми, цифровыми или электронными. Базовый набор, как правило, состоит из детектора, передающего устройства и индикатора, самописца или запоминающего устройства.
Аналоговые устройства — самые старые из используемых инструментов. Хотя они надежны для статических и стабильных измерений, они не подходят для динамических и переходных условий. Кроме того, они довольно громоздкие и имеют ограничения из-за использования стрелочной индикации.
Электронные инструменты реагируют быстрее и способны мгновенно обнаруживать динамические изменения тока в сети. Примером является цифровой мультиметр, который способен измерить значения тока в динамическом или переходном режиме за секунды.
Виды погрешностей амперметра
Чтобы понять размер погрешности в измерениях, нужно сравнить полученные результаты с эталонными.
В метрологии используют для всех электротехнических измерителей, как для амперметров, так и для вольтметров, несколько видов погрешностей: абсолютную, относительную и приведенную.
Абсолютная погрешность амперметра — это разность Δ между результатом измерения, полученного на шкале прибора (Xи) и действительным значением силы тока в цепи (Xд). Абсолютная погрешность амперметра описывается простой формулой и выражается в единицах тока А.
Δх = Xд−Xи, А
где:
- Δх — дельта Х
- Xд — действительное показание силы тока, принимаемой по образцовому прибору;
- Xи — измеренное значение на шкале прибора.
Относительная погрешность (δ) — отношение абсолютной погрешности амперметра Δх к действительному показанию силы тока, принимаемому по образцовому прибору. Оно может быть указано как в процентах, тогда частное умножается на 100, либо выражаться в относительных единицах.
δ = (Δх : Xд)×100, %
Приведенная погрешность — это значение приведенное к диапазону измерения амперметра, приравненного к его шкале. Его получают в виде частного от абсолютной погрешности Δх и нормируемого значения (Xн), в значениях соответствующим абсолютной погрешности Δх умноженной на 100 %:
δпр = (Δх : Xн)×100, %
Класс точности
Это основная характеристика амперметра, которая согласно еще советскому действующему ГОСТ 1845-59, определяет границы возможных погрешностей.
Для всех электроизмерительных приборов, к которым он относится, класс точности (Кл) обозначается в числовом виде по значению, соответствующему предельной допустимой приведенной погрешности δпр, в %.
Все электрические амперметры подразделяются по точности на 8 классов, а затем по группам, которые является важным признаком их классификации:
- Образцовые: 0.05–0.1–0.2;
- лабораторные: 0.5–0.1;
- технические: 1.5–2.0–4.0.
Обратить внимание! Все приборы, у которых погрешность превышает 4%, являются внеклассными.
Образцовые применяют в электроизмерительных процессах для определения класса точности технических и лабораторных амперметров. Лабораторные применяются в научно-технических процессах при электротехнических исследованиях контроля ведения режимов, например на котельных, ГЭС, ТЭЦ и АЭС.
Важно! На панели амперметра класс точности указывается в кружках, квадратах и звездочках. Если он имеет неравномерную шкалу измерения, Кл обозначается ломаной линией.
Как определить класс точности
Согласно действующих государственных норм, производители амперметров обязаны гарантировать его относительную погрешность измерения, полученную по классу точности, указанной на измерительной панели и в паспорте на прибор. Кроме того, все измерительные приборы должны проходить периодическую поверку в метрологических центрах, на соответствие заводскому классу точности. Если такую аттестацию он не проходит, то не может использоваться в измерительных процессах.
Зная абсолютную погрешность и показание силы тока на шкале, можно просто получить реальную силу тока, действующую в цепи. При этом шкала для применения абсолютной погрешности считается равномерной.
Важно! При выборе шкалы стрелочного амперметра, нужно чтобы рабочее значение тока находилось, примерно, в 2/3 диапазона шкалы. Если стрелка будет находиться практически на 0 или на максимальном показатели шкалы, то относительная погрешность будет очень высокой, то есть доверять таким показаниям не рекомендуется.
Пример нахождения показания амперметра по приведенной погрешности
Для примера рассматривается аналоговый измеритель со шкалой до 25 А.
На шкале имеется обозначение класса точности 2.5, кружок или квадрат отсутствует, поэтому эта погрешность приведенная.
Y=Dх/Xп×100=+/- p
При Хп= 25А и значении p = 2.5 можно рассчитать абсолютную погрешность:
Δх =25/100×2.5=0.625 A
Если пользователь обнаружит на панели класс точности заключенный в квадрат, то погрешность нужно будет определять в процентном выражении от измеренного значения.
При показаниях по шкале Iи = 10 А, погрешность прибора не должна превышать
Δх =10×2.5/100=0.25
При показаниях по шкале Iи=2 А погрешность будет иной:
Δх =2×2.5/100=0.05
При показаниях по шкале Iи=25 А погрешность будет максимальной:
Δх =25×2.5/100=0.625
Вот почему важно, чтобы аналоговый прибор работал при измерениях в 2/3 рабочей шкалы.
Пример нахождения показания амперметра по относительной погрешности
Для того чтобы узнать погрешность для амперметра, имеющего класс точности 0.05/0.02, шкалу измерения 0…25 А. Δх определяют по измеряемому показанию на шкале 10А.
Поскольку класс точности задан как c/d, то расчет будет выполняться по формуле:
δ пр =+/-(с+d(xk/(x-1)))
Где:
- xk=25 А;
- х=10 А;
- с=0.05;
- d=0.02.
δ пр =100 Δх / xN
Нормирующее значение xN=xk=25 A,
δ пр =+/-(0.05+0.02(25/(10-1)))=0.105
Δх = δ пр×xN/100=0.105×25/100=0.026 A
Выбор амперметра по метрологическим характеристикам
Наиболее частым источником ошибки при измерении тока считается то, что амперметр имеет ненулевое входное сопротивление. Напряжение, возникающее на измерителе, приводит к снижению напряжения на тестируемом устройстве. Если уменьшение будет значительным, это приведет к значительно меньшему протеканию тока. Другими словами, измеритель не показывает ток, который фактически протекает в сети.
Для того чтобы максимально нивелировать эту погрешность, применяют два основных типа архитектуры измерения: шунтирующие амперметры и с обратной связью.
Погрешность, вызванная шунтирующим измерителем, определяемая в виде частного напряжения амперметра, деленная на выходное сопротивление.
Амперметры с обратной связью ближе к «идеальным». Он вырабатывает напряжение на пути обратной связи операционного усилителя с высоким коэффициентом усиления. Это напряжение также пропорционально измеряемому току, но не появляется на входе прибора. В результате чувствительные измерители с обратной связью, такие как электрометры и пикоамперметры, имеют нагрузку по напряжению, обычно ограниченную до 200 мкВ.
Для промышленных измерений наиболее часто применяются амперметры аналогового панельного типа. При их выборе следует учитывать такие моменты:
- Выбор типа. При измерении І постоянного, следует выбрать измеритель постоянного тока, то есть с магнитоэлектрическим измерительным механизмом. При измерении переменного тока нужно обратить внимание на форму волны и частоту. Если это синусоида, то измеряют только эффективное значение, с последующим преобразованием в максимальное или среднее значение.
- Класс точности. Чем более высокий класс точности измерителя, тем выше его цена, тем сложнее у него ремонт и метрологическая аттестация. Поэтому для выполнения большинства инженерных измерений достаточно класса точности 1.5, не стоит применять образцовые или лабораторные приборы.
- Выбор шкалы. Чтобы в полной мере использовать возможности амперметра по классу точности, измеряемый показатель должен быть в интервале 1/2 ~ 2/3 максимальной шкалы.
Важно! Внутреннее сопротивление — определяющая величина при выборе измерителя. Ее следует принимать в соответствии с величиной измеряемого импеданса, иначе это приведет к большим ошибкам измерения. Поскольку внутреннее сопротивление отражает энергопотребление самого измерителя, при измерении тока прибор с внутренним сопротивлением следует выбирать, как можно меньшим.