Как найти абсолютную систематическую погрешность

Как найти абсолютную систематическую погрешность

Абсолютная погрешность

  1. Причины возникновения погрешности измерения
  2. Систематическая и случайная погрешности
  3. Определение абсолютной погрешности
  4. Алгоритм оценки абсолютной погрешности в серии прямых измерений
  5. Значащие цифры и правила округления результатов измерений
  6. Примеры

Причины возникновения погрешности измерения

Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.

Обычно «истинное» значение неизвестно, и можно только оценить погрешность, приняв в качестве «истинного» среднее значение, полученное в серии измерений. Таким образом, процесс оценки проводится статистическими методами.

Виды погрешности измерений

Причины

Инструментальная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Погрешность метода

Определяется несовершенством методов и допущениями в методике.

Теоретическая погрешность

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Погрешность оператора

Определяется субъективным фактором, ошибками экспериментатора.

Систематическая и случайная погрешности

Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.

Систематическая погрешность всегда имеет знак «+» или «-», т.е. говорят о систематическом завышении или занижении результатов измерений.

Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.

Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.

Случайные погрешности неизбежны и всегда присутствуют при измерениях.

Определение абсолютной погрешности

Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:

$$ Delta x = |x_{изм}-x_{ист} | $$

Например:

При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:

$m_i,г$

98,4

99,2

98,1

100,3

98,5

$Delta m_i, г$

1,6

0,8

1,9

0,3

1,5

Граница абсолютной погрешности – это величина h: $ |x-x_{ист}| le h $

Для оценки границы абсолютной погрешности на практике используются статистические методы.

Алгоритм оценки абсолютной погрешности в серии прямых измерений

Шаг 1. Проводим серию из N измерений, в каждом из которых получаем значение измеряемой величины $x_i, i = overline{1, N}$.

Шаг 2. Находим оценку истинного значения x как среднее арифметическое данной серии измерений:

$$ a = x_{cp} = frac{x_1+x_2+ cdots +x_N}{N} = frac{1}{N} sum_{i = 1}^N x_i $$

Шаг 3. Рассчитываем абсолютные погрешности для каждого измерения:

$$ Delta x_i = |x_i-a| $$

Шаг 4. Находим среднее арифметическое абсолютных погрешностей:

$$ Delta x_{cp} = frac{Delta x_1+ Delta x_2+ cdots + Delta x_N}{N} = frac{1}{N} sum_{i = 1}^N Delta x_i $$

Шаг 5. Определяем инструментальную погрешность при измерении как цену деления прибора (инструмента) d.

Шаг 6. Проводим оценку границы абсолютной погрешности серии измерений, выбирая большую из двух величин:

$$ h = max {d; Delta x_{cp} } $$

Шаг 7. Округляем и записываем результаты измерений в виде:

$$ a-h le x le a+h или x = a pm h $$

Значащие цифры и правила округления результатов измерений

Значащими цифрами – называют все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.

Например:

0,00501 – три значащие цифры 5,0 и 1.

5,01 – три значащие цифры.

5,0100 – пять значащих цифр; такая запись означает, что величина измерена с точностью 0,0001.

Внимание!

Правила округления.

Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу (округление по избытку, “ceiling”).

Округлять результаты измерений и вычислений нужно так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.

Например: если при расчетах по результатам серии измерений получена оценка истинного значения a=1,725, а оценка абсолютной погрешности h = 0,11, то результат записывается так:

$$ a approx 1,7; h approx ↑0,2; 1,5 le x le 1,9 или x = 1,7 pm 0,2 $$

Примеры

Пример 1. При измерении температура воды оказалась в пределах от 11,55 ℃ до 11,63 ℃. Какова абсолютная погрешность этих измерений?

По условию $11,55 le t le 11,63$. Получаем систему уравнений:

$$ {left{ begin{array}{c} a-h = 11,55 \ a+h = 11,63 end{array} right.} Rightarrow {left{ begin{array}{c} 2a = 11,55+11,63 = 23,18 \ 2h = 11,63-11,55 = 0,08 end{array} right.} Rightarrow {left{ begin{array}{c} a = 11,59 \ h = 0,04end{array} right.} $$

$$ t = 11,59 pm 0,04 ℃ $$

Ответ: 0,04 ℃

Пример 2. По результатам измерений найдите границы измеряемой величины. Инструментальная погрешность d = 0,1.

$x_i$

15,3

16,4

15,3

15,8

15,7

16,2

15,9

Находим среднее арифметическое:

$$ a = x_{ср} = frac{15,3+16,4+ cdots +15,9}{7} = 15,8 $$

Находим абсолютные погрешности:

$$ Delta x_i = |x_i-a| $$

$ Delta x_i$

0,5

0,6

0,5

0

0,1

0,4

0,1

Находим среднее арифметическое:

$$ Delta x_{ср} = frac{0,5+0,6+ cdots + 0,1}{7} approx 0,31 gt d $$

Выбираем большую величину:

$$ h = max {d; Delta x_{ср} } = max⁡ {0,1; 0,31} = 0,31 $$

Округляем по правилам округления по избытку: $h approx ↑0,4$.

Получаем: x = 15, $8 pm 0,4$

Границы: $15,4 le x le 16,2$

Ответ: $15,4 le x le 16,2$

Пример 3*. В первой серии экспериментов было получено значение $x = a pm 0,3$. Во второй серии экспериментов было получено более точное значение $x = 5,631 pm 0,001$. Найдите оценку средней a согласно полученным значениям x.

Более точное значение определяет более узкий интервал для x. По условию:

$$ {left{ begin{array}{c} a-0,3 le x le a+0,3 \ 5,630 le x le 5,632 end{array} right.} Rightarrow a-0,3 le 5,630 le x le 5,632 le a+0,3 Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} a-0,3 le 5,630 \ 5,632 le a+0,3 end{array} right.} Rightarrow {left{ begin{array}{c} a le 5,930 \ 5,332 le a end{array} right.} Rightarrow 5,332 le a le 5,930 $$

Т.к. a получено в серии экспериментов с погрешностью h=0,3, следует округлить полученные границы до десятых:

$$ 5,3 le a le 5,9 $$

Ответ: $ 5,3 le a le 5,9 $

Источник

При прямых измеренияхзначение
измеряемой величины отсчитывается
непосредственно по шкале измерительного
прибора. Ошибка в отсчете может достигать
нескольких десятых долей деления шкалы.
Обычно при таких измерениях величину
систематической погрешности считают
равной половине цены деления шкалы
измерительного прибора. Например, при
измерении штангенциркулем с ценой
деления 0,05 мм величина приборной
погрешности измерения принимают равной
0,025 мм.

Цифровые измерительные приборы дают
значение измеряемых ими величин с
погрешностью, равной значению одной
единицы последнего разряда на шкале
прибора. Так, если цифровой вольтметр
показывает значение20,45 мВ, то абсолютная
погрешность при измерении равна
мВ.

Систематические погрешности возникают
и при использовании постоянных величин,
определяемых из таблиц. В подобных
случаях погрешность принимается равной
половине последнего значащего разряда.
Например, если в таблице значение
плотности стали дается величиной, равной
7,9∙103кг/м3, то абсолютная
погрешность в этом случае равнакг/м3.

Некоторые особенности в расчете приборных
погрешностей электроизмерительных
приборов будут рассмотрены ниже.

При определении систематической
(приборной) погрешности косвенных
измеренийфункциональной величиныиспользуется
формула

,
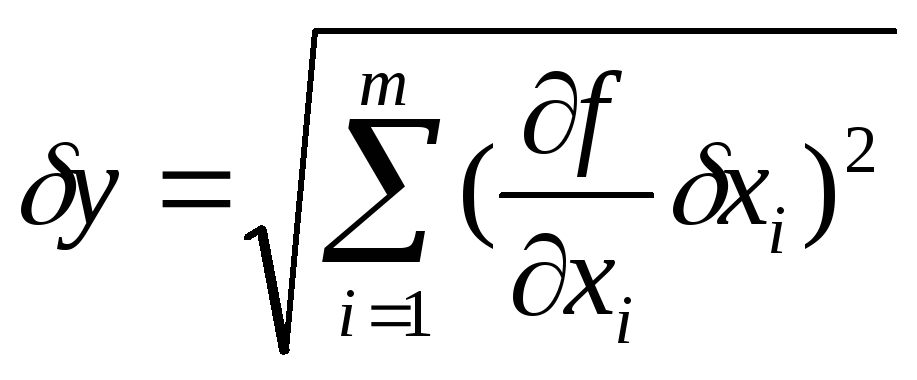(1)

где
– приборные ошибки прямых измерений
величины,–
частные производные функции по переменной.

В качестве примера, получим формулу для
расчета систематической погрешности
при измерении объема цилиндра. Формула
вычисления объема цилиндра имеет вид

.

Частные производные по переменным d
и hбудут равны

,.

Таким образом, формула для определения
абсолютной систематической погрешности
при измерении объема цилиндра в
соответствии с (2. ..) имеет следующий вид

,

где
иприборные
ошибки при измерении диаметра и высоты
цилиндра

3. Оценка случайной погрешности. Доверительный интервал и доверительная вероятность

Д

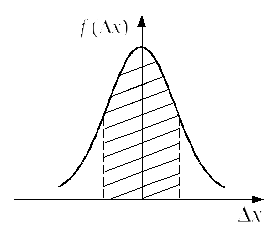
Рис. 1

ля подавляющего большинства простых
измерений достаточно хорошо выполняется
так называемый нормальный закон случайных
погрешностей (закон Гаусса), выведенный
из следующих эмпирических положений.

  1. погрешности измерений могут принимать
    непрерывный ряд значений;

  2. при большом числе измерений погрешности
    одинаковой величины, но разного знака
    встречаются одинаково часто,

  3. чем больше величина случайной погрешности,
    тем меньше вероятность ее появления.

График нормального закона распределения
Гаусса представлен на рис.1. Уравнение
кривой имеет вид

,
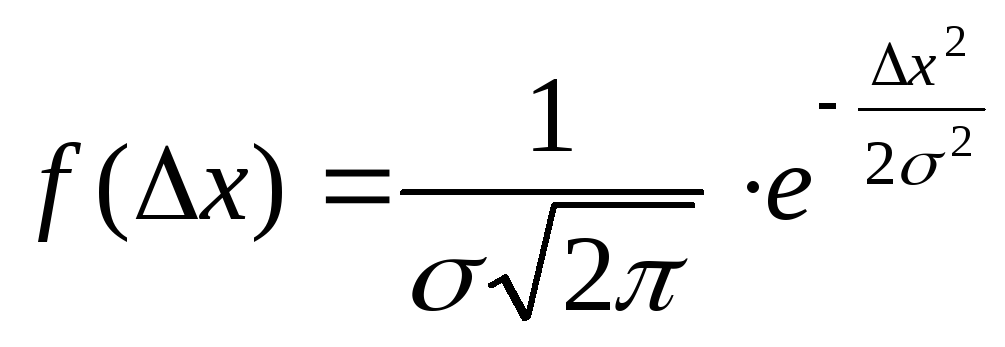(2)

где
– функция распределения случайных ошибок
(погрешностей), характеризующая
вероятность появления ошибки,σ– средняя
квадратичная ошибка.

Величина σне
является случайной величиной и
характеризует процесс измерений. Если
условия измерений не изменяются, то σ
остается постоянной величиной. Квадрат
этой величины называютдисперсией
измерений.Чем меньше дисперсия, тем
меньше разброс отдельных значений и
тем выше точность измерений.

Точное значение средней квадратичной
ошибки σ, как
и истинное значение измеряемой величины,
неизвестно. Существует так называемая
статистическая оценка этого параметра,
в соответствии с которой средняя
квадратичная ошибка равняется средней
квадратичной ошибке среднего
арифметического.
Величина которой определяется по формуле

,
(3)

где
– результатi-го
измерения;–
среднее арифметическое полученных
значений;n – число
измерений.

Чем больше число измерений, тем меньше
и тем больше оно приближается кσ.
Если истинное значение измеряемой
величины μ, ее среднее арифметическое
значение, полученное в результате
измерений ,
а случайная абсолютная погрешность,
то результат измерений запишется в виде.

Интервал значений от
до,
в который попадает истинное значение
измеряемой величины μ, называетсядоверительным интервалом.Посколькуявляется случайной величиной, то истинное
значение попадает в доверительный
интервал с вероятностью α, которая
называетсядоверительной вероятностью,илинадежностью измерений. Эта
величина численно равна площади
заштрихованной криволинейной трапеции.
(см. рис.)

Все это справедливо для достаточно
большого числа измерений, когда
близка к σ. Для отыскания доверительного
интервала и доверительной вероятности
при небольшом числе измерений, с которым
мы имеем дело в ходе выполнения
лабораторных работ, используетсяраспределение вероятностей Стьюдента.
Это распределение вероятностей
случайной величины,
называемойкоэффициентом Стьюдента,
дает значение доверительного интервалав долях средней квадратичной ошибки
среднего арифметического.

.

(4)

Распределение вероятностей этой величины
не зависит от σ2, а существенно
зависит от числа опытовn.С увеличением числа опытовnраспределение
Стьюдента стремится к распределению
Гаусса.

Функция распределения табулирована
(табл.1). Значение коэффициента Стьюдента
находится на пересечении строки,
соответствующей числу измерений n,
и столбца, соответствующего доверительной
вероятности α

Таблица 1.

n

α

n

α

0,8

0,9

0,95

0,98

0,8

0,9

0,95

0,98

3

1,9

2,9

4,3

7,0

6

1,5

2,0

2,6

3,4

4

1,6

2,4

3,2

4,5

7

1,4

1,9

2,4

3,1

5

1,5

2,1

2,8

3,7

8

1,4

1,9

2,4

3,9

Пользуясь данными таблицы, можно:

  1. определить доверительный интервал,
    задаваясь определенной вероятностью;

  2. выбрать доверительный интервал и
    определить доверительную вероятность.

При косвенных измерениях среднюю
квадратичную ошибку среднего
арифметического значения функции
вычисляют по формуле

.
(5)

Доверительный интервал и доверительная
вероятность определяются так же, как и
в случае прямых измерений.

Оценка суммарной погрешности измерений.
Запись окончательного результата.

Суммарную погрешность результата
измерений величины Х будем определять
как среднее квадратичное значение
систематической и случайной погрешностей

,
(6)

где δх – приборная погрешность, Δх
– случайная погрешность.

В качестве Х может быть как непосредственно,
так и косвенно измеряемая величина.

Окончательный результат измерений
рекомендуется представлять в следующем
виде

,
α=…, Е=…(7)

Следует иметь в виду, что сами формулы
теории ошибок справедливы для большого
число измерений. Поэтому значение
случайной, а следовательно, и суммарной
погрешности определяется при малом nс большой ошибкой. При вычислении Δхпри числе измеренийрекомендуется
ограничиваться одной значащей цифрой,
если она больше 3 и двумя, если первая
значащая цифра меньше 3. Например, если
Δх= 0,042, то отбрасываем 2 и пишем
Δх=0,04, а если Δх=0,123, то пишем
Δх=0,12.

Число разрядов результата и суммарной
погрешности должно быть одинаковым.
Поэтому среднее арифметическое
погрешности должно быть одинаковым.
Поэтому среднее арифметическое
вычисляется вначале на один разряд
больше, чем измерение, а при записи
результата его значение уточняется до
числа разрядов суммарной ошибки.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Результат любого измерения содержит ошибку. Это непреложная истина. Обратите внимание, что я сказал ошибку, а не погрешность. Проблема заключается в том, что мы не можем определить величину этой ошибки, так как нам неизвестно точное значение измеряемой физической величины. Парадоксальность ситуации заключается в том, что если нам известно точное, истинное, значение, то и измерять уже ничего не нужно. А раз мы измеряем, значит истинное значение величины нам неизвестно.

Исключением из этого правила можно считать проверку метрологических параметров измерительного прибора (средства измерения) во время выполнения процедуры поверки. Во время поверки результат измерения полученный с помощью поверяемого прибора сравнивается с условным эталоном, который и измеряется. Почему эталон условный? Дело в том, что, во первых, в самом лучшем случае используется не эталон, а копия эталона. Во вторых, в качестве эталонного значения чаще используется просто результат измерения намного более точным прибором. Впрочем, о поверке мы поговорим в отдельной статье.

Я долго думал, с чего начать долгий разговор о погрешностях и ошибках. Дело в том, что это очень обширная и многогранная тема. Причем в ней все взаимосвязано. И у меня даже есть несколько начатых, но незаконченных статей, довольно проработанных. В конечном итоге было принято решение “начать издалека”, с общего взгляда. Что бы у читателей сложилось представление о вопросе в целом, а не о наборе разрозненных (на первый взгляд) частностей. Иногда, что бы лучше разглядеть что-то, надо отойти подальше и окинуть взглядом картину в целом.

Это пятая статья цикла “Нескучная метрология”. В первых четырех мы больше разбирались со шкалами, которые являются очень важной частью любого измерения и измерительного прибора. И к информации из этих статей мы будем постоянно обращаться на протяжении всего цикла.

Давайте немного постреляем. В тире

Рассказывать об ошибках и погрешностях можно на разных примерах, как умозрительных, так и практических. И с разной степенью наглядности. Наиболее наглядной, на мой взгляд, является аналогия со стрельбой в тире.

Стрельба по мишени, единичный выстрел, и неточное попадание. Иллюстрация моя
Стрельба по мишени, единичный выстрел, и неточное попадание. Иллюстрация моя

Центр мишени, собственно цель, является аналогом истинного значения измеряемой физической величины. В центр мишени можно попасть. Для обычного стрелка это, скорее всего, будет случайностью. Для снайпера, закономерностью. Но даже снайпер не сможет при каждом выстреле попадать точно в одно и тоже место.

Место попадания в мишень является аналогом “результата измерения”. Почему в кавычках? Скоро узнаете. Видно, что стрелок промазал, не по мишени вообще, а по центру мишени. Расстояние от центра мишени до места попадания дает нам величину ошибки нашего “измерения”. Учитывать будем только расстояние, направление не важно.

По результату одиночного выстрела нельзя судить ни о качестве оружия, ни о подготовке стрелка. Точно так же, по результату одно измерения нельзя судить о точности измерительного прибора. И сейчас мы будем разбираться, что с этим делать. Но поскольку мы занимаемся метрологией, а это точная наука, нам нужно сначала договориться о терминологии.

Наблюдение и измерение

Мы уже договорились считать центр мишени аналогом истинного, эталонного, значения измеряемой физической величины. Соответственно, стрельба будет аналогом “измерения” физической величины.

А теперь, разберемся с кавычками. Дело в том, нашу стрельбу по мишени нельзя назвать ни измерением, ни даже аналогом измерения. С точки зрения метрологии это лишь наблюдение. И место попадания это не результат измерения, а наблюдаемое значение. И это наблюдаемое значение, что важно, определяется для единичного наблюдения.

Измерение отличается от наблюдения тем, что оно должно выполняться в соответствии с регламентированной процедурой. Это кажется лишь казуистической уловкой метрологов, но на самом деле чрезвычайно важно. Давайте рассмотрим это на простом примере измерения температуры.

Температуру можно измерить “на ощупь”. Действительно, прикасаясь к чему либо, будем называть это физическим телом, мы можем примерно оценить его температуру. Причем не на уровне горячее/холодное, даже более менее точно, до пары градусов, в некотором диапазоне температур. И это именно наблюдение, но не измерение.

Температуру можно определить “на глаз”. Например, нагретый до высокой температуры металл начинает светиться. По интенсивности свечения и цвету мы можем сделать заключение о температуре. Более низкие температуры металла можно определить по “цветам побежалости”. И это тоже наблюдение, а не измерение.

Мы можем взять термометр, даже довольно точный, например, лабораторный ртутный, и использовать его. Будем ли мы по прежнему наблюдать или, наконец то, измерять? Представим, что нам надо измерить температуру капли воды массой 1 грамм (объемом 1 мл). Что будет, если мы используем лабораторный ртутный термометр, чувствительная часть которого гораздо больше капли? Правильно, температура капли просто станет равной температуре чувствительной части термометра. Своей попыткой “измерения” мы существенно изменили сам объект измерения.

Измеряя температуру тела человека мы должны не просто использовать медицинский термометр, но соблюсти массу дополнительных условий. Расположить его правильно и в правильном месте. Само измерение занимает определенное время. Вот это и есть та самая регламентированная процедура. Какой то результат мы получим и соблюдая ее, и не соблюдая. Но говорить о достоверности этого результата мы можем только в том случае, если соблюдены определенные правила, та самая регламентированная процедура.

Не соблюдая правила мы наблюдаем. Соблюдая правила мы измеряем. На бытовом, любительском уровне, разница между наблюдением и измерением зачастую не видна. Например, какая разница, как подключить вольтметр для измерения напряжения? На самом деле большая, поскольку сам выбор вольтметра должен учитывать внутренне сопротивление участка цепи, на котором мы измеряем напряжение. Иначе он внесет искажения в процессы на этом участке цепи.

Измеряя сопротивление резистора многие прижимаю его к щупам омметра пальцами. Тем самым получая неверный результат. Да, многое понимают, что тело человека проводит электрический ток. Вряд ли ошибусь, если скажу, что многие даже “измеряли” свое сопротивление. А значит, измеряя сопротивление высокоомного резистора к одному из его выводов прикасаются только щупом.

А если сопротивление резистора не большое? Например, возьмем резистор с номинальными сопротивлением 3.3 кОм ± 5%. Не прикасаясь к выводам резистора и щупов измерим его сопротивление. У меня получилось 3.297 кОм. А теперь измерим сопротивление “как обычно”, прижав щупы к выводам резистора пальцами. Результат будет иным, 3.291 кОм. Разница невелика, но она есть.

Для стрелочных измерительных приборов на показания влияет и расположение стрелочной головки в пространстве. Если прибор должен работать при горизонтальном положении шкалы, то установив его вертикально, или под углом к горизонтали, мы получим неверный результат.

Регламентированная процедура это не обязательно нечто записанное на бумаге и скрепленное множеством подписей и печатей. Если конечно речь не идет о метрологической лаборатории. Это просто набор правил, соблюдение которых позволяет получить достоверный результат.

А насколько хорош этот стрелок?

Возвращаемся в тир! Раз результат одно выстрела ничего не позволяет сказать о стрелке и его оружии, значит нужно провести достаточное количество выстрелов. Может быть промах был случайным…

Результат серии выстрелов по мишени. Иллюстрация моя
Результат серии выстрелов по мишени. Иллюстрация моя

Вот теперь все гораздо интереснее. Во первых, видно, что стрелок все время попадает примерно в одно и тоже место. Во вторых, это место расположено не в центре мишени. В результатах стрельбы стала видна некоторая система. Давайте присмотримся повнимательнее.

В результатах стрельбы теперь видна некоторая система. Иллюстрация моя
В результатах стрельбы теперь видна некоторая система. Иллюстрация моя

У стрелков есть понятие кучности. Кучность оружия это свойство группировать попадания на некоторой ограниченной площади. Но есть еще и кучность стрелка, которая уже является свойством стрелка, а не оружия. И разброс попаданий определяется совокупной кучностью стрелка и оружия. Это для нас важно.

Почему выстрелы не могут попадать точно в одно и тоже место? Потому что вмешивается случайность. Скорость пули при выходе из ствола оружия немного разная. Она зависит и от количества пороха в патроне. И от сопротивления, которое пуля испытывает проходя по каналу ствола. А это включает, в том числе, колебания наружного диаметра пули. Диаметр канала ствола зависит от температуры, которая повышается при каждом выстреле и снижается между выстрелами. Ствол при каждом выстреле немного колеблется. Тоже самое касается и стрелка, для него тоже можно привести довольно большой список случайностей, которые влияют на результат.

Каждое из этих возмущающих событий случайно и невелико. Но на результат стрельбы влияет их совокупность. И именно случайный характер дает тот самый неизбежный разброс результатов, который мы не можем предсказать.

Еще раз отмечу важный для нас факт. Разброс результатов стрельбы, вызванный случайными событиями, является совокупностью случайностей оружия и стрелка. То есть, разброс попаданий имеет две составляющие, в нашем случае.

Тем не менее, можно заметить, что разброс попаданий тоже имеет некоторую закономерность. Попадания не просто сгруппированы, они сгруппированы вокруг некоего центра. И мы можем выделить этот центр, как место максимальной плотности попаданий. И из этого центра провести окружность, которая охватит большую часть попаданий. Что я и сделал на иллюстрации. Центр окружности, точку максимальной плотности попаданий, можно считать условным местом попадания всей стрельбы. Это место попадания, результат всей серии выстрелов, будет иметь вероятностный характер. Для его определения используются методы математической статистики. Но об этом будет отдельная статья.

Итак, кучность стрельбы определяется случайными факторами. И поскольку у нас теперь не один выстрел, а множество, мы имеем и множество ошибок, свою для каждого единичного выстрела. Давайте выделим в этих ошибках случайную составляющую как расстояние от центра нашей окружности, вероятностного результата всей стрельбы, до каждого отдельного попадания.

Совокупность всех случайных составляющих ошибок можно назвать погрешностью. Причем погрешностью случайной.

Но мы можем видеть, что попадания, в целом, смещены относительно центра мишени. И это уже не влияние случайных факторов. Это смещение носит системный, регулярный характер.

Мы можем для каждого единичного выстрела определить ошибку, величину промаха, расстояние до центра мишени. Для полученной совокупности ошибок мы можем найти среднюю величину промаха. И эта величина промаха будет, условно, соответствовать расстоянию от центра мишени до вероятностного результата стрельбы, центра той самой окружности, что мы провели ранее. Почему условно? Потому что эта величина тоже будет вероятностной.

Среднее значение совокупности ошибок, расстояний от места попадания до центра окружности, смещение вероятностного результата стрельбы от центра мишени, можно назвать систематической погрешностью.

В отличии от погрешности случайной, систематическая погрешность поддается прогнозированию. И не только прогнозированию, но и корректировке. Так для нашего случая мы можем выбрать другую точку прицеливания, расположенную не в центре мишени. Или откорректировать положение прицела.

Причем, как и случайная погрешность, погрешность систематическая имеет несколько составляющих. В частности, у оружия может быть сбит прицел. И это погрешность именно оружия. Но ведь и при точном прицеле стрелок может неправильно целиться? И это уже погрешность стрелка.

Ошибка и погрешность

Давайте опять на время покинем тир и займемся терминологией. И сначала разберемся, чем отличается ошибка от погрешности. Ведь это понятия достаточно близкие, на первый взгляд.

Если мы знаем истинное значение измеряемой величины, то мы можем сравнить его с результатом единичного измерения, с измеренным значением. Разность между истинным и измеренным значением и даст нам величину ошибки единичного измерения. Однако, проблема в том, что мы обычно не знаем истинного значения измеряемой физической величины. А значит, просто не в состоянии определить ошибку каждого измерения.

И тут нам на помощь приходит математическая статистика в лице теории ошибок. Мы можем в метрологической лаборатории провести серию испытаний нашего измерительного прибора, в которых будем измерять точно известные, эталонные, значения. После множества проведенных измерений мы получим результаты, которые будут обработаны методами математической статистики.

И мы получим статистические, вероятностные, величины тех ошибок, которые вносит наш измерительный прибор. Вот эти статистические величины ошибок и называют погрешностями.

Погрешность, как и ошибка измерения, показывает разницу между истинным значением и измеренным. Но, в отличии от ошибки, она показывает не точное значение ошибки, а границы неопределенности значения измеряемой физической величины. И это очень важное отличие.

То есть, проведя измерение неизвестного значения физической величины мы можем, обращаясь к погрешности, определить диапазон значений ошибки. Диапазон, а не конкретное значение. Точное значение ошибки будет находится где то внутри этого диапазона. И будет иметь вероятностный характер. Причем ошибка каждого конкретного измерения может не просто лежать в диапазоне, определяемом погрешностью, но и быть равной нулю. С некоторой долей вероятности.

Погрешность случайная и систематическая

Итак, погрешность это статистическая величина. И мы уже, на примере стрельбы в тире, видели, что ее можно разделить на случайную и систематическую. Каждая из этих двух составляющих обладает свои свойствами, которые мы будет рассматривать в отдельных статьях. Сегодня мы только разберемся с определениями.

Случайная погрешность, как и следует из ее названия, изменяется случайным образом. Причем случайным образом изменяется и величина погрешности, и ее знак. Каждое измерение будет отличаться от предыдущего, и последующего, на некоторую, пусть и очень малую величину. Ту самую случайную погрешность.

Мы можем знать источники случайной погрешности. Можем попытаться снизить их влияние. Но полностью устранить случайную погрешность нельзя. Так в нашей стрельбе в тире случайную погрешность создавали, например, колебания ствола оружия и не совсем точная дозировка пороха в патроне. При электрических измерениях случайную погрешность вносят электромагнитные помехи. В приборах с стрелочными шкалами случайную погрешность вносит направление взгляда оператора на шкалу из-за явления параллакса. В электронных измерительных приборах (не обязательно цифровых) случайную погрешность привносит неизбежный шумовой сигнал.

Систематическая погрешность, в противоположность случайной, остается неизменной при последовательных измерениях одного и того же значения физической величины. А при измерении изменяющейся физической величины систематическая погрешность или остается неизменной, или изменяется по какому-либо известному закону.

Другими словами, систематическая погрешность предсказуема и поддается корректировке. В нашем тире мы видели, что систематическую погрешность мог вносить сбитый прицел. Не смотря на разброс попаданий от каждого выстрела, все они были смещены в одну сторону и на одно расстояние, если убрать случайную составляющую погрешности.

В одной из последующих статей, которая будет посвящения систематической погрешности, мы увидим, что ее тоже можно разделить на две составляющие – относительную систематическую погрешность и абсолютную систематическую погрешность. Не буду забегать вперед, ограничусь лишь кратким упоминанием, что относительная погрешность зависит от измеренного значения физической величины, а абсолютная нет.

Погрешности приборные и метода измерения (методические)

Помните, чуть ранее мы говорили, что результат стрельбы зависит как от собственно оружия, так и от стрелка? Точно так же, погрешность результата измерения зависит как от погрешности измерительно прибора, так и от метода, который используется для измерения. Кроме того, влияют и математические модели процессов, которые используются при измерении, или которые собственно и измеряют.

Поскольку при выполнении измерений можно сменить как измерительный прибор, так и изменить метод (методику) измерения, имеет смысл разделять вносимые ими погрешности.

Приборной погрешностью называют погрешность вносимую собственно измерительными прибором. Именно приборная погрешность указывается в паспорте измерительного прибора. Например, если мы будем измерять ток измеряя падение напряжения на токовом шунте, приборная погрешность будет относиться только к вольтметру. Она не будет учитывать погрешность сопротивления токового шунта, ни в каком виде.

Теперь давайте вспомним, что измерение от наблюдения отличается соблюдением регламентирующей процедуры. Эта процедура учитывает множество нюансов. Но обязательным является указание метода проведения измерения. То есть, как именно мы будем выполнять измерение.

Под методом измерения понимают специальный прием или совокупность приемов сравнения измеряемой физической величины с ее единицей. Например, метод измерения сопротивления с помощью измерения падения напряжения на резисторе при протекании через него тока заданной величины. Или метод измерения силы тока, протекающего через резистор, при приложении к нему заданного напряжения.

Кроме метода измерения регламентирующая процедура может включать в себя и методологию измерения. Например, измерение температуры жидкости метом измерения сопротивления платинового термометра сопротивления, это метод. А необходимость перемешивания жидкости, что бы обеспечивать равенство ее температуры во всем объеме, это методология. И все вместе это включается в регламентирующую процедуру.

Погрешность метода, методическая, это погрешность вносимая в результат измерения несовершенством метода измерения. Например, ток, протекающий через резистор при измерении сопротивления, может быть задан с некоторой ошибкой (погрешностью). Погрешность метода не учитывает погрешность приборную.

А результирующая погрешность измерения будет совокупностью погрешности метода и приборной погрешности. Погрешности математической модели (и расчетов) могут учитываться отдельно или включаться в методическую погрешность.

Отдельно погрешность метода (методическую) не всегда можно выделить. Например, измерение напряжения вольтметром, прямое измерение (это тема отдельного разговора) можно считать имеющим только приборную погрешность. Равно как и измерение сопротивления омметром. Измерение температуры внешним датчиком будет уже учитывать и погрешность датчика (метода) и приборную погрешность.

В случае с нашей стрельбой, приборные погрешности это погрешности оружия. А погрешности метода, пожалуй, погрешности стрелка. Мы можем дать то же самое оружие в руки другого стрелка и результат будет иным. Можем дать в руки нашему стрелку другое оружие и результат тоже изменится.

Определяем лучшего стрелка

Возвращаемся в наш тир. Давайте теперь устроим соревнование в поисках лучшего стрелка. У нас будет 4 кандидата. Вот их результаты

Результаты стрельбы в тире четырех разных стрелков. Иллюстрация моя
Результаты стрельбы в тире четырех разных стрелков. Иллюстрация моя

У двух стрелков, 1 и 2, результаты кучные, но второй отстрелялся по центру мишени, а второй со смещением. Однако, есть еще и стрелок 3, который, в среднем, отстрелялся по центу мишени, но вот с кучностью у него проблемы. Последний стрелок и по центу мишени не попал, и кучность никуда не годится.

Какой стрелок лучший? Очевидно, что стрелок 2. Но на чем основано это решение? В обиходе мы говорим, что стрелок 2 более точен. Но что такое точность? И как оценить кучность, с точки зрения метрологии? А значит,Ю нам снова надо покинуть тир и заняться метрологией.

Точность и прецизионность

Мы легко, не задумываясь, говорим о точности измерительных приборов или измерений. Часто можно встретить и термин прецизионный прибор. Но что обозначают эти термины и какая между ними разница? Давайте начнем с прецизионности.

Официальное определение прецизионности оперирует понятиями математической статистики, что неудивительно, как мы теперь понимаем. Прецизионность является некоторым аналогом кучности, о которой мы сегодня уже говорили.

Прецизионность это степень близости друг к другу независимых результатов измерений. А измерения, как мы помним, выполняются в регламентированных условиях и регламентированными методами. Независимые измерения, как мы знаем из статьи

не зависят от результатов предыдущих измерений. И не влияют на последующие.

Очень важным является то, что прецизионность определяется только случайными погрешностями. На нее совершенно не влияют погрешности систематические. Не важно, насколько далек результат измерений от истинного значения физической величины. Важно лишь то, насколько близки результат измерений друг к другу.

Если вернуться к результатам из тира, то теперь понятно, что у стрелков 1 и 2 прецизионность почти одинакова, и выше, чем у других стрелков. Ну а самая низкая прецизионность у стрелка 4.

Количественная оценка прецизионности может быть разной. Здесь опять вмешиваются различные регламенты. Но, в общем случае, прецизионность выражается через стандартные отклонения. Чаще всего, через среднеквадратичное отклонение.

Точность, в отличии от прецизионности, определяет, насколько близок результат измерений к истинному значению физической величины. Понятие точности ближе всего к тому, что мы и понимаем под точностью в бытовом смысле. Но, естественно, определение точности оперирует понятиями математической статистики.

Точность это степень близости результата измерений к истинному значению. И опять, измерения выполняются в соответствии с регламентирующей процедурой. В определении точности можно встретить и ссылки на математическое ожидание. Если не вдаваться в тонкости плотностей распределения вероятностей, то это среднее значение результата измерения для совокупности измерений. Тот самый центр условной окружности, который мы рисовали для результатов стрельбы.

Если вернуться к результатам из тира, то можно сказать, что у стрелков 2 и 3 точность примерно одинакова. Что может показаться странным, с бытовой точки зрения. Но вот у стрелка 2, по сравнению с остальными, выше и точность, и прецизионность. Поэтому он и является победителем. Наконец то мы смогли обосновать наше решение метрологически.

Точность и прецизионность не просто являются метрологическими и математическими понятиями. Они являются понятиями вероятностными, статистическими. Как и погрешности. А значит, вводятся не для единичного измерения, а для совокупности, множества, измерений. И не зря метрологи требуют выполнять много измерений одного и того же, причем по строгой процедуре, которая гарантирует, в том числе, независимость этих измерений. Это не прихоть метролога, это требования математической статистики.

Правильность, повторяемость, воспроизводимость

В предельном случае, когда измерений выполняется очень много, точность становится правильностью. Точное количество измерений определяется регламентами. Например, вполне может быть, что для определения точности достаточно 20 измерений, а для определения правильности нужно 2000 измерений. Или даже 20000.

В отличии от правильности, для повторяемости не требуется очень большого количества измерений. Повторяемость означает, что прецизионность результатов измерений, с точки зрения математической статистики, выполняемых с одним и тем же образцом (значением физической величины), на одном и том же оборудовании, в одних и тех же условиях, одним и тем же человеком, в течении некоторого ограниченного отрезка времени, должна сохраняться.

Другими словами, мы можем выполнить серию измерений, сделать перерыв, например, 5 минут, повторить серию измерений. И прецизионность для этих двух серий измерений должна быть одинаковой.

Кроме того, есть еще понятие воспроизводимости. Воспроизводимость означает, что выполненные в разных метрологических лабораториях измерения, одним и тем же методом, для идентичных объектов (значений, эталонов) измерения, с точки зрения математической статистики, должны иметь одинаковую прецизионность.

Заключение

Пожалуй, на этом сегодня стоит остановиться. Как бы ни была наглядна аналогия с тиром, как бы она не позволяла ощутить, почти осязаемо, сложные метрологические понятия, обилие определений и новых терминов может утомить читателей. Или вовсе отвратить от знакомства с метрологией.

Рассмотренные сегодня типы погрешностей могут показаться нелогичными и запутанными. Но на самом деле, все очень логично, все необходимо. Пожалуй, для большинства, лишними будут только повторяемость, правильность и воспроизводимость.

В последующих статьях мы рассмотрим разные погрешности подробнее. Но без излишнего погружения в детали и зубодробильной математики. В конечном итоге, этот цикл статей не является учебником метрологии. И даже не пытается претендовать на сколь нибудь полное, подробное, или точное, изложение основ метрологии.

Будет интересно!

До новых встреч!

Источник

Абсолютная и относительная погрешность


Абсолютная и относительная погрешность

4.2

Средняя оценка: 4.2

Всего получено оценок: 2187.

4.2

Средняя оценка: 4.2

Всего получено оценок: 2187.

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Опыт работы учителем математики – более 33 лет.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

  • при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
  • при делении и умножении чисел требуется сложить относительные погрешности;
  • при возведении в степень относительную погрешность умножают на показатель степени.

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Заключение

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Тест по теме

Доска почёта

Доска почёта

Чтобы попасть сюда – пройдите тест.

  • Светлана Лобанова-Асямолова

    10/10

  • Валерий Соломин

    10/10

  • Анастасия Юшкова

    10/10

  • Ксюша Пономарева

    7/10

  • Паша Кривов

    10/10

  • Евгений Холопик

    9/10

  • Guzel Murtazina

    10/10

  • Максим Аполонов

    10/10

  • Olga Bimbirene

    9/10

  • Света Колодий

    10/10

Оценка статьи

4.2

Средняя оценка: 4.2

Всего получено оценок: 2187.

А какая ваша оценка?

Источник

Погре́шность измере́ния — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.

Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного. Это отклонение принято называть ошибкой измерения.[1] Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. На практике вместо истинного значения используют действительное значение величины хд, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него[1]. Такое значение обычно вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому при записи результатов измерений необходимо указывать их точность. Например, запись T = 2,8 ± 0,1 с; P = 0,95 означает, что истинное значение величины T лежит в интервале от 2,7 с до 2,9 с с доверительной вероятностью 95 %.

Количественная оценка величины погрешности измерения — мера «сомнения в измеряемой величине» — приводит к такому понятию, как «неопределённость измерения». В то же время иногда, особенно в физике, термин «погрешность измерения» (англ. measurement error) используется как синоним термина «неопределённость измерения» (англ. measurement uncertainty)[2].

Классификация погрешностей измерений[править | править код]

По способу выражения[править | править код]

Абсолютная погрешность[3]
Абсолютной погрешностью называют величину, выраженную в единицах измеряемой величины. Её можно описать формулой {displaystyle Delta X=X_{text{измеряемый}}-X_{text{истинный}}.} Вместо истинного значения измеряемой величины на практике пользуются действительным значением {displaystyle {X_{text{д}}},} которое достаточно близко к истинному и которое определяется экспериментальным путём и может приниматься вместо истинного. Из-за того, что истинное значение величины всегда неизвестно, можно лишь оценить границы, в которых лежит погрешность, с некоторой вероятностью. Такая оценка выполняется методами математической статистики[4].
Относительная погрешность[3]
Относительная погрешность выражается отношением {displaystyle delta X={frac {Delta X}{X_{text{д}}}}.} Относительная погрешность является безразмерной величиной; её численное значение может указываться, например, в процентах.

По источнику возникновения[править | править код]

Инструментальная погрешность[5]
Эта погрешность определяется несовершенством прибора, возникающим, например, из-за неточной калибровки.
Методическая погрешность[5]
Методической называют погрешность, обусловленную несовершенством метода измерений. К таким можно отнести погрешности от неадекватности принятой модели объекта или от неточности расчётных формул.
Субъективная погрешность[5]
Субъективной является погрешность, обусловленная ограниченными возможностями, ошибками человека при проведении измерений: проявляется, например, в неточностях при отсчёте показаний со шкалы прибора.

По характеру проявления[править | править код]

Случайная погрешность
Это составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведённых в одних и тех же условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, всегда присутствуют в результате измерения, однако их влияние обычно можно устранить статистической обработкой. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики.

Математически случайную погрешность, как правило, можно представить белым шумом: как непрерывную случайную величину, симметричную относительно нуля, независимо возникающую в каждом измерении (некоррелированную по времени).

Основным свойством случайной погрешности является то, что искажения искомой величины можно уменьшить путём усреднения данных. Уточнение оценки искомой величины при увеличении количества измерений (повторных экспериментов) означает, что среднее случайной погрешности при увеличении объёма данных стремится к 0 (закон больших чисел).

Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельности слабо влияет на результат измерения. По этой причине распределение случайной погрешности часто полагают «нормальным» (см. «Центральная предельная теорема»). «Нормальность» позволяет использовать в обработке данных весь арсенал математической статистики.

Однако априорная убеждённость в «нормальности» на основании центральной предельной теоремы не согласуется с практикой — законы распределения ошибок измерений весьма разнообразны и, как правило, сильно отличаются от нормального.[источник не указан 727 дней]

Случайные погрешности могут быть связаны с несовершенством приборов (например, с трением в механических приборах), с тряской в городских условиях, с несовершенством самого объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления).

Систематическая погрешность
Это погрешность, изменяющаяся по определённому закону (в частности, постоянная погрешность, не изменяющаяся от измерения к измерению). Систематические погрешности могут быть связаны с неисправностью или несовершенством приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.

Систематическую ошибку нельзя устранить повторными измерениями. Её устраняют либо с помощью поправок, либо «улучшением» эксперимента.

Деление погрешностей на случайные и систематические достаточно условно. Например, ошибка округления при определённых условиях может носить характер как случайной, так и систематической ошибки.

Грубая погрешность
Так называют погрешность, существенно превышающую ожидаемую. Как правило она проявляется в результате явной ошибки в проведении измерений, что обнаруживается при повторных проверках. Результат измерения с грубой погрешностью исключают из рассмотрения и не используют при дальнейшей математической обработке[6].

Оценка погрешности при прямых измерениях[править | править код]

При прямых измерениях искомая величина определяется непосредственно по отсчётному устройству (шкале) средства измерения. В общем случае измерения проводятся по определённому методу и при помощи некоторых средств измерений. Эти компоненты несовершенны и вносят свой вклад в погрешность измерения[7]. Если тем или иным путём погрешность измерения (с конкретным знаком) удаётся найти, то она представляет собой поправку, которую просто исключают из результата. Однако достичь абсолютно точного результата измерения невозможно, и всегда остаётся некоторая «неопределённость», которую можно обозначить, оценив границы погрешности[8]. В России методики оценки погрешности при прямых измерениях стандартизированы ГОСТом Р 8.736-2011[9] и Р 50.2.038-2004[10].

В зависимости от имеющихся исходных данных и свойств погрешностей, которые подвергаются оценке, используют различные способы оценки. Случайная погрешность, как правило, подчиняется закону нормального распределения, для нахождения которого необходимо указать математическое ожидание M и среднеквадратическое отклонение sigma. В связи с тем, что при измерении проводится ограниченное число наблюдений, находят только наилучшие оценки этих величин: среднее арифметическое (то есть конечный аналог математического ожидания) результатов наблюдений {bar {x}} и среднеквадратическое отклонение среднего арифметического {displaystyle S_{bar {x}}}[11][9]:

{displaystyle {bar {x}}={frac {sum _{i=1}^{n}x_{i}}{n}}}; {displaystyle S_{bar {x}}={sqrt {frac {sum _{i=1}^{n}(x_{i}-{bar {x}})^{2}}{n(n-1)}}}.}

Доверительные границы varepsilon оценки погрешности, полученной таким способом, определяются умножением среднеквадратического отклонения на коэффициент Стьюдента t, выбранный для заданной доверительной вероятности {displaystyle P:}

{displaystyle varepsilon =tS_{bar {x}}.}

Систематические погрешности в силу своего определения не могут быть оценены путём проведения многократных измерений[12]. Для составляющих систематической погрешности, обусловленной несовершенством средств измерений, как правило, известны только их границы, представленные, например, основной погрешностью средства измерения[13].

Итоговая оценка границ погрешности получается суммированием вышеприведённых «элементарных» составляющих, которые рассматриваются как случайные величины. Эта задача может быть математически решена при известных функциях распределений этих случайных величин. Однако в случае систематической погрешности такая функция, как правило, неизвестна и форму распределения этой погрешности задают как равномерную[14]. Основная трудность заключается в необходимости построения многомерного закона распределения суммы погрешностей, что практически невозможно уже при 3—4 составляющих. Поэтому используются приближённые формулы[15].

Суммарную неисключённую систематическую погрешность (метода, средств измерения, других источников), когда она состоит из нескольких m компонентов, определяют по следующим формулам[9]:

{displaystyle Theta _{sum }=pm sum _{i=1}^{m}left|Theta _{i}right|} (если {displaystyle m<3});
{displaystyle Theta _{sum }(P)=pm k{sqrt {sum _{i=1}^{m}Theta _{i}^{2}}}} (если {displaystyle mgeqslant 3}),
где коэффициент k для доверительной вероятности {displaystyle P=0{,}95} равен 1,1.

Суммарная погрешность измерения, определяемая случайной и систематической составляющей, оценивается как[16][9]:

{displaystyle Delta =K{sqrt {S_{bar {x}}^{2}+{frac {Theta _{sum }^{2}}{3}}}}} или {displaystyle Delta =K{sqrt {S_{bar {x}}^{2}+left({frac {Theta _{sum }(P)}{k{sqrt {3}}}}right)^{2}}}},
где {displaystyle K={frac {varepsilon +Theta _{sum }}{S_{bar {x}}+{frac {Theta _{sum }}{sqrt {3}}}}}} или {displaystyle K={frac {varepsilon +Theta _{sum }(P)}{S_{bar {x}}+{frac {Theta _{sum }(P)}{k{sqrt {3}}}}}}.}

Окончательный результат измерения записывается как[17][9][18][19] {displaystyle Apm Delta (P),} где A — результат измерения ({displaystyle {bar {x}},}) Delta  — доверительные границы суммарной погрешности, P — доверительная вероятность.

Оценка погрешности при косвенных измерениях[править | править код]

При косвенных измерениях искомая величина не измеряется непосредственно — вместо этого она вычисляется по известной функциональной зависимости (формуле) от величин (аргументов), получаемых прямыми измерениями. Для линейной зависимости методика проведения таких измерений математически строго разработана[20]. При нелинейной зависимости применяются методы линеаризации или приведения. В России методика расчёта погрешности при косвенных измерениях стандартизирована в МИ 2083-90[19].

См. также[править | править код]

  • Измерение
  • Класс точности
  • Метрология
  • Отклонение от круглости
  • Мультипликативная погрешность
  • Неопределённость измерения

Примечания[править | править код]

  1. ↑ 1 2 В ряде источников, например в Большой советской энциклопедии, термины ошибка измерения и погрешность измерения используются как синонимы, но, согласно рекомендации РМГ 29-99, термин ошибка измерения, считающийся менее удачным, не рекомендуется применять, а РМГ 29-2013 его вообще не упоминает. См. «Рекомендации по межгосударственной сертификации 29-2013. ГСИ. Метрология. Основные термины и определения Архивная копия от 8 сентября 2016 на Wayback Machine».
  2. ↑ Olive K. A. et al. (Particle Data Group). 38. Statistics. — В: 2014 Review of Particle Physics // Chin. Phys. C. — 2014. — Vol. 38. — P. 090001.
  3. ↑ 1 2 Фридман, 2008, с. 42.
  4. ↑ Фридман, 2008, с. 41.
  5. ↑ 1 2 3 Фридман, 2008, с. 43.
  6. ↑ Клюев, 2001, p. 15.
  7. ↑ Рабинович, 1978, p. 19.
  8. ↑ Рабинович, 1978, p. 22.
  9. ↑ 1 2 3 4 5 ГОСТ Р 8.736-2011 ГСИ. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения / ВНИИМ. — 2011.
  10. ↑ Р 50.2.038-2004 ГСИ. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений. Дата обращения: 9 марта 2021. Архивировано 24 июля 2020 года.
  11. ↑ Рабинович, 1978, p. 61.
  12. ↑ Фридман, 2008, с. 82.
  13. ↑ Рабинович, 1978, p. 90.
  14. ↑ Рабинович, 1978, p. 91.
  15. ↑ Новицкий, 1991, p. 88.
  16. ↑ Рабинович, 1978, p. 112.
  17. ↑ МИ 1317-2004 ГСИ. Рекомендация. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров / ВНИИМС. — Москва, 2004. — 53 с.
  18. ↑ Р 50.2.038-2004 Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений / ВНИИМ. — 2011. — 11 с.
  19. ↑ 1 2 МИ 2083-90 ГСИ. Измерения косвенные определение результатов измерений и оценивание их погрешностей / ВНИИМ. — 11 с.
  20. ↑ Фридман, 2008, с. 129.

Литература[править | править код]

  • Машиностроение. Энциклопедия. Измерения, контроль, испытания и диагностика / В. В. Клюев, Ф. Р. Соснин, В. Н. Филинов и др.; Под общей редакцией В. В. Клюева. — 2-е изд., перераб. и доп.. — М.: Машиностроение, 2001. — Т. III-7. — 464 с.
  • Якушев А. И., Воронцов Л. Н., Федотов Н. М. Взаимозаменяемость, стандартизация и технические измерения. — 6-е изд., перераб. и доп.. — М.: Машиностроение, 1986. — 352 с.
  • Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др. Лабораторные занятия по физике. Учебное пособие / под ред. Гольдина Л. Л.. — М.: Наука. Главная редакция физико-математической литературы, 1983. — 704 с.
  • Назаров Н. Г. Метрология. Основные понятия и математические модели. — М.: Высшая школа, 2002. — 348 с. — ISBN 5-06-004070-4.
  • Деденко Л. Г., Керженцев В. В. Математическая обработка и оформление результатов эксперимента. — М.: МГУ, 1977. — 111 с. — 19 250 экз.
  • Рабинович С. Г. Погрешности измерений. — Ленинград, 1978. — 262 с.
  • Фридман А. Э. Основы метрологии. Современный курс. — Санкт-Петербург: НПО «Профессионал», 2008. — 284 с.
  • Новицкий П. В., Зограф И. А. Оценка погрешностей результатов измерений. — Л.: Энергоатомиздат, 1991. — 304 с. — ISBN 5-283-04513-7.

Ссылки[править | править код]

  • Погрешность и неопределённость Архивная копия от 8 мая 2013 на Wayback Machine
  • Что означает класс точности измерительного прибора Архивная копия от 5 июля 2014 на Wayback Machine
  • Рекомендация МОЗМ № 34. Классы точности средств измерений
Источник

Добавить комментарий