Как найти абсолютную температуру газа формула

Уравне́ние состоя́ния идеа́льного га́за (иногда уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

,

где

Уравнение состояния идеального газа можно записать в виде:

,

где  — масса,  — молярная масса, (так как количество вещества ):

или в виде

,

где  — концентрация частиц (атомов или молекул) – количество частиц,  — постоянная Больцмана.

Эта форма записи носит имя уравнения (закона) Клапейрона — Менделеева.

Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную значение которой необходимо было измерять для каждого газа:

Менделеев обнаружил, что прямо пропорциональна , коэффициент пропорциональности он назвал универсальной газовой постоянной.^{[источник не указан 1458 дней]}

Связь с другими законами состояния идеального газа[править | править код]

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта — Изотермический процесс.

 — Закон Гей-Люссака — Изобарный процесс.

 — закон Шарля (второй закон Гей-Люссака, 1808 г.) — Изохорный процесс

В форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое.

С точки зрения химика этот закон может звучать несколько иначе: объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:

.

1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:

.

Закон Бойля — Мариотта

Закон Бойля — Мариотта

назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.

В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме

где  — показатель адиабаты,  — внутренняя энергия единицы массы вещества.

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. Это обстоятельство может быть прояснено на основании молекулярных представлений.

С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.

С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение немного уменьшается. При очень высоких давлениях большую роль играет первое обстоятельство и произведение увеличивается.

См. также[править | править код]

• Совершенный газ
• Реальный газ
• Уравнение состояния реального газа

Примечания[править | править код]

Литература[править | править код]

• Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высшая школа, 2009. — 527 с. — ISBN 978-5-06-006161-1.

Микро- и макропараметры системы

Атомы и молекулы, взаимодействую друг с другом, образуют разнообразные вещества (системы). Если число частиц невелико (десятки, сотни), то мы имеем микросистему. Если число частиц системы во много раз больше (миллионы и более), то такую систему называют макросистемой. Например, газ, состоящий из очень большого числа молекул — это макросистема. Большое число частиц системы приводит к появлению у нее новых свойств, которыми отдельные частицы не обладают. Например, давление газа есть результат непрерывного действия всех молекул на стенки сосуда, хотя не каждая молекула сталкивается со стенками. Для описания состояния макросистемы вводят параметры, которые называются параметрами состояния. Различают микропараметры и макропараметры состояния.

Микропараметры — это параметры, характеризующие отдельную частицу. Например, масса молекулы, ее скорость, энергия.

Макропараметры

Макропараметры — это параметры, характеризующие систему в целом. Например, объем V, давление p, средняя скорость молекул (~leftlangle upsilon rightrangle), температура T, концентрация n и т.д. Значения этих параметров могут быть установлены с помощью измерительных приборов.

Объем газа V — это объем сосуда, в котором газ находится. В Си измеряется в м³. Часто используется несистемная единица измерения 1 литр: 1 л = 10^-3 м³.

Давление р — скалярная физическая величина, равная отношению силы F к значению площади S площадки, на которую эта сила действует[~p = dfrac{F}{S}]. Газ оказывает давление вследствие столкновений молекул со стенками сосуда. В Си единица давления 1 Н/м² = 1 Па (Паскаль). Внесистемные единицы измерения — 1 мм.рт.ст и 1 атмосфера. Нормальное давление равно одной физической атмосфере. 1 физическая атмосфера = 1 атм = 760 мм.рт.ст, 1 техническая атмосфера = 1 ат = 736 мм.рт.ст. 1 мм.рт.ст. = 133Па.

• Более строгое определение давления: давление р — скалярная физическая величина, равная отношению проекции силы на направление нормали к площадке, на которую сила действует, к значению площади этой площади.

Концентрация молекул n — это число молекул N в единице объема, т.е. (~n = dfrac{N}{V}). Измеряется в 1/м³ = м^–3.

Температура — скалярная физическая величина, характеризующий степень нагретости тела.

По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС). За 1 ºС принята одна сотая промежутка от температуры плавления льда (0 ºС) до температуры кипения воды (100 ºС).

Абсолютная температурная шкала — шкала температур, в которой за начало отсчета принят абсолютный нуль. Температура здесь обозначается буквой T, измеряется в кельвинах (К). За единицу измерения в этой шкале принят один градус Цельсия, т.е. изменение на один кельвин (1 К) равно изменению на один градус Цельсия.

T = (t + 273) К или t = (T – 273) ºС,

где T — абсолютная термодинамическая температура (К); t — температура по шкале Цельсия (ºС).

Средние скорости молекул газов

Движение молекул газа подчиняется законам статистической физики. В каждый момент времени скорости отдельных молекул могут значительно отличаться друг от друга, но их средние значения одинаковы и при расчетах используются не мгновенные скорости отдельных молекул, а не которые средние значения. Различают среднюю арифметическую (~ leftlangle upsilon rightrangle) и среднюю квадратичную (~leftlangle upsilon_{KB} rightrangle) скорости хаотического движения молекул.

Пусть имеется N молекул, скорости которых соответственно υ₁, υ₂, …, υ_N. Средняя арифметическая скорость хаотического движения молекул (при грубом приближении) по модулю определяется как сумма модулей скоростей молекул газа, деленная на их общее число:

(~leftlangle upsilon rightrangle = dfrac{upsilon_1 + upsilon_2 + ldots + upsilon_N}{N} .)

Средняя квадратичная скорость хаотического движения молекул

(~leftlangle upsilon_{KB} rightrangle = sqrt{leftlangle upsilon^2 rightrangle} = sqrt{dfrac{upsilon^2_1 + upsilon^2_2 + ldots + upsilon^2_N}{N}} ,)

где (~leftlangle upsilon^2 rightrangle) — средний квадрат скорости движения молекул. Его не следует смешивать с квадратом средней скорости[~leftlangle upsilon^2 rightrangle ne leftlangle upsilon rightrangle^2].

• Как показывают расчеты, (~leftlangle upsilon rightrangle = sqrt{dfrac{8R cdot T}{pi M}}); (~leftlangle upsilon_{KB} rightrangle = sqrt{dfrac{3R cdot T}{M}}) , где R — универсальная газовая постоянная, Μ — молярная масса.

• Более строгое определение средней скорости дано тут.

См. также

1. Аксенович Л.А. и др. Физика в средней школе //6.12. Температура и тепловое равновесие системы
2. Аксенович Л.А. и др. Физика в средней школе //6.13. Измерение температуры
3. Аксенович Л.А. и др. Физика в средней школе //6.14. Абсолютная температурная шкала. Абсолютный нуль
4. Кикоин А. Температура, теплота, термометр //Квант. — 1990. — № 8. — С. 10-19
5. Мякишев Г.Я. Давление газа в сосуде //Квант. — 1987. — № 9. — С. 41-42
6. Температура

Идеальный газ

Рассмотрим свойства газов на основе МКТ. Для этого введем физическую модель идеального газа, в которой приняты следующие допущения:

1) размеры молекул малы по сравнению со средним расстоянием между ними; молекулы можно принимать за материальные точки;

2) силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях;

3) молекулы сталкиваются друг с другом как абсолютно упругие шары, движение которых описывается законами механики.

Таким образом, идеальным называется газ, в котором можно пренебречь собственным объемом молекул и межмолекулярным взаимодействием (кроме столкновений).

При небольших давлениях и не очень низких температурах реальные газы близки к идеальному газу. Например, водород, кислород при нормальных условиях в атмосфере можно рассматривать как идеальные газы.

При высоких давлениях молекулы газа находятся так близко, что между ними возникают заметные силы взаимодействия. Пренебречь их собственным объемом нельзя, и газ уже не является идеальным.

Основное уравнение МКТ идеального газа — это уравнение, связывающее микро- и макропараметры идеального газа. Одно из этих уравнений имеет вид:

(~p = dfrac{1}{3} n cdot m_0 cdot leftlangle upsilon^2 rightrangle , quad (1))

где p — давление газа (Па); n — концентрация молекул (м^–3); m₀ — масса одной молекулы газа (кг); 〈v² 〉 — среднее значение квадрата скорости молекул (м/с²). Это уравнение называют еще уравнением Клаузиуса.

Давление можно выразить через среднюю кинетическую энергию молекул[~leftlangle E_k rightrangle = dfrac{m_0 cdot leftlangle upsilon^2 rightrangle}{2},] где 〈E_k 〉 – средняя кинетическая энергия одной молекулы газа (Дж). Подставляя 〈E_k 〉 в уравнение Клаузиуса, получаем

(~p = dfrac 23 n cdot leftlangle E_k rightrangle. quad (2))

Вывод основного уравнения

1. Аксенович Л.А. и др. Физика в средней школе // 6.11. Основное уравнение МКТ идеального газа

1. Кикоин А.К. Давление идеального газа //Квант. — 1983. — № 10. — С. 35-37

Температура – мера средней кинетической энергии молекул

Можно провести следующий эксперимент. Взять сосуды с разными газами. Определить предварительно их объемы, массы и рассчитать число молекул (по формуле (~N = dfrac mM cdot N_A)), затем поместить сосуды в тающий лед. После наступления теплового равновесия определить давление p и рассчитать отношение (~dfrac{p cdot V}{N}). Опыт показывает, что оно одинаково для всех газов. Затем эти сосуды помещают в кипящую воду. Опять это отношение для всех газов одинаковое, но большее первого значения. Проделав опыт несколько раз при разных температурах, можно заметить, что отношение (~dfrac{p cdot V}{N} sim T). Обозначим коэффициент пропорциональности k, тогда:

(~dfrac{p cdot V}{N} = k cdot T ) или (~p = dfrac{N}{V} cdot k cdot T = n cdot k cdot T, quad (3))

где p — давление газа (Па); n — концентрация молекул (м^–3); T — температура газа (К); k — постоянная Больцмана, равная 1,38·10^–23 Дж/К.

Сравнивая выражения (3) и (2), получаем

( dfrac 23 n cdot leftlangle E_k rightrangle = n cdot k cdot T, ) или (~leftlangle E_k rightrangle = dfrac 32 k cdot T. )

Данная формула верна для расчёта средней энергии поступательного движения молекулы или для расчёта средней кинетической энергии одноатомной молекулы. Если учитывать, наряду с поступательным движением и вращение молекулы, то средняя кинетическая энергии молекулы с жесткой связью (без колебании атомов в молекуле) будет равна

(~leftlangle E_k rightrangle = dfrac i2 k cdot T, )

где i — степень свободы. Для одноатомного газа (например, инертные газы) i = 3, для двухатомного — i =5.

• Понятие числа степеней свободы тела, т.е. число независимых координат, необходимо для однозначного задания его положения в пространстве. На каждую степень свободы в состоянии термодинамического равновесия в среднем приходится одна и та же энергия ( dfrac{k cdot T}{2}). Оказывается, что этот результат имеет универсальный характер: средняя кинетическая энергия, приходящаяся на каждую степень свободы, одинакова и равна ( dfrac{k cdot T}{2}). Это утверждение относится не только к газам, оно справедливо для теплового движения молекул в жидкостях и твердых телах, ионов и электронов в плазме и даже для макроскопических тел, совершающих броуновское движение в результате хаотических ударов молекул окружающей среды.

Температура – это величина, характеризующая среднюю кинетическую энергию поступательного движения молекул идеального газа:

(~T = dfrac{2 leftlangle E_k rightrangle}{k}.)

Эта формула позволяет установить физический смысл абсолютной температуры Т. Этот макроскопический параметр характеризует среднее значение кинетической энергии хаотического теплового движения одной молекулы в состоянии термодинамического равновесия. Интересно отметить, что средняя энергия теплового движения молекул зависит только от температуры газа. При данной температуре средняя кинетическая энергия поступательного хаотического движения молекул не зависит ни от химического состава газа, ни от массы молекул, ни от давления газа, ни от объема, занимаемого газом.

Так как абсолютная температура не может равняться нулю, то и средняя энергия теплового движения молекул то же не может равняться нулю, т.е. молекулы находятся в постоянном движении.

См. также

1. Аксенович Л.А. и др. Физика в средней школе //6.12. Температура и тепловое равновесие системы
2. Аксенович Л.А. и др. Физика в средней школе //6.13. Измерение температуры
3. Аксенович Л.А. и др. Физика в средней школе //6.14. Абсолютная температурная шкала. Абсолютный нуль
4. Городецкий Е.Е. Идеальный газ — универсальная физическая модель //Квант. — 1991. — № 9. — С. 33-36
5. Кикоин А. Температура, теплота, термометр //Квант. — 1990. — № 8. — С. 10-19
6. *Стасенко А.Л. Кладовые энергии молекулы //Квант. — 1995. — № 5. — С. 36-38

1

Формула выглядит следующим образом: p•Vm = R•T, где p — это давление, Vm — молярный объем газа, R — это универсальная газовая постоянная, а Т — абсолютная температура идеального газа.
2

Выясняем, какие данные нам доступны для того, чтобы использовать формулу, таким образом: Т = (p•Vm)/ R.
3

В случае если нам не известен молярный объем газа, мы можем найти его по формуле:
Vm = V/ν. В этой формуле ν представляет собой количество вещества, Найти эту величину можно разделив массу газа на его молярную массу.
4

Формула, которая носит название закон Менделеева-Клапейрона, записывается именно в таком виде: p•V = (m/М) • R•T.
5

Видоизменяем эту формулу, чтобы найти температуру газа: T = (p•V • М) /(R• m).
6

Находим все величины, которые требуются нам для подстановки в формулу. Выполняем расчеты и находим искомую температуру идеального газа.

Как найти температуру газа

Для того чтобы найти абсолютную температуру идеального газа, можно воспользоваться уравнением, которое широко известно, как уравнение Клапейрона-Менделеева. Эта формула позволяет установить зависимость между давлением, температурой газа и его молярным объемом.

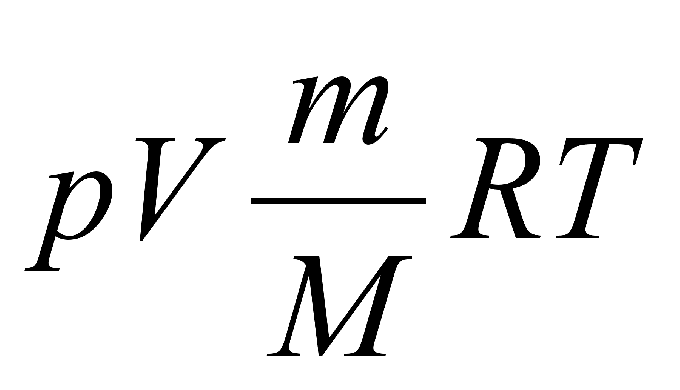
Вам понадобится

• Лист бумаги, ручка.

Инструкция

Формула выглядит следующим образом: p•Vm = R•T, где p — это давление, Vm — молярный объем газа, R — это универсальная газовая постоянная, а Т — абсолютная температура идеального газа.

Выясняем, какие данные нам доступны для того, чтобы использовать формулу, таким образом: Т = (p•Vm)/ R.

В случае если нам не известен молярный объем газа, мы можем найти его по формуле:
Vm = V/?. В этой формуле ? представляет собой количество вещества, Найти эту величину можно разделив массу газа на его молярную массу.

Формула, которая носит название закон Менделеева-Клапейрона, записывается именно в таком виде: p•V = (m/М) • R•T.

Видоизменяем эту формулу, чтобы найти температуру газа: T = (p•V • М)/(R• m).

Находим все величины, которые требуются нам для подстановки в формулу. Выполняем расчеты и находим искомую температуру идеального газа.

Обратите внимание

Внимательно разберитесь в условных обозначениях, чтобы из-за неправильно распознанного символа в формуле не допустить ошибки в расчетах.

Полезный совет

Закон Менделеева-Клапейрона также называют объединенным газовым законом, именно из него выводятся законы Шарля и Гей-Люссака, а также Бойля-Мариотта.

Источники:

• Здесь вы найдете не только информацию, которая касается непосредственно поиска абсолютной температуры идеального газа, но и массу информации о свойствах газов.
• как определить температуру газа
• Температура газовой плиты

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Модель идеального газа в МКТ

Идеальный газ — это теоретическая модель газа, в которой пренебрегают размерами и взаимодействиями частиц газа и учитывают лишь их упругие столкновения.

Другими словами, предполагается, что внутренняя энергия идеального газа определяется лишь кинетической энергией его частиц (т. е. потенциальной энергией взаимодействия молекул пренебрегают).

Модель идеального газа была предложена в 1847 г. Дж. Герапатом. На основе этой модели были теоретически выведены газовые законы (закон Бойля—Мариотта, закон Гей-Люссака, закон Шарля, закон Авогадро), которые ранее были установлены экспериментально. Модель идеального газа была положена в основу молекулярно-кинетической теории газа.

Основными законами идеального газа являются уравнение состояния и закон Авогадро, в которых впервые были связаны макрохарактеристики газа (давление, температура, масса) с массой молекулы (уравнение Менделеева-Клапейрона, или уравнение состояния идеального газа).

В современной физике ее используют также для описания ансамблей любых слабовзаимодействующих частиц. Модель идеального газа справедлива для реальных классических газов при достаточно высоких температурах и разрежениях, когда среднее расстояние между молекулами много больше размеров самих молекул. В этом случае силами притяжения можно пренебречь. Силы же отталкивания проявляются лишь при столкновении друг с другом в течение ничтожно малых интервалов времени.

В простейшей модели газа молекулы рассматриваются как очень маленькие твердые шарики, обладающие массой. Движение отдельных молекул подчиняется законам механики Ньютона. Конечно, не все процессы в разреженных газах можно объяснить с помощью такой модели, однако давление газа вычислить с ее помощью можно.

Основное уравнение МКТ (давление газа)

Основное уравнение молекулярно-кинетической теории устанавливает связь между давлением идеального газа и средней кинетической энергией его молекул.

Вывод основного уравнения МКТ основывается на допущениях модели идеального газа и утверждении: давление газа является результатом ударов молекул о стенку сосуда.

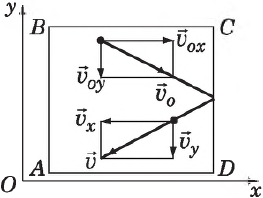
Определим давление газа на стенку площадью $S$ сосуда $ABCD$.

Каждая молекула массой $m_0$, отскакивая от стенки после упругого соударения со стенкой, передает ей импульс $2m_{0}υ_x$, где $υ_x$ — проекция скорости молекулы $υ↖{→}$ на ось $О_х$, перпендикулярную стенке. Всего за одну секунду суммарный импульс, получаемый стенкой от всех молекул, равен $2m_{0}υ_{x}Z$, где $Z$ — число таких столкновений (за $1$ с) всех молекул. Очевидно, что $Z=n={N}/{V}$, где $n$ — концентрация молекул в единице объема; $N$ — число всех молекул. Число $Z$ пропорционально также скорости молекул $υ_x$ и площади стенки $S:Z∼nυ_{x}S$. Поскольку все направления при хаотичном движении молекул газа равновероятны, то из всех молекул, имеющих составляющую скорости $υ_x$, только половина движется в сторону стенки $CD$ вторая половина — в сторону $АВ$ (т. е. в обратную). Поэтому $Z={1}/{2}nυ_{x}S$, а полный импульс, переданный стенке за $1$ с, равен $2m_{0}nυ_x^{2}S$. Поскольку изменение импульса точки (тела) за единицу времени равно действующей на него силе $F={∆(mυ)}/{∆t}$, то $F=m_{0}nυ_x^{2}S$. В действительности, поскольку речь идет о большом количестве молекул, движущихся с разными скоростями, силу следует усреднить: $F↖{-}={m_{0}nυ_x^{2}S}↖{-}$.

Сила эта зависит, таким образом, от среднего квадрата скорости ${υ_x^{2}}↖{-}$.

Поскольку вследствие хаотичности движения все направления равноправны, то

${υ_x^{2}}↖{-}={υ_y^{2}}↖{-}={υ_z^{2}}↖{-}$

С другой стороны, известно, что квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат, поэтому:

$υ^2=υ_x^{2}+υ_y^{2}+υ_z^{2}$

Усредняя это выражение по всем молекулам и учитывая $υ^2=υ_x^{2}+υ_y^{2}+υ_z^{2}$, получим:

${υ^2}↖{-}={υ_x^{2}}↖{-}+{υ_y^{2}}↖{-}+{υ_z^{2}}↖{-}=3{υ_x^{2}}↖{-}$

Отсюда:

${υ_x^{2}}↖{-}={1}/{3}{υ_^2}↖{-}$

С учетом последней формулы $F↖{-}={1}/{3}m_{0}n{υ^2}↖{-}$

Следовательно, давление на стенку сосуда равно:

$p={F}/{S}={1}/{3}m_{0}n{υ^2}↖{-}$

Это основное уравнение молекулярно-кинетической теории. Это уравнение — первое количественное соотношение, полученное в МКТ.

Уравнение $p={F}/{S}={1}/{3}m_{0}n{υ^2}↖{-}$ позволяет получить связь между давлением и средней кинетической энергией молекул ${E_k}↖{-}={m_{0}{υ^2}↖{-}}/{2}:$

$p={2}/{3}n{E_k}↖{-}$

Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

Важно подчеркнуть, что здесь речь идет о средней кинетической энергии молекул газа. Это означает, что давление газа — величина, органически связанная с тем, что газ состоит из большого числа молекул. Нет смысла говорить о давлении, создаваемом несколькими молекулами. Давление газа — понятие, имеющее статистический характер (так называют понятия, имеющие смысл только для систем с очень большим числом частиц).

Абсолютная температура

Согласно основному уравнению МКТ, давление $р$ прямо пропорционально средней кинетической энергии $E↖{-}$ поступательного движения молекул:

$p={2}/{3}n{E}↖{-}$

где $n$ — объемная концентрация молекул. Заменив в $p={2}/{3}n{E}↖{-}$ $n$ отношением числа молекул $N$ к объему газа $V(n={N}/{V})$, получим:

${pV}/{N}={2}/{3}{E}↖{-}$

В состоянии теплового равновесия при постоянном объеме средняя кинетическая энергия данной массы газа должна иметь вполне определенное значение, как и температура. Согласно формуле ${pV}/{N}={2}/{3}{E}↖{-}$, это означает, что отношение ${pV}/{N}$ для данной температуры должно быть одним и тем же для любых идеальных газов. То, что это действительно так, было подтверждено экспериментально для разных газов, находящихся в условиях теплового равновесия при постоянном объеме (измерялось давление).

Таким образом, величина $Θ={pV}/{N}$, которую, в отличие от микропараметра ${E}↖{-}$, легко измерить, является вполне однозначной характеристикой теплового состояния газа, как и температура. Измеряется $Θ$ (как и энергия) в джоулях. Зависит она только от температуры и может рассматриваться как естественная мера температуры. Однако в силу укоренившейся привычки измерять температуру в градусах был введен коэффициент пропорциональности $k$ между температурой $Θ$, выраженной в энергетических единицах, и температурой $Т$, выраженной в градусах:

$Θ=kT$

или

${pV}/{N}=kT$

Температура $Т$, определяемая равенством $Θ=kT$, называется абсолютной температурой.

Значения температуры, определенной по формуле ${pV}/{N}={2}/{3}{E}↖{-}$, всегда положительны в силу положительности $Θ={pV}/{N}$ (ни давление, ни объем, ни число частиц отрицательными быть не могут). Поэтому минимальным значением температуры является нуль. Температура может равняться нулю, если давление либо объем равны нулю. Из принятого определения температуры следует, что нулем температуры является температура, при которой прекращается хаотическое движение молекул. Она называется абсолютным нулем температуры.

Температура, как и давление, определяется средней кинетической энергией молекул идеального газа. Поэтому температура, как и давление, является статистической величиной (статистической называется величина, имеющая смысл только для систем, содержащих очень большое число частиц). Нельзя говорить о температуре одной или нескольких молекул.

Абсолютную шкалу температур ввел английский ученый У. Кельвин в 1850 г. Нулевая температура по абсолютной шкале (ее называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.

Единица абсолютной температуры является одной из семи основных единиц СИ и измеряется в кельвинах (обозначается буквой $К$).

Связь между температурами, измеренными по шкалам Цельсия $t$ и Кельвина $Т$, описывается формулой:

$T(K)=t(°C)+273.15K$

Абсолютный нуль равен $-273.15°$С. Как правило, при расчетах пользуются округленным значением абсолютного нуля ($-273°$С).

Коэффициент пропорциональности к в формуле $Θ=kT$ называется постоянной Больцмана в честь Л. Больцмана — одного из основателей молекулярно-кинетической теории газа. Этот коэффициент составляет $k=1.38^{-23}$ Дж/К.

Постоянная Больцмана связывает температуру $Θ$ в энергетических единицах с температурой $Т$ в кельвинах. Это одна из наиболее важных постоянных в молекулярно-кинетической теории.

Температура как мера кинетической энергии

Из основного уравнения молекулярно-кинетической теории, записанного в форме $p={2}/{3}{E}↖{-}$

${pv}/{N}={2}/{3}{E}↖{-}$

и определения абсолютной температуры согласно ${pV}/{N}=kt$

${pv}/{N}=kT$

получим:

$E↖{-}={3}/{2}kT$

Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.

Из полученного результата однозначно следует, что абсолютная температура есть мера средней кинетической энергии движения молекул.

Соотношение между температурой и кинетической энергией справедливо не только для разреженных газов (идеальных газов), но также для любых тел, подчиняющихся законам механики Ньютона. Оно справедливо и для жидкостей, и для твердых тел, атомы которых колеблются около положения равновесия.

Уравнение $р = nkТ$

Из формулы $p={2}/{3}n{E_k}↖{-}$ может быть получена зависимость давления газа от абсолютной температуры $Т$ и концентрации его молекул, если воспользоваться выражением для средней кинетической энергии:

$p=nkT$

где $k$ — постоянная Больцмана.

Из формулы $p=nkT$ очевидно, что при одинаковых давлениях и температурах концентрация молекул у всех газов одинакова.

Отсюда следует известный закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

Средняя скорость теплового движения молекул может быть также выражена через абсолютную температуру, если в формуле $E↖{-}={3}/{2}kT$ заменить $E↖{-}$ на ${m_{0}{υ^2}↖{-}}/{2}$:

${m_{0}{υ^2}↖{-}}/{2}={3}/{2}kT→{υ^2}↖{-}=3{kT}/{m_0}$

Квадратный корень из этой величины называется средней квадратичной скоростью:

$υ↖{-}=√{{3kT}/{m_0}}$

Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)

Уравнение состояния идеального газа — это зависимость между параметрами идеального газа — давлением $р$, объемом $V$ и абсолютной температурой $Т$, определяющими его состояние:

$pV=BT$

где $В$ зависит от массы газа $m$ и его молекулярной массы $М$. В таком виде уравнения впервые получено в 1834 г. французским ученым Б. П. Э. Клапейроном и называется уравнением Клапейрона.

В 1874 г. Д. И. Менделеев вывел уравнение состояния для одного моля идеального газа: $pV=RT$, где $R$ — универсальная газовая постоянная. Если молярная масса газа $М$, то

$pV={m}/{M}RT$

Уравнение состояния в форме $pV={m}/{M}RT$ называется уравнением Клапейрона-Менделеева. Оно объединяет газовые законы Гей-Люссака, Бойля—Мариотта, Авогадро, Шарля.

Уравнение состояния $pV={m}/{M}RT$ может быть получено из зависимости давления от температуры $p=nkT$, если в нее подставить концентрацию молекул $n$ из выражения

$n={N}/{V}={1}/{V}·{m}/{M}N_A$

где $N_А$ — постоянная Авогадро, $N$ — число молекул в теле.

В результате получим:

$pV={m}/{M}kN_{A}T$

где $kN_A=R$ — универсальная газовая постоянная, равная $8.31$ Дж/моль$·$К; $k$ — постоянная Больцмана, равная $1.38·10^{-23}$ Дж/К. Заменив в $pV={m}/{M}kN_{A}T$ $kN_A$ на $R$, получаем уравнение состояния в виде $pV={m}/{M}RT$. Отношение уравнений $pV={m}/{M}RT$ или $pV=BT$ при двух наборах параметров $p_1,V_1,T_1$ и $p_2,V_2,T_2$ дает:

${p_1V_1}/{T_1}={p_2V_2}/{T_2}=const$

Внутренняя энергия идеального одноатомного газа

Поскольку молекулы идеального газа не взаимодействуют друг с другом, их потенциальная энергия считается равной нулю. Внутренняя энергия идеального газа определяется только кинетической энергией беспорядочного поступательного движения его молекул. Для ее вычисления нужно умножить среднюю кинетическую энергию одного атома $E↖{-}={3}/{2}kT$ на число атомов $N={m}/{M}N_A$.

Учитывая, что $kN_A=R$, получим значение внутренней энергии идеального газа:

$U={3}/{2}·{m}/{M}RT$

Внутренняя энергия идеального одноатомного газа прямо пропорциональна его температуре.

Если воспользоваться уравнением Клапейрона-Менделеева, то выражение для внутренней энергии идеального газа можно представить в виде:

$U={3}/{2}pV$

Следует отметить, что, согласно выражению для средней кинетической энергии одного атома $(E↖{-}={3}/{2}kT)$ и в силу хаотичности движения, на каждое из трех возможных направлении движения или каждую степень свободы по оси $X,Y$ и $Z$ приходится одинаковая энергия ${kT}/{2}$.

Число степеней свободы — это число возможных независимых направлений движения молекулы.

Газ, каждая молекула которого состоит из двух атомов, называется двухатомным. Каждый атом может двигаться по трем направлениям, поэтому общее число возможных направлений движения — $6$. За счет связи между молекулами число степеней свободы уменьшается на одну, поэтому число степеней свободы для двухатомной молекулы равно пяти.

Средняя кинетическая энергия двухатомной молекулы равна ${5}/{2}kT$. Соответственно внутренняя энергия идеального двухатомного газа равна:

$U={5}/{2}·{m}/{M}RT={5}/{2}pV$

Формулы для внутренней энергии идеального газа можно обобщить:

$U={i}/{2}·{m}/{M}RT={i}/{2}pV$

где $i$ — число степеней свободы молекул газа ($i = 3$ для одноатомного и $i=5$ для двухатомного газа).

Для идеальных газов внутренняя энергия зависит только от одного макроскопического параметра — температуры и не зависит от объема, т. к. потенциальная энергия равна нулю (объем определяет среднее расстояние между молекулами).

Для реальных газов потенциальная энергия не равна нулю. Поэтому внутренняя энергия в термодинамике в общем случае однозначно определяется параметрами, характеризующими состояние этих тел: объемом ($V$) и температурой ($Т$).

Закон Дальтона

Закон Дальтона для смеси идеальных газов гласит: давление смеси газов равно сумме парциальных давлений ее компонент.

Парциальным давлением какого-либо газа — компонента газовой смеси называется давление, которое оказывал бы этот газ, если бы он один занимал весь объем, занимаемый смесью.

Для доказательства закона Дальтона перепишем уравнение $p=nkT$ в виде:

$pV=NkT$

Рассмотрим сосуд объемом $V$, в котором имеется смесь нереагирующих химически газов, находящихся в состоянии теплового равновесия. Уравнение состояния для такой смеси имеет вид:

$pV=(N_{1}+N_{2}+N_{3}+…)kT$

где $N_{1},N_{2},N_{3}…$ — числа компонент смеси.

Очевидно, что

$N_{1},N_{2},N_{3}+…=N$

где $N$ — общее число молекул в сосуде.

Давление смеси газа получим, поделив обе части $pV=(N_{1}+N_{2}+N_{3}+…)kT$ на объем $V$:

$p={N_1}/{V}kT+{N_2}/{V}kT+{N_3}/{V}kT+…$

Слагаемые этой суммы представляют собой давления каждой из компонент смеси, занимающей объем $V$, т. е. являются парциальными давлениями компонент смеси $р_1 р_2, р_3, …$ что и утверждает закон Дальтона:

$p=р_1+р_2+р_3+…$

То, что каждая группа молекул оказывает давление, не зависящее от давления, оказываемого другими группами, обусловлено отсутствием взаимодействия между молекулами. Последнее реально выполняется только для газов при невысоких давлениях, которые приближаются к идеальному газу.