Специальные условные знаки используются для изображения рельефа местности на картах и планах местности.
Перед тем как изобразить горы и равнины, холмы и впадины, необходимо определить абсолютную и относительную высоту нужных точек.
Абсолютная высота — высота точки над уровнем океана (моря).

Абсолютная высота (а), относительная высота (б), абсолютная глубина (в) в метрах
Уровень моря принимают за (0) метров, так как все моря и океаны сообщаются между собой и находятся примерно на одном уровне.
Абсолютная высота отдельных вершин на суше обозначается точкой и числом. Число показывает высоту над уровнем моря. Глубина показывается только числом и так же отсчитывается от уровня Мирового океана:


В России точкой отсчёта является средний уровень Балтийского моря, определённого на основе многолетних наблюдений в городе Кронштадте (нуль Кронштадтского футштока).

Нуль Кронштадтского футштока
Москва в среднем находится на (156) м выше уровня моря, Санкт-Петербург — на (3) м выше уровня моря.
Абсолютные высоты наиболее важных объектов на планах и картах подписаны цифрой и обозначены точкой — отметкой высоты.
На суше есть впадины, которые лежат ниже уровня моря. В этом случае перед значением высоты ставят знак «(-)», например (-)(27).
Глубину морей и океанов также отсчитывают от уровня моря.

Наибольшие высоты материков и глубины океанов в метрах
Относительная высота — превышение одной точки поверхности над другой.

Если абсолютная высота холма равна (200) м над уровнем моря, а абсолютная высота равнины — (50) м, то относительная высота холма равна (150) м ((200 – 50 = 150)).
Перейти к содержанию
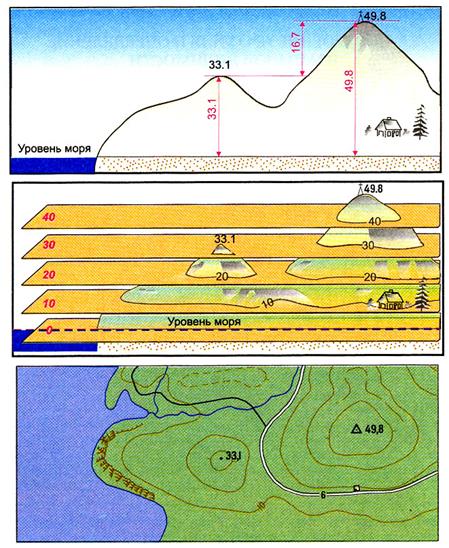
Абсолютная высота — высота точки земной поверхности над уровнем моря; определяется по отметкам высот и горизонталей (на рис. 9 это высоты с отметками 33,1 и 49,8).
Высота сечения рельефа — расстояние по высоте между двумя смежными секущими плоскостями.
Относительная высота (взаимное превышение точек) — высота точки местности над другой, она определяется как разность абсолютных высот этих точек (на рис. 9 относительная высота равна 16,7 (49,8-33,1)).
Читать полный конспект Чтение топографических карт. Рельеф
В статье речь пойдет о том, что такое высота – абсолютная и относительная. Высота – это термин, используемый в географии. На примере будут показаны различия между двумя этими понятиями. После прочтения статьи у вас сложится устойчивое понятие о двух видах высот в географии, и будет легче ориентироваться на местности и решать практические задачи.
Что такое высота и зачем ее используют в географии?
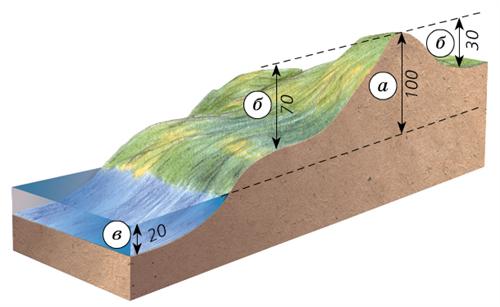
Любой географический объект, расположенный на поверхности Земли, обладает определенным набором координат (широта и долгота), а также высотными характеристиками. Рельеф нашей планеты неоднороден, где-то доминируют высокие горы, где-то глубоко вниз уходят бездонные впадины и ущелья. Понятие высоты было придумано людьми, чтобы максимально точно описать те или иные особенности рельефа земной поверхности.
Кроме того, понятие высоты используется на топографических и высотных картах. Подписанная высота позволяет отобразить на плоской поверхности карты объемный рельеф. Как правило, все высоты измеряются в метрах – стандартизированной единице из международной системы. Высоты могут принимать как положительные, так и отрицательные значения. На земной поверхности диапазон высот колеблется от -400 метров (впадина Мертвого моря) до 8848 метров (высочайшая вершина мира – гора Эверест). Для того чтобы лучше понять, чем отличаются высоты, необходимо ввести понятие абсолютная и относительная высота.
Абсолютная высота
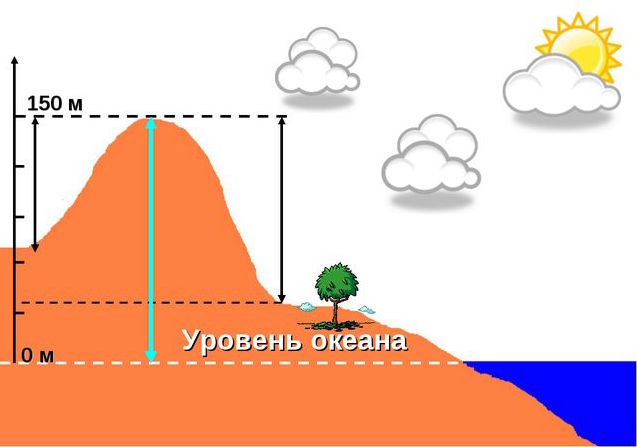
Понятие абсолютной высоты тождественно понятию высоты над уровнем моря, или высоты н.у.м. Так, абсолютная высота той или иной точки земной поверхности представляет собой превышение этой точки над среднегодовым уровнем моря в той или иной системе морских высот. В России все абсолютные высоты измеряются относительно нулевой отметки в Кронштадте, которая расположена у самой кромки воды в этом северо-западном городе.
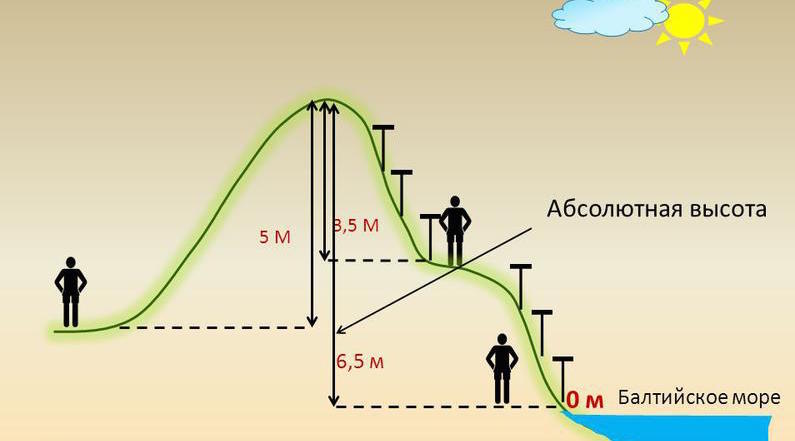
В других странах существуют иные нулевые уровни, однако суть понятия абсолютной высоты от этого не меняется. Абсолютная высота измеряется в метрах над уровнем моря. Она может принимать как положительные, так и отрицательные значения. На рисунке выше абсолютная высота холма показана голубой стрелочкой. Нет строгого соотношения понятий и значений абсолютной и относительной высоты. Абсолютная высота может быть больше, меньше или равна относительной.
Относительная высота
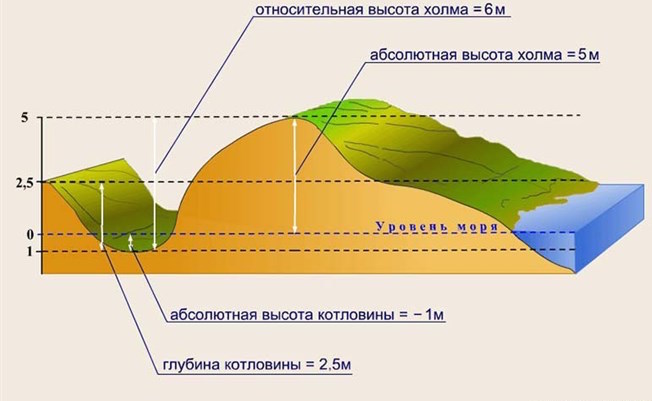
Относительная высота по определению представляет собой превышение двух любых точек земной поверхности относительно друг друга. Сразу следует отметить, что в отличие от абсолютной высоты, относительная всегда принимает строго положительные значения, поскольку численно равняется разности точек с большей и меньшей абсолютными высотами.
Если обратиться, к примеру, к рисунку выше, можно заметить, что абсолютная высота холма составляет 5 метров, при этом относительная высота того же самого холма равняется уже 6 метрам. Как так вышло? Все довольно просто и следует из понятия относительной высоты. Так, авторы данного рисунка решили измерить относительное превышение холма (положительной формы рельефа с положительной величиной высоты) над котловиной (отрицательной формой рельефа с отрицательными значениями абсолютной высоты). Для этого они вычли из абсолютной высоты самой высокой точки (холма, 5 м) абсолютную высоту самой низкой точки, над которой искали превышение холма (-1 м). По правилу сложения и вычитания, 5 – (-1) = 6. Именно 6 метров составляет превышение холма над котловиной, и этому значению равняется абсолютная высота.
Строго говоря, у холма может быть бесконечно большое количество относительных высот, все зависит от того, относительно чего мы будем ее измерять. Для примера найдем относительную высоту самого высокого холма (на рисунке справа) от холма пониже, он показан в левой части. Из разницы абсолютных высот этих положительных форм рельефа (5 метров для высокого и 2,5 метра для низкого холмов) получаем, что относительная высота самого большого холма от низкого холма составляет 5-2,5=2,5 метра. По аналогии с данным примером можно найти относительные высоты чего угодно. Теперь можно ответить на вопрос, как определить абсолютную и относительную высоты.
Как измеряют относительные высоты?
Теперь вы поняли, чем абсолютная высота отличается от относительной в географии. Для определения относительных высот удобно пользоваться специальным прибором – рейкой. Для этого в начальной точке, относительно которой ищется превышение, ставится рейка. Условно эта точка принимается за высоту с отметкой 0. Далее, как показано на рисунке выше, необходимо двигаться вверх по холму или горе до тех пор, пока вы не достигнете высоты рейки, и самая высокая ее точка не окажется ниже уровня ваших ног.
Тогда необходимо зафиксировать точку на холме, которая соответствует положению самой высокой точки рейки, стоящей на нулевом уровне, и сместить рейку в данную точку. Таким образом, на второй точке относительная высота будет равна 1 высоте рейки. Операцию нужно проделать до тех пор, пока вы не достигнете самой высокой точки холма. В этом случае относительная высота будет равняться сумме всех высот переставляемой рейки.
Вместо рейки можно использовать любой предмет, высота которого известна заранее. Если под рукой нет совсем ничего, относительную высоту можно измерить по своему собственному росту, проделав описанные выше манипуляции. Кроме того, относительную высоту легко можно измерить как разность абсолютных высот, если они заранее известны.
Как измеряют абсолютные высоты?
Абсолютную высоту измерить таким способом в полевых условиях не получится. Конечно, можно было бы, однако для этого потребовалось бы наличие в непосредственной близости поверхности моря. Чтобы найти абсолютную высоту, необходимо воспользоваться картой местности или приборами спутникового позиционирования, в которых есть возможность автоматического определения высоты.
Теперь у вас есть устойчивое представление о том, чем отличаются абсолютная высота и относительная высота. Успехов в решении практических географических задач и в повседневном ориентировании в условиях окружающей среды!
Высоты
точек местности по карте определяют по
горизонталям, используя имеющиеся на
ней высотные отметки.
Если
определяемая точка расположена на
горизонтали, то ее абсолютная высота,
очевидно, равна высоте этой горизонтали.
Если же точка находится между горизонталями,
то надо определить отметку ближайшей
к ней нижней горизонтали и прибавить
к этой отметке превышение данной точки
над горизонталью. Это превышение
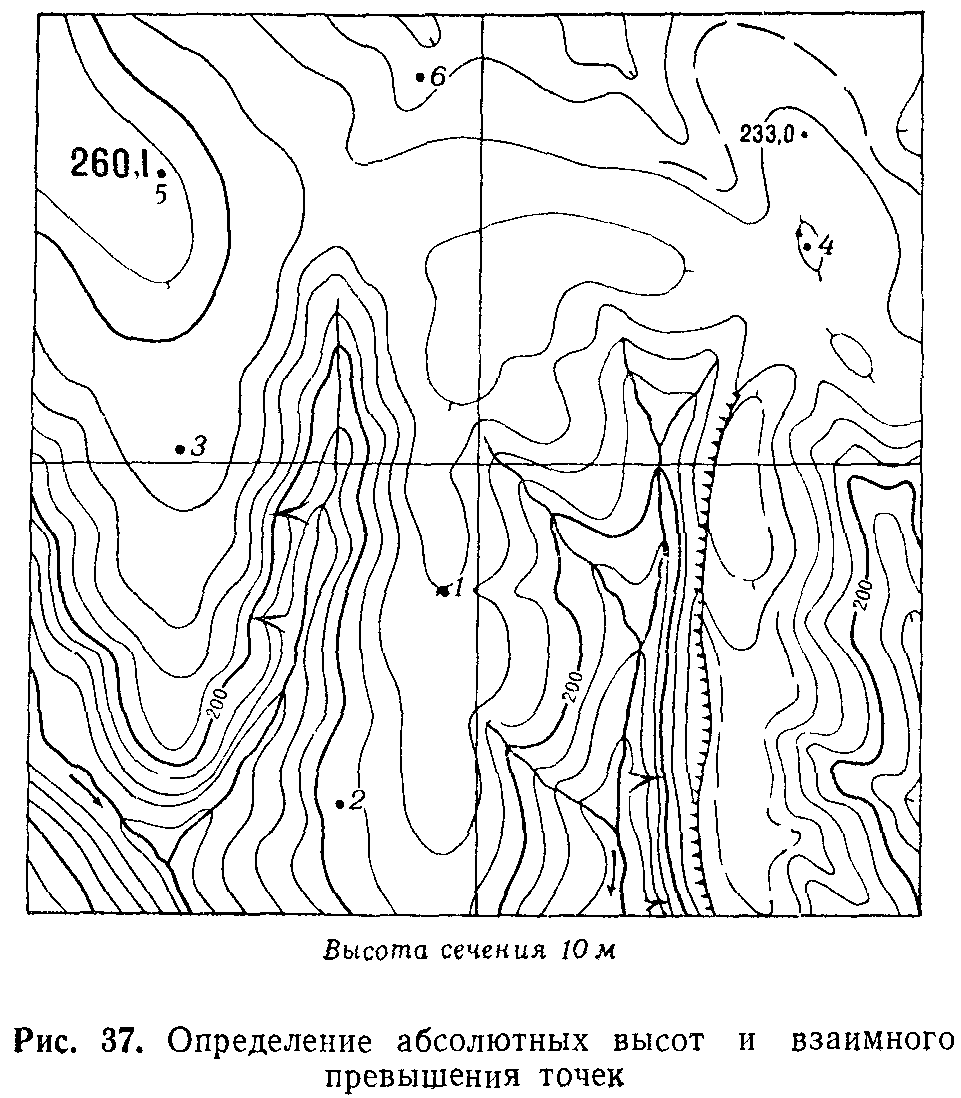
определяется на глаз. Например, (рис.
37), абсолютная высота точки 1
будет
230 м, так как горизонталь, на которой она
расположена, лежит на три высоты сечения
выше горизонтали с отметкой 200 м.
Высота точки 2
равна
205 м: она расположена посредине между
горизонталями, одна из которых имеет
высоту 200 м (утолщенная горизонталь), а
другая 210 м. Точки 3
и
4 имеют примерно одну и ту же высоту –
242 м.
Превышение
одной точки над другой определяется
как разность их абсолютных высот.
Если же точки расположены на одном и
том же скате, то задача решается просто
путем подсчета числа промежутков между
горизонталями этих точек: превышение
между ними равно произведению высоты
сечения на полученное число промежутков
между горизонталями. Например, точка 5
на
рис. 37 расположена выше точки 6
на
45 м (4,5 промежутка между горизонталями)
и выше точки 2
на
55 м.
Точность
определения высот точек, отметки которых
не подписаны на карте, равна: для
характерных точек рельефа, расположенных
на вершинах, гребнях, водосливах, бровках
и пологих скатах неровностей, – примерно
0,3 – 0,5 высоты сечения, а для точек,
расположенных на крутых скатах, где
невозможно проведение полугоризонталей,
она примерно в 3-4 раза меньше.
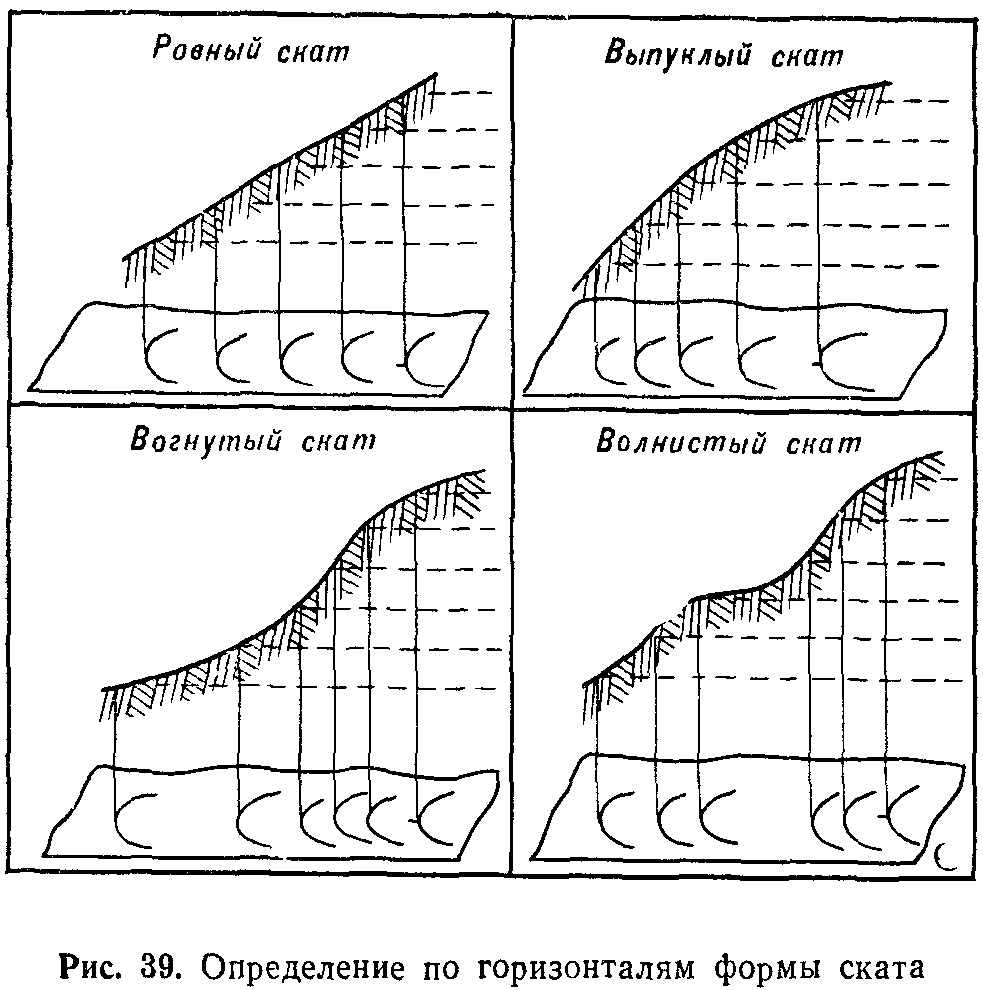
Определение формы и крутизны скатов
Форма
ската определяется по взаимному
расположению горизонталей на скате
(рис. 39). Если скат ровный, то его
горизонтали на карте располагаются
на равных расстояниях одна от другой;
при вогнутом скате они учащаются к
вершине, а при выпуклом, наоборот, – к
подошве. При волнистом скате горизонтали
учащаются и разреживаются в нескольких
местах в зависимости от количества
перегибов ската.
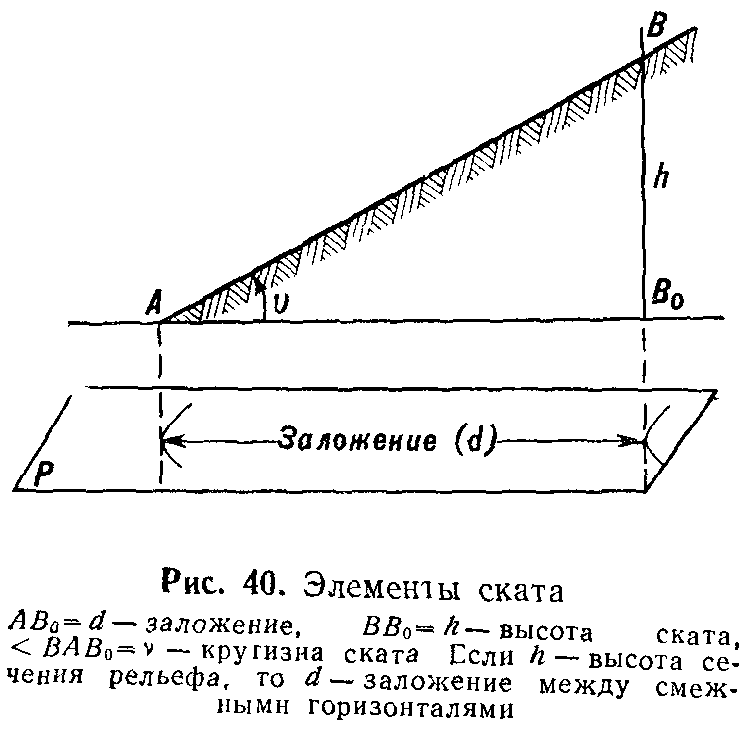
Крутизна
ската, т. е. угол его наклона v (рис. 40),
вычисляется по формуле
![]() (1)
(1)
Приближенно
угол v, если он не больше 25°, может быть
подсчитан по формуле
![]() (2)
(2)
Эти
зависимости и лежат в основе всех
способов определения крутизны скатов.
Наиболее употребительны из них следующие.
А
Определение
крутизны скатов по шкале заложений (рис
41) шкалой заложений называется график,
который печатается на всех листах
топографических карт масштаба 1 : 100 000
и круп нее – рядом с линейным масштабом.
Вдоль основания графика подписана
крутизна скатов в градусах. На
перпендикулярах к основанию отложены
в масштабе карты соответствующие им
заложения: в левой части шкалы – заложения
при основной высоте сечения, а в
правой – при пятикратной, т.
е.
заложения между двумя смежными утолщенными
горизонталями.
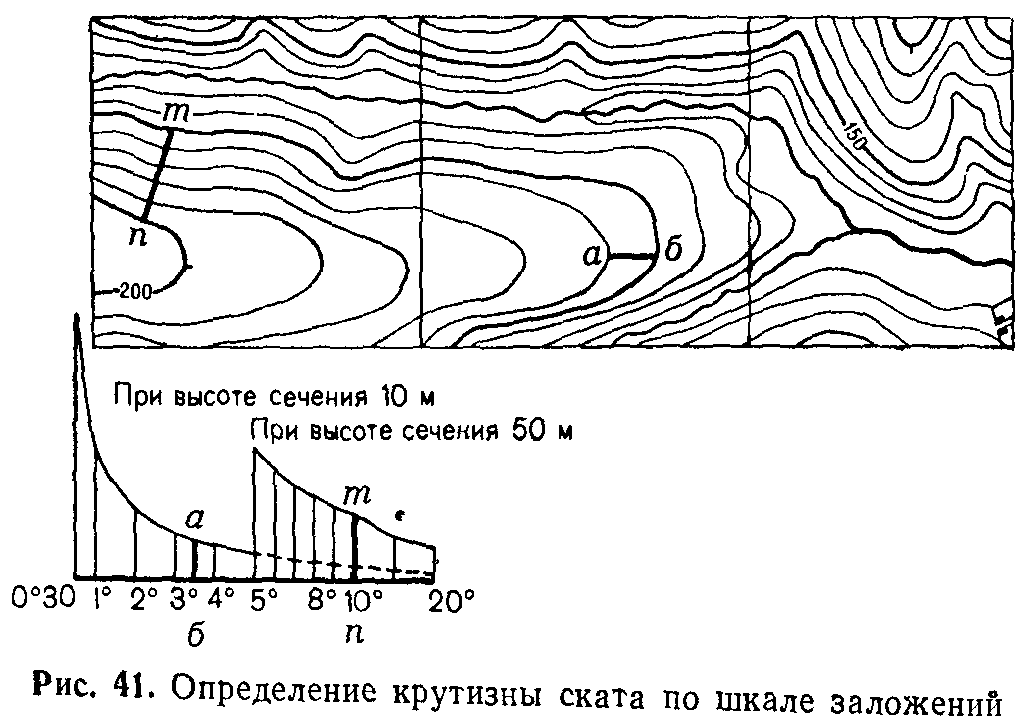
Для
определения крутизны ската надо взять
циркулем или с помощью полоски бумаги
расстояние между двумя смежными
горизонталями на интересующем нас
скате и затем, приложив этот отрезок к
шкале, как показано на рис. 41, прочитать
внизу число градусов крутизны. В нашем
примере крутизна ската вдоль отрезка
ab
равна
3°,5.
Если
горизонтали на скате расположены очень
близко одна к другой и взять циркулем
расстояние между ними затруднительно,
тогда удобнее пользоваться правой
частью шкалы, беря при этом по карте
заложения между соседними утолщенными
горизонталями. В нашем примере
крутизна ската по отрезку mn
равна
10°.
Точность
определения крутизны скатов по шкале
заложений равна
примерно 0,3-0,4 цены деления этой шкалы
в том ее интервале, в котором
определяется крутизна данного ската.
Б.
Оценка
крутизны скатов на глаз. Расчеты
по формуле (2) показывают, что на всех
топографических картах с нормальной
высотой основного сечения (т. е. при Л =
0,02 величины масштаба карты) заложению
в 1 см соответствует крутизна ската в
1°,2 или округленно в 1°, а заложению в 1
мм соответствует крутизна ската в 10°.
Поэтому на указанных картах применимо
следующее общее правило для приближенного
определения крутизны ската на глаз:
определяемая
крутизна ската во столько раз больше
(меньше) 1°, во сколько раз его заложение
между смежными сплошными горизонталями
меньше (больше) 1 см.
Например,
на карте масштаба 500 м в 1 см с высотой
сечения 10 м крутизна ската будет примерно
равна: при заложении ската 0,5 см – 2°,
при заложении 0,1 см– 10°, при заложении
2 см – 0°,5.
Это
правило применимо и на картах, на которых
высота сечения отличается от
нормальной. При этом, однако, надо
полученное по указанному правилу
число градусов увеличить (уменьшить)
во столько же раз, во сколько высота
основного сечения на карте больше
(меньше) нормальной. Если она больше
нормальной, то для уточнения надо в
полученный при этом результат ввести
поправку, прибавив по 1° на каждые 4°.
Например,
на карте масштаба 1:25 000 с высотой основного
сечения 10 м (нормальная высота сечения
5 м) заложению в 0,5 см соответствует 5°
(4+1), а заложению в 1 мм – 25° (20 + 5).
16
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
