Как найти адекватность математической модели

Как найти адекватность математической модели


Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Современное развитие математической науки, требования которые к ней сейчас предъявляются, заставляет ученых не только фиксировать и строить свои предположения на основании ранее открытых математических моделей, но и самостоятельно открывать новые, которые смогли бы объяснить многие явления и характер математических действий.

Так, возникло понятие «адекватность» и стало необходимым при проверке математических моделей.

Любая математическая модель характеризуется в первую очередь, необходимостью математических вычислений, что повлекло за собой появление вычислительного эксперимента. Во время планирования вычислительного эксперимента задействуют различные методы математического моделирования. Причем от методов, которые употребляются в математической статистике до методов, присущих теории катастроф.

С середины двадцатого века центром математического моделирования становится понятие адекватности.

«Если математика является “чистым порождением ума” (своеобразной “игрой в бисер”), то непонятно, почему мир обязан с ней сообразовываться. Если же она является формой абстрагирования в “аминокислотном” человеческом сознании присущих миру (или возможных в нем при отсутствии запрещающих ограничений) структур и отношений, то возникает вопрос об “адекватности”, “изоморфности” математических структур структурам реальности» (Д. Гильберт) [1].

Адекватность математической модели – свойство правильно отражать реальные процессы, протекающие в синтезируемом объекте.

Адекватность математической модели особенно важна в задачах эксплуатации, где непосредственно можно сопоставлять расчетные и фактические значения параметров и проверять правильность модели. По многим причинам теоретические значения некоторых коэффициентов в этих соотношениях существенно отличаются от фактических. Точнее, теоретическая модель оказывается недостаточно хорошей для описания реального объекта.

Адекватность математической модели – это соответствие модели моделируемой задаче или процессу принятия решений, причем адекватность рассматривают по тем свойствам модели, которые для лица принимающего решения являются наиболее важными в данный момент времени.

Адекватность математической модели проверяется при помощи F – критерия Фишера.

F-тестом или критерием Фишера (F-критерием, φ*-критерием) — называют любой статистический критерий, тестовая статистика которого при выполнении нулевой гипотезы имеет распределение Фишера (F-распределение доверительного интервала [2].

Критерий Фишера является очень удобным в проверке адекватности математических моделей. Удобство использования критерия Фишера состоит в том, что проверку гипотезы можно свести к сравнению с табличным значением. Если рассчитанное значение F-критерия не превышает табличного, то, с соответствующей доверительной вероятностью, модель можно считать адекватной. При превышении табличного значения эту приятную гипотезу приходится отвергать. Этот способ расчета дисперсии адекватности, подходит, если опыты в матрице планирования не дублируются, а информация о дисперсии воспроизводимости извлекается из параллельных опытов в нулевой точке или из предварительных экспериментов.

Важны два случая:

1) опыты во всех точках плана дублируются одинаковое число раз (равномерное дублирование),

2) число параллельных опытов не одинаково (неравномерное дублирование).

Проверка адекватности математической модели системы (или ее отдельных элементов) осуществляется путем проведения экспериментальных исследований и сопоставления их результатов с результатами аналитических расчетов, выполненных для конкретных условий проведения эксперимента[3].

Итак, целью анализа является получение некоторой оценки, с помощью которой можно было бы утверждать, что при некотором уровне α полученное уравнение регрессии – статистически надежно. Для этого используется коэффициент детерминации R2.

Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель как уже было выше сказано считается значимой.

где m – число факторов в модели.

Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:

Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α.

Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.

Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01.

Например, табличное значение критерия со степенями свободы k1=1 и k2=48, Fтабл = 4

Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.

В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.

Пример. По совокупности 25 предприятий торговли изучается зависимость между признаками: X — цена на товар А, тыс. руб.; Y — прибыль торгового предприятия, млн. руб. При оценке регрессионной модели были получены следующие промежуточные результаты:

∑(yi-yx)2 = 46000; ∑(yi-yср)2 = 138000.

Какой показатель корреляции можно определить по этим данным? Рассчитайте величину этого показателя, на основе этого результата и с помощью F-критерия Фишера сделайте вывод о качестве модели регрессии.

Решение. По этим данным можно определить эмпирическое корреляционное отношение:

,

где ∑(yср-yx)2 = ∑(yi-yср)2 – ∑(yi-yx)2 = 138000 – 46000 = 92 000.

η2 = 92 000/138000 = 0.67, η = 0.816 (0.7 < η < 0.9 – связь между X и Y высокая).

F-критерий Фишера: n = 25, m = 1.

R2 = 1 – 46000/138000 = 0.67, F = 0.67/(1-0.67)x(25 – 1 – 1) = 46.

Fтабл(1; 23) = 4.27

Поскольку фактическое значение F > Fтабл, то найденная оценка уравнения регрессии статистически надежна.

Таким образом, доказывается адекватность математической модели.

Такие проверки, несмотря на их трудоемкость, проводятся регулярно и, как правило, дают вполне удовлетворительные результаты, подтверждая пригодность всех моделей для практического использования[4]

Из всего вышесказанного можно сделать вывод, что понятие «адекватность» имеет полное право занять достойное место, среди четких математических определений. Именно с помощью этого понятия можно внести в хаотический мир некоторых математических понятий порядок [1].

Список используемых источников

1. Бурбаки, Н. Очерки по истории математики: учебное пособие / Н. Бурбаки ; ред. К. А. Рыбников ; пер. с фр. И. Г. Башмакова. – Москва : Изд-во иностр. лит-ры, 1963. – 292 с

2. Вяхирев, Р. Российская газовая энциклопедия: учебное пособие/ Р. Вяхирев; ред. Р.И. Вяхирев; Изд-во Большая Российская Энциклопедия, 2004г.

3. Адекватность и точность математических моделей. Верификация результатов моделирования [Электронный ресурс] – Режим доступа: http://studopedia.ru/ 4. F-статистика. Критерий Фишера [Электронный ресурс] – Режим доступа: http://math.semestr.ru/corel/fisher.php

Источник

Хороший теоретик может объяснить почти любые полученные результаты, верные или невер­ ные, и, по крайней мере, может потерять массу времени на выяснение того, верны они или нет.

Р. Хемминг

Под адекватностью математической модели будет пониматься степень соответствия результатов, полученных по разработанной модели, данным эксперимента или тестовой задачи. Прежде чем пе­ реходить к проверке адекватности модели, необходимо убедиться в правильном комплексном функционировании всех алгоритмов и программ модели, выполнить независимое тестирование и отладку всех отдельных алгоритмов (например, используемых программных модулей, реализующих используемый численный метод).

Проверка адекватности модели преследует две цели:

1) убедиться в справедливости совокупности гипотез, сформу­ лированных на этапах концептуальной и математической постано­ вок. Переходить к проверке гипотез следует лишь после проверки использованных методов решения, комплексной отладки и устра­ нения всех ошибок и конфликтов, связанных с программным обес­ печением;

2) установить, что точность полученных результатов соответ­ ствует точности, оговоренной в техническом задании.

Проверка разработанной математической модели выполняется путем сравнения с имеющимися экспериментальными данными о реальном объекте или с результатами других, созданных ранее и хо­ рошо себя зарекомендовавших моделей. В первом случае говорят о проверке путем сравнения с экспериментом, во втором —о сравне­ нии с результатами решения тестовой задачи.

Решение вопроса о точности моделирования зависит от требо­ ваний, предъявляемых к модели, и ее назначения. При этом долж­ на учитываться точность получения экспериментальных результа­ тов или особенности постановок тестовых задач. В моделях, пред­ назначенных для выполнения оценочных и прикидочных расчетов, удовлетворительной считается точность 10—15%. В моделях, исполь­ зуемых в управляющих и контролирующих системах, требуемая точность может быть 1—2% и даже более.

Как правило, различают качественное и количественное совпа­ дение результатов сравнения. При качественном сравнении требу­

ется лишь совпадение некоторых характерных особенностей в рас­ пределении исследуемых параметров (например, наличие экстре­ мальных точек, положительное или отрицательное значение пара­ метра, его возрастание или убывание и т.д.). Фактически при каче­ ственном сравнении оценивается совпадение лишь вида функции распределения параметров (убывающая или возрастающая, с одним экстремумом или с несколькими). Вопрос о количественном срав­ нении можно ставить лишь после удовлетворительного ответа на вопрос о качественном соответствии результатов. При количествен­ ном сравнении большое значение следует придавать точности ис­ ходных данных для моделирования и соответствующих им значе­ ний сравниваемых параметров.

Неадекватность результатов моделирования возможна, по край­ ней мере, по трем причинам:

а) значения задаваемых параметров модели не соответствуют до­ пустимой области этих параметров, определяемой принятой систе­ мой гипотез. Например, в задаче о баскетболисте гипотезу об от­ сутствии сопротивления воздуха можно использовать лишь при от­ носительно малых (менее 5 м/с) скоростях движения тела. При больших значениях начальной скорости мяча влияние силы сопро­ тивления будет существенным;

б) принятая система гипотез верна, но константы и параметры в использованных определяющих соотношениях установлены не точно. Например, в случае задачи о баскетболисте значение уско­ рения свободного падения g может быть уточнено в зависимости от широты местности, где находится баскетболист;

в) неверна исходная совокупность гипотез.

Все три случая требуют дополнительного исследования как мо­ делируемого объекта (с целью накопления новой дополнительной информации о его поведении), так и исследования самой модели (с целью уточнения границ ее применимости).

Замечание. В данном случае не анализируется влияние выбран­ ного численного метода на точность получаемого решения, а значит, и на адекватность модели. Вопрос о сходимости алгоритма и устой­ чивости получаемого выбранным численным методом решения, а также накопление погрешностей, связанных с ошибками округления при использовании ЭВМ, здесь не рассматривается.

При возникновении проблем, связанных с адекватностью мо­ дели, ее корректировку требуется начинать с последовательного ана­ лиза всех возможных причин, приведших к расхождению результа­ тов моделирования и результатов эксперимента. В первую очередь

требуется исследовать модель и оценить степень ее адекватности при различных значениях варьируемых параметров (начальных и граничных условиях, параметров, характеризующих свойства объек­ тов моделирования). Если модель неадекватна в интересующей ис­ следователя области параметров, то можно попытаться уточнить значения констант и исходных параметров модели. Если же и в этом случае нет положительных результатов, то единственной возмож­ ностью улучшения модели остается изменение принятой системы гипотез. Данное решение фактически означает возвращение ко вто­ рому этапу процесса разработки модели и может повлечь не только серьезное изменение математической постановки задачи, но и ме­ тодов ее решения (например, переход от аналитических к числен­ ным), полной переработки программного обеспечения и нового цикла проверки модели на адекватность. Поэтому решение об из­ менении принятой системы гипотез должно быть всесторонне взве­ шено и приниматься только в том случае, если исчерпаны все про­ чие возможности по улучшению адекватности модели.

Примечание. Надлежит предостеречь начинающих исследователей от попыток «перепрыгнуть» рассмотренный этап моделирования, от желания быстрее перейти к решению «настоящей задачи». Как пока­ зывает собственный опыт авторов, подобный образ действий приво­ дит к огромным временным издержкам (не говоря уже о психологи­ ческих). Особенно опасной является ситуация, в которой при реше­ нии реальной задачи с использованием не проверенной должным образом модели получаются правдоподобные результаты. Для других условий модель может дать качественно неверные результаты, но истоки ошибок разработчики будут искать уже не в модели…

Пример. Проверка адекватности решения задачи о баскетболисте.

Соотношения (2.10) являются аналитическим решением задачи о баскетболисте и позволяют определить значения координат и ско­ ростей центра масс мяча в любой момент времени. Для координат х и у соотношения (2 .1 0 ) есть уравнения параболы в параметрической

форме. Мяч при броске движется по траектории, близкой к парабо­ ле. Поэтому в данном случае можно говорить о качественном совпа­ дении результатов моделирования и экспериментальных данных. Вопрос о количественном совпадении результатов моделирования и эксперимента скорее всего будет решен отрицательно, так как отказ от учета силы сопротивления воздуха является грубым предположе­ нием. Для удовлетворительной оценки точности попадания мяча в корзину расхождение результатов моделирования и эксперимента не должно превышать 1—2 см. Поэтому гипотезу об отсутствии силы со­ противления воздуха в концептуальной постановке задачи заменим

новой: сила сопротивления воздуха прямо пропорциональна скоро­ сти мяча:

где ксопр —коэффициент сопротивления, зависящий от свойств сре­ ды и формы тела.

Для тела в форме шара коэффициент сопротивления определял­ ся по формуле Стокса:

*сопр = б щ т г ,

где |i —динамическая вязкость среды (для воздуха при температуре 20°С и давлении 1 атм р = 0,0182 Н с/м2).

В соответствии с принятыми в баскетболе правилами длина ок­ ружности мяча может изменяться от 0,749 до 0,780 м, что соответ­ ствует изменению радиуса мяча от 0,119 до 0,124 м. Масса мяча дол­ жна быть в пределах от 0,567 до 0,650 кг. Примем для определенно­ сти радиус мяча R = 0,12 м, а массу мяча /я = 0,6 кг. Тогда коэффициент сопротивления среды составляет £сопр = 0,0247 Н с/м.

Соотношения (2.5) в математической постановке задачи следует заменить на новые:

dv

,

dx

т –

X

= -*conpvx>

V*= —

dt

dt

dv

V

dy

‘conpV

= — ■

vy

f t ‘

Разделяя переменные и интегрируя с учетом начальных условий (2 .6 ), можно получить решение в следующем виде:

у = тк(mkg+ ) (l – exp(-t/mk))- mkgt,

ух= у*оехр Н Ч ) –

(213)

vy ={mkS +V )exP(-/K

)- mk8>

где mk = m/kconp.

Для определения дальности броска следует второе соотношение в (2.13) записать в виде

Ук = тк {mkS +v0 sina0)(1-exp (~t/mk))- mkgt,

где yk —координата центра корзины. При ук = 0 получим нелиней­ ное уравнение относительно времени

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Динамическая идентификация объектов управления

Время на прочтение
8 мин

Количество просмотров 15K

Введение

Идентификация объектов управления — совокупность методов для построения математических моделей объекта по данным наблюдений.

Математическая модель в данном контексте означает математическое описание поведения какого-либо объекта или процесса в частотной или временной области, к примеру, физических процессов (движение механической системы под действием внешней силы [1]), экономического процесса (влияние смены курса валют на потребительские цены на товары [2]).

В настоящее время эта область теории управления находит широкое применение на практике и поэтому интересна для рассмотрения.

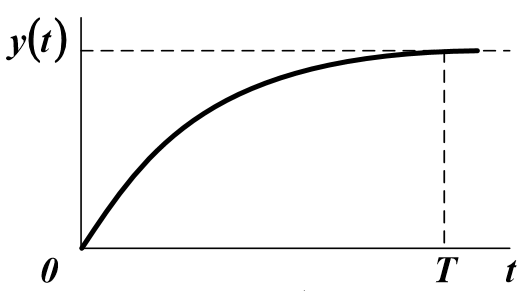
Область динамической идентификации объектов управления в связи с различной природой самих объектов достаточно обширна, поэтому для начала ограничимся рассмотрением методов обработки так называемой кривой разгона.

Кривой разгона называют процесс изменения во времени выходной переменной, вызванный ступенчатым входным воздействием. Кривая разгона служит для определения динамических свойств объекта.

Постановка задачи

1. Построить математические модели динамической идентификации объекта управления по нормированной переходной характеристике (кривой разгона):

• Методом наименьших квадратов с использованием производных;
• Модифицированным методом площадей.

2. Определить и сравнить адекватность полученных математических моделей объекту управления.

Теория

Идентификация состоит в отыскании для объекта адекватной ему модели. Различают структурную и параметрическую идентификацию. При структурной идентификации определяется форма модели из некоторого заданного класса функций, при параметрической идентификации определяются параметры модели.

Если выходные сигналы объекта Y(t) полностью определяются наблюдаемыми входными воздействиями X(t), то для его идентификации достаточно использовать методы активного эксперимента.

Исходной информацией является экспериментально снятая кривая разгона – реакция объекта Y(t) на поданное входное воздействие X(t) в интервале времени 0≤t≤T.

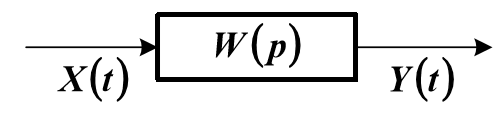
Это структурная схема модели объекта с операторной передаточной функцией W(p). Уравнение динамической характеристики объекта можно условно представить в следующем виде:

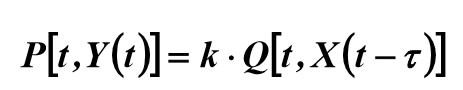
(1)
где – время запаздывания объекта, которое проходит от момента подачи сигнала на вход объекта до момента появления сигнала на его выходе; k – коэффициент усиления (или коэффициент передачи) объекта.

Схема для определения времени запаздывания и коэффициента усиления объекта:

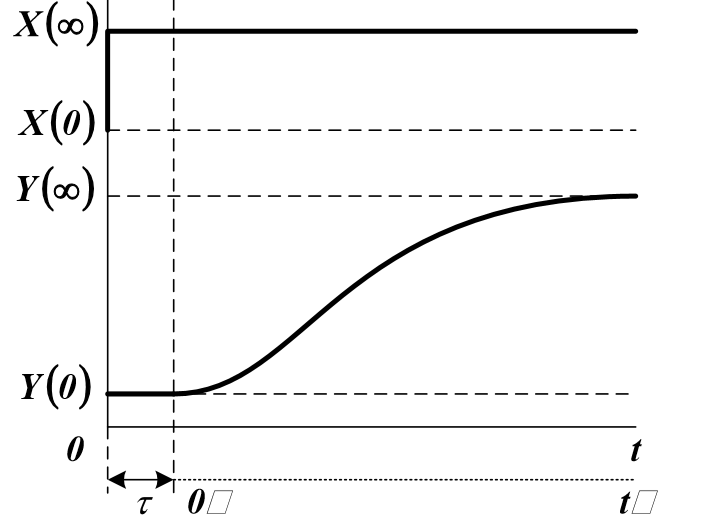
Входные и выходные величины, как правило, масштабируются в стандартном диапазоне от 0 до 1 (нормируются):

После определения k и можно исследовать объект в нормированных координатах и без запаздывания, сместив шкалу времени вправо на величину [3].

Структурная идентификация объекта

При структурной идентификации априорная информация об объекте используется для определения структуры модели.

Уравнение динамики, как правило, выбирается из класса линейных или линеаризованных характеристик. В нормированных координатах модель объекта с сосредоточенными параметрами, одним входным и одним выходным сигналом является обыкновенным дифференциальным уравнением с постоянными коэффициентами:

(2)

где коэффициенты и имеют размерность времени в степени, равной порядку производной соответствующего слагаемого. В физически реализуемых системах n≥m

По виду кривой разгона можно приближённо определить порядок будущей модели, например, для объекта первого порядка:

Для объектов более высоких порядков:

Обычно X(t) – ступенчатая функция, поэтому порядок уравнения (1) может быть приближенно определен по форме кривой разгона объекта. Если эта характеристика не имеет точек перегиба, то n = 1. Если есть перегиб при t = tп, и tп / T <0,1…0,15, то n = 2.В противном случае считают n> 2. Однако можно снизить порядок модели, вводя фиктивное запаздывание.

Вывод

Влияние погрешности измерения X(t) и Y(t) и погрешности численных методов обработки информации обычно делает нецелесообразным использование моделей выше третьего-четвертого порядка.

Параметрическая идентификация объекта

При параметрической идентификации данные об объекте обрабатываются для получения о нем апостериорной информации. При этом оцениваются параметры выбранной модели. В простейших случаях такая оценка может выполняться по графику переходной характеристики.

Параметрическая идентификация методом наименьших квадратов с использованием производных

Для идентификации объекта произвольного порядка используется метод наименьших квадратов, требующий минимизации среднего квадрата невязки правой и левой частей уравнения (2):

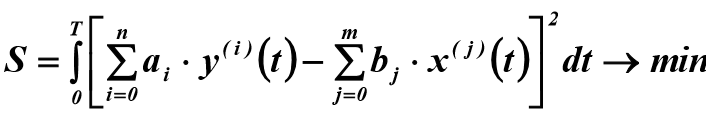(3)

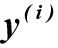где: и 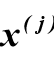– производные i-го и j-го порядка от функций выходного и входного сигналов.

Решение задачи (3) сводится к решению системы:

(4)

Преобразуя (4) в соответствии с уравнением (3), можно получить систему линейных алгебраических уравнений:

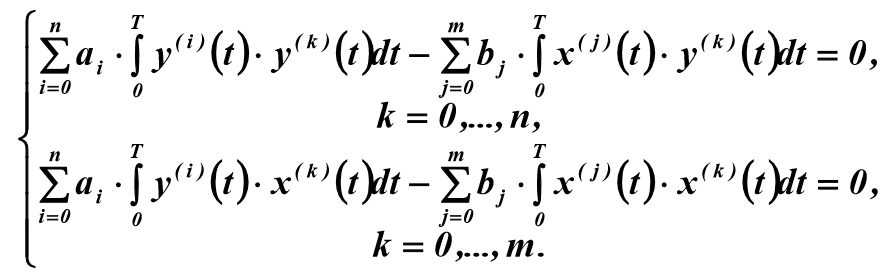(5)

Для решения системы (5) относительно неизвестных параметров необходимо знать производные входного и выходного сигналов объекта, которые находятся в результате сглаживания функций X(t) и Y(t) на отрезке 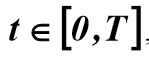. Для расчета коэффициента 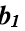используется формула:

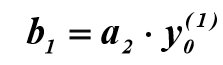
Вывод

Погрешность численного дифференцирования, как правило, достаточно высока, поэтому схему определения коэффициентов, нужно использовать дифференцирование аналитических выражений для X(t) и Y(t).

Параметрическая идентификация модифицированным методом площадей

Для создания модели средствами Python, модификация метода площадей состоит в неизменном масштабе времени. В классическом варианте вводят новый масштаб времени, что при численном решении приводит к дополнительной погрешности.

Обычно, выражение для передаточной функции ищут в виде одной из трех математических моделей:

Выражение 1/W(p), обратное передаточной функции модели, можно разложить в ряд по степени р:

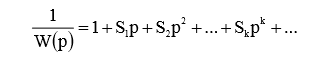
Коэффициенты a,b приведенных передаточных функций связаны с коэффициентами S следующей системой уравнений:

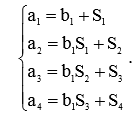
Коэффициенты Si связаны с переходной функцией h(t) соотношениями:

(6)

Вывод

Соотношения (6) оптимальны для решения средствами Python при интерполяции h(t) кубическими сплайнами, что будет доказано на примерах.

Оценка адекватности математических моделей идентификации объектов управления

Для выбора оптимальной модели достаточно использовать показатель адекватности второго порядка:

(7)

где 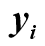– данные, снятые с кривой разгона, 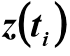– значения, рассчитанные по действительной части Re(W(i×w)) передаточной функции модели (переход из частотной области во временную):

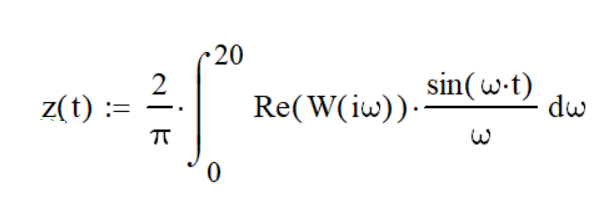(8)
Лучшей следует считать модель, обеспечивающую максимальное значение

Учитывая существенную погрешность численного дифференцирования при решении системы уравнений (5), реализуем символьное дифференцирование. Для этого применим интерполяцию полиномом в соответствии со следующим листингом:

# -*- coding: utf8 -*-
import matplotlib.pyplot as plt# для построение графика
import time
start = time.time()
import scipy as sp# для интерполяции полиномом
import numpy as np# для операций с матрицами производных от КР
from sympy import *# для символьного дифференцирования КР
import scipy.integrate as spint
from scipy.integrate import quad
x=[0.0, 0.4, 0.8, 1.2, 1.6 ,2.0, 2.4, 2.8 ,3.2, 3.6]#время
y=[0.00, 0.11, 0.36, 0.61, 0.79, 0.89, 0.94, 0.98, 0.99, 1.00]# отклик системы
fp, residuals, rank, sv, rcond = sp.polyfit(x, y,4, full=True)# интерполяция полиномом
a=round(fp[0],4);b=round(fp[1],4);c=round(fp[2],4)
d=round(fp[3],4);e=round(fp[4],4)
t=symbols('t ' ,real=True)
def h(t):# аналитическая форма переходной характеристики h(t)
         return a*t**4+b*t**3+c*t**2+d*t+e
''' Символьное вычисление производных'''
L1=integrate(h(t).diff(t)*h(t).diff(t,t),(t,0,3.6)) 
L2=integrate(h(t).diff(t,t)*h(t).diff(t,t),(t,0,3.6))
L3=integrate(h(t).diff(t)*h(t).diff(t),(t,0,3.6))
L4=integrate((1-h(t))*h(t).diff(t,t),(t,0,3.6))
L5=integrate((1-h(t))*h(t).diff(t),(t,0,3.6))
""" Матричная форма решения системы уравнений (5) с учётом критерия (3)"""
P= np.zeros([2,2])
P[0,0]=L2;P[0,1]=L1
P[1,0]=L1;P[1,1]=L3
Q= np.zeros([2,1])
Q[0,0]=L4;Q[1,0]=L5
P=np.matrix(P);
Q=np.matrix(Q)
C=P.I*Q
''' Коэффициенты передаточной функции объекта'''
a2=C[0,0]
a1=C[1,0]
b1=C[0,0]*h(t).diff(t).subs(t,0)
a2=round(C[0,0],3)
a1=round(C[1,0],3)
b1=round(C[0,0]*h(t).diff(t).subs(t,0),3)    
""" Переход из частотной области во временную по соотношению (8)"""
def ff(x,t):
        j=(-1)**0.5
        return (2/np.pi)*( ((b1*x*j+1)/(a2*(x*j)**2+a1*x*j+1)).real)*(np.sin(x*t)/x)
z=np.array([round(quad(lambda x: ff(x,t),0, 20)[0],2) for t in x])
"""Определение адекватности модели идентификации по соотношению (7) """
k=round(1-sum([(y[i]-z[i])**2 for i in np.arange(0,len(y)-1,1)])/sum([(y[i])**2 for i in np.arange(0,len(y)-1,1)]),5)
stop = time.time()
print ("Время работы программы :",round(stop-start,3))
plt.title('Идентификация методом наименьших квадратовn Адекватность модели -%s'%k)
plt.plot(x, y,'o', label='Снятая экспериментально КР')
plt.plot(x, z,'r', label=' W=(%s*p+1)/(%s*p**2+%s*p+1)'%(b1,a2,a1))
plt.legend(loc='best')
plt.grid(True)
plt.show()

Получим:

Время работы программы: 0.802

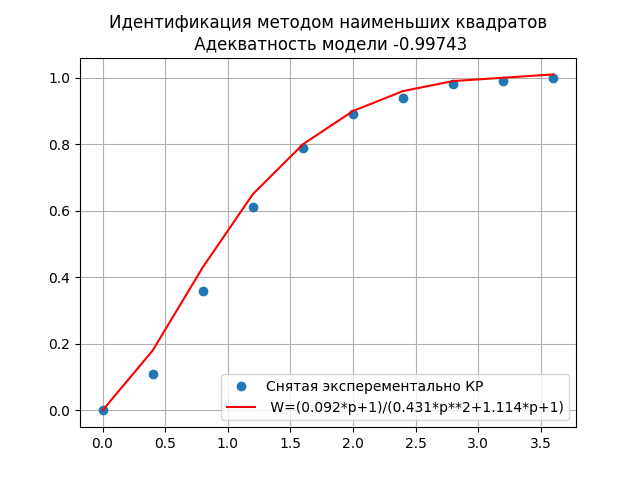
Высокая степень адекватности модели 0.99743 свидетельствует о том, что полученная передаточная функция:

W=(0.092*p+1)/(0.431*p**2+1.114*p+1),

достаточно точно отображает динамические свойства объекта.

Кривая разгона получена экспериментально, поэтому дельнейшие исследование систем управления объектом на устойчивость [4] и определения параметров регуляторов [5] приобретают практическое значение.

Реализация средствами Python задачи идентификации объекта модифицированным методом площадей

Для решения этой задачи можно использовать численные методы поскольку модель не содержит дифференцирования, а предложенный метод решения согласно соотношениям (6) не предполагает смены координаты времени. Кроме этого, применим интерполяцию сплайном в соответствии со следующим листингом:

# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
import time
start = time.time()
from scipy.interpolate import splev, splrep
import scipy.integrate as spint
import numpy as np
from scipy.integrate import quad
xx =np.array([0.0, 0.4, 0.8, 1.2, 1.6 ,2.0, 2.4, 2.8 ,3.2, 3.6])
yy =np.array([0.00, 0.11, 0.36, 0.61, 0.79, 0.89, 0.94, 0.98, 0.99, 1.00])
""" Интерполяция переходной характеристики при помощи сплайнов"""
def h(x):         
         spl = splrep(xx , yy )
         return splev(x, spl)
""" Численное интегрирование без смены координаты времени в соответствии с (6)"""
S1=(spint.quad(lambda x:1-h(x),xx[0],xx[len(xx)-1])[0])
S2=(spint.quad(lambda x:(1-h(x))*(S1-x),xx[0],xx[len(xx)-1])[0])
S3=(spint.quad(lambda x:(1-h(x))*(S2-S1*x+(1/2)*x**2),xx[0],xx[len(xx)-1])[0])
S4=(spint.quad(lambda x:(1-h(x))*(S3-S2*x+S1*(1/2)*x**2-(1/6)*x**3),xx[0],xx[len(xx)-1])[0])
""" Определение коэффициентов передаточной функции"""
b1=-S4/S3
a1=b1+S1
a2=b1*S1+S2
a3=b1*S2+S3
""" Возврат во временную область"""
def ff(x,t):
        j=(-1)**0.5
        return (2/np.pi)*( ((b1*x*j+1)/(a3*(x*j)**3+a2*(x*j)**2+a1*x*j+1)).real)*(np.sin(x*t)/x)
y=np.array([round(quad(lambda x: ff(x,t),0, 20)[0],2) for t in xx])
""" Определение критерия адекватности модели """
k=round(1-sum([(yy[i]-y[i])**2 for i in np.arange(0,len(yy)-1,1)])/sum([(yy[i])**2 for i in np.arange(0,len(yy)-1,1)]),5)
stop = time.time()
print ("Время работы программы :",round(stop-start,3))
plt.title('Идентификация модифицированным методом площадей.n Адекватность модели -%s'%k)
plt.plot(xx, yy,'o', label='Нормированная кривая разгона (КР)')
plt.plot(xx, y,'r', label='W=(%s*p+1)/(%s*p**3+%s*p**2+%s*p+1)'%(round(b1,3),round(a3,3),round(a2,3),round(a1,3)))
plt.legend(loc='best')
plt.grid(True)
plt.show()

Получим:

Время работы программы: 0.238

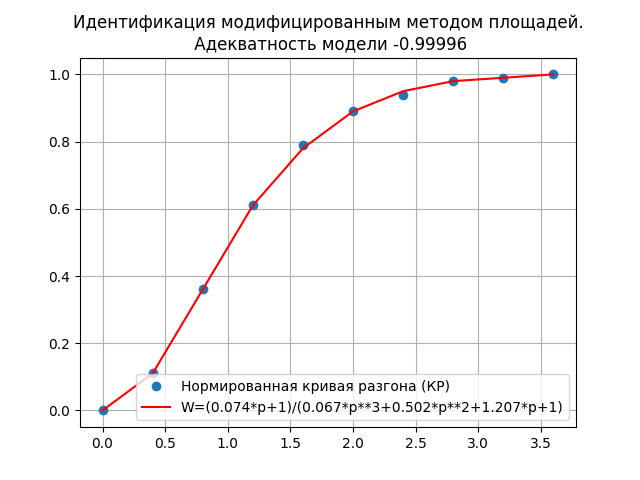
Высокая степень адекватности модели 0.99996 и большее быстродействие, чем при символьном дифференцировании, позволяет утверждать, что передаточная функция:

W= (0.074*p+1)/(0.067*p**3+0.502*p**2+1.207*p+1)),

полученная модернизированным методом площадей лучше отображает динамические свойства объекта.

Выводы

1. Публикация знакомит с основами динамической идентификации объекта управления.

2. Реализация решения задачи идентификации на свободно распространяемом языке программирования Python с примерами использования явного представления переходной функции полиномом и сплайнами будет способствовать расширению области применения Python.

3. Для численных решений задач идентификации, можно предложить использование соотношений (6), которые позволяют получить результат без изменения координаты времени.

Ссылки

  1. Модель колебательного звена с применением символьного и численного решений дифференциального уравнения на SymPy и NumPy.
  2. Математическая модель динамики финансового рынка.
  3. Определение параметров модели методом площадей.
  4. Определение устойчивости систем автоматического управления промышленными роботами.
  5. Модель ПИД регулятора на Python.
Источник

Проверка адекватности математической модели выполняется путем сравнения дисперсии адекватности и дисперсии воспроизводимости.

, где K-количество коэффициентов модели (K = 10),

N – количество экспериментов.

Дисперсия воспроизводимости высчитывается следующим образом:

Сравнение дисперсий выполняется по критерию Фишера. Чтобы воспользоваться сравнением с критерием Фишера, нужно рассчитать переменную Фишера:

Квантили распределения Фишера для уровня значимости 0,05

f2

f1

1

2

3

4

5

6

1

164.4

199.5

215.7

224.6

230.2

234

2

18.5

19.2

19.2

19.3

19.3

19.3

3

10.1

9.6

9.3

9.1

9

8.9

4

7.7

6.9

6.6

6.4

6.3

6.2

5

60.6

5.8

5.4

5.2

5.1

5

6

6

5.1

4.8

4.5

4.4

4.3

7

5.6

4.7

4.4

4.1

4

3.9

8

5.3

4.5

4.1

3.8

3.7

3.6

9

5.1

4.3

3.9

3.6

3.5

3.4

10

5

4.1

3.7

3.5

3.3

3.2

11

4.8

4

3.6

3.4

3.2

3.1

12

4.8

3.9

3.5

3.3

3.1

3

13

4.7

3.8

3.4

3.2

3

2.9

14

4.6

3.7

3.3

3.1

3

2.9

15

4.5

3.7

3.3

3.1

2.9

2.8

Критическим значением для нашей выборки является F=2,9

Если переменная Фишера меньше критического значения критерия Фишера, то дисперсии однородны, а модель адекватная.

Вывод:

Построенная нами модель по заданным значениям адекватна.

Проверка значимости коэффициента модели

Проверка значимости коэффициентов заключается в том, что по критерию Стъюдента оценивается, не является ли математическое ожидание каждого коэффициента нулевыми. Для этого мы рассматриваем переменную Стъюдента:

, где -среднеквадратическая погрешность коэффициента

,

где – диагональный коэффициент матрицы ошибок.

Матрица ошибок размерности [kxk]

0,289

0

0

0

-0,111

-0,111

-0,111

0

0

0

0

0,111

0

0

0

0

0

0

0

0

0,111

0

0

0

0

0

0

0

0

0,111

0

0

0

0

-0,111

0

0

0

0,389

-0,111

-0,111

0

0

0

-0,111

0

0

0

-0,111

0,389

-0,111

0

0

0

-0,111

0

0

0

-0,111

-0,111

0,389

0

0

0

0

0

0

0

0

0

0

0,125

0

0

0

0

0

0

0

0

0

0

0,125

0

0

0

0

0

0

0

0

0

0

0,125

Для сопротивления продавливанию:

b0

b1

b2

b3

b11

b22

b33

b12

b13

b23

0,289

0,1

0,1

0,1

0,389

0,389

0,389

0,125

0,125

0,125

166,523

37,943

15,624

24,761

0,833

15,268

0,146

1,001

6,461

0,63

Для разрушающего усилия при сжатии:

b0

b1

b2

b3

b11

b22

b33

b12

b13

b23

0,289

0,1

0,1

0,1

0,389

0,389

0,389

0,125

0,125

0,125

88,884

8,979

10,249

3,759

4,634

5,141

9,096

6,134

2,357

7,242

Критическое значение критерия Стъюдента

Если меньше , то она есть проявление всех случайных чисел и от 0 отличается незначительно. Если больше , то коэффициент значим.

После проверки значимости незначимые коэффициенты должны быть исключены из уравнения регрессии. И в случае необходимости оставшиеся коэффициенты должны быть заново рассчитаны по методу наименьших квадратов.

Из этого следует, что после проведения необходимых расчетов коэффициенты будут следующие:

Для сопротивления продавливанию:

b0= 855,503, b1=114,467, b2= 47,133, b3=74,7, b13= -21,792, b22= -90,963,

Для разрушающего усилия при сжатии кольца:

b0= 397,281, b1=23,567, b2= 26,900, b3=-9,867, b11=-24,018, b12= 18,

b13= -6,917, b22= 26,648, b23=-21,250, b33=47,148

Источник

УДК 629.735.015:531.5:681.3:001.891.573

ПРОВЕРКА АДЕКВАТНОСТИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

М.С. КУБЛАНОВ

Предлагаются формулировки основных терминов, устоявшихся в практике математического моделирования задач динамики полета летательных аппаратов. Обсуждаются способы проверки адекватности.

Ключевые слова: математическое моделирование, технические системы, динамика полета, адекватность.

Введение

В последние годы математическое моделирование как метод исследования сложных систем находит широкое применение для различных задач. Как показала практика, понятие адекватности математических моделей (ММ) и сопутствующие термины нуждаются в том, чтобы их уточненная формулировка была единообразно понимаемой и продуктивной. Именно из-за различий в понимании этой терминологии, к сожалению, появляются исследования, претендующие на научность, но таковыми не являющиеся ввиду отсутствия адекватности.

Терминология

В теории моделирования [1-7] под адекватностью модели понимают соответствие результатов, полученных на модели, поведению реального объекта. (В [8] дается определение адекватности ММ как соответствия ММ экспериментальным данным по выбранному критерию.) Это соответствие следует оценивать с точки зрения целей исследования, поэтому для моделей в различных областях знаний могут использоваться совершенно непохожие приемы, методы и критерии проверки адекватности.

Общее понятие модели сводится к тому, что модель – это заместитель оригинала, позволяющий изучить некоторые его свойства в определенных условиях. Заметим, что в этом определении оговаривается не только назначение модели, но и ее заведомо ограниченные возможности – ограниченные целями исследования.

Особенностью ММ является то, что получение с их помощью каких-либо результатов связано с вычислениями, т.е. с получением результатов вычислительного эксперимента (ВЭ). ВЭ -это получение результатов с помощью ММ для какого-либо конкретного случая исследований. Таким образом, адекватность ММ – это соответствие результатов ВЭ поведению реального объекта. Для проверки адекватности ММ служит контрольный ВЭ, воспроизводящий реальный известный случай поведения оригинала в конкретных условиях.

Что касается иностранизмов, то они не вносят в теорию никаких принципиально новых понятий. Так, например, верификация – это процесс проверки адекватности модели (независимо от результата). Валидация модели – установление факта удовлетворения модели заявленным свойствам (самой модели, может быть независимо от оригинала). Это понятие, скорее, административное, чем научное.

При проверке соответствия модели оригиналу (проверке адекватности, верификации) для технических систем и процессов, характеризующихся измеримыми величинами – параметрами – необходимо провести сравнение соответствующих параметров модели и оригинала в одних и тех же условиях. Какими критериями оценивать это соответствие (или несоответствие, ошибочность), подсказывает определение ММ как заместителя оригинала. ММ должна быть инструментом получения информации в виде числовых данных и функциональных зависимостей, характеризующих поведение оригинала. Полная аналогия с теорией ошибок измерений, которая на основании центральной предельной теоремы теории вероятностей [9] утверждает, что ошибка при многократных измерениях распределена по нормальному закону – закону ошибок. Итак,

если мы покажем, что рассогласование ММ и оригинала ведет себя как простая малая ошибка измерений, то тем самым положительно ответим на вопрос об адекватности. Поэтому для адекватности ММ поведению оригинала достаточно убедиться в выполнении двух свойств: точности и непротиворечивости [4-6].

Приведенные выше термины применимы для любых моделей в любых областях деятельности человека. Однако для применения на практике необходима конкретизация этих понятий для определенных видов задач.

Точность

Точность в технических задачах означает, что обобщенная характеристика рассогласования соответствующего параметра модели и оригинала (Ли = имодели – иоригинала) должна быть не больше, чем заранее заданное значение приемлемой погрешности. В качестве такой характеристики может выступать наибольшее по модулю значение рассогласования, среднее значение рассогласования, но чаще всего используется доверительный интервал для математического ожидания рассогласования [4-6]. Заметим, что доверительный интервал дает только оценку разброса значений рассогласования с заданной доверительной вероятностью, например, рассогласование результатов ВЭ с поведением реального объекта не выходит за границы (- 0,52 км/ч; + 0,27 км/ч) с вероятностью 0,99 или в относительных величинах – за границы (- 0, 104 %; + 0,054 %) в 99 % случаев.

Очевидно, что доверительный интервал не дает единой жесткой числовой характеристики адекватности, как хотелось бы авторам работы [10], предложившим понятие “степени адекватности” в виде дополнительной величины в процентах к относительной приведенной погрешности (при молчаливом задании доверительной вероятности) Л; = (1 – Лт/т;тах)х100%, где Л; -степень адекватности ММ по 1-му параметру; Лт; – максимальное отклонение ьго расчетного параметра от математического ожидания с заданной вероятностью Р = 0,95; т1тах – максимальное значение ьго расчетного параметра в исследуемом диапазоне времени. Универсальной такая оценка “степени адекватности” быть не может, т.к. в некоторых задачах величина т;тах, стоящая в знаменателе, может обращаться в ноль, а доверительная вероятность 0,95 может не удовлетворять исследователя.

Простейший пример проверки адекватности на основании одной только точности и одновременно пример единственной числовой оценки точности приведен в статье [11], выдержки из которой приведены ниже.

Необходимость расширить возможности модели на случаи прерванного взлета и посадки с учетом отказов систем самолета, оказывающих влияние на параметры движения по ВПП, наталкивается на непреодолимые трудности получения результатов качественных данных линейных испытаний (ЛИ). Практически единственным источником информации для этого оказывается Руководство по летной эксплуатации самолета (РЛЭ) [12].

Проверку адекватности ММ и решение задачи идентификации приходится проводить на основе точечных данных о значениях некоторых нормируемых показателей движения воздушного судна (ВС), т.к. зависимостей параметров полета от времени в РЛЭ нет. В этих условиях в качестве сравниваемых параметров можно использовать данные о дистанциях исследуемых этапов, а в качестве идентифицируемых параметров модели – законы управления, также регламентированные РЛЭ.

При проверке адекватности по единичным значениям параметров требование непротиворечивости отпадает, и адекватность становится эквивалентной точности, которую единственно и следует оценить.

Расчет дистанций прерванного взлета в РЛЭ [12] проводится с помощью номограмм для угла отклонения закрылков 5з = 28°. Для проверки адекватности были выбраны крайние случаи для продолженного взлета самолета массой 110 т и 90 т. Дистанция прерванного взлета по номограммам определяется с точностью до 50 м. Расчетные условия ВЭ соответствовали

РЛЭ. Совпадение дистанций обеспечено лишь соблюдением предписанного РЛЭ порядка процедур прерванного взлета. Результаты ВЭ представлены в табл. 1.

Таблица 1

Сравнение расчетов дистанций прерванного взлета самолета Ту-154М с данными РЛЭ

Расчетные варианты Взлетная дистанция

температура высота масса У v отк РЛЭ ВЭ

МСА – 15° 3000 м 110 т 259 км/ч 3860 м 3889 м

МСА + 30° 0 м 110 т 259 км/ч 3800 м 3834 м

МСА + 30° 2500 м 90 т 239 км/ч 3800 м 3815 м

МСА + 20° 3000 м 90 т 239 км/ч 3570 м 3578 м

Представленные результаты своим рассогласованием, не превосходящим 0,8 %, свидетельствуют о высокой степени адекватности математической модели прерванного взлета самолета Ту-154М данным РЛЭ.

Конец выдержки из работы [11].

Следует особо отметить, что в приведенном примере достигается погрешность не более 34 м, что существенно меньше, чем погрешность данных РЛЭ в 50 м. При таком итоге оценки погрешности безусловно достаточно для доказательства адекватности ММ.

Итак, ранее мы отметили, что одной характеристики точности для проверки адекватности недостаточно. Только в случаях выражения результатов ВЭ в виде одного числа (а не функции) точность может служить единственной проверкой адекватности. В подавляющем большинстве современных задач требуется воспроизведение в ММ сложных функциональных зависимостей, причем подчас важнее, чтобы эти зависимости имели логическое объяснение, а точность – вопрос второстепенный.

Более того, точность не может быть самоцелью, т.к. существует множество причин, оправдывающих существование значительных систематических погрешностей, как например, в летной эксплуатации при нерегистрируемом изменении высоты местности, эксплуатационной потере тяги двигателей и т.п. [6]. Ниже приводится фрагмент раздела 7.5 этой работы, включая графики (об упоминаемых понятиях идентификации и эвристического метода см. далее).

В 1994 г. была проведена идентификация ММ движения самолета Ил-76ТД № 76473 по записи системы регистрации полета реального рейса 7257 от 16.03.94 г. Вообще говоря, записи системы регистрации полета не годятся в качестве данных для идентификации, т.к. большое количество информации об условиях полета в них не содержится. Однако отобранная запись была разъяснена и дополнена экипажем.

В ММ использованы характеристики самолета, предоставленные АК им. С.В. Ильюшина. Конфигурация самолета (отклонения стабилизатора 5ст, закрылков 5з, предкрылков 5пр) и способы пилотирования (моменты и скорости перекладки руля высоты и режима работы двигателей) принимались такими же, как в реальном полете.

Идентификация ММ проводилась только в продольном канале управления по значениям следующих параметров полета: Нг – высота по радиовысотомеру; Упр – скорость полета по прибору; S – угол тангажа; ny – вертикальная перегрузка; 5В – угол отклонения руля высоты.

Как выявили результаты контрольного ВЭ, взлет был осуществлен с “роллинг-старта” (без остановки на исполнительном старте на ВПП после руления), причем зарегистрированному взлетному режиму соответствовала тяга двигателей примерно на 10 % меньшая стендовой. В последствии пилоты подтвердили правоту этих фактов.

САМОЛЕТ Ил-76ТД N1 76473 N РЕР1СН: 7257 №ТЙ: 16. 3. Ь

я

я

я

я

а

й

$5 60 80 100

Ьрамя

САМОЛЕТ Ил-76ТД N1 76473 N РЕПСЯ: 7257 ДАТА: 16. 3. 4

о ■ – – – ■”■ –‘ ” —V ч _

N о

ц э 6 3 8 э 1 30

и. □

□

а с

САМОЛЕТ Ил-76ТД N1 76473

время

N РЕИСН: 7257 ДАТА: 16. 3. 4

А ч

•1

/ ?

__,—А 6 Э 8 I) 1 30

Ьремя

САМОЛЕТ Ил-76ТД N1 76473 N РЕПСА: 7257 ДАТА: 16. 3. 4

– -_ ——-

со А

– -о. у ■

4 1 я Э 8 3 1 зо

Ьремя

Рис. 1

В момент времени 16.53.21 (на рис. 1 – 21 с) на скорости около 60 км/ч режим работы двигателей был переведен с номинального на взлетный, и начался разбег. С этого момента времени и до 16.54.40 (до высоты 600 м) осуществлялось воспроизведение всех упомянутых выше процедур пилотирования с целью получения идентифицируемых параметров с максимально возможной точностью. Однако согласно алгоритму эвристического метода идентификации это возможно не всегда, но всегда нуждается в логическом объяснении. Так по данным системы регистрации полета характеры поведения угла тангажа $ и угла атаки а на высоте более 120 м противоречат друг другу, что может объясняться влиянием внешних атмосферных условий. На высоте более 300 м наблюдается значительный перепад высоты (замеренной радиовысотомером), находящийся в явном противоречии с поведением что в последствии оказалось связанным с профилем местности.

Анализ степени адекватности ММ реальному взлету удобно проводить с помощью графического представления параметров полета, совмещенных по времени на общих осях координат.

Пунктирной линией на графиках изображены данные системы регистрации полета, а сплошной – результаты ВЭ.

Как нетрудно убедиться, даже чисто визуальное сравнение параметров полета свидетельствует о достаточно высокой степени адекватности результатов ММ данным реального полета, по крайней мере, до высоты 120 м. Следует учесть, что зубцы в записях системы регистрации полета отвечают дискретности записи и вполне характеризуют точность регистрации параметров полета. Расхождения заметны только по приборной скорости на ВПП и по углу атаки на ВПП и небольшой высоте. Это объясняется тем, что приборная скорость менее 170 км/ч – 200 км/ч и угол атаки в пределах аэродинамического влияния поверхности земли регистрируются с очень большой погрешностью.

Конец фрагмента раздела 7.5 [6].

Таким образом, точность в технических задачах следует оценивать с помощью доверительного интервала для величины рассогласования значений соответствующих параметров, полученных на ММ и в эксперименте на оригинале. Удобство такой оценки точности заключается в том, что даются одновременно и диапазон погрешности, который удобно сравнивать с “нормативом” типа допустимой погрешности, и вероятность ее (оценки) выполнения. Недостаток такой оценки кроется в том, что для построения доверительного интервала необходимо знание закона распределения оцениваемой случайной величины, в данном случае рассогласования. То есть перед оценкой точности необходимо провести другую процедуру. Но для оценки точности с помощью доверительного интервала не всегда достаточно данных, в этих случаях приходится довольствоваться простейшими грубыми оценками, например, по максимуму.

Непротиворечивость

Непротиворечивость подразумевает идентичный характер изменения соответствующих параметров, т.е. идентичный вид основных свойств функциональных зависимостей на отдельных участках, как-то: возрастание, убывание, экстремумы, выпуклость и т.п. При более глубоком рассмотрении этого понятия становится очевидным многообразие возможных критериев проверки непротиворечивости.

Однако центральная предельная теорема подсказывает универсальный метод проверки непротиворечивости – с помощью проверки подчиненности рассогласования закону ошибок. То есть для того чтобы рассогласование между оригиналом и моделью не описывало бы какую-либо закономерность, рассогласование должно вести себя вполне хаотически, иначе говоря, подчиняться нормальному закону распределения с нулевым математическим ожиданием. Для такой проверки существуют известные статистические критерии, в частности, критерий Пирсона х2. Такой подход оправдан для технических систем и процессов: регистрация параметров на оригинале часто сопряжена с наложением шума – влиянием неучитываемых факторов, в том числе и погрешностей регистрирующей аппаратуры.

Если будет доказана вышеупомянутая подчиненность нормальному закону распределения такого интегрального рассогласования, то тем самым, с одной стороны, будет доказана непротиворечивость ММ, а, с другой стороны, проверенный закон распределения можно будет использовать при построении доверительного интервала для рассогласования. Таким образом, в итоге будет доказана адекватность ММ, т.е. модель будет находиться в поле “хорошего измерительного инструмента”.

Статистическая проверка адекватности

Пример проверки адекватности ММ посадки самолета Ту-154Б записям параметров летных испытаний (ЛИ) с помощью статистических методов проверки непротиворечивости и точности приводится в [13; 5; 6]. Результаты показаны в табл. 2.

Таблица 2

Уровень значимости критериев: .00100 Доверительная вероятность: .90000 Имя файла данных “ЛИ”: Г_19_2 Имя файла данных “ММ”: А1

N анализируемого параметра: 186 — путев. скорость Число анализируемых точек: 59 Шаг по времени в секундах: .50000 Начальный момент в “ЛИ”: .00000 Начальный момент в “ММ”: .00000

При уровне значимости .001 нет оснований отвергнуть гипотезу о нормальном распределении рассогласования с математическим ожиданием = 0 и со среднеквадратическим отклонением = 1.7488 при 12 интервалах

Наблюдаемый критерий = 14.316 предельный критерий = 29.600

При уровне значимости .001 нет оснований отвергнуть гипотезу о нулевом мат.ожидании рассогласования

Наблюдаемый критерий = -2.997 предельный критерий = 3.460

Доверительный интервал с вероятностью .900 для среднеквадратического отклонения рассогласования: 1.1309 2.1239

Задача идентификации

В [7] было показано, что для ММ движения ВС исчерпывающую информацию о поведении объекта исследования в конкретном случае собрать практически невозможно. В условиях неопределенности добиться адекватности результатов ВЭ реальному поведению ВС можно только с помощью решения задачи идентификации. Идентификацией называется процесс определения неизвестных или уточнения недостаточно точно известных параметров ММ с целью обеспечения ее адекватности экспериментальным данным. Для ММ динамики полета (ДП) летательных аппаратов (ЛА) общее количество таких недостаточно точно известных параметров может исчисляться десятками.

Таким образом, идентификация ММ ДП ВС сводится к “интерпретации” исходного приближенного числового материала и моделей тех отдельных элементов, которые не описываются законами природы.

Этот важнейший для дальнейших построений принцип вытекает из работ научной школы академика А.Н. Тихонова, обязанной своими успехами в теории обратных задач четкому пониманию, что любое решение обратной задачи (как, например, идентификации) следует рассматривать не более чем “интерпретацию данных наблюдений” [14]. Для отыскания хотя бы одного частного решения необходимо прибегать к методу проверки гипотез. На этом фоне задача проверки адекватности ММ выглядит весьма простой, и решать ее приходится совместно с задачей идентификации.

Согласно [11] помочь здесь может только эвристический подход, использующий подробный “физический” анализ качественной взаимосвязи управляющих воздействий и параметров движения с целью получения наиболее близких к ЛИ результатов расчетов. Такой подход в общих чертах был сформулирован в [13; 15] и получил окончательный вид в [5] и [6]. Эвристический метод идентификации ММ представляет собой ряд последовательных этапов анализа:

1) разделение задачи в различных степенях свободы (продольного и бокового, поступательного и вращательного движений, как это практикуется в ДП);

2) выбор данных ЛИ, соответствующих рассматриваемому виду движения;

3) выявление и устранение возможных внутренних несогласованностей в данных ЛИ (устранение несогласованностей подразумевает не исправление данных, а лишь замену одних параметров другими, известным образом с ними связанными);

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

4) выявление особенностей выполнения исследуемого этапа реального полета (характерных моментов времени и действий);

5) выбор факторов ЛИ, по которым требуется обеспечить адекватность ММ (с их изменением по траектории должно быть качественно согласовано изменение результатов расчетов);

6) выдвижение гипотез об идентифицируемых параметрах (возможных причинах их отклонения от штатных или зарегистрированных);

7) проведение ВЭ (подбор идентифицируемых параметров методом последовательных приближений);

8) анализ результатов расчетов и оценка проверяемых гипотез.

Эвристическим методом идентификации ММ решено множество прикладных задач летной эксплуатации, в том числе для самолетов Ил-96 [16; 17], Ту-154 [18-21], вертолета Ми-8МТВ [22].

Заключение

В результате анализа опыта математического моделирования для решения задач ДП ЛА дана система терминов, их формулировки и рассмотрены способы проверки адекватности математических моделей.

ЛИТЕРАТУРА

1. Дыхненко Л.М., Кабаненко И.В., Кузьмин И.В. [и др.]. Основы моделирования сложных систем: учеб. пособие для втузов. – Киев: Вища школа, 1981.

2. Лебедев А.Н. Моделирование в научно-технических исследованиях. – М.: Радио и связь, 1989.

3. Ибрагимов И.А. и др. Моделирование систем: учеб. пособие. – Баку: Азинефтехим, 1989.

4. Кубланов М.С. Математическое моделирование. Методология и методы разработки математических моделей механических систем и процессов: учеб. пособие. – 4-е изд. – М.: МГТУ ГА, 2013. – Ч. I.

5. Кубланов М.С. Разработка теории и методов повышения уровня адекватности математических моделей на основе идентификации параметров движения для обеспечения летной эксплуатации самолетов гражданской авиации: дисс. … док. техн. наук. – М., 2000.

6. Кубланов М.С. Математическое моделирование задач летной эксплуатации воздушных судов на взлете и посадке: монография. – М.: МГТУ ГА, 2013.

7. Кубланов М.С. Об адекватности математических моделей и задаче идентификации // Научный Вестник МГТУ ГА, серия Аэромеханика и прочность. – 2009. – № 138. – С. 101-106.

8. ГОСТ 24026-80. Исследовательские испытания. Планирование эксперимента. Термины и определения. -М.: Изд-во стандартов, 1980.

9. Вентцель Е.С. Теория вероятностей: учебник для вузов. – 6-е изд., стер. – М.: Высшая школа, 1999.

10. Ермаков А.Л., Жеребятьев А.В. Разработка и применение адаптивной объектно-ориентированной математической модели повышенной степени адекватности // Научный Вестник МГТУ ГА, серия Аэромеханика и прочность. – 2005. – № 81. – С. 96-101.

11. Гришин А.А., Стрелец И.В., Кубланов М.С. Идентификация математической модели взлета и посадки самолета Ту-154М по данным руководства по летной эксплуатации // Научный Вестник МГТУ ГА, серия Аэромеханика и прочность. – 2003. – № 59. – С. 32-38.

12. Руководство по летной эксплуатации самолета Ту-154М. – М., 1986. – Кн. 1.

13. Кубланов М.С. Идентификация математической модели посадки самолета Ту-154Б по данным летных испытаний // Научный Вестник МГТУ ГА, серия Аэромеханика и прочность. – 1999. – № 15. – С. 27-36.

14. Тихонов А.Н., Кальнер В.Д., Гласко В.Б. Математическое моделирование технологических процессов и метод обратных задач в машиностроении. – М.: Машиностроение, 1990.

15. Кубланов М.С. Идентификация математических моделей по данным летных испытаний самолета Ил-96-300 // Решение прикладных задач летной эксплуатации ВС методами математического моделирования: сб. науч. тр. -М.: МГТУ ГА, 1993. – С. 3-10.

16. Разработка общих рекомендаций по летной эксплуатации самолета Ил-96-300 в ожидаемых условиях эксплуатации и режимах, выходящих за ожидаемые условия эксплуатации, на этапах взлета, захода на посадку и по-

садки: отчет о НИР (заключительный) / Руководитель В.Г. Ципенко, ответственный исполнитель М.С. Кубланов. № ГР 01930010176; Инв. № 02940003177. – М.: МИИГА, 1993.

17. Обоснование рекомендаций и предложений по летной эксплуатации самолета Ил-96Т на этапах взлета и посадки вблизи минимально-эволютивных скоростей, на больших углах атаки, с учетом аэроупругости конструкции: отчет о НИР (заключительный) / Руководитель В.Г. Ципенко, ответственный исполнитель М.С. Кубланов. № ГР 01960000315. – М.: МГТУ ГА, 1996.

18. Применение системы математического моделирования динамики полета летательных аппаратов (СММ ДП ЛА) к исследованию эксплуатационных ограничений ВС при взлете и посадке: отчет о НИР (промежуточный) / Руководитель В.Г. Ципенко, Ответственный исполнитель М.С. Кубланов. – М.: МГТУ ГА, 2001.

19. Проведение вычислительных экспериментов по ослаблению эксплуатационных ограничений ВС при взлете и посадке в условиях высокогорья и высоких температур окружающего воздуха: отчет о НИР (промежуточный) / Руководитель В.Г. Ципенко, ответственный исполнитель М.С. Кубланов. – М.: МГТУ ГА, 2001.

20. Разработка предложений и рекомендаций по летной эксплуатации ВС при взлете и посадке в условиях высокогорья и высоких температур окружающего воздуха: отчет о НИР (заключительный) / Руководитель В.Г. Ципенко, ответственный исполнитель М.С. Кубланов. – М.: МГТУ ГА, 2002.

21. Бехтина Н.Б. Применение усовершенствованной математической модели работы шасси в системе математического моделирования для расследования инцидента при посадке самолета Ту-154 // Научный Вестник МГТУ ГА, серия Аэромеханика и прочность. – 2009. – № 138. – С. 183-190.

22. Ефимов В.В., Ивчин В.А. Оценка адекватности математической модели динамики вертолета Ми-8МТВ // Научный Вестник МГТУ ГА, серия Аэромеханика и прочность. – 2011. – № 172. – С. 57-64.

CHECK OF THE MATHEMATICAL MODEL ADEQUACY

Kublanov M.S.

The wording of key terms established in the practice of mathematical modeling of the aircraft flight dynamics is proposed. We discuss the methods for adequacy checking.

Keywords: mathematical modeling, engineering systems, flight dynamics, adequacy.

Сведения об авторе

Кубланов Михаил Семенович, 1945 г.р., окончил МГУ (1968), доктор технических наук, профессор кафедры аэродинамики, конструкций и прочности летательных аппаратов МГТУ ГА, автор более 130 научных работ, область научных интересов – механика, математические методы моделирования.

Источник

Добавить комментарий