Как найти адсорбцию раствора

ЗАДАЧИ НА АДСОРБЦИЮ

ЗАДАЧИ НА АДСОРБЦИЮ

1. Вычислите величину адсорбции пропионовой кислоты из раствора при 15 °С. Поверхностное натяжение раствора и воды при 15 °С равны соответственно 6,33·10^–2 и 7,35·10^–2  Н/м.

Решение.

,

где Г – искомая адсорбция, моль/м²; σ(р-ра) и σ(H₂O) – поверхностное натяжение раствора и воды соответственно, Н/м; R = 8,13 Дж/(моль·К) – универсальная газовая постоянная; T – температура, К.

Ответ: 2,13·10^–6 моль/м²

2. Определить адсорбцию при 15 °C для водного раствора ацетона, если поверхностное натяжение раствора составляет 5,94·10^–2 Н/м, а для воды оно равно 7,35·10^–2 Н/м.

Решение.

,

где Г – искомая адсорбция, моль/м²; σ(р-ра) и σ(H₂O) – поверхностное натяжение раствора и воды соответственно, Н/м; R = 8,13 Дж/(моль·К) – универсальная газовая постоянная; T  – температура, К.

Ответ: 5,88·10^–9 моль/м²

3. Определить величину и знак адсорбции при растворении в воде серной кислоты, если поверхностное натяжение раствора 7,520·10^–2 Н/м, поверхностное натяжение воды 7,305·10^–2 Н/м, температура  18 °С.

Решение.

,

где Г – искомая адсорбция, моль/м²; σ(р-ра) и σ(H₂O) – поверхностное натяжение раствора и воды соответственно, Н/м; R = 8,13 Дж/(моль·К) – унивеерсальная газовая постоянная; T  – температура, К.

Ответ:–4,44·10^–7 моль/м².

4. Поверхностное натяжение водного раствора, содержащего поверхностно-активное вещество (ПАВ) с концентрацией c₁ = 0,056 моль/л при 293 К равно 4,33·10^–2 Н/м. Вычислите величину адсорбции ПАВ из раствора с концентрацией c₂ = 0,028 моль/л при 293 К. σ(H₂O) = 7,28·10^–2 Н/м.

Решение.

,

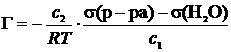
Ответ: 6,06·10^–6 моль/м²

5. При уменьшении концентрации новокаина в растворе с 0,20 моль/л до 0,15 моль/л поверхностное натяжение возросло с σ₁ = 6,9·10^–2 Н/м до σ₂ = 7,1·10^–2 Н/м, а у раствора кокаина при аналогичном уменьшении концентрации поверхностное натяжение возросло с 6,5·10^–2 Н/м до 7,0·10^–2 Н/м. Сравните величины адсорбции двух веществ в данном интервале концентраций при 293 К.

Решение.

.

Ответ: Г_нов = 2,87·10^–6 моль/м² < Г_кок = 7,19·10^–6 моль/м²

6. Используя уравнение Ленгмюра, найти величину адсорбции при 298 К, если величина предельной адсорбции 7,85·10^–6 моль/м², равновесная концентрация = 0,75 моль/л, а константа равновесия «адсорбция ⇄ десорбция» составляет 0,42 моль/л.

Решение.

,

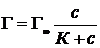
где Г – искомая адсорбция, моль/м²; Г_∞ – предельная адсорбция,  кмоль/м²; с –равновесная концентрация, моль/л; К – константа равновесия «адсорбция ⇄ десорбция», моль/л

Ответ: 5,03·10^–6 моль/м²

7. По уравнению Ленгмюра найти величину максимальной адсорбции, если при равновесной концентрации 0,03 моль/л величина адсорбции равна 6·10^–3 кмоль/м², а константа равновесия равна 0,8 моль/л.

Решение.

,

где Г – адсорбция, кмоль/м²; Г_∞ – искомая величина максимальной адсорбции,  кмоль/м²; с – равновесная концентрация, моль/л; К – константа равновесия «адсорбция ⇄ десорбция», моль/л.

Ответ: 0,16 кмоль/м².

8. Какая масса холестерина (M = 386,6 г/моль) адсорбируется 1 граммом адсорбента АДБ из плазмы крови, содержащей 4,8 мкмоль/мл холестерина, если константа равновесия равна 2 мкмоль/мл? Величина емкости адсорбента АДБ по холестерину составляет 0,7 мкмоль/г.

,

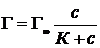
где Г – адсорбция, мкмоль/г; Г_∞ – величина емкости адсорбента АДБ по холестерину, мкмоль/г; с – равновесная концентрация холестерина, мкмоль/мл; К – константа равновесия «адсорбция ⇄ десорбция», мкмоль/мл.

m = Гm(АДБ)M,

где m – искомая масса холестерина, мкг; m(АДБ) – масса адсорбента АДБ, г; M – молярная масса холестерина, г/моль.

Ответ: 191 мкг

9. Установлено, что величина максимальной адсорбции на угле составляет 3,0·10^–3 моль/г, величина константы равновесия равна 6,0·10^–2 моль/л. Какая масса пропионовой кислоты (адсорбата) адсорбировалась из раствора, в котором установилась равновесная концентрация 0,1 моль/л, если масса угля равна 1 г?

Решение.

,

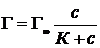
где Г – адсорбция, моль/г; Г_∞ – величина максимальной адсорбции на угле, моль/г; с – равновесная концентрация адсорбата, моль/л; К – константа равновесия «адсорбция ⇄ десорбция», моль/л.

m = Гm(угля)M,

где m – искомая масса адсорбата, г; m(угля) – масса адсорбента, г; M – молярная масса адсорбата, г/моль.

Ответ: 0,139 г.

10. Найти равновесную концентрацию уксусной кислоты, для которой удельная адсорбция по уравнению Фрейндлиха равна 0,012 моль/г, К = 0,25; n = 3,1.

Решение.

,

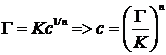
где Г – удельная адсорбция, моль/г; К и n – константы уравнения Фрейндлиха; с – искомая равновесная концентрация кислоты, моль/л.

Ответ: 8,16·10^–5 моль/л.

11. Найти величину равновесной концентрации серина, если удельная адсорбция равна 0,022 моль/г, К = 0,35, n = 4,0.

Решение.

,

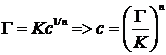
где Г – удельная адсорбция, моль/г; К и n – константы уравнения Фрейндлиха;        с – искомая равновесная концентрация серина, моль/л.

Ответ: 1,56·10^–5 моль/л

12. Таблетка активированного угля массой 2,50 г помещена в 50,0 мл 0,200 М раствора уксусной кислоты. Рассчитать количество вещества (моль) кислоты,  адсорбируемой 1,00 г угля, если на титрование 10,0 мл вышеуказанного раствора после прохождения адсорбции ушло 6,00 мл 0,0500 М раствора NaOH.

Решение.

,

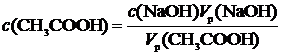
где  – равновесная концентрация кислоты, моль/л; – концентрация NaOH, моль/л;  – объем раствора NaOH, мл;  – объем оттитрованного раствора кислоты, мл.

,

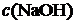
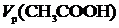
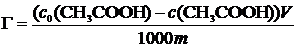
где Г – удельная адсорбция, моль/г; 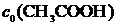– начальная (до адсорбции) концентрация кислоты, моль/л; V – исходный объем раствора кислоты, мл; 1000 мл/л – пересчетный коэффициент; m – масса таблетки адсорбента, г.

 Гm(угля),

где 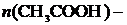искомое количество вещества кислоты, моль; m(угля) – заданная масса адсорбента, г.

Ответ: 0,068 моль

Адсорбция из
раствора на твердом адсорбенте.

Цель занятия:

1. Проводить качественные опыты по
адсорбции.

2. Количественно характеризовать
зависимость степени адсорбции от
концентрации адсорбтива.

3. Обрабатывать результаты опытов, делая
обобщения и выводы.

Воспитательная цель:

привить умение пользоваться справочной
литературой, аккуратное и экономное
отношение к химическим реактивам и
посуде.

Значение темы:

Адсорбция в широком смысле этого слова-
это процесс самопроизвольного изменения
концентрации веществ на поверхности
раздела фаз. Гетерогенные системы
чрезвычайно широко распространены в
природе, промышленности и, естественно,
их существованию сопутствуют процессы
адсорбции. Так, например, процесс любого
гетерогенного катализа начинается с
адсорбции субстрата на активных центрах
фермента. Это в одинаковой степени
относится как к промышленному, так и к
ферментативному катализу. Достаточно
сказать, что фотосинтез начинается с
адсорбции углекислого газа. Адсорбция
лежит в основе таких промышленных
процессов, как улавливание ценных паров
и газов; осветления вин, сахара, глюкозы,
фармакологических препаратов,
нефтепродуктов; крашение волокон;
флотационное обогащение руд, препаративная
хроматография.

Трудно переоценить биологическую роль
адсорбционных процессов. В качестве
примеров можно назвать следующие
явления: различная адсорбируемость
токсинов, сопровождающая избирательным
поражением органов; абсолютная
избирательность взаимодействия
«антитело-антиген», поражение ядами
активных ферментов (например, отравление
тяжелыми металлами, цианидами, монооксидами
углерода); транспорт белками крови
адсорбированных ими витаминов, гормонов,
металлов, перенос кислорода гемоглобином,
аминокислот эритроцитами и т.д. Действие
ряда фармакологических препаратов
связано с явлением адсорбции. Это,
например, карболен (активированный
уголь), применяющийся при отравлениях;
гемодез и полиглюкин (кровезаменитель
и дезинтоксикационный препарат).

Необходимый исходный уровень знаний
и умений студентов.

Студенты должны знать:

1. Второй закон термодинамики и его
следствия.

2. Полярные и неполярные группы.

3. Межмолекулярное взаимодействие.

4. Основы метода нейтрализации.

Студенты должны уметь:

1. Определять концентрацию кислоты
методом нейтрализации.

2. Производить необходимые расчеты.

3. Делать выводы на основании полученных
результатов.

Учебно-целевые вопросы.

1. Поверхностная энергия.

2. Следствие второго начала термодинамики
о самопроизвольном уменьшении системой
поверхностной энергии.

3. Возникновение поверхностного натяжения.

4. Поверхностно-активные вещества (ПАВ).
Моющее действие ПАВ и биологическая
роль. Правило Траубе. Закон Гиббса.

5. Адсорбция. Теория адсорбции (Ленгмюра,
Поляни, БЭТ).

6. Избирательная и ионообменная адсорбция.

7. Биологическое значение адсорбции и
ее практическое применение.

Практическая часть.

Адсорбцией называется изменение
концентрации какого-либо вещества в
поверхностном слое по сравнению с
объемной фазой, отнесенной к единице
поверхности этого слоя. Адсорбция
наблюдается на поверхности раздела
фаз: твердое вещество- жидкость, твердое
вещество- газ, жидкость – жидкость.

адсорбирующего вещества можно использовать
уравнение Гиббса, устанавливающее связь
между величиной адсорбции Г, концентрацией
С и уменьшением поверхностного с ростом
концентрации адсорбтива:

Г=- С/RT∙ dG/dс
(1)

График Г=f(с) при Т=const
(изотерма адсорбции) имеет вид кривой,
которая выходит из начала координат и
возрастает с увеличением концентрации
сначала быстро, а затем всё медленнее
и медленнее, так что кривая асимптотически
приближается к некоторой прямой,
параллельной оси абсцисс:

Рис.1

Уравнение Гиббса в принципе применимо
ко всем случаям адсорбции; однако на
практике оно применимо лишь к системам
жидкость-газ, в которых поверхностное
натяжение G легко поддается
измерению. Когда же дело имеет с
практически важной адсорбцией на твердых
поверхностях, для которых отсутствуют
методы непосредственного определения
G, пользуются другими
уравнениями, например, уравнением
Ленгмюра:

Г=Г_∞∙ КС/1+КС
(2)

где Г- величина адсорбции ;

Г_∞– предельное количество
адсорбирующего вещества;

С- равновесная концентрация растворенного
вещества после адсорбции, моль/л;

к – константа равновесия, равная
отношению констант скоростей адсорбции
и десорбции.

Некоторые случаи адсорбции на твердых,
особенно пористых поверхностях, которые
не могут быть описаны ни уравнением
Гиббса, ни уравнением Фрейндлиха:

Г=βxс^α (3)

где Г- количество вещества в миллимолях,
адсорбированного граммом твердого
адсорбтива;

С- равновесная концентрация растворенного
вещества после адсорбции, моль/л;

β и α – константы, причем α всегда меньше
единицы.

Построенная по уравнению (3) кривая
Г=f(с) отличается от изотермы
Гиббса и Ленгмюра тем, что лишена
начального участка и не дает предельного
значения адсорбции. Другими словами,
уравнение Фрейндлиха справедливо только
в интервале средних концентраций.

Лабораторная
работа.

Адсорбция уксусной
кислоты на угле.

Реактивы и оборудование:

Растворы: уксусная кислота – 0,4н; 0,5 н;

Оборудование: кол-во штук из расчета на
двух студентов:

Колбы плоскодонные конические 100мл –
10 шт;

Фильтры- 10 шт;

Пробирки- 10шт;

Воронки- 2 шт;

Штативы с бюретками- 6 шт;

Пипетки на 10мл – 6 шт.

Цель работы:

1. Изучить адсорбцию уксусной кислоты
на твердом адсорбенте-угле. Построить
изотерму адсорбции по данным опыта.

2. Определить предельное значение
удельной адсорбции, используя уравнение
Ленгмюра и постоянную «К» этого уравнения.

3. Вычислить удельную поверхность
твердого адсорбента.

Ход работы.

Разбавлением 0,4 н раствора уксусной
кислоты приготовить растворы концентраций,
указанных в таблице №1.

Приготовление исходных растворов.

№ колб	1	2	3	4
Концентрация кислоты	0,4н	0,2н	0,1н	0,05н
Объем растворов, мл	20	10	5	2,5
Объем воды, мл	0	10	15	17,5

Для определения точных значений
полученных концентраций кислоты Со из
каждой колбы отбирают пипеткой по 5 мл
полученного раствора и титруют 0,1н
раствором NаОН в присутствии
фенолфталеина до устойчивой розовой
окраски.

Концентрация кислоты определяется по
формуле:

С=С_NаОН∙ V_NаОН
/ V_к-ты = 0,1 ∙ V_NаОН
/ 5, (1)

Где С_NаОН –
концентрация щелочи;

V_NаОН
– объем щелочи, пошедший на титрование;

V_к-ты – Объем кислоты,
взятой на титрование, в нашем случае 5
мл.

Для определения величины адсорбции в
4 пробирки, в которых находится по 15 мл
полученных растворов кислоты, вносят
по 0,5 г адсорбента активированного угля,
встряхивают в течении 10-15 минут. Затем
раствор отфильтровывают через складчатый
фильтр. Определяют точную концентрацию
кислоты после адсорбции (С) титрованием
0,1н раствором NаОН.

По данным опыта рассчитывают удельную
адсорбцию:

Г ‘ = x/m=
(Со-С)∙V/m
(г)

где Г ‘ = x/m
– удельная адсорбция из опыта;

Со – концентрация кислоты до адсорбции;

С – равновесная концентрация кислоты
после адсорбции;

V – объем кислоты (в нашем
случае 15 мл);

m – навеска угля 0,5 г.

Полученные экспериментальные данные,
а также результаты вычислений внести
в таблицу №2

Результаты эксперимента.

Таблица №2

№ колб	Со	Vср (из 3-х)	С	Г ‘ = x/m	С/ Г ‘	Г ‘∞	К	S, см2

Обработка результатов эксперимента:

1. Используя полученные данные, построить
изотерму адсорбции Г=f(с),

где С- равновесная концентрация кислоты
после адсорбции (рис.1).

2. По уравнению Ленгмюра

Г=Г_∞∙ КС/1+КС

Рассчитать значение предельной удельной
адсорбции и константу «К». Для этого
можно применить графический метод.

Преобразовав уравнение Ленгмюра в
уравнение прямой:

С/Г=С/Г_∞ + 1/КГ_∞

где 1/Г_∞
= const; 1/КГ_∞
= const;

Построим график С/Г= f(с),
откладывая на оси абсцисс значения
концентраций С, а на оси ординат величины
С/Г (рис2).

Рис2.

Котангенс угла α, образуемого этой
прямой с осью абсцисс, равен Г_∞,
отрезок оа = 1/КГ_∞ , откуда можно
найти значение «К», подставляя сюда
значение Г_∞, Котангенс угла
находят из графика как отношение
прилежащего катета к противолежащему,
взяв величины катетов с учетом масштабов.

3. Зная Г_∞, вычисляем удельную
поверхность адсорбента, выражая ее в
см²/г по формуле:

Sуд.= Г_∞^∙Nа
∙q

где Nа – число Авогадро
(6,02 ∙10²³);

q – площадь поперечного
сечения молекул ПАВ (q=
25∙ 10^-16 см²)

Соседние файлы в предмете Химия

• #
• #
• #
• #
• #
• #

Для расчетапараметров молекул в адсорбционном слое прежде всего необходимо провести определение адсорбции ПАВ на поверхности водного раствора. Для этого обычно используют один из двух методов, основанных на обработке изотермы поверхностного натяжения.

Поверхностное натяжение растворов ПАВ определяют одним из описанных выше методов. Полученные данных используют для построения изотермы поверхностного натяжения, пример которой показан на рис. 1.20.

Для расчета адсорбции используют уравнение (1.1.100) изотермы адсорбции Гиббса. Для этого находят поверхностную активность 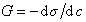в нескольких точках изотермы поверхностного натяжения.

Для нахождения G к заданным точкам кривой s= f(c) проводят касательные, как это показано на рис. 1.20, определяют тангенс угла наклона касательных, который равен ds/dc. По найденной поверхностной активности для разных концентраций рассчитывают по уравнению Гиббса адсорбцию (моль/м²). Затем строят изотерму адсорбции в области возможно наименьших концентраций, так как уравнение изотермы Гиббса в форме уравнения 1.1.100 справедливо в области малых концентраций растворов. Для расчета максимальной адсорбции Г_max можно воспользоваться одним из двух вариантов линейной формы уравнения изотермы адсорбции Ленгмюра:

Если единицу поделить на левую и правую часть уравнения (1.1.113), то получаем уравнение

. (1.1.122 )

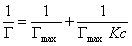
После построения изотермы адсорбции в координатах этого уравнения находят предел адсорбции Г_max как величину, обратную отрезку, отсекаемому на оси ординат. Этот метод обычно связан с высокой погрешностью определения Г_max, так как величина отрезка бывает небольшой. В этой связи часто прибегают к обработке экспериментальных данных по линейной форме изотермы адсорбции Ленгмюра, получающейся при делении равновесной концентрации раствора на левую и правую части уравнения (1.1.113). В этом случае получается уравнение

. ( 1.1.123)

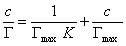
Линейная зависимость с/Г = f(с) отсекает на ординате отрезок, позволяющий найти 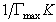, а тангенс угла наклона прямой к оси абсцисс равен 1/Г_max.

После нахождения предела адсорбции рассчитывают параметры молекул ПАВ в адсорбционном слое.

Определить предел адсорбции и постоянной равновесия адсорбцииможно такжеc помощью уравнения Шишковского (как описано выше, при обсуждении этого уравнения).

В табл. 1.1 приведены поверхностное натяжение некоторых жидкостей, их межфазовые натяжения на границе с водой при температуре 293,2 K, температурные коэффициенты поверхностного и межфазового натяжений, а также работа адгезии жидкости к воде.

Таблица 1.1

Поверхностное и межфазовое натяжение (s), работа адгезии

органической жидкости в воде (W₁₂₃), температурный коэффициент

поверхностного и межфазового натяжения –ds/dT