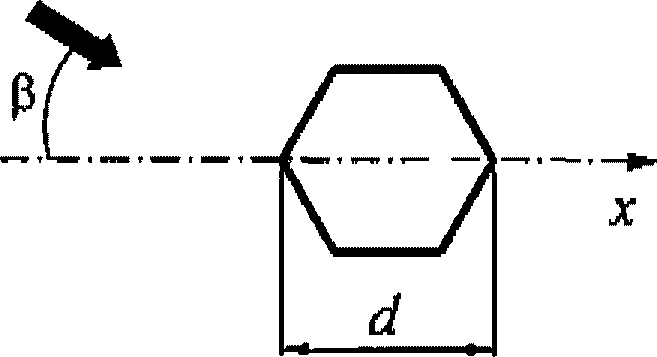
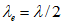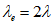Ветровые нагрузки
Если со снеговой нагрузкой обычно проблем не возникает – эту нагрузку видно, её можно пощупать и даже взвесить – то с ветровой нагрузкой всё наоборот. Очевидно, что ветер оказывает какое-то воздействие на конструкции, и порой даже весьма разрушительное: срывает крыши, заваливает каркасы стен и заборы, скручивает рекламные баннеры. Но как можно учесть эту силу? И поддаётся ли она в принципе расчёту? Поддаётся! Но, ветровую нагрузку непрофессионалы считать очень не любят и тому есть объяснение – её расчёт значительно сложнее, чем расчёт снеговой нагрузки. Если в СП 20.13330.2011 расчёту снеговой нагрузки уделено 2,5 страницы, то расчёт ветровой нагрузки втрое больше + обязательное приложение на 19 страниц с аэродинамическими коэффициентами. Ну а для Беларуси всё ещё страшнее – документ TKP_EN_1991-1-4-2009 “Ветровые воздействия” объёмом 120 страниц!
С Еврокодом (EN 1991-1-4-2009) по ветровым воздействиям мало кому захочется разбираться в масштабах постройки частного дома (интересующимся лучше скачать и изучать его непосредственно), поэтому здесь я постараюсь использовать по возможности упрощённое представление на основе Российского СП 20.13330.2011 со специфическими данными для Беларуси из актуального Национального приложения Еврокода. Считаю, что для примерной оценки ветровых воздействий этого будет более, чем достаточно (особенно в сравнении с ничем вообще).
Воздействия ветра
Для зданий и сооружений необходимо учитывать следующие воздействия ветра:
-
основной тип ветровой нагрузки (в дальнейшем – «ветровая нагрузка»);
-
пиковые значения ветровой нагрузки, действующие на конструктивные элементы ограждения и элементы их крепления;
-
резонансное вихревое возбуждение;
-
аэродинамические неустойчивые колебания типа галопирования, дивергенции и флаттера.
Резонансное вихревое возбуждение и аэродинамические неустойчивые колебания типа галопирования необходимо учитывать для зданий и сплошностенчатых сооружений, у которых высота в 10 и более раз больше характерного поперечного размера. Т.е. для частного домостроения последние два пункта рассчитывать не стоит.
Нормативная ветровая нагрузка
Нормативное значение ветровой нагрузки ω следует определять как сумму средней ωm и пульсационной ωр составляющих:
ω = (ωm + ωp ) · γf
Нормативная средняя составляющая ветровой нагрузки ωm
Нормативное значение средней составляющей ветровой нагрузки ωm в зависимости от эквивалентной высоты zе над поверхностью земли следует определять по формуле:
ωm = ω0 · k(zе) · c,
где ω0 – нормативное значение ветрового давления;
k(ze) – коэффициент, учитывающий изменение ветрового давления для высоты zе;
c – аэродинамический коэффициент.
Теперь разберёмся с каждым из этих коэффициентов:
Нормативное значение ветрового давления ω0
Нормативное значение ветрового давления ω0 принимается в зависимости от ветрового района по таблице:
На карте представлена только Россия, так как СНиП 2.01.07-85 действует только на территории РФ, для Беларуси данные будут немного ниже.
Так же СП 20.13330.2011 допускает определять нормативное значение ветрового давления ω0 по формуле:
ω0 = 0,43 · ν²
где ν² – давление ветра, соответствующее скорости ветра, м/с, на уровне 10 м над поверхностью земли для местности типа А, определяемой с 10-минутным интервалом осреднения и превышаемой в среднем один раз в 50 лет.
Для Беларуси такой карты нет, и по Еврокоду используется несколько иная терминология. Так, для РБ идентичный параметр называется скоростным напором. Значение базового скоростного напора определяется по формуле:
qb = 0.5 · ρ · νb²
где ρ – плотность воздуха = 1,25 кг/м³;
νb – базовое значение скорости ветра, принимаемое по карте (Изменение №2 ТКП EN 1991-1-4-2009 от 9.04.2015)
Если подставить все значения в формулу, получим для Беларуси два значения:
-
1 ветровой район (жёлтый по карте) – 0,28 кПа;
-
2 ветровой район (зелёный по карте) – 0,33 кПа.
w0
Коэффициент k(ze)
Коэффициент k(ze) определяется по формуле:
k(ze) = k10 · (ze/10)^(2·a)
где ze – эквивалентная высота, для нашего случая равная высоте дома;
k10, a – зависят от типа местности и берутся из таблицы ниже.
Принимаются следующие типы местности:
-
А – открытые побережья морей, озер и водохранилищ, сельские местности, в том числе с постройками высотой менее 10 м, пустыни, степи, лесостепи, тундра;
-
В – городские территории, лесные массивы и другие местности, равномерно покрытые препятствиями высотой более 10 м;
-
С – городские районы с плотной застройкой зданиями высотой более 25 м.
Сооружение считается расположенным в местности данного типа, если эта местность сохраняется с наветренной стороны сооружения на расстоянии 30h – при высоте сооружения h до 60 м и на расстоянии 2 км – при h > 60 м.
Примечание – Типы местности могут быть различными для разных расчетных направлений ветра.
kz
Например: высота дома 7 м в сельской местности с постройками в округе ниже 10 м (Тип А) и в лесном массиве (Тип В):
А) k(ze) = 1 · (7/10)^(2·0,15) = 1 · 0,7^0,3 = 0,9. В) k(ze) = 0,65 · (7/10)^(2·0,2) = 0,65 · 0,7^0,4 = 0,56.
Аэродинамический коэффициент с
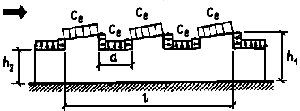
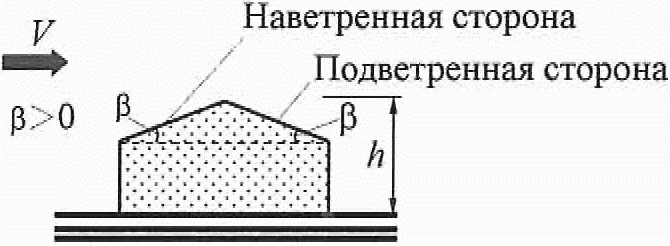
Определение аэродинамического коэффициента по СП 20.13330.2011 сводится к выбору соответствующей формы строения и выбору участка поверхности этого строения. Здесь нужно просто найти картинку, наиболее похожую на требуемую конструкцию и из таблички взять значение коэффициента. Конечно, Свод Правил описывает множество различных вариантов, но я, для простоты понимания, ограничусь лишь наиболее распространённой формой – прямоугольным в плане зданием с двускатной кровлей. Индекс се используется для обозначения внешнего давления ветра, бывает ещё ci, cf, cx, cy, и cz, но, как я уже упоминал, для простоты изложения их мы не рассматриваем. Знак “минус” у коэффициента соответствует направлению ветра от рассчитываемой поверхности (отсос).
c90
Нормативная пульсационная составляющая ветровой нагрузки ωр
Нормативное значение пульсационной составляющей ветровой нагрузки ωр на эквивалентной высоте zе следует определять исходя из частот собственных колебаний. Но, согласно примечания для этого раздела СП “При расчёте многоэтажных зданий высотой до 40 м …. пульсационную нагрузку допускается определять по формуле…”, т.е. мы можем не выяснять собственные частоты колебаний нашего частного одно-двухэтажного дома и воспользоваться формулой:
ωр = ωm · ζ(zе) · ν,
где ωm – нормативная средняя составляющая ветровой нагрузки, которую мы вычислили в предыдущем разделе;
ζ(ze) – коэффициент пульсации давления ветра;
ν – коэффициент пространственной корреляции пульсаций давления ветра.
Теперь разберёмся с последними двумя коэффициентами:
Коэффициент ζ(ze)
Коэффициент ζ(ze) определяется по формуле:
ζ(ze) = ζ10 · (ze/10) ^ -a
где ze – эквивалентная высота, для нашего случая равная высоте дома;
ζ10, a – зависят от типа местности и берутся из таблицы ниже.
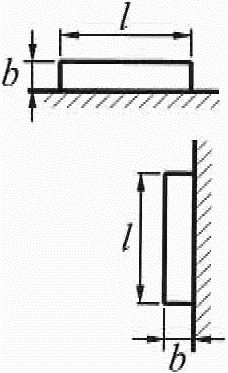
ez
Например: высота дома 7 м в сельской местности с постройками в округе ниже 10 м (Тип А) и в лесном массиве (Тип В):
А) ζ(ze) = 0,76 · (7/10) ^ -0,15 = 0,8. В) ζ(ze) = 1,06 · (7/10) ^ -0,2 = 1,14.
Коэффициент пространственной корреляции пульсаций давления ν
Коэффициент пространственной корреляции пульсаций давления ν следует определять для расчетной поверхности сооружения или отдельной конструкции, для которой учитывается корреляция пульсаций. Расчетная поверхность включает в себя те части наветренных и подветренных поверхностей, боковых стен, кровли и подобных конструкций, с которых давление ветра передается на рассчитываемый элемент сооружения.
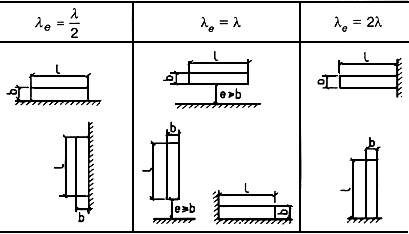
Определение этого коэффициента слегка запутанное. Для начала, смотрим на рисунок 11.2 (слева) и определяем плоскость, наиболее параллельно которой расположена наша расчётная поверхность. Тут может быть три варианта:
-
поверхность стены расположена перпендикулярно направлению ветра (zoy);
-
поверхность стены расположена параллельно направлению ветра (zox);
-
расчётная поверхность – это крыша (xoy).
Теперь определяем дополнительные параметры ρ и χ по таблице:
Коэффициент ν определяем по следующей таблице в зависимости от вычисленных параметров ρ и χ:
Например: дом с двускатной крышей, высота в коньке 7 м, уклон скатов 30°, размер дома в плане 9х11 м, Ориентация конька восток-запад. Приоритетное направление ветра – западное (дует в стену с фронтоном, α=90°). Дом в лесном массиве (тип местности В). Определим параметры ρ, χ и коэффициент ν:
-
для западной и восточной стен (плоскость zoy) ρ = b = 9 м; χ = h = 7м; ν = 0,84.
-
для северной и южной стен (плоскость zoх) ρ = 0,4а = 4,4 м; χ = h = 5м; ν = 0,89.
-
для скатов крыши (плоскость хoy) ρ = b = 9 м; χ = а = 11м; ν = 0,84.
Коэффициент надёжности γf
Свод правил СП 20.13330.2011 предписывает принимать коэффициент надежности по ветровой нагрузке γf = 1,4.
Пиковая ветровая нагрузка
Для элементов ограждения и узлов их крепления необходимо учитывать пиковые положительные ω+ и отрицательные ω– воздействия ветровой нагрузки, нормативные значения которых определяются по формуле:
ω+(–) = ω0 · k(ze) · [1 + ζ(ze)] · cp,+(–) · ν+(–)
где ω0 – расчетное значение давления ветра;
ze – эквивалентная высота;
k(ze) – коэффициент, учитывающий изменение давления ветра на высоте ze;
ζ(ze) – коэффициент, учитывающий изменение пульсаций давления ветра на высоте ze;
cp,+(–) – пиковые значения аэродинамических коэффициентов положительного давления (+) или отсоса (–);
ν+(–) – коэффициенты корреляции ветровой нагрузки, соответствующие положительному давлению (+) и отсосу (–);
Осталось определить последние два коэффициента.
Коэффициенты корреляции ветровой нагрузки ν+(–) зависят от площади
поверхности (А), с которой собирается ветровая нагрузка и определяются
по табличке справа:
Для стен прямоугольных в плане зданий положительное пиковое значение аэродинамического коэф. ср,+ =1,2.
Пиковые значения отрицательного аэродинамического коэффициента ср,– для стен и плоских покрытий приведены в табличке ниже в зависимости от участка поверхности.
Пример
Как вы уже поняли, расчёт ветровой нагрузки предполагает разбиение расчётной поверхности на участки, где ветер оказывает воздействие сильнее (на углах и кромках), где слабее (в центре поверхности) и для каждого случая необходим отдельный расчёт. Можно, конечно, просто рассчитать максимально напряжённые участки, но это не совсем верно, т.к. углы здания обычно являются тоже самыми жёсткими элементами стены, и для них повышенное ветровое воздействие не так страшно, как для большой площади стены без внутренних перегородок и рёбер жёсткости. Однако, проводить в рамках статьи подробный расчёт тоже смысла нет, мало кто и до сюда-то дочитал 🙂
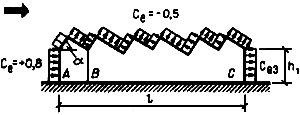
Для примера я возьму уже упоминавшийся выше дом с двускатной крышей, высота в коньке 7 м, уклон скатов 30°, размер дома в плане 9х11 м, Ориентация конька восток-запад. Приоритетное направление ветра – западное (дует в стену с фронтоном, α=90°). Дом в лесном массиве (тип местности В).
Определим нормативную величину ветровой нагрузки и пиковую ветровую нагрузку для максимально напряжённых участков стены и крыши, чтобы в принципе понять о каких силах идёт речь.
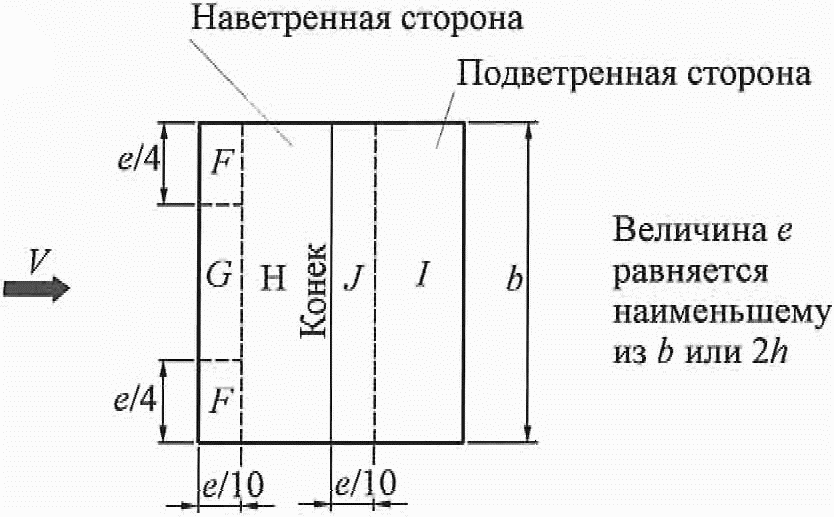
Для расчёта нормативной ветровой нагрузки ω я изобразил на нашем условном доме зоны с распределением аэродинамических коэффициентов:
-
Определим нормативную среднюю составляющую ветровой нагрузки:
ωm = ω0 · k(zе) · c
где ω0 = 0,28 кПа (определили выше);
k(zе) = 0,56 (определили выше);
аэродинамические коэффициенты для различных участков здания берём из таблиц:
с(A) = –1,0 (боковая стена); ωm(А) = –0,16 кПа;
с(В) = –0,8 (боковая стена); ωm(В) = –0,13 кПа;
с(С) = –0,5 (боковая стена); ωm(С) = –0,08 кПа;
с(D) = 0,8 (наветренная стена); ωm(D) = +0,13 кПа;
с(Е) = –0,5 (подветренная стена); ωm(E) = –0,08 кПа;с(F) = –1,1 (крыша);
ωm(F) = –0,17 кПа;
с(G) = –1,4 (крыша); ωm(G) = –0,22 кПа;
с(H) = –0,8 (крыша); ωm(H) = –0,13 кПа;
с(I) = –0,5 (крыша); ωm(I) = –0,08 кПа;
-
Определим нормативную пульсационную составляющую ветровой нагрузки:
ωр = ωm · ζ(zе) · ν
где ωm мы только что определили для всевозможных участков строения;
ζ(zе) = 1,14 (определили здесь)
ν = 0,84 (для стен с фронтонами [D, Е] (плоскость zoy) ρ = b = 9 м; χ = h = 7м);
ν = 0,89 (для боковых стен [A, B, C] (плоскость zoх) ρ = 0,4а = 4,4 м; χ = h = 5м);
ν = 0,84 (для скатов крыши [F, G, H, I] (плоскость хoy) ρ = b = 9 м; χ = а = 11м);
ωp(А) = –0,16 кПа (боковая стена);
ωp(В) = –0,13 кПа (боковая стена);
ωp(С) = –0,08 кПа (боковая стена);ωp(D) = +0,12 кПа (наветренная стена);
ωp(E) = –0,08 кПа (подветренная стена);ωp(F) = –0,21 кПа (крыша);
ωp(G) = –0,17 кПа (крыша);
ωp(H) = –0,12 кПа (крыша);
ωp(I) = –0,08 кПа (крыша); -
Определим нормативную ветровую нагрузку для каждого участка:
ω = (ωm + ωp ) · γf
где γf = 1,4 (коэффициент надёжности по ветровой нагрузке);
ω(А) = –0,44 кПа (боковая стена);
ω(В) = –0,35 кПа (боковая стена);
ω(С) = –0,22 кПа (боковая стена);
ω(D) = +0,34 кПа (наветренная стена);
ω(E) = –0,21 кПа (подветренная стена);
ω(F) = –0,60 кПа (крыша);
ω(G) = –0,47 кПа (крыша);
ω(H) = –0,34 кПа (крыша);
ω(I) = –0,21 кПа (крыша);
-
Определим пиковую ветровую нагрузку:
ω+(–) = ω0 · k(ze) · [1 + ζ(ze)] · cp,+(–) · ν+(–)
где ω0 = 0,28 кПа (определили выше);
k(zе) = 0,56 (определили выше);
ζ(zе) = 1,14 (определили здесь);
Сp,+ = 1,2;
Сp,– = -2,2 (участки шириной 0,9 м на углах всех стен);
Сp,– = -1,2 (остальные участки стен);Сp,– = -3,4 (участки шириной 0,9 м на углах скатов крыши);
Сp,– = -2,4 (участки шириной 0,9 м на наружных краях крыши, за исключением углов);
Сp,– = -1,5 (вся крыша кроме краёв и углов);
площадь любых стен нашего дома > 20 м², значит для всех стен коэффициент корреляции ν одинаков:
ν+ = 0,75;
ν– = 0,65;
ω+ = 0,3 кПа;
ω–(углы стен) = –0,48 кПа;
ω–(стены) = –0,26 кПа;
ω–(углы крыши) = –0,74 кПа;
ω–(края крыши) = –0,52 кПа;
ω–(крыша) = –0,33 кПа.
Вывод:
-
максимальная нормативная ветровая нагрузка от давления ветра на наветренной стене 0,34 кПа;
-
максимальная нормативная нагрузка отсоса ветра на боковой стене -0,44 кПа; на крыше -0,6 кПа;
-
максимальная пиковая нагрузка на углах стен -0,48 кПа;
-
максимальная пиковая нагрузка на углах крыши -0,74 кПа.
Аэродинамические коэффициенты профиля
10.2.1. Общие понятия об аэродинамических коэффициентах профиля
Аэродинамические коэффициенты – безразмерные величины, характеризующие аэродинамические силу и момент, действующие на тело, движущееся в жидкой или газообразной среде.
Аэродинамические коэффициенты силы CR находят как отношение аэродинамической силы R к скоростному напору ρv2/2 и характерной площади S, а эродинамические коэффициенты момента CМ – как отношение аэродинамического момента М к ρv2/2, S и к характерной длине l , т. е.
где ρ – плотность среды, в которой движется тело, v – скорость тела относительно этой среды.
Характерные размеры выбираются достаточно произвольно, например для самолёта S – площадь несущих крыльев (в плане), а l – длина хорды крыла; для ракеты S – площадь миделевого сечения, а l – длина ракеты.
Выражение аэродинамических сил и моментов в форме аэродинамических коэффициентов имеет большое значение для аэродинамических исследований и расчётов, существенно их упрощая. Так, например, аэродинамическая сила, действующая на самолёт, может достигать значений в сотни и тысячи кн (десятки и сотни mс), та же сила, действующая на модель этого самолёта, испытываемую в аэродинамической трубе, составляет десятки ньютонов (н), но аэродинамические коэффициенты для самолёта и для модели равны между собой. Или, например, аэродинамическая сила, действующая на шар, падающий с большой высоты на землю, зависит от высоты и скорости падения шара, а аэродинамический коэффициент является постоянной величиной.
Рекомендуемые материалы
Вода при температуре t из резервуара А подается в резервуар В со скоростью υ по стальному трубопроводу диаметром d1 и длиной l1. Уровень воды в баке А поддерживается постоянным Н1. Коэффициенты сопротивления: входа в трубу ξвх, крана ξкр, колена бе
Вода при 5°С (слой глубиной Н=2,4м) вытекает из открытого бака в атмосферу. Заданы коэффициенты гидравлических потерь вентиля ξвент=4,5 и сопла ξс=0,09, длины труб L1=15м, L2=5,0м, L3=L4=12м, их диаметры d1= d2=d3=90мм, d4=120мм, d=35мм – диаметр соп
Курсовая работа мжг 41вариант “Гидравлический расчет гидросистемы комплекса средств обеспечения мобильной доставки питьевой воды населению”
В емкость вместимостью V, бензин заливается из резервуара при напоре Н по трубе переменного сечения (l1, d1, l2, d2, ∆1, ∆2) имеющей три колена (ξк=0,8) и два вентиля (ξв=7,5), коэффициенты местных сопротивлений: ξвх=0,5; ξвых=1,0; внезапного сужения
Определение аэродинамических характеристик изолированного профиля в дозвуковом плоском потоке
Вариант 1 (41, 42) ” Гидравлический расчет гидросистемы комплекса средств обеспечения мобильной доставки питьевой воды населению”
Для аппаратов больших размеров, летящих на малой высоте с дозвуковой скоростью, для которых М-число М < 0,2, аэродинамические коэффициенты зависит только от формы летательного аппарата и угла атаки (угла между характерной плоскостью и направлением скорости полёта). В общем случае аэродинамические коэффициенты зависят от вязкости и сжимаемости газа, характеризуемой безразмерными критериями подобия: М-числом и Рейнольдса числом.
10.2.2. Определение аэродинамических коэффициентах профиля
Если аэродинамическую силу и момент разложить на составляющие по осям, то соответственно будем иметь: аэродинамические коэффициенты сопротивления – Cx, подъёмной и боковой сил – Су и Cz, а также аэродинамические коэффициенты моментов крена, рыскания и тангажа.
Аэродинамическое сопротивление – лобовое сопротивление, сила, с которой газ (например, воздух) действует на движущееся в нём тело; эта сила направлена всегда в сторону, противоположную скорости, и является одной из составляющих аэродинамической силы. Знание Л. с. необходимо для аэродинамического расчёта летательных аппаратов, т. к. от него зависит, в частности, скорость движения при заданных тяговых характеристиках двигательной установки.
Аэродинамическое сопротивление – результат необратимого перехода части кинетической энергии тела в тепло. Зависит аэродинамическое сопротивление от формы и размеров тела, ориентации его относительно направления скорости, значения скорости, а также от свойств и состояния среды, в которой происходит движение. В реальных средах имеют место: вязкое трение в пограничном слое между поверхностью тела и средой, потери на образование ударных волн при около- и сверхзвуковых скоростях движения (волновое сопротивление) и на вихреобразование. В зависимости от режима полёта и формы тела будут преобладать те или иные компоненты аэродинамическое сопротивление. Например, для затупленных тел вращения, движущихся с большой сверхзвуковой скоростью, Аэродинамическое сопротивление определяется в основном волновым сопротивлением. У хорошо обтекаемых тел, движущихся с небольшой скоростью, аэродинамическое сопротивление определяется сопротивлением трения и потерями на вихреобразование.
В аэродинамике аэродинамическое сопротивление характеризуют безразмерным аэродинамическим коэффициентом сопротивления Cx, с помощью которого аэродинамическое сопротивление Х определяется как
где r¥ – плотность невозмущённой среды, v¥ – скорость движения тела относительно этой среды, S – характерная площадь тела.
Коэффициент Cx тела заданной формы при известной ориентации его относительно потока зависит от безразмерных критериев подобия: М-числа, числа Рейнольдса и др. (рис. 1 и 2).
Рис. 1. Зависимость коэффициента аэродинамического сопротивления конуса от числа М
Рис. 2. Зависимость коэффициента аэродинамического сопротивления шара от числа Re
Численные значения Cx обычно определяют экспериментально, измеряя А. с. моделей в аэродинамических трубах и других установках, используемых при аэродинамическом эксперименте. Теоретическое определение аэродинамическое сопротивление возможно лишь для ограниченного класса простейших тел.
Коэффициент подъемной силы су – безразмерный коэффициент, зависящий от формы тела, его ориентации в среде и чисел Рейнольдса Re и Маха М. Значение су определяют теоретическим расчётом или экспериментально.
Так, согласно теории Жуковского, для крыла в плоскопараллельном потоке при небольших углах атаки:
су=2m(α-α0),
где α – угол атаки (угол между направлением скорости набегающего потока и хордой крыла);
α0 – угол нулевой подъемной силы;
m – коэффициент, зависящий от формы профиля крыла, например для тонкой слабо изогнутой пластины m=p.
В случае крыла конечного размаха L коэффициент m = p, где l = L / b – удлинение крыла.
В реальной жидкости в результате влияния вязкости величина m меньше теоретической, причём эта разница возрастает по мере увеличения относительной толщины профиля; значение угла α0 также меньше теоретического.
Кроме того, с увеличением угла α зависимость су от α (рис. 2) перестает быть линейной и величина монотонно убывает, становясь равной нулю при угле атаки acr , которому соответствует максимальная величина коэффициента подъемной силы – су,мах .
Дальнейшее увеличение а ведёт к падению су вследствие отрыва пограничного слоя от верхней поверхности крыла. Величина cymax имеет существенное значение, т.к. чем она больше, тем меньше скорость взлёта и посадки самолёта.
Рис. 2. Зависимость су от a.
При больших, но докритических скоростях, т. е. таких, для которых М < Мкр (Mkp — значение числа М набегающего потока, при котором вблизи поверхности профиля местные значения числа М = 1), становится существенной сжимаемость газа. Для слабо изогнутых и тонких профилей при малых углах атаки сжимаемость можно приближённо учесть, положив
,
.
При сверхзвуковых скоростях характер обтекания существенно меняется. Так, при обтекании плоской пластины у передней кромки на верхней поверхности образуются волны разрежения, а на нижней – ударная волна (рис. 3).
Рис. 3. Схема сверхзвукового обтекания пластинки:
nв > n1, рв < p1; n2 < nв, р2 > рв; nн < n1, рн > n1; n3> nн, p3 < рн.
В результате давление рн на нижней поверхности пластины становится больше, чем на верхней (рв); возникает суммарная сила, нормальная к поверхности пластины, составляющая которой, перпендикулярная к скорости набегающего потока, и есть подъёмная сила.
Для малых М>1 и малых α подъемная сила пластины может быть вычислена по формуле:
.
Эта формула справедлива и для тонких профилей произвольной формы с острой передней кромкой.
Аналогично определяют аэродинамические коэффициенты сопротивления боковой силы Cz, а также аэродинамические коэффициенты моментов крена, рыскания (небольшие угловые отклонения от курса (попеременно в обе стороны) относительно вертикальной оси летательного аппарата, судна) и тангажа (угловое движение летательного аппарата или судна относительно главной поперечной оси инерции).
Обратите внимание на лекцию “2 Услуги Интернет”.
ЗАКЛЮЧЕНИЕ
В лекции рассмотрены законы движения жидкостей и газов и применение этих законов к решению практических задач. Настоящая лекция является теоретической базой для студентов-теплоэнергетиков, т. к. знание гидрогазодинамик (технической гидромеханики) необходимо для решения многочисленных инженерных задач, в том числе в теплогазоснабжении и вентиляции, в частности, для расчета трубопроводов, проектирование котельных агрегатов, печных и сушильных установок, воздухо- и газоочистных аппаратов, теплообменных аппаратов.
Аэродинамические коэффициенты
HomeАэродинамические коэффициенты
Д.1 Аэродинамические коэффициенты
Д.1.1 Отдельностоящие плоские сплошные конструкции
Отдельностоящие плоские сплошные конструкции на земле (стены, заборы и т.д.)
Для различных участков конструкций (рисунок Д.1) коэффициент сх определяется по таблице Д.1;
ze = h.
|
Участки плоских сплошных конструкций на земле (см. рисунок Д.1) |
|||
|
А |
В |
С |
D |
|
2,1 |
1,8 |
1,4 |
1,2 |
Рекламные щиты
Для рекламных щитов, поднятых над землей на высоту не менее d/4 (рисунок Д.2): сх = 2,5kl, где kl – определено в Д.1.15.
Равнодействующую нагрузку, направленную по нормали к плоскости щита, следует прикладывать на высоте его геометрического центра с эксцентриситетом в горизонтальном направлении е = ± 0,25b.
ze = zg + d/2.
Д.1.2 Прямоугольные в плане здания с двускатными покрытиями
Вертикальные стены прямоугольных в плане зданий
|
Боковые стены |
Наветренная стена |
Подветренная стена |
||
|
Участки |
||||
|
А |
В |
С |
D |
Е |
|
-1,0 |
-0,8 |
-0,5 |
0,8 |
-0,5 |
Для наветренных, подветренных и различных участков боковых стен (рисунок Д.3) аэродинамические коэффициенты се приведены в таблице Д.2.
Для боковых стен с выступающими лоджиями аэродинамический коэффициент трения сf = 0,1.
Двускатные покрытия
Для различных участков покрытия (рисунок Д.4) коэффициент се определяется по таблицам Д.3, а и Д.3, б в зависимости от направления средней скорости ветра.
Для углов 15° £ b £ 30° при a = 0° необходимо рассмотреть два варианта распределения расчетной ветровой нагрузки.
Для протяженных гладких покрытий при a = 90° (рисунок Д.4, б) аэродинамические коэффициенты трения сf = 0,02.
Таблица Д.3а
|
Уклон b |
F |
G |
Н |
I |
J |
|
15° |
-0,9 |
-0,8 |
-0,3 |
-0,4 |
-1,0 |
|
0,2 |
0,2 |
0,2 |
|||
|
30° |
-0,5 |
-0,5 |
-0,2 |
-0,4 |
-0,5 |
|
0,7 |
0,7 |
0,4 |
|||
|
45° |
0,7 |
0,7 |
0,6 |
-0,2 |
-0,3 |
|
60° |
0,7 |
0,7 |
0,7 |
-0,2 |
-0,3 |
|
75° |
0,8 |
0,8 |
0,8 |
-0,2 |
-0,3 |
Таблица Д.3б
|
Уклон b |
F |
С |
Н |
I |
|
0° |
-1,8 |
-1,3 |
-0,7 |
-0,5 |
|
15° |
-1,3 |
-1,3 |
-0,6 |
-0,5 |
|
30° |
-1,1 |
-1,4 |
-0,8 |
-0,5 |
|
45° |
-1,1 |
-1,4 |
-0,9 |
-0,5 |
|
60° |
-1,1 |
-1,2 |
-0,8 |
-0,5 |
|
75° |
-1,1 |
-1,2 |
-0,8 |
-0,5 |
Д.1.3 Прямоугольные в плане здания со сводчатыми и близкими к ним по очертанию покрытиями
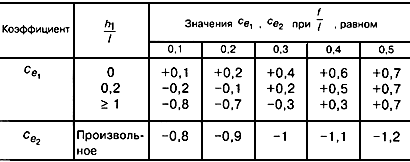
Примечание – При 0,2 £ f/d £ 0,3 и hl/l ³ 0,5 необходимо учитывать два значения коэффициента се1.
Распределение аэродинамических коэффициентов по поверхности покрытия приведено на рисунке Д.5.
Аэродинамические коэффициенты для стен принимаются в соответствии с таблицей Д.2.
При определении эквивалентной высоты (11.1.5) и коэффициента v в соответствии с 11.1.1: h = h1 + 0,7f.
Д.1.4 Круглые в плане здания с купольными покрытиями
Значения коэффициентов се в точках А и С, а также в сечении ВВ приведены на рисунке Д.6. Для промежуточных сечений коэффициенты се определяются линейной интерполяцией.
При определении эквивалентной высоты (11.1.5) и коэффициента v в соответствии с 11.1.1: h = h1 + 0,7f.
Д.1.5 Здания с продольными фонарями
Для участков А и В (рисунок Д.7) коэффициенты се следует определять в соответствии с таблицами Д.3, а и Д.3, б.
Для фонарей участка С при l £ 2 сх = 0,2; при 2 £ l £ 8 для каждого фонаря сх = 0,1l; при l > 8 сх = 0,8, здесь l = a/hf.
Для остальных участков покрытия се = -0,5.
Для вертикальных поверхностей и стен зданий коэффициенты се следует определять в соответствии с таблицей Д.2.
При определении эквивалентной высоты zе (11.1.5) и коэффициента v (11.1.1) h = h1.
Д.1.6 Здания с зенитными фонарями
Для наветренного фонаря коэффициент се следует определять в соответствии с таблицами Д.3, а и Д.3, б.
Для остальных фонарей коэффициенты сх определяются так же, как и для участка С (раздел Д.1.5).
Для остальной части покрытия се = -0,5.
Для вертикальных поверхностей и стен зданий коэффициенты се следует определять в соответствии с таблицей Д.2.
При определении эквивалентной высоты ze (11.1.5) и коэффициента v (11.1.1) h = h1.
Д.1.7 Здания с шедовыми покрытиями
Для участка А коэффициент се следует определять в соответствии с таблицами Д.3, а и Д.3, б.
Для остальной части покрытия се = -0,5.
Для вертикальных поверхностей и стен зданий коэффициенты се следует определять в соответствии с таблицей Д.2.
При определении эквивалентной высоты ze (11.1.5) и коэффициента v (11.1.1) h = h1.
Д.1.8 Здания с уступами
Для участка С коэффициент се = 0,8.
Для участка А коэффициент се следует принимать в соответствии с таблицей Д.2.
Для участка В коэффициент се следует определять линейной интерполяцией.
Для остальных вертикальных поверхностей коэффициент се необходимо определять в соответствии с таблицей Д.2.
Для покрытия зданий коэффициенты се определяются в соответствии с таблицами Д.3, а и Д.3, б.
Д.1.9 Здания, постоянно открытые с одной стороны
При проницаемости ограждения m £ 5 % сi1 = ci2 = ± 0,2. Для каждой стены здания знак «плюс» или «минус» следует выбирать из условия реализации наиболее неблагоприятного варианта нагружения.
При m ≥ 30 % сi1 = -0,5; ci2 = 0,8.
Коэффициент се на внешней поверхности следует принимать в соответствии с таблицей Д.2.
Примечание – Проницаемость ограждения m следует определять как отношение суммарной площади имеющихся в нем проемов к полной площади ограждения.
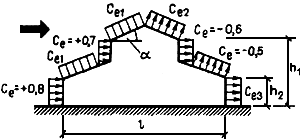
Д.1.10 Навесы
Аэродинамические коэффициенты се для четырех типов навесов (рисунок Д.12) без сплошностенчатых вертикальных ограждающих конструкций определяются по таблице Д.4.
Таблица Д.4
|
Тип схемы |
a, град |
Значения коэффициентов |
|||
|
ce1 |
ce2 |
ce3 |
ce4 |
||
|
I |
10 |
0,5 |
-1,3 |
-1,1 |
0 |
|
20 |
1,1 |
0 |
0 |
-0,4 |
|
|
30 |
2,1 |
0,9 |
0,6 |
0 |
|
|
II |
10 |
0 |
-1,1 |
-1,5 |
0 |
|
20 |
1,5 |
0,5 |
0 |
0 |
|
|
30 |
2 |
0,8 |
0,4 |
0,4 |
|
|
III |
10 |
1,4 |
0,4 |
– |
– |
|
20 |
1,8 |
0,5 |
– |
– |
|
|
30 |
2,2 |
0,6 |
– |
– |
|
|
IV |
10 |
1,3 |
0,2 |
– |
– |
|
20 |
1,4 |
0,3 |
– |
– |
|
|
30 |
1,6 |
0,4 |
– |
– |
|
|
Примечания 1 Коэффициенты се1, се2, се3, се4 соответствуют суммарному давлению на верхнюю и нижнюю поверхности навесов. 2 Для отрицательных значений се1, се2, се3, се4 направление давления на схемах следует изменять на противоположное. 3 Для навесов с волнистыми покрытиями аэродинамический коэффициент трения cf = 0,04. |
Д.1.11 Сфера
Аэродинамические коэффициенты лобового сопротивления сх сферы при zg > d/2 (рисунок Д.13) приведены на рисунке Д.14 в зависимости от числа Рейнольдса Re и относительной шероховатости d = D/d, где D, м, – шероховатость поверхности (см. Д.1.15). При zg < d/2 коэффициент сх следует увеличить в 1,6 раза.
Коэффициент подъемной силы сферы сz принимается равным:
при zg > d/2 – cz = 0;
при zg < d/2 – сz = 0,6.
Опечатка
Эквивалентная высота (11.1.5) ze = zg + d/2.
При определении коэффициента v в соответствии с 11.1.11 следует принимать
b = h = 0,7d.
Число Рейнольдса Re определяется по формуле
где d, м, – диаметр сферы;
w0, Па, – определяется в соответствии с 11.1.4;
ze, м, – эквивалентная высота;
k(ze) – определяется в соответствии с 11.1.6;
- gf
Д.1.12 Сооружения и конструктивные элементы с круговой цилиндрической поверхностью
Аэродинамический коэффициент се1 внешнего давления определяется по формуле
ce1 = kl1cb,
где kl1 = 1 при сb > 0; для сb < 0 – kl1 = kl, определено в Д.1.15.
Распределение коэффициентов сb по поверхности цилиндра при d = D/d < 5×10-4 (см. Д.1.16) приведено на рисунке Д.16 для различных чисел Рейнольдса Re. Значение указанных на этом рисунке углов bmin и bb, а также соответствующее им значение коэффициентов сmin и сb приведены в таблице Д.5.
Значения аэродинамических коэффициентов давления се2 и сi (рисунок Д.14) приведены в таблице Д.6. Коэффициент сi следует учитывать для опущенного покрытия («плавающая кровля»), а также при отсутствии покрытия.
Аэродинамические коэффициенты лобового сопротивления определяются по формуле
cX = klcx¥,
где kl – определено в Д.1 в зависимости от относительного удлинения сооружения (см. Д.1.15). Значения коэффициентов cx¥ приведены на рисунке Д.17 в зависимости от числа Рейнольдса Re и относительной шероховатости D = d/d (см. Д.1.16).
|
Re |
bmin |
cmin |
bb |
cb |
|
5×105 |
85 |
-2,2 |
135 |
-0,4 |
|
2×106 |
80 |
-1,9 |
120 |
-0,7 |
|
107 |
75 |
-1,5 |
105 |
-0,8 |
|
h/d |
1/6 |
1/4 |
1/2 |
1 |
2 |
³ 5 |
|
ce2, ci |
-0,5 |
-0,55 |
-0,7 |
-0,8 |
-0,9 |
-1,05 |
Для проводов и тросов (в том числе покрытых гололедом) сх = 1,2.
Аэродинамические коэффициенты наклонных элементов (рисунок Д.18) определяются по формуле
схb = cхsin2bsin2q.
где сх – определяется в соответствии с данными рисунка Д.17;
ось х параллельна скорости ветра V;
ось z направлена вертикально вверх;
- bXYи осью х;
- qz.
При определении коэффициента v в соответствии с 11.1.1:
b = 0,7d; h = h1 + 0,7f.
Число Рейнольдса Re определяется по формуле, приведенной в Д.1.11, где zе = 0,8h для вертикально расположенных сооружений;
ze равно расстоянию от поверхности земли до оси горизонтально расположенного сооружения.
Д.1.13 Призматические сооружения
Опечатка
Аэродинамические коэффициенты лобового сопротивления призматических сооружений определяются по формуле
cX = klcX¥,
где kl определено в Д.1.15 в зависимости от относительного удлинения сооружения lе.
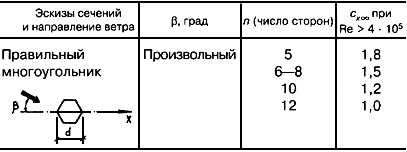
Значения коэффициента cX¥ для прямоугольных сечений приведены на рисунке Д.19, а для n-угольных сечений и конструктивных элементов (профилей) – в таблице Д.7.
|
Эскизы сечений и направлений ветра |
b, град. |
п (число сторон) |
cx¥ при Re > 4×105 |
|
Правильный многоугольник
|
Произвольный |
5 |
1,8 |
|
6 – 8 |
1,5 |
||
|
10 |
1,2 |
||
|
12 |
1,0 |
Аэродинамические коэффициенты решетчатых конструкций отнесены к площади граней пространственных ферм или площади контура плоских ферм.
Направление оси х для плоских ферм совпадает с направлением ветра и перпендикулярно плоскости конструкции; для пространственных ферм расчетные направления ветра показаны в таблице Д.8.
Аэродинамические коэффициенты сх отдельностоящих плоских решетчатых конструкций определяются по формуле
где cxi – аэродинамический коэффициент i-го элемента конструкций, определяемый в соответствии с указаниями Д.1.13 для профилей и Д.1.12, в для трубчатых элементов; при этом kl = 1;
Ai – площадь проекции i-го элемента конструкции;
Аk – площадь, ограниченная контуром конструкции.
Ряд плоских параллельно расположенных решетчатых конструкций
Для наветренной конструкции коэффициент cxl определяется так же, как и для отдельностоящей фермы.
Для второй и последующих конструкций сх2 = сх1h.
Для ферм из профилей из труб при Re <4×105 коэффициент h определяется по таблице Д.8 в зависимости от относительного расстояния между фермами b/h (рисунок Д.19) и коэффициента проницаемости ферм
|
j |
b/h |
||||
|
1/2 |
1 |
2 |
4 |
6 |
|
|
0,1 |
0,93 |
0,99 |
1 |
1 |
1 |
|
0,2 |
0,75 |
0,81 |
0,87 |
0,9 |
0,93 |
|
0,3 |
0,56 |
0,65 |
0,73 |
0,78 |
0,83 |
|
0,4 |
0,38 |
0,48 |
0,59 |
0,65 |
0,72 |
|
0,5 |
0,19 |
0,32 |
0,44 |
0,52 |
0,61 |
|
0,6 |
0 |
0,15 |
0,3 |
0,4 |
0,5 |
Для ферм из труб при Re ³ 4×105 h = 0,95.
Примечание – Число Рейнольдса Re следует определять по формуле в подразделе Д.1.11, где d – средний диаметр трубчатых элементов.
Решетчатые башни и пространственные фермы
Аэродинамические коэффициенты сl решетчатых башен и пространственных ферм определяются по формуле
сl = сх(1 + h)k1,
где сх – определяется так же, как и для отдельностоящей фермы;
- h
Значения коэффициента k1 приведены в таблице Д.9.
|
Форма контура поперечного сечения и направление ветра |
k1 |
|
|
1 |
|
|
0,9 |
|
|
1,2 |
Д.1.15 Учет относительного удлинения
Значения коэффициента kl в зависимости от относительного удлинения lе элемента или сооружения приведены на рисунке Д.23. Относительное удлинение le зависит от параметра l = l/b и определяется по таблице Д.10; степень проницаемости
|
||
|
|
|
|
|
Примечание – l, b – соответственно максимальный и минимальный размеры сооружения или его элемента в плоскости, перпендикулярной направлению ветра. |
Д.1.16 Учет шероховатости внешней поверхности
Значения коэффициента D, характеризующего шероховатость поверхностей конструкций, в зависимости от их обработки и материала, из которого они изготовлены, приведены в таблице Д.11.
|
Тип поверхности |
Относительная шероховатость d, мм |
Тип поверхности |
Относительная шероховатость d, мм |
|
Стекло |
0,0015 |
Оцинкованная сталь |
0,2 |
|
Полированный металл |
0,002 |
Шлифованный бетон |
0,2 |
|
Тонкомолотая масляная краска |
0,006 |
Шероховатый бетон |
1,0 |
|
Распыленная краска |
0,02 |
Ржавчина |
2,0 |
|
Литейный чугун |
0,2 |
Каменная кладка |
3,0 |
Д.1.17 Пиковые значения аэродинамических коэффициентов для прямоугольных в плане зданий
а) Для стен прямоугольных в плане зданий пиковое положительное значение аэродинамического коэффициента ср,+ = 1,2.
б) Пиковые значения отрицательного аэродинамического коэффициента ср,– для стен и плоских покрытий (рисунок Д.24) приведены в таблице Д.12.
|
Участок |
А |
В |
С |
D |
Е |
|
сp,- |
-2,2 |
-1,2 |
-3,4 |
-2,4 |
-1,5 |
Д.2 Резонансное вихревое возбуждение
Д.2.1 Для однопролетных сооружений и конструктивных элементов интенсивность воздействия F(z), действующего при резонансном вихревом возбуждении по i-й собственной форме в направлении, перпендикулярном средней скорости ветра, определяется по формуле
Н/м, (Д.2.1)
где d, м, – размер сооружения или конструктивного элемента в направлении, перпендикулярном средней скорости ветра;
Vcr,i, м/с, – см. 11.3.2;
сy,cr – аэродинамический коэффициент поперечной силы при резонансном вихревом возбуждении;
- d
- dd
z – координата, изменяющаяся вдоль оси сооружения;
ji(z) – i-я форма собственных колебаний в поперечном направлении, удовлетворяющая условию
max[j(z)] = 1. (Д.2.2)
Примечание – Воздействие при резонансном вихревом возбуждении (в первую очередь высотных зданий) рекомендуется уточнить на основе данных модельных аэродинамических испытаний.
Д.2.2 Аэродинамические коэффициенты су поперечной силы определяются следующим образом:
а) Для круглых поперечных сечений су = 0,3.
б) Для прямоугольных поперечных сечений при b/d > 0,5:
cy = 1,1 для Vcr,i/Vmax(zэк) < 0,8;
су = 0,6 для Vcr,i/Vmax(zэк) ³ 0,8,
здесь b – размер сооружения в направлении средней скорости ветра.
При b/d £ 0,5 расчет на резонансное вихревое возбуждение допускается не проводить.
Д.2.3 При расчете сооружения на резонансное вихревое возбуждение наряду с воздействием (Д.2.1) необходимо учитывать также действие ветровой нагрузки, параллельной средней скорости ветра. Средняя wm,cr и пульсационная wp,cr составляющие этого воздействия определяются по формулам:
wm,cr = (Vcr/Vmax)2wm; wp,cr = (Vcr/Vmax)2wp, (Д.2.3)
где Vmax – расчетная скорость ветра на высоте zэк, на которой происходит резонансное вихревое возбуждение, определяемое по формуле (11.13);
wm и wp – расчетные значения средней и пульсационной составляющих ветровой нагрузки, определяемые в соответствии с указаниями 11.1.
Д.2.4 Критические скорости Vcr,i могут иметь достаточно большую повторяемость в течение расчетного срока эксплуатации сооружения и, в связи с этим, резонансное вихревое возбуждение может привести к накоплению усталостных повреждений.
Для предотвращения резонансного вихревого возбуждения могут быть использованы различные конструктивные мероприятия: установка вертикальных и спиралевидных ребер, перфорация ограждения и установка соответствующим образом настроенных гасителей колебаний.
#G0Но-
мер схе-
мы
Схемы зданий,
сооружений, элементов конструкций и
ветровых нагрузок
Определение
аэродинамических коэффициентов
Примечания
1
Отдельно стоящие плоские сплошные
конструкции.
Вертикальные и отклоняющиеся от
вертикальных не более чем на 15°
поверхности:
–
наветренные
=+0,8
подветренные
=-0,6
2
Здания
с двускатными покрытиями
1. При ветре, перпендикулярном
торцу зданий, для всей поверхности
покрытия
=-0,7.
2. При определении
коэффициента
в соответствии с п.6.9
3
Здания со сводчатыми и близкими к ним
по очертанию покрытиями
Значение
принимается по схеме 2
1. См. примеч.1 к схеме 2.
2.
При определении коэффициента
в соответствии с п.6.9
4
Здания
с продольным фонарем
Коэффициенты
,
и
следует определять в соответствии с
указаниями к схеме 2
1. При расчете поперечных рам зданий
с фонарем и ветроотбойными щитами
значение суммарного коэффициента
лобового сопротивления системы
“фонарь-щиты” принимается равным
1,4.
2. При определении
коэффициента
в соответствии с п.6.9
5
Здания
с продольными фонарями
Для покрытия здания на
участке
коэффициенты
следует принимать по схеме 4.
Для фонарей участка
при
;
при
для каждого фонаря
;
при
,
здесь
.
Для
остальных участков покрытия
=-0,5
1. Для наветренной, подветренной и
боковых стен зданий коэффициенты
давления следует определять в
соответствии с указаниями к схеме 2.
2. При определении
коэффициента
в соответствии с п.6.9
6
Здания с продольными фонарями различной
высоты
Коэффициенты
,
и
следует определять в соответствии с
указаниями к схеме 2, где при определении
за
необходимо принимать высоту наветренной
стены здания.
Для участка
следует определять так же, как для
участка
схемы 5, где за
необходимо принимать высоту фонаря
См. примеч.1
и 2 к схеме 5
7
Здания
с шедовыми покрытиями
Для
участка
следует определять в соответствии с
указаниями к схеме 2.
Для
участка
=-0,5#S
1. Силу трения необходимо
учитывать при произвольном направлении
ветра, при этом
=0,04.
2. См. примеч.1 и 2 к схеме 5
8
Здания
с зенитными фонарями
Для наветренного фонаря
коэффициент
следует определять в соответствии с
указаниями к схеме 2, для остальной
части покрытия – как для участка
схемы 5
См. примеч.1
и 2 к схеме 5
9
Здания,
постоянно открытые с одной стороны
При
%
;
при
%
следует принимать равным
,
определенному в соответствии с
указаниями к схеме 2;
1. Коэффициенты
на внешней поверхности следует
принимать в соответствии с указаниями
к схеме 2.
2. Проницаемость ограждения
следует определять как отношение
суммарной площади имеющихся в нем
проемов к полной площади ограждения.
Для герметичного здания следует
принимать
В зданиях, указанных в п.6.1, в, нормативное
значение внутреннего давления на
легкие перегородки (при их поверхностной
плотности менее 100 кг/м
)
следует принимать равным 0,2
,
но не менее 0,1 кПа (10 кгс/м
).
3. Для каждой стены здания
знак “плюс” или “минус” для
коэффициента
при
%
следует определять исходя из условия
реализации наиболее неблагоприятного
варианта нагружения
10
Уступы
зданий при
Для участка
=0,7.
Для участка
следует определять линейной
интерполяцией значений, принимаемых
в точках
и
.
Коэффициенты
и
на участке
следует принимать в соответствии с
указаниями к схеме 2 (где
и
– размеры в плане всего здания).
Для вертикальных
поверхностей коэффициент
необходимо определять в соответствии
с указаниями к схемам 1 и 2
–
11
Навесы
1. Коэффициенты
,
,
,
следует относить к сумме давлений на
верхнюю и нижнюю поверхности навесов.
Для отрицательных значений
,
,
,
направление давления на схемах следует
изменять на противоположное.
2. Для навесов с волнистыми
покрытиями
=0,04
12а
Сфера
Продолжение
=1,3 при
=0,6 ”
=0,2 ”
где
– число Рейнольдса;
– диаметр сферы, м;
– определяется в
соответствии с п.6.4, Па;
– определяется в
соответствии с п.6.5;
– расстояние, м, от
поверхности земли до центра сферы;
– определяется в
соответствии с п.6.11
1. Коэффициенты
приведены при
.
2. При определении
коэффициента
в соответствии с п.6.9 следует принимать
12б
Сооружения с круговой цилиндрической
поверхностью
где
=1 при
>0;
необходимо принимать
при
по графику:
1.
следует определять по формуле к схеме
12 а, принимая
.
2. При определении
коэффициента
в соответствии с п.6.9 следует принимать:
3. Коэффициент
следует учитывать при опущенном
покрытии (“плавающая кровля”), а
также при отсутствии его
13
Призматические сооружения
Таблица 1
необходимо определять по табл.2.
Таблица 2
В табл.2
,
где
,
– соответственно максимальный и
минимальный размеры сооружения или
его элемента в плоскости, перпендикулярной
направлению ветра.
Таблица 3
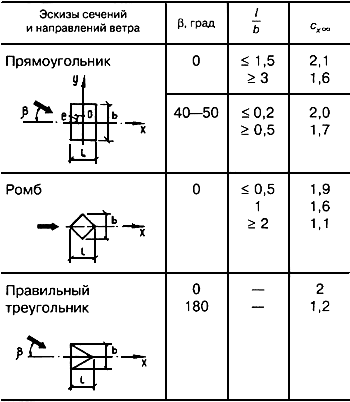
Таблица 4
1. Для стен с лоджиями при
ветре, параллельном этим стенам
=0,1; для волнистых покрытий
=0,04.
2. Для прямоугольных в плане зданий
при
=0,1-0,5 и
=40°-50°
=0,75;
равнодействующая ветровой нагрузки
приложена в точке 0, при этом
эксцентриситет
3.
следует определять по формуле к схеме
12а, принимая
,
– диаметр описанной окружности.
4. При определении
коэффициента
в соответствии с п.6.9
– высота сооружения,
– размер в плане по оси
14
Сооружения и их элементы с круговой
цилиндрической поверхностью
(резервуары, градирни, башни, дымовые
трубы), провода и тросы, а также круглые
трубчатые и сплошные элементы сквозных
сооружений
где
– определяется по табл.1 схемы 13;
– определяется по
графику:
Для
проводов и тросов (в том числе и
покрытых гололедом)
1.
следует определять по формуле к схеме
12а, принимая
,
– диаметр сооружения.
Значения
принимаются: для деревянных конструкций
=0,005 м; для кирпичной кладки
=0,01 м; для бетонных и железобетонных
конструкций
=0,005 м; для стальных конструкций
=0,001 м; для проводов и тросов диаметром
; для ребристых поверхностей с ребрами
высотой
.
2. Для волнистых покрытий
=0,04.
3. Для проводов и тросов
20
мм, свободных от гололеда, значение
допускается снижать на 10%
15
Отдельно стоящие плоские решетчатые
конструкции
,
где
– аэродинамический коэффициент i-го
элемента конструкций; для профилей
=1,4; для трубчатых элементов
следует определять по графику к схеме
14, при этом необходимо принимать
(см. табл.2 схемы 13);
–
площадь проекции i-го элемента на
плоскость конструкции;
–
площадь, ограниченная контуром
конструкции
1. Аэродинамические коэффициенты к
схемам 15-17 приведены для решетчатых
конструкций с произвольной формой
контура и
2. Ветровую нагрузку
следует относить к площади, ограниченной
контуром
.
3. Направление оси
совпадает с направлением ветра и
перпендикулярно плоскости конструкции
16
Ряд плоских параллельно расположенных
решетчатых конструкций
Для
наветренной конструкции коэффициент
определяется так же, как для схемы
15.
Для
второй и последующих конструкций
.
Для
ферм из труб при
=
0,95.
1. См.примеч.1-3 к схеме 15.
2.
следует определять по формуле к схеме
12а, где
– средний диаметр трубчатых элементов;
– допускается принимать равным
расстоянию от поверхности земли до
верхнего пояса фермы.
3. В таблице к схеме 16:
– минимальный размер
контура; для прямоугольных и
трапециевидных ферм
– длина наименьшей стороны контура;
для круглых решетчатых конструкций
– их диаметр; для эллиптических и
близких к ним по очертанию конструкций
– длина меньшей оси;
– расстояние между соседними фермами.
4. Коэффициент
следует определять в соответствии с
указаниями к схеме 15.
17
Решетчатые
башни и пространственные фермы
где
– определяется так же, как для схемы
15;
– определяется так
же, как для схемы 16.
1. См. примеч.1 к схеме 15.
2.
относится
к площади контура наветренной грани.
3. При направлении ветра
по диагонали четырехгранных квадратных
башен коэффициент
для стальных башен из одиночных
элементов следует уменьшать на 10%;
для деревянных башен из составных
элементов – увеличивать на 10%
18
Ванты и наклонные трубчатые элементы,
расположенные в плоскости потока
где
– определяется в соответствии с
указаниями к схеме 14
–
В.1 Аэродинамические коэффициенты
В.1.1 Отдельно стоящие плоские сплошные конструкции
(стены, заборы и т.д.)
Для различных участков конструкций (рисунок В.1) коэффициент cx определяется по таблице В.1;
ze = h.
Рисунок В.1
Таблица В.1
|
Участки плоских сплошных конструкций на земле (см. рисунок В.1) |
|||
|
A |
B |
C |
D |
|
2,1 |
1,8 |
1,4 |
1,2 |
Рекламные щиты
Для рекламных щитов, поднятых над землей на высоту не менее d/4 (рисунок В.2):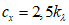 
, где 
– определено в В.1.15.
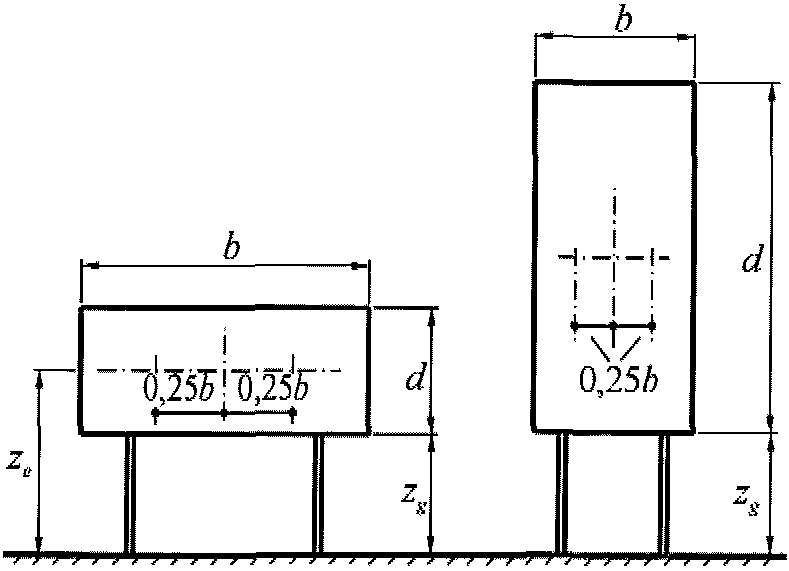
Рисунок В.2
Равнодействующую нагрузку, направленную по нормали к плоскости щита, следует прикладывать на высоте его геометрического центра с эксцентриситетом в горизонтальном направлении e = +/- 0,25b.
ze = zg + d/2.
В.1.2 Прямоугольные в плане здания с двускатными покрытиями
Вертикальные стены прямоугольных в плане зданий
Таблица В.2
|
Боковые стены |
Наветренная стена |
Подветренная стена |
||
|
Участки |
||||
|
A |
B |
C |
D |
E |
|
-1,0 |
-0,8 |
-0,5 |
0,8 |
-0,5 |
Для наветренных, подветренных и различных участков боковых стен (рисунок В.3) аэродинамические коэффициенты ce приведены в таблице В.2. Для стен с отрицательным уклоном при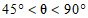 
(см. рисунок В.3) аэродинамические коэффициенты определяются так же, как и для вертикальных стен.
Для боковых стен с выступающими лоджиями аэродинамический коэффициент трения cf = 0,1.
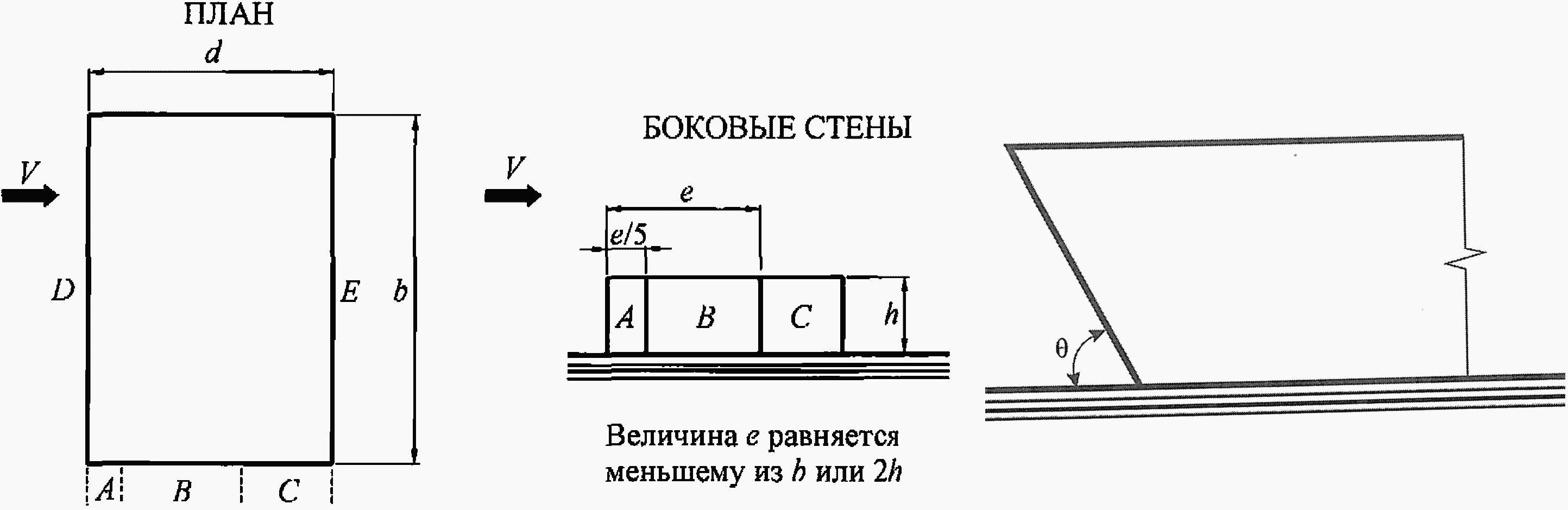
Рисунок В.3
Двускатные покрытия
Для различных участков покрытия (рисунок В.4) коэффициент ce определяется по таблице В.3а и В.3б в зависимости от направления средней скорости ветра.
Для углов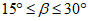 
при 
необходимо рассмотреть два варианта распределения расчетной ветровой нагрузки.
Для протяженных гладких покрытий при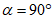 
(рисунок В.4, б) аэродинамические коэффициенты трения cf = 0,02.
а)
б)
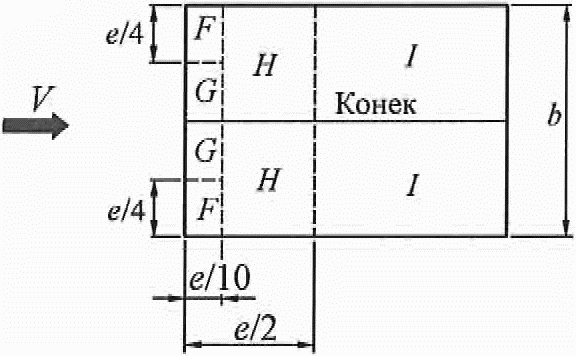
Рисунок В.4
Таблица В.3а
|
Уклон |
F |
G |
H |
I |
J |
|
0° |
-1,8 |
-1,3 |
-0,7 |
-0,5 |
-0,5 |
|
15° |
-0,9 |
-0,8 |
-0,3 |
-0,4 |
-1,0 |
|
0,2 |
0,2 |
0,2 |
|||
|
30° |
-0,5 |
-0,5 |
-0,2 |
-0,4 |
-0,5 |
|
0,7 |
0,7 |
0,4 |
|||
|
45° |
0,7 |
0,7 |
0,6 |
-0,2 |
-0,3 |
|
60° |
0,7 |
0,7 |
0,7 |
-0,2 |
-0,3 |
|
75° |
0,8 |
0,8 |
0,8 |
-0,2 |
-0,3 |
Таблица В.3б
|
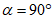
Уклон |
F |
G |
H |
I |
|
0° |
-1,8 |
-1,3 |
-0,7 |
-0,5 |
|
15° |
-1,3 |
-1,3 |
-0,6 |
-0,5 |
|
30° |
-1,1 |
-1,4 |
-0,8 |
-0,5 |
|
45° |
-1,1 |
-1,4 |
-0,9 |
-0,5 |
|
60° |
-1,1 |
-1,2 |
-0,8 |
-0,5 |
|
75° |
-1,1 |
-1,2 |
-0,8 |
-0,5 |
В.1.3 Прямоугольные в плане здания со сводчатыми
и близкими к ним по очертанию покрытиями
Примечание – При 0,2 <= f/l <= 0,3 и h1/l >= 0,5 необходимо учитывать два значения коэффициента ce1.
Рисунок В.5
Распределение аэродинамических коэффициентов ce по поверхности покрытия приведено на рисунке В.5.
Аэродинамические коэффициенты ce для стен принимаются в соответствии с таблицей В.2.
При определении эквивалентной высоты ze, см. 11.1.5 и коэффициента 
в соответствии с 11.1.11: h = h1 + 0,7f.
В.1.4 Круглые в плане сооружения
с купольными и коническими покрытиями
а) Для купольных покрытий значения коэффициентов ce принимают постоянными вдоль сечений, параллельных B-B. Их значения в точках A и C, а также в сечении B-B, приведены на рисунке В.6, а. Для промежуточных сечений коэффициенты ce определяют линейной интерполяцией.
б) Для конических покрытий значения аэродинамических коэффициентов внешнего давления ce при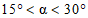 
определяются (см. рисунок В.6, б) следующим образом:
– для участка A коэффициент ce = -1,5;
– для участка B коэффициент ce = -1,0;
– для участка C коэффициент ce = -1,1;
– для участка D коэффициент ce = -2,0;
– для участка E коэффициент ce = -0,7;
– для купольных и конических покрытий при определении эквивалентной высоты ze в соответствии с 11.1.5 и коэффициента v в соответствии с 11.1.11 h = h1 + 0,7f.
Рисунок В.6
В.1.5 Здания с продольными
фонарями и здания переменной высоты
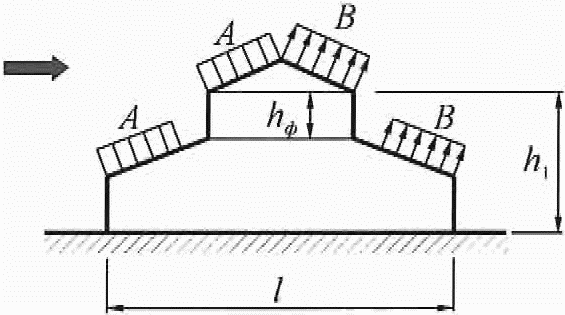
а)
б)
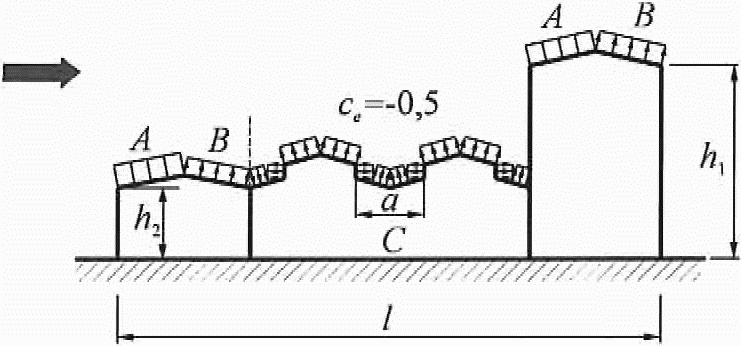
Рисунок В.7
Для участков A и B (рисунок В.7) коэффициенты ce следует определять в соответствии с таблицами В.3а и В.3б.
Для фонарей участка C при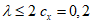 
; при 
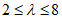для каждого фонаря 
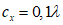; при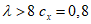 
, здесь 
.
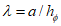Для остальным участков покрытия ce = -0,5.
Для вертикальных поверхностей и стен зданий коэффициенты ce следует определять в соответствии с таблицей В.2.
При определении эквивалентной высоты ze, см. 11.1.5 и коэффициента в соответствии с 11.1.11: h = h1.
В.1.6 Здания с зенитными фонарями
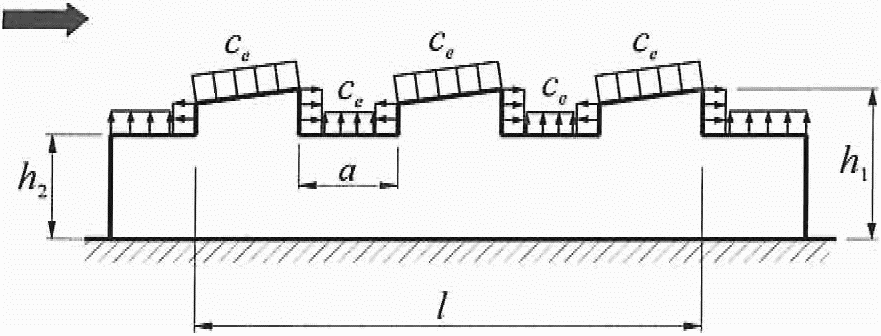
Рисунок В.8
Для наветренного фонаря коэффициент ce следует определять в соответствии с таблицами В.3а и В.3б.
Для остальных фонарей коэффициенты cx определяются так же, как и для участка C (раздел В.1.5).
Для остальной части покрытия ce = -0,5.
Для вертикальных поверхностей и стен зданий коэффициенты ce следует определять в соответствии с таблицей В.2.
При определении эквивалентной высоты ze, см. 11.1.5 и коэффициента в соответствии с 11.1.11 h = h1.
В.1.7 Здания с шедовыми покрытиями
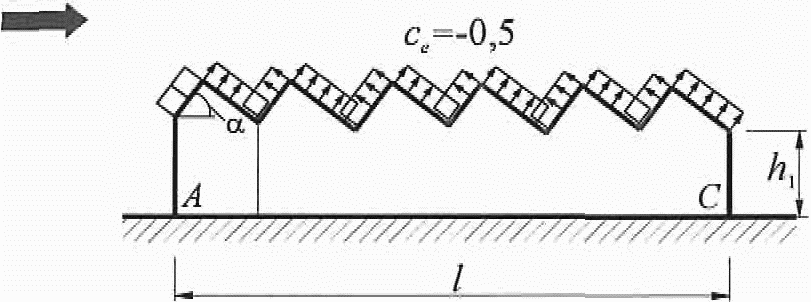
Рисунок В.9
Для участка A коэффициент ce следует определять в соответствии с таблицами В.3а и В.3б. Для остальной части покрытия ce = -0,5.
Для вертикальных поверхностей и стен зданий коэффициенты ce следует определять в соответствии с таблицей В.2.
При определении эквивалентной высоты ze (11.1.5) и коэффициента (11.1.11) h = h1.
Для шедовых покрытий аэродинамический коэффициент трения cf = 0,04.
В.1.8 Здания с уступами
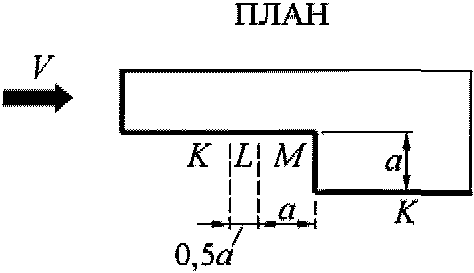
Рисунок В.10
Для участка M коэффициент ce = 0,8.
Для участка K коэффициенты ce следует принимать в соответствии с таблицей В.2.
Для участка L коэффициент ce следует определять линейной интерполяцией.
Для остальных вертикальных поверхностей коэффициент ce необходимо определять в соответствии с таблицей В.2.
Для покрытия зданий коэффициенты ce определяются в соответствии с таблицами В.3а и В.3б.
В.1.9 Учет внутреннего давления
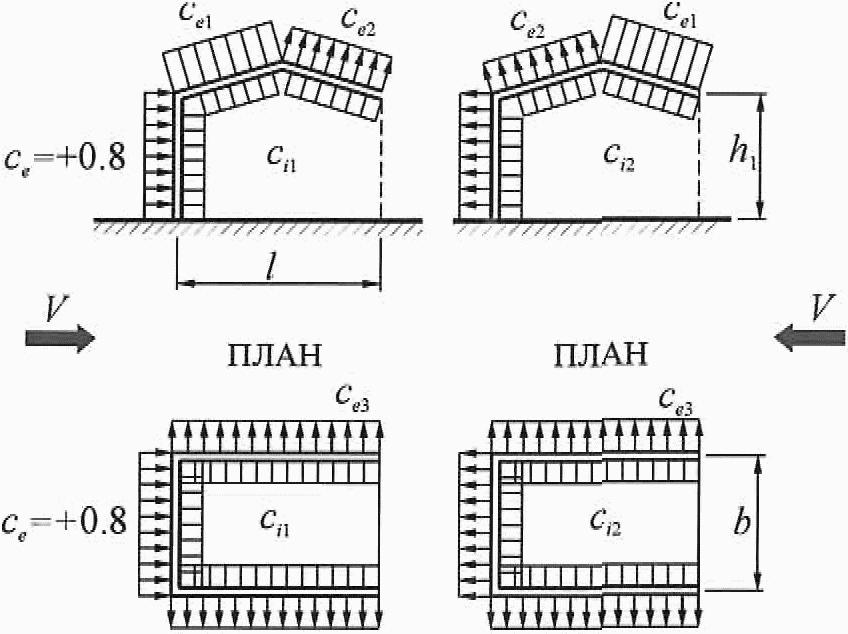
Рисунок В.11
При проницаемости ограждения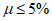 
ci1 = ci2 = +/- 0,2. Для каждой стены здания знак “плюс” или “минус” следует выбирать из условия реализации наиболее неблагоприятного варианта нагружения.
При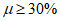 
ci1 = -0,5; ci2 = 0,8.
Аэродинамические коэффициенты для внешней поверхности следует принимать в соответствии с В.1.2 – В.1.7.
Примечание – Проницаемость ограждения 
следует определять как отношение суммарной площади имеющихся в нем проемов к полной площади ограждения.
В.1.10 Навесы
Аэродинамические коэффициенты cp для четырех типов навесов (рисунок В.12) без сплошностенчатых вертикальных ограждающих конструкций определяются по таблице В.4.
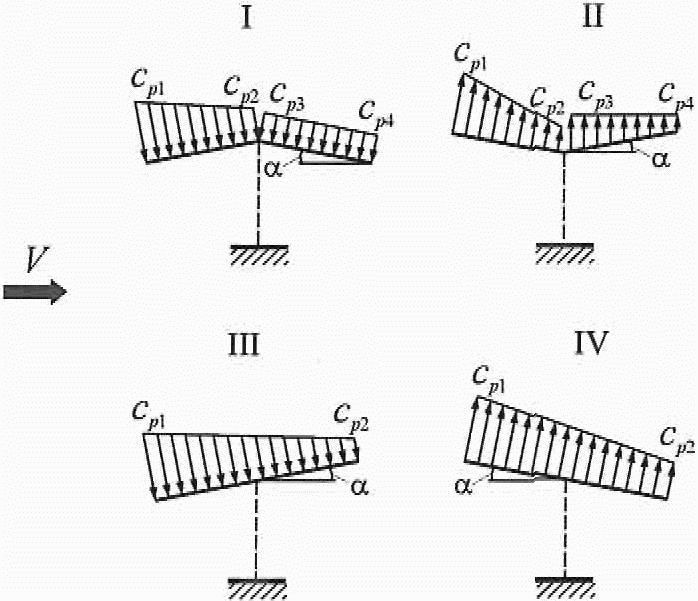
Рисунок В.12
Таблица В.4
|
Тип схемы |
|
Значения коэффициентов |
|||
|
cp1 |
cp2 |
cp3 |
cp4 |
||
|
I |
10 |
0,5 |
-1,3 |
-1,1 |
0 |
|
20 |
1,1 |
0 |
0 |
-0,4 |
|
|
30 |
2,1 |
0,9 |
0,6 |
0 |
|
|
II |
10 |
0 |
-1,1 |
-1,5 |
0 |
|
20 |
1,5 |
0,5 |
0 |
0 |
|
|
30 |
2 |
0,8 |
0,4 |
0,4 |
|
|
III |
10 |
1,4 |
0,4 |
– |
– |
|
20 |
1,8 |
0,5 |
– |
– |
|
|
30 |
2,2 |
0,6 |
– |
– |
|
|
IV |
10 |
1,3 |
0,2 |
– |
– |
|
20 |
1,4 |
0,3 |
– |
– |
|
|
30 |
1,6 |
0,4 |
– |
– |
|
|
Примечания 1 Коэффициенты cp1, cp2, cp3, cp4 соответствуют суммарному давлению на верхнюю и нижнюю поверхности навесов. 2 Для отрицательных значений cp1, cp2, cp3, cp4 направление давления на схемах следует изменять на противоположное. 3 Для навесов с волнистыми покрытиями аэродинамический коэффициент трения cf = 0,04. 4 Для горизонтально расположенных навесов необходимо рассмотреть два варианта нагружения, соответствующих схемам III и IV при |
, град
.В.1.11 Сфера
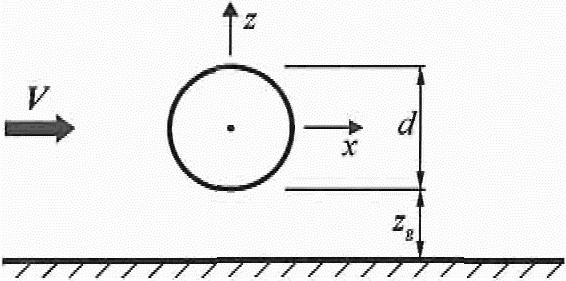
Рисунок В.13
Аэродинамические коэффициенты лобового сопротивления cx сферы при zg > d/2 (рисунок В.13) приведены на рисунке В.14 в зависимости от числа Рейнольдса Re и относительной шероховатости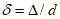 
, где 
, м, – шероховатость поверхности (см. В.1.16). При zg < d/2 коэффициент cx следует увеличить в 1,6 раза.
Коэффициент подъемной силы сферы cz принимается равным:
при zg > d/2 – cz = 0;
при zg < d/2 – cz = 0,6.
Эквивалентная высота, см. 11.1.5 ze = zg + d/2.
При определении коэффициента в соответствии с 11.1.11 следует принимать
b = h = 0,7d.
Число Рейнольдса Re определяется по формуле
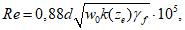(В.1)
где d, м, – диаметр сферы;
w0, Па, – определяется в соответствии с 11.1.4;
ze, м, – эквивалентная высота;
k(ze) – определяется в соответствии с 11.1.6;
– коэффициент надежности по нагрузке (см. преамбулу к разделу 11).
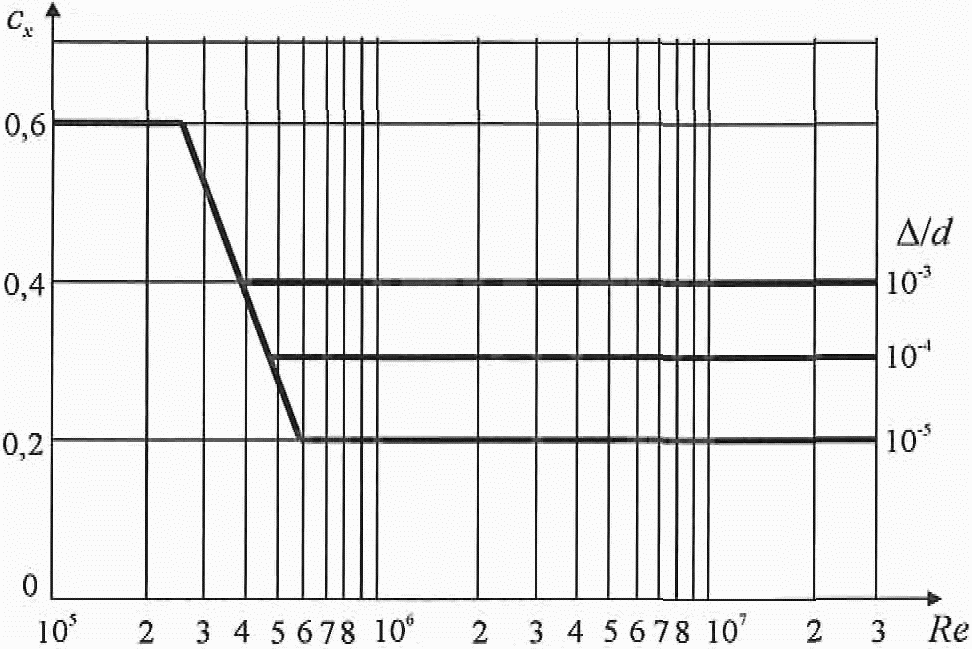
Рисунок В.14
В.1.12 Сооружения и конструктивные элементы с круговой
цилиндрической поверхностью
Аэродинамический коэффициент ce1 внешнего давления определяется по формуле
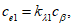(В.2)
где 
при 
; для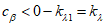 
, определено в В.1.15.
Распределение коэффициентов 
по поверхности цилиндра при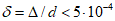 
(см. В.1.16) приведены на рисунке В.16 для различных чисел Рейнольдса Re. Значение указанных на этом рисунке углов 
и 
, а также соответствующее им значение коэффициентов cmin и ch приведены в таблице В.5.
Значения аэродинамических коэффициентов давления ce2 и ci (рисунок В.15) приведены в таблице В.6. Коэффициент ci следует учитывать для опущенного покрытия (“плавающая кровля”), а также при отсутствии покрытия.
Аэродинамические коэффициенты лобового сопротивления cx определяются по формуле
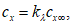(В.3)
где – определено в В.1 в зависимости от относительного удлинения сооружения (см. В.1.15). Значения коэффициентов 
приведены на рисунке В.17 в зависимости от числа Рейнольдса Re и относительной шероховатости 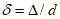(см. В.1.16); для цилиндрических сооружений с ребрами – высота ребра.
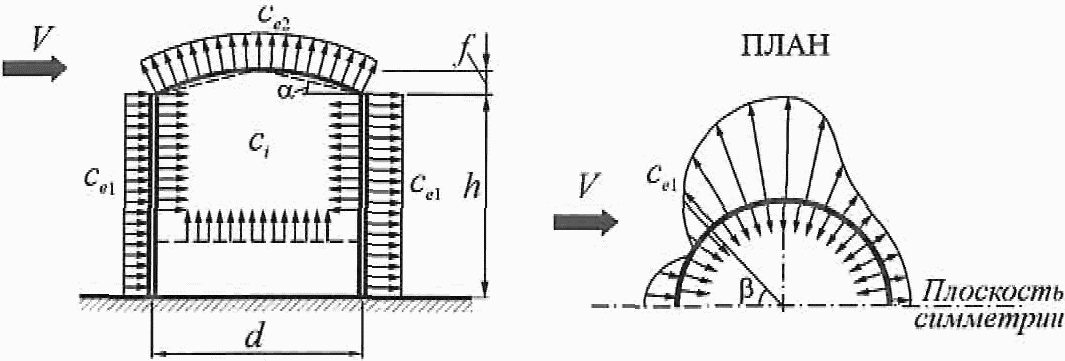
Рисунок В.15
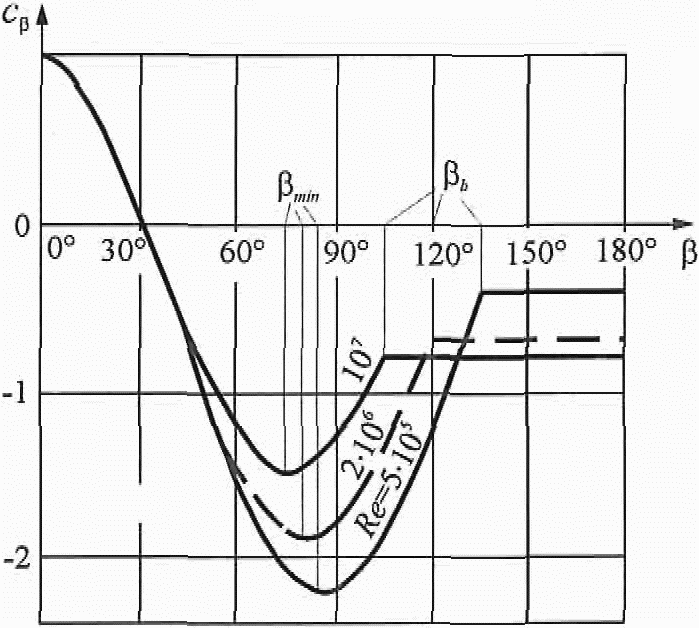
Рисунок В.16
Таблица В.5
|
Re |
|
cmin |
|
cb |
|
5·105 |
85 |
-2,2 |
135 |
-0,4 |
|
2·106 |
80 |
-1,9 |
120 |
-0,7 |
|
107 |
75 |
-1,5 |
105 |
-0,8 |
Таблица В.6
|
h/d |
1/6 |
1/4 |
1/2 |
1 |
2 |
>= 5 |
|
ce2, ci |
-0,5 |
-0,55 |
-0,7 |
-0,8 |
-0,9 |
-1,05 |
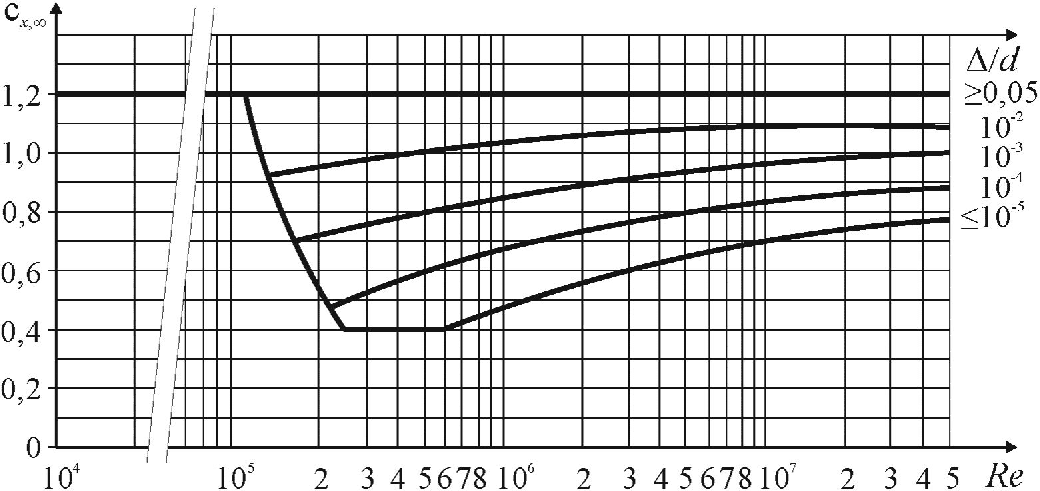
Рисунок В.17
Для проводов и тросов (в том числе покрытых гололедом) cx = 1,2.
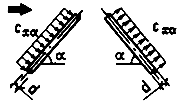
Аэродинамические коэффициенты лобового сопротивления наклонных элементов (рисунок В.18) определяются по формуле
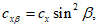(В.4)
где cx – определяется в соответствии с данными В.1.12, В.1.13 и В.1.14;
– угол между осью элемента и скоростью ветра V, направленной вдоль оси x.
Рисунок В.18
При определении коэффициента в соответствии с 11.1.11:
b = 0,7d; h = h1 + 0,7f.
Число Рейнольдса Re определяется по формуле, приведенной в В.1.11, где ze = 0,8h для вертикально расположенных сооружений;
ze равно расстоянию от поверхности земли до оси горизонтально расположенного сооружения.
В.1.13 Призматические сооружения и конструктивные элементы
Аэродинамические коэффициенты лобового сопротивления призматических сооружений определяются по формуле
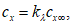(В.5)
где определено в В.1.15 в зависимости от относительного удлинения сооружения 
.
Значения коэффициента для прямоугольных сечений приведены на рисунке В.19, а для n-угольных сечений и конструктивных элементов (профилей) – в таблице В.7.
Аэродинамические коэффициенты лобового сопротивления для конструкционных профилей принимаются равными 1,4 (cx = 1,4).
Таблица В.7
|
Эскизы сечений и направлений ветра |
|
n (число сторон) |
Re > 4·105 |
|
Правильный многоугольник
|
Произвольный |
5 |
1,8 |
|
6 – 8 |
1,5 |
||
|
10 |
1,2 |
||
|
12 |
1,0 |
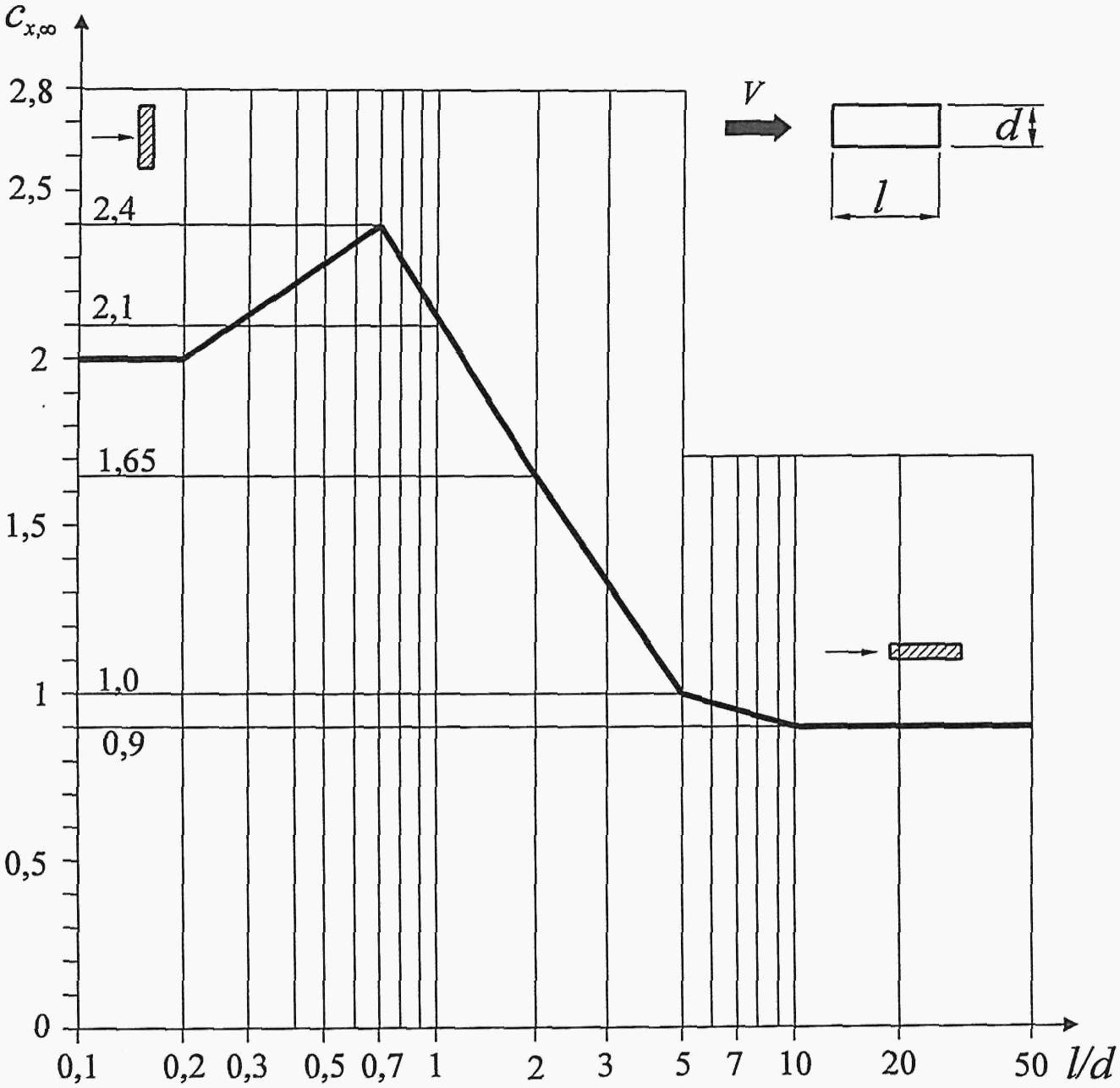
Рисунок В.19
В.1.14 Решетчатые конструкции
Аэродинамические коэффициенты решетчатых конструкций отнесены к площади граней пространственных ферм или площади контура плоских ферм.
Направление оси x для плоских ферм совпадает с направлением ветра и перпендикулярно плоскости конструкции; для пространственных ферм расчетные направления ветра показаны в таблице В.8.
Аэродинамические коэффициенты cx отдельно стоящих плоских решетчатых конструкций определяются по формуле
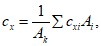(В.6)
где cxi – аэродинамический коэффициент i-го элемента конструкции, принимаемый равным 1,4 (cxi = 1,4) для профилей и определяемый в соответствии с указаниями В.1.12 и В.1.13 для элементов с круглым и прямоугольным поперечными сечениями, соответственно; при этом 
;
Ai – площадь проекции i-го элемента конструкции;
Ak – площадь, ограниченная контуром конструкции.
Рисунок В.20
Ряд плоских параллельно расположенных
решетчатых конструкций
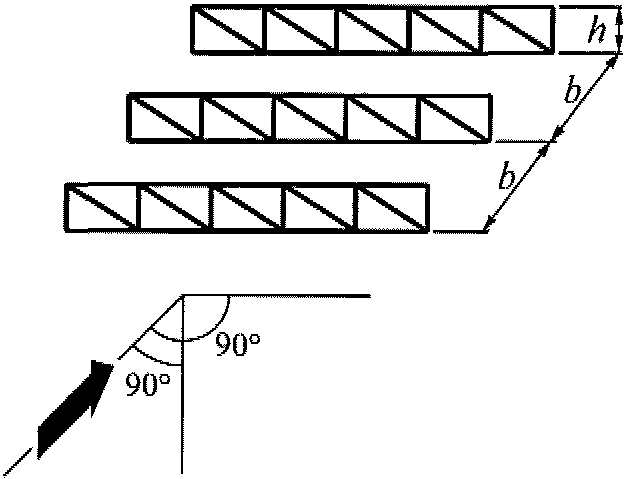
Рисунок В.21
Для наветренной конструкции коэффициент cx1 определяется так же, как и для отдельно стоящей фермы.
Для второй и последующих конструкций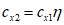 
.
Для ферм из профилей из труб при Re < 4·105 коэффициент 
определяется по таблице В.8 в зависимости от относительного расстояния между фермами b/h (рисунок В.19) и коэффициента заполнения ферм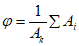 
.
Таблица В.8
|
|
b/h |
||||
|
1/2 |
1 |
2 |
4 |
6 |
|
|
0,1 |
0,93 |
0,99 |
1 |
1 |
1 |
|
0,2 |
0,75 |
0,81 |
0,87 |
0,9 |
0,93 |
|
0,3 |
0,56 |
0,65 |
0,73 |
0,78 |
0,83 |
|
0,4 |
0,38 |
0,48 |
0,59 |
0,65 |
0,72 |
|
0,5 |
0,19 |
0,32 |
0,44 |
0,52 |
0,61 |
|
>= 0,6 |
0 |
0,15 |
0,3 |
0,4 |
0,5 |
Для ферм из труб при Re >= 4·105 коэффициент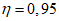 
.
Примечание – Число Рейнольдса Re следует определять по формуле в В.1.11, где d – средний диаметр трубчатых элементов.
Решетчатые башни и пространственные фермы
Рисунок В.22
Аэродинамические коэффициенты ct решетчатых башен и пространственных ферм определяются по формуле
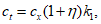(В.7)
где cx – определяется так же, как и для отдельно стоящей фермы;
– определяется так же, как и для ряда плоских ферм.
Значения коэффициента k1 приведены в таблице В.9.
Таблица В.9
|
Форма контура поперечного сечения и направление ветра |
k1 |
|
|
1 |
|
|
0,9 |
|
|
1,2 |
В.1.15 Учет относительного удлинения
Значения коэффициента в зависимости от относительного удлинения элемента или сооружения приведены на рисунке В.23. Относительное удлинение зависит от параметра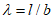 
и определяется по таблице В.10; степень заполнения .
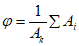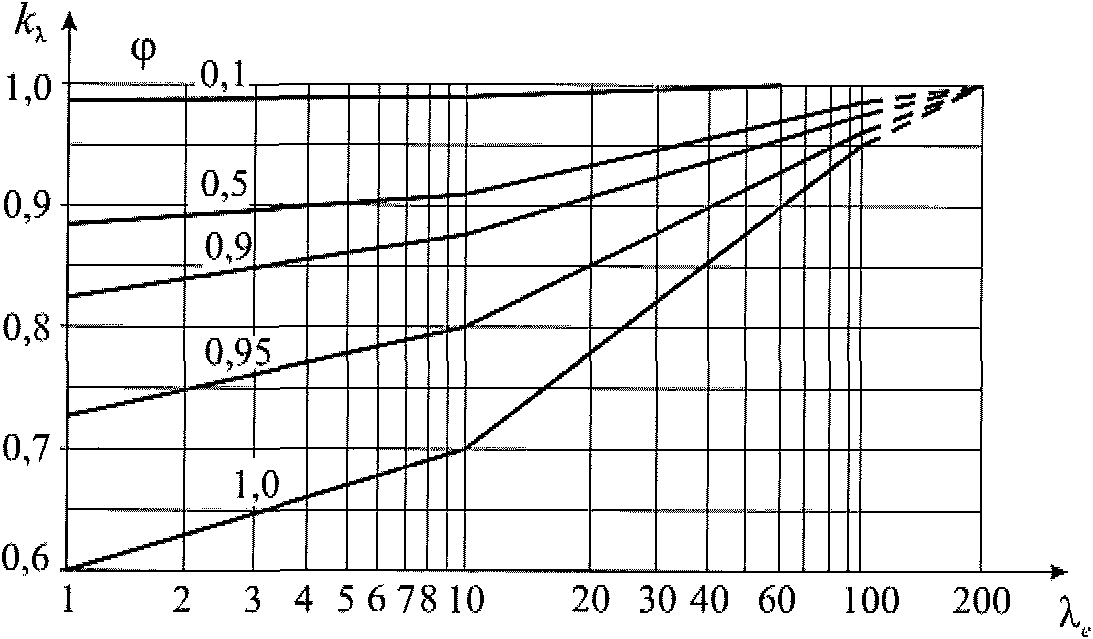
Рисунок В.23
Таблица В.10
|
|
|
|
|
|
|
|
|
|
|
Примечание – l, b – соответственно максимальный и минимальный размеры сооружения или его элемента в плоскости, перпендикулярной направлению ветра. |
В.1.16 Учет шероховатости внешней поверхности
Шероховатость поверхностей конструкций, в зависимости от их обработки и материала, из которого они изготовлены, приведены в таблице В.11.
Таблица В.11
|
Тип поверхности |
Шероховатость |
Тип поверхности |
Шероховатость |
|
Стекло |
1,5·10-6 |
Оцинкованная сталь |
2·10-4 |
|
Полированный металл |
2·10-6 |
Шлифованный бетон |
2·10-4 |
|
Тонкомолотая масляная краска |
6·10-6 |
Шероховатый бетон |
10-3 |
|
Распыленная краска |
2·10-5 |
Ржавчина |
2·10-3 |
|
Литейный чугун |
2·10-4 |
Каменная, кирпичная кладка |
3·10-3 |
, мВ.1.17 Пиковые значения аэродинамических коэффициентов
для прямоугольных в плане зданий
а) Для стен прямоугольных в плане зданий пиковое положительное значение аэродинамического коэффициента cp,+ = 1,2.
б) Пиковые значения отрицательного аэродинамического коэффициента cp,- для стен и плоских покрытий (рисунок В.24) приведены в таблице В.12.
Таблица В.12
|
Участок |
A |
B |
C |
D |
E |
|
cp,- |
-2,2 |
-1,2 |
-3,4 |
-2,4 |
-1,5 |
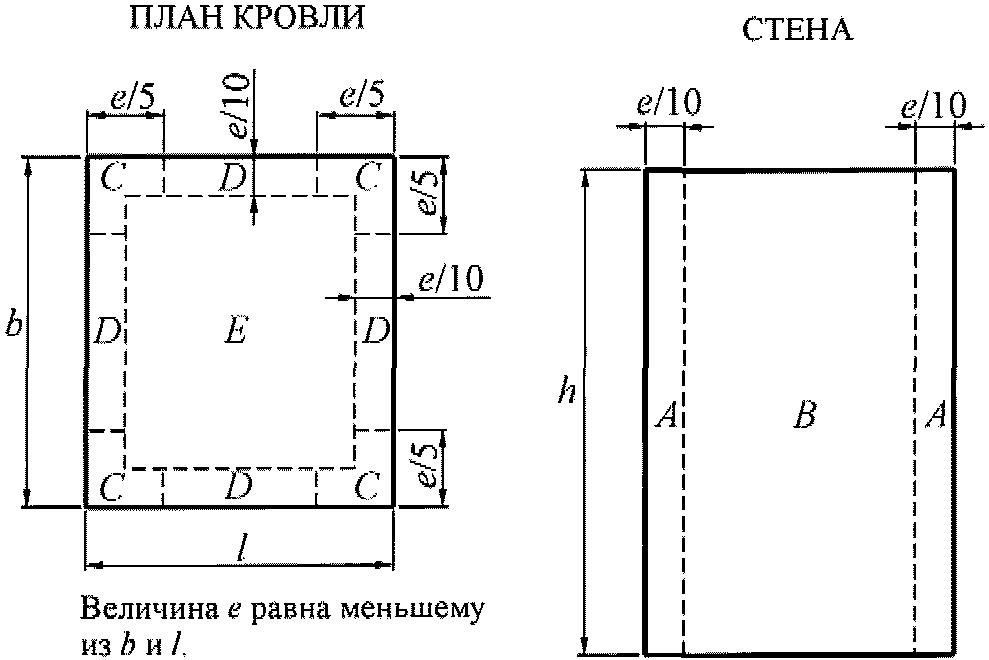
Рисунок В.24
Скачать документ целиком в формате PDF
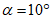