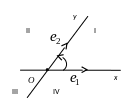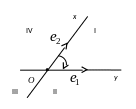Как найти аффинные координаты

Как найти аффинные координаты

Аффинные координаты

Аффинная система координат на прямой, на плоскости, в пространстве

Пусть в пространстве фиксирована точка O. Совокупность точки O и базиса называется аффинной (декартовой) системой координат:

– аффинная система координат на прямой (рис.2.1,а) – это точка O и ненулевой вектор vec{e} на прямой (базис на прямой);

– аффинная система координат на плоскости (рис.2.1,6) – это точка O и два неколпинеарных вектора vec{e}_1,vec{e}_2, взятые в определенном порядке (базис на плоскости);

– аффинная система координат в пространстве (рис.2.1,в) – это точка O и три некомпланарных вектора vec{e}_1,vec{e}_2,vec{e}_3, взятые в определенном порядке (базис в пространстве).

Аффинная система координат на прямой, на плоскости и в пространстве

Точка O называется началом координат. Прямые, проходящие через начало координат в направлении базисных векторов, называются координатными осями: Ox_1 — ось абсцисс, Ox_2 — ось ординат, Ox_3 — ось аппликат. Плоскости, проходящие через две координатные оси, называются координатными плоскостями.

Аффинная система координат в пространстве (или на плоскости) называется правой, если ее базис является правым, и левой, если её базис — левый.

Координаты векторов и точек в аффинной системе координат

Координатами вектора в заданной системе координат называются, как и ранее, коэффициенты в разложении вектора по базису (см. разд.1.3.1; 1.3.2; 1.3.3).

Для любой точки A в заданной аффинной системе координат можно рассмотреть вектор overrightarrow{OA} начало которого совпадает с началом координат, а конец – с точкой A (рис.2.1,а,б,в). Этот вектор называется радиус-вектором точки A.

Координатами точки A в заданной системе координат называются координаты радиус-вектора этой точки относительно заданного базиса. В пространстве это координаты вектора overrightarrow{OA} в базисе vec{e}_1,vec{e}_2,vec{e}_3, т.е. коэффициенты a_1,a_2,a_3 в разложении overrightarrow{OA}=a_1cdotvec{e}_1+a_2cdotvec{e}_2+a_3cdotvec{e}_3 (рис.2.1,в). Координаты точки записывают в виде A(a_1,a_2,a_3). Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой. На плоскости и на прямой координаты записывают в виде A(a_1,a_2) и A(a) согласно разложениям overrightarrow{OA}=a_1cdotvec{e}_1+a_2cdotvec{e}_2 (рис.2.1,6), overrightarrow{OA}=acdotvec{e} (рис.2.1,а). Координаты точки A, или, что то же самое, координаты ее радиус-вектора overrightarrow{OA} представляют в виде координатного столбца (матрицы-столбца):

begin{pmatrix}a_1\a_2\a_3end{pmatrix} в пространстве, begin{pmatrix}a_1\a_2end{pmatrix} на плоскости.

Разность векторов в аффинной системе координат

Найдем координаты вектора overrightarrow{AB} с началом в точке A(a_1,a_2,a_3) и концом в точке B(b_1,b_2,b_3). Рассмотрим треугольник OAB (рис.2.2). Радиус-векторы overrightarrow{OA} и overrightarrow{OB} представляются в виде overrightarrow{OA}=a_1cdotvec{e}_1+a_2cdotvec{a}_2+a_3cdotvec{e}_3, overrightarrow{OB}=b_1cdotvec{e}_1+b_2cdotvec{a}_2+b_3cdotvec{e}_3. По правилу треугольника (см. разд. 1.1.2) вычитания векторов получаем overrightarrow{AB}=overrightarrow{OB}-overrightarrow{OA}=(b_1-a_1)vec{e}_1+(b_2-a_2)vec{e}_2+(b_3-a_3)vec{e}_3, т.е. вектор overrightarrow{AB} имеет координаты b_1-a_1,b_2-a_2,b_3-a_3. Этим доказано следующее правило: чтобы найти координаты вектора,нужно из координат его конца вычесть соответствующие координаты его начала. Это же правило справедливо для аффинных систем координат на плоскости и на прямой.

Замечания 2.1.

1. В заданной системе координат каждой точке можно поставить в соответствие её координаты, причем это соответствие взаимно однозначное:

(точка) leftrightarrow (её координаты).

В частности, разным точкам соответствуют разные наборы координат.

2. Если вектор vec{v} с координатами v_1,v_2,v_3 отложить от точки A(a_1,a_2,a_3), то конец вектора overrightarrow{AB}=vec{v} будет иметь координаты B(a_1+v_1,a_2+v_2,a_3+v_3).

3. Координаты точки M, которая делит отрезок AB в отношении frac{AM}{MB}=frac{beta}{alpha}, находятся по координатам его концов A(a_1,a_2,a_3) и B(b_1,b_2,b_3):

M!left(frac{alphacdot a_1+betacdot b_1}{alpha+beta},frac{alphacdot a_2+betacdot b_2}{alpha+beta},frac{alphacdot a_3+betacdot b_3}{alpha+beta}right).

В частности, координаты середины M отрезка AB равны среднему арифметическому соответствующих координат концов отрезка (alpha+beta):

M!left(frac{a_1+b_1}{2},frac{a_2+b_2}{2},frac{a_3+b_3}{2}right).

Координаты точки M которая “делит” площадь треугольника ABC в отношении S_{MBC}:S_{MCA}:S_{MAB}=alpha:beta:gamma alpha>0,,beta>0,,gamma>0, находятся по координатам его вершин A(a_1,a_2,a_3),,B(b_1,b_2,b_3),,C(c_1,c_2,c_3):

M!left(frac{alphacdot a_1+betacdot b_1+gammacdot c_1}{alpha+beta+gamma},frac{alphacdot a_2+betacdot b_2+gammacdot c_2}{alpha+beta+gamma},frac{alphacdot a_3+betacdot b_3+gammacdot c_3}{alpha+beta+gamma}right).

В частности, координаты точки M пересечения медиан треугольника ABC равны среднему арифметическому соответствующих координат вершин треугольника (alpha=beta=gamma):

M!left(frac{a_1+b_1+c_1}{3},frac{a_2+b_2+c_2}{3},frac{a_3+b_3+c_3}{3}right).

Эти формулы следуют из свойств 2,4 аффинных и выпуклых комбинаций (см. разд. 1.6.1). Они остаются справедливыми и на координатной плоскости, если аппликаты всех точек положить равными нулю. Например, координаты середины M отрезка ABcolon M!left(frac{a_1+b_1}{2},frac{a_2+b_2}{2}right), или координаты точки M пересечения медиан треугольника ABCcolon M!left(frac{a_1+b_1+c_1}{3},frac{a_2+b_2+c_3}{3}right)

Пирамида в аффинной системе координат

Пример 2.1. В некоторой аффинной системе координат известны координаты вершин треугольной пирамиды ABCD (см. рис.2.3): A(1;1;3), B(3;5;4), C(-1;3;2), D(5;3;-1). Найти координаты (в той же системе координат):

а) точки M пересечения медиан треугольника ABC;

б) точки Z, которая делит отрезок DN в отношении DZ:ZM=3:1 (beta=3;~alpha=1).

Решение. Учитывая пункт 3 замечаний 2.1, получаем:

а) M!left(frac{1+3+(-1)}{3},frac{1+5+3}{3},frac{3+4+2}{3}right), то есть M(1,3,3);

б) Z!left(frac{1cdot5+3cdot1}{1+3},frac{1cdot3+3cdot3}{1+3},frac{1cdot(-1)+3cdot3}{1+3}right), то есть Z(2,3,2).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

§ 1. Аффинная система координат

Определение
1.
Аффинной
системой координат
или аффинным
репером
называется совокупность некоторой
точки О
и некоторого базиса (
,
).
(аффинное = родственное, репер = метка).

Точка
О
называется началом
координат,

и

– координатными
векторами.

Если
базис (
,
)
– правый, то аффинная система координат
называется правой,
если базис левый, то – левой.

Определение
2. Осью
называется прямая с выбранным на ней
направлением, началом отсчета и единичным
отрезком. Две оси, проходящие через
начало координат и имеющие направления
векторов

и

,
называются соответственно осью
абсцисс
и осью
ординат
или координатными
осями.

Четыре
части, на которые они делят плоскость,
называются координатными
углами
или квадрантами.

Обозначения:
ось абсцисс –

,

;

ось
ординат –

,

;

система
координат –

,

.

Правая
система координат

Левая
система координат

Определение
3.
Радиус-вектором
точки М
плоскости называется вектор

.
Его координаты x
и y
в базисе (
,
)
называются координатами
точки М
в аффинной системе координат, при этом
х
называется абсциссой,
у
– ординатой.

Обозначение:

,


,


.

По
определению:



.

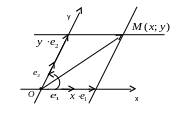
Определение
4.
Плоскость называется ориентированной,
если на ней выбрана какого-либо вида
аффинная система координат – правая
или левая и, следовательно, определено
направление отсчета углов (против или
по часовой стрелке). Система координат
выбранного вида называется положительно
ориентированной,
а выбранное направление отсчета углов
– положительным.

Замечание.
Будем считать плоскость положительно
ориентированной, на ней выбрана правая
система координат
и, следовательно, положительным
направлением отсчета углов
– против
часовой стрелки.

§ 2. Деление отрезка в данном отношении

Определение.
Пусть на прямой лежат направленный
отрезок

и произвольная точка М.
Отношением,
в котором эта точка делит данный отрезок,
называется такое число λ, что:

(1)

Обозначение:
λ=(AB,M)

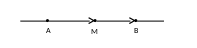
ЧАСТНЫЕ
СЛУЧАИ:

1)

λ>0


,
точка М
лежит внутри
отрезка АВ,

.

λ=1


,
М
– середина
отрезка
АВ.

2)

λ=0


,

– точка М
совпадает с началом А
отрезка АВ.

3)

λ<0


,
точка М
лежит вне
отрезка АВ,

.

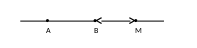
Замечание:

λ
-1

, т. к. в этом случае

или

и

и

,
то есть

.

Теорема.
Если точка M(x;y)
делит в отношении λ
-1
направленный отрезок с началом А(х1;у1)
и концом В(х2;у2),
то


,

.
(2)

Доказательство.

– согласно определению. Перейдем к
координатам:

,


.

Из
условия равенства векторов

и

имеем:

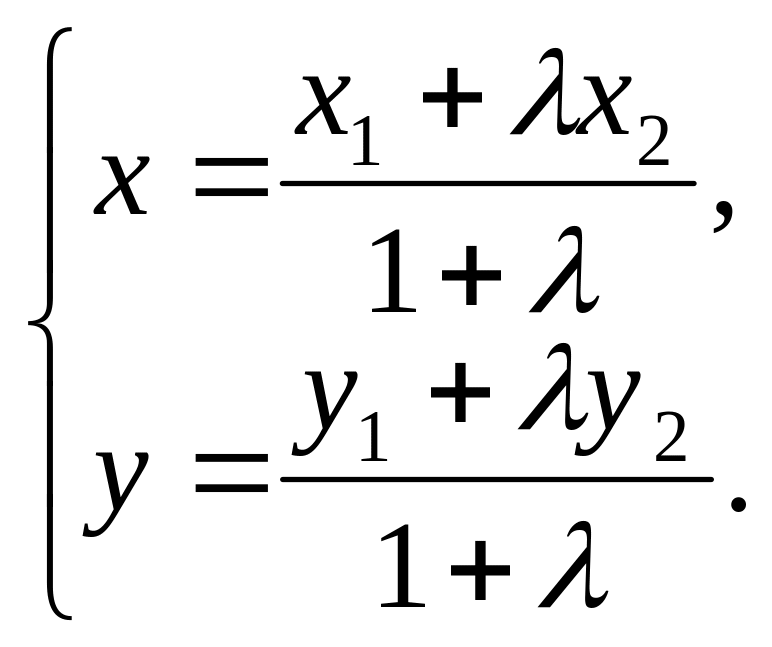
Теорема
доказана.

Следствие.
Если М
– середина направленного отрезка

,
то λ=1 и

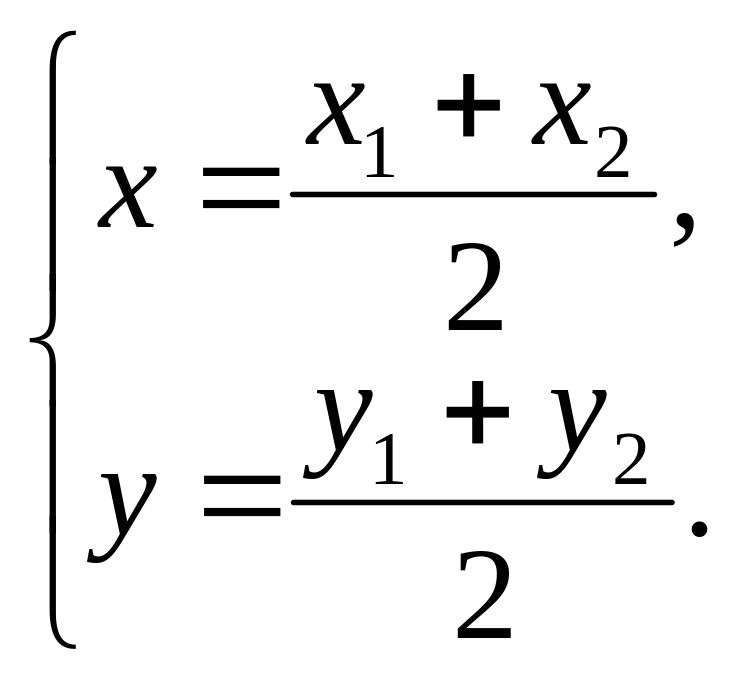
(3)

§ 3. Переход к новой аффинной системе координат

Рассмотрим
две аффинные системы координат. Одну
из них обозначим

и назовем старой,
другую обозначим

и назовем ее новой.

Теорема.
Пусть 1) начало координат и координатные
векторы новой системы имеют в старой
системе координаты:

,

,

;
2) произвольная точка М
имеет в старой системе координаты x,
y,
а в новой системе координаты

.
Тогда имеют место формулы:


,
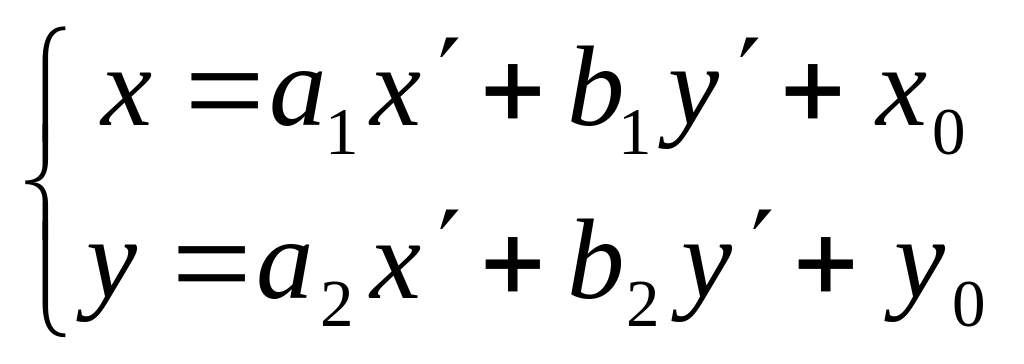
где

. (*)

Доказательство.

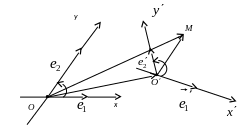
СТАРАЯ
СИСТЕМА НОВАЯ СИСТЕМА

КООРДИНАТ
КООРДИНАТ

По
определению координат точек и векторов
имеем для старой системы координат

:


;
(1)

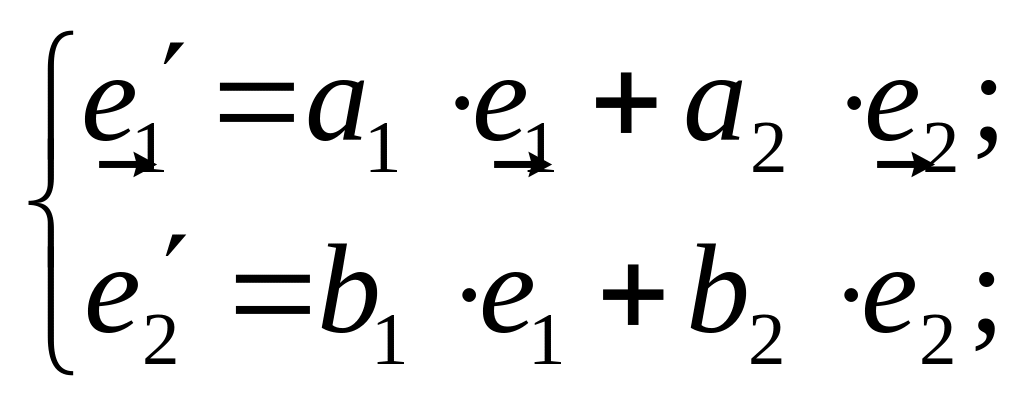
(2)

.
(3)

Для
новой системы координат аналогично
имеем:


.
(4)

Подставим
выражения

и

из (2) в (4):


.
(5)

По
правилу треугольника имеем:


.
(6)

Подставим
в это равенство выражения (3), (1) и (5):



+
+
+
+
+
.

Приведем
подобные члены:



+

=

+

.

Так
как координаты вектора в данном базисе
определены однозначно, то формулы (*)
справедливы:

(*)

Теорема
доказана.

Замечания.

1)
в правой части равенств (*) коэффициентами
при

служат координаты

и

вектора

в старой системе координат, коэффициентами
при

– координаты

и

вектора

в старой системе координат, свободными
членами – координаты нового начала

в старой системе координат;

2)
по определению базиса векторы

и

неколлинеарны,
а по теореме из §3: определитель из их
координат отличен от нуля:

.

Можно
доказать, что если старая и новая системы
координат одного
типа
(например, обе правые), то

,
если же разных
типов,
то

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Макеты страниц

ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ

§ 1. Определение аффинной системы координат

1. Аффинная система координат на плоскости. Общая, или аффинная, система координат на плоскости задается точкой О (начало координат) и парой приложенных к ней неколлинеарных векторов (рис. 31), данных в определенном порядке: есть первый, а — второй вектор; векторы определяют две оси, пересекающиеся в точке О, — первую и вторую ось координат — и являются по определению единичными векторами этих осей. Первая ось называется также осью абсцисс или осью , а вторая — осью ординат или осью данной координатной системы. Сама система координат обозначается через или через .

Рис. 31.

Пусть М — какая-нибудь точка плоскости; обозначим через проекции точки М соответственно на первую и вторую ось координат (проекции на каждую ось берутся вдоль другой оси) (Рис. 32).

Рис. 32.

Алгебраические значения векторов являются соответственно первой и второй координатой (абсциссой и ординатой) точки М.

Любая пара чисел х, у однозначно определяет точку М, для которой х является первой, а у — второй координатой. В самом деле, искомая точка М является концом вектора ОМ, проектирующегося

на векторы . Значит,

т. е. вектор ОМ есть диагональ параллелограмма, построенного на , чем точка М определена однозначно. Точка М с координатами обозначается так: . Система координат включает в себя базис многообразия всех векторов на плоскости. Координаты произвольного вектора и относительно базиса называются координатами вектора и относительно системы координат они являются алгебраическими значениями проекций вектора и на оси координат и не зависят от выбора начала координат (рис. 33). Вектор и с координатами обозначается так: тогда

Условие характеризует векторы, коллинеарные оси ординат, а условие характеризует векторы, коллинеарные оси абсцисс.

Рис. 33.

Очевидно, координаты любой точки М в данной системе координат суть координаты вектора ОМ в этой системе координат. Замечание 1. Если точка О отлична от точки О, то

поэтому координаты точек (в отличие от координат вектора) зависят от выбора начала координат.

Начало координат О разбивает каждую из координатных осей на две полуоси: положительную, идущую от начала координат в положительном направлении (т. е. в направлении единичного вектора этой оси), и отрицательную.

Ось абсцисс состоит из всех точек, ординаты которых раины нулю; она разбивает плоскость на две полуплоскости; та, в которой лежит положительная полуось оси ординат, характеризуется тем, что ординаты лежащих в ней точек положительны; во второй полуплоскости лежат точки с отрицательными ординатами.

Аналогично ось ординат состоит из всех точек, абсциссы которых равны нулю; она разбивает плоскость на две полуплоскости; точки той из них, в которой лежит положительная полуось оси абсцисс, имеют положительные абсциссы; точки другой полуплоскости имеют отрицательные абсциссы.

Совокупность обеих координатных осей разбивает плоскость на четыре области, называемые «квадрантами» (рис. 34); в первом квадранте лежат точки, обе координаты которых положительны, во втором — точки с отрицательной абсциссой и положительной ординатой, в третьем — точки, обе координаты которых отрицательны, и в четвертом — точки, у которых абсцисса положительна, а ордината отрицательна. Обе координаты начала координат, очевидно, равны нулю:

Замечание 2. Система координат на плоскости с началом О и единичными векторами определяет на каждой координатной оси свою систему координат, началом которой является точка О, а единичным вектором — лежащий на данной оси вектор или . Очевидно, каждая из координат точки М есть координата проекции этой точки на соответствующую координатную ось.

Аналогично координаты вектора суть координаты проекций и этого вектора на оси координат, т. е. алгебраические значения векторов и на соответствующей оси.

Два вектора АВ и CD равны тогда и только тогда, когда равны их соответствующие координаты.

Если , то для координат вектора АВ имеем:

Рис. 34.

Достаточно доказать первое из этих равенств. Координата есть алгебраическое значение вектора на оси абсцисс (рис. 35):

кроме того, . По лемме Шаля имеем

т. е. , откуда утверждение следует.

2. Аффинная система координат в пространстве. Все сказанное с очевидными изменениями применяется и к случаю пространства. Аффинная система координат в пространстве состоит из точки О («начало координат») и приложенных к этой точке трех некомпланарных векторов (рис. 36), данных в определенном порядке — первый, второй, — третий) — единичных векторов данной системы координат. Каждый из этих векторов определяет проходящую через начало О ось, единичным вектором которой он является; эти оси называются первой, второй и третьей осью координат или соответственно «осью (осью абсцисс), «осью (осью ординат) и «осью (осью аппликат – последнее название, впрочем, употребляется нечасто). Каждые две координатные оси определяют проходящую через них координатную плоскость. Так, оси определяют координатную плоскость или и т. д.

Рис. 35.

Рис. 36.

Первой, второй, третьей координатой данного вектора и называются соответствующие его координаты относительно базиса , т. е. соответствующие коэффициенты в представлении

Они равны алгебраическим значениям проекций вектора и на оси, определенные соответственно векторами (проекции на каждую ось берутся вдоль плоскости, несущей две другие оси).

Координаты вектора не зависят от выбора начала координат О.

Координаты точки М суть по определению координаты вектора ОМ (рис. 37). Если суть проекции точки — проекции вектора ОМ на оси координат, то координаты х, у, z точки М суть алгебраические значения векторов . Тогда

Векторы, коллииеарные данной координатной оси, характеризуются тем, что равны нулю их координаты, соответствующие двум другим осям.

Мы уже знаем из главы II, что при сложении векторов их одноименные координаты складываются, а при умножении вектора и на число Я на это А умножается каждая координата вектора и. Отсюда (и из главы II, § 4, предложение 5) сразу следует, что два вектора тогда и только тогда коллинеарны, когда координаты одного из ник пропорциональны координатам другого.

Рис. 35.

Каждая тройка чисел х, у, z (данных в определенном порядке) Однозначно определяет точку М пространства, тройкой координат которой она является. Для получения этой точки М надо приложить к точке О вектор , т. е. взять диагональ параллелепипеда, построенного на векторах . Точка М с координатами х, у, z обозначается так: М=(х, у, z).

По определению координат точки М вектор ОМ имеет те же координаты, что и его конец М. Вообще, если то вектор АВ имеет координаты доказательство совершенно аналогично тому, которое мы провели в случае плоскости.

Рис. 38.

Координатная плоскость характеризуется тем, что ее точки имеют коордикату Эта плоскость разбивает пространство на два полупространства; координата z у всех точек одного из этих полупространств положительна, у точек другого — отрицательна. Аналогичные утверждения справедливы и для других координатных плоскостей.

Каждое из двух полупространств, на которое пространство разбито плоскостью , двумя другими координатными плоскостями разбивается на четыре области, соответствующие четырем квадрантам, на которые плоскость разбивается осями . Всего, таким образом, получаем восемь областей, называемых октантами, на которые пространство разбивается совокупностью трех координатных плоскостей (рис. 38). Точки каждого октанта характеризуются распределением знаков своих координат следующим образом:

Кроме того, имеем для точек плоскости для плоскости для плоскости на оси имеем на оси имеем на оси имеем . Для начала координат О имеем

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
  • § 1. Отношение отрезков
  • § 2. Направленные отрезки (векторы); их отношение
  • § 3. Ось. Алгебраическое значение (координата) вектора на оси
  • § 4. Сложение векторов на прямой
  • § 5. Система координат на прямой
  • § 6. Деление отрезка в данном отношении
  • § 7. Пропорциональность пар чисел
  • § 8. Бесконечно удаленная точка прямой
  • § 9. Пропорциональность двух последовательностей, состоящих из и чисел
  • ГЛАВА II. ВЕКТОРЫ
  • § 1. Равенство векторов. Свободный вектор
  • § 2. Линейные операции над векторами (сложение и умножение на число)
  • § 3. Проекции
  • § 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
  • § 5. Линейная зависимость и независимость векторов
  • § 6. Геометрический смысл линейной зависимости векторов
  • § 7. Векторные многообразия
  • ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
  • § 1. Определение аффинной системы координат
  • § 2. Перенос начала координат
  • § 3. Деление отрезка в данном отношении
  • ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
  • § 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
  • § 2. Скалярное произведение векторов; угол между двумя векторами
  • § 3. Угол от одного вектора до другого на плоскости
  • § 4. Полярная система координат на плоскости
  • § 5. Полярная система координат в пространстве
  • ГЛАВА V. ПРЯМАЯ ЛИНИЯ
  • § 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
  • § 2. Расположение двух прямых на плоскости
  • § 3. Частные случаи общего уравнения прямой
  • § 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
  • § 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
  • § 6. Две полуплоскости, определяемые данной прямой на плоскости
  • § 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
  • § 8. Расстояние от точки до прямой (на плоскости)
  • § 9. Углы, образуемые двумя прямыми на плоскости
  • § 10. Прямая в пространстве, снабженном прямоугольной системой координат
  • ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
  • § 1. Парабола
  • § 2. Определение и каноническое уравнение эллипса
  • § 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
  • § 4. Эллипс как проекция окружности и как сечение круглого цилиндра
  • § 5. Определение гиперболы. Каноническое уравнение гиперболы
  • § 6. Основной прямоугольник и асимптоты гиперболы
  • § 7. Директрисы эллипса и гиперболы
  • § 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
  • § 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
  • ГЛАВА VII. ДЕТЕРМИНАНТЫ
  • § 1. Плошадь ориентированного параллелограмма и треугольника
  • § 2. Детерминант второго порядка. Матрицы
  • § 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
  • § 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
  • § 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
  • § 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
  • § 8. Правило Крамера для решений систем и уравнений с n неизвестными
  • § 9. Общее определение миноров матрицы. Теорема Лапласа
  • § 10. Умножение детерминантов
  • § 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
  • ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
  • § 1. Переход от одной аффинной системы координат к другой
  • § 2. Перемножение матриц. Новое определение обратной матрицы
  • § 3. Переход от одной прямоугольной системы координат к другой
  • § 4. Действия над матрицами в общем случае
  • ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
  • § 1. Ориентация пространства (плоскости)
  • § 2. Углы Эйлера
  • § 3. Объем ориентированного параллелепипеда
  • § 4. Векторное произведение двух векторов
  • ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
  • § 1. Уравнения плоскости
  • § 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
  • § 3. Взаимное расположение двух плоскостей
  • § 4. Прямая как пересечение двух плоскостей
  • § 5. Пучок плоскостей
  • § 6. Взаимное расположение двух прямых в пространстве
  • § 7. О двух полупространствах, определяемых данной плоскостью
  • § 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
  • § 9. Угол между прямой и плоскостью; угол между двумя плоскостями
  • § 10. Две задачи
  • ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
  • § 1. Определение движений и аффинных преобразований
  • § 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
  • § 3. Аналитическое выражение аффинных преобразований
  • § 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
  • § 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
  • § 6. Движения как изометрические преобразования
  • § 7. Преобразования подобия
  • § 8. Классификация движений прямой и плоскости
  • ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
  • § 1. Определение векторного пространства
  • § 2. Размерность. Базис. Координаты
  • § 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
  • § 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
  • § 5. Алгебраическая (в частности, прямая) сумма подпространств
  • § 6. Линейные отображения векторных пространств
  • § 7. Теорема о ранге матрицы
  • § 8. Системы линейных однородных уравнения
  • ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
  • § 1. Линейные функции
  • § 2. Билинейные функции и билинейные формы
  • § 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
  • § 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
  • § 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
  • ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
  • § 1. Определение n-мерного аффинного пространства
  • § 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
  • § 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
  • § 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
  • § 5. Системы линейных уравнений
  • § 6. Аффинные преобразования n-мерного аффинного пространства
  • ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
  • § 1. Определение алгебраических линий и поверхностей
  • § 2. Преобразование многочлена второй степени при преобразовании координат
  • § 3. Аффинная эквивалентность линий и поверхностей
  • § 4. Комплексная плоскость
  • § 5. Прямая линия на комплексной плоскости
  • § 6. Замечание о действительных и мнимых линиях
  • § 7. Комплексное пространство
  • § 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
  • § 9. Несколько заключительных замечаний о линиях и поверхностях
  • ГЛАВА XVI. Различные виды кривых второго порядка
  • § 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
  • § 2. Инварианты многочлена второй степени
  • § 3. Центральный случай
  • § 4. Параболический случай
  • § 5. Аффинная классификация кривых второго порядка
  • § 6. Несколько заключительных замечаний
  • ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
  • § 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
  • § 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
  • § 3. Асимптотические направления кривых второго порядка
  • § 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
  • § 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
  • § 6. Центр кривой второго порядка
  • § 7. Диаметры кривой второго порядка
  • § 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
  • § 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
  • § 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
  • § 11. Оси симметрии и главные направления кривой второго порядка
  • § 12. Основная теорема об аффинных преобразованиях
  • ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
  • § 1. Распадающиеся поверхности
  • § 2. Цилиндрические поверхности
  • § 3. Конусы второго порядка
  • § 4. Эллипсоиды и гиперболоиды
  • § 5. Параболоиды
  • § 6. Прямолинейные образующие
  • ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
  • § 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
  • § 2. Пересечение поверхности второго порядка с плоскостью
  • § 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
  • § 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
  • § 5. Центр поверхности второго порядка
  • ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
  • § 1. Диаметральные плоскости. Особые направления
  • § 2. Диаметральные плоскости поверхностей различных видов
  • § 3. Сопряженные направления
  • § 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
  • § 5. Теорема единственности
  • § 6. Главные направления
  • § 7. Приведение к каноническому виду уравнения поверхности второго порядка
  • § 8. Аффинная классификация поверхностей второго порядка
  • ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
  • § 1. Перспективное соответствие между плоскостью и связкой
  • § 2. Однородные координаты точек на плоскости и лучел в связке
  • § 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
  • § 4. Принцип двойственности для проективной плоскости
  • § 5. Проективная система координат в связке и на проективной плоскости
  • § 6. Проективные преобразования и отображения проективной плоскости
  • § 7. Проективные координаты на прямой. Проективные отображения прямой
  • § 8. Двойное отношение
  • ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
  • § 1. Определение. Теорема единственности
  • § 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
  • § 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
  • § 4. Поляры и полюсы
  • § 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
  • § 6. Диаметры как поляры несобственных точек
  • § 7. Автополярный треугольник
  • § 8. Проективная классификация кривых второго порядка
  • ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
  • § 1. Проективное пространство; его плоскости и прямые
  • § 2. Проективные координаты. Проективные преобразования.
  • § 3. Понятие об n-мерном проективном пространстве
  • § 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
  • § 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
  • § 6. Полюсы и полярные плоскости
  • § 7. Проективная классификация поверхностей второго порядка
  • § 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
  • ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
  • § 1. Введение. Ортогональные матрицы
  • § 2. Положительно определенные симметричные билинейные функции в векторном пространстве
  • § 3. Определение евклидовых пространств и простейших относящихся к ним понятий
  • § 4. Неравенство Коши—Буняковского и его следствия. Углы
  • § 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
  • ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
  • § 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
  • § 2. Ортогональные преобразования n-мерного евклидова пространства
  • § 3. Движения трехмерного евклидова пространства
  • § 4. Преобразования подобия. Дальнейшие проблемы
  • § 5. Самосопряженные операторы
  • § 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
  • § 7. Билинейные и квадратичные формы в евклидовых пространствах
  • § 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
  • ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
  • § 1. Перестановки
  • § 2. Множества
  • § 3. Отображения или функции
  • § 4. Разбиение множества на подмножества. Отношение эквивалентности
  • § 5. Определение группы
  • § 6. Простейшие теоремы о группах
  • § 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
  • ЗАДАЧИ
  • Задачи к главе IV
  • Задачи к главе V
  • Задачи к главе VI
  • Задачи к главе VIII
  • Задачи к главе IX
  • Задачи к главе X
  • Задачи к главе XI
  • Задачи к главе XII
  • Задачи к главе XIII
  • Задачи к главе XIV
  • Задачи к главе XV
  • Задачи к главам XVI и XVII
  • Задачи к главе XVIII
  • Задачи к главам XIX и XX
  • Задачи к главе XXI
  • Задачи к главе XXII
Источник

Точка М на аффинной плоскости.

Аффи́нная систе́ма координа́т (от лат. affinis «соприкасающийся, близкий, смежный»), также косоуго́льная система координат — прямолинейная система координат в аффинном пространстве.

В n-мерном пространстве она задаётся упорядоченной системой линейно независимых векторов {vec {e}}_{1},;ldots ,;{vec {e}}_{n}, выходящих из одной точки O. Аффинными координатами точки M называют такие числа x_{i}, что

{vec {OM}}=x_{1}{vec {e}}_{1}+ldots +x_{n}{vec {e}}_{n}.

Tочку O и систему векторов {vec {e}}_{1},;ldots ,;{vec {e}}_{n} называют репером или аффинным базисом; прямые, проходящие через вектора {vec {e}}_{1},;ldots ,;{vec {e}}_{n} — координатными осями.

На аффинной плоскости (n=2) координату x_{1} называют абсциссой, а x_{2} — ординатой точки M. В пространстве же координаты точки называют её абсциссой, ординатой и аппликатой. Аналогичным образом именуют и координатные оси.

Источник

В этой статье я опишу аффинные и евклидовы пространства, а также введу декартову систему координат в евклидовом пространстве. Все будет описано именно в этом логически последовательном порядке. В абстрактном математическом смысле и аффинное, и евклидово пространства являются хаусдорфовыми пространствами, удовлетворяющими сильной аксиоме отделимости: любые две точки хаусдорфова пространства обладают непересекающимися окрестностями. А это уже говорит об их метризуемости, причем аффинное – это метризуемое, а евклидово – уже метризованное пространства. Оба являются сепарабельными пространствами, т.к. в них можно определить счетное всюду плотное подмножество, такое, что в любой окрестности любой точки будет содержаться точка из этого множества. И оба не являются компактными топологическими пространствами, т.к. существуют последовательности открытых подмножеств, не имеющие предела.

Далее. И аффинное, и евклидово пространства оперируют объектами двух типов: векторами и точками. В комплексе они составляют объект типа “свободного вектора”, привязанного к произвольной точке пространства.

Рис.1. Изображение свободного вектора AB аффинного пространства, привязанного началом к определенной точке A в некоторой системе координат.
Рис.1. Изображение свободного вектора AB аффинного пространства, привязанного началом к определенной точке A в некоторой системе координат.

Это отличает их от векторных пространств, в которых все векторы привязаны к единственной точке, точнее – все векторы имеют одну и ту же начальную точку. Все свойства векторных пространств наследуются и этими пространствами. Но операция скалярного произведения в аффинном пространстве не определяется.

И в аффинном, и в евклидовом пространствах определены понятия различимых точек (см. хаусдорфовость), существования сходящихся к любой точке бесконечной последовательности ее убывающих окрестностей, параллельности прямых, плоскостей и т.д., параллельного переноса объектов. Но в аффинном пространстве невозможно определить перпендикулярность.

На прямой можно определить отношение “находится между”. Но в аффинном пространстве, кроме как на одномерной прямой, невозможно определить метрические отношения: на прямой можно определить операции последовательного откладывания заранее определенного отрезка этой же прямой и деления ее на любое целое число частей, и в предельном переходе – определить вещественное отношение двух отрезков на прямой и параллельных ей прямых. Через это отношение можно определить понятие координаты любой точки относительно некоторой выделенной точки, называемой началом системы отсчета (координат) O (см. рис. 2). Преобразования координат, допустимые в аффинном пространстве, те же, что и в евклидовом пространстве (см. формулу 2 – далее), только вместо ортонормированной матрицы g ⁱ ⱼ можно использовать любую невырожденную матрицу.

Метрические отношения между любыми отрезками можно определить в евклидовом пространстве. В ней же, в дополнение к параллельности, можно определить понятия перпендикулярности и угла. Как следствие, в ней также можно определить декартову ортонормированную систему координат (см. рис. 2). Для определения координаты точки (см. рис. 2) в таком пространстве необходимо провести перпендикуляры к осям координат x, y, z и определить расстояние от начала координат O до точек пересечения этих перпендикуляров с осями координат, с учетом знаков. Для примера, координаты точки A будут равны (x, y, z). Кроме такой записи координат точки, применяется и тензорная форма записи в виде (r¹, r², r³).

2.Аффинное и евклидово пространства. Декартова система координат

Декартова система координат отличается от общей с.к. наличием понятия “расстояние” между любыми двумя точками абсолютного пространства с наиболее простой для его вычисления формулой:

2.Аффинное и евклидово пространства. Декартова система координат

Пространство с введенной таким образом метрикой является однородным и изотропным пространством. Свойства всех точек пространства одни и те же.

Все с.к., оставляющие инвариантными выражение (1) для определения расстояния, составляют множество ортонормированных с.к. К преобразованиям координат, оставляющим эту форму инвариантной, относятся трансляции по вектору и повороты пространства, т.е. группа ортонормированных преобразований координат. Математически в общем случае эти преобразования записываются так:

2.Аффинное и евклидово пространства. Декартова система координат

где r ⁱ – координата точки пространства,

r₀ⁱ – вектор смещения новой с.о.,

g ⁱ ⱼ– ортонормированная матрица (тензор) поворота новой с.о.

С т.з. тензорной алгебры, особенностью декартовой с.к. является то, что в ней можно не отличать ко- и контравариантные тензорные объекты, т.к их элементы имеют одни и те же значения, т.е. верхние и нижние индексы не отличаются.

Ну а как здесь с физикой? С материей, временем и пространством? Если принимать триединство “пространства, времени и материи”, то никак: оба пространства однородны и изотропны. Выделить в них материю невозможно из-за их однородности и изотропности без дополнительных структурных построений с целью “включения” в нее материального. Более того, пространство в них есть – но “времени” в них нет. Для исключения такого несоответствия придется “расширить” данные пространства, что выведет их за пределы определений аффинного и евклидова пространств.

Да и с “масштабом” метрики евклидова пространства проблемы в смысле материализации. Как известно, в реальном мире этот масштаб имеется, и оно определяется, в общем то, фундаментальными константами ПВМ. Если грубо, то это скорость света, размеры и массы атомов, частоты их линий излучения. В рассматриваемом галилеевом пространстве, также как и в аффинном и евклидовом пространствах, эти константы не определяются. Их можно только выбрать.

Источник

Добавить комментарий