Содержание:
Электрические цепи синусоидального тока:
В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.
При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.
Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
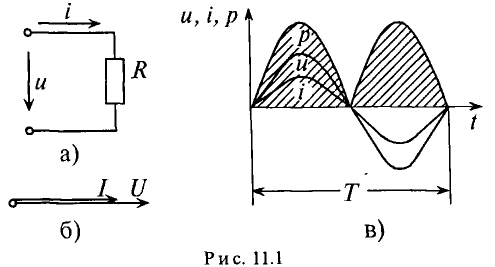
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение 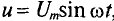
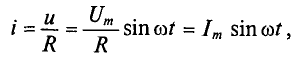
где 
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (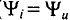 = 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 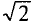 =1,41.
=1,41.
Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.
Активная мощность
Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.
Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.
Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
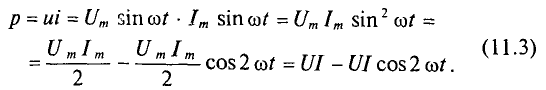
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 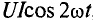 , изменяющейся с двойной частотой.
, изменяющейся с двойной частотой.
Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть
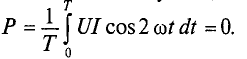
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
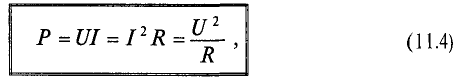
где U- действующее значение напряжения; I— действующее значение тока.
Единицей активной мощности является ватт:
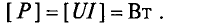
Поверхностный эффект и эффект близости
Сопротивление проводника постоянному току 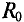 называют омическим сопротивлением и определяют выражением (2.8)
называют омическим сопротивлением и определяют выражением (2.8) 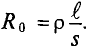 Сопротивление проводника переменному току R называют активным.
Сопротивление проводника переменному току R называют активным.
Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е. 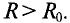
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).
На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.
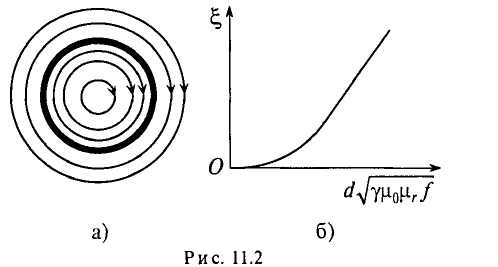
Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.
Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 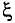 (кси)
(кси)
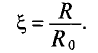
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости 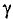 , магнитной проницаемости материала проводника
, магнитной проницаемости материала проводника 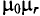 и частоты переменного тока
и частоты переменного тока  , проходящего по проводнику, показан на рис. 11.26.
, проходящего по проводнику, показан на рис. 11.26.
При токах большой частоты  (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
(радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
На величину активного сопротивления проводника R оказывает влияние и эффект близости.
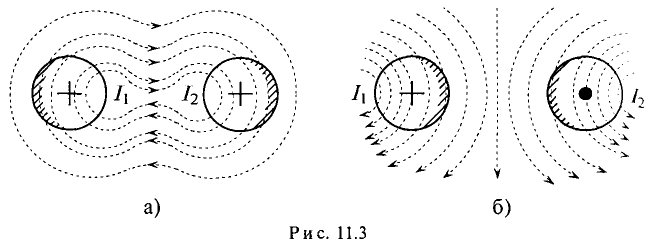
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.
Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).
Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.
Цепь с идеальной индуктивностью
Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.
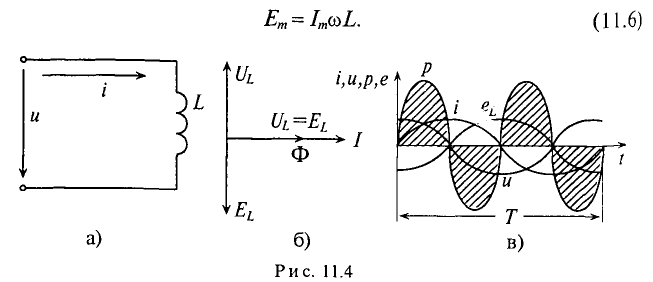
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток 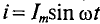 , то этот ток создает в катушке синусоидальный магнитный поток
, то этот ток создает в катушке синусоидальный магнитный поток 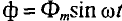 , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
, который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
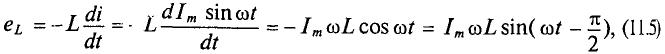
так как 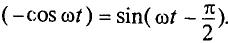
Очевидно, эта ЭДС достигает своего амплитудного значения 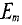 тогда, когда
тогда, когда 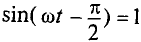 :
:
Тогда 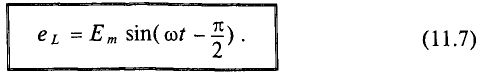
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 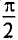 (рис. 11.46, в).
(рис. 11.46, в).
По второму закону Кирхгофа для мгновенных значений можно записать

Откуда 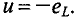
Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):
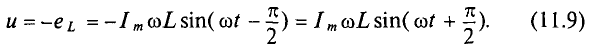
Очевидно, напряжение достигает своего амплитудного значения Um тогда, когда 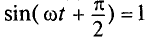 :
:

Следовательно, 
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 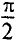 (рис. 11.46, в).
(рис. 11.46, в).
Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).
Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 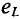 противодействует изменению тока.
противодействует изменению тока.
Если уравнение (11.10) разделить на 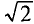 =1,41, то получается
=1,41, то получается 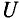 =
=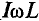 , откуда
, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.
Таким образом,

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
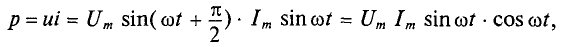
где 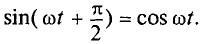
Следовательно, 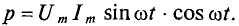
Полученное уравнение умножают и делят на 2:
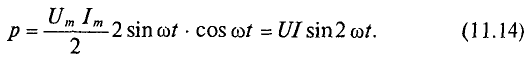
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.
Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (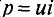 ) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно
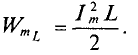
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.
Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.
Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
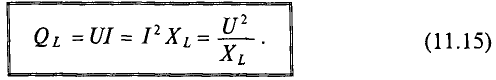
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. XL.
Цепь с емкостью
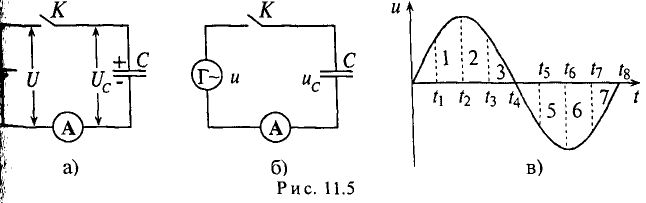
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе Uc не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).
Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе Uc отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
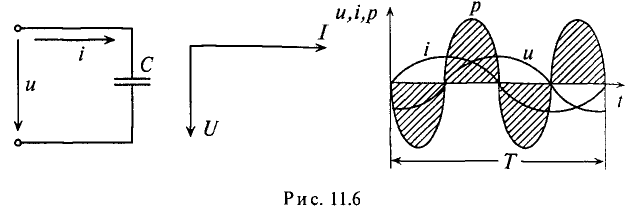
Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 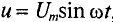 , то в цепи конденсатора проходит ток i (рис. 11.6а):
, то в цепи конденсатора проходит ток i (рис. 11.6а):
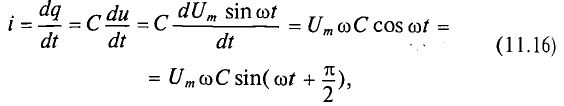
где q= Си согласно (6.3).
Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда 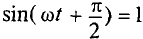 :
:

Тогда 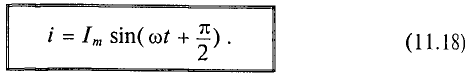
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=
Следовательно, напряжение отстает по фазе от тока на 90° =  (рис. 11.66).
(рис. 11.66).
Если уравнение (11.17) разделить на 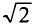 = 1,41, то получится равенство
= 1,41, то получится равенство 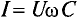 или
или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.
Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление – это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).
Реактивная мощность в цепи с конденсатором
Если в цепи конденсатора емкостью 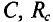 = 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
= 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
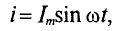
Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно
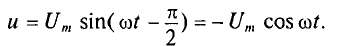
Мгновенная мощность в цепи с конденсатором
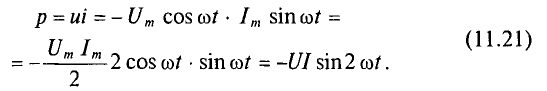
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).
Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.
Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
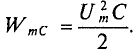
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.
Величина реактивной мощности в цепи конденсатора определяется выражением
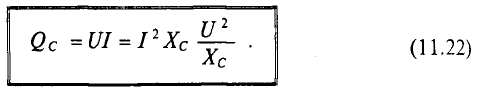
Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) – аналитическом выражении мгновенной мощности в цепи с конденсатором.
Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Хс).
Расчет линейных электрических цепей синусоидального тока
Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.
Цепь с активным сопротивлением и индуктивностью
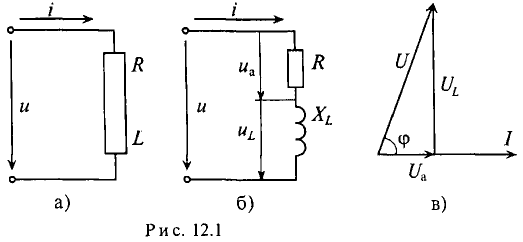
Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 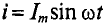 (рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки
(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки 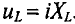
Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением XL (рис. 12.16).
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано 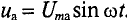 . Индуктивное напряжение
. Индуктивное напряжение 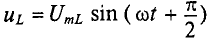 опережает ток на угол 90° =
опережает ток на угол 90° = 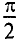 .
.
Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 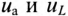 согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
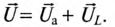
Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).
Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 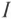 на угол ф. Мгновенное значение этого напряжения может быть записано:
на угол ф. Мгновенное значение этого напряжения может быть записано:
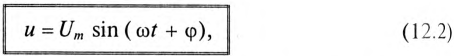
где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение
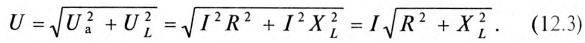
Откуда

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Zk — полное, или кажущееся, сопротивление реальной катушки.
Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.
Треугольники напряжений, сопротивлений, мощностей
Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).
Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:
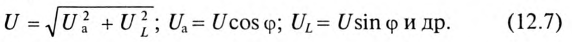
Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:
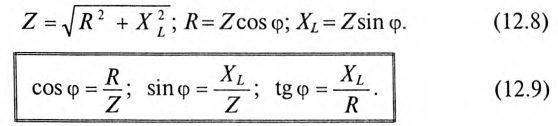
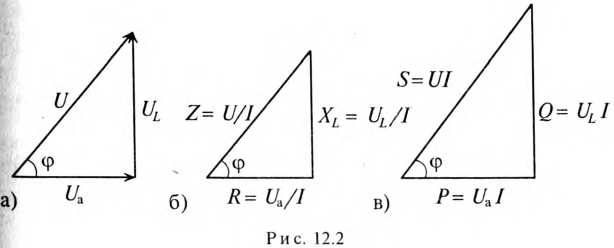
Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).
Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).
Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е. 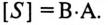
Однако потребляется в цепи только часть полной мощности – активная мощность
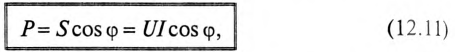
где cos ф показывает, какая часть полной мощности 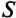 потребляется в цепи, поэтому cos ф называют коэффициентом мощности:
потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:
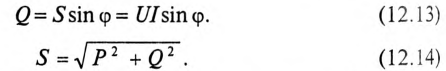
Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.
Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток 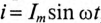 , то он создает падение напряжения на активном сопротивлении
, то он создает падение напряжения на активном сопротивлении 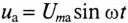 и на емкостном сопротивлении
и на емкостном сопротивлении 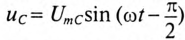 . Векторная диаграмма для этой цепи изображена на рис. 12.36.
. Векторная диаграмма для этой цепи изображена на рис. 12.36.
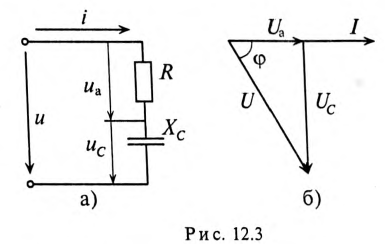
Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф < 90°, т. е.

Действующее значение напряжения U, приложенного к этой цепи, определяется по векторной диаграмме (рис. 12.3):
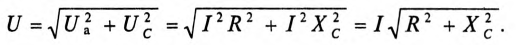
Откуда математическое выражение закона Ома для этой цепи:
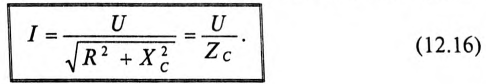
Пример 12.1
К цепи с последовательно включенными сопротивлениями R= 8 Ом и Хс= 6 Ом (рис. 12.3а) приложено напряжение U= 220 В. Определить ток цепи I, напряжение на активном 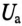 и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
Решение
Для определения тока вычислим полное сопротивление цепи
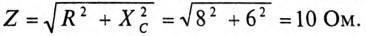
Тогда ток будет равен
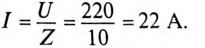
Напряжения на участках:
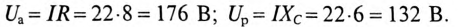
Полная мощность 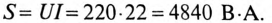
Активная мощность 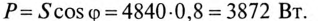
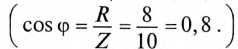
Реактивная мощность 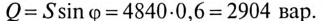
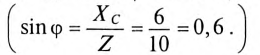
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток 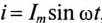 , то он создает падение напряжения на всех участках цепи:
, то он создает падение напряжения на всех участках цепи: 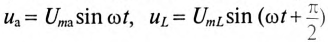 и
и 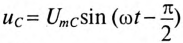 .
.
Мгновенное значение напряжения цепи определяется по формуле
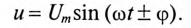
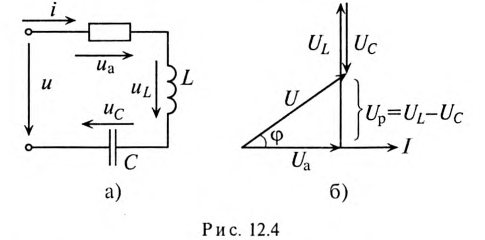
Так как в рассматриваемой цепи включены два реактивных сопротивления XL и Хс, то возможны три режима работы цепи: 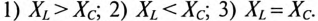
Векторная диаграмма цепи для режима 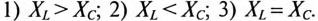 изображена на рис. 12.46.
изображена на рис. 12.46.
Знак перед углом сдвига фаз ф зависит от режима работы цепи Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т. е. 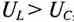 , то цепь имеет индуктивный характер и напряжение U опережает по фазе ток
, то цепь имеет индуктивный характер и напряжение U опережает по фазе ток 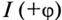 .
.
Если в цепи преобладает емкостное напряжение (сопротивление), т.е. 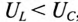 , то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
, то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
Из векторной диаграммы (рис. 12.46) следует:
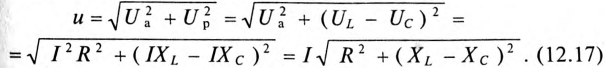
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:
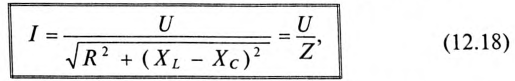
где Z — полное (или кажущееся) сопротивление неразветвленной цепи с R, L и С, т. е.
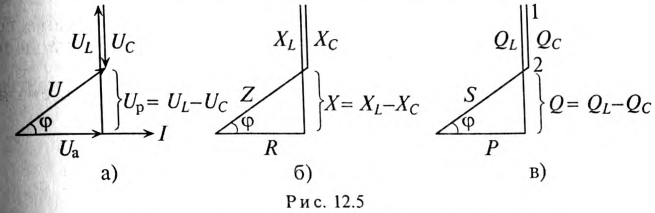
На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла ф можно определить из треугольника сопротивлений (рис. 12.56):
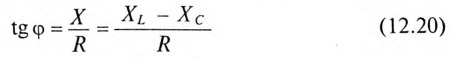
или
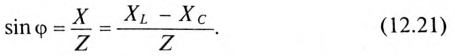
Из выражений (12.20) и (12.21) видно, что если 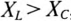 , то угол ф положителен (+ф), если
, то угол ф положителен (+ф), если 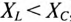 , то угол ф отрицательный (—ф).
, то угол ф отрицательный (—ф).
Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности 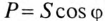 имеется реактивная мощность
имеется реактивная мощность 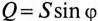 . Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
. Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= QL– Qc. Эта реактивная мощность (энергия) колеблется между источником и магнитным полем катушки индуктивности, так как 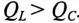
Полная мощность цепи определяется по формуле

Колебательный контур
Электрические цепи, в которых происходят периодические изменения токов, напряжений, энергии называются колебательными.
Для того чтобы исследовать резонансные явления, необходимо иметь представления о процессах в колебательном контуре, состоящем из идеальной катушки и конденсатора без потерь.
Если конденсатор емкостью С зарядить до напряжения Um, то в электрическом поле этого конденсатора накопится энергия, максимальное значение которой согласно выражению (6.21):
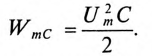
Если к заряженному конденсатору подключить индуктивность L замыканием ключа К (рис. 12.6), то конденсатор будет
разряжаться через индуктивность переменным током i. При этом в индуктивности L создается ЭДС самоиндукции eL, и в магнитном поле ее накапливается энергия, максимальное значение которой (9.12):
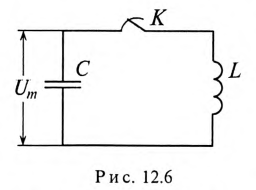
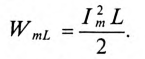
Источником энергии в этом контуре является конденсатор. Ток в контуре, состоящем из индуктивности L и конденсатора С, не прекращается даже когда конденсатор полностью разрядится. За счет ЭДС самоиндукции и энергии, накопившейся в магнитном поле индуктивности, конденсатор будет заряжаться, и энергия магнитного поля индуктивности переходит в электрическое поле конденсатора. При этом источником энергии в этом контуре является индуктивность. Дальше процесс повторяется.
Таким образом, в замкнутом контуре, состоящем из индуктивности и емкости, происходит колебание энергии между электрическим полем конденсатора С и магнитным полем индуктивности L. Поэтому такой замкнутый контур называется колебательным контуром.
Колебание энергии в колебательном контуре происходит с определенной частотой 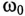 , которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
, которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
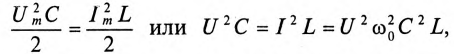
так как из (11.19) в цепи переменного тока с емкостью 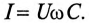
Откуда
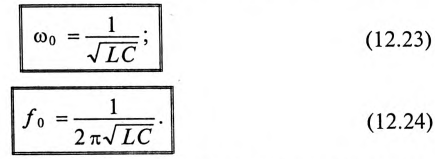
Таким образом, частота собственных колебаний колебательного контура определяется параметрами этого контура L и С.
Если в колебательном контуре отсутствуют потери (идеальный контур), то колебания в нем будут незатухающими с неизменной амплитудой. Если в колебательном контуре имеется активное сопротивление, т.е. возникают потери, то колебания энергии в нем будут затухающие, с уменьшающейся амплитудой, если эти потери не компенсируются.
Резонанс напряжений
Если в цепи синусоидального тока с последовательно соединенными конденсатором емкостью С и катушкой с сопротивлением R И индуктивностью L (рис. 12.7а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.

Из (12.25) следует 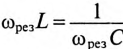 , тогда частота резонанса опреляется выражением
, тогда частота резонанса опреляется выражением

Из (12.26) следует, что резонанс напряжений имеет место в неразветвленной цепи с L и С тогда, когда частота вынужденных колебаний (частота источника) 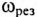 будет равна частоте собственных колебаний резонансного контура
будет равна частоте собственных колебаний резонансного контура 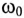 . Следовательно, добиться резонанса напряжений можно изменением частоты источника
. Следовательно, добиться резонанса напряжений можно изменением частоты источника 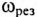 или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний
или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний 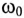 .
.
Полное (кажущееся) сопротивление цепи (рис. 12.7а) при резонансе напряжений определяется по формуле
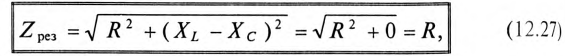
так как XL-Xc=0.
То есть полное сопротивление неразветвленной цепи при резонансе напряжений 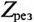 становится минимальным и равным активному сопротивлению цепи R.
становится минимальным и равным активному сопротивлению цепи R.
Следовательно, ток в неразветвленной цепи при резонансе напряжений максимальный:

Реактивные сопротивления при резонансе напряжений равны между собой, т. е.
(12.29)
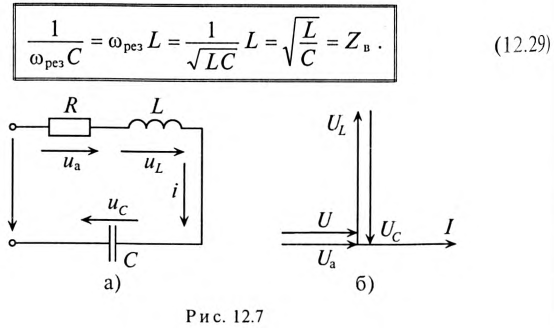
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению 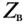 , которое называют характеристическим сопротивлением:
, которое называют характеристическим сопротивлением:
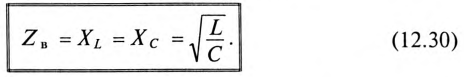
Напряжения на индуктивности UL и на емкости Uc при резонансе напряжений равны между собой, так как равны сопротивления, см. (12.25).
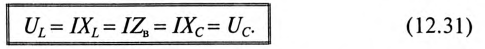
Равенство (12.31) определяет название «резонанс напряжений».
Так как UL и Uc изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении 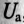 , т. е.
, т. е. 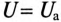 , что видно на векторной диаграмме (рис. 12.76).
, что видно на векторной диаграмме (рис. 12.76).
При резонансе напряжений каждое из реактивных напряжений UL и Uc может оказаться большим, чем напряжение цепи U.
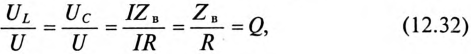
где Q — добротность резонансного контура.
Добротность контура Q показывает, во сколько раз напряжение на индуктивности UL и емкости Uc (каждое) больше напряжения цепи U.
Высокая добротность резонансного контура (при малом активном сопротивлении контура) нашла широкое применение в радиотехнике, в частности в антенном контуре.
Из векторной диаграммы (рис. 12.76) видно, что при резонансе напряжение цепи U совпадает по фазе с током 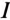 , угол между
, угол между 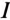 и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:
и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:

Колеблющаяся между магнитным полем индуктивности и электрическим полем емкости мощность (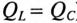 ) не является реактивной, так как не загружает источник и провода.
) не является реактивной, так как не загружает источник и провода.
Из выражения (12.33) следует, что при отсутствии активной Мощности Р (активного сопротивления R) резонансный контур становится при резонансе идеальным колебательным контуром. Следовательно, при наличии активного сопротивления R источник расходует свою мощность на компенсацию потерь в контуре, за счет чего колебания в цепи будут незатухающими.
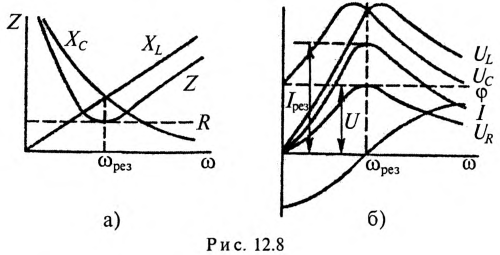
Кроме активного сопротивления R резонансной цепи и напряжения, приложенного к ней, все параметры резонансной цепи (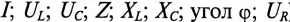 ) изменяются с изменением частоты сети
) изменяются с изменением частоты сети 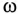 .
.
Эти изменения параметров резонансной цепи наглядно иллюстрируются резонансными кривыми, изображенными на рис. 12.8.
На резонансных кривых четко просматриваются значения этих параметров при частоте резонанса 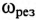 .
.
Общий случай неразветвленной цепи
Для неразветвленной цепи, содержащей несколько активных и реактивных сопротивлений различного характера (рис. 12.9а), справедливо геометрическое равенство напряжений (баланс напряжений)
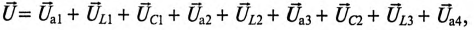
которое лежит в основе построения векторной диаграммы (рис. 12.96).
Таким образом, напряжение цепи равно геометрической сумме напряжений на всех участках этой цепи.
Из векторной диаграммы следует (рис. 12.96)
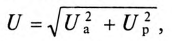
где 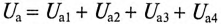 — активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи;
— активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи; 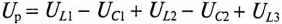 — реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
— реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
Те же рассуждения можно отнести и к сопротивлениям:
– полное сопротивление цепи 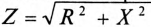 ;
;
– активное сопротивление цепи 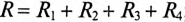 ;
;
– реактивное сопротивление цепи 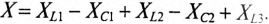
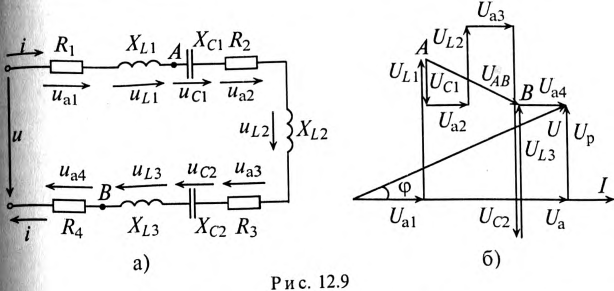
Напряжение на каком-либо участке неразветвленной цепи (рис. 12.9а), например на участке АВ, определяется так:_
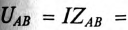
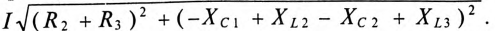
Вектор напряжения UAB показан на векторной диаграмме (рис. 12.96).
Пример 12.2
Напряжение, приложенное к неразветвленной цепи (рис. 12.10) U=220 В, частота тока сети f = 50 Гц. Начальная фаза тока 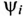 = 0.
= 0.
Сопротивление участков цепи: 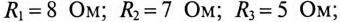
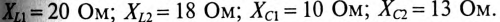
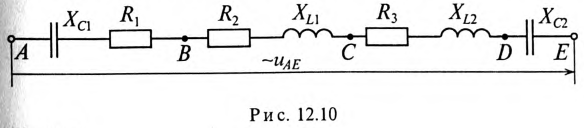
Требуется:
1. Вычислить ток цепи I и записать его мгновенное значение.
2. Записать мгновенное значение напряжения цепи иАЕ, определив предварительно угол ср и характер цепи.
3. Определить напряжение между точками АВ и CD.
4. Построить в масштабе векторную диаграмму цепи, определив едварительно напряжение на каждом сопротивлении.
5. Определить мощности S, Р и Q цепи.
6. Определить частоту, при которой в цепи наступит резонанс напряжений, и ток при резонансе.
7. Определить максимальную энергию, запасенную в магнитном поле катушек WmL и электрическом поле конденсаторов WmC. Как нужно изменить емкость конденсаторов, чтобы в цепи пил резонанс напряжений при частоте f = 50 Гц?
Решение
1. Для определения тока цепи I необходимо вычислить полное сопротивление цепи:
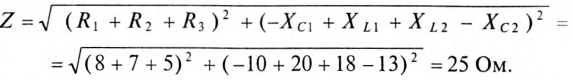
Действующее значение тока 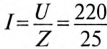 = 8,8 А, а амплитудное значение тока
= 8,8 А, а амплитудное значение тока 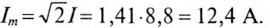
Угловая частота 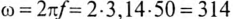 рад/с.
рад/с.
Мгновенное значение тока цепи:
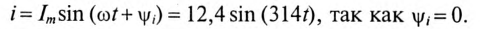
2. Угол сдвига фаз ф и характер цепи определяется через tg ф:
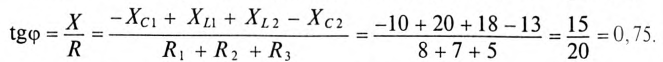
Таким образом, угол ф = 37° (из таблицы), характер цепи индуктивный (+ф).
Тогда мгновенное значение напряжения цепи
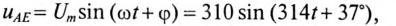
где 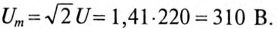
3. Напряжение на участках:
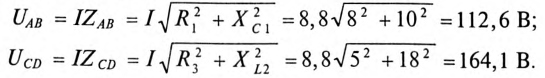
4. Для построения векторной диаграммы определяются напряжения:
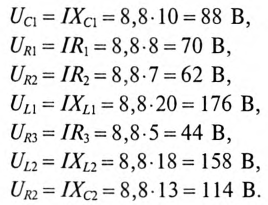
Векторная диаграмма цепи (отображает только характер участков, но не величины напряжений на них) изображена на рис. 12.11.
5. Полная мощность цепи 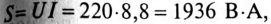 активная мощность Р=
активная мощность Р=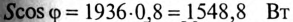 (так как
(так как 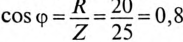 ), реактивная мощность
), реактивная мощность 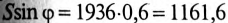 вар, (так как
вар, (так как 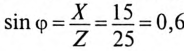 ).
).
6. Для определения частоты резонанса вычисляется индуктивность L и емкость С цепи:
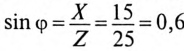
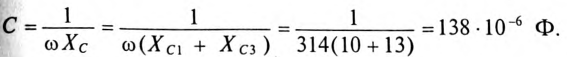
Тогда
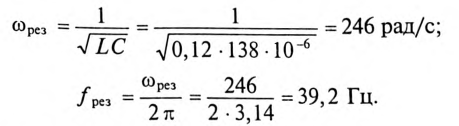
Ток цепи при резонансе 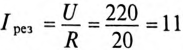 А.
А.
7. Максимальная энергия, запасенная в магнитном поле катушек:
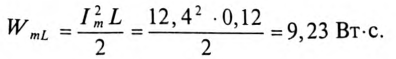
Максимальная энергия, запасенная в электрическом поле конденсаторов:
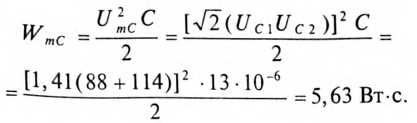
8. Условие резонанса XL = XC.
По условию задачи 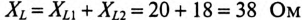 , а
, а 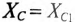
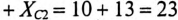 Ом. Этому Хс соответствует емкость С =
Ом. Этому Хс соответствует емкость С = 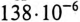 Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
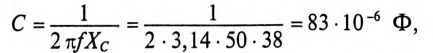
т. е. емкость конденсаторов нужно уменьшить на
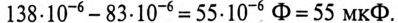
Разветвленная цепь синусоидального тока
Активный и реактивный токи:
Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.
Если к цепи, содержащей активное сопротивление R и индуктивное XL (рис. 13.1а), приложено синусоидальное напряжение 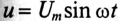 , то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в),
, то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в), 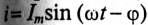 .
.
Векторная диаграмма в этом случае изображена на рис. 13.16.
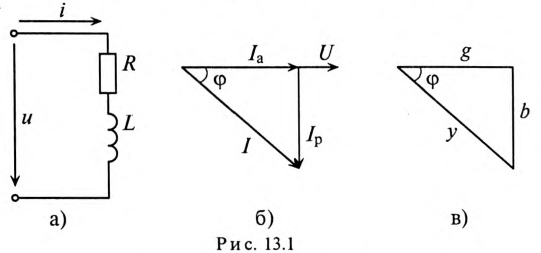
Ток цепи I (рис. 13.16) раскладывается на две составляющие, одна из которых  совпадает по фазе с напряжением, другая
совпадает по фазе с напряжением, другая  — сдвинута на 90°. Составляющая тока
— сдвинута на 90°. Составляющая тока  , совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока
, совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока  , имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
, имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
Активный и реактивный токи физического смысла не имеют. Они являются расчетными величинами, так как в неразветвленной цепи (рис. 13.1а) ток на всех участках имеет одинаковое значение. Однако понятия активный  и реактивный
и реактивный  токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
13.2. Проводимости
Из треугольника токов для рассматриваемой цепи (рис. 13.16) следует: 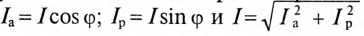 .
.
С другой стороны, известно, что 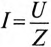 (см. (12.6)), a
(см. (12.6)), a 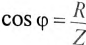 и
и 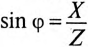 (см. (12.9)).
(см. (12.9)).
Тогда
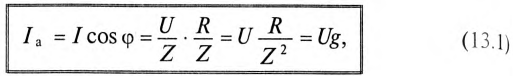
где g — активная проводимость цепи, равная

Величина, на которую умножают напряжение, чтобы получить ток, называют проводимостью.
А так как g определяет активный ток 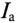 , то ее и называют активной проводимостью.
, то ее и называют активной проводимостью.
Таким образом, активная проводимость g определяется величиной активного сопротивления, деленного на квадрат полного (кажущегося) сопротивления цепи.
Величина реактивного тока определяется выражением
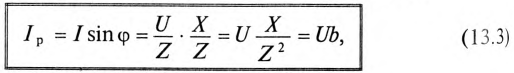
где b — реактивная проводимость цепи, равная

Величина полного тока цепи равна
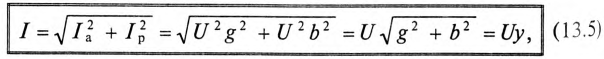
где 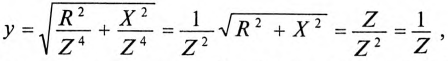 так как для цепи синусоидального тока с
так как для цепи синусоидального тока с 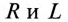 (рис. 13.1а)
(рис. 13.1а) 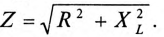
Таким образом, у — полная, или кажущаяся, проводимость цепи:

Полная (кажущаяся) проводимость цепи «у» является обратной величиной полного (кажущегося) сопротивления цепи.
Активная 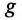 и реактивная
и реактивная 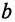 проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е.
проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е. 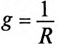 и
и 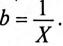
Если же в неразветвленной цепи (или ветви) включены сопротивления 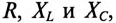 то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
Параллельное соединение катушки и конденсатора
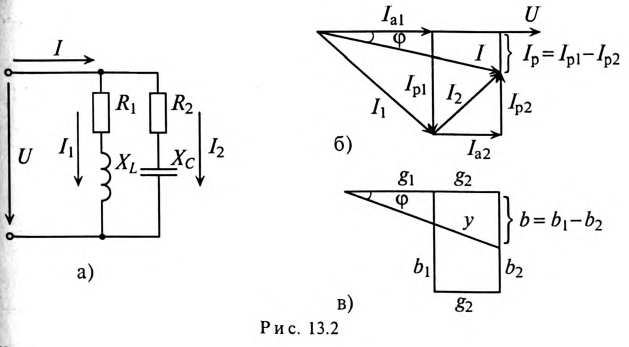
Если к источнику синусоидального напряжения 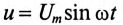 подключить параллельно реальную катушку с активным сопротивлением
подключить параллельно реальную катушку с активным сопротивлением 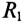 и индуктивным
и индуктивным 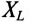 и конденсатор с активным сопротивлением
и конденсатор с активным сопротивлением 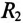 и емкостным
и емкостным 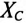 (рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
(рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
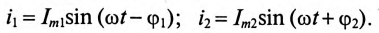
Действующие значения этих токов будут соответственно равны
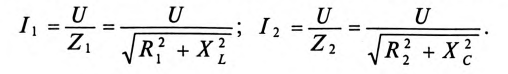
Ток в неразветвленной цепи 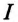 равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
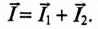
Для определения этого тока строится векторная диаграмма цепи (рис. 13.26), из которой следует:
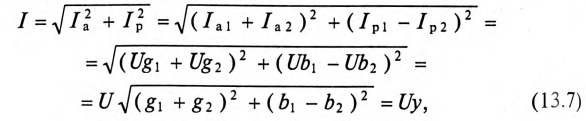
где 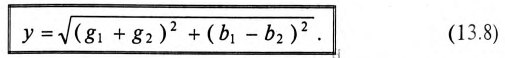
Таким образом, ток в неразветвленной части цепи 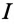 определяется произведением напряжения U и полной проводимости цепи
определяется произведением напряжения U и полной проводимости цепи 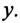
Реактивные проводимости в ветвях имеют различные знаки, так как сопротивления в ветвях различного характера (индуктивное и емкостное).
Треугольник проводимостей рассматриваемой цепи изображен на рис. 13.2в.
Характер разветвленной цепи определяется так же, как и неразветвленной. Если ток цепи 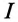 отстает от напряжения
отстает от напряжения 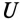 (как в рассматриваемом случае), то цепь индуктивного характера, если же ток
(как в рассматриваемом случае), то цепь индуктивного характера, если же ток 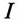 опережает напряжение
опережает напряжение 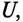 то цепь емкостного характера.
то цепь емкостного характера.
Резонанс токов
Резонанс токов в цепи (рис. 13.2а) с параллельным включением катушки и конденсатора (в различных ветвях) возникает при равенстве реактивных проводимостей в ветвях:
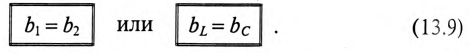
Выражение (13.9) является условием резонанса токов в разветвленных цепях синусоидального тока. Полная (кажущаяся) проводимость при этом условии
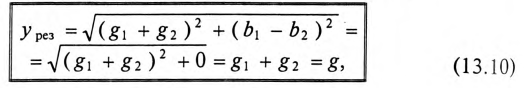
так как 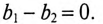
Таким образом, полная проводимость цепи при резонансе токов 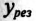 минимальна по величине и равна активной проводимости
минимальна по величине и равна активной проводимости 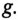 Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину
Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину

Реактивные токи в ветвях при резонансе токов равны между собой

Это равенство и определяет название «резонанс токов».
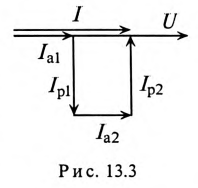
На основании равенства (13.12) строится векторная диаграмма при резонансе токов (рис. 13.3). Реактивные токи находятся в противофазе, поэтому ток в неразветвленной части цепи 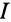 при резонансе токов равен активному току
при резонансе токов равен активному току 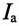 и совпадает по фазе с напряжением, т.е.
и совпадает по фазе с напряжением, т.е. 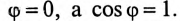 Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
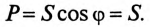
Эта активная мощность компенсирует потери на активном сопротивлении в параллельном резонансном контуре. Мощность (энергия), которая колеблется между электрическим полем конденсатора и магнитным полем индуктивности при резонансе, не является реактивной, так как не загружает источник и провода.
Частота резонанса токов в параллельном резонансном контуре может быть определена из условия резонанса токов, т. е. равенства реактивных проводимостей в ветвях 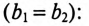
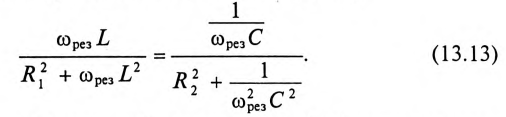
После ряда преобразований равенства (13.13) определяется частота резонанса токов
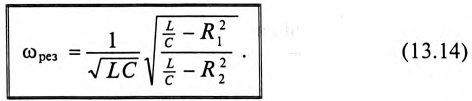
Резонансная частота зависит не только от параметров колебательного контура 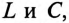 но и от активных сопротивлений в ветвях реального резонансного контура.
но и от активных сопротивлений в ветвях реального резонансного контура.
Если в резонансном контуре отсутствуют активные сопротивления в ветвях, то частота резонанса токов 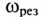 становится равной частоте собственных колебаний идеального резонансного контура
становится равной частоте собственных колебаний идеального резонансного контура
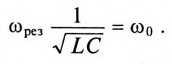
Если в резонансном контуре 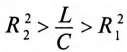 или
или 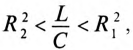 то резонанса токов добиться невозможно.
то резонанса токов добиться невозможно.
Резонанс токов нашел широкое применение в радиотехнике и выпрямительной технике (в резонансных фильтрах) и др.
Пример 13.1
Напряжение, приложенное к параллельно включенным катушке и конденсатору (рис. 13.4а), 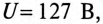 частота сети
частота сети 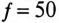 Гц. Параметры цепи:
Гц. Параметры цепи: 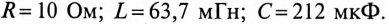 Определить:
Определить:
1) токи всех участков цепи: 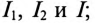
2) углы сдвига фаз этих токов относительно напряжения: 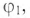
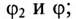
3) полную S, активную Р и реактивную Q мощности цепи;
4) частоту, при которой наступит резонанс токов в этой цепи. Построить векторную диаграмму.
Решение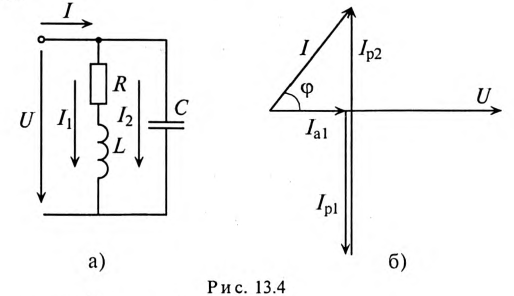
1. Сопротивление участков цепи:
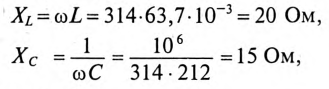
где 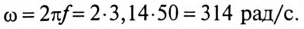
Сопротивление 1-й ветви:
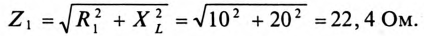
Токи в ветвях соответственно равны
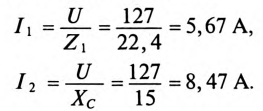
Для определения тока 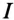 в неразветвленной части цепи определяются проводимости:
в неразветвленной части цепи определяются проводимости:
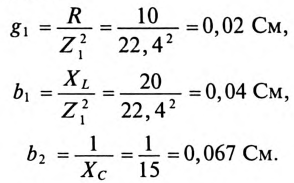
Тогда полная проводимость цепи будет равна
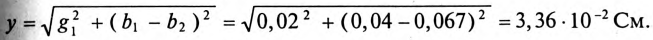
Ток в неразветвленной части цепи
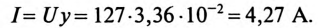
2. Углы сдвига фаз:
.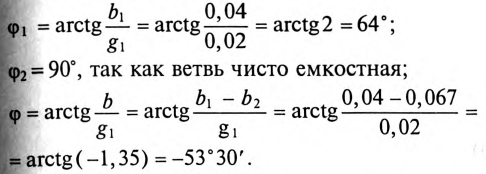
Знак «минус» перед значением угла 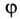 параллельного контура означает, что цепь имеет емкостной характер, так как
параллельного контура означает, что цепь имеет емкостной характер, так как 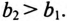
3. Полная мощность цепи 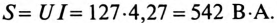
Активная мощность цепи 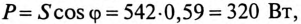 так как
так как 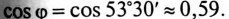
Реактивная мощность цепи 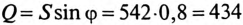 вар, так как
вар, так как 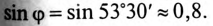
4. Угловая частота резонанса токов в цепи равна
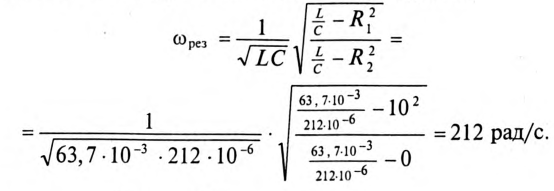
Откуда 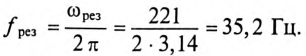
Для построения векторной диаграммы определяют активные и реактивные токи в ветвях:

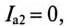 так как в ветви с емкостью отсутствует активное сопротивление, т.е.
так как в ветви с емкостью отсутствует активное сопротивление, т.е. 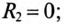
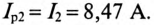
Векторная диаграмма для рассматриваемой цепи изображена на рис. 13.46.
На векторной диаграмме видно, что ток I опережает напряжение U на угол 53°30′ (цепь емкостного характера).
Коэффициент мощности
Номинальные параметры, т.е. мощность источника 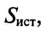 мощность потребителя
мощность потребителя 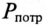 и коэффициент мощности
и коэффициент мощности 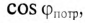 связаны следующим соотношением
связаны следующим соотношением

Из (13.15) следует, что чем меньше 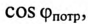 тем большую мощность
тем большую мощность 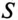 должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
Ток в цепи потребителя с определенным 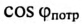 согласно выражению (12.11) равен
согласно выражению (12.11) равен
Из (13.16) видно, что чем меньше 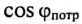 , тем больше ток потребителя
, тем больше ток потребителя 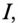 тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
Таким образом, низкий коэффициент мощности потребителя 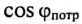 приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.
приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.  должен быть равен или больше 0,93
должен быть равен или больше 0,93 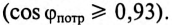
Однако  большинства электрических потребителей переменного тока меньше этой нормы. Так, например,
большинства электрических потребителей переменного тока меньше этой нормы. Так, например,  асинхронных двигателей, в зависимости от нагрузки, составляет
асинхронных двигателей, в зависимости от нагрузки, составляет 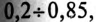 трансформаторов –
трансформаторов – 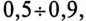 выпрямителей –
выпрямителей – 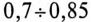 и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения 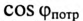 параллельно с ним подключаются конденсаторы (рис. 13.5а).
параллельно с ним подключаются конденсаторы (рис. 13.5а).
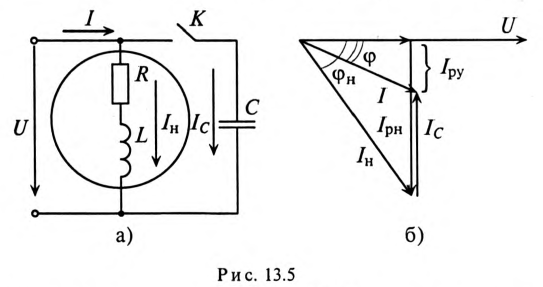
Из векторной диаграммы (рис. 13.56) видно, что с подключением конденсатора С (ключ К замкнут) появляется 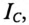 за счет которого уменьшается угол
за счет которого уменьшается угол 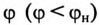 и увеличивается
и увеличивается 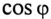 установки. При этом уменьшается ток цепи
установки. При этом уменьшается ток цепи 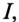 который до подключения конденсатора был равен току нагрузки
который до подключения конденсатора был равен току нагрузки 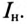
Для повышения коэффициента мощности 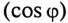 конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения
конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения 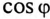 конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
Коэффициент мощности можно повысить, увеличив активную нагрузку. При этом увеличивается потребляемая энергия, что экономически нерационально (уменьшается КПД установки).
Пример 13.2
Асинхронный двигатель, включенный в сеть с напряжением 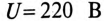 и частотой
и частотой 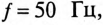 развивает на валу мощность
развивает на валу мощность 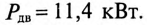 КПД двигателя
КПД двигателя 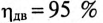 при
при 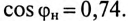 Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить
Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить 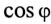 установки до 0,95.
установки до 0,95.
Решение
Мощность, потребляемая двигателем из сети:
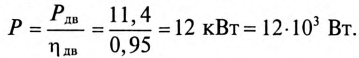
Ток нагрузки 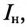 т.е. ток двигателя (рис. 13.5а), равен
т.е. ток двигателя (рис. 13.5а), равен
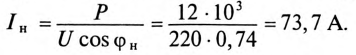
Реактивная составляющая тока двигателя 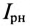 (рис. 13.56)
(рис. 13.56)
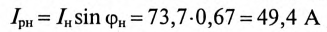
(по таблице 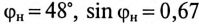 ).
).
Ток установки 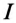 при подключении конденсатора, т. е. при
при подключении конденсатора, т. е. при 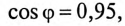 будет равен
будет равен

При 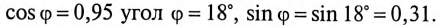 Реактивная составляющая тока установки (рис. 13.56)
Реактивная составляющая тока установки (рис. 13.56)
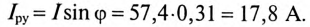
Ток конденсатора 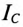 (рис. 13.56)
(рис. 13.56)
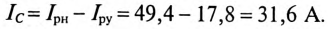
Емкостное сопротивление конденсаторов
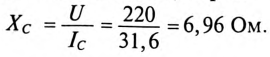
Емкость конденсаторов, которые нужно подключить параллельно двигателю для улучшения 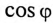 до 0,95:
до 0,95:
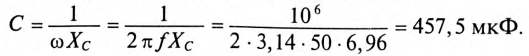
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле
Расчет электрических цепей переменного тока
Для электрической цепи, схема которой соответствует варианту задания и изображена на рис. 1.1-1.50, по заданным в табл. 1 параметрам и приложенному к цепи напряжению, определить токи во всех ветвях цепи. Определить активную, реактивную и полную мощности цепи. Построить в масштабе векторную диаграмму токов и напряжений.
Методические указания
Для правильного решения поставленной задачи необходимо изучить теорию электрических цепей однофазного синусоидального тока, усвоить основные формулы сопротивлений, проводимостей токов, напряжений; научиться применять для анализа и расчета закон Ома, уравнения Кирхгофа, метод проводимостей.
Все предлагаемые заданием электрические цепи являются смешанными, т.е. содержат последовательную ветвь и две параллельные. В каждой ветви имеются различные сопротивления, величины которых заданы.
Для примера рассмотрим обобщенную цепь, представленную на рис. 1.
 Общий ход решения задач подобного типа следующий. Необходимо преобразовать последовательно-параллельную цепь в простую последовательную цепь, заменив разветвленный участок цепи эквивалентной последовательной цепочкой.
Общий ход решения задач подобного типа следующий. Необходимо преобразовать последовательно-параллельную цепь в простую последовательную цепь, заменив разветвленный участок цепи эквивалентной последовательной цепочкой.
Прежде всего, необходимо методом проводимости определить параметры эквивалентной цепочки, которой может быть замещен разветвленный участок цепи.
В эквивалентной цепочке реактивное сопротивление будет индуктивным или емкостным в зависимости от знака эквивалентной реактивной проводимости. Дальнейшее решение сводится к определению активного и реактивного сопротивления цепи, а по ним полного сопротивления цепи.
По каждому сопротивлению цепи и заданному напряжению определяется общий потребляемый ток в цепи  . Чтобы определить ток в отдельных ветвях разветвленного участка, находим сначала напряжение между узловыми точками
. Чтобы определить ток в отдельных ветвях разветвленного участка, находим сначала напряжение между узловыми точками  , а затем и токи в ветвях
, а затем и токи в ветвях  .
.
После чего находим напряжение на указанном участке, активную, реактивную и полную мощности в цепи. Заканчиваем расчет построением векторной диаграммы токов и напряжений.
Возможно вам будут полезны данные страницы:
Алгоритм расчета
1. Вычисляем величины сопротивлений отдельных элементов цепи:

где 
 — в Генри (Гн),
— в Генри (Гн),  — в Фарадах (Ф).
— в Фарадах (Ф).
ВНИМАНИЕ: в задании L дается в мГн, С — в мкФ.
2. Вычисляем полные сопротивления ветвей:
 где
где 
3. Вычисляем активные проводимости параллельных ветвей:

4. Вычисляем общую эквивалентную активную проводимость  :
:

5. Вычисляем реактивные проводимости ветвей и общую эквивалентную проводимость  :
:

6. Изобразим эквивалентную схему, на которой сопротивления заменим проводимостями (рис.2).
 7. Заменим эквивалентные проводимости эквивалентными сопротивлениями, включенными последовательно (рис.З).
7. Заменим эквивалентные проводимости эквивалентными сопротивлениями, включенными последовательно (рис.З).
 8. Найдем общее сопротивление всей цепи: при сложении (реактивных сопротивлений учитывать знаки).
8. Найдем общее сопротивление всей цепи: при сложении (реактивных сопротивлений учитывать знаки).

9. Найдем общий потребляемый ток:

10. Найдем напряжение, приложенное к параллельному участку цепи:


12. Найдем напряжение на сопротивлении  :
:

13. Вычисляем мощности цепи:
 где
где 
Строим векторную диаграмму токов и напряжений, предварительно определив масштаб для векторов напряжений и векторов тока (рис.4).
 В качестве исходного вектора удобно принимать вектор напряжения, приложенного к параллельным ветвям, вектор
В качестве исходного вектора удобно принимать вектор напряжения, приложенного к параллельным ветвям, вектор  .
.
Относительно вектора  откладываем вектора токов ветвей
откладываем вектора токов ветвей  , предварительно определив углы
, предварительно определив углы  из уравнений:
из уравнений:

Ток в неразветвленной части цепи  (общий ток), находим векторным сложением токов
(общий ток), находим векторным сложением токов  . При построении векторов учитывать, что опережающий ток откладывается против часовой стрелки относительно вектора напряжения U
. При построении векторов учитывать, что опережающий ток откладывается против часовой стрелки относительно вектора напряжения U  а отстающий по фазе — по часовой стрелке.
а отстающий по фазе — по часовой стрелке.
Строим треугольник напряжений (масштабы для векторов токов и напряжений выбираем разные, выбирая их согласно полученных значений).
Так как  , необходимо определить угол (
, необходимо определить угол (  из уравнения:
из уравнения: 
Для построения вектора  из конца вектора
из конца вектора  проводим пунктирную линию параллельно
проводим пунктирную линию параллельно  , под углом
, под углом  к ней откладываем вектор
к ней откладываем вектор 
Если  положительная величина, вектор откладывается против часовой стрелки, если отрицательная величина — по часовой стрелке. Соединяем начало вектора
положительная величина, вектор откладывается против часовой стрелки, если отрицательная величина — по часовой стрелке. Соединяем начало вектора  с концом вектора
с концом вектора  и находим вектор
и находим вектор  , т.е.
, т.е. 
Пример с решением № 2
Для электрической цепи, схема которой изображена на рис. 2.1 — 2.17 (СМ. ВАРИАНТ ЗАДАНИЯ), по заданным в табл. 2 параметрам, определить фазные и линейные токи, ток в нейтральном проводе (для четырехпроводной схемы), активную мощность всей цепи и каждой фазы отдельно. Построить векторную диаграмму токов и напряжений.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Прежде чем приступить к расчету задания № 2, необходимо изучить теорию трехфазных цепей при соединении потребителей электрической энергии по схеме «звезда» и «треугольник». При этом надо особо обратить внимание на соотношение фазных и линейных напряжений при соединении потребителей звездой и соотношение фазных и линейных токов при соединении треугольником.

Для соединения потребителей треугольником:

Рассмотрим примеры расчета трехфазной цепи при соединении потребителей звездой и треугольником.
Электрическая цепь при соединении «звездой».
 Алгоритм расчета
Алгоритм расчета
1. Находим полное сопротивление фаз:

2. Находим фазные (линейные) токи:
 где
где 
3. Находим углы сдвига по фазе из выражений:

4. Находим активные мощности фаз:

5. Находим полную активную мощность цепи:

Строим с учетом масштаба векторную диаграмму токов относительно фазных напряжений (рис.6) и находим графически ток в нейтральном проводе:
 Диаграмму строим посредством отметок циркулем, предварительно задавшись масштабом, начав построение с фазных напряжений, например, из точки 0 (угол между направлением векторов 120°). Вычислив фазные токи, задавшись масштабом для токов, откладываем фазные токи под соответствующим углом сдвига по фазе относительно одноименного фазного напряжения.
Диаграмму строим посредством отметок циркулем, предварительно задавшись масштабом, начав построение с фазных напряжений, например, из точки 0 (угол между направлением векторов 120°). Вычислив фазные токи, задавшись масштабом для токов, откладываем фазные токи под соответствующим углом сдвига по фазе относительно одноименного фазного напряжения.
Проводим сложение векторов токов по правилам силового многоугольника и находим ток в нейтральном проводе  , измерив длину вектора в выбранном масштабе.
, измерив длину вектора в выбранном масштабе.
Пример 2. Электрическая цепь при соединении треугольником.
 Алгоритм расчета
Алгоритм расчета
1. Находим полное сопротивление каждой фазы:


где 
1. Находим значение углов сдвига по фазе из выражений:

4. Находим активные мощности каждой фазы:

5. Находим активную мощность всей цепи:
 Вт.
Вт.
6. Строим векторную диаграмму токов относительно векторов фазных напряжений для этой цепи, используя полученные цифровые данные (рис.8). Откладываем значения вычисленных фазных токов с учетом сдвига по отношению к своим фазным напряжениям.
 7. Определяем линейные токи.
7. Определяем линейные токи.
Линейные токи определяются графически с учетом масштаба. Каждый из линейных токов равен геометрической разности фазных токов согласно приведенных ранее уравнений для соединения потребителей энергии треугольником.
Вектор линейного тока соединяет концы векторов фазных токов, отложенных из точки О и направленных к уменьшаемому.
На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Источник
АКТИВНАЯ, РЕАКТИВНАЯ И ПОЛНАЯ МОЩНОСТИ ЦЕПИ
Умножив стороны треугольников напряжений (см. векторные диаграммы рис. 2.9, б, 2.10, б, 2.11, б) на ток I, получим треугольники мощностей.
Стороны треугольников мощностей соответственно означают:
— Р = UrI = I 2 r — активная мощность цепи, Вт, кВт (рис 2.9, г, 2.10, г, 2.11,г и ж);
— QL = ULI = I 2 xL — реактивная индуктивная мощность цепи, обусловленная энергией магнитного поля, вар, квар (рис. 2.9, г);
— QС = UСI = I 2 хС — реактивная емкостная мощность цепи, обусловленная энергией электрического поля, вар, квар (рис. 2.10, г);
— Q = QL — QС = I 2 x — реактивная мощность цепи, вар, квар (рис 2.11, г и ж), это та мощность, которой приемник обменивается с сетью;
— S = UI = I 2 z — полная мощность цепи. В • А, кВ • А (рис. 2.9, г, 2.10, г, 2.11, г и ж);
— cos φ = r/z = P/S — коэффициент мощности цепи (рис. 2.9, г, 2.10, г, 2.11, г и ж).
Из треугольников мощностей можно установить следующие связи между Р, Q, S и cos φ:
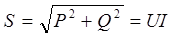
За единицу активной мощности принят ватт (Вт) или киловатт (кВт), реактивной мощности — вольтампер реактивный (вар) или киловольтампер реактивный (квар), полной мощности — вольтампер (ВА) или киловольтампер (кВ • А).
Реактивные (индуктивная, емкостная) мощности, обусловленные соответственно энергией магнитного поля индуктивности и электрического поля емкости, не совершают никакой полезной paботы, однако они оказывают существенное влияние на режим работы электрической цепи. Циркулируя по проводам трансформаторов, генераторов, двигателей, линий передач, они нагревают их. Поэтому расчет проводов и других элементов устройств переменного тока производят, исходя из полной мощности S, которая учитывает активную и реактивную мощности.
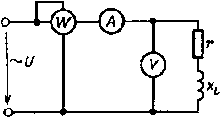
Рис. 2.13. Схема включения приборов для измерения активной, реактивной и полной мощностей цепи, а также ее параметров
Коэффициент мощности имеет большое практическое значение: он показывает, какая часть полной мощности является активной мощностью. Полная мощность и коэффициент мощности наряду с другими параметрами являются расчетными величинами и в конечном счете определяют габаритные размеры трансформаторов, генераторов, двигателей и других электротехнических устройств.
Измерение активной, реактивной, полной мощностей и cos φ, а также параметров цепи, например r и L, можно произвести с помощью ваттметра, амперметра и вольтметра, включенных в цепь по схеме, изображенной на рис. 2.13.
Ваттметр измеряет активную мощность Р цепи. Полная мощность цепи равна произведению показаний вольтметра и амперметра.
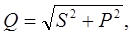
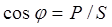
Активное сопротивление находят из формулы:
Полное сопротивление цепи
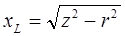
Индуктивность L определяют из формулы
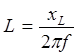
Пример 2.1. Приборы, включенные в цепь рис 2.13, показывают Р = 500 Вт, I = 5 А, U= 400 В.
Определить активное сопротивление r и индуктивность цепи L, если частота сети f = 50Гц.
Решение. Активное сопротивление цепи
r = P/I 2 = 500/5 2 = 20 Ом.
Индуктивное сопротивление цепи
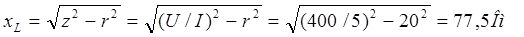
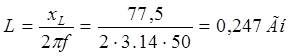
Пример 2.2. Определить ток, полную, активную и реактивную мощности, а также напряжения на отдельных участках цепи, изображенной на рис. 2.11, а. если r = 40 Ом. L = 0,382 Гн, С = 35,5 мкФ, U = 220 В, частота сети f = 50 Гц.
Решение. Индуктивное сопротивление цепи
Емкостное сопротивление цепи
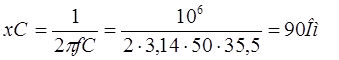
Полное сопротивление цепи
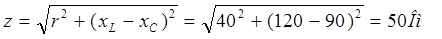
Ток в цепи:
I = U/z = 220/50 = 4,4 А.
Коэффициент мощности цепи:
Полная, активная и реактивная мощности:
S = UI = I 2 z = 220 • 4,4 = 4,42 • 50 = 970 В • А.
Р = S cos φ = I 2 r = 970 • 0,8 = 4,42 • 40 = 775 Вт;
Q = S sin φ = I 2 (xL — xС) = 970 • 0,56 = 4,42 (120 — 90) = 580 вар.
Напряжения на отдельных участках цепи:
Пример 2.3. Определить характер нагрузки, полную, активную и реактивную мощности цепи, в которой мгновенные значения напряжения и тока составляют:
Решение. Угол начальной фазы напряжения (ψ1 = 60°) больше, чем тока (ψ2 = 30°), поэтому напряжение опережает по фазе ток на угол φ = ψ1 — ψ2 = 60 — 30 = 30° и нагрузка имеет активно-индуктивный характер.
Полная мощность цепи:
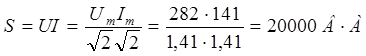
Активная мощность цепи:
Р = S cos φ = 20 000 cos 30° = 20 000 ( 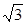 /2) — 17 300 Вт
/2) — 17 300 Вт
Реактивная мощность цепи:
Q = S sin φ = 20 000 sin 30° = 20000 • 0,5 = 10 000 вар.
Электрическая нагрузка.
Электрическая нагрузка — это нагрузка создаваемая в электрической сети включенными для работы в сети электроприемниками, она выражается в единицах тока или мощности. Присоединяются к электрическим сетям электроприемники в одиночку либо группами. Электроприемники могут входить в состав группы не только одинакового, а также различного назначения и режима работы. Зависит режим работы системы электроснабжения одинаковых приемников и их групп от режима работы или его сочетаний одиночных приемников либо их групп.
Характер нагрузки в сети может в процессе работы электроприемников оставаться неизменным, изменяться во всех или отдельных фазах, сопровождаться возникновением высших гармоник напряжения или тока. Ввиду этого электрическая нагрузка в сети бывает следующих типов:
— спокойная симметричная (преобладающее большинство трехфазных электроприемников);
К специфическим нагрузкам относятся резкопеременная, нелинейная и несимметричная нагрузка.
Резкими набросами и провалами тока или мощности характеризуется резкопеременная электрическая нагрузка. Неравномерная нагрузка фаз характерна для несимметричной нагрузки, вызывается она однофазными и трехфазными (реже) приемниками с неравномерной загрузкой фаз. В сети при несимметричной нагрузке возникают токи, которые имеют прямую, нулевую и обратную последовательности. Электроприемниками с нелинейной вольт-амперной характеристикой создается нелинейная нагрузка, при в сети ней появляются высшие гармоники напряжения или тока, происходит искажение синусоидальной формы напряжения или тока.
Созданию специфических нагрузок способствует работа электродуговых печей, полупроводниковых преобразовательных установок или сварочных установок. В основном эти установки принадлежат промышленным. Как известно, электрические сети промышленных предприятий связаны через трансформаторные подстанции с сетями сельскохозяйственного назначения, тогда можно считать, что на электросети сельскохозяйственного назначения оказывают влияние специфические электрические нагрузки промышленных предприятий.
Электроприемники сельскохозяйственного назначения по мощности подразделяются на три группы:
1. Большой мощности (больше 50 кВт)
2. Средней мощности (от 1 до 50 кВт)
3. Малой мощности (до 1 кВт)
Для работы некоторые электроприемники используют постоянный ток, а также токи повышенной частоты (до 400 Гц) или высокой (до 10 кГц).
Перерывы в электроснабжении могут допускать во время работы некоторые группы приемников, но существуют такие группы для которых перерыв в электроснабжении недопустим.
Электроприемники по надежности и бесперебойности электроснабжения разделены на 3 категории.
Первая категория включает электроприемники и комплексы электроприемников, при перерыве в электроснабжении которых может возникнуть опасность для жизни людей, расстройство технологического процесса, повреждение основного оборудования. Для этих приемников необходима возможность обеспечения электроэнергией не меньше, чем от двух независимых источников питания. На время автоматического восстановления электроснабжения от второго источника питания, допускается нарушение их электроснабжения.
Вторую категорию представляют электроприемники и комплексы электроприемников, при перерыве электроснабжения которых наблюдается массовый недовыпуск продукции, простои механизмов и рабочих.
От двух независимых источников питания необходимо обеспечивать электроснабжение приемников второй категории, допускается перерыв в электроснабжении только на время, необходимое для автоматического переключения на второй источник.
К третьей категории относятся электроприемники и комплексы электроприемников, которые не попадают по определение первых двух категорий. Их электроснабжение может осуществляться лишь от одного источника питания. На требующееся для проведения восстановительных работ время, но не больше суток допускается перерыв их электроснабжения.
Потреблением из сети не только активной, но также и реактивной мощности сопровождается работы подавляющего большинства электроприемников. Преобразуется активная мощность в механическую мощность на валу рабочей машины или теплоту, а на создание магнитных полей в электроприемниках расходуется реактивная мощность. Основными ее потребителями являются трансформаторы, асинхронные двигатели, индукционные печи, в которых отстает ток по фазе напряжения. Характеризуется потребление реактивной мощности коэффициентом мощности сosφ, представляющим отношение активной мощности Р к полной мощности S. Является удобным показателем коэффициент реактивной мощности tgφ, который выражает отношение реактивной мощности Q к активной Р (показывает, происходящее потребление реактивной мощности на единицу активной мощности).
Источниками реактивной мощности являются установки с опережающим током, они применяются для компенсации реактивной нагрузки с индуктивным характером цепи.
Электрическая нагрузка таким образом в электросети представляется активными и реактивными нагрузками.
При возникновении электрической нагрузки в распределительной сети, может возникать нагрев токоведущих частей (кабелей, проводов, обмоток трансформаторов и электродвигателей). Их чрезмерный нагрев приводит к преждевременному износу изоляции, поэтому не должна температура токоведущих частей превышать допустимые значения. Сечения кабелей и проводов необходимо выбирать по допустимому (расчетному) току нагрузки, для определения которого требуется определить расчетную мощность нагрузки.
При проектировании и эксплуатации СЭС за расчетную электрическую нагрузку принимается неизменная во времени нагрузка – Iрсч, вызывающая характеризующийся установившейся температурой максимальный нагрев токоведущих и с ними соседних частей. Допустимые значения нагрев превышать не должен. Для большинства кабелей и проводов установившееся тепловое состояние обычно наступает за 30 минут (около трех постоянных времени нагрева – 3Т, т. е. постоянная времени нагрева Т = 10 мин). В установках, имеющих номинальный ток нагрузки больше 1000 А, не менее 60 минут достигается установившаяся температура.
Параметры сети и характер нагрузки
Номинальным напряжением приемников электрической энергии называется напряжение, при котором они предназначены для нормальной работы.
Каждая электрическая сеть характеризуется номинальным напряжением приемников электрической энергии, в том числе и трансформаторов, которые от нее питаются. Отличие действительного напряжения на выводах приемника электрической энергии от номинального напряжения является одним из основных показателей качества электрической энергии. Напряжение у потребителя (подстанция, завод, трансформаторный пункт) или у отдельного приемника (электродвигатель, лампа накаливания) никогда не остается постоянным в течение суток. В процессе нормальной эксплуатации электрической сети наблюдаются плавные, закономерные отклонения напряжения от среднего уровня или резкие кратковременные колебания напряжения, вызванные внезапным изменением режимов работы приемников. Поддержать напряжение у потребителей неизменным и равным номинальному практически невозможно. Пределы допустимых отклонений напряжения, которые удобно выражать в процентах от номинального напряжения (δU), пользуясь формулой:

Очевидно, что отклонение напряжения положительно, когда напряжение у приемника U2 выше номинального Uн и отрицательно — в противоположном случае. Ответить на вопрос, какое из отклонений, положительное или отрицательное, лучше, в ряде случаев весьма трудно. Для этого каждый приемник рассматривают с точки зрения его назначения, места установки и режима работы, так как совсем не безразлично, применена ли лампа накаливания в светильнике наружного освещения или над рабочим местом в цехе. Во всех случаях следует руководствоваться нормами предельно допустимых отклонений напряжения у приемников.

Из таблицы видно, для одних и тех же приемников, например ламп накаливания, в условиях жилых помещений можно допустить отклонения в пределах ± 5%, так как это практически не отразится на жителях, в то время как снижение напряжения больше чем на 2,5 % у ламп рабочего освещения недопустимо из-за возможного брака. При снижении напряжения на 5 % номинального светового потока лампы накаливания снижается до 82,5 %, а люминесцентные лампы перестают работать устойчиво. При повышении напряжения, например, на 5 % срок службы лампы снижается до 350 часов вместо нормальных 1000 часов. Мощность нагревательных приборов, вращающий момент асинхронных двигателей и мощность конденсаторов изменяются пропорционально квадрату, то есть второй степени напряжения. Поэтому даже незначительные изменения напряжения резко ухудшают основные характеристики этих приемников.
Параметры электрической сети включают в себя параметры линейных элементов (индуктивные) сопротивления проводов и кабелей, и те же параметры трансформаторов. При решении вопросов, связанных с регулированием напряжения сети, составляется расчетная схема замещения, в простейшем случае представляющая собой последовательное соединение всех активных и индуктивных сопротивлений. для превращения схемы сети в схему замещения необходимо определить параметры линейных элементов, для чего необходимо знать протяженность линий, марку провода и его сечение, а также расстояние между проводами. К параметрам линейных элементов сети, оказывающим влияние на величину напряжения у приемников, относятся величины:
r0 — активное сопротивление на каждый километр, Ом;
x0 — индуктивное (реактивное) сопротивление на каждый километр линии, Ом.
Индуктивное сопротивление x0 для трехфазной линии тем больше, чем чем больше расстояние между проводами. Это объясняется тем, что соединение провода своим магнитным потоком уменьшают ЭДС самоиндукции в проводах и тем в большей степени, чем они ближе друг к другу. Для кабельных линий или проводов, расположенных в одной трубе, расстояние между отдельными жилами незначительно и поэтому x0, близко к 0,08 Ом/км. В линиях постоянного тока индуктивное сопротивление отсутствует, так как там нет переменного магнитного поля. Для заводских сетей, проложенных на изоляторах или роликах, при расстояниях между проводами 50-150 мм индуктивное сопротивление составляет примерно 0,3 Ом/км, а для воздушных сетей близко к 0,4 Ом/км.
Сопротивления линий могут быть легко получены по формулам:

где l — протяженность линии, км.
В заводских сетях схема замещения силового трансформатора, связывающего сеть высокого и низкого напряжений, принимаются состоящей только из последовательно соединенных активного Rт и индуктивного Xт сопротивлений. Для определения этих параметров необходимо воспользоваться следующими данными заводского паспорта трансформатора или по данным ГОСТ: номинальная мощность трансформатора Sн, кВА; номинальное линейной напряжение обмотки низшего или высшего напряжения Uн, кВ; потери в обмотках или потери короткого замыкания ΔPкз, кВт; напряжение короткого замыкания, uк, %.
Для расчета используются формулы:

Электроснабжение промышленных предприятий осуществляется, как правило, по распределительной воздушной или кабельной сети 6, 10 или 35 кВ. Распределительная сеть высокого напряжения через трансформаторы связана с сетью низкого напряжения. параметры сети высокого, низкого напряжений и самого трансформатора можно только тогда связывать электрической схемой замещения, когда все они предварительно будут рассчитаны или, как говорят, приведены к одному напряжению, принятому за базисное. Пересчет сопротивлений на «базисное» напряжение и получение «приведенных» сопротивлений производится по формулам:

где R’, X’ — приведенные величины активного и реактивного сопротивлений; U’ — базисное, обычно высшее напряжение трансформатора; Uн — номинальное напряжение того участка сети, на котором находится пересчитываемое сопротивление.
После приведения сопротивлений к одному напряжению сеть, имеющую одну ступень трансформации, можно рассматривать как сеть одного базисного напряжения. Схема замещения для сети с одной ступенью трансформации приведена на рисунке ниже.

Приемники электрической энергии могут быть разделены на две группы.
К первой из них следует отнести приемники, в которых электрическая энергия целиком переходит в тепло, например лампы накаливания, дуговые печи, нагревательные приборы обычного типа.
Ко второй группе относятся приемники, действие которых невозможно без наличия переменного магнитного поля. К ним относятся все электродвигатели переменного тока, индукционные печи, трансформаторы и т.д. В этих приемниках энергии в течение четверти периода накапливается магнитное поле, в течение следующей четверти уходит из магнитного поля обратно к источнику. Эти чередующиеся перемещения энергии в линии вызывают протекание по линии дополнительного тока, называемого намагничивающим или реактивным Iр. Ток этот отстает по времени от напряжения на четверть периода (0,005 секунд). Для пояснения процессов, происходящих в цепях переменного тока, принято пользоваться тригонометрическим соотношением между сторонами прямоугольного треугольника ОАВ (рисунок ниже).

При этом ток I рассматривается как вектор, совпадающий с гипотенузой треугольника, а катеты рассматриваются как составляющие тока — активная Iа и реактивная Iр. Амперметр, включенный в рассечку линии, показывает величину тока I, проходящего по цепи, из которого только часть Iа обеспечивает развитие активной мощности. Реактивная слагающая тока Iр есть следствие процесса перетока энергии магнитного поля, которая загружает сеть, создавая в ней дополнительные потери энергии и напряжения. Чтобы судить об экономичности использования сети и оборудования по величине тока и напряжения при наличии реактивной составляющей тока, используется как называемый коэффициент мощности, который из векторной диаграммы определяется как:
cosф = P/ S или cosф = Iа / I.
Подобные соотношения справедливы и для мощности одной фазы трехфазной системы. Активная слагающая тока Iа = I·cosф входит в выражение активной мощности, определяя ее при заданном напряжении U:
Реактивная слагающая тока Iр = I· sinф входит в выражение реактивной мощности, определяя ее при заданном напряжении U:
Коэффициент мощности для осветительной или, как говорят, чисто активной нагрузки близок к единице. При выборе способа и средств регулирования напряжения на зажимах трехфазного приемника с симметричной нагрузкой фаз необходимо, кроме параметров питающей линии, установить характер самой нагрузки, то есть активную и реактивную составляющие тока (мощности). проще всего это можно осуществить с помощью имеющихся практически у каждого потребителя электросчетчиков «активной» и «реактивной» энергии.
Для школьников.
Рассмотренные в предыдущих трёх статьях электрические цепи переменного тока. содержащие только активное, только емкостное и только индуктивное сопротивления были взяты для того, чтобы полнее раскрыть свойства перечисленных сопротивлений.
В реальных электрических цепях присутствуют все перечисленные сопротивления: активное, индуктивное, емкостное.
Сейчас будем говорить о цепях, содержащих последовательно соединённые активное сопротивление, катушку индуктивности и конденсатор.
Нам предстоит найти полное сопротивление показанной на рисунке цепи и разность фаз между действующими значениями тока и напряжения в ней.
Мгновенное значение приложенного к цепи напряжения (на зажимах цепи) складывается из мгновенных значений напряжений на каждом сопротивлении, то есть будет равно сумме мгновенных напряжений на активном, индуктивном и емкостном сопротивлениях:
Но действующее значение напряжения на зажимах цепи U не будет равно алгебраической сумме напряжений на каждом участке цепи из-за разности фаз между током и напряжением U на каждом сопротивлении (активном, индуктивном, емкостном).
Для нахождения связи между перечисленными напряжениями удобно пользоваться векторной диаграммой.
Векторная диаграмма – это графическое изображение значений периодически изменяющихся величин и соотношений между ними при помощи направленных отрезков – векторов.
Например, мы знаем, что напряжение на зажимах цепи переменного тока меняется по синусоидальному закону, то есть колебания напряжения сети изображается синусоидой.
Мгновенные значения напряжения внешнего источника можно рассматривать ещё как проекции вектора напряжения U (вектора ОВ) на вертикальную ось при равномерном вращении этого вектора против часовой стрелки.
Точно также векторами можно изобразить переменный ток в цепи, переменные напряжения на активном сопротивлении, на емкостном и индуктивном сопротивлениях.
Колебания перечисленных величин имеют одну частоту, но сдвинуты по фазе относительно друг друга.
Их взаимное расположение со временем не меняется. Тогда все перечисленные вектора можно показать на одной диаграмме.
Действующее значение вектора напряжения внешнего источника U будет равно геометрической сумме векторов напряжений на каждом сопротивлении цепи.
Такое сложение векторов значительно проще сложения синусоид, поэтому векторные диаграммы применяют очень часто.
Ниже рассказано как построена диаграмма, изображённая на рис. 15, которая решает задачу нахождения полного сопротивления рассматриваемой электрической цепи и нахождения сдвига фаз между током и напряжением.
Как видим из формулы закона Ома, полное сопротивление цепи не равно простой сумме активного R и реактивного сопротивлений.
Индуктивное и емкостное напряжения имеют разные знаки – они направлены навстречу друг другу.
Итак, полное сопротивление цепи переменного тока:
Индуктивное сопротивление:
Емкостное сопротивление:
На рис 15 прямоугольный треугольник векторной диаграммы составлен следующими векторами: вектором активного напряжения,
вектором индуктивного напряжения
вектором емкостного напряжения:
и вектором действующего напряжения U стороннего источника.
Из диаграммы, применив закон Пифагора, получим выражение для действующего напряжения:
Если каждое из этих напряжений (рис. 15) разделить на ток, то получим такой же треугольник, составленный сопротивлениями.
Прилежащий к углу катет даёт активное сопротивление цепи R, противолежащий катет – общее реактивное сопротивление цепи X, а гипотенуза треугольника даёт полное сопротивление цепи Z, состоящей из последовательно соединённых активного, индуктивного и ёмкостного сопротивлений..
Из представленного треугольника сопротивлений получаем соотношение:
то есть сдвиг фаз (угол фи) между током и напряжением в цепи определяется отношением реактивного сопротивления цепи к её активному сопротивлению.
Возможны следующие случаи:
Когда индуктивное сопротивление больше емкостного, то есть когда в цепи преобладает индуктивность, то ток отстаёт от напряжения на угол “фи”.
Когда индуктивное сопротивление меньше емкостного, то есть когда в цепи преобладает емкостное сопротивление, то ток опережает напряжения на угол “фи”.
Из треугольника сопротивлений получаем ещё такое выражение:
то есть
определяется отношением активного сопротивления цепи к её полному сопротивлению. Его называют коэффициентом мощности.
Значение коэффициента мощности определяет активную (полезную) мощность цепи.
Посмотрим, как получают выражение для мощность цепи переменного тока.
Мгновенное значение мощности равно произведению мгновенных значений напряжения и силы тока, которые выражаются формулами:
Взяв произведение мгновенных значений тока и напряжения и проанализировав полученное выражение, придём к выводу, что мощность может быть как положительной (когда энергия от источника поступает в цепь), так и отрицательной (когда уходит из цепи в источник).
Практически важно знать среднюю за период мощность, так как только средняя мощность характеризует энергию, потребляемую цепью за единицу времени.
После математических преобразований получается следующее выражение для средней мощности, которую можно называть просто мощностью цепи:
то есть мощность электрической цепи переменного тока равна произведению действующих значений напряжения и силы тока на косинус угла между током и напряжением,
Косинус сдвига фаз между током и напряжением назвали коэффициентом мощности.
Видим, что коэффициент мощности оказывает очень большое влияние на мощность электрической цепи.
Коэффициент мощности достигает максимального значения, равного единице, при угле “фи” (сдвиге фаз) равном нулю или когда индуктивное сопротивление равно емкостному сопротивлению:
При этом условии цепь переменного тока имеет минимальное сопротивление, равное активному сопротивлению цепи.
Ток же в цепи в этом случае достигает максимального значения (явление резонанса).
Приложенное к цепи напряжение U равно активному напряжению (напряжению на активном сопротивлении R).
Но при этом есть и индуктивное напряжение и равное ему по модулю, но противоположное по направлению (сдвинутое по фазе на половину периода) емкостное напряжение.
Причём они могут достигать достаточно больших значений, гораздо больших, чем напряжение сети U. Реактивные напряжения (индуктивное, емкостное) будут превышать напряжение сети U во столько раз, во сколько раз реактивные сопротивления (индуктивное, емкостное) будут больше активного сопротивления R.
Поэтому рассмотренное явление резонанса называется резонансом напряжений.
При резонансе мгновенные мощности в реактивных участках цепи (в катушке индуктивности и конденсаторе) равны и противоположны по знаку. Это значит, что увеличение энергии магнитного поля в катушке индуктивности происходит в результате уменьшения электрической энергии запасённой в конденсаторе, и наоборот, а энергия генератора расходуется только на активном сопротивлении.
Для электрической цепи промышленного тока резонанс вреден, так как может привести к пробою изоляции катушки и конденсатора.
По этой причине коэффициент мощности на предприятиях поднимают до 0,9 – 0,95, чтобы получить большую мощность, но чтобы не получить явление резонанса.
Какие меры применяются для повышения коэффициента мощности на промышленных предприятиях будет сказано позднее.
Пример.
В цепь переменного тока (120В, 50 Гц) последовательно включены катушка с активным сопротивлением 3 Ом и индуктивным сопротивлением 4 Ом и конденсатор. При какой ёмкости конденсатора наступит резонанс напряжений? Какими будут при этом ток в цепи, активное, индуктивное и емкостное напряжения?
При резонансе емкостное сопротивление равно индуктивному:
Емкостное сопротивление равно 4 Ом:
Отсюда найдём ёмкость конденсатора, при которой наступит резонанс в цепи. Эта ёмкость равна 0,0008 Ф.
Ток в цепи:
равен 40 А.
Анодное напряжение:
равно 120 В.
Емкостное напряжение
(и равное ему по модулю, но противоположное по направлению) индуктивное напряжение, будут иметь значения по 160 В, то есть больше напряжения сети, равного 120 В.
Таким образом, при последовательном соединении активного сопротивления, индуктивности и ёмкости (при равенстве индуктивного и емкостного сопротивлений) наступает резонанс напряжений, когда индуктивное и емкостное напряжения больше напряжения на источнике, в чём убедились, рассмотрев пример.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись : Катушка индуктивности в цепи переменного тока. Индуктивное сопротивление.
Следующая запись : Расчёт цепей переменного тока, содержащих активное сопротивление, индуктивность и ёмкость,
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58 .
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70. .
Электрический ток проводимости в
металлах представляет собой направленное
движение свободных электронов. Скорость
электронов и направление их движения
определяется значением и полярностью
приложенного к проводнику напряжения.
При движении электроны сталкиваются
с атомами проводника, и их кинетическая
энергия превращается в тепловую энергию,
которая идет на нагрев проводника и
рассеивание в окружающую среду. Этот
активный процесс является необратимым
и количественно определяется сопротивлением
R. Поэтому его называют
активным сопротивлением. Как правило,
различают активное и омическое
сопротивления. При рассмотрении цепей
переменного тока сопротивление R
называют активным, так как оно больше
сопротивления постоянному току. При
рассмотрении цепей постоянного тока
сопротивление R называют
омическим.
(Если через один и тот же проводник
пропускать переменный и постоянный
ток, то для того, чтобы выделилось одно
и то же количество теплоты, величина
переменного тока должна быть больше,
чем постоянного).
Элементы электрической цепи, обладающие
только активным сопротивлением R,
называют резисторами. Все элементы
электрической цепи – провода, обмотки,
реостаты – обладают активным
сопротивлением, все они нагреваются
при пропускании тока.
Кроме активного сопротивления существует
еще индуктивное, емкостное, реактивное,
полное.
Пусть к зажимам цепи с активным
сопротивлением R приложено
напряжение источника питания.

По закону Ома для мгновенных значений
для этой цепи
![]()
,
отсюда
![]()
![]()
![]()
– закон Ома для амплитудных значений.
Разделив левую и правую части этого
выражения на
,
получим
![]()
– закон Ома для действующих значений
(![]()
,![]()
– связь действующего значения с
амплитудным).
![]()
– закон Ома в комплексной форме.
Комплексное действующее значение тока
![]()
.
Поскольку ток и напряжение совпадают
по фазе, как видно из формул для мгновенных
значений, то можно представить изменение
тока и напряжения на временной диаграмме
следующим образом:
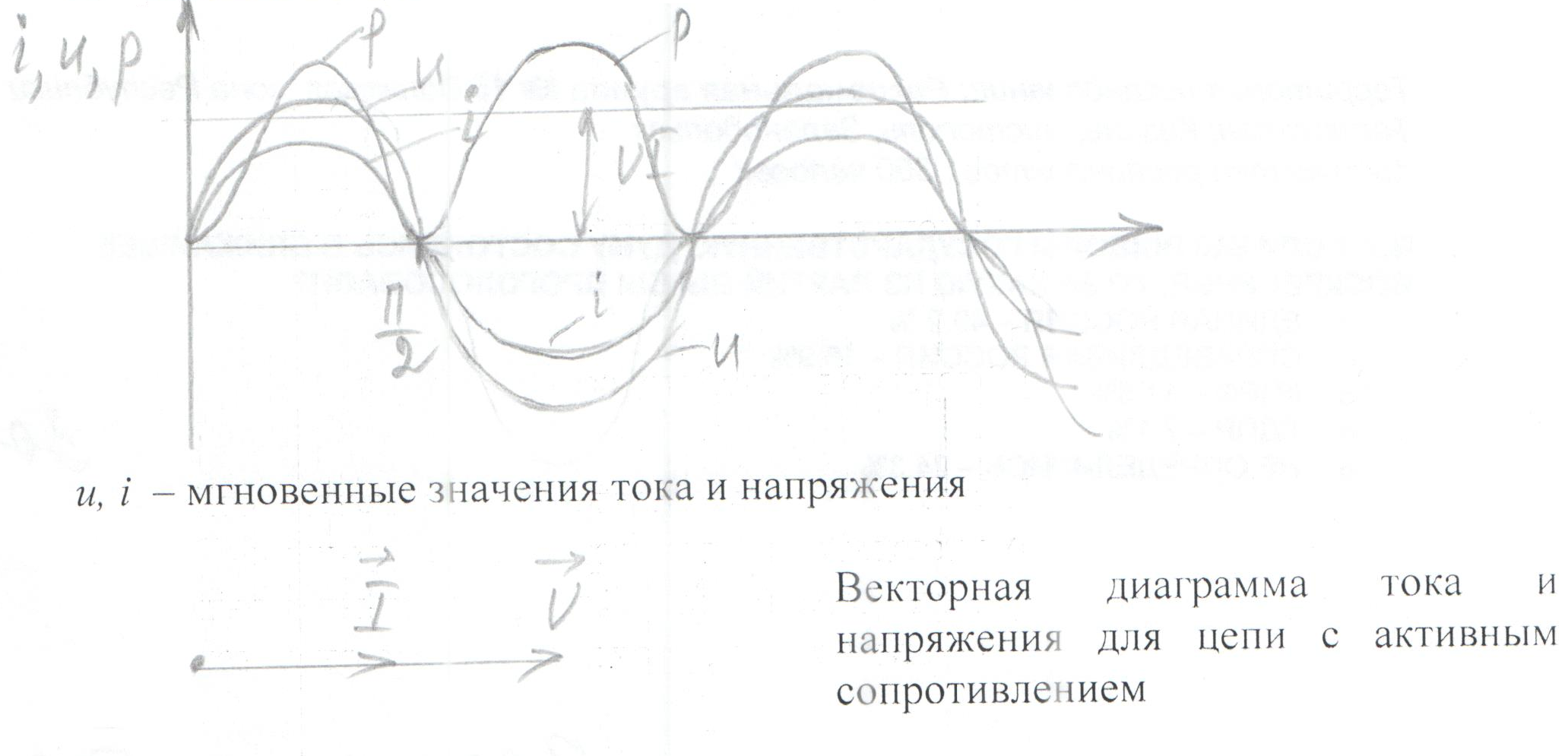
5. Мощность в цепи с активным сопротивлением
Мгновенная мощность
Мощность определяет
скорость расхода энергии, и для цепей
переменного тока также является
переменной величиной.
![]()
Т.к.
![]()
,
то
![]()
![]()
Из формулы
видно:мгновенная мощность остается
всегда положительной и колеблется около
уровня UI
(см. график).
С энергетической
точки зрения, положительная мощность
– это мощность, которая поступает из
генератора в нагрузку, а отрицательная
– та, которая возвращается обратно.
Первая мощность называется активной,
вторая – реактивной. Через активное
сопротивление проходит только активная
мощность.
Средняя мощность
Для определения
расхода энергии за длительное время
пользуются средним значением мощности.
Такую мощность еще называют активной
P
= UI.
Активная мощность
обозначается [P],
единица измерения Ватт (Вт), (кВт), (МВт).
6. Электрическая цепь с индуктивностью
Индуктивность
можно определить как меру магнитной
инерции элемента в отношении
электромагнитного поля. По смыслу
индуктивность в электротехнике можно
сравнить с массой в механике. Чем больше
индуктивность элемента, тем медленнее
и тем большую энергию магнитного поля
он запасает.
Индуктивностью,
индуктивным сопротивлением обладают
в разной мере все элементы электрической
цепи переменного тока. Особенно велика
она у обмоток или катушек, состоящих из
большого числа витков. В цепях постоянного
тока индуктивность равна нулю, поскольку
ток не меняется со временем и проявляется
лишь при переходных режимах.
Рассмотрим электрическую цепь, состоящую
из источника и катушки индуктивности.
|
|
Под действием |
В результате этого
вокруг катушки возникает переменное
магнитное поле, и в катушке наводится
э.д.с. самоиндукции.
Если R
= 0, то напряжение источника целиком идет
на уравновешивание этой э.д.с. Следовательно,
![]()
Т.к. по закону
электромагнитной индукции
![]()
,
то
![]()
или
![]()
,
где
![]()
.
Сопоставив
выражения для мгновенных значений тока
и напряжения, можно видеть, что напряжение
в цепи с индуктивностью опережает по
фазе ток на
![]()
.
Т.О, временная
диаграмма для тока и напряжения выглядит:
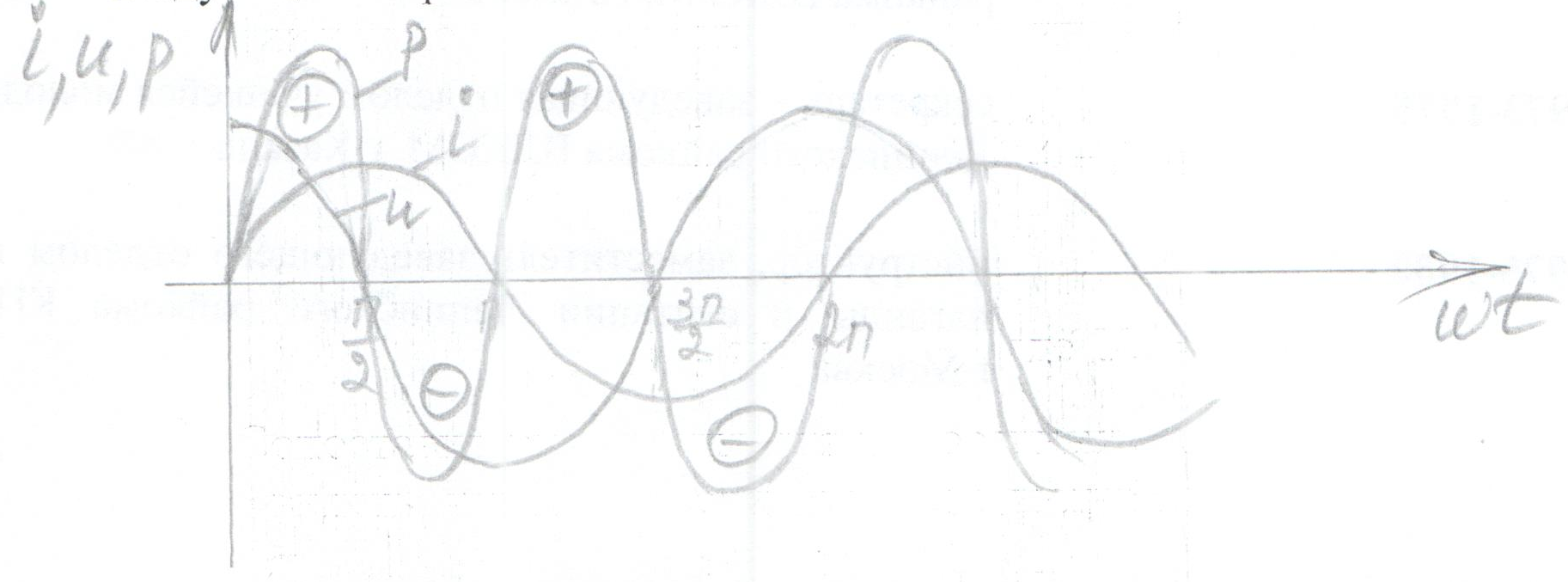
|
|
Векторная |
,
![]()
– индуктивное
сопротивление цепи;
![]()
:
видно, что с увеличением частоты
увеличивается индуктивное сопротивление.
Закон Ома для цепи
с индуктивностью
Закон Ома для
амплитудных значений для цепи с
индуктивностью:
![]()
.
Разделив левую и
правую части этого выражения на
,
получим закон Ома для действующих
значений
![]()
.
Закон Ома в
комплексной форме
![]()
,
j
обеспечивает
сдвиг фаз на
между I
и U
на комплексной плоскости.