Что такое активное сопротивление катушки
Содержание
- 1 Катушка
- 2 Конструкция и разновидности
- 3 Принцип работы
- 4 Индуктивность
- 5 Активное сопротивление
- 6 Постоянный ток
- 7 Переменный ток
- 8 Замер сопротивления и формула расчета
- 9 Заключение
- 10 Видео по теме
Одной из наиболее важных радиотехнических деталей является катушка индуктивности. Статья раскроет тему, что такое активное сопротивление катушки. Также будет дана информация о назначении и принципе действия этого элемента, приведена формула расчета сопротивления.
Катушка
Катушка индуктивности представляет собой металлический или ферритный сердечник, на который намотано несколько витков медного провода. Элемент обладает следующими свойствами:
- За счет индуктивности ограничивается скорость изменения токов.
- С увеличением частоты тока катушка способна увеличить свое сопротивление (скин-эффект).
- Создает магнитное поле.
- Увеличивает и накапливает напряжение.
- Создает сдвиг фаз переменного тока.
- Пропорционально скорости движения тока создает ЭДС самоиндукции.

Все эти свойства находят применение при разработке радиоприемных устройств, генераторов частоты, тестеров, магнитометров и других видов сложного оборудования.
Конструкция и разновидности
Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
- Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
- Тороидальная. В такой катушке соленоид выполнен в форме «тора».
- Многослойный тип, имеет несколько рядов обмотки.
- Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
- Универсальная, может совмещать сразу несколько вариантов обмотки.

Независимо от конструкции, все катушки работают по одному и тому же принципу.
Принцип работы
Катушка индуктивности работает только при прохождении электрического тока через набор витков обмотки. При подключении элемента к электрической цепи, по витку начинает двигаться ток. За счет взаимодействия провода с металлическим сердечником создается магнитный поток. Поток полностью пропорционален индуктивности катушки и величине тока. Величину магнитного потока можно рассчитать по следующей формуле: Ф=L×I.
Элементами формулы являются:
- «Ф» — величина магнитного потока.
- «L» — индукция.
- «I» — величина тока.

Количество витков влияет на величину ЭДС самоиндукции. Витки взаимодействуют не только с сердечником, но и между собой, что приводит к увеличению ЭДС.
В цепи переменного напряжения, величина ЭДС способна спровоцировать разность фаз напряжения и тока вплоть до 90 градусов.
Индуктивность
Индуктивностью катушки является способность к накапливанию электричества. Этот параметр зависит от:
- Числа витков.
- Сечения и длины провода.
- Конструктивных особенностей детали.
- От материала, длины, диаметра и формы сердечника.
- От расстояния между витками.
- Наличия экрана.
В радиоэлектронике не принято указывать значение индуктивности. Производители маркируют детали числом витков и указывают тип сердечника.
Активное сопротивление
Катушка индуктивности, не подключенная к электрической цепи, имеет только активное сопротивление.

Оно создается медным проводом и зависит от его длины, сечения. Активное сопротивление способно нарастать только после подключения в цепь. В этом случае процессы, протекающие внутри элемента, зависят от типа тока.
Постоянный ток
В подключенной к постоянному току катушке индуктивности создается магнитное поле. Его величина зависит от числа витков на сердечнике. При этом, ЭДС самоиндукции возникает при движении магнитного потока, который в зависимости от своей силы и скорости, выталкивает часть напряжения на поверхность обмотки.

За счет образования ЭДС, возникает эффект занижения нарастания тока в этой цепи. Ток, имея определенную силу, не способен нарасти мгновенно, так как на него действует сопротивление катушки. Постепенно преодолевая ограничение, ток плавно нарастает и достигает нормальных значений. Скорость такого переходного процесса рассчитывается с использованием следующих значений:
- «L» — индуктивность, генри;
- «R» — сопротивление электрической цепи, ом. Берется значение всей схемы с катушкой;
- «t» — время переходного процесса, сек.
Формула расчета выглядит следующим образом: t=L/R. В этой формуле также используется число витков элемента. Например, t=5×0.7/70=0.05 секунд, где 5 — число витков.
Для катушек индуктивности с первичной и вторичной обмоткой, ЭДС индуктивности протекает немного иным способом. Это различие создается за счет разницы сечений витков. В такой детали ЭДС не препятствует увеличению напряжения, а направляется вместе с прерванным током в одном направлении.
В трансформаторах первичная обмотка создает эффект сильного увеличения напряжения на контактах выхода. Этого удается достичь за счет изменения силы тока на первичной обмотке. Учитывая мгновенно изменение силы тока (одномоментное размыкание), во вторичной обмотке наводится импульс э.д.с амплитудой в десятки киловольт. Примером такого явления является катушка зажигания автомобиля. Ее магнитное поле позволяет достичь напряжения в тысячи вольт, несмотря на то, что сама она работает от аккумулятора с напряжением 12 вольт.
Переменный ток
Переменный ток сильно отличается от постоянного. Поэтому и его влияние на катушку индуктивности так же будет сильно отличаться. Помимо активного сопротивления, катушка подключенная к источнику переменному току, обладает еще и индуктивным.

Активное сопротивление не подключенной в цепь катушки зависит только от марки провода, его длины и сечения. При замере сопротивления отключенной от цепи катушки, тестер покажет только способность самого провода сопротивляться прохождению тока. По своей сути, активное сопротивление этого элемента будет равно 0 + подключенный резистор. При таком соотношении, катушка с ее 0 сопротивлением является идеальной. Для более точного измерения сопротивления в состоянии покоя, важно чтобы деталь была полностью отключена от цепи. При замере на схеме, сопротивление будет увеличено за счет параметров других радиодеталей.

Индуктивное сопротивление возникает только после подключения катушки в цепь переменного тока. Оно зависит от частоты тока и числа витков. Индуктивное сопротивление можно определить, используя простую формулу: XL=2×π×f×L. В данном выражении:
- «XL» — индуктивное сопротивление.
- «π» — число «пи», равное 3.14.
- «f» — частотная характеристика тока.
- «L» — индуктивность.
При прохождении переменного тока по виткам катушки, создается эффект вытеснения магнитными потоками доли токов. Это свойство схоже с влиянием постоянного тока. Главное отличие заложено в боковом вытеснении. Магнитное поле каждого витка оказывает давление на поле последующего витка. Таким образом происходит увеличение активного сопротивления.
Данный эффект увеличивается в зависимости от сечения провода, его проводимости и температуры. Эффект близости, сильно влияющий на увеличение активного сопротивления, снижают за счет подбора сечения обмоточного провода. Снижение эффекта близости недопустимо за счет увеличения расстояния между витками. Такой подход влияет на реактивное сопротивление и мощность магнитного поля.

В итоге активное сопротивление при подключении катушки к источнику переменного тока обладает следующими свойствами:
- Взаимодействует с параметрами индуктивного сопротивления.
- Способно занижать скорость магнитного потока.
- Создает сдвиг фаз напряжения и тока.
- При работе в условиях больших токов, активное сопротивление катушки увеличивает температуру самого компонента и всей цепи в целом. Нагрев часто происходит по причине непрочных контактов, неправильно подобранного сечения проводов на выходе и сильной нагрузки в общей сети.
В электротехнике существует ряд разновидностей экранированных катушек индуктивности. Такие экран часто делают из стали или алюминия. Они необходимы для снижения воздействия магнитного поля на ближайшие элементы схемы. У экранов есть и обратная функция. С помощью них катушка защищает себя от воздействия смежных компонентов схемы. Таким образом производители могут уменьшить определенную часть помех. Воздействие магнитного поля неэкранированной катушки можно услышать, например, если поднести элемент к включенному радиоприемнику. У экрана есть и один существенный недостаток. Он сильно увеличивает активное сопротивление самой детали.
Замер сопротивления и формула расчета
Замерить активное сопротивление катушки индуктивности можно только в обесточенном виде. Делается это при помощи мультиметра.
- Мультиметр надо перевести в режим омметра.
- Красный измерительный щуп соединить с первым выходом катушки.
- Черный измерительный щуп соединить со вторым выходом.
- Прибор покажет только активное сопротивление обмотки.

При помощи тестера можно определить только целостность витков. Если элемент включен в цепь под напряжением, то величину сопротивления находят за счет простого вычисления по формуле: Z=U/I.
Для расчета по этой формуле, при помощи тестера определяют сначала величину тока (I) и напряжения (U). Активное сопротивление измеряется в Омах.
Зная формулу расчета активного и индуктивного сопротивления, полное сопротивление элемента может быть найдено с помощью формулы:
Z= 2×(R×R+XL×XL)
В этом выражении R является активным сопротивлением, а XL — индуктивным.
Заключение
Расчет активного сопротивления катушки несет в себе большую практическую пользу. Радиолюбители и инженеры могут определить наименьший коэффициент сопротивляемости элемента, что помогает настроить частотные характеристики электронной аппаратуры.
Видео по теме
Что такое сопротивление
Ток, протекая через провода и различные радиодетали, тратит свою энергию. Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.
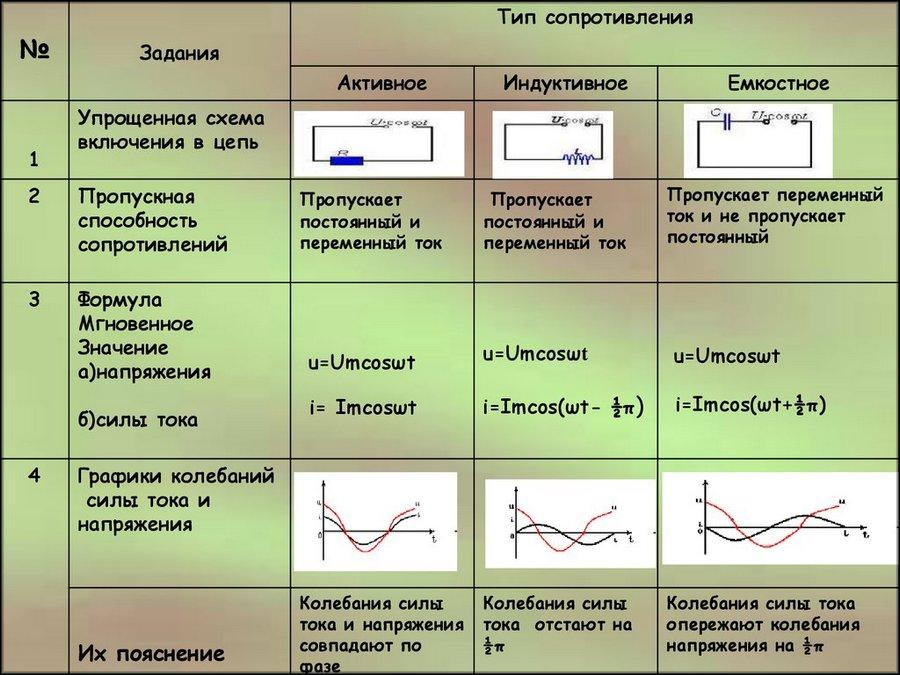
Второй тип сопротивления имеет более сложную природу и возникает в момент включения или выключения потребителя электроэнергии в сеть переменного или постоянного тока. В цепи с реактивным сопротивлением энергия электрического тока частично превращается в другую форму, а затем переходит обратно, то есть, наблюдается периодический колебательный процесс. Полное сопротивление цепи включает в себя активный и реактивный типы, которые учитываются по особым правилам.
Виды сопротивления
В электротехнике рассматривается активное электрическое сопротивление, а также две разновидности реактивного: индуктивное и ёмкостное.

Какое сопротивление называется реактивным, какое активным
Активное электросопротивление — это важный параметр электрической сети, который обуславливает превращение электрической энергии, поступающей в участок электроцепи или в отдельный элетроэлемент в любой другой тип энергии: химическую, механическую, тепловую, электромагнитную. Процесс превращения при этом считаю необратимым.
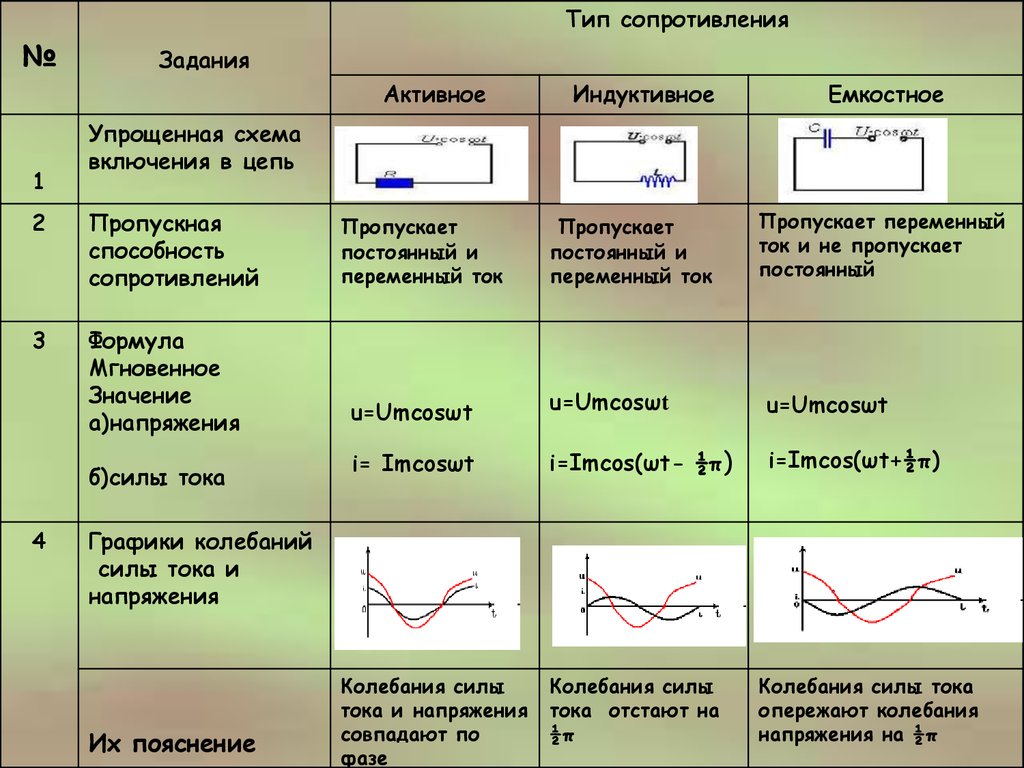
Типы рассматриваемой величины и формулы ее расчета
Реактивное сопротивление по-другому называется реактансом и представляет собой сопротивляемость элементов электроцепи, которые вызывается измерением силы электротока или напряжения из-за имеющейся емкости или индуктивности этого элемента. При реактансе происходит обменный процесс между отдельным компонентом сети и источником энергии. Часто это понятие относят к простому электрическому сопротивлению, однако оно отличается некоторыми моментами.
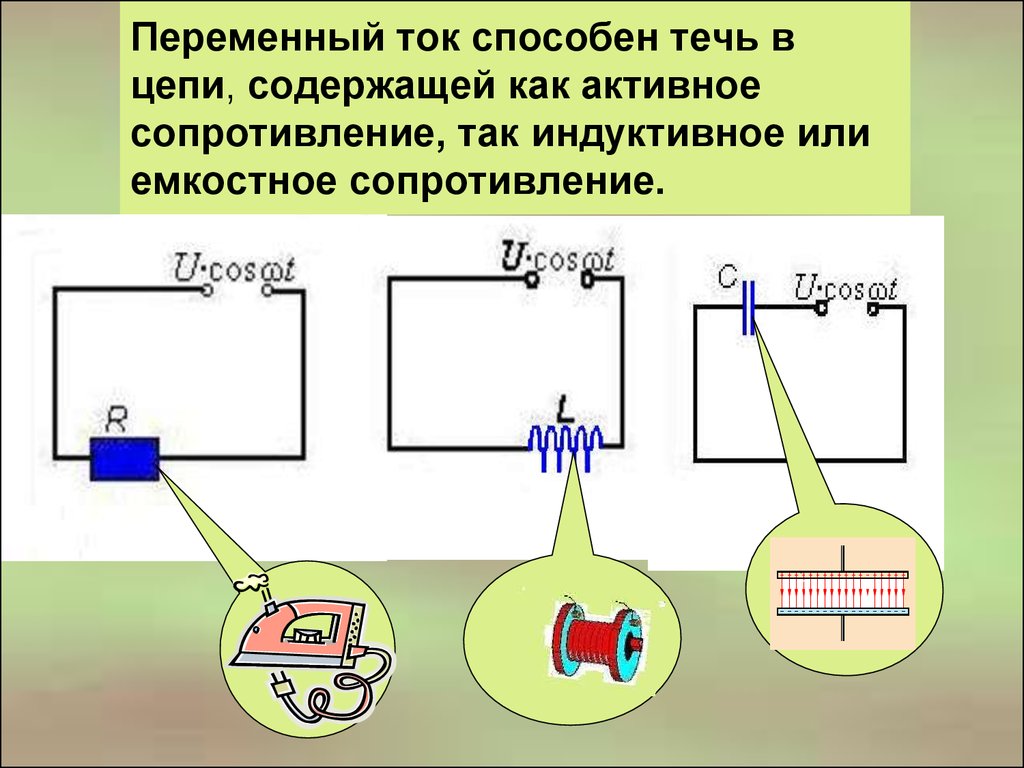
Течение переменного электротока не зависит от типа сопротивляемости элементов и всей сети
Какие отличия
Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.

Индуктивная величина и ее формулы
Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть.
Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.

Комплексная сопротивляемость отдельного элетроэлемента сети R
В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.
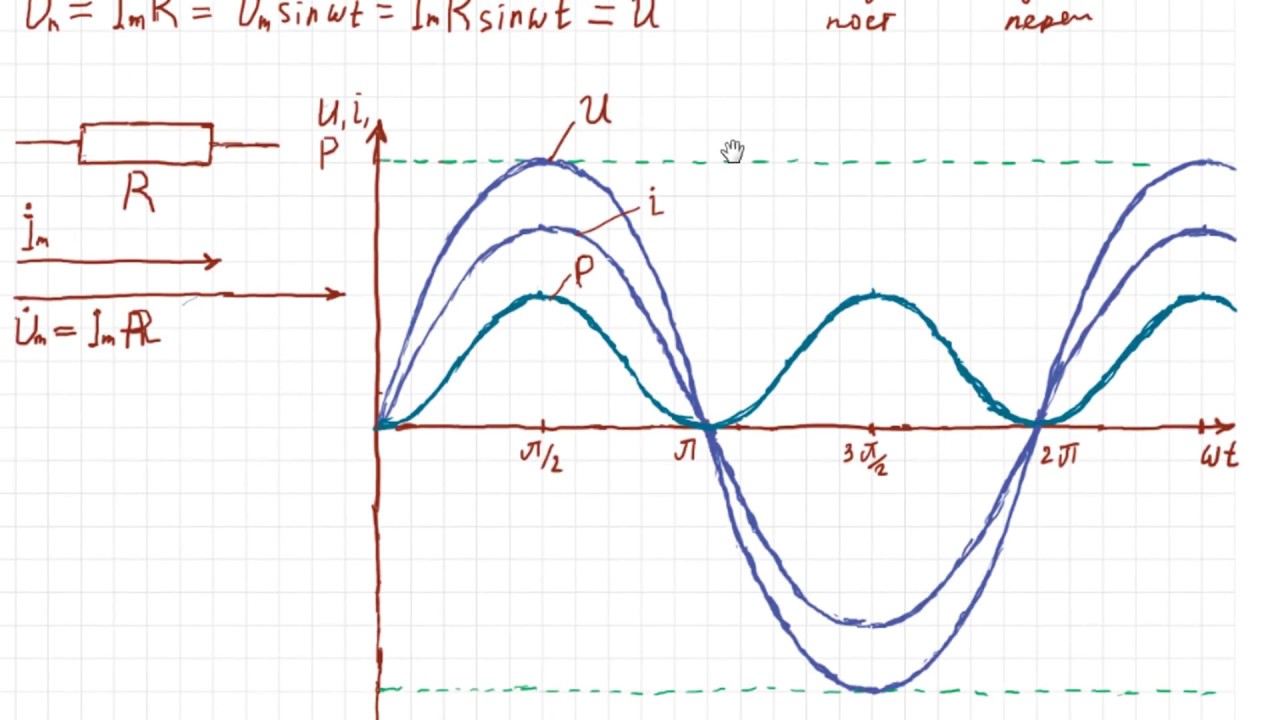
Активная сопротивляемость в цепи переменного синусоидального тока
Области проявления
Реактанс электросопротивления проявляется в емкости и индукции. Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.
Вам это будет интересно Особенности активно-емкостной нагрузки
Сопротивляемость, которую оказывает проводник переменному току и электродвижущей силе самоиндукции, называется индуктивным. Оно зависит от индуктивности потребителя. Чем выше его индуктивность и выше частота переменного электротока, тем выше индуктивное электросопротивление. Выражается оно формулой: xl = ωL, где xl — это электросопротивление индукции, L — индуктивность, а ω — угловая частота тока.
Емкостный реактанс электросопротивление проявляется, например, в конденсаторе, который накапливает электроэнергию в виде электромагнитного поля между своими обкладками. Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.
Активностным же электросопротивлением может обладать любой резистор, линии электропередач, обмотки трансформатора или электрического двигателя.

Индукция ЭДС может наблюдаться в дросселе
Таким образом, активный резист и реактанс во многом отличаются друг от друга не только разницей по названию, но и по физическим свойствам. Первый вид превращает электроэнергию в другой вид и отдает ее в окружающую среду. Второй же — возвращает ее обратно в электросеть.
Переменный ток
Для того чтобы понять, что такое активное сопротивление, необходимо разобраться в самом явлении переменного тока. Переменным является такой тип тока, который непрерывно изменяет направление своего протекания. Во время протекания потенциалы переменного тока постоянно изменяются. Это происходит благодаря работе генератора, а точнее за счет взаимодействия магнитного поля с медной обмоткой. Движение хорошо прослеживается при помощи осциллографа. Своей формой оно напоминает синусоиду.
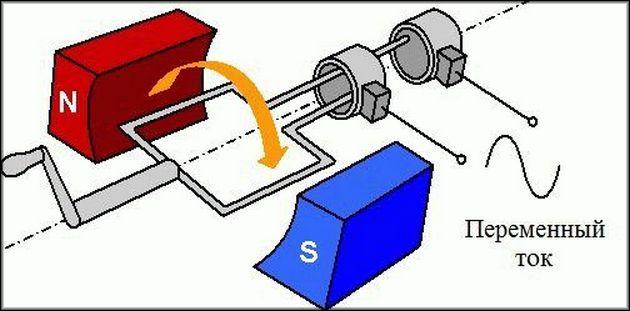
Роль переменного тока сложно переоценить. Главное его достоинство заключается в простоте передачи от источника к потребителю, возможность занижать или увеличивать напряжение при помощи трансформаторов. Также, переменные электрические токи можно доставлять потребителю с гораздо меньшими затратами.
Активное сопротивление
Переменный ток доставляется потребителю с целью его преобразования в иные виды энергии, например, тепло и свет. В бытовых сетях преобладает использование однофазного переменного тока. При подключении потребителя создается активное сопротивление.
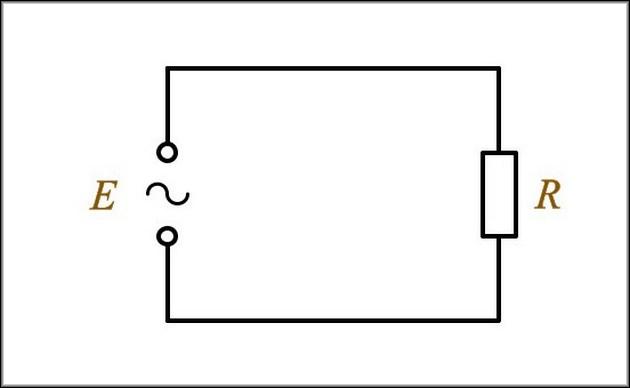
Простые цепи переменного тока с активным сопротивлением включает в себя генератор тока и идеальный резистор. При этом должны соблюдаться необходимые условия для идеальной цепи:
- Активное сопротивление не должно равняться нулю, обязательное условие.
- Емкость и индуктивность цепи должны быть равны нулю.
Также, для идеального активного сопротивления должны соблюдаться следующие условия:
- Соблюдаются закон Ома для мгновенных, среднеквадратичных и амплитудных параметров цепи.
- Значение полностью независимо от амплитудных колебаний.
- Между током и напряжением отсутствует сдвиг фаз.
- Элемент, находящийся под напряжением, выделяет долю тепловой энергии, то есть нагревается.
Все эти условия позволяют электрическим приборам работать в пределах точно установленных параметров с максимальным КПД. Любое изменение может быть причиной отсутствия надежного контактного соединения или неисправностью самого потребителя.
Для того чтобы рассчитать величину активного сопротивления в цепи, необходимо знать величину напряжения и силы тока. Для расчета используется формула: R=U/I. Формула состоит из следующих значений:
- «R» — сопротивление, Ом;
- «U» — величина напряжения, вольт;
- «I» — величина силы тока, ампер.
Далее можно сделать простой расчет. В качестве потребителя выступает электрическая печь, включенная в цепь однофазного переменного тока:
- Напряжение цепи 240 вольт.
- При замере силы тока получено значение 4 ампера.
- R= 240/4=60 Ом.
Расчетная величина активного сопротивления — это не окончательное значение. На нее влияет прежде всего сечение проводов включенных в цепь, схема взаимодействия между цепями емкостных и полупроводниковых элементов.
Активное значение цепи также вызывает безвозвратную потерю первоначальной электрической энергии, а так же приводит к снижению мощности.
Зависимость
Величина активного сопротивления во многом зависит от диаметра проводников. При подаче высокочастотных токов, сопротивление проводника может быть снижено, только если его поверхностный слой намного тоньше основного. Для того чтобы добиться идеального сечения, этот слой должен состоять из материала с очень высокой проводимостью, например, золота или серебра. Данный эффект возникает по причине взаимодействия напряжения и магнитного поля, образованного им. Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.
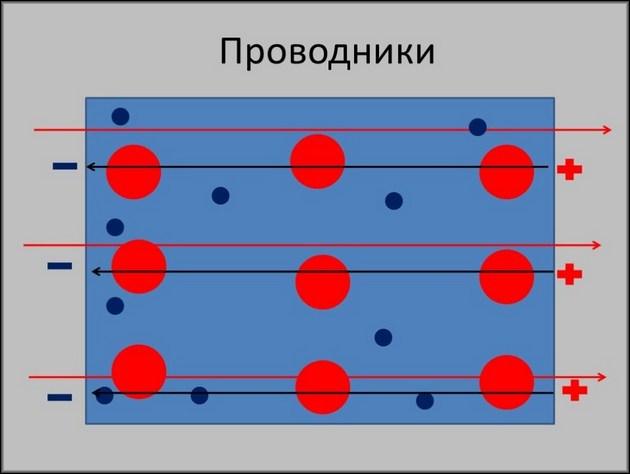
Так же присутствуют следующие эффекты: потери утечки и диэлектрические потери. Оба эффекта связаны с наличием конденсатора в цепи. Диэлектрические потери возникают за счет увеличения температуры диэлектрика внутри конденсатора. Потеря утечки возникает в следствии доли пробоя изолятор конденсатора.
Гистерезис. Это тоже тип потери энергии переменного тока. Такая потеря возникает при формировании магнитного поля вокруг предметов из металла. Электромагнитное воздействие приводит к нагреванию металла, а значит преобразованию энергии.
Последним фактором утечки является радиоизлучение. Радиоволны появляются по причине сильного магнитного поля и его взаимодействия с металлами цепи. Для подавления, особенно в радиоаппаратуре, используются экраны, которые впитывают часть поля и отталкивают остальную долю.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём 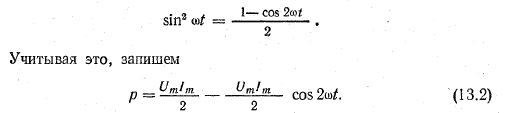
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2,то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°: 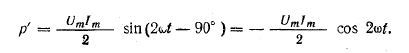
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р= UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I2R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода: 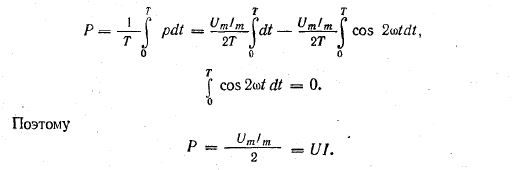
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
В чем измеряется реактивное сопротивление
Само по себе, явление реактанса характерно только для цепей с электрическим током переменного типа. Обозначается оно латинской буквой «X» и измеряется в Омах. В отличие от активностного варианта, реактанс может иметь как положительное, так и отрицательное значение. Знак «+» или «-» соответствует знаку, по которому сдвигается фаза электротока и напряжения. Знак положительный, когда ток отстает от напряжения и отрицателен, когда кот опережает напряжение.
Важно! Абсолютно чистое реактивное электросопротивление имеет сдвиг фазы на ± 180/2. То есть, фаза «двигается» на π/2.

Как правильно измерять сопротивление
При работе с радиоаппаратурой иногда требуется измерять не только активностное, но и реактивное электросопротивление (индуктивность и емкость). Для измерений применяют косвенный метод использования мультиметра, а более точные значения получают при мостовом методе.

Косвенный метод наиболее прост в своей реализации, так как не требует дополнительных схем включения. Одна требуется наличие трех отдельных приборов: амперметра, вольтметра и ваттметра. Если измерить напряжение и силу электротока в цепи, то можно получить полное электросопротивление: Z=U*I После измерения активностной мощности P, можно получить величину активного сопротивления отдельного элемента: R= P/I².

Катушка
Катушка индуктивности представляет собой металлический или ферритный сердечник, на который намотано несколько витков медного провода. Элемент обладает следующими свойствами:
- За счет индуктивности ограничивается скорость изменения токов.
- С увеличением частоты тока катушка способна увеличить свое сопротивление (скин-эффект).
- Создает магнитное поле.
- Увеличивает и накапливает напряжение.
- Создает сдвиг фаз переменного тока.
- Пропорционально скорости движения тока создает ЭДС самоиндукции.

Все эти свойства находят применение при разработке радиоприемных устройств, генераторов частоты, тестеров, магнитометров и других видов сложного оборудования.
Конструкция и разновидности
Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
- Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
- Тороидальная. В такой катушке соленоид выполнен в форме «тора».
- Многослойный тип, имеет несколько рядов обмотки.
- Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
- Универсальная, может совмещать сразу несколько вариантов обмотки.

Независимо от конструкции, все катушки работают по одному и тому же принципу.
Замер сопротивления и формула расчета
Замерить активное сопротивление катушки индуктивности можно только в обесточенном виде. Делается это при помощи мультиметра.
- Мультиметр надо перевести в режим омметра.
- Красный измерительный щуп соединить с первым выходом катушки.
- Черный измерительный щуп соединить со вторым выходом.
- Прибор покажет только активное сопротивление обмотки.

При помощи тестера можно определить только целостность витков. Если элемент включен в цепь под напряжением, то величину сопротивления находят за счет простого вычисления по формуле: Z=U/I.
Для расчета по этой формуле, при помощи тестера определяют сначала величину тока (I) и напряжения (U). Активное сопротивление измеряется в Омах.
Зная формулу расчета активного и индуктивного сопротивления, полное сопротивление элемента может быть найдено с помощью формулы:
Z= 2×(R×R+XL×XL)
В этом выражении R является активным сопротивлением, а XL — индуктивным.
Активное сопротивление катушки
Активное сопротивление обуславливается омической характеристикой проводов обмотки. При работе на низких частотах, омическое сопротивление не зависит от частоты. В мощных устройствах необходимо учитывать эффект близости, который заключается в том, что токи и образуемое ими магнитное поле вызывают вытеснение тока в проводах соседних витков. В результате, снижается эффективное используемое сечение провода и растет его омическое сопротивление.
Обратите внимание! На высоких частотах проявляется скин-эффект, который заключается в том, что ток вытесняется в поверхностные слои провода. В результате этого снижается используемое сечение кабеля. Для снижения скин-эффекта вместо одного проводника используют жгут из нескольких более тонких – литцендрат, либо поверхность провода покрывают слоем серебра, поскольку оно обладает наименьшим удельным сопротивлением.
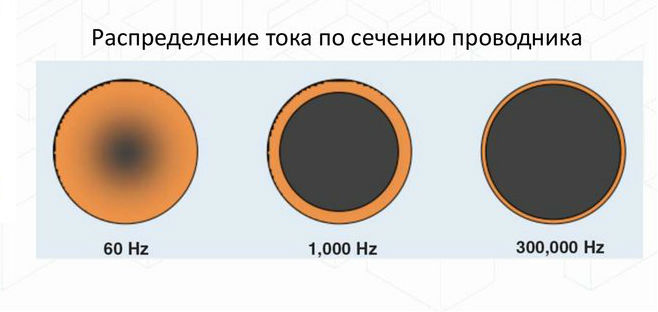
Скин-эффект
В мощных электромагнитных системах (ускорители частиц) для снижения активного сопротивления, используется свойство сверхпроводимости – полное исчезновение сопротивления при охлаждении некоторых материалов ниже критической температуры.

Провод литцендрат
Во многих случаях применения катушек индуктивности следует учитывать влияние активного сопротивления обмоток. Данный параметр может отрицательно влиять не только путем снижения добротности, но и вызывать повышенный нагрев проводников обмоток в том случае, когда устройство работает с большими токами.
Определение активного сопротивления проводов
Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.
Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:
где:
- γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
- s – номинальное сечение провода(кабеля),мм2;
- l – длина линии, м;
- ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].
Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].
Формулы, зависимости и виды индуктивности
Электрическая индуктивность L – это величина, равная коэффициенту пропорциональности между током I, протекающим в замкнутом контуре, и создаваемым им магнитным потоком, иначе называемым потокосцеплением Y:
Y = LI.
Если к выводам катушки на некоторое время приложить напряжение, то в ней начнёт протекать ток I и формироваться магнитное поле. Чем меньше индуктивность L, тем быстрее протекает данный процесс. В итоге рассматриваемый двухполюсник накопит некоторое количество потенциальной энергии. При отключении питания он будет стремиться её вернуть. В результате на выводах катушки образуется ЭДС самоиндукции E, которая многократно превышает изначально приложенное напряжение. Подобная технология ранее использовалась в магнето систем зажигания ДВС, а сейчас широко встречается в повышающих DC-DC преобразователях.
Формула ЭДС самоиндукции, здесь t – это время, в течение которого ток I уменьшится до нуляПростой DC-DC повышающий преобразователь
Катушка (она же – дроссель) – это радиодеталь с ярко выраженной индуктивностью, ведь именно для этого её и создавали. Однако подобным свойством обладают в принципе все элементы. Например, конденсатор, резистор, кабель, просто кусок провода и даже тело человек также имеют некоторую индуктивность. В расчетах ВЧ схем это обязательно принимается во внимание.
Важно! Проводя измерение индуктивности специализированным прибором, стоит помнить, что нельзя держаться руками за оба его вывода. В противном случае показания могут измениться и будут неверными. Вызвано это включением в измеряемую цепь тела человека с его собственной индуктивностью.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними
Главная > Теория > Индуктивное сопротивление
Если подключить катушку индуктивности в цепь электротока переменного типа, то этот ток будет изменяться под влиянием непрерывного изменения электронапряжения. Такие изменения являются генераторами магнитного поля, которое убывает и возрастает периодами. Магнитное поле влияет на катушку, которая создает встречное электронапряжение, что препятствует изменению тока. Соответственно, ток протекает по цепи с постоянным противодействием, которое называется индуктивным сопротивлением.

Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Рассматривая примеры включения катушек в различные цепи мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:

Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
U_L = IR_а
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление будет равно:
X_L = 2pi f L = 0
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давай разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
u = iR + u_L
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -varepsilon_L = Lfrac{di}{dt}
И мы получаем для напряжения на реальной катушке индуктивности:
u = iR + Lfrac{di}{dt}
Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Q = frac{X_L}{R}
Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Итак, активное сопротивление катушки мы рассмотрели, давайте перейдем к следующему вопросу.
Формулы, зависимости и виды
Такое сопротивление напрямую зависит от значения индуктивности и частоты приложенного электрического напряжения. Поэтому индуктивное сопротивление представляется формулой:
XL=2π*f*L= ωL, где:
- XL – сопротивление индуктивного типа;
- π – математическая постоянная;
- ω – угловая частота (измеряется в радианах в секунду – рад/сек);
- L – индуктивность, которая измеряется в Генри (Гн);
- f – частота напряжения, измеряется в Герцах (Гц).
На заметку. Такая зависимость позволяет вывести из вышеприведенной формулы индуктивность или частоту.

Переменный электроток, проходя через проводниковый элемент, создает вокруг этого элемента переменное электромагнитное поле. Под воздействием этого поля в проводнике возникает электродвижущая сила противоположного направления, которая именуется ЭДС самоиндукцией. Противодействие, которое оказывает переменному электротоку ЭДС, называется реактивным индуктивным сопротивлением.
Следует учесть, что индуктивное сопротивление, зависящее от множества дополнительных факторов, имеет некоторые скрытые зависимости. Например, на нее влияет не только сила электротока в собственном проводниковом компоненте, но и в соседствующих проводах. Если увеличится расстояние между фазными проводами, то увеличится и сопротивление с одновременным снижением степени воздействия соседних проводов (в простейшей цепи такое явление можно продемонстрировать добавлением в цепь к катушке резисторов).
Во многих сферах энергетики применяется такое понятие, как индуктивное погонное сопротивление. Формула сопротивления такого вида выглядит следующим образом:
X0 = ω*(4,61g* (Dср/R) + 0,5μ)*10-4, где:
- ω – угловая частота;
- μ – магнитная проницаемость;
- Dср – среднее геометрическое расстояние между фазами ЛЭП;
- R – радиус провода.

Важно! Индуктивное погонное сопротивление полностью зависит от радиуса проводника в проводе, а не от его общего сечения. Когда такой радиус увеличивается, данная величина уменьшается.
Энергия катушки индуктивности.
Электрический ток, протекающий через катушку способствует накоплению энергии в магнитном поле катушки. При пропадании/отключении тока эта энергия будет возвращена в электрическую цепь. С этим мы и столкнулись при рассмотрении катушек индуктивности в цепях постоянного тока. Больше тут добавить особо нечего, просто приведу формулу, по которой можно определить величину накопленной энергии катушки индуктивности:
W = frac{LI^2}{2}
Давайте переходить к вариантам соединения катушек между собой… Все расчеты мы будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0 и его необходимо учитывать при проведении любых расчетов.
Принцип работы катушки зажигания
Катушку зажигания на простом языке можно назвать обычным повышающим напряжение трансформатором. Её задача преобразовать низковольтное напряжение (6-15В) в высокое (20-30кВ). Она, как и трансформатор, состоит из двух обмоток — первичной и вторичной. Первичная низковольтная катушка состоит из небольшого количества витков, а вторичная из большего.
Но есть ещё один нюанс. Витки в катушке расположены определённым образом, что позволяет катушке, кроме индуктивности, иметь ещё и ёмкость. То есть, своего рода — колебательный контур.

При подаче тока в первичную обмотку в катушке генерируется магнитное поле. Наведенное напряжение генерируется в катушке путем самоиндукции. В момент воспламенения ток в катушке прерывается выходным каскадом (в старых системах — контактами прерывателя). Мгновенно сворачивающееся магнитное поле генерирует высокое индукционное напряжение в первичной обмотке. Оно трансформируется на вторичной обмотке катушки и преобразуется в соотношении — количество витков вторичной обмотки отнесенное к количеству витков первичной обмотки. В свече зажигания происходит высоковольтный разряд с ионизацией искрового промежутка и прохождением тока. Это продолжается, пока накопленная энергия не будет истрачена.
Эти все физические явления, наверное, мало кому интересны, поэтому давайте отвлечёмся и посчитаем, на мой взгляд, интересные факты. Сколько раз свеча зажигания «производит» искру за свой срок службы?
Количество искрообразований = «об/мин» умножить на «количество цилиндров» и всё это разделить на 2. Возьмём обычный 4-цилиндровый 4-тактный двигатель. Допустим, обороты двигателя составляют 3000 об/мин. Значит количество искрообразований = 3000 х 4/2 = 6000 искр / мин!
Свечи я меняю раз в 30000 км.
Если пройденное расстояние составляет 30 000 км со средней частотой вращения коленчатого вала двигателя 3000 об/мин при средней скорости 60 км/ч, то количество искрообразований составляет 45 000 000 на каждую свечу зажигания! Во как трудится катушка зажигания! Как Золушка, прям
Поэтому катушка зажигания вполне заслуженно может когда-нибудь устать и молча выйти из строя.
Последовательное соединение катушек индуктивности.

При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
L_0 = L_1 + L_2
Вроде бы все просто, проще некуда, но тут есть один важный момент. Данная формула справедлива только в том случае, если катушки расположены на на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:

Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация совсем другая. Возможно два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек — начало второй катушки подключается к концу первой. А второй вариант называют встречным включением — конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом «*«. Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
L = L_1 + L_2 + 2M
Где M — взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2medspace-medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу — уменьшается на ту же самую величину.
СОДЕРЖАНИЕ
В зависимости от назначения катушки индуктивности различают:
— контурные катушки (образующие совместно с конденсаторами колебательный контур);
— катушки связи (передающие высокочастотные колебания из одной цепи в другую);
— высокочастотные дроссели (катушки индуктивности, преграждающие путь токам высокой частоты).
По конструктивным признакам катушки могут быть разделены на цилиндрические, спиральные, тороидальные, однослойные, многослойные, с сердечником или без сердечника, экранированные, с постоянной или переменной индуктивностью.
На принципиальных электрических схемах рядом с условным графическим изображением катушки индуктивности помещают ее символическое буквенное обозначение (латинская прописная буква L) с порядковым цифровым (иногда буквенным) индексом. Значение индуктивности на схеме обычно не указывают (рис. 4.1).
| Катушка индуктивности | Катушка индуктивности с отводами | Катушки индуктивности с магнитопроводом (L6 — с медным) |
| Катушка индуктивности экранированная | Ферровариометр | Индуктивно связанные катушки (ВЧ трансформатор) |
Рис. 4.1. Обозначения катушек индуктивности на схемах
Дроссели имеют такое же графическое изображение, но обозначаются буквами Др.
Параллельное соединение катушек индуктивности.

При параллельном соединении катушек индуктивности также возможны три варианта:
- Магнитное поле одной катушки не пересекает витков второй катушки, тогда: frac{1}{L_0} = frac{1}{L_1} +frac{1}{L_2} или L_0 = frac{L_1L_2}{L_1 + L_2}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены согласно (как изображено на рисунке — то есть начала обеих катушек подключены к одному узлу). В этом случае: L_0 = frac{L_1L_2medspace-medspace M^2}{L_1 + L_2medspace-medspace 2M}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены встречно. В этом случае: L_0 = frac{L_1L_2medspace-medspace M^2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом мы и заканчиваем рассмотрение катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающие все эти элементы в разных комбинациях
Сопротивлением в электротехнике называют физическую величину, характеризующую свойства проводника препятствовать прохождению электрического тока и равную отношению напряжения на концах проводника к силе тока, протекающего по нему.
Но сопротивление бывает активным и реактивным. В чем разница и где используется каждое из понятий и пойдет речь в этой статье.
Активное сопротивление
Активное сопротивление – это сопротивление элемента или участка цепи электрическому току, обусловленное необратимыми превращениями электрической энергии в другие формы, например, механическую в электродвигателях или тепловую, когда речь идёт о нагреве чего-либо или просто потерях или другие виды энергии. Выражается в Омах и в формулах обозначается буквой R.
Активное сопротивление характерно для проводников, а его величина зависит от свойств этих самых проводников:
- Материал — обычно проводники выполняются из металла (или из графита, как щетки электрических машин) и у каждого проводника есть удельное сопротивление, оно измеряется в Ом·мм²/м.
- Длина и площадь поперечного сечения. Следует из предыдущего. Чем больше площадь поперечного сечения (мм²) – тем меньше сопротивление, или чем длиннее проводник – тем оно больше.
- Температура. Чем больше температура – тем больше сопротивление проводника.
Согласно закону Ома, сопротивление участка электрической цепи можно рассчитать, если известны ток и напряжение по формуле: R=U/I.
Сопротивление проводника, определенной длины и сечения определяется по формуле: R=p*l/S,
где p (ро) – удельное сопротивление, l – длина, S – площадь поперечного сечения.
При протекании тока через активное сопротивление в любом случае происходят потери в виде тепла. По этой причине греются провода и кабельные линии под нагрузкой, трансформаторы, электродвигатели и так далее… Величина этих потерь определяется по формуле: P=U²/R. Кроме потерь в виде тепла на линии, а вернее сказать, на активном сопротивлении линии происходит падение напряжения (просадки), величина которых также рассчитывается по закону Ома: Uпад=I*Rл,
где Uпад – падение напряжение на линии, Rл – сопротивление линии.
Напряжение и ток в активном сопротивлении совпадают по фазе, соответственно коэффициент мощности у активной нагрузки в идеальном случае равен 1. Это можно пронаблюдать на иллюстрации выше, как и то, что векторы U и I также совпадают по направлению, и между ними нет угла.
Под «идеальным случаем» понимается используемое в физике понятие «идеальный», то есть, когда объекту характерен какой-то единый набор свойств. Например, когда говорят «идеальный резистор» — это значит, такой резистор в котором есть только активное сопротивление, а реактивные составляющие отсутствуют. А «идеальная индуктивность» — это такая индуктивность, у которой нет активного сопротивления проводника, которым она намотана, а также паразитной ёмкости. То есть идеальная катушка, обладает только индуктивностью.
Подведем итоги — активное сопротивление характерно для нагрузки ток и напряжение в которой совпадают по фазе, это могут быть: провода, резисторы, ТЭНы и другие нагревательные элементы, лампы накаливания…
Реактивное сопротивление
Согласно энциклопедическому определению, реактивное сопротивление — это сопротивление элемента схемы, вызванное изменением тока или напряжения из-за индуктивности или ёмкости этого элемента. Отсюда следует, что реактивное сопротивление присуще только индуктивной или емкостной нагрузке. Измеряется оно также в Омах, но обозначается буквой X.
Также следует вспомнить законы коммутации:
- Ток на индуктивности не может изменяться скачком.
- Напряжение на ёмкости не может измениться мгновенно.
Другими словами, в индуктивности ток отстаёт от напряжения по фазе, а в ёмкости наоборот — ток опережает напряжение.
Реактивное сопротивление индуктивности
В цепи постоянного тока это вносит влияние в работу системы преимущественно при её коммутации (включении или отключении), а также при резком изменении режима работы и потребления тока и такого понятия как реактивное сопротивление для постоянного тока нет.
Но в цепи переменного тока реактивное сопротивление оказывает значительное влияние. При протекании переменного тока I в катушке, возникает магнитное поле. Оно создаёт в витках катушки ЭДС, которое в свою очередь препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении – положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
Выше мы рассматривали график тока и напряжения в активном сопротивлении, и они совпадали по фазе, ниже приведен график тока и напряжения для катушки индуктивности.
На рисунке 2.б видно, что ток и напряжение в индуктивности не совпадают по фазе. В идеальной индуктивности ток отстаёт от напряжения на 90 градусов, что более наглядно иллюстрирует векторная диаграмма на рисунке 2.в.
Сопротивление, которое индуктивность оказывает переменному току вычисляется по формуле: XL=ω*L=2*pi*f*L,
где ω — угловая частота (рад/с), L — индуктивность (Гн), pi – число пи (3.14), f — частота (Гц).
То есть чем больше частота переменного тока, тем большее сопротивление ему оказывает индуктивность.
Реактивное сопротивление ёмкости
В ёмкостной нагрузке дело обстоит также, но наоборот. На рисунке 3.б видно, что ток опережает напряжение, а на 3.в видно, что опережает на угол в 90˚.
При протекании переменного тока в конденсаторе циклически происходят процессы заряда и разряда, или накопления и отдачи энергии электрическим полем между его обкладками. Конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное.
В момент когда напряжение достигнет амплитудного значения, ток будет равен нулю. Таким образом, напряжение на идеальном конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
То есть емкостное сопротивление — это сопротивление изменению напряжения. Оно определяется по формуле: Xс=1/(ω*C)=1/(2*pi*f*c),
где ω — угловая частота (рад/с), C — ёмкость (Ф), pi – число пи (3.14), f — частота (Гц).
То есть чем меньше частота переменного тока, тем большее сопротивление оказывает ему ёмкость.
Но отклонение напряжения от тока по фазе на 90 градусов только в цепях с идеальной индуктивностью, на практике же такого нет.
Полное сопротивление
Так как и активное сопротивление, и индуктивность, и ёмкость влияют на токи и напряжения в электрической цепи по-своему, то при их соединении их сопротивления также складываются. Так, например полное реактивное сопротивление равно: X=XL-Xс
Таким образом реактивные сопротивления ёмкости и индуктивности приводятся к общему значению, то есть какое из них больше, такой характер и будет у цепи (индуктивный или емкостной).
В любой реальной цепи присутствуют все три составляющие: активная, емкостная и индуктивная. Тогда говорят о полном сопротивление цепи. Оно обозначается буквой Z и вычисляется по формуле:
где Z – полное сопротивление, r – активное, XL – индуктивное, Xc – емкостное.
Эта формула должна была вам напомнить теорему Пифагора, где квадрат гипотенузы равен сумме квадратов катетов. И это неспроста. Дело в том, что если на векторной диаграмме изобразить активное и полное реактивное сопротивление, то мы получим т.н. треугольник сопротивлений, где гипотенузой будет полное сопротивление цепи.
Угол Фи — это и есть угол, на который ток отстаёт от напряжения, а косинус этого угла (cosФ) называют коэффициентом мощности. Это опережение или отставание тока и напряжение приводит к тому, что этот ток возвращается обратно к источнику питания, а не выполняет какую-то работу в потребителе. Это приводит к излишней нагрузке на электросеть, то есть ток протекает полный, а работу выполняет только активная его часть.
Большая часть электрооборудования (электродвигатели, электромагниты и прочее) носит индуктивный характер, что приводит к значительному повышению нагрузки на электросеть и потребления реактивной мощности.
Чтобы бороться с этим явлением используются компенсаторы реактивной мощности — конденсаторные установки, синхронные двигатели, синхронные компенсаторы. То есть подключают какую-то нагрузку с емкостным характером, она нужна, чтобы уменьшить угол между током и напряжением и в итоге повысить коэффициент мощности.
Ну и напоследок ознакомьтесь с подборкой советских плакатов, которые иллюстрируют параметры электрических цепей со смешанной нагрузкой, а также их векторные диаграммы (треугольники сопротивлений, напряжения и мощности).
Активное сопротивление любого проводника определяется:
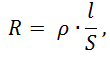
где ρ = 1,7∙10-8 Ом∙м – удельная проводимость материала (в данном случае – меди),
l – длина проводника, м,
S – площадь поперечного сечения проводника, м2.
Определим длину проводника. Для этого рассчитаем длину витка и умножим её на число витков. При этом длина витка будет равна длине окружности:
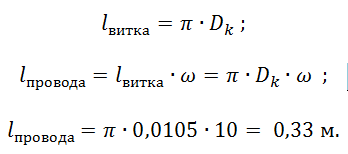
Определим площадь поперечного сечения проводника. В реальности проводник имеет круглое сечение, Maxwell же рассчитывает потери для всей области занятой катушкой, т.е. предполагается, что проводники полностью заполняют область. В случае, если необходим точный расчёт для катушек, намотанных проводом круглого сечения, каждый проводник катушки должен быть прорисован отдельным объектом.
Исходя из вышесказанного, будем условно считать, что катушка намотана проводником прямоугольного сечения. В этом случае площадь поперечного сечения проводника будет определяться:
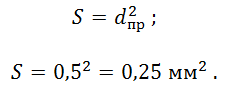
Определим сопротивление обмотки:
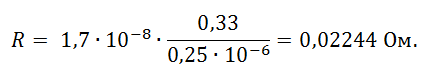
Построим геометрию модели из Примера 1 в 3D. Для этого нажимаем ПКМ на проекте модели 2D примера 1 и выбираем Create 3D Design. После чего модель будет автоматически преобразована в 3D.
1. Создадим сечение для задания возбуждения катушки.
Для этого выделим объект катушки и применим к нему операцию “сечение” (меню Modeler > Surface > Section, выбираем плоскость сечения YZ). Получим объект, состоящий из двух сечений. Для задания возбуждения необходимо одно сечение, поэтому разделим получившийся объект (меню Modeler > Boolean > Separate Bodyes). Второе сечение не нужно, и его можно удалить.
Последнему сечению назначим величину тока, равную 10 ампер-виткам (ПКМ по сечению > Assign Excitation > Current > Value), тип обмотки – распределённая (Stranded).
2. Задание граничных условий.
В 3D постановке задачи в Maxwell по умолчанию действует условие обнуления поля на границах модели. В отличии от 2D постановки задачи открытых границ (условие Balloon) в 3D нет. Поэтому расчётную область иногда приходится увеличивать до тех пор, пока результат расчёта модели не перестанет ощутимо изменяться.
Создадим область для расчёта: Create Region  (Создание региона), в открывшемся окне выберем Pad Individual Direction и по каждой оси отступим 40% от объектов модели:
(Создание региона), в открывшемся окне выберем Pad Individual Direction и по каждой оси отступим 40% от объектов модели:
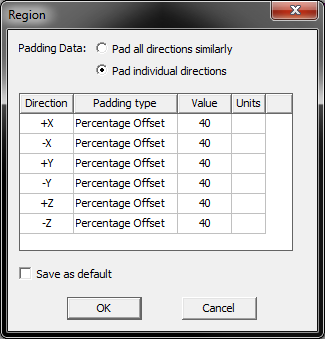
Граничные условия для модели не задаём, т.к. действует граничное условие по умолчанию (присваивается нулевая величина поля на границе расчётной модели).
3. Создание сетки элементов и задания на расчёт.
Далее – создаём сетку конечных элементов, предварительно выделив все объекты модели (Assign Mesh Operation > Inside Selection > Length Based… )
Создаём новое задание на расчёт с параметрами по умолчанию (ПКМ на Analysis > Add Solution Setup)
Запускаем задачу на расчёт.
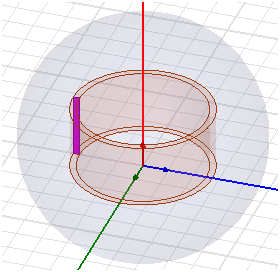
Рисунок П.2.1 – 3D модель рассчитываемой катушки
4. Расчёт омических потерь катушки.
Запустим калькулятор поля (ПКМ на Field Overlays > Calculator…)
В калькуляторе поля (Рисунок П.2.2), необходимо задать следующее выражение:
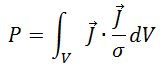
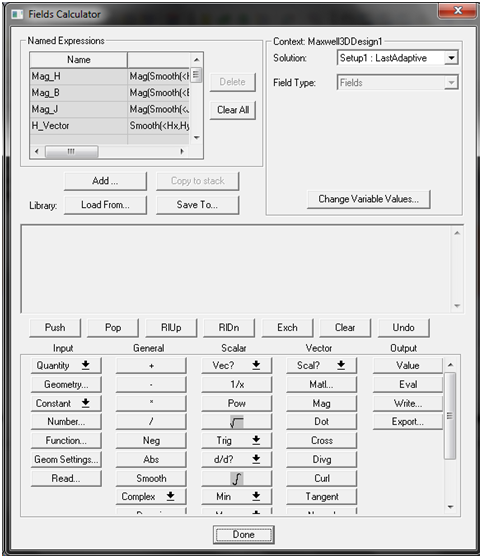
Рисунок П.2.2 – Калькулятор поля Maxwell
где V – объём, в котором рассчитываются потери (обмотка);
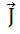 – вектор плотности тока в обмотке;
– вектор плотности тока в обмотке;
σ = 1/ρ = 58∙106 См/м – удельная проводимость материала (в данном случае – меди).
Запишем искомое выражение в калькуляторе поля, набрав следующую последовательность команд:
| Quantity > J | Выбираем вектор плотности тока |
| Push | Дублируем |
| Number > Scalar > Value 58000000 | Вводим величину удельной проводимости меди |
| / | Делим плотность тока на проводимость |
| Dot | Перемножаем |
| Geometry > Volume > Coil | Выбираем объём катушки (вместо Coil выбрать название катушки) |
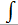 |
Интегрируем выражение по объёму. |
В строке выражений получится:
Scl : Integrate(Volume(Coil), Dot(<Jx,Jy,Jz>, /(<Jx,Jy,Jz>, 58000000)))
Получившееся выражение сохраняем в качестве переменной (Named Expression): PowerLoss (кнопка Add..)
Разделим получившиеся потери на квадрат тока ( I = 1 А ) в проводнике (выбираем PowerLoss в списке переменных > Copy to Stack > Eval > Number > Scalar > 1 > / (операция деления).
Получим результат: R = 0,022687 Ом.
Сравним с теоретическим результатом: R = 0,02244 Ом, погрешность составила: 0,1%.
Примечание: Нельзя забывать, что сечение электропроводящего материала в катушках, намотанных проводником круглого сечения, не будет соответствовать реальному сечению катушки. Поэтому нельзя в модели строить сечение катушек по реальным данным, т.к. это приведёт к уменьшению активного сопротивление катушки. В модели сечение катушки должно совпадать с сечением электропроводящего материала (медь, алюминий). Это сечение можно рассчитать, перемножив сечение провода на число витков в катушке.
Автор материалов: Drakon (С) 2014. Редактор: Админ
