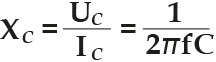Что такое емкостное сопротивление
Содержание
- 1 Определение
- 2 Принцип работы
- 3 Расчет
- 4 Характеристики элемента
- 5 Импеданс
- 6 Расчет
- 7 Применение
- 8 Измерение и проверка
- 8.1 Проверка
- 8.2 Замер
- 8.3 Измерение емкости
- 9 Заключение
- 10 Видео по теме
При проектировании электрический цепей, оборудования и электроприборов учитываются многие свойства проводников. Одним из важных свойств считается емкостное сопротивление.
В данной статье будет подробно описано — что такое емкостное сопротивление конденсатора. Так же будет приведена формула расчета такого параметра, описана работа конденсатора в цепи переменного тока и сферы применения ёмкостного сопротивления.
Определение
Сопротивлением называют физический эффект противодействия протеканию тока по любой электрической цепи. Этим свойством обладают все проводники электрического тока. Данная величина измеряется в Ом.
Емкостное электрическое сопротивление является величиной, благодаря которой можно понять, что в цепи присутствует конденсатор. Емкостные сопротивления конденсатора рассчитываются только для цепей переменного тока, без учета наличия в них резисторов.
Конденсатор обозначается на схеме буквой «С», а его ёмкостное сопротивление «Xc».
Принцип работы
Конденсатор с определенной ёмкостью работает по принципу периода, который состоит из заряда и разряда элемента. Период делится на 4 части:
- Первая часть предполагает рост напряжения. В этот момент сопротивление конденсатора минимально, а зарядный ток очень высокий.
- Во второй четверти происходит наполнение его ёмкости за счет зарядного тока.
- В третьей четверти конденсатор полностью заряжается, при этом происходит снижение тока вплоть до 0. ЭДС возрастает с эффектом смены своей направленности.
- В последней четверти происходит разряд элемента. На этом этапе ЭДС будет в пределах 0, а ток постепенно нарастать.
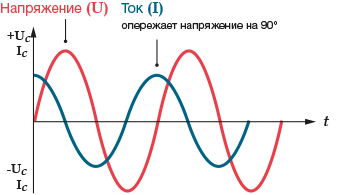
Все описанные процессы за один период определяют дальнейший фазный сдвиг на 90 градусов.
Природа возникновения емкостного сопротивления полностью зависит от нескольких факторов:
- Обязательно наличие конденсатора в цепи.
- По цепи должен течь только переменный ток.
- Сопротивление проводника должно быть меньше емкости конденсатора.
Все эти факторы помогают рассчитать наиболее правильное значение ёмкостных характеристик для наиболее эффективной работы электроцепи.
Расчет
Расчет электрического емкостного сопротивления цепи делается по формуле. Она состоит из следующих значений:
- «Xc» — является емкостным сопротивлением в Омах.
- «1» — период полного заряда и разряда элемента.
- «w» — круговая частота переменного тока с емкостью, рад/сек.
- «C» — емкость конденсатора, единицы измерения Фарад.
Сама формула при этом выглядит следующим образом:
При помощи этой формулы легко рассчитывается Xc. Для этого требуется просто умножить циклическую частоту переменного тока на известную величину емкости конденсатора. Далее необходимо будет один период разделить на полученное значение. Таким образом можно всегда найти сопротивление конденсатора в Ом.
Рассчитываться емкостное сопротивление может так же с помощью и другой формулы, которая приведена на рисунке ниже.
При расчетах по данной формуле прослеживаются следующие зависимости:
- Емкость конденсатора и частота тока всегда выше сопротивления.
- От величин емкости и частоты зависит скорость одного периода заряда/разряда конденсатора.
Также стоит учесть, что после подключения конденсатора в цепь постоянного тока, его сопротивление сильно увеличивается. Объясняется причина такого явления довольно просто — отсутствует частота протекания электричества.
Характеристики элемента
Для того чтобы понять, что такое емкостное сопротивление, необходимо разобраться с его основной характеристикой, которая называется емкостью. Емкостью называется накопительная способность элемента. Она заключается в накоплении определенной доли электрического тока за определённый промежуток времени. Единицей измерения этой величины является Фарад (Ф или F).
Элемент заряжается электричеством до определенного момента, после которого он начинает разряжаться и отдавать ток дальше по электроцепи. Время полного разряда напрямую зависит от величины сопротивления цепи. Чем выше это значение, тем меньше времени тратится на разрядку элемента. Для расчета ёмкостной характеристики используется следующее выражение:
Так же конденсаторы обладают рядом дополнительных характеристик. К ним относят:
- Общую удельную емкость. Является отношением массы диэлектрических пластин и емкостных параметров.
- Напряжение. Параметр определяется как рабочее напряжение, которое способен выдержать элемент.
- Температурная стойкость или стабильность. Это температурный параметр, который не влияет на изменение емкости.
- Изоляционное сопротивление. Является величиной точки утечки и саморазряда.
- Эквивалентная нагрузка. Значение, определяющее потери на выводе или контактах устройства.
- Абсорбция. Разность потенциалов в момент разряда до 0.
- Полярность. Параметр свойственен элементам, которые работают строго при подаче на обкладку потенциала определенного значения (плюс или минус).
- Индуктивность. Свойство конденсатора образовывать на контактах индуктивное сопротивление. Такое свойство может наделить элемента параметрами колебательного контура.
Все эти значения строго учитываются при проектировании цепей или схем электрического оборудования.
Импеданс
Кроме емкостного, конденсатор еще имеет общее сопротивление или импеданс. Данное значение определяется с учетом значений трех параметров: индуктивного, резистивного и емкостного сопротивления.
Для вычисления импеданса применяется следующая формула:
В данном выражении используются следующие сопротивления:
- xL — индуктивное;
- xC — емкостное;
- R — активное.
Активное сопротивление цепи появляется вследствие возникновения в ней ЭДС. Так как переменный ток по своей природе импульсный, то электромагнитный поток может довольно незначительно изменяться, а это приводит к сдвигу постоянного значения ЭДС.
Емкостные и индуктивные величины взаимосвязаны. По разнице между ними легко находят реактивную составляющую цепи.
Отсюда легко проследить, от чего зависит само реактивное сопротивление:
- Если реактивная величина больше 0, то устройство больше нагружено индуктивным значением.
- Если реактивное значение равно 0, то емкость не нагружается активным сопротивлением.
- Если реактивность меньше 0, то элемент имеет высокое емкостное сопротивление.
Активное сопротивление считается невосполнимой величиной. Она тратится на преобразование тока в иной вид энергии. Реактивная величина неизменна для актуальной цепи переменного тока.
Расчет
Узнав, по какой формуле делаются необходимые вычисления и поняв смысл емкостного сопротивления, можно заняться расчетом данной величины.
Например, сделаем расчет на основе следующих данных:
- Емкость конденсатора C=1мкФ;
- В цепи также имеется активное сопротивление R, которое равно 5 кОм;
- Индуктивное сопротивление цепи xL составляет 4.5 кОм;
- Частота переменного тока равна 50 Гц;
- Напряжение 50 вольт.
На основе этих данных необходимо будет найти сопротивление конденсатора.
Емкостное сопротивление определим следующим образом:
xC=1/(2πfC)=1/(2×3.14×50×1×10-6)=3184 Ом или округленно 3.2 кОм.
Для определения величины тока в этой цепи воспользуемся законом Ома:
I=U/xC=50/3184=0.0157 ампер или 15.7мА.
После этого определяются параметры общего сопротивления:
Z=(R²+(xL-xC)²)½=(5000²+(4500–3184)²)½=5170 Ом или 5.1 кОм.
По данным расчётам можно определить влияние емкостного элемента на электроцепь. Главное понимать, какие физические величины используются в данных формулах для выполнения правильных вычислений.
Применение
В электронных цепях очень часто конденсатор используется в качестве фильтрующего элемента. При этом инженеры учитывают способ подключения данного элемента:
- При параллельном соединении конденсатора с цепью, устройство способно задерживать ток высокой частоты. Такой фильтр работает по принципу зависимости сопротивления от частоты тока. Чем выше частота, тем ниже будет сопротивление.
- При последовательном включении фильтр уже отсеивает низкочастотные импульсы. Вторым свойством такого фильтра является возможность не пропускать постоянный ток.
Также большая доля использования таких устройств приходится на звуковые усилители. Конденсатор способен отделить переменный и постоянный ток, а значит работать в качестве усилителя низкой частоты. При этом подбираются элементы с наименьшей емкостью.
Так же устройства используются для блоков питания постоянного тока или стабилизаторов. Тут применяется свойство разделения постоянной и переменной составляющей. Например, разделение ее между потребителями с помощью отдельных выходов для постоянного и переменного тока. В таких устройствах конденсатор разряжается, если нагрузка на цепь увеличивается за счет подключения нового устройства. Тем самым общая пульсация в цепи сглаживается. При необходимости можно передать ток обоих значений по одному проводнику. Делается это следующим образом — контакты с постоянным напряжением подключают к выводу емкости для прямого контакта с переменным напряжением. Таким образом происходит фильтрация частоты, сглаживание импульсов и передача постоянного тока потребителю. Такая схема используется в антенных усилителях, которые подключаются к телевизорам.
Измерение и проверка
Измерить целостность конденсатора и его сопротивление можно при помощи мультиметра. Перед этим элемент обязательно необходимо отсоединить от цепи.
Проверка
Диагностика целостности конденсатора начинается с визуально осмотра его состояния. Любые трещины, вздутия или деформации корпуса можно считать неисправностью элемента. Если визуальный осмотр не дал никаких результатов, то элемент проверяется на пробой при помощи тестера.
Делается такая проверка следующим образом:
- Элемент необходимо выпаять из схемы, а его контактные выводы замкнуть металлическим предметом для разрядки.
- Мультиметр перемести в режим замера сопротивления.
- Измерительные щупы соединить с контактами устройства.
- Сопротивление исправного элемента будет измеряться бесконечным значением, которое будет превышать значение сопротивления утечки. Величина этой утечки при этом составляет 2 кОм.
Если показания меньше этого значения, значит элемент неисправен и пробит.
Замер
Замерить сопротивление можно так же с помощью мультиметра. Его надо будет перевести в режим измерения сопротивлений более 100 кОм. Далее необходимо соединить щупы прибора с контактами устройства. Некоторое время потребуется на полную зарядку элемента. После этого он покажет конечный результат, который не должен быть выше 100 кОм. Если этот порог преодолен, то можно сделать однозначный вывод о неисправности элемента.
Измерение емкости
Для замера емкости потребуется тестер с режимом СX. Если такого режима нет, проверить элемент будет невозможно. Далее требуется:
- Полностью разрядить конденсатор.
- На мультиметре выбирается режим СX.
- Измерительные щупы соединить с контактными выводами устройства, строго соблюдая полярность.
- Прибор должен показать величину больше 1, но при этом ее значение должно быть в пределах тех значений, которые указаны на корпусе детали. Если значение равняется 0 или находится за пределами указанных значений, то конденсатор можно признать неисправным.
Полученные мультиметром данные также можно считать ёмкостным значением, так как в момент проверки элемент проходит зарядку током.
Заключение
Емкостным сопротивлением обладают все цепи, в которых задействованы конденсаторы. Зная, какой по параметрам элемент включен в данную цепь, можно легко рассчитать его емкостное влияние на цепь, используя представленные в статье формулы для расчётов.
Видео по теме
Калькулятор электрического сопротивления ёмкости
При подключении конденсатора в цепь переменного тока возникает совокупность процессов заряда и разряда ёмкости,
т.е. накопление и отдача энергии электрическим полем между обкладками. По мере заряда ёмкости, ток через нее уменьшается.
Конденсатор будет заряжаться до максимального значения, пока ток не сменит направление на противоположное.
В моменты максимального значения напряжения на конденсаторе, ток в нём будет равен нулю.
Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
Ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току Xc.
X C — сопротивление, Ом;
f — частота, Гц;
C — ёмкость, Ф.
Сопротивление конденсатора переменному току это отношение действующих значений напряжения к току.
Оно обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Фазы кривых тока и напряжения на конденсаторе смещены на 90 градусов, при этом ток опережает напряжение.
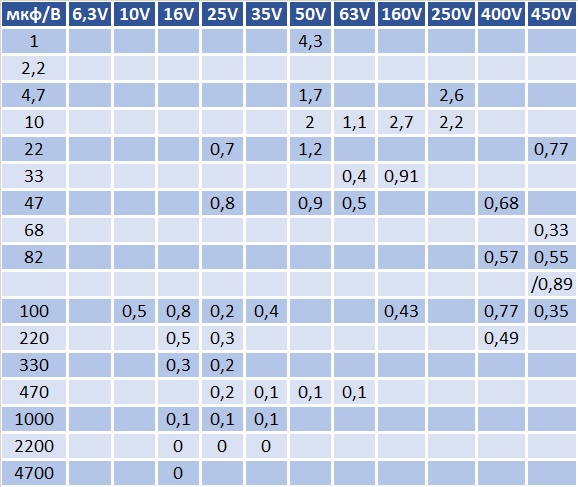
Расчет электрического сопротивления ёмкости
Для расчета введите значение ёмкости конденсатора и частоту переменного тока
Калькулятор вычисления действующих значений тока или напряжения на конденсаторе.
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Емкостное сопротивление конденсатора – величина, измеряемая в омах, создается непосредственно самим конденсатором, который включен в любую цепь. Оно должно иметь большую величину, то есть быть большим. Если на них происходит подача переменного тока, в устройстве происходят процессы заряда и последующего разряда. Последнее происходит по требованию цепи. При включении электрического тока, напряжение будет равно 0. Само устройство при этом начнет заряжаться, следовательно его величина напряжения постепенно растет. В случае необходимости, при достижении максимального заряда, произойдет разряд конденсатора.
В статье, посвященной теме расчета сопротивления конденсатора, приведена вся информация о процессе, как происходит заряд-разряд. В качестве бонуса есть интересный материал по теме, который можно скачать, и видеоролик в конце статьи.
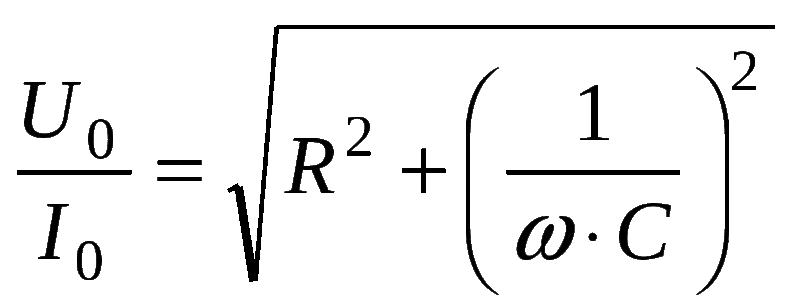
Формула сопротивления
Формула ёмкостного сопротивления выводится следующим образом:
- Вначале следует вычислить угловую частоту. Для этого частоту протекающего по цепи тока (в герцах) необходимо умножить на удвоенное число «пи».
- Затем полученное число следует перемножить на ёмкость конденсатора в фарадах.
Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление. Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.

Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
- Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
- Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
- Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.
В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.

Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними. Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
[stextbox id=’info’]Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.[/stextbox]
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Материал в тему: все о переменном конденсаторе.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
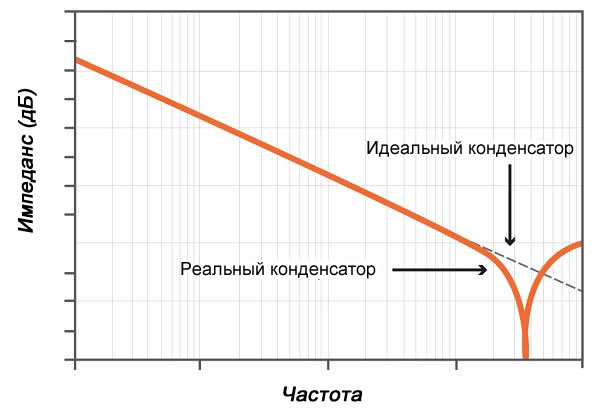
Пример расчёта
Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R 2 +Xc 2 ) ½.
Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.
Стоит почитать: все об электролитических конденсаторах.
В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет
Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.
По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.
Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (50002+32002)½ = 5 936 Ом =5,9 кОм.
[stextbox id=’info’]Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.[/stextbox]
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
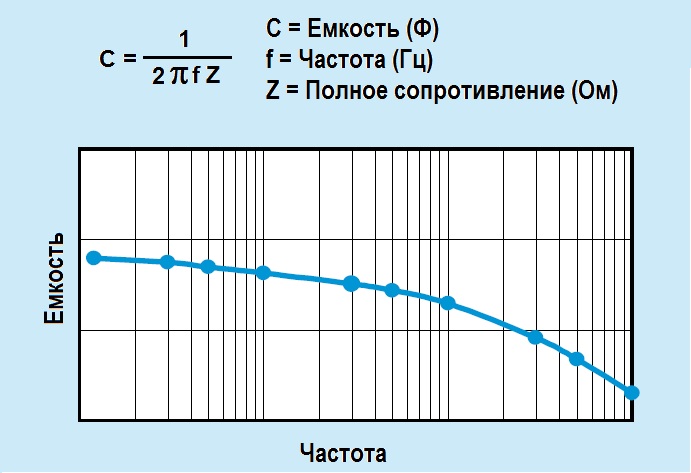
Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
[stextbox id=’info’]Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.[/stextbox]
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:
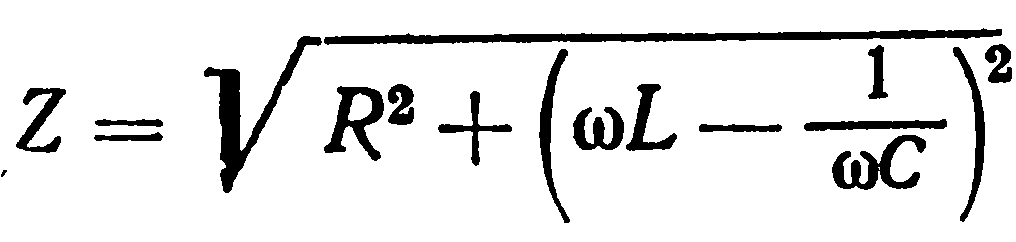
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:
- X > 0 – элемент проявляет свойства индуктивности .
- X = 0 – элемент имеет чисто активное сопротивление .
- X < 0 – элемент проявляет ёмкостные свойства.
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.
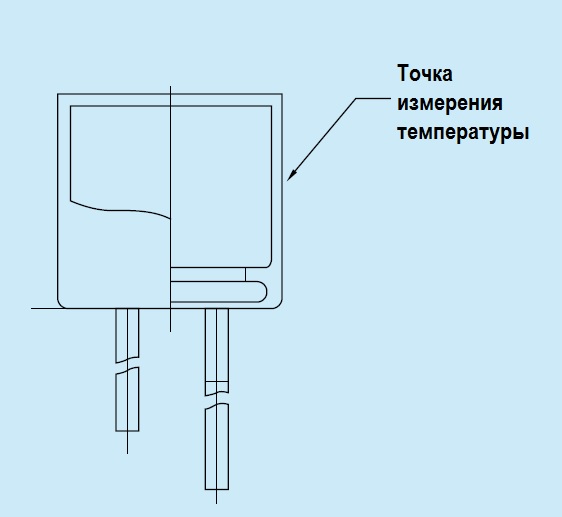
Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
Заключение
В данной статье были рассмотрены основные вопросы расчета сопротивления конденсаторов. Больше информации можно найти в скачиваемой версии учебника по электромеханике “Что такое конденсаторы”
В нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессиональных электронщиков. Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vk.com/electroinfonet. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:
www.amperof.ru
www.eduspb.com
www.beasthackerz.ru
www.electroandi.ru
www.websor.ru
Предыдущая
КонденсаторыСколько стоят керамические конденсаторы?
Следующая
КонденсаторыЧто такое ионистор?
В этой статье мы поведем речь о таких параметрах, как активное и реактивное сопротивление.
Активное сопротивление
И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента — резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, «активный — это деятельный, энергичный, проявляющий инициативу». Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.
То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.
Как смотреть силу тока в цепи через осциллограф
Чем же резистор отличается от катушки индуктивности и конденсатора? Понятное дело, что выполняемыми функциями, но этим все не ограничивается. Итак, давайте рассмотрим самую простую схемку во всей электронике:
На схеме мы видим генератор частоты и резистор.
Давайте визуально посмотрим, что у нас творится в этой схеме. Для этого, как я уже сказал, нам понадобится генератор частоты
А также цифровой осциллограф:
С помощью него мы будем смотреть напряжение и силу тока.
Что?
Силу тока?
Но ведь осциллограф предназначен для того, чтобы рассматривать форму сигнала напряжения? Как же мы будем рассматривать форму сигнала силы тока? А все оказывается просто). Для этого достаточно вспомнить правило шунта.
Кто не помнит — напомню. Имеем обыкновенный резистор:
Что будет, если через него прогнать электрический ток?
На концах резистора у нас будет падение напряжения. То есть, если замерить с помощью мультиметра напряжение на его концах, мультиметр покажет какое-то значение в Вольтах
И теперь главный вопрос: от чего зависит падение напряжения на резисторе? В дело опять же вступает закон Ома для участка цепи: I=U/R. Отсюда U=IR. Мы видим зависимость от номинала самого резистора и от силы тока, текущей в данный момент в цепи. Слышите? От СИЛЫ ТОКА! Так почему бы нам не воспользоваться таким замечательным свойством и не глянуть силу тока через падение напряжения на самом резисторе? Ведь номинал резистора у нас постоянный и почти не изменяется с изменением силы тока 😉
Осциллограмма силы тока на активном сопротивлении
В данном опыте нам не обязательно знать номинал силы тока в цепи. Мы будем просто смотреть, от чего зависит сила тока и изменяется ли вообще?
Поэтому, наша схема примет вот такой вид:
В этом случае шунтом будет являться резистор сопротивлением в 0,5 Ом. Почему именно 0,5 Ом? Да потому что он не будет сильно греться, так как обладает маленьким сопротивлением, а также его номинал вполне достаточен, чтобы снять с него напряжение.
Осталось снять напряжение с генератора, а также со шунта с помощью осциллографа. Если вы не забыли, со шунта мы снимаем осциллограмму силы тока в цепи. Красная осциллограмма — это напряжение с генератора Uген , а желтая осциллограмма — это напряжение с шунта Uш , в нашем случае — сила тока. Смотрим, что у нас получилось:
Частота 28 Герц:
Частота 285 Герц:
Частота 30 Килогерц:
Как вы видите, с ростом частоты сила тока у нас осталась такой же.
Давайте побалуемся формой сигнала:
Как мы видим, сила тока полностью повторяет форму сигнала напряжения.
Итак, какие можно сделать выводы?
1) Сила тока через активное (омическое) сопротивление имеет такую же форму, как и форма напряжения.
2) Сила тока и напряжение на активном сопротивлении совпадают по фазе, то есть куда напряжение, туда и ток. Они двигаются синфазно, то есть одновременно.
3) С ростом частоты ничего не меняется (если только на очень высоких частотах).
Конденсатор в цепи переменного тока
Ну а теперь давайте вместо резистора поставим конденсатор.
Смотрим осциллограммы:
Как вы видите, конденсатор обладает сопротивлением, так как сила тока в цепи значительно уменьшилась. Но обратите внимание, что произошел сдвиг желтой осциллограммы, то бишь осциллограммы силы тока.
Вспоминаем алгебру старшие классы. Итак, полный период T — это 2П
Теперь давайте прикинем, какой сдвиг фаз у нас получился на графике:
Где-то примерно П/2 или 90 градусов.
Почему так произошло? Во всем виновато физическое свойство конденсатора. В самые первые доли секунд, конденсатор ведет себя как проводник с очень малым сопротивлением, поэтому сила тока в этот момент будет максимальна. В этом можно легко убедиться, если резко подать на конденсатор напряжение и в начальный момент времени посмотреть, что происходит с силой тока
Красная осциллограмма — это напряжение, которое мы подаем на конденсатор, а желтая — это сила тока в цепи конденсатора. По мере заряда конденсатора сила тока падает и достигает нуля при полном заряде конденсатора.
К чему приведет дальнейшее увеличение частоты? Давайте посмотрим:
50 Герц.
100 Герц
200 Герц
Как вы видите, с увеличением частоты, у нас сила тока в цепи с конденсатором возрастает.
Реактивное сопротивление конденсатора
Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:
где
Хс — реактивное сопротивление конденсатора, Ом
П — постоянная и приблизительно равна 3,14
F — частота, Гц
С — емкость конденсатора, Фарад
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.
Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
Все с точностью наоборот! Можно даже сказать, что катушка — это полная противоположность конденсатору 😉
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц
34 Килогерца
17 Килогерц
10 Килогерц
Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Реактивное сопротивление катушки индуктивности
Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле
где
ХL — реактивное сопротивление катушки, Ом
П — постоянная и приблизительно равна 3,14
F — частота, Гц
L — индуктивность, Генри
Мощность в цепи с реактивными радиоэлементами
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность — это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком «плюс», а напряжение со знаком «минус». В итоге плюс на минус дает минус. Получается мощность со знаком «минус». А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем «плющить» пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно — это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо — это уже другая история.
В третий промежуток времени t3 и ток и напряжение у нас со знаком «минус». Минус на минус — это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL — это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L — собственно сама индуктивность катушки
С — межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r — сопротивление диэлектрика и корпуса между обкладками
С — собственно сама емкость конденсатора
ESR — эквивалентное последовательное сопротивление
ESI (ESL) — эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Резюме
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением.
В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов.
Сопротивление катушки вычисляется по формуле
Сопротивление конденсатора вычисляется по формуле:
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Реальные катушка и конденсатор имеют в своем составе паразитные параметры, которые имеют некоторое сопротивление. Поэтому реальные катушка и конденсатор не обладают чисто реактивным сопротивлением.
Для школьников.
Кроме активного сопротивления, в цепях переменного тока возможно существование емкостного и индуктивного сопротивлений. Про индуктивное сопротивление будет говориться в следующей статье, а сейчас речь пойдёт об емкостном сопротивлении.
Рассмотрим опыты, позволяющие увидеть существование емкостного сопротивления.
Две маленькие одинаковые электрические лампочки подключались к источникам одинакового напряжения. Но одна (правая) подключалась к источнику постоянного тока (аккумуляторной батарее), а другая (левая) – к источнику переменного тока.
Лампочки светили одинаково, так как количество выделяющегося тепла не зависит от того, какой ток протекает по нитям лампочек (постоянный или переменный).
Подсоединение в цепи конденсаторов большой ёмкости (рис. б) показало, что лампочка, включенная в цепь переменного тока, светила также ярко, а лампочка, включенная в цепь постоянного тока, не светила совсем.
При постоянном источнике тока результат понятен – конденсатор разрывает электрическую цепь, его сопротивление постоянному току бесконечно велико.
Но что происходит, когда цепь, состоящая из лампочки и конденсатора подсоединена к источнику переменного тока, почему лампочка при этом светит или почему конденсатор не препятствует прохождению по цепи переменного тока?
Опыты показывают, что конденсатор пропускает переменный ток, но оказывает ему сопротивление. Это сопротивление назвали емкостным сопротивлением).
Существование емкостного сопротивления обнаружено, например, при проведении следующего опыта.
Конденсатор ёмкостью 10 мкФ, с последовательно соединённым с ним амперметром, включали в городскую осветительную сеть переменного тока с частотой 50 Гц и напряжением 220 В.
Амперметр показал ток 0,69 А. Подсчитали сопротивление конденсатора переменному току, разделив напряжение 220 В на показание амперметра.
Оно оказалось равным 319 Ом.
Расчёт и опыт показали, что емкостное сопротивление для синусоидального тока находится по формуле :
(Формула для емкостного сопротивления получена путём сравнения выражений закона Ома для участка цепи постоянного тока, содержащего активное сопротивление и закона Ома для участка цепи переменного тока, содержащего конденсатор).
Таким образом, емкостное сопротивление зависит от ёмкости конденсатора и частоты переменного тока.
Емкостное сопротивление конденсатора тем меньше, чем больше его ёмкость и чем больше частота переменного тока (чем меньше период).
Чем больше ёмкость, тем больший электрический заряд накапливается на его обкладках при зарядке.
Чем больше частота переменного тока, тем за более короткое время этот заряд будет проходить по проводам, тем больший ток будет пропускать конденсатор.
Посмотрим, что происходит в цепи переменного тока, содержащей только ёмкость.
Если цепь переменного тока содержит только емкостное сопротивление
то ток и напряжение в цепи колеблются с одинаковой частотой, но ток опережает напряжение по фазе на “пи” пополам (на 90 градусов), поэтому в уравнении тока сдвиг по фазе записываем со знаком “плюс”(см. уравнение ниже).
На рисунке синусоиды тока и напряжения смещены в соответствии с записанными уравнениями для мгновенных значений напряжения и тока
Поясним, почему ток в такой цепи (содержащей источник переменного тока и конденсатор) опережает напряжение, воспользовавшись следующим рисунком
По оси ординат откладываются мгновенные значения приложенного к цепи напряжения (напряжение на зажимах источника) и мгновенные значения возникающего в цепи тока в согласии с приведёнными выше формулами для мгновенных значений тока и напряжения, когда в цепи источника переменного тока находится только конденсатор.
Конденсатор заряжается от источника, между его обкладками возникает напряжение, которое в каждый момент времени равное напряжению на клеммах источника, так как ток распространяется по цепи с огромной скоростью (скоростью света).
Когда конденсатор заряжен до максимума (напряжение на нём и напряжение источника имеют максимальные значения), ток равен нулю, а вся энергия цепи есть электрическая энергия заряженного конденсатора (точка а на рисунке).
При уменьшении напряжения источника уменьшается напряжение между обкладками конденсатора, то есть конденсатор начинает разряжаться. В цепи появляется ток, направленный навстречу напряжению источника. На рисунке он изображён как отрицательный (точки лежат ниже оси времени).
К моменту времени Т/4 конденсатор полностью разряжен (напряжение между его обкладками равно нулю), а ток в цепи достигает максимального значения (точка в). В этот момент электрическая энергия становится равной нулю, вся энергия цепи сводится к энергии магнитного поля, создаваемого током.
Затем напряжение источника изменяет знак (заряд на обкладках изменился на обратный), ток начинает ослабевать, сохраняя прежнее направление.
Когда напряжение источника (и конденсатора) достигнет максимума, вся энергия цепи снова становится электрической, а ток равным нулю (точка с).
В дальнейшем напряжение источника (и конденсатора) начинает убывать, конденсатор разряжается, ток нарастает, имея теперь положительное направление (совпадающее с напряжением между обкладками конденсатора), ток достигает максимального значения (точка d) и т. д.
Рассуждая так (сравнивая синусоиды тока и напряжения), видим, что ток раньше, чем напряжение, достигает максимума и проходит через нуль, то есть ток опережает напряжение по фазе на 90 градусов (или на”пи” пополам), или по времени на четверть периода Т/4.
Можно сказать ещё так: при замыкании цепи сначала ток приносит заряд на обкладки конденсатора, а уж потом появляется напряжение на конденсаторе, то есть ток является первичным, а напряжение вторичным, то есть ток опережает напряжение на участке цепи содержащей электрическую ёмкость.
Свойством конденсатора брать из сети ток, опережающий напряжение, широко пользуются на практике для повышения коэффициента мощности сети.
Таким образом, если электрическая цепь переменного тока состоит только из конденсатора, то роль конденсатора сводится к периодическому накоплению им электрической энергии (при зарядке) и возвращению этой энергии обратно источнику тока (при разрядке).
На следующем рисунке показано, как в цепи, содержащей только емкостное сопротивление, меняется мощность в зависимости от времени (пунктирная синусоида).
Мгновенные значения мощности находятся через произведение мгновенных значений тока и напряжения.
Из рисунка видно, что мощность цепи переменного тока, содержащая только конденсатор, изменяется с двойной частотой.
Из рисунка также видно, что в первую и третью части периода, когда напряжение между обкладками конденсатора растёт, мощность цепи с конденсатором положительна (горизонтально заштрихованная площадь). В эти части периода конденсатор получает энергию от источника тока.
Во вторую и четвёртую части периода, когда напряжение между обкладками конденсатора уменьшается, мощность цепи с конденсатором имеет отрицательный знак (вертикально заштрихованная площадь). В эти части периода конденсатор возвращает энергию источнику тока.
Средняя мощность за период цепи с конденсатором равна нулю.
Таким образом, в конденсаторе в каждый момент времени либо запасается энергия от источника (при зарядке), либо возвращается обратно источнику тока (при разрядке конденсатора).
Для электрической цепи промышленного тока факт возвращения энергии источнику тока является отрицательным. Энергия, поступающая в цепь, должна использоваться ею наиболее полно, а не возвращаться источнику.
Рассмотренную мощность называют реактивной емкостной мощностью.
Реактивной её называют потому что она не совершает никакой работы в цепи и не превращается в другие виды энергии, например в тепло (конденсатор остаётся холодным).
Напряжение на конденсаторе:
Ток в цепи, содержащей только конденсатор, равен отношению напряжения на зажимах источника к емкостному сопротивлению цепи:
Пример.
Конденсатор ёмкостью 10 мкФ включен в цепь переменного тока напряжением 120 В и частотой 50 Гц. Какой ток будет проходить через конденсатор и какую мощность будет брать этот конденсатор из сети?
Используя приведённые ниже формулы, получим ответ на поставленные вопросы.
Ответ: 0,4 А; 51 Вт.
Итак, присутствие электрической ёмкости С в цепи переменного тока приводит к сдвигу фаз между током и напряжением (колебания тока опережают колебания напряжения).
Емкостная мощность не совершает механической работы, не нагревает проводники.
Процесс прохождения переменного тока через конденсатор – это многократное повторение зарядки и разрядки конденсатора. При зарядке конденсатора источник отдаёт ему некоторое количество энергии, которая запасается в конденсаторе в виде энергии электрического поля. При разрядке конденсатор возвращает эту энергию источнику (в сеть).
Ещё можно сказать, что замкнутость цепи переменного тока, содержащей конденсатор, объясняется существованием между обкладками конденсатора тока смещения, составной частью которого является ток поляризации в диэлектрике.
О токе смещения и токе поляризации говорится в статьях: “Какое одинаковое свойство имеют изменяющееся во времени электрическое поле. Направление тока поляризации” и “Вектор электрического смещения. Замкнутость цепи переменного тока с конденсатором током смещения”
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Предыдущая запись: Характеристики переменного тока. Переменный ток в цепях, содержащих только активное сопротивление.
Следующая запись :Катушка индуктивности в цепи переменного тока. Индуктивное сопротивление.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70.