12. Активное сопротивление вл определяется в соответствии с паспортными данными оборудования по формуле:
|
|
(5) |
где
r020 – удельное
активное сопротивление на 1 км провода
при его температуре 20 С,
Ом/км;
L – длина линии,
км;
– средняя
температура провода за базовый период,
С;
nЦ
– количество
параллельных цепей, шт.
В
формуле (5) принимается, что при средней
загрузке линий ниже экономической
плотности тока, температура провода
приблизительно равна температуре
воздуха.
При
отсутствии данных о температуре провода,
она принимается равной 20 0С.
13. Активное сопротивление
КЛ определяется в соответствии с
паспортными данными по формуле:
|
|
(6) |
где
r0 – удельное
активное сопротивление на 1 км кабеля,
Ом/км;
L – длина кабеля, км;
nЦ
– количество параллельных цепей, шт.
14. Активное сопротивление шинопровода определяется по формуле:
|
|
(7) |
где
– удельное сопротивление шинопровода,
Оммм2/м;
l
– длина шинопровода, м;
s
– сечение шинопровода, мм2;
kи, с – температурный
коэффициент изменения сопротивления
(для меди и алюминия kи, с
= 0,004);
– средняя
температура за базовый период, при
которой определяют сопротивление
шинопровода, С.
При
отсутствии данных о температуре
шинопровода, она принимается равной 20
0С.
Если
в паспортных данных шинопровода указано
значение удельного активного сопротивления
на 1 км шинопровода, то активное
сопротивление определяется произведением
значений удельного активного сопротивления
и длины шинопровода.
15. Активное сопротивление двухобмоточного трехфазного трансформатора определяется в соответствии с паспортными данными оборудования по формуле:
|
|
(8) |
где
РКЗ
– потери мощности короткого замыкания,
кВт;
UB
ном –
номинальное напряжение высшей обмотки,
кВ;
Sном
–номинальная мощность трехфазного
трансформатора, МВА.
В
случае двухобмоточных однофазных
трансформаторов, образующих трехфазную
группу, активное сопротивление
определяется по формуле:
|
|
(9) |
где
Sном тр –
номинальная мощность двухобмоточного
однофазного трансформатора, МВА.
16.
Активные сопротивления трехобмоточного
трехфазного трансформатора
(автотрансформатора) при равных мощностях
обмоток высшего, среднего и низшего
напряжений определяются в соответствии
с паспортными данными оборудования по
формуле:
|
|
(10) |
где
РКЗ В-С,
РКЗ В-Н,
РКЗ С-Н
– потери мощности короткого замыкания
для пар обмоток, кВт;
Sном
– номинальная мощность трехобмоточного
трехфазного трансформатора, МВА.
Активные
сопротивления трехобмоточного трехфазного
трансформатора с обмотками различной
номинальной мощности, определяются в
соответствии с паспортными данными
оборудования по формуле:
|
|
(11) |
где
– коэффициент, учитывающий приведение
потерь короткого замыкания для
трансформаторов с обмотками
различной номинальной мощности
к мощности обмотки
высшего напряжения:
|
|
(12) |
где
UВном,
UСном
– номинальное напряжение высшей и
средней обмотки, кВ.
Если
паспортные данные оборудования содержат
одно из трех значений потерь короткого
замыкания, то расчет активных сопротивлений
выполняется с использованием «сквозного
активного сопротивления» с последующим
его разделением по ветвям схемы замещения
в пропорциях, определяемых отношениями
номинальных мощностей обмоток,
представленных в таблице 11.
Сквозное активное
сопротивление определяется по формуле:
|
|
(13) |
где
РКЗ
– потери короткого замыкания при
номинальной нагрузке обмотки высшего
напряжения, кВт.
Таблица 11
Соотношение
мощностей и активных сопротивлений
трехобмоточного трансформатора
|
Мощность |
Активное |
||||
|
SВ |
SС |
SН |
RТ |
RТ |
RТ |
|
100 |
100 |
100 |
0,5Rскв |
0,5Rскв |
0,5Rскв |
|
100 |
67 |
100 |
0,5 |
0,75 |
0,5 |
|
100 |
100 |
67 |
0,5 |
0,5 |
0,75 |
|
100 |
67 |
67 |
0,55 |
0,82 |
0,82 |
|
100 |
100 |
50 |
0,5 |
0,5 |
Rскв |
|
100 |
50 |
50 |
0,5 |
Rскв |
Rскв |
|
100 |
100 |
33 |
0,5 |
0,5 |
1,5 |
Двухобмоточные трансформаторы
Двухобмоточные трансформаторы характеризуются сопротивлением короткого замыкания ![]()
и проводимостью шунта намагничивания ![]() схема замещения — Г-образная (рисунок 1) с идеальным трансформатором ИТ, не имеющим сопротивления и характеризующимся только коэффициентами трансформации:
схема замещения — Г-образная (рисунок 1) с идеальным трансформатором ИТ, не имеющим сопротивления и характеризующимся только коэффициентами трансформации: ![]()
Рисунок 1 Г- Образная схема замещения 2 обмоточного трансформатора с идеальным трансформатором ИТ
В программах расчета установившегося режима коэффициент трансформации может определяться, например, как соотношение напряжений 2-го и 1-го узлов данной связи, то есть может быть определен по формуле приведенной выше так и обратным соотношением, в зависимости от того, какой из узлов задан в качестве начала ветви, а какой — в качестве конца ветви (в RastrWin такой принцип расчета коэффициента трансформации).
Для трансформаторов, имеющих регулирование напряжения, в частности регулирование напряжения под нагрузкой, коэффициент трансформации должен соответствовать реальному положению переключателя отпайки: ![]() для i-й отпайки трансформатора.
для i-й отпайки трансформатора.
В такой схеме замещения сопротивление Zт не зависит от k, хотя в действительности такая зависимость имеется.
Активное сопротивление обмоток двухобмоточного трансформатора определяют по известным потерям мощности в обмотках трансформатора, которые в практических расчетах обычно принимают равными потерям короткого замыкания при номинальном токе трансформатора. Выражение для активного сопротивления трансформатора следующее:![]() где: Pk — потери короткого замыкания на трансформаторе, кВт,
где: Pk — потери короткого замыкания на трансформаторе, кВт,
Uном — номинальное напряжение соответствующей обмотки трансформатора, кВ,
Sном — номинальная мощность трансформатора. МВА.
Полное сопротивление обмоток трансформатора: ![]() где: uk — напряжение короткого замыкания трансформатора, выраженное в процентах его от номинального напряжения,
где: uk — напряжение короткого замыкания трансформатора, выраженное в процентах его от номинального напряжения,
Uном — номинальное напряжение соответствующей обмотки трансформатора, кВ,
Sном — номинальная мощность трансформатора, МВА.
Отсюда можно определить индуктивное сопротивление рассеяния обмоток трансформатора: ![]() Для мощных трансформаторов (мощностью выше 1000 кВА), имеющих очень небольшое активное сопротивление, по сравнению с индуктивным), обычно индуктивное сопротивление определяется приближенно Xт=Zт.
Для мощных трансформаторов (мощностью выше 1000 кВА), имеющих очень небольшое активное сопротивление, по сравнению с индуктивным), обычно индуктивное сопротивление определяется приближенно Xт=Zт.
Для мощных трансформаторов можно также считать Yт=0, так как потери холостого хода пренебрежительно малы. При необходимости эти потери могут быть учтены: 
![]() где: Pх — потери холостого хода (потери в стали), кВт,
где: Pх — потери холостого хода (потери в стали), кВт,
Sном — номинальная мощность трансформатора, МВА,
iх — ток холостого хода, %,
Iном, Uном — номинальные ток и напряжение трансформатора, А, кВ,
Таки образом, при моделировании двухобмоточного трансформатора для расчета установившегося режима обычно вводятся четыре параметра: Rт, Xт, Gт и Bт, рассчитываемые по паспортным данным трансформаторов по вышеприведенным формулам.
В различных программах расчета режима есть свои особенности ввода данных по трансформаторам. После определения расчетных параметров трансформаторов вашей сети k,Rт, Xт, Gт, Bт необходимо ввести их в расчетную схему согласно инструкции, приложенной к используемой программе. Особо следует обратить внимание на коэффициент трансформации, и на то, к какому узлу приводится сопротивление трансформатора и параметры его шунта намагничивания.
Поэтому расчетные параметры трансформаторов необходимо вводить в расчетную схему k, Rт, Xт, Gт, Bт согласно инструкции, приложенной к используемой программе, если инструкция не содержит указаний по этому поводу, можно сделать локальный расчет режима для одного трансформатора, и проследить, чтобы он был близок к оценочным параметрам данного трансформатора. Так, рассчитанные программой потери холостого хода должны быть близки (а при номинальном напряжении — совпадать) с Pхх в паспортных данных или в данных справочника r и x трансформатора должно быть близко к рассчитанным в справочнике для трансформатора данного типа r и x, для этой цели можно использовать справочную литературу.
Сопротивление элементов схемы замещения в сети 0,4 кВ
Содержание
Для того чтобы рассчитать токи КЗ в сети до 1000 В, следует первоначально составить схему замещения, которая состоит из всех сопротивлений цепи КЗ. Активные и индуктивные сопротивления всех элементов схемы замещения выражают в миллиомах (мОм).
Как определять сопротивления отдельных элементов схемы замещения, об этом вы и узнаете в этой статье.
1. Определение сопротивлений питающей энергосистемы
Активные и индуктивные сопротивления питающей энергосистемы рассчитывают на стороне ВН понижающего трансформатора и приводят к стороне НН по формуле 2-6 [Л3. с. 28].

На практике можно не учитывать активное сопротивление энергосистемы, а значение индуктивного сопротивления приравнивать как к полному сопротивлению энергосистемы (на точность расчетов это никак не скажется). В этом случае значение (в Омах) индуктивное (полное) сопротивление энергосистемы определяется по формуле 2-7 [Л3. с. 28].

После того как определили индуктивное сопротивление системы по формуле 2-7 [Л3. с. 28], данное сопротивление нужно привести к стороне НН по формуле 2-6 [Л3. с. 28].
Индуктивное сопротивление системы, также можно определить по формулам представленных в ГОСТ 28249-93:
Как мы видим формула 1 из ГОСТ 28249-93 соответствует формулам 2-6, 2-7 из [Л3. с. 28].
Определить сопротивление энергосистемы, учитывая, что ток КЗ со стороны энергосистемы на зажимах ВН трансформатора 6/0,4 кВ составляет в максимальном режиме – 19 кА, в минимальном – 13 кА.
Определяем индуктивное сопротивление энергосистемы по формулам 2-6, 2-7.
Сопротивление энергосистемы в максимальном режиме, приведенное к напряжению 0,4 кВ:
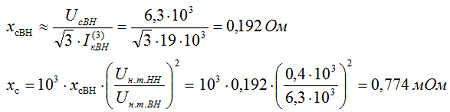
Сопротивление энергосистемы в минимальном режиме, приведенное к напряжению 0,4 кВ:
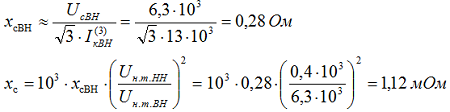
2. Определение сопротивлений трансформаторов
Значения (в мОм) полного (zт), активного (rт) и индуктивного (хт) сопротивления понижающего трансформатора приведенных к стороне НН определяются по формулам: 2-8, 2-9, 2-10 [Л3. с. 28].

На большинстве трансформаторов 10(6)/0,4 кВ имеется возможность регулирования напряжения путем переключения без возбуждения (ПБВ) при отключенном от сети трансформаторе как со стороны высшего так и низшего напряжения. Напряжение регулируется со стороны высшего напряжения на величину ±2х2,5% от номинального значения.

Для трансформаторов с пределом регулирования ПБВ ±2х2,5%, полное сопротивление будет изменятся в пределах:

Значения индуктивного и активного сопротивления трансформатора по ГОСТ 28249-93 определяются по формулам:

Как видно, формулы из ГОСТ 28249-93 совпадают с формулами приведенными в [Л3. с. 28].
Для упрощения расчета активного и индуктивного сопротивления тр-ра, можно использовать таблицу 2-4 [Л3. с. 29] для схем соединения обмоток трансформатора Y/Yo и ∆/Yo. Причем для схем соединения обмоток трансформатора ∆/Yo, значения активного (r0) и индуктивного (х0) сопротивления нулевой последовательности равны значениям активного и индуктивного сопротивления прямой последовательности: r0 = rт и х0 = хт.
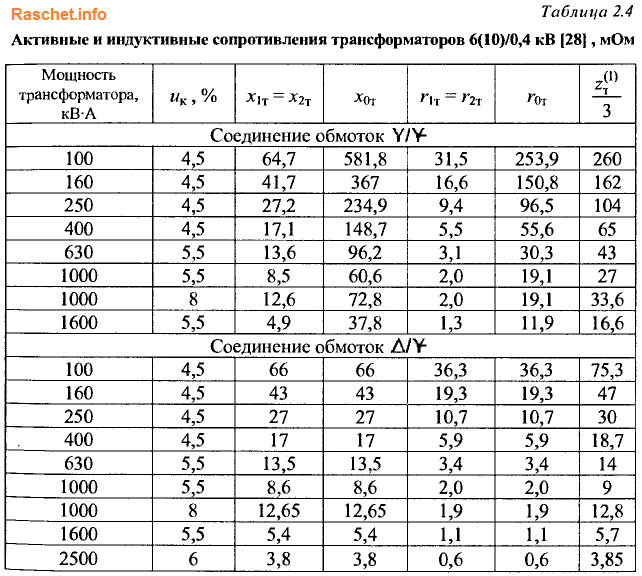
Определить сопротивление трансформатора ТМ 50/6 со схемой соединения обмоток ∆/Yо.
По справочным данным определяем технические данные трансформатора: Sном. = 50 кВА, Uном.ВН = 6,3 кВ, Uном.НН = 0,4 кВ, Uкз = 4%, ∆Ркз=1,1 кВт.
Определяем полное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-8:
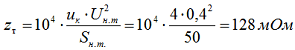
Определяем активное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-9:
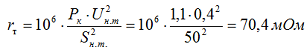
Определяем индуктивное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-10:

3. Определение сопротивлений кабелей
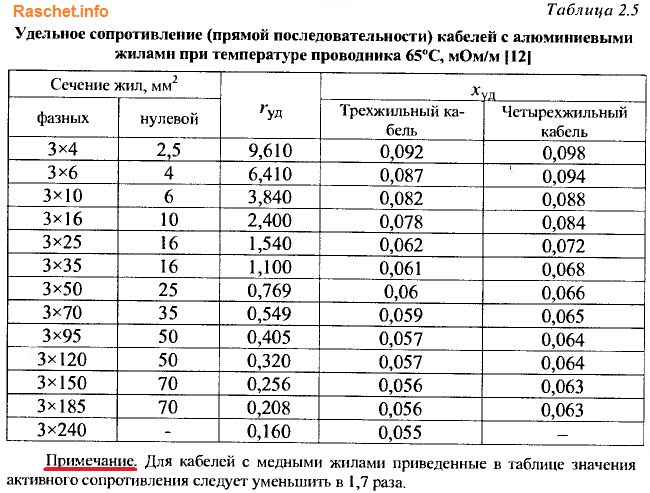
Значения активного и индуктивного сопротивления кабелей определяются по формуле 2-11 [Л3. с. 29].

4. Определение сопротивлений шин и шинопроводов
Сопротивление шин и шинопроводов длиной 5м и меньше, можно не рассчитывать, так как они не влияют на значение токов КЗ.
Значения активного и индуктивного сопротивления шин и шинопроводов определяется аналогично кабелям.

Зная расстояние между прямоугольными шинами, можно приближенно определить индуктивное сопротивление (мОм/м) по формуле 2-12 [Л3. с. 29].
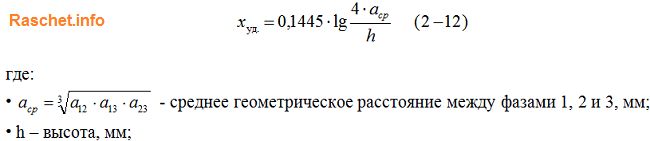
Определить активное и индуктивное сопротивление алюминиевых шин сечением 60х8 мм2 от трансформатора ТМ-630/6 до распределительного щита 0,4 кВ, общая длина проложенных от трансформатора до РП-0,4 кВ составляет 10 м. В данном примере определим сопротивление шин, когда шины находятся как в горизонтальном положении, так и в вертикальном.
4.1 Определим активное и индуктивное сопротивление шин при горизонтальном расположении.
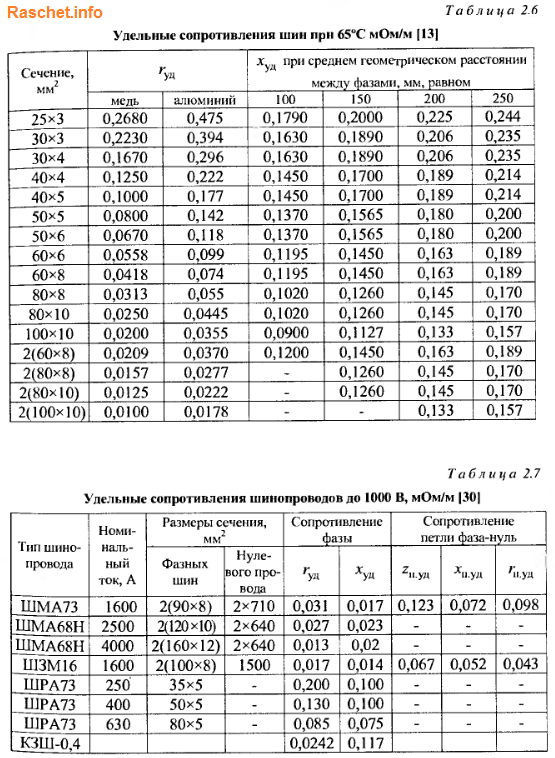
По таблице 2.6 определяем погонное активное сопротивление rуд. = 0,074 мОм/м, индуктивное сопротивление определяем по формуле 2-12 [Л3. с. 29].
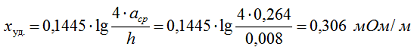
где: расстояние между шинами первой и второй фазы а12 = 200 мм, между второй и третью а23 = 200 мм, между первой и третью а13 = 200 + 60 + 200 = 460 мм, а среднегеометрическое расстояние:
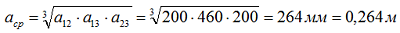
Сопротивление шин от тр-ра до РП-0,4 кВ:

4.2 Определим активное и индуктивное сопротивление шин при вертикальном расположении
При вертикальном расположении шин, активное сопротивление не изменяется, а индуктивное сопротивление составляет:
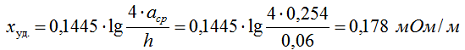
где: расстояние между шинами первой и второй фазы а12 = 200 мм, между второй и третью а23 = 200 мм, между первой и третью а13 = 200 + 8 + 200 = 408 мм, а среднегеометрическое расстояние:
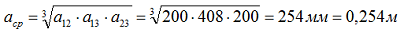
Сопротивление шин от тр-ра до РП-0,4 кВ:
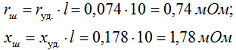
5. Определение сопротивлений воздушных линии
Активное и индуктивное сопротивления линий определяется по той же формуле 2-11 [Л3. с. 29], что и кабели.
Значение индуктивного сопротивления для проводов из цветных металлов можно приближенно принимать равным 0,3 мОм/м, активного по табл. 2.8.
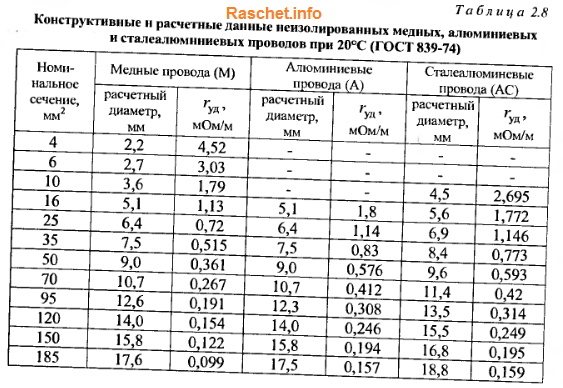
Для стальных проводов активное и индуктивное сопротивление определяется исходя из конструкции провода и значения протекающего по нему тока. Зависимость эта сложная и математическому расчету не поддается, из-за большого количества переменных (сечение провода, температура окружающего воздуха, которая постоянно меняется в течении года, времени суток; нагревом провода током КЗ), которые влияют на значение сопротивление стальных проводов.
Поэтому учесть все эти зависимости практически не возможно и на практике активное сопротивление условно принимают при температуре 20°С и определяют по кривым зависимости стальных проводов от проходящего по ним токам, представленных в приложениях П23-П27 [Л4. с. 80-82].
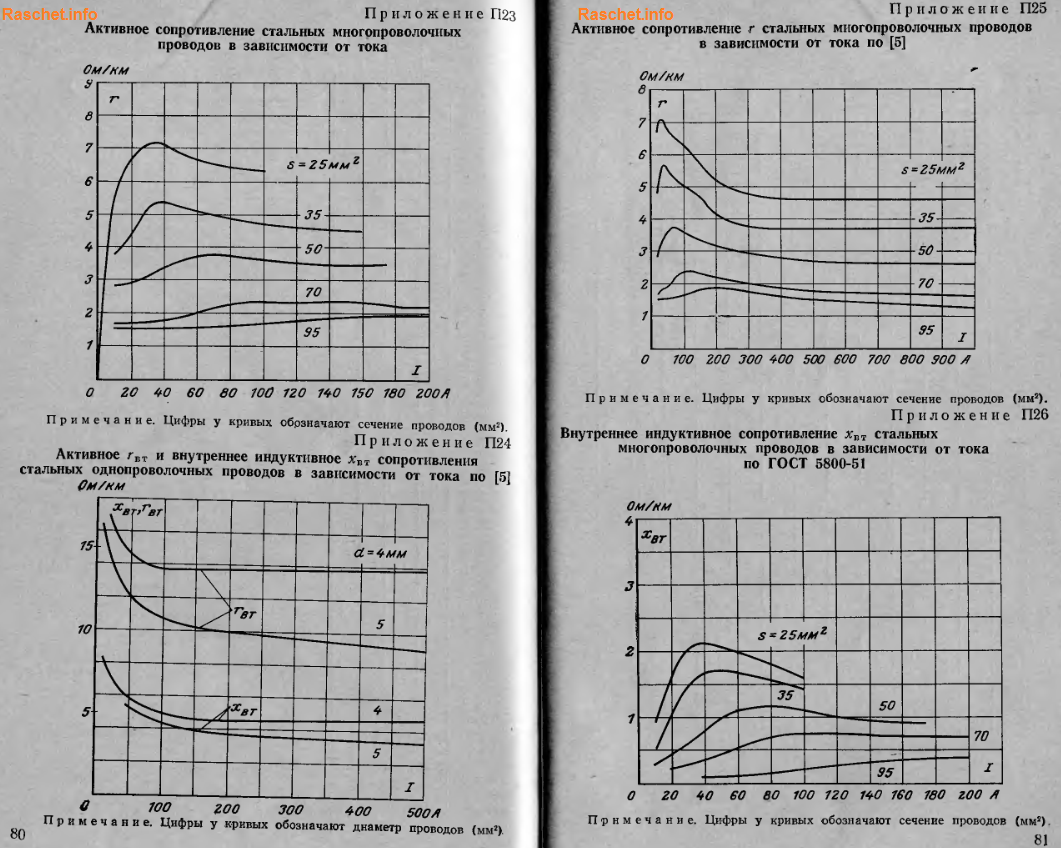

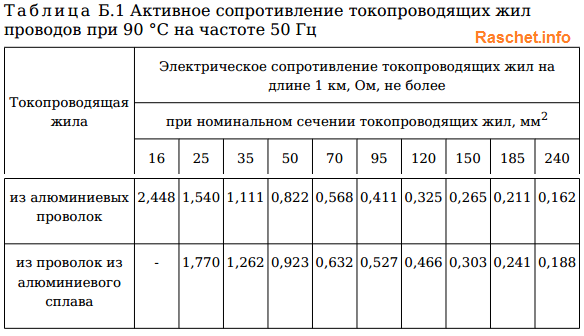
Активное и индуктивное сопротивление для проводов самонесущих изолированных (СИП) определяют по таблицам Б.1, Б.2 [Л5. с. 23-26].
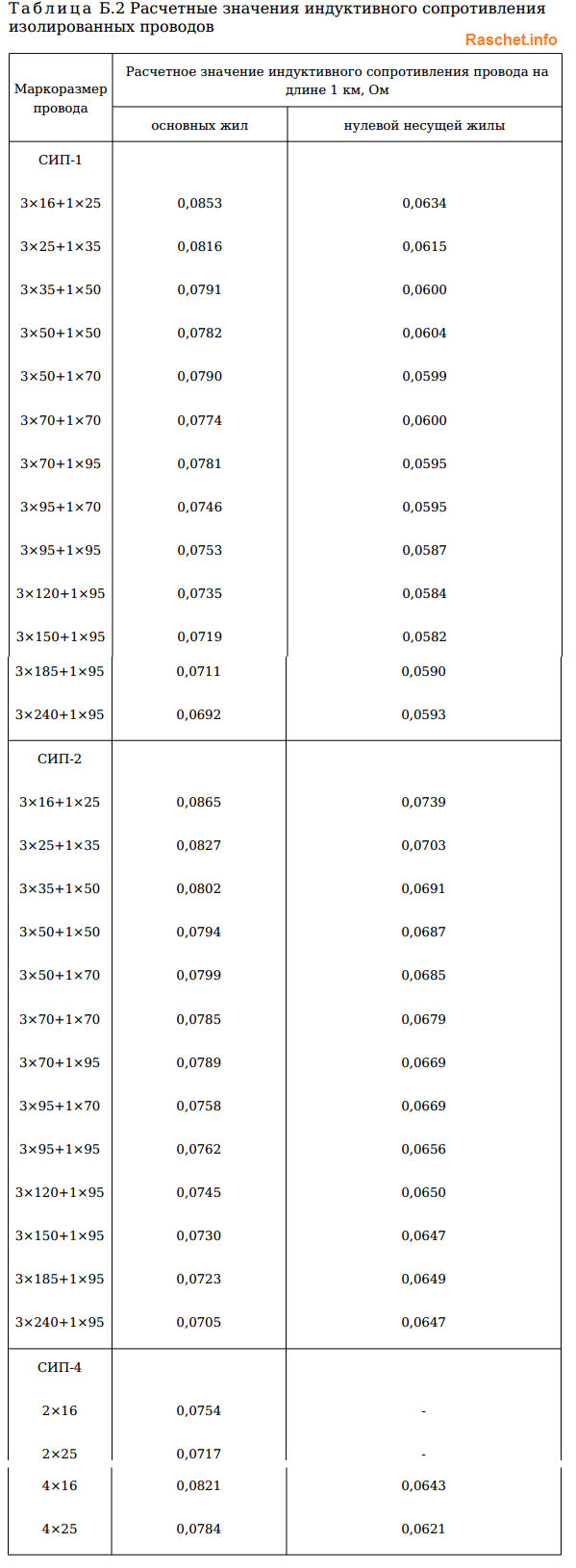
6. Определение сопротивлений реакторов
Номинальные параметры реактора уже заданы в обозначении самого реактора типа РТТ и РТСТ. Например у реактора типа РТТ-0,38-100-0,15:
- 0,38 – номинальное напряжение 380 В;
- 100 – номинальный ток 100 А;
- 0,15 – индуктивное сопротивление при частоте 50 Гц равно 150 мОм.
Активное сопротивление для исполнения У3 (алюминиевая обмотка) — 17 мОм, для исполнения Т3 (медная обмотка) – 16 мОм.
7. Определение сопротивлений трансформаторов тока
Значения активных и индуктивных сопротивлений трансформаторов тока принимаются по приложению 5 таблица 20 ГОСТ 28249-93. Активным и индуктивным сопротивлением одновитковых трансформаторов (на токи более 500 А) при расчетах токов КЗ можно пренебречь.
Согласно [Л3. с. 32] для упрощения расчетов, сопротивления трансформаторов тока не учитывают ввиду почти незаметного влияния на токи КЗ.

8. Определение сопротивлений автоматических выключателей, рубильников, разъединителей
Приближенные значения сопротивлений разъемных контактов коммутационных аппаратов напряжением до 1 кВ определяются по приложению 4 таблица 19 ГОСТ 28249-93. При приближенном учете сопротивление коммутационных аппаратов принимают — 1 мОм.
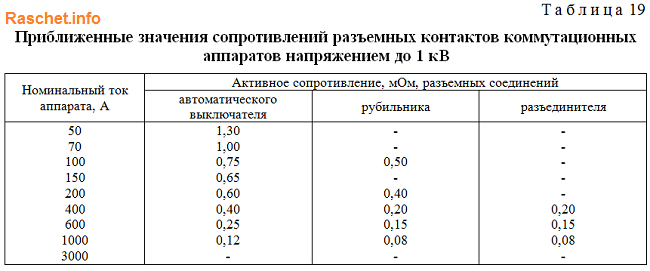
9. Определение сопротивлений контактных соединений кабелей и шинопроводов
Значения сопротивления контактных соединений кабелей и шинопроводов определяют по приложению 4 таблицы 17,18 ГОСТ 28249-93. Для упрощения расчетов, данными сопротивлениями можно пренебречь. При приближенном учете сопротивлений контактов принимают: • rк = 0,1 мОм — для контактных соединений кабелей;
• rк = 0,01 мОм — для шинопроводов.
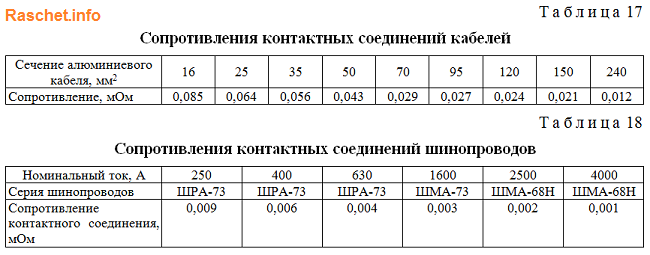
10. Список литературы
1. Рекомендации по расчету сопротивления цепи «фаза-нуль». Главэлектромонтаж. 1986 г.
2. ГОСТ 28249-93 – Методы расчета в электроустановках переменного тока напряжением до 1 кВ.
3. Беляев А.В. Выбор аппаратуры, защит и кабелей в сети 0,4 кВ. Учебное пособие. 2008 г.
4. Голубев М.Л. Расчет токов короткого замыкания в электросетях 0,4 — 35 кВ. 2-e изд. 1980 г.
5. ТУ 16-705.500-2006. Провода самонесущие изолированные и защищенные для воздушных линий электропередач.
Источник
Расчетные формулы основных параметров трансформаторов
Представляю вашему вниманию таблицу с расчетными формулами для определения основных параметров силовых трансформаторов, а также таблицу коэффициента изменения потерь kн.п. в трансформаторах.
Таблица 1 – Расчетные формулы для определения основных параметров трансформаторов
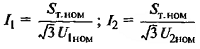
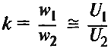
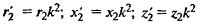
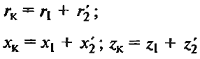
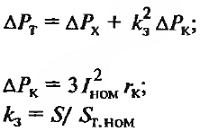
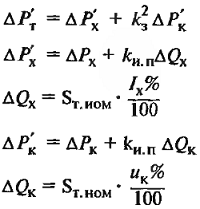
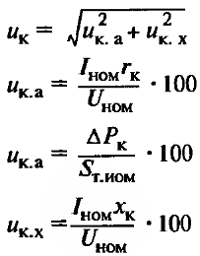
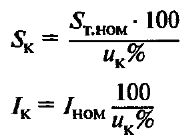
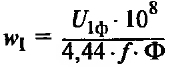
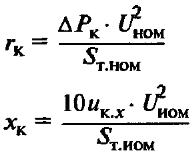
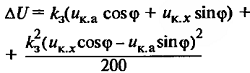
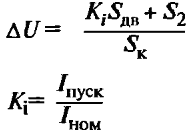
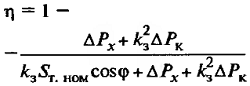

Исходные данные, которые приводятся в паспорте (шильдике) на трансформатор:
- Потери холостого хода ∆Рх, кВт;
- Потери короткого замыкания ∆Pк, кВт;
- Напряжения короткого замыкания Uк, %;
- Ток холостого хода Iхх,%.
Таблица 2 – Коэффициент изменения потерь в трансформаторах
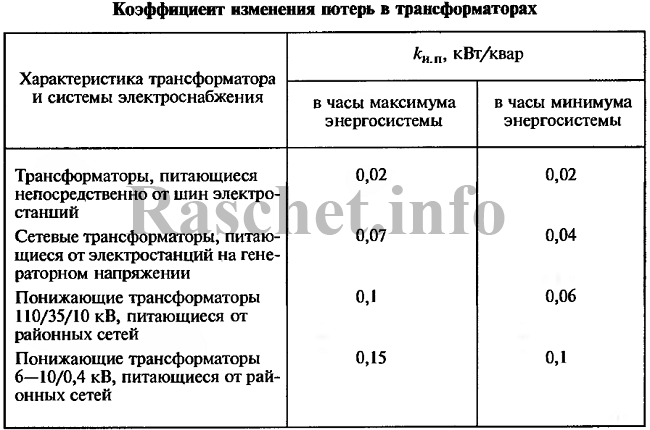
1. Справочная книга электрика. В.И. Григорьева, 2004 г.
Поделиться в социальных сетях
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding» и «PayPal» .
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.

Разобравшись в предыдущей статье с принципом действия и конструкцией УЗО. Теперь перейдем.

В предыдущей статье мы рассмотрели условия выбора плавких предохранителей. В этой же статье, речь.
В данном примере требуется выбрать сечение проводов (по нагреву, по току и по потере напряжения) для.

Выбор сечения кабеля на напряжение до 1000 В независимо это электродвигатель или другая нагрузка. Сводится.

Потеря напряжения в трехфазной линии с несколькими нагрузками вдоль линии определяется как сумма потерь.
Отправляя сообщение, Вы разрешаете сбор и обработку персональных данных.
Политика конфиденциальности.
Источник
➤Adblock
detector
| Наименование величин | Формулы | Обозначение |
|---|---|---|
| Токи обмоток | I1, I2 — токи первичной и вторичной обмоток, А; U1, U2 — то же линейное напряжение, В; |
|
| Коэффициент трансформации | rк, хк, zк – активные, реактивные и полное сопротивления КЗ фазы трансформатора | |
| Активные потери мощности в трансформаторе при нагрузке | ∆Рх – активные потери холостого хода, кВт; ∆Рк – активные нагрузочные потери в обмотках при номинальном токе, кВт; kз – коэффициент загрузки; Sт.ном. – номинальная мощность трансформатора. |
|
| Приведенные активные потери мощности в трансформаторе при нагрузке | S – фактическая нагрузка трансформатора; kи.п. – коэффициент изменения потерь, кВт/квар; ∆Qх – реактивные потери мощности холостого хода; ∆Qк – реактивные потери мощности КЗ; Значения kи.п. даны ниже. |
|
| Напряжение КЗ | Uк – напряжение КЗ, В или %; Uк.а, Uк.х – активная и реактивная составляющие напряжения КЗ, В или %. |
|
| Мощность и ток КЗ трансформатора | U1ф – фазное напряжение первичной обмотки, В Ф – фазный поток; Ф = Вст*Qст мкс; Вст –индукция в стержне; Вст = 13 – 14,5 103 Гс; Qст – активное сечение стержня, см 2 |
|
| Активное и реактивное сопротивление двухобмоточного трансформатора, Ом | Если нагрузка смешанная (активная и индуктивная), то вторым членом можно пренебречь | |
| Потери напряжения при пуске асинхронного короткозамкнутого двигателя (приближенно) | ∆U – потеря напряжения, %; Sдв. – номинальная мощность двигателя, кВА; S2 – мощность других потребителей, присоединенных к шинам трансформаторов, кВА; Ki – кратность пускового тока относительно номинального. |
|
| КПД трансформатора |
Всем доброго времени суток! В прошлых статьях я рассказывал о тепловых расчетах при проектировании трансформатора(Часть 1. Часть 2.). На тепловой режим трансформатора влияет множество параметров трансформатора электрические и электромагнитные. Об этом сегодняшняя статья.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Векторная диаграмма трансформатора
Для упрощения расчётов напряжений и токов в трансформаторе используют векторную диаграмму, которая является графическим изображением всех уравнений трансформатора на комплексной плоскости. Векторную диаграмму строят на основе эквивалентной схемы замещения и уравнений трансформатора.
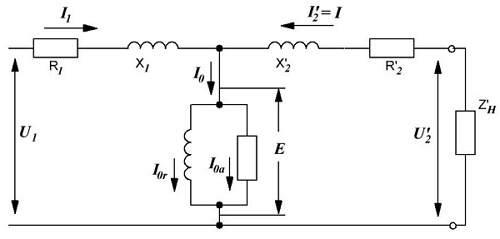
Эквивалентная схема трансформатора.
Обозначения на схеме: U1, I1, R1, X1 – напряжение, ток, активное и реактивное сопротивление первичной обмотки, U/2, I/2, X/2, R/2, Z/H – приведённые напряжение, ток, активное, реактивное сопротивление и полное сопротивление нагрузки вторичной обмотки, Е – ЭДС трансформатора, I0 – намагничивающий ток трансформатора, I0r и I0a – реактивная и активная составляющая намагничивающего тока.
Построение векторной диаграммы начинается с вектора основного магнитного потока Ф, начальная фаза которого принимается равной нулю, вектор ЭДС Е = Е/2 отстаёт от вектора Ф на 90°. Вектор тока намагничивания I0 опережает вектор магнитного потока на угол α, зависящий от магнитных потерь в сердечнике и содержит две составляющие I0r и I0a.
![]()
Для определения направлений векторов I и U/2 на вторичной обмотке можно определить из углов φн и φ/1
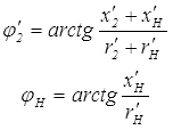
где x/2, r/2 – приведённое реактивное и активное сопротивление вторичной обмотки,
x/Н, r/Н – приведённое реактивное и активное сопротивление нагрузки.
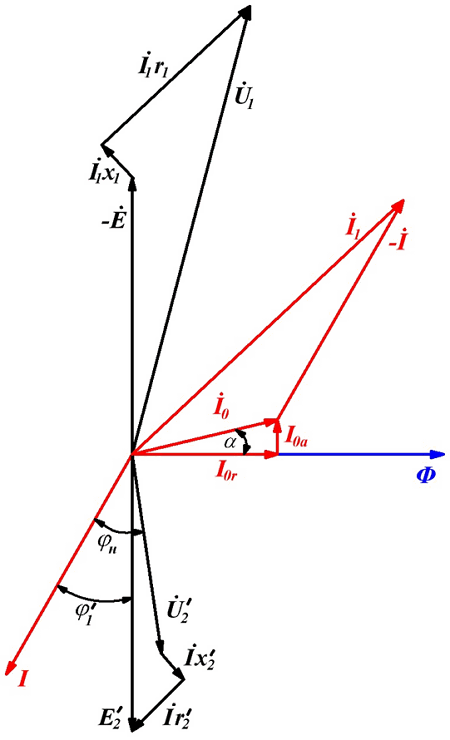
Векторная диаграмма трансформатора.
Данные выражения позволяют построить вектор напряжения на выходе трансформатора U/2, на активном сопротивлении обмотки I/2r/2 и реактивном сопротивлении обмотки I/2jх/2.
![]()
Для продолжения построения необходимо воспользоваться уравнениями трансформатора. Вектор I1 равен геометрической сумме векторов I0 и –I. Произведём суммирование и изобразим на диаграмме
![]()
Вектор (-I) откладывается от конца вектора I0 параллельным переносом вектора I, но в противоположном направлении. В результате вектор I1 откладывается от начала координат и до конца вектора (-I).
Вектор напряжения на первичной обмотке
![]()
Вектор (–Е) строится от начала координат в направлении противоположном вектору Е, то есть он опережает вектор Ф на 90°, вектор I1x1 откладывается от конца вектора (–Е) перпендикулярно вектору тока I1, а вектор I1r1 – параллельно.
Построенная векторная диаграмма имеет общий характер, но её можно перестроить в зависимости от режимов работы трансформатора и позволяет определить электрические параметры трансформатора в этих режимах.
Намагничивающий ток трансформатора
Влияние намагничивающего тока I0 на параметры мощных трансформаторов (более нескольких кВт) обычно незначительно и составляет 2 – 5% от номинального. Чаще всего при расчётах им пренебрегают. В случае трансформаторов малой мощности ток намагничивания порой сравнивается с рабочим током, поэтому требует учёта и анализа.
Из эквивалентной схемы приведённой выше видно, что намагничивающий ток I0 содержит две составляющие: реактивную I0r, которая обеспечивает намагничивающую силу для создания магнитного потока в сердечнике Φ (Φ = I0rω), и активную I0a, зависящая от потерь мощности в сердечнике ∆Р (∆Р = I0aRc). Тогда
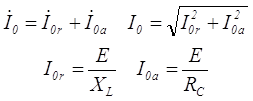
Использование абсолютных значений намагничивающего тока: полного I0, активной I0a и реактивной I0r составляющих не всегда удобно, поэтому используют эти значения относительно приведённого тока вторичной обмотки I
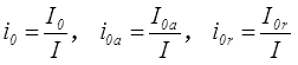
Тогда относительная реактивная составляющая намагничивающего тока i0r может быть выведена из следующих выражений
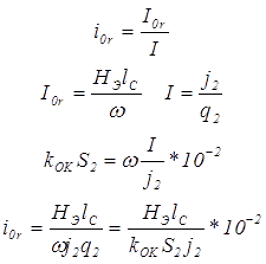
где НЭ – эквивалентная напряженность магнитного поля в сердечнике,
lC – длина средней магнитной линии сердечника.
Часто при расчетах трансформаторов используют выражения для геометрических изображений (подробнее здесь), в основе которых стоит некоторый базовый параметр а. Поэтому выразим реактивную составляющую через базовый параметр
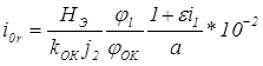
Относительная активная составляющая i0a, после преобразований и используя метод геометрических изображений, будет иметь вид
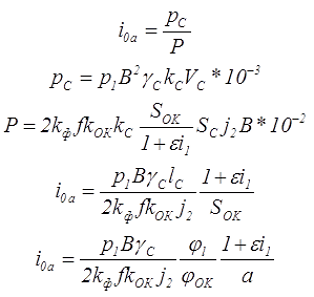
где γС – удельный вес сердечника.
Из приведённых выражений видно, что намагничивающий ток и его составляющие растут при уменьшении базового размера а, то есть размеров трансформатора. То есть при достаточно малой величине базового размера а, намагничивающий ток может достигать значительных величин. Однако с ростом частоты намагничивающий ток оказывается значительно ниже, чем в трансформаторах промышленной частоты.
С учётом данного факта необходимо уточнить выражение для мощности трансформатора путём ввода коэффициента учёта распределения окна между обмотками – n. Тогда выражение для мощности трансформатора будет иметь вид
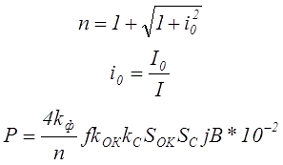
где I0 – ток намагничивания трансформатора,
I – приведённый вторичный ток,
i0 – относительный намагничивающий ток.
Падения напряжения трансформатора
Для трансформатора малой мощности большое значение играет изменение выходного напряжения под нагрузкой ∆U. Данная величина характеризует стабильность выходного напряжения и показывает, на сколько изменяется выходное напряжение при изменении выходного тока от нуля до номинального. Падение напряжения зависит от сочетания следующих факторов: активные и реактивные сопротивления обмоток, cos φ нагрузки и первичного тока. В общем случае падение напряжение оценивается следующими выражениями
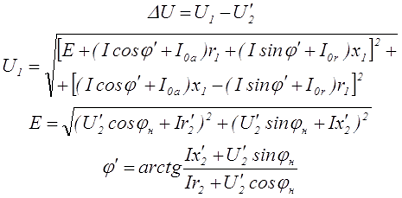
где U1, r1, x1 – напряжение, активное и реактивное сопротивление первичной обмотки, U/2, x/2, r/2 – приведённые напряжение, активное, реактивное сопротивление, Е – ЭДС трансформатора, I = I/2 – приведённый ток вторичной обмотки трансформатора, I0r и I0a – реактивная и активная составляющая намагничивающего тока, φн – фазовый угол нагрузки.
Данные выражения позволяют вычислить падение напряжение при любых условиях, однако в зависимости от типа трансформатора можно их упростить. Для этого рассмотрим составляющие падания напряжению – активную часть ∆Ua и реактивную часть ∆Uх.
![]()
Они показывают падение напряжения на активных и реактивных сопротивлениях обмоток.
Так же как и для намагничивающего тока для анализа и расчета лучше использовать относительные значения падения напряжения.
Относительное значение падения напряжения на активных сопротивлениях обмоток
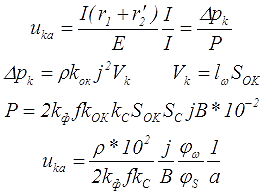
где ρ – удельное электрическое сопротивление,
j – плотность тока в обмотках,
kф – коэффициент формы напряжения,
f – частота переменного напряжения,
kс – коэффициент заполнения сердечника,
В – магнитная индукция в сердечнике,
φω – геометрическое изображение средней длины витка катушки трансформатора,
φS – геометрическое изображение сечения сердечника,
a – базисный параметр трансформатора.
Относительное значение падения напряжения на реактивных сопротивлениях обмоток
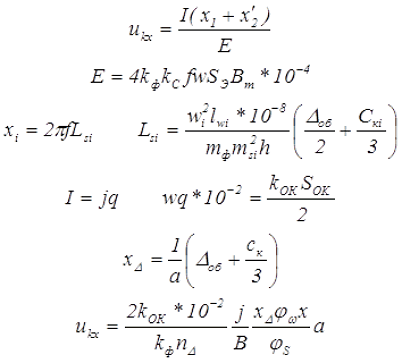
где kОК – коэффициент заполнения окна сердечника,
j – плотность тока в обмотках,
kф – коэффициент формы напряжения,
В – магнитная индукция в сердечнике,
n∆ — число сечений катушек в окне, для БТ n∆ = 1, для СТ, ТТ n∆ = 2,
∆об – толщина межобмоточной изоляции,
φω – геометрическое изображение средней длины витка катушки трансформатора,
φS – геометрическое изображение сечения сердечника,
a – базисный параметр трансформатора.
сК – толщина одной катушки (на одну сторону),
х – относительная ширина окна.
Полученные выражения показывают, что при постоянной геометрии трансформатора и его размерах относительное значение активной составляющей падения напряжения uка уменьшается с ростом частоты, а величина относительного значения реактивной составляющей uкх практически не зависит от частоты (она немного возрастает из-за роста отношения j/B). В тоже время при увеличении базовой величины а (а значит и размеров трансформатора) активная составляющая uка значительно уменьшается, а реактивная uкх – возрастает. Однако в большинстве случаев для трансформаторов малой мощности основное значение в падении напряжения играет активная составляющая.
Величина падения напряжения может быть различной в зависимости от назначения или условий работы трансформатора. Типовым значением падения напряжения считается u = 0,1, но в отдельных случаях при жестких требованиях к стабильности выходного напряжения может уменьшаться до u = 0,05, или даже u = 0,01…0,02.
Соотношение плотностей тока в обмотке
Соотношение плотностей тока в обмотках трансформатора ε определяется следующим выражением
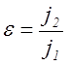
где j1 и j2 – плотность тока в первичной и вторичной обмотке.
Проблема выбора оптимального соотношения плотностей тока в обмотках является одной из важных в теории и практике проектирования трансформатора. Обычно принято считать что ε ≈ 1 (j1 = j2), однако это справедливо для очень больших трансформаторов. Однако для трансформатора малой мощности данное условие не является оптимальным и вот почему.
Обычно к таким трансформаторам предъявляют противоречивые требования в зависимости от условия проектирования.
Так при условии обеспечения требуемого теплового режима (перегрева) трансформатора оптимальное значение ε определяются потерями активной мощности в обмотках. Например, для трансформатора малой мощности выступают требования минимальных потерь при заданной мощности, либо максимальной мощности при заданных потерях, либо минимальный вес и объем при заданной мощности и перегреве. Таким образом, ключевым условием в данном случае является получение минимальных потерь в обмотках, поэтому выражение для оптимального соотношения плотностей тока εо в обмотках будет иметь вид
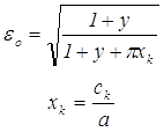
где х – относительная ширина сердечника,
y – относительная толщина сердечник,
а – базовый размер сердечника,
сk – толщина одной катушки (на одну сторону).
Из данного выражения можно сделать вывод, что εо < 1, но конкретные значения определяются геометрией трансформатора. Рост потерь в обмотках трансформатора происходит при отклонении от оптимального значения, как в большую, так и в меньшую сторону. Практически часто приходится отступать от оптимальных значений ε из-за дискретности ряда диаметров проводов. Поэтому без заметного отклонения величина отношения плотностей тока может изменяться в следующих пределах -15…+25% от εо.
Иначе при заданном падении напряжения трансформатора предъявляются следующие требования: минимальное падение напряжения при заданной мощности или максимальная мощность при заданном падении напряжения, либо минимальный вес и объём при заданной мощности и падении напряжении. В данном случае оптимальное значение отношения плотностей тока εо будет иметь вид
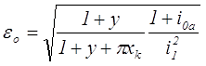
где i0a – активная составляющая относительного значения тока намагничивания,
i1 – относительное значение тока первичной обмотки.
В данном случае оптимальное значение εо также меньше 1. Значение εо тем меньше, чем больше i1 и зависит от геометрии трансформатора, определяемой параметрами хk и y. Рост падения напряжения происходит при отклонении от оптимального значения εо особенно в меньшую сторону. То есть за счет правильного выбора соотношения плотностей тока (сечения провода) можно добиться снижения падения напряжения и повышения КПД трансформатора.
Как определить мощность трансформатора?
Чаще всего для мощности трансформатора Р используется выражение, полученное при условии следующих упрощений:
— намагничивающий ток не учитывают, I0 = 0, I1 = I;
— плотность тока первичной и вторичной обмоток считают равными, j1 = j2 = j;
— окно сердечника делится пополам между обмотками, S1 = S2 = Sок/2.
Таким образом мощность трансформатора может быть определена следующими выражениями
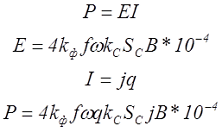
где kф – коэффициент формы кривой напряжения,
f – частота переменного напряжения, Гц,
w – число витков в обмотке,
kC – коэффициент заполнения магнитным материалом сердечника,
SC – сечение сердечника, см2,
В – магнитная индукция в сердечнике (амплитудное значение), Тл,
j – плотность тока в обмотке, А/мм2,
q – сечение проводника в обмотке, мм2.
Данное выражение можно несколько упростить
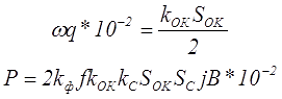
где kОК – коэффициент заполнения окна сердечника,
SOK – площадь окна сердечника, см2.
Данные выражения показывают, что при постоянных kC, kОК, j и В мощность трансформатора пропорциональна частоте f и произведению площадей сердечника и окна SCSOK. Следует отметить, что коэффициенты j и В не постоянны, а сложным образом зависят от мощности трансформатора. Однако видно, что при тех же размерах трансформатора SC и SOK при увеличении частоты мощность трансформатора можно существенно увеличить. Или же другими словами трансформатор той же мощности при повышенной частоте имеет существенно меньшие размеры, чем трансформатор промышленной частоты (50 Гц). Это основная причина широкого распространения трансформаторов повышенной и высокой частоты.
Чаще всего для трансформаторов, ε = 1, однако это условие не является оптимальным. Однако если считать, что ε ≠ 1, то вышеописанные выражения теряют силу, потому что окно сердечника распределяется не пополам и не в отношении n, а в зависимости от величины ε. В результате необходимо вводить дополнительные коэффициенты заполнения окна первичной и вторичной обмоток kОК1 и kОК2. В результате данных условий получаем наиболее общее выражение для электромагнитной мощности трансформатора
![]()
где j2 – плотность тока вторичной обмотки,
S2 – площадь окна занятая только вторичной обмотки,
kОК2 – коэффициент заполнения площади S2.
Площадь S2 определяется следующим выражением
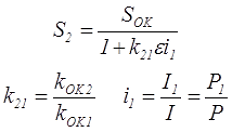
где I1 – относительный ток первичной обмотки,
I – приведённый вторичный ток,
Р1 – полная мощность, потребляемая трансформатором от сети,
Р – электромагнитная мощность.
Тогда получим наиболее строгое выражение для электромагнитной мощности
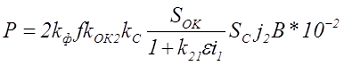
Разница значений kОК1 и kОК2 обычно незначительна и не дает больших отличий, поэтому можно принять kОК1 = kОК2 = kОК, k21 = 1.
Тогда площадь окна занятая вторичной обмоткой составит
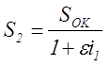
В соответствие с данным выражением для обычных условий получим следующее выражение для электромагнитной мощности трансформатора
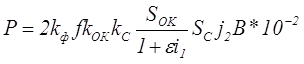
Как определить мощность вторичной обмотки трансформатора?
Мощность, отдаваемая вторичной обмоткой трансформатора в общем случае равна
![]()
где Р – электромагнитная мощность трансформатора,
φ/ — угол между векторами ЭДС и тока,
рК2 и рS2 – потери активной и реактивной мощности во вторичной обмотке.
При работе трансформатора на активную нагрузку φ/ = 0, и потери реактивной мощности рS2 = 0 (у трансформаторов малой мощности они незначительны). Поэтому выражение мощности отдаваемой вторичной обмоткой будет следующее
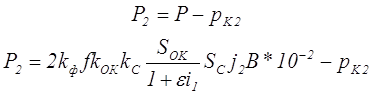
Данное выражение наиболее общее для обычных условий работы основное уравнение вторичной мощности.
В следующей статье я продолжу рассматривать параметры трансформатора, такие как, плотность тока в обмотках трансформатора, электромагнитную индукцию сердечника и т.д.
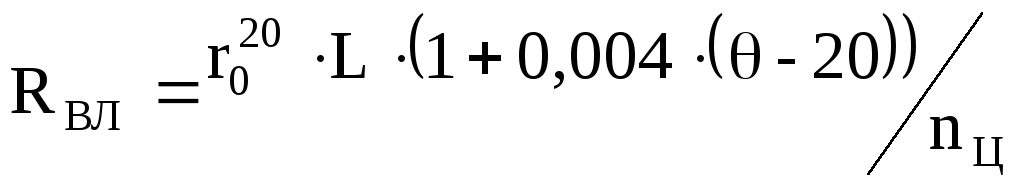 ,
, ,
,



 ,
,
