Как найти активность если известен период полураспада - Сайт, где вы сможете решить свои вопросы

Активность и
единицы ее измерения.

Закон
радиоактивного распада
для любых превращений ядер устанавливает,
что за единицу времени распадается
всегда одна и та же доля нераспавшихся
ядер данного радионуклида. Эту долю
называют постоянной
распада
и обозначают l.
В общем виде этот закон выражается
экспоненциальной зависимостью:

,
(2.1)

где
N – число ядер, распавшихся за время t;
N₀
– начальное число ядер радионуклида;
е = 2,718; l
– постоянная распада и соответствующий
ей период полураспада зависят только
от устойчивости ядер.

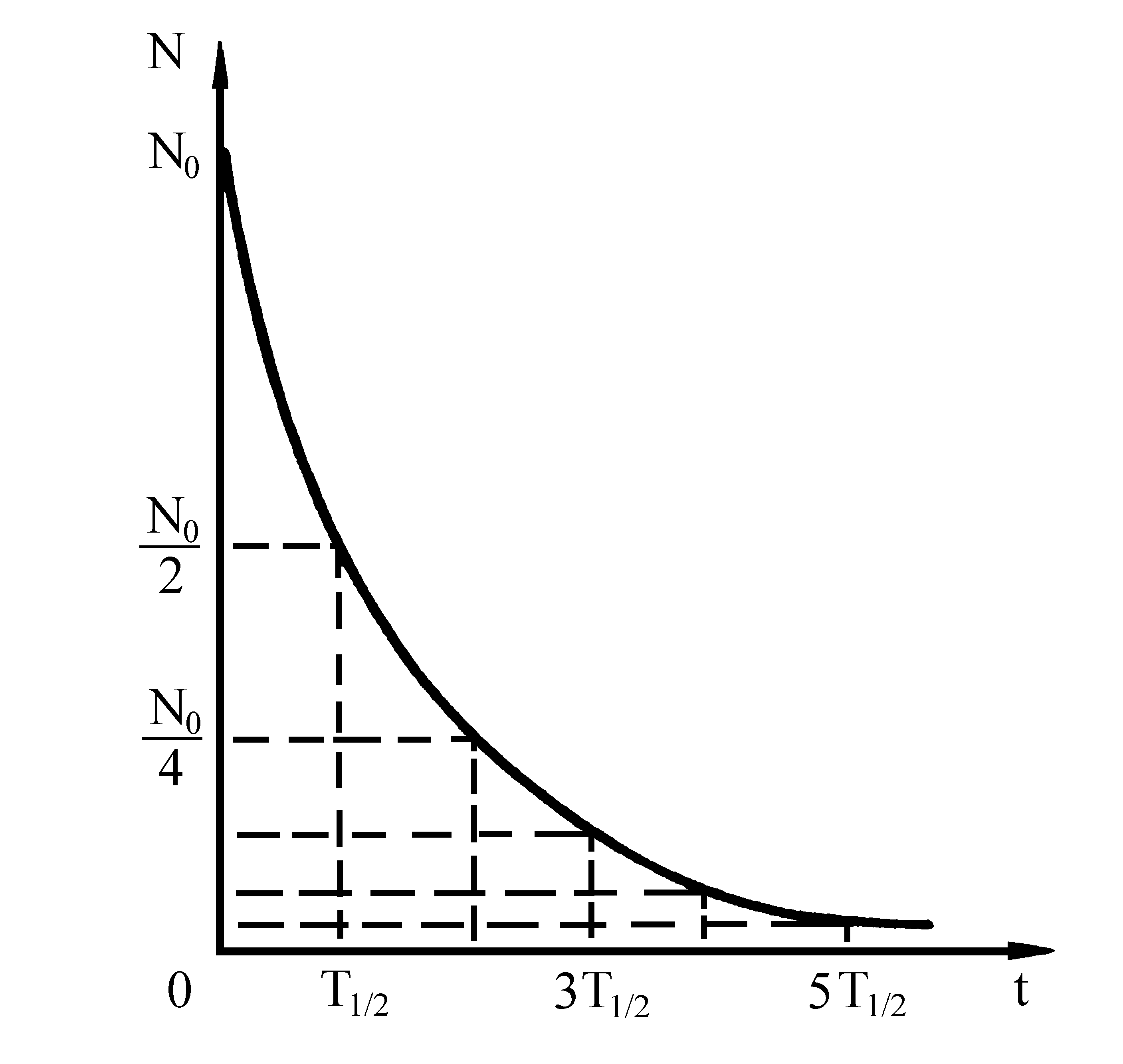
Этот закон,
выражающий уменьшение количества ядер
атомов радиоактивного вещества во
времени, называется законом радиоактивного
распада (рис. 4).

Для любого момента времени

,
(2.2)

,
(2.3)

где N₁ и N₂
– число ядер материнского и дочернего
радионуклидов; N₀ –
число ядер материнского радионуклида
в начальный момент времени; l₁
и l₂ – постоянные
распада материнского и дочернего
радионуклидов.

Для
характеристики устойчивости ядер
радиоактивного вещества относительно
распада используется понятие период
полураспада,
т.е.–
промежуток времени, в течение которого
в результате радиоактивного распада
количество ядер данного радиоактивного
вещества уменьшается в два раза.

.
(2.4)

Рис. 4. График радиоактивного распада:

N₀
– исходное количество радиоактивного
вещества; Т_1/2
– период

полураспада вещества

Величина,
обратная постоянной распада, называется
средним
временем жизни
t
радиоактивного ядра:

.
(2.5)

Период полураспада
для различных радионуклидов имеет
протяженность от долей секунды до
миллиардов лет. Соответственно и
радиоактивные вещества разделяют на
короткоживущие (часы, дни) и долгоживущие
(многие годы).

Например:
Po
имеет Т_1/2
= 1,6´10^-4с;

U
имеет Т_1/2
= 4,47´10¹⁰
лет.

Период
полураспада – одна из основных
характеристик радиоактивных веществ,
которую учитывают при их практическом
применении. Так при гамма-терапии
предпочтение отдают радиоактивным
веществам с большим периодом полураспада,
например
Cs
(Т_1/2 = 30 лет),

Co
(Т_1/2 = 5,25
года). При введении радиоактивных веществ
в организм с диагностической целью
стремятся свести к минимуму дозу
облучения органов и тканей, поэтому
используют радиоактивные вещества,
период полураспада которых невелик,
например
Na
(Т_1/2
=
14,9 ч),
I
(Т_1/2
=
2,3 ч).

Активность и единицы измерения

Активность
есть мера интенсивности распада
радионуклида и определяется как
количество распадов ядер атомов
радиоактивного вещества в единицу
времени, т.е. как скорость распада ядер.

Если
радиоактивное вещество содержит N атомов
и его постоянная распада, выражающая
долю распадающихся атомов в единицу
времени, l,
то активность будет равна

А_n.
(2.6)

Известно,
что постоянная радиоактивного распада
и период полураспада Т_1/2
связаны соотношением

.
(2.7)

Моль
вещества содержит 6,02´10²³
атомов. В массе m вещества с массовым
числом А число атомов

.
(2.8)

Тогда активность
источника выражается формулой

А_n
,
(2.9)

где
А_n
– активность радионуклида, Бк; m
– масса радионуклида, г; А – массовое
число радионуклида; Т – период полураспада
радионуклида, с.

Активность
источника,
в котором содержатся радиоактивные
ядра одного вида, уменьшается во времени
по экспоненциальному закону:

А_n
= А₀,
(2.10)

где
А₀
– активность источника в начальный
момент времени (t = 0); t – текущее время,
которому соответствует активность
вещества A_n.

Чем меньше период
полураспада, тем большая доля ядер
атомов радионуклида распадается в
единицу времени.

Число
распадов в единицу времени в данном
количестве радиоактивного вещества
выражает активность
вещества. Поэтому количество радиоактивного
вещества удобнее выражать не в весовых
единицах, а в единицах активности.
Единицей измерения активности в
Международной системе единиц (СИ)
является Беккерель
(Бк).
Беккерель равен активности нуклида в
радиоактивном
источнике, в котором за время 1 с происходит
1 распад, т.е. 1 Бк = 1 расп./с.

В практике большое
применение получила внесистемная
единица измерения активности –
Кюри (Ки).
Кюри равен активности нуклида в
радиоактивном источнике, в котором за
время 1 с происходит 3,7´10¹⁰
распадов, т.е. 1 Ки = 3,7´10¹⁰
Бк, такой активностью обладает 1 г радия
и радиоактивность 1 г Rа
была принята за единицу измерения Кюри.

1
Бк =
1 расп./с = 2,703´10^-11
Ки.

Вес радионуклида
активностью 1 Ки тем больше, чем медленнее
распадается вещество, т.е. чем больше
период его полураспада. Так для
Nа
(Т_1/2
= 15 ч) масса = 0,1 г; для
Рu
(Т_1/2
= 24,4 тыс. лет) масса = 16 г; для
U
(Т_1/2=
4,5 млрд. лет) масса = 3 т.

Для характеристики
загрязненности продуктов питания, воды,
строительных материалов, почвы и т.д.
используется: удельная активность А_m
= А_n/m,
объемная активность А_v
= А_n/V
и поверхностная активность А_s
= А_n/S,
где m
и V соответственно масса и объем препарата
пробы с активностью А_n,
а S – площадь загрязненной поверхности.

Удельная активность
А_m
измеряется в единицах СИ в Бк/кг, объемная
активность А_v
– в Бк/м³,
поверхностная активность в Бк/м².
На практике также используются
внесистемные единицы активности (табл.
1).

Выбор единиц этих величин определяется
конкретной задачей.

Например, допустимую
концентрацию радионуклидов в воде
(объемную активность) удобнее выражать
Бк/л, а в воздухе в Бк/м³.

Если плотность пробы
r
= 1 кг/л например воды, измеренные значения
объемной активности А_v,
Бк/л численно совпадают с удельной
активностью А_m,
Бк/кг. Если плотность пробы отличается
от 1кг/л, удельную активность пробы можно
найти по формуле

А_m
= А_v/r.
(2.11)

Таблица
1. Единицы
измерения радиоактивности

Величина	Название и обозначение	Соотношение между единицами
единица СИ	внесистемная
Активность	А	Бк	А	Ки	1 Бк = 1расп./с = = 2,703´10^-11 Ки 1 Ки = 3,7´10¹⁰ Бк
Удельная Активность	А_m	Бк/кг	А_уд	Ки/кг	1 Бк/кг = 0,27´10^-10Kи/кг 1 Kи/кг = 3,7´10¹⁰ Бк/кг
Объемная Активность	А_v	Бк/м³	А_об	Ки/л	1 Бк/м³ = 0,27´10^-7 Kи/л, 1 Ки/л = 3,7´10⁷ Бк/м³
Поверхностная активность (степень загрязнения)	А_s	Бк/м²	А_пов	Ки/км²	1 Бк/см² =10⁴ Бк/м² = = 0,27 Ки/км² 1 Ки/км² = 3,7´10⁴ Бк/м² = = 3,7 Бк/см²

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 февраля 2021 года; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Активность.

Акти́вность радиоакти́вного исто́чника — число элементарных радиоактивных распадов в единицу времени^[1].

Производные величины[править | править код]

Удельная активность — активность, приходящаяся на единицу массы вещества источника.

Объёмная активность — активность, приходящаяся на единицу объёма источника.
Удельная и объёмная активности используются, как правило, в случае, когда радиоактивное вещество распределено по объёму источника.

Поверхностная активность — активность, приходящаяся на единицу площади поверхности источника. Эта величина применяется для случаев, когда радиоактивное вещество распределено по поверхности источника.

Единицы измерения активности[править | править код]

В Международной системе единиц (СИ) единицей активности является беккерель (русское обозначение: Бк; международное: Bq); 1 Бк = с⁻¹. В образце с активностью 1 Бк происходит в среднем 1 распад в секунду.

Внесистемными единицами активности являются:

кюри (русское обозначение: Ки; международное: Ci); 1 Ки = 3,7⋅10¹⁰ Бк (точно).
резерфорд (русское обозначение: Рд; международное: Rd); 1 Рд = 10⁶ Бк (точно). Единица используется редко.

Удельная активность измеряется в беккерелях на килограмм (Бк/кг, Bq/kg), иногда Ки/кг и т. д. Системная единица объёмной активности — Бк/м³, часто используются также Бк/л. Системная единица поверхностной активности — Бк/м², часто используются также Ки/км² (1 Ки/км² = 37 кБк/м²).

Существуют также устаревшие внесистемные единицы измерения объёмной активности (применяются только для альфа-активных нуклидов, обычно газообразных, в частности для радона):

махе; 1 махе = 13,5 кБк/м³;
эман; 1 эман = 0,1 нКи/л = 3,7 Бк/л = 3700 Бк/м³.

Зависимость активности от времени[править | править код]

Активность (или скорость распада), то есть число распадов в единицу времени, согласно закону радиоактивного распада зависит от времени следующим образом:

${displaystyle A(t)=-{frac {dN}{dt}}=lambda N={frac {ln 2}{T_{1/2}}},N_{0},2^{-{frac {t}{T_{1/2}}}}={frac {ln 2}{T_{1/2}}},{frac {m}{mu }},N_{A},2^{-{frac {t}{T_{1/2}}}}=A_{0},2^{-{frac {t}{T_{1/2}}}},}$

где

N_A — число Авогадро,
T_1/2 — период полураспада,
N(t) — количество радиоактивных ядер данного типа,
N₀ — их начальное количество,
λ — постоянная распада,
μ — молярная масса радиоактивных ядер данного типа,
m — масса образца (радиоактивных ядер данного типа).

Здесь предполагается, что в образце не появляются новые ядра данного радионуклида, в противном случае зависимость активности от времени может быть более сложной. Так, хотя период полураспада радия-226 всего 1600 лет, активность ²²⁶Ra в образце урановой руды совпадает с активностью урана-238 в течение почти всего времени существования образца (кроме первых 1-2 миллионов лет до установления векового равновесия, когда активность радия даже растёт).

Вычисление активности источника[править | править код]

Зная период полураспада (T_1/2) и молярную массу (μ) вещества, из которого состоит образец, а также массу m самого образца, можно вычислить значение числа распадов, произошедших в образце за период времени t по следующей формуле (полученной из уравнения радиоактивного распада):

${displaystyle N(t)=N_{0}left(1-2^{-{frac {t}{T_{1/2}}}}right),}$

где $N_{0}={frac {m}{mu }}N_{A}$ — начальное количество ядер^[2]. Активность равна (с точностью до знака) производной по времени от N(t):

${displaystyle A=-dN(t)/dt={frac {N_{0}ln 2}{T_{1/2}}}cdot 2^{-{frac {t}{T_{1/2}}}}.}$

Если период полураспада велик по сравнению с временем измерений $(tll T_{{1/2}}),$ активность можно считать постоянной. В этом случае формула упрощается:

$A={frac {N_{0}ln 2}{T_{{1/2}}}}.$

При этом удельная активность

${displaystyle a={frac {A}{m}}={frac {N_{A}ln 2}{mu cdot T_{1/2}}}.}$

Величина $lambda ={frac {ln 2}{T_{{1/2}}}}$ называется константой распада (или постоянной распада) радионуклида. Обратная ей величина $tau =1/lambda ={frac {T_{{1/2}}}{ln 2}}$ называется временем жизни (совпадает с периодом полураспада с точностью до коэффициента 1/ln 2 ≈ 1/0,69 ≈ 1,44; её физический смысл — время, в течение которого количество радионуклида уменьшается в е раз).

Зачастую на практике приходится решать обратную задачу — определять период полураспада радионуклида, из которого состоит образец. Один из методов решения этой задачи, подходящий для коротких периодов полураспада, — измерения активности исследуемого препарата через различные промежутки времени. Для определения длинных периодов полураспада, когда активность за время измерения практически постоянна, необходимо измерить активность и количество атомов распадающегося радионуклида^[3]:

$T_{{1/2}}={frac {N_{0}ln 2}{A}}.$

Примеры[править | править код]

Удельная активность радия-226 — 1 Ки/г.
Типичная объёмная активность радона в воздухе над материками — 10…100 Бк/м³.
Поверхностная активность цезия-137 в 30-километровой зоне вокруг Чернобыльской АЭС достигает десятков Ки/км².

Примечания[править | править код]

↑ Активность радиоактивного источника // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 39. — 707 с. — 100 000 экз.
↑ Здесь предполагается, что вещество состоит либо из одинаковых радиоактивных атомов, либо из молекул, в каждой из которых содержится ровно один радиоактивный атом. В противном случае N₀ необходимо домножить на коэффициент ν, равный среднему количеству радиоактивных атомов данного вида, приходящемуся на одну молекулу рассматриваемого вещества. Например, для сверхтяжёлой (тритиевой) воды T₂O при вычислении активности трития ν = 2, а для природного калия при вычислении активности калия-40 (содержание которого в природной смеси изотопов равно 0,0117 %) этот коэффициент равен 1,17×10⁻⁴.
↑ Фиалков Ю. Я. Применение изотопов в химии и химической промышленности. — Киев: Техніка, 1975. — С. 52. — 240 с. — 2000 экз.

Литература[править | править код]

Применения ядерной химии и изотопных методов (Методы изотопного разбавления) // Основные законы химии: В 2-х томах. Пер. с англ / Дикерсон Р., Грей Г., Хейт Дж. — М.: Мир, 1982. — Т. II. — С. 428–429. — 652 с.

См. также[править | править код]

Банановый эквивалент

Источник

Скачать материал

Сейчас обучается 268 человек из 65 регионов

Сейчас обучается 389 человек из 62 регионов

Описание презентации по отдельным слайдам:

1 слайд

Радиоактивный распад. Активность
2 слайд

Ядро Х – материнское; Y – дочернее. Под частицей a в основном понимают α-частицу и β+ -частицу.
Радиоактивный распад, явление квантомеханическое, и он является свойством ядра. Повлиять на ход процесса радиоактивного распада нельзя, не изменив состояние ядра. Следовательно, для данного радиоактивного ядра, находящегося в определенном состоянии, вероятность распада постоянна. Эта вероятность носит название постоянной распада – λ (вероятность распада в единицу времени) =с-1
3 слайд

Количество радиоактивных ядер в зависимости от времени подчиняется exp закону:

где No – число радиоактивных ядер в момент времени t = 0, Т1/2 -период полураспада – время, в течение которого распадается половина радиоактивных ядер.
4 слайд

Кроме используют величину среднего времени жизни радиоактивных ядер –
По физическому смыслу среднее временя жизни радиоактивных ядер – это время, за которое число радиоактивных ядер и скорость распада уменьшается в e раз. На практике более удобно использовать период полураспада Т1/2 – это время, за которое количество радиоактивности уменьшится вдвое.

(ln 2  0.693)
5 слайд

Активность
Обозначив λN0 как С0, где С0 – активность материала в момент времени t=0, получаем, что активность уменьшается во времени по экспоненциальному закону:
6 слайд

Если имеется радиоактивное вещество массой M и массовым числом A с постоянной распада  (или периодом полураспада ), то для того, чтобы определить активность этого вещества, необходимо вычислить количество радиоактивных ядер, содержащихся в массе M этого вещества, а затем умножить на постоянную распада

где Na — число Авогадро; A–массовое число.
Пользуясь этим выражением, можно решить обратную задачу – определить массу радиоактивного нуклида, зная его измеренную активность:
8 слайд

Задача 1
Постоянные радиоактивного распада урана, радия и радона соответственно равны 4,9·10-18; 1,37·10-11 и 2,09·10-6 сек-1. Вычислить среднее время жизни данных ядер и их периоды полураспада.
Ответ:6,5·109; 2300 лет и 5, 52 суток, периоды полураспада 4,5·109; 1590лет и 3,8 сут.
9 слайд

Задача 2
Найти постоянную распада элемента если его период полураспада равен 1602 лет.
10 слайд

Задача 3

β-активный изотоп 90Sr (стронций) имеет период полураспада 20 лет. Подсчитать какая доля первоначального количества ядер данного изотопа останется через 10 и 100 лет?
N(t)=N0exp(-t·ln2/T1/2)
Ответ: 0,708; 0,0313
11 слайд

Задача 4
Какая доля первоначальноного количества ядер радиоактивного препарата со средним временем жизни τ:
останется через интервал времени, равный 10 τ.
распадется за интервал времени между t1= τ и t2=2τ
12 слайд

Решение
Число ядер препарата к моменту времени t:
N(t)=N0exp(-t/ τ)
Доля ядер, оставшихся к моменту t=10τ,
N(10τ) /N0 = exp(-10)
Доля ядер, распавшихся за интервал времени ∆t=t2 –t1
13 слайд

Задача 5

Вычислить постоянную распада, среднее время жизни и период полу распада радиоактивного нуклида, активность которого уменьшается в 1,07 раза за 100 дней.
14 слайд

Активность по определению – число распадающихся ядер в единицу времени: А=dNd /dt
где Nd – число ядер, которые должны испытать распад за время t,
Nd(t) = N0 – N(t) = N0(1 – e-λt)
Продифференцируя последнее выражение по времени, получим
А(t) = λ N0 e-λt = А0 e-λt,
где А0 = λN0 – активность в начальный момент времени.
Таким образом,

Решая последнее уравнение относительно λ, получим
15 слайд

Задача 6
Определить возраст древних деревянных предметов, у которых удельная активность 14С составляет 3/5 удельной активности этого же нуклида в только что срубленных деревьях.
16 слайд

Решение
Радиоактивный углерод 14С, период полураспада которого Т1/2 = 5730 лет, непрерывно образуется в верхних слоях атмосферы Земли из азота 14N под действием космического излучения. Благодаря ветрам и океанским течениям равновесная концентрация 14С в различных местах земного шара одинакова и равна примерно 14 распадам в минуту на каждый грамм углерода природного состава. Пока организм жив, концентрация 14С в нем остается постоянной из-за круговорота веществ в природе. После смерти организма усвоение 14С прекращается и его количество начинает убывать по обычному закону радиоактивного распада, что позволяет определить дату их смерти или, как говорят археологи, возраст.
17 слайд

Задача 7
Свежеприготовленный препарат содержит 1,4 мкг радиоактивного нуклида 24Nа. Какую активность он буде иметь через сутки?
18 слайд

Решение
Согласно С(t) = λ·N0·e-λt = С0e -λt,
1 а. е. м. ≈ 1,660 540 2∙10−27 кг = 1,660 540 2∙10−24 г.
19 слайд

Задача 8
Определить число радиоактивных ядер в свежеприготовленном препарате 82Br, если известно, через сутки его активность стала равной С(t)= 7,4·10-9 Бк (0,4 Ки).
23 слайд

Эквивалентная доза
24 слайд

Эквивалентная доза

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 261 947 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

12.12.2020
927
17

05.12.2020
505
5

01.12.2020
124
0

27.09.2020
126
0

26.08.2020
91
0

25.08.2020
133
0

12.08.2020
674
18

29.07.2020
117
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Основы туризма и гостеприимства»
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
Курс профессиональной переподготовки «Клиническая психология: организация реабилитационной работы в социальной сфере»
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
Курс повышения квалификации «Правовое регулирование рекламной и PR-деятельности»
Курс повышения квалификации «Страхование и актуарные расчеты»
Курс повышения квалификации «Финансы предприятия: актуальные аспекты в оценке стоимости бизнеса»
Курс повышения квалификации «Источники финансов»
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
Курс профессиональной переподготовки «Гражданско-правовые дисциплины: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Управление качеством»

Источник

Активность и единицы измерения

Производные величины[править | править код]

Единицы измерения активности[править | править код]

Зависимость активности от времени[править | править код]

Вычисление активности источника[править | править код]

Примеры[править | править код]

Примечания[править | править код]

Литература[править | править код]

См. также[править | править код]

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Вам будут интересны эти курсы:

Вам также может понравиться

Как найти макдональдс рядом

Как составить covering letter

Как найти срок оборота

Добавить комментарий Отменить ответ