Как найти акустическое сопротивление среды

Удельное акустическое сопротивление упругой среды — величина, равная отношению амплитуды звукового давления в среде к колебательной скорости её частиц при прохождении через среду звуковой волны:

${displaystyle Z_{S}={p_{0} over v}}$

Единица измерения — паскаль-секунда на метр (Па•с/м). Удельное акустическое сопротивление можно рассчитать через плотность среды ρ и скорость звука c в ней:

Z_S = ρc

Например:

Z_S = 417 Па•с/м для сухого воздуха при 15 °C и стандартном атмосферном давлении ρ = 1,225 кг/м³, c = 340,3 м/с.
Z_S = 600 Па•с/м для резины.
Z_S = 150•10⁴ Па•с/м для воды.
Z_S = 4180•10⁴ Па•с/м для меди.
Z_S = 4600•10⁴ Па•с/м для стали.

См. также[править | править код]

Интенсивность звука
Волновое сопротивление
Акустический импеданс

Для улучшения этой статьи желательно:

Найти и оформить в виде сносок ссылки на независимые авторитетные источники, подтверждающие написанное.
Дополнить статью (статья слишком короткая либо содержит лишь словарное определение).
Добавить иллюстрации.

После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.

Словари и энциклопедии	Britannica (онлайн)

Источник

Акустический импеданс

Вновь рассмотрим акустическую волну, распространяющуюся вдоль оси z . Мгновенные значения компонентов акустического поля могут быть получены выделением реальной части из выражений

(2.20), (2.21):

pa (z,t)= pam cos(ωt − k z),	(2.24)
vr(z,t)= zr0vzm cos(ωt − k z).	(2.25)

Из полученных выражений видно, что акустическое давление и колебательная скорость изменяются синфазно. Связь амплитуд колебательной скорости частиц среды и акустического давления может

быть определена из уравнения движения частиц (2.1):
		∂vr +	1	grad pa = 0 .		(2.26)

			∂t	ρ0
После дифференцирования по времени выражения (2.25) и вы-
числения grad p	= zr	∂ pa	(Прил. 1) выражение (2.26) принимает вид
a		0	∂ z
−zr v		ω sin (ωt − k z)+ zr	1	p	am	k sin (ωt − k z)= 0.

0 m				0 ρ	0

Последнее выражение позволяет определить связь между амплитудами акустического давления и колебательной скорости плоской волны:

p	am	=	ρ0νmω	= (ρ0V l )νm .	(2.27)
		k

Коэффициентом связи является произведение невозмущенной плотности среды и скорости распространения акустической волны в среде, в данном случае скорости продольной акустической волны. Этот коэффициент пропорциональности принято называть акустическим сопротивлением среды для плоской волны. Данный термин связан с аналогией акустических и электрических величин как разных видов колебательных процессов в природе.

В теории электромагнитного поля для анализа распространения волн в линиях передачи вводится понятие волнового сопротивления. Это некий коэффициент, равный отношению напряжения и тока волны в линии передачи. Поскольку напряжение в линии имеет размерность вольт (В), а ток – ампер (А), их отношение имеет размерность ом (Ом). По этой причине коэффициент, связывающий эти параметры, получил наименование «волновое сопротивление» и обозначается Z0 .

Акустическое сопротивление, или акустический импеданс, – это коэффициент, связывающий между собой акустическое давление и колебательную скорость частиц среды:

Давление

н м2

кг

Z a =

(2.28)

м с

м3

м2

Скорость

Формула (2.28) справедлива как для продольных, так и для сдвиговых акустических волн, распространяющихся в упругой среде, причем не только плоских волн.

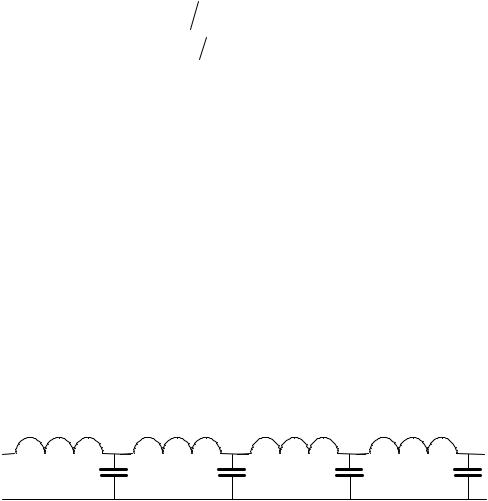
Если сравнивать между собой уравнения, описывающие распространение волны тока и напряжения в электрической линии передачи, называемые «телеграфными уравнениями», и уравнения для бегущей акустической волны (Табл.2.1), можно сделать вывод об их очевидной схожести. В курсе “Основы теории электрических цепей” показано, что любую достаточно длинную линию передачи можно представить в виде периодической структуры из последовательно включенных индуктивностей L и параллельно включенных емкостей C

(рис.2.1).

Рис. 2.1. Эквивалентная схема электрической линии передачи

Эти индуктивности и емкости называются погонными, т.е. относящимися к единице длины линии передачи.

Для плоской акустической волны, распространяющейся вдоль оси z (выражения (2.20)–(2.21)), и эквивалентных напряжений и то-

ков плоской электромагнитной волны, распространяющейся вдоль оси z , можно составить следующую сравнительную таблицу, иллюстрирующую связь акустических и электромагнитных параметров.

Таблица 2.1 Связь параметров акустических волн и волн напряжения и тока

в линии

Для акустических волн

Для волн напряжения и тока

∂ pa (z)

dU (z)

= j ωρ0 v

(z)

= − j ωL I (z)

∂ z

d z

∂v&(z) = j ω pa

d I (z) = − j ωC U& (z)

∂ z

d z

k = ω

ρ0

β = ω

Z a =

ρ0 K

Z 0 =

Сравнивая между собой выражения, стоящие в левом и правом столбцах приведенной выше таблицы, можно заметить, что при взаимных заменах pa ↔U, v ↔ I , ρ0 ↔ L, 1K ↔ C уравнения для

электромагнитной волны в линии передачи и плоской акустической волны поменяются местами, т.е. полученные выражения полностью эквивалентны.

Таким образом, упругой волне, распространяющейся в среде, можно поставить в соответствие некоторую эквивалентную линию передачи и для решения задач с акустическими волнами широко использовать разработанные алгоритмы и программы анализа распространения волн в электрических цепях.

Для плоской продольной волны выражение для расчета акустического сопротивления среды с учетом (2.27) может быть записано следующим образом:

Z a = pam = ρ0Vl .

Полученное соотношение остается верным и для плоских сдвиговых волн, если в нем скорость распространения продольной волны Vl за-

менить на скорость распространения сдвиговой волны Vt .

При нормальном атмосферном давлении и температуре t = 200 C

акустическое сопротивление воздуха Z a = 420	кг	. В расходящихся

	м2 с

сферических и цилиндрических волнах акустическое давление и колебательная скорость частиц среды изменяются несинфазно и акустическое сопротивление становится комплексным:

Z&a = Ra + j X a = Z&a e j ϕ,

где ϕ – сдвиг по фазе между давлением pa	и колебательной скоро-
стью частиц среды v .
Для сферической волны модуль акустического сопротивления
	Z&a	= ρ0V l cosϕ, tg ϕ =	1

k r

не превышает акустического сопротивления этой же среды для плоской волны.

Для цилиндрической волны

Z&a		= ρ0V l cosϕ, tg ϕ =	1	.

	2 k r

Разность фаз ϕ между давлением и колебательной скоростью в сферических и цилиндрических волнах быстро уменьшается с ростом расстояния r и увеличением частоты. В дальней зоне (r >> λ) сдвиг фаз ϕ = 0, акустическое сопротивление становится вещественным и

равным по величине акустическому сопротивлению среды для плоской волны.

Уравнение баланса энергии акустической поля. Интенсивность акустической волны

Для вывода закона сохранения энергии акустической волны воспользуемся уравнением движения частиц среды (2.1)

∂v	+	1	grad pa = 0	(2.29)
∂t
	ρ0

и уравнением закона сохранения массы вещества (2.2)

∂ρa	+ρ0 div vr	= 0 .	(2.30)

∂t

Величину акустической плотности из (2.3) выразим через давление и скорость распространения волны

ρ	a	=	pa	(2.31)

	V l2

и подставим это значение в уравнение (2.30). Перепишем исходные уравнения (2.29) и (2.30) в следующем виде:

∂vr
ρ0 ∂t +grad pa = 0,	(2.32)
1		∂pa	+div vr	= 0 .	(2.33)
ρ0V l2
∂t

Умножим скалярно уравнение (2.32) на v , а уравнение (2.33) на pa .

Суммируя полученные уравнения,

с учетом

Прил. 1, получим соот-

ношение

∂

ρ0

+ div (pa v )= 0 .

(2.34)

∂t

ρ0V l2

Выражение в квадратных скобках представляет собой энергию аку-

стической волны в единице объема среды, Дж :

м3

w =	1	ρ		vr	2+	1	pa	2	,	(2.35)

2	0		2	ρ0V l2

Энергия акустической волны состоит из двух видов энергии: кинетической и потенциальной. Потенциальная энергия (энергия упругой деформации) определяется максимальным смещением колеблющихся частиц среды относительно положения равновесия и связана с силой, приложенной для перемещения частиц среды. Наглядная мо-

дель для данного случая – растянутая или сжатая пружина. Объемная

плотность потенциальной энергии вычисляется по формуле, Дж :

м3

1 p2 wп = 2 ρ a 2 ,

0V l

Кинетическая энергия запасается в движущихся частицах среды и

ееобъемная плотность равна, Дж :

м3

wк =	1	ρ0	r	2

2		v	.

Произведение pa vr, входящее в (2.34), определяет плотность по-

тока энергии акустической волны, переносимую волной за единицу времени через единицу площади поверхности, перпендикулярной на-

правлению распространения волны. Вектор J называется вектором Умова-Пойнтинга:

	Jr = pa vr.		(2.36)
С учетом (2.35), (2.36) уравнение (2.34) принимает вид
	∂w	+div Jr	= 0	(2.37)

	∂t

и выражает закон сохранения энергии в дифференциальной форме. Проинтегрируем (2.37) по выделенному объему V среды, ограниченному поверхностью S . С учетом теоремы Остроградского-Гаусса (Прил. 1) для второго слагаемого уравнения (2.37) получим

∂		r	r
	∫w dv + ∫ J ds	= 0 .	(2.38)
∂t
V	S

Приведенное выражение представляет собой запись закона сохранения энергии в интегральной форме (закон сохранения энергии для выделенного объема среды).

Модуль вектора Умова-Пойнтинга, Вт/м2:

J =	J	= pa	vr	= pa v .	(2.39)

называется интенсивностью (силой) звука. Другое название этой величины – плотность потока энергии акустической волны.

Для расчета интенсивности акустической волны, изменяющейся во времени по гармоническому закону, воспользуемся комплексным представлением

pa = 12 p&a e jωt + 12 pa* e− jωt ,

v = 12 v&e jωt + 12 v e− jωt .

Звездочкой в этих выражениях обозначено комплексное сопряжение. Средняя за период интенсивность звука может быть вычислена

следующим образом:

Jср =	1 T	pa v dt =	1	&	*	).	(2.40)
4	∫	2 Re(pa v
		0

Мощность, переносимая акустической волной через поверхность S , охватывающую выделенный объем среды, равна

P = ∫JсрdS .

Для сферических и цилиндрических волн акустическое давление и колебательная скорость зависят от расстояния от источника до точки наблюдения вследствие расходимости волн, т.е.

p&a = pam (r)e− jkr , v& = vam (r)e− jkre− jϕ ,

где ϕ – сдвиг по фазе между акустическим давлением и колебатель-

ной скоростью.

Акустическое давление и колебательная скорость связаны между собой через акустическое сопротивление. Это позволяет получить еще одну полезную формулу


	1	p2	(r)
Jср =		am		cosϕ.	(2.41)
2		Z&a

Для плоской звуковой волны, распространяющейся в идеально упругой среде, акустическое сопротивление,

Za = ρ0 V l ,

сдвиг фаз между давлением и колебательной скоростью ϕ = 0, амплитуда не зависит от расстояния и средняя за период интенсивность

				Jср = 1	pam2	=	1 vm2 ρ0 V l .

				2 ρ0 V l	2
В акустике звуковых колебаний принято говорить об уровне ин-
тенсивности звука, дБ, и характеризовать его как
					L =10 lg		J
					Jст

относительно	стандартного нулевого	уровня с	интенсивностью
Jст =10	−12	,	Вт	. Величина Jст получена на частоте	f =1кГц для са-
	м2

мых слабых звуков (порог слышимости человеческого уха) при акустическом давлении pam = 2 10−5 Па и акустическом сопротивлении

воздуха Z a = ρ0 Vl = 420 кг . м2 с

Относительный уровень интенсивности, дБ, в логарифмическом масштабе рассчитывается по формуле

∆ L = L1 − L2 =10 lg J1 .

Особенности восприятия акустических волн различной интенсивности и частоты человеческим ухом и субъективные параметры звуковых волн рассматриваются в разд.6.

Для оценки качества экранировки звукового потока слоем материала вводится понятие коэффициента звукоизоляции. Коэффициентом звукоизоляции называется разность уровней интенсивности звука до и после прохождения звукоизоляционного материала. Коэффициент звукоизоляции, дБ:

D =10 lg J1 .

Численные значения коэффициента звукоизоляции приведены в табл.2.2.

Таблица 2.2 Численные значения коэффициента звукоизоляции

некоторых строительных материалов

Вид материала		Толщина,	D, дБ
			см
Кирпичная стена,	оштукатуренная	в	9	42
1/4 кирпича

Кирпичная стена,	оштукатуренная	в	15	44
1/2 кирпича

Бетонная плита			16	48
Толстое стекло			0,6	29
Одинарное окно				15
Двойное окно				30
Одинарная дверь				до 20
Двойная дверь				40

В случае нескольких источников звука равной интенсивности L полный уровень интенсивности равен, дБ:

LΣ = L +10 lg n .

При сложении двух волн равного уровня общий уровень интенсивности увеличивается на 3 дБ. Интенсивность звука пропорциональна квадрату частоты и высоким частотам ультразвукового диапазона соответствуют большие интенсивности, что приводит к нагреву тел, подвергающихся воздействию ультразвука. Для цилиндрических волн интенсивность за счет расходимости звукового потока обратно пропорциональна расстоянию от источника, а для сферических волн – квадрату расстояния. Для стоячей волны интенсивность равна нулю.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Поверхностные волны обусловлены колебанием частиц со значительной амплитудой на поверхности тела и постепенным ее уменьшением при удалении частиц от поверхности. Если продольная волна падает перпендикулярно на плоскую границу раздела двух сред, обладающих различным акустическим сопротивлением, то одна часть ее энергии переходит во вторую среду, а другая отражается в первую. Доля отраженной энергии тем больше, чем больше разность акустических сопротивлений сред. Если продольная волна попадает на границу раздела двух твердых сред под углом, то отраженная и прошедшая волны преломляются и трансформируются в продольные и сдвиговые, распространяющиеся в первой и второй средах под различными углами. Законы отражения и преломления волн аналогичны законам геометрической оптики. [c.194]

В выражение для амплитуды звукового давления входит произведение плотности р среды на скорость с в ней звука, т. е. волновое сопротивление рс (см. 57). В случае звуковых волн его принято называть акустическим сопротивлением среды. [c.227]

Таким образом, интенсивность звука равна отношению квадрата амплитуды звукового давления к удвоенному акустическому сопротивлению среды. [c.227]

Величина рС — удельное акустическое сопротивление среды, определяющее во многом ее акустические свойства. [c.21]

При падении ультразвуковой волны на границу раздела двух сред в общем случае часть энергии ультразвуковой волны отражается, а часть — преломляется, проходит во вторую среду. Степень преломления падающей волны во второй среде определяется соотношением акустических сопротивлений сред (акустическое сопротивление представляет произведение плотности среды на скорость распространения ультразвука в ней). Чем больше разница акустических сопротивлений,тем больше интенсивность отраженной волны. Для отражения ультразвуковой волны от не-сплошностей в контролируемом металле необходимо, чтобы размеры несплошности были соизмеримы с длиной волны или больше ее. Если размеры дефекта меньше длины волны, то ультразвуковая волна огибает его. [c.503]

ГИИ переходит во вторую среду, а часть энергии отражается в первую. При этом проходящая и отраженная волны будут того же вида, что и падающая. Отраженная энергия тем больше, чем больше разница акустических сопротивлений сред. При неровной поверхности раздела с неровностями более 0,1 мм наблюдается диффузное отражение (рис. 4.9). [c.119]

Таким образом, избыточное звуковое давление равно произведению акустического сопротивления среды на скорость колебательного движения частиц. [c.394]

Из этой формулы видно, что качество приемника ультразвука как преобразователя определяется не только отношением 1Цр, но и соотношением импеданса приемника X и акустического сопротивления среды рс. [c.332]

К линейным характеристикам звукового поля в жидкостях н газах относят звуковое давление, смещение частиц среды, скорость колебаний и акустическое сопротивление среды. [c.8]

Волны растяжения возникают в объектах типа стержня. Тогда частицы колеблются вдоль направления распространения волн и перпендикулярно к нему. Поверхностные волны обусловлены колебанием частиц со значительной амплитудой на поверхности тела и постепенным ее уменьшением при удалении частиц от поверхности. Если продольная волна падает перпендикулярно на плоскую границу раздела двух сред, обладающих различным акустическим сопротивлением, то одна часть ее энергии переходит во вторую среду, а другая отражается в первую. Доля отраженной энергии тем больше, чем больше разность акустических сопротивлений сред. Если продольная волна попадает на границу раздела двух твердых сред под углом, го отраженная и прошедшая волны преломляются и трансформируются в продольные и сдвиговые, распространяющиеся в первой и второй средах под различными углами. Законы отражения и преломления волн аналогичны законам геометрической оптики. Свойства упругих волн учитываются при разработке технологии и средств контроля изделий. [c.58]

Коэффициент отражения i не зависит от угла падения волны и растет с увеличением разницы акустических сопротивлений сред. Явление отражения ультразвуковой волны от границы перехода в среду с малым акустическим сопротивлением широко используется в ультразвуковой дефектоскопии. Например, при переходе ультразвуковой волны из стали в воздух интенсивность отраженной волны составляет более 90 %. Аналогичный эффект возникает при обнаружении внутри металла областей (объемов) с малым акустическим со- [c.145]

Величина рс называется удельным акустическим сопротивлением среды. Так, при температуре 20° С для воздуха оно равно 41 гс1 см -сек), для воды 1,5-10 гс1 см -сек), для стали — 4,8-10 гс/ см -сек). Чтобы звук был слышен, он должен при [c.5]

Акустическое сопротивление среды — величина, пропорциональная скорости распространения с и плотности вещества с, [c.299]

Из приведённого выше выражения для активного сопротивления излучения, определяющего излучаемую акустическую мощность, видно, что пропорционально акустическому сопротивлению среды рс и площади поверхности 5. Следовательно, излучаемая акустическая мощность тем больше, чем больше акустическое сопротивление среды рг. Этим, в частности, объясняется тот факт, что для излучения в воздух большой акустической мощности требуется гораздо большая энергия, чем для излучения той же акустической мощности в воду, поскольку для воздуха, как мы указывали ранее, рс —41 ед. GS, а для воды рс= 150 ОоО ед. GS (см. стр. 274). [c.114]

Для получения полного отражения от зеркала необходимо, чтобы акустическое сопротивление материала зеркала рс) было значительно больше, чем акустическое сопротивление среды (рс) , поскольку коэффициент отражения при этом приближается к единице. (Суш,ественно именно различие в величинах рс зеркала и среды сами же значения плотности материала зеркала и скорости звука в нём в отдельности роли не играют.) В воздухе это требование легко удовлетворяется благодаря малому (рс) воздуха и большому (рс) твёрдых тел, из которых делаются зеркала. Если же средой является вода, то для увеличения коэффициента отражения от зеркала часто применяются зеркала из двух слоёв твёрдого тела, между которыми имеется воздушный промежуток (см., например, рис. 220). [c.304]

Линзы в акустике начали применяться давно так, например, для фокусировки звука в воздухе применялись линзы из углекислого газа, скорость звука в котором меньше, чем в воздухе. Развитие ультразвуковой техники привело к более широкому применению акустических линз. Для того чтобы линза была акустически прозрачна, т.е. потери звуковой энергии при прохождении звука через линзу были минимальны, акустическое сопротивление материала линзы должно примерно равняться акустическому сопротивлению среды. Этому требованию удовлетворить гораздо труднее, чем требованию (рс)з (рс)с> которое необходимо для хорошей работы рефлектора. [c.307]

Произведение рс называют акустическим сопротивлением среды. Акустические сопротивления стали и пластмасс относятся приблизительно как 10 I. Следовательно, коэффициент отражения энергии ультразвуковой волны при сварке пластмасс составляет – 0,8. [c.212]

Из формулы (16.17) видно, что чем больше отличаются акустические сопротивления сред, тем большая часть энергии звуковой волны отразится от границы раздела двух сред. Этим условием определяются и возможность, и эффективность выявления нарушений сплошности материала (включений среды с акустическим сопротивлением, отличающимся от сопротивления контролируемого материала). [c.288]

Для характеристики физических свойств среды, в которой распространяется ультразвуковая волна, вводится понятие акустическое сопротивление среды г, под которым понимают произведение скорости ультразвука V на плотность среды р, т. е. г—ри. Акустическое сопротивление называют также акустическим импедансом. В табл. 17 приведены скорости распространения ультразвуковых волн и акустические сопротивления некоторых материалов. [c.152]

Углы, при которых исчезают те или иные волны, называют критическими углами. По мере )гвеличения угла падения продольной волны р, начиная с некоторого исчезает продольная преломленнсш волна С/ (а = 90°), и контроль может осуществляться только преломленной поперечной волной. При дальнейшем увеличении р исчезает и поперечная преломленная волна — Q (а, = 90°), что соответствует второму критическому углу Р рз (см. рис. 6.20). Контроль только поперечной преломленной волной для системы оргстек-ло-сталь может происходить при расчетных Р р, в диапазоне 27…56°, что облегчает методику его проведения. Коэффициенты отражения и прохождения ультразвука зависят от соотношения акустических сопротивлений. С уве-личс нием разности акустических сопротивлений двух сред увеличивается коэффициент отражения (обычно дефекты имеют резко отличное акустическое сопротивление среды и поэтому отражают УЗК). [c.171]

Вращающий момент, действующий па диск, пропорцноиален квадрату амплитуды скорости частиц в волне. Поэтому, измеряя вращающий момент по углу поворота диска, можно определить амплитуду скорости частиц в волне, а следовательно, и амплитуду звукового давления. Зная а.милитуду звукового давления II акустическое сопротивление среды, по формуле (60.6) вычисляют интенсивность звука. [c.228]

Пространство, в котором распространяются УЗ волны, называют акустическим (ультразвуковым) полем. Распространени . волны в нем связано с переносом энергии. Количество энергии, переносимой волной за единицу времени через единицу площади, перпендикулярной к направлению распространения, называют интенсивностью ультразвука, которая в плоской волне пропорциональна квадрату амплитуды звукового давления и обратно пропорциональна акустическому сопротивлению среды [c.21]

Полную акустическую прозрачность пластинки, помещенной в среду с отличным от волнового сопротивления пластинки своим волновым сопротивлением Z pi, согласно [1], [3], [4] и [5], [6], обеспечивает возникновение резонанса в исследуемом слое при условии (7) или (8). При этом резко уменьшается количество энергии, требующееся от генератора колебаний, что без особого труда можно зарегистрировать известными методами. Коэффициент отражения по интенсивности ультразвуковой волны R, согласно выводам Ре-лея [1], зависит как от акустических сопротивлений сред, так и от их геометрических размеров [c.294]

Выведите формулу для амплитуды избыточного звукового давления. Что называется акустическим сопротивлением среды и как с этой величиной скязана амплитуда избыточного давления [c.410]

Малое акустическое сопротивление среды требует настолько больших амплитуд, что они не могут быть обеспечены твердыми продольно колеблющимися излучателями. Так, для создания в воздухе интенсивности звука 1 втп1см (160 дб) на частоте 8 кгц необходима амплитуда колебаний 0,1 мм. Для никелевого излучателя максимальное относительное удлинение составляет 4-10 , т. е. при работе такого полуволнового вибратора можно получить амплитуду колебаний всего лишь б-10 мм. Поэтому интенсивность излучения оказывается в 250 раз меньше (136 дб). [c.9]

Величина = называется удельным волновым (акустическим) сопротивлением среды. Такое названне связано с тем, что коэффициент 0(,Го р уравнениях (111.10) и (111.11) определяет величину колебательной скорости при заданном акустическом давлении. Сила давления, действующая на площади S, равна Fp = p roSi . Соответственно величина po oS может быть названа полным акустическим сопротивлением среды на площали S [c.46]

Если на пути ультразвукового поля, расщ)остраняющегося в среде с акустическим сопротивлением Р1С1, встречается среда с другим акустическим сопротивлением раСг, то часть энергии проходит во вторую среду, а часть отражается в первую. Распределение энергии между отраженной волной и прошедшей определяется соотношением удельных акустических сопротивлений сред. [c.16]

Из приведенного выше выражения для aiiTHBHoro сопротивления излучения, определяюш,его излучаемую акустическую мощность, видно, чтопропорционально акустическому сопротивлению среды рс и площади Поверхности S. Следовательно, излучаемая акустическая мощность тем больше, чем больше акустическое сопротивление среды рс. Этим, в частности, объясняются лучшие условия излучения звука в воду, чем в воздух, поскольку для воздуха, как мы указывали ранее, рс = 41 ед. GS, а для воды рс = 150 ООО ед. GS. [c.129]

Источник

Акустическое сопротивление, его влияние на отражение ультразвука • Важнейшей характеристикой биологической среды является акустическое сопротивление , которое определяется как произведение плотности среды и скорости звука в ней: . • Акустические сопротивления замечательны тем, что их различие определяет характер отражения на границе сред.

• Введем понятие коэффициента отражения по амплитуде , определяемого следующим отношением: где и уровни давления отраженной и падающей УЗ волны соответственно.

• При перпендикулярном падении УЗ волны на плоскую границу сред (см. вышеприведенный рисунок) коэффициент вычисляется с помощью выражения • Здесь и акустические сопротивления граничащих сред, знак модуля ( | | ) показывает, что берется абсолютная величина вычисленного отношения.

• Эта простая формула позволяет очень наглядно проиллюстрировать характер формирования отраженных сигналов на границе сред и пояснить особенности и ограничения, свойственные УЗ методам исследований. • Для мягких тканей и крови различие акустических сопротивлений лежит в пределах ± 15%. • Если первая среда имеет относительное сопротивление = 0, 95, а вторая = 1, 05, то = 0, 05 (или 5%). • Это означает, что только малая часть энергии падающей УЗ волны вернется в виде отраженной УЗ волны, а существенно большая часть будет распространяться вглубь тканей, достигая следующих неоднородностей и опять частично отражаясь от них, постепенно затухая.

• Если среды меняются местами, т. е. первая имеет = 1, 05, а вторая = 0, 95, то, как следует из вышеприведенной формулы, результат не изменится: = 0, 05.

• Таким образом, коэффициент отражения зависит только от разности акустических сопротивлений сред и не зависит от того, какая из сред находится дальше другой с большим или меньшим акустическим сопротивлением. • Этот факт необходимо усвоить всем начинающим специалистам, которые иногда склонны объяснять эхогенность тканей (т. е. уровень отраженных от них сигналов) тем, что глубже расположенные ткани имеют более высокое акустическое сопротивление (или большую плотность), чем ткани, расположенные ближе к границе раздела. • Еще раз отметим, что уровень отраженного сигнала зависит только от степени акустической неоднородности граничащих тканей, которая определяется разницей их акустических сопротивлений.

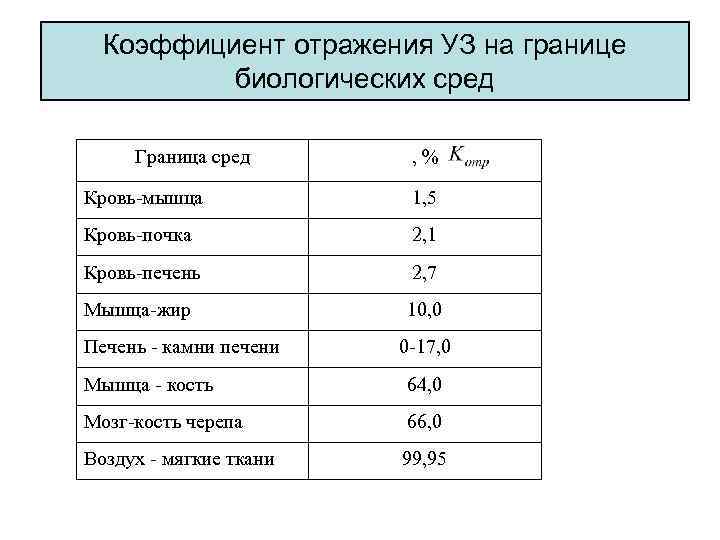
Коэффициент отражения УЗ на границе биологических сред Граница сред , % Кровь-мышца 1, 5 Кровь-почка 2, 1 Кровь-печень 2, 7 Мышца-жир 10, 0 Печень – камни печени 0 -17, 0 Мышца – кость 64, 0 Мозг-кость черепа 66, 0 Воздух – мягкие ткани 99, 95

• Из таблицы следует, что для мягких тканей коэффициент отражения по амплитуде не превышает 10%, снижаясь иногда до нуля, если соседствующие ткани не отличаются по акустическому сопротивлению. • Более высокий коэффициент отражения на границе жировых тканей с другими мягкими тканями иллюстрирует факт, что наблюдение структур, расположенных за многочисленными жировыми прослойками, сопряжено с определенными трудностями.

• Отражения от границы мягкая ткань камни (печени, почек или желчного пузыря) могут меняться в широких пределах в зависимости от вида камня и его акустического сопротивления. • Чем плотнее камень и чем больше скорость звука в нем, тем больше уровень отражения на его границе и тем легче его обнаружить. • При большом акустическом сопротивлении камня отражения от него могут быть очень высокого уровня, так что в результате за ним образуется область акустической тени, т. е. область с низким уровнем отраженных сигналов, что обусловлено малым уровнем энергии прошедшей через камень УЗ волны. • Наличие акустической тени является одним из диагностических признаков наличия камня в органах.

• Если камень имеет структуру, близкую к структуре мягких тканей, то обнаружить его иногда затруднительно вследствие малого уровня отраженного сигнала. • Это случай акустически прозрачного плохо диагностируемого камня. • Как правило, такие камни хорошо выявляются с помощью рентгеновской диагностики.

• На границе воздух мягкие ткани УЗ волна отражается практически полностью, и дальше этой границы получить информацию невозможно. • Поэтому при обследовании пациента на рабочую поверхность датчика наносится акустический гель, исключающий воздушную прослойку и обеспечивающий акустический контакт между датчиком и телом пациента. • Вследствие практически полного отражения на границе газовых образований и мягких тканей газосодержащие структуры (легкие, желудок, кишечник), а также ткани, находящиеся за этими структурами, с помощью ультразвука исследовать почти невозможно, что является серьезным ограничением для УЗ диагностики.

• Возвращаясь к отражению на границе мягких тканей с различным акустическим сопротивлением, заметим, что границы неоднородностей располагаются под произвольным углом к направлению распространения ультразвука (совпадающему с осью УЗ луча), не всегда равным 90°. • Поэтому основная энергия отраженного сигнала может распространяться не в сторону датчика, что ухудшает возможности наблюдения. • Положение облегчается тем, что границы неоднородностей, как правило, не являются гладкими, и, следовательно, отраженные от них УЗ волны распространяются в различных направлениях, в том числе и в направлении на датчик, что обеспечивает прием эхо сигналов и получение акустического изображения.

• Чаще всего неоднородности в мягких тканях имеют сложную форму и различные размеры, причем их ориентация носит случайный характер. • УЗ изображения в основном формируются волнами, рассеянными на относительно мелких структурах. • Если размеры неоднородностей сравнимы с длиной волны ультразвука или меньше ее (в большинстве случаев в биологических тканях это условие имеет место), то взаимодействие ультразвука со средой характеризуется сложными эффектами. • Основными из них являются дифракция и интерференция.

Затухание ультразвука в биологических тканях • Затухание ультразвука, т. е. снижение энергии УЗ волн в процессе их распространения вглубь тканей, существенным образом влияет на акустическое изображение, прежде всего на максимальную глубину, с которой еще можно получать информацию, и на качество изображения. • Основными причинами затухания УЗ волн являются: отражение и рассеяние УЗ волн на неоднородностях, поглощение УЗ волн. • Дополнительное затухание имеет место из за расходимости УЗ луча, т. е. увеличения площади сечения луча с глубиной. • Затухание из за расходимости луча обычно по величине много меньше, чем вследствие отражения, рассеяния и поглощения УЗ волн.

• Затухание из за отражения и рассеяния определяется геометрическими размерами, свойствами и пространственным распределением акустических неоднородностей. • Поглощение обусловлено вязкостью, теплопроводностью биологических тканей, а также сложными процессами, полное понимание которых пока отсутствует.

• На базе обширных экспериментальных исследований получены основные закономерности и количественные оценки величин затухания в различных биологических тканях. • В зависимости от расстояния (глубины) амплитуда давления УЗ волны из за рассеяния и поглощения уменьшается по экспоненциальному закону: где х – расстояние, пройденное УЗ волной, p 0 начальная амплитуда давления (при х = 0), р – амплитуда давления на расстоянии , коэффициент затухания.

• В общем случае = р + п, где р и п коэффициенты затухания, соответствующие рассеянию и поглощению ультразвука. • Раздельно измерить каждый из коэффициентов довольно трудно. • Поэтому обычно анализируется суммарный коэффициент затухания . • Для биологических тканей и воды он зависит от частоты, увеличиваясь с повышением частоты ультразвука.

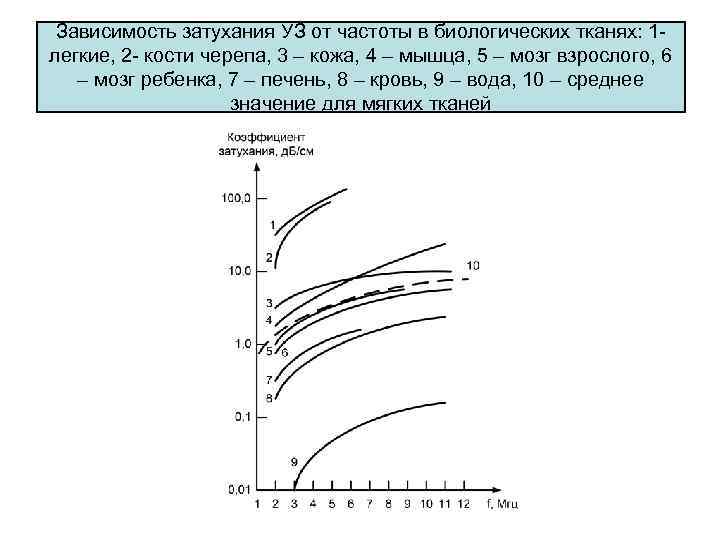
Зависимость затухания УЗ от частоты в биологических тканях: 1 легкие, 2 кости черепа, 3 – кожа, 4 – мышца, 5 – мозг взрослого, 6 – мозг ребенка, 7 – печень, 8 – кровь, 9 – вода, 10 – среднее значение для мягких тканей

• С увеличением частоты величина затухания увеличивается вследствие частотнозависимого характера затухания: уровень излученного датчиком сигнала на данной глубине уменьшается. • В той же мере уменьшается уровень эхо сигнала, полученного в результате отражения на этой глубине по мере прохождения им того же пути, но уже в обратном направлении к датчику. • На частоте f = 3, 5 МГц затухание на глубине 10 см не приводит к серьезным последствиям эхо сигналы, принимаемые датчиком с этой глубины, имеют уровень, достаточный для их уверенного наблюдения. • На частоте f = 5 МГц на той же глубине наблюдение очень слабых эхо сигналов в ряде случаев может быть затруднено. • На частоте = 7, 5 МГц нередко становится невоз можно наблюдать даже сильные отражения они неразличимы на фо не случайных шумов и помех. • Поэтому предельная глубина наблюдения для частоты 7, 5 МГц составляет 70 90 мм.

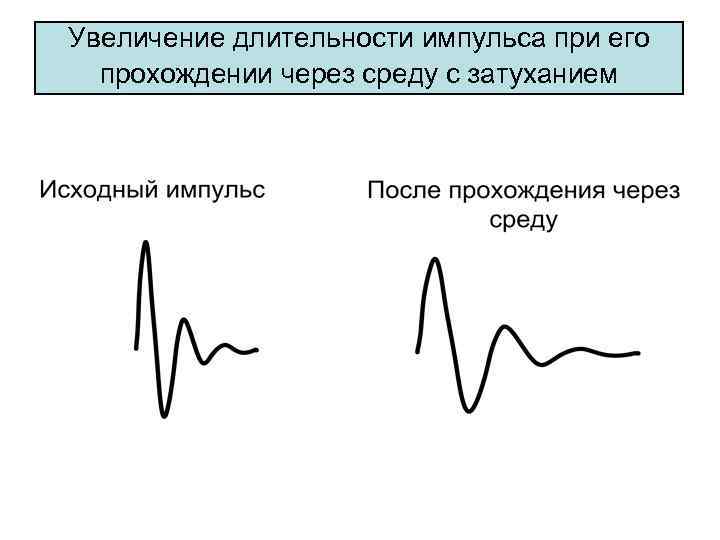
• Частотнозависимый характер затухания в биологических тканях, особенно в мягких, приводит к тому, что вид импульсного УЗ сигнала изменяется по мере увеличения расстояния, которое он проходит. • Это связано с тем, что более высокочастотные составляющие сигнала ослабляются сильнее, чем низкочастотные. • В результате средняя частота сигнала смещается по мере увеличения глубины в сторону более низких частот, а период колебаний и длительность сигнала увеличиваются

Увеличение длительности импульса при его прохождении через среду с затуханием

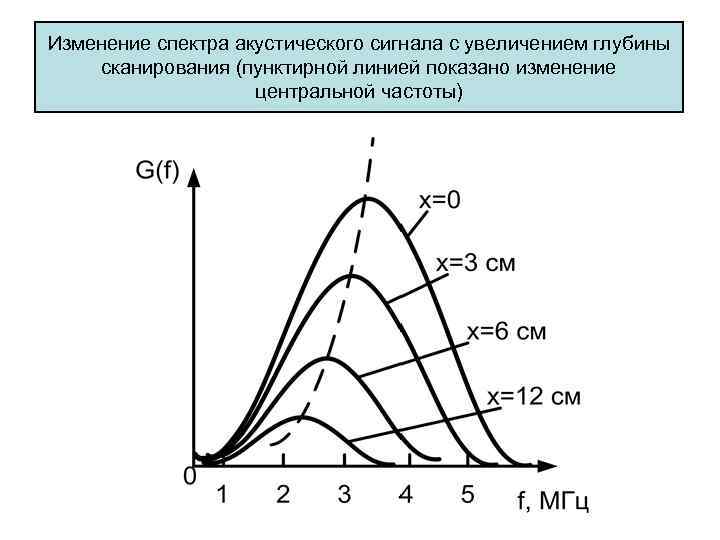
Изменение спектра акустического сигнала с увеличением глубины сканирования (пунктирной линией показано изменение центральной частоты)

• Смещение спектра эхо сигнала в сторону низких частот с увеличением глубины должно учитываться при создании диагностического прибора. • Поэтому во всех современных УЗ приборах используется автоматическая подстройка частоты приемника эхо сигналов в зависимости от глубины или, что то же самое, от времени прихода эхо сигналов.

Приборы ультразвуковой диагностики • Среди всех средств медицинской интроскопии или, другими словами, средств визуализации внутренних органов и структур ультразвуковые диагностические приборы занимают особое место. • Это объясняется рядом существенных достоинств ультразвукового метода исследований, основные из которых следует перечислить.

• Высокая диагностическая информативность, обусловленная чувствительностью к физическим и физиологическим изменениям характеристик биологических тканей. • Способность оценивать динамические характеристики движущихся структур, прежде всего кровотока. • Безвредность обследований для пациента и врача, что обеспечивается достаточно низким уровнем излучаемой мощности ультразвука. • Относительно небольшие размеры и вес аппаратуры.

• Известны ограничения и недостатки ультразвукового метода диагностики: невозможность получения информации о газосодержащих структурах (легкие, кишечник); трудность получения диагности ческих данных при наблюдении через структуры со значительным отражением, а также затуханием и рассеянием ультразвука (костные ткани, уже упоминавшиеся газосодержащие структуры); малая чувствительность при исследовании органов и тканей с незначительным различием акустических характеристик.

Классификация ультразвуковых приборов • Количество моделей ультразвуковых приборов, выпускаемых различными фирмами, достаточно велико, и для того, чтобы ориентироваться в этом многообразии, полезно ввести определенную классификацию приборов. • Естественно систематизировать приборы по функциональным возможностям и назначению, а также по техническому уровню и качеству выполняемых функций. • Имея в виду функциональные возможности и назначение, можно выделить универсальные и специализированные ультразвуковые приборы.

• Универсальные приборы можно разделить на три основных типа в зависимости от используемых в них режимов работы. 1. Ультразвуковые сканеры. Приборы, предназначенные прежде всего для получения двухмерного черно белого акустического изображения. • Основные режимы работы (modes): В (или 2 D) двухмерное изображение; М (или ТМ) одномерная яркостная эхограмма с разверткой во времени. • Дополнительные режимы: В + В, В + М.

2. Ультразвуковые сканеры со спектральным допплером. Иногда они называются дуплексными приборами. Отличаются от обычных ультразвуковых сканеров тем, что дополнительно имеют возможность оценивать спектр скоростей кровотока допплеровским методом. • Основные режимы работы: B(2 D); М (ТМ); D спектральный анализ скоростей кровотока с использованием импульсноволнового допплера (PW) и в ряде случаев непрерывноволнового допплера (CW). • Дополнительные режимы: В + В, В + М, В + D (дуплексный).

3. Ультразвуковые системы с цветовым допплеровским картированием. Иногда они называются приборами с цветовым допплером. Это приборы с максимальным количеством функций. Помимо режимов, которые имеются в сканерах со спектральным допплером, этот класс приборов имеет возможность отображения двухмерного распределения скоростей кровотока, выделяемых цветом на двухмерном серошкальном изображении тканей. • Основные режимы работы: В (2 D); М (ТМ); D (PW и CW); CFM цветовое допплеровское картирование кровотока. • Дополнительные режимы: В + В, В + М, В + D (дуплексный), В + D + CFM (триплексный).

• Помимо перечисленных могут использоваться специальные режимы: PD энергетический допплер; TD тканевый допплер; 3 D трехмерное изображение; тканевая (нативная) гармоника. • Имеется группа специализированных ультразвуковых диагностических приборов к которой относятся приборы достаточно ограниченного медицинского применения.

• Функциональные возможности перечисленных выше универсальных и специализированных приборов определяются не только имеющимися в них режимами работы, но и набором датчиков и дополнительных устройств, которые могут быть подключены к прибору, вычислительными программами, устройствами запоминания, архивирования и регистрации диагностической информации.

• Области медицинского применения в основном определяются типом датчиков, работающих с ультразвуковым прибором и наличием специализированных режимов работы. • Качество получаемой информации зависит от технического уровня прибора чем сложнее и совершеннее прибор, тем выше качество диагностической информации. • Как правило, по техническому уровню приборы делят на четыре группы: 1) простые приборы; 2) приборы среднего класса; 3) приборы повышенного класса; 4) приборы высокого класса (иногда называемого high end).

• В простых (как правило, переносных) ультразвуковых сканерах число каналов передачи приема не более 16, в приборах среднего и повышенного класса 32, 48 и 64. • В приборах высокого класса число каналов может быть более 64, например 128, 256, 512 и даже более. • Как правило, ультразвуковые сканеры высокого и повышенного класса являются приборами с цветовым допплеровским картированием. • Приборы высокого класса обычно используют в максимальной мере современные возможности цифровой обработки сигналов, начиная практически с выхода датчиков. • По этой причине такие приборы называют цифровыми системами или платформами (digital system).

Источник

From Wikipedia, the free encyclopedia

Sound measurements
Characteristic	Symbols
Sound pressure	p, SPL,L_PA
Particle velocity	v, SVL
Particle displacement	δ
Sound intensity	I, SIL
Sound power	P, SWL, L_WA
Sound energy	W
Sound energy density	w
Sound exposure	E, SEL
Acoustic impedance	Z
Audio frequency	AF
Transmission loss	TL

v t e

Acoustic impedance and specific acoustic impedance are measures of the opposition that a system presents to the acoustic flow resulting from an acoustic pressure applied to the system. The SI unit of acoustic impedance is the pascal-second per cubic metre (Pa·s/m³), or in the MKS system the rayl per square metre (rayl/m²), while that of specific acoustic impedance is the pascal-second per metre (Pa·s/m), or in the MKS system the rayl.^[1] There is a close analogy with electrical impedance, which measures the opposition that a system presents to the electric current resulting from a voltage applied to the system.

Mathematical definitions[edit]

Acoustic impedance[edit]

For a linear time-invariant system, the relationship between the acoustic pressure applied to the system and the resulting acoustic volume flow rate through a surface perpendicular to the direction of that pressure at its point of application is given by:^{[citation needed]}

or equivalently by

where

p is the acoustic pressure;
Q is the acoustic volume flow rate;
is the convolution operator;
R is the acoustic resistance in the time domain;
G = R⁻¹ is the acoustic conductance in the time domain (R⁻¹ is the convolution inverse of R).

Acoustic impedance, denoted Z, is the Laplace transform, or the Fourier transform, or the analytic representation of time domain acoustic resistance:^[1]

$Z(s){stackrel {{mathrm {def}}}{{}={}}}{mathcal {L}}[R](s)={frac {{mathcal {L}}[p](s)}{{mathcal {L}}[Q](s)}},$

$Z(omega ){stackrel {{mathrm {def}}}{{}={}}}{mathcal {F}}[R](omega )={frac {{mathcal {F}}[p](omega )}{{mathcal {F}}[Q](omega )}},$

$Z(t){stackrel {{mathrm {def}}}{{}={}}}R_{{mathrm {a}}}(t)={frac {1}{2}}!left[p_{{mathrm {a}}}*left(Q^{{-1}}right)_{{mathrm {a}}}right]!(t),$

where

Acoustic resistance, denoted R, and acoustic reactance, denoted X, are the real part and imaginary part of acoustic impedance respectively:^{[citation needed]}

where

i is the imaginary unit;
in Z(s), R(s) is not the Laplace transform of the time domain acoustic resistance R(t), Z(s) is;
in Z(ω), R(ω) is not the Fourier transform of the time domain acoustic resistance R(t), Z(ω) is;
in Z(t), R(t) is the time domain acoustic resistance and X(t) is the Hilbert transform of the time domain acoustic resistance R(t), according to the definition of the analytic representation.

Inductive acoustic reactance, denoted X_L, and capacitive acoustic reactance, denoted X_C, are the positive part and negative part of acoustic reactance respectively:^{[citation needed]}

$X(s)=X_{L}(s)-X_{C}(s),$

$X(omega )=X_{L}(omega )-X_{C}(omega ),$

$X(t)=X_{L}(t)-X_{C}(t).$

Acoustic admittance, denoted Y, is the Laplace transform, or the Fourier transform, or the analytic representation of time domain acoustic conductance:^[1]

$Y(s){stackrel {{mathrm {def}}}{{}={}}}{mathcal {L}}[G](s)={frac {1}{Z(s)}}={frac {{mathcal {L}}[Q](s)}{{mathcal {L}}[p](s)}},$

$Y(omega ){stackrel {{mathrm {def}}}{{}={}}}{mathcal {F}}[G](omega )={frac {1}{Z(omega )}}={frac {{mathcal {F}}[Q](omega )}{{mathcal {F}}[p](omega )}},$

$Y(t){stackrel {{mathrm {def}}}{{}={}}}G_{{mathrm {a}}}(t)=Z^{{-1}}(t)={frac {1}{2}}!left[Q_{{mathrm {a}}}*left(p^{{-1}}right)_{{mathrm {a}}}right]!(t),$

where

Z⁻¹ is the convolution inverse of Z;
p⁻¹ is the convolution inverse of p.

Acoustic conductance, denoted G, and acoustic susceptance, denoted B, are the real part and imaginary part of acoustic admittance respectively:^{[citation needed]}

where

in Y(s), G(s) is not the Laplace transform of the time domain acoustic conductance G(t), Y(s) is;
in Y(ω), G(ω) is not the Fourier transform of the time domain acoustic conductance G(t), Y(ω) is;
in Y(t), G(t) is the time domain acoustic conductance and B(t) is the Hilbert transform of the time domain acoustic conductance G(t), according to the definition of the analytic representation.

Acoustic resistance represents the energy transfer of an acoustic wave. The pressure and motion are in phase, so work is done on the medium ahead of the wave. Acoustic reactance represents the pressure that is out of phase with the motion and causes no average energy transfer.^{[citation needed]} For example, a closed bulb connected to an organ pipe will have air moving into it and pressure, but they are out of phase so no net energy is transmitted into it. While the pressure rises, air moves in, and while it falls, it moves out, but the average pressure when the air moves in is the same as that when it moves out, so the power flows back and forth but with no time averaged energy transfer.^{[citation needed]} A further electrical analogy is a capacitor connected across a power line: current flows through the capacitor but it is out of phase with the voltage, so no net power is transmitted into it.

Specific acoustic impedance[edit]

For a linear time-invariant system, the relationship between the acoustic pressure applied to the system and the resulting particle velocity in the direction of that pressure at its point of application is given by

or equivalently by:

where

p is the acoustic pressure;
v is the particle velocity;
r is the specific acoustic resistance in the time domain;
g = r⁻¹ is the specific acoustic conductance in the time domain (r⁻¹ is the convolution inverse of r).^{[citation needed]}

Specific acoustic impedance, denoted z is the Laplace transform, or the Fourier transform, or the analytic representation of time domain specific acoustic resistance:^[1]

$z(s){stackrel {{mathrm {def}}}{{}={}}}{mathcal {L}}[r](s)={frac {{mathcal {L}}[p](s)}{{mathcal {L}}[v](s)}},$

$z(omega ){stackrel {{mathrm {def}}}{{}={}}}{mathcal {F}}[r](omega )={frac {{mathcal {F}}[p](omega )}{{mathcal {F}}[v](omega )}},$

$z(t){stackrel {{mathrm {def}}}{{}={}}}r_{{mathrm {a}}}(t)={frac {1}{2}}!left[p_{{mathrm {a}}}*left(v^{{-1}}right)_{{mathrm {a}}}right]!(t),$

where v⁻¹ is the convolution inverse of v.

Specific acoustic resistance, denoted r, and specific acoustic reactance, denoted x, are the real part and imaginary part of specific acoustic impedance respectively:^{[citation needed]}

where

in z(s), r(s) is not the Laplace transform of the time domain specific acoustic resistance r(t), z(s) is;
in z(ω), r(ω) is not the Fourier transform of the time domain specific acoustic resistance r(t), z(ω) is;
in z(t), r(t) is the time domain specific acoustic resistance and x(t) is the Hilbert transform of the time domain specific acoustic resistance r(t), according to the definition of the analytic representation.

Specific inductive acoustic reactance, denoted x_L, and specific capacitive acoustic reactance, denoted x_C, are the positive part and negative part of specific acoustic reactance respectively:^{[citation needed]}

$x(s)=x_{L}(s)-x_{C}(s),$

$x(omega )=x_{L}(omega )-x_{C}(omega ),$

$x(t)=x_{L}(t)-x_{C}(t).$

Specific acoustic admittance, denoted y, is the Laplace transform, or the Fourier transform, or the analytic representation of time domain specific acoustic conductance:^[1]

$y(s){stackrel {{mathrm {def}}}{{}={}}}{mathcal {L}}[g](s)={frac {1}{z(s)}}={frac {{mathcal {L}}[v](s)}{{mathcal {L}}[p](s)}},$

$y(omega ){stackrel {{mathrm {def}}}{{}={}}}{mathcal {F}}[g](omega )={frac {1}{z(omega )}}={frac {{mathcal {F}}[v](omega )}{{mathcal {F}}[p](omega )}},$

$y(t){stackrel {{mathrm {def}}}{{}={}}}g_{{mathrm {a}}}(t)=z^{{-1}}(t)={frac {1}{2}}!left[v_{{mathrm {a}}}*left(p^{{-1}}right)_{{mathrm {a}}}right]!(t),$

where

z⁻¹ is the convolution inverse of z;
p⁻¹ is the convolution inverse of p.

Specific acoustic conductance, denoted g, and specific acoustic susceptance, denoted b, are the real part and imaginary part of specific acoustic admittance respectively:^{[citation needed]}

where

in y(s), g(s) is not the Laplace transform of the time domain acoustic conductance g(t), y(s) is;
in y(ω), g(ω) is not the Fourier transform of the time domain acoustic conductance g(t), y(ω) is;
in y(t), g(t) is the time domain acoustic conductance and b(t) is the Hilbert transform of the time domain acoustic conductance g(t), according to the definition of the analytic representation.

Specific acoustic impedance z is an intensive property of a particular medium (e.g., the z of air or water can be specified); on the other hand, acoustic impedance Z is an extensive property of a particular medium and geometry (e.g., the Z of a particular duct filled with air can be specified).^{[citation needed]}

Acoustic ohm[edit]

The acoustic ohm is a unit of measurement of acoustic impedance. In SI units, pressure is measured in pascals and flow in m³/s, so the acoustic ohm is equal to 1 Pa·s/m³.

The acoustic ohm can be applied to fluid flow outside the domain of acoustics. For such applications a hydraulic ohm with an identical definition may be used. A hydraulic ohm measurement would be the ratio of hydraulic pressure to hydraulic volume flow.

Relationship[edit]

For a one dimensional wave passing through an aperture with area A, the acoustic volume flow rate Q is the volume of medium passing per second through the aperture; if the acoustic flow moves a distance dx = v dt, then the volume of medium passing through is dV = A dx, so:^{[citation needed]}

$Q={frac {{mathrm {d}}V}{{mathrm {d}}t}}=A{frac {{mathrm {d}}x}{{mathrm {d}}t}}=Av.$

If the wave is one-dimensional, it yields

$Z(s)={frac {{mathcal {L}}[p](s)}{{mathcal {L}}[Q](s)}}={frac {{mathcal {L}}[p](s)}{A{mathcal {L}}[v](s)}}={frac {z(s)}{A}},$

$Z(omega )={frac {{mathcal {F}}[p](omega )}{{mathcal {F}}[Q](omega )}}={frac {{mathcal {F}}[p](omega )}{A{mathcal {F}}[v](omega )}}={frac {z(omega )}{A}},$

$Z(t)={frac {1}{2}}!left[p_{{mathrm {a}}}*left(Q^{{-1}}right)_{{mathrm {a}}}right]!(t)={frac {1}{2}}!left[p_{{mathrm {a}}}*left({frac {v^{{-1}}}{A}}right)_{{mathrm {a}}}right]!(t)={frac {z(t)}{A}}.$

Characteristic acoustic impedance[edit]

Characteristic specific acoustic impedance[edit]

The constitutive law of nondispersive linear acoustics in one dimension gives a relation between stress and strain:^[1]

${displaystyle p=-rho c^{2}{frac {partial delta }{partial x}},}$

where

p is the acoustic pressure in the medium;
ρ is the volumetric mass density of the medium;
c is the speed of the sound waves traveling in the medium;
δ is the particle displacement;
x is the space variable along the direction of propagation of the sound waves.

This equation is valid both for fluids and solids. In

fluids, ρc² = K (K stands for the bulk modulus);
solids, ρc² = K + 4/3 G (G stands for the shear modulus) for longitudinal waves and ρc² = G for transverse waves.^{[citation needed]}

Newton’s second law applied locally in the medium gives:^[2]

${displaystyle rho {frac {partial ^{2}delta }{partial t^{2}}}=-{frac {partial p}{partial x}}.}$

Combining this equation with the previous one yields the one-dimensional wave equation:

${displaystyle {frac {partial ^{2}delta }{partial t^{2}}}=c^{2}{frac {partial ^{2}delta }{partial x^{2}}}.}$

The plane waves

{displaystyle delta (mathbf {r} ,,t)=delta (x,,t)}

that are solutions of this wave equation are composed of the sum of two progressive plane waves traveling along x with the same speed and in opposite ways:^{[citation needed]}

{displaystyle delta (mathbf {r} ,,t)=f(x-ct)+g(x+ct)}

from which can be derived

${displaystyle v(mathbf {r} ,,t)={frac {partial delta }{partial t}}(mathbf {r} ,,t)=-c{big [}f'(x-ct)-g'(x+ct){big ]},}$

${displaystyle p(mathbf {r} ,,t)=-rho c^{2}{frac {partial delta }{partial x}}(mathbf {r} ,,t)=-rho c^{2}{big [}f'(x-ct)+g'(x+ct){big ]}.}$

For progressive plane waves:^{[citation needed]}

${begin{cases}p({mathbf {r}},,t)=-rho c^{2},f'(x-ct)\v({mathbf {r}},,t)=-c,f'(x-ct)end{cases}}$

${begin{cases}p({mathbf {r}},,t)=-rho c^{2},g'(x+ct)\v({mathbf {r}},,t)=c,g'(x+ct).end{cases}}$

Finally, the specific acoustic impedance z is

$z({mathbf {r}},,s)={frac {{mathcal {L}}[p]({mathbf {r}},,s)}{{mathcal {L}}[v]({mathbf {r}},,s)}}=pm rho c,$

$z({mathbf {r}},,omega )={frac {{mathcal {F}}[p]({mathbf {r}},,omega )}{{mathcal {F}}[v]({mathbf {r}},,omega )}}=pm rho c,$

$z({mathbf {r}},,t)={frac {1}{2}}!left[p_{{mathrm {a}}}*left(v^{{-1}}right)_{{mathrm {a}}}right]!({mathbf {r}},,t)=pm rho c.$

^{[citation needed]}

The absolute value of this specific acoustic impedance is often called characteristic specific acoustic impedance and denoted z₀:^[1]

$z_{0}=rho c.$

The equations also show that

${frac {p({mathbf {r}},,t)}{v({mathbf {r}},,t)}}=pm rho c=pm z_{0}.$

Effect of temperature[edit]

Temperature acts on speed of sound and mass density and thus on specific acoustic impedance.^{[citation needed]}

Effect of temperature on properties of air

Celsius temperature θ (°C)	Speed of sound c (m/s)	Density of air ρ (kg/m³)	Characteristic specific acoustic impedance z₀ (Pa·s/m)
35	351.88	1.1455	403.2
30	349.02	1.1644	406.5
25	346.13	1.1839	409.4
20	343.21	1.2041	413.3
15	340.27	1.2250	416.9
10	337.31	1.2466	420.5
5	334.32	1.2690	424.3
0	331.30	1.2922	428.0
−5	328.25	1.3163	432.1
−10	325.18	1.3413	436.1
−15	322.07	1.3673	440.3
−20	318.94	1.3943	444.6
−25	315.77	1.4224	449.1

Characteristic acoustic impedance[edit]

For a one dimensional wave passing through an aperture with area A, Z = z/A, so if the wave is a progressive plane wave, then:^{[citation needed]}

$Z({mathbf {r}},,s)=pm {frac {rho c}{A}},$

$Z({mathbf {r}},,omega )=pm {frac {rho c}{A}},$

$Z({mathbf {r}},,t)=pm {frac {rho c}{A}}.$

The absolute value of this acoustic impedance is often called characteristic acoustic impedance and denoted Z₀:^[1]

$Z_{0}={frac {rho c}{A}}.$

and the characteristic specific acoustic impedance is

${frac {p({mathbf {r}},,t)}{Q({mathbf {r}},,t)}}=pm {frac {rho c}{A}}=pm Z_{0}.$

If the aperture with area A is the start of a pipe and a plane wave is sent into the pipe, the wave passing through the aperture is a progressive plane wave in the absence of reflections, and the usually reflections from the other end of the pipe, whether open or closed, are the sum of waves travelling from one end to the other.^[3] (It is possible to have no reflections when the pipe is very long, because of the long time taken for the reflected waves to return, and their attenuation through losses at the pipe wall.^[3]) Such reflections and resultant standing waves are very important in the design and operation of musical wind instruments.^[4]

References[edit]

^ ^a ^b ^c ^d ^e ^f ^g ^h Kinsler L, Frey A, Coppens A, Sanders J (2000). Fundamentals of Acoustics. Hoboken: Wiley. ISBN 0-471-84789-5.
^ Attenborough K, Postema M (2008). A pocket-sized introduction to acoustics. Kingston upon Hull: University of Hull. doi:10.5281/zenodo.7504060. ISBN 978-90-812588-2-1.
^ ^a ^b Rossing TD, Fletcher NH (2004). Principles of Vibration and Sound (2nd ed.). Heidelberg: Springer. ISBN 978-1-4757-3822-3. OCLC 851835364.
^ Fletcher NH, Rossing TD (1998). The physics of musical instruments (2nd ed.). Heidelberg: Springer. ISBN 978-0-387-21603-4. OCLC 883383570.

External links[edit]

The Wave Equation for Sound
What Is Acoustic Impedance and Why Is It Important?

Источник

См. также[править | править код]

Акустический импеданс