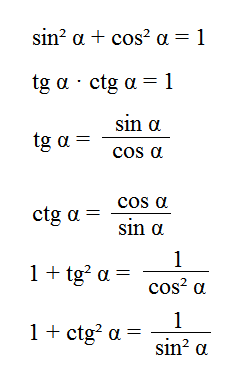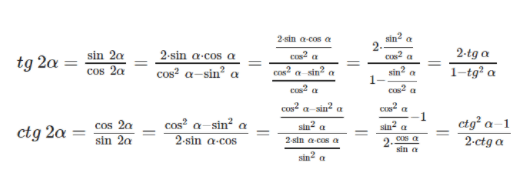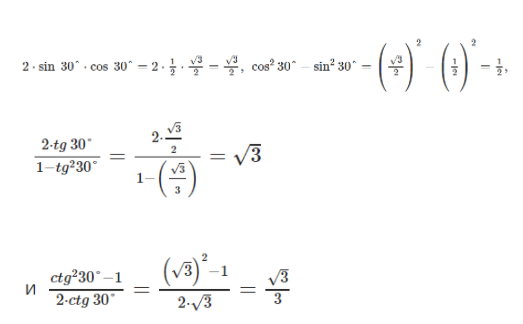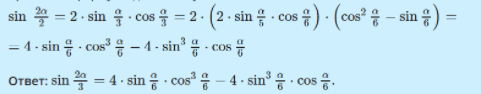Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2α, используя тригонометрические функции угла α. Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид nα записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin nαимеет то же значение, что и sin (nα). При обозначении sinn α имеем аналогичную запись(sin α)n. Использование записи применимо для всех тригонометрических функций со степенями n.
Ниже приведены формулы двойного угла:
sin 2α=2·sin α·cos αcos 2α=cos2 α-sin2 α, cos 2α=1-2·sin2 α, cos 2α=2·cos2 α-1tg 2α=2·tg α1-tg2 αctg 2α-ctg2 α-12·ctg α
Отметим, что данные формулы sin и cos применимы с любым значением угла α. Формула тангенса двойного угла справедлива при любом значении α, где tg 2α имеет смысл, то есть α≠π4+π2·z, z является любым целым числом. Котангенс двойного угла существует при любом α, где ctg 2α определен на α≠π2·z.
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin (α+β)=sin α ·cos β+cos α·sin βи косинуса суммы cos (α+β)=cos α ·cos β-sin α·sin β. Предположим, что β=α, тогда получим, что
sin (α+α)=sin α ·cos α+cos α·sin α=2·sin α·cos α и cos (α+α)=cos α ·cos α-sin α·sin α=cos2α-sin2α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2α= 2·sin α·cos α и cos 2α=cos2α-sin2α.
Остальные формулы cos 2α=1-2·sin2 α и cos 2α=2·cos2 α-1 приводят к виду cos 2α=cos 2α=cos2 α-sin2 α, при замене 1 на сумму квадратов по основному тождествуsin2 α+cos2 α=1. Получаем, что sin2 α+cos2 α=1. Так 1-2·sin2 α=sin2 α+cos2 α-2·sin2 α=cos2 α-sin2 α и 2·cos2 α-1=2·cos2 α-(sin2 α+ cos2 α)=cos2 α-sin2 α.
Для доказательства формул двойного угла тангенса и котангенса применим равенства tg 2α=sin 2αcos 2α и ctg 2α=cos 2αsin 2α. После преобразования получим, что tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α и ctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos α. Разделим выражение на cos2 α, где cos2 α≠0 с любым значением α, когда tg α определен. Другое выражение поделим на sin2 α, где sin2 α≠0 с любыми значениями α, когда ctg 2α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
tg 2α=sin 2αcos 2α=2·sin α·cos αcos2 α-sin2 α=2·sin α·cos αcos2 αcos2 α-sin2 αcos2 α=2·sin2 αcos2 α1-sin2 αcos2 α=2·tg α1-tg2 αctg 2α=cos 2αsin 2α=cos2 α-sin2 α2·sin α·cos=cos2 α-sin2 αsin2 α2·sin α·cos αsin2 α=cos2 αsin2 α-12·cos αsin α=ctg2 α-12·ctg α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2α для α=30°, применим значения тригонометрических функций для этих углов. Если α=30°, тогда 2α=60°. Проверим значения sin 60°=2·sin 30°·cos 30°, cos 60°=cos2 30°-sin2 30°.
Подставив значения, получим tg 60°= 2·tg 30°1-tg2 30° и ctg 60°=ctg230°-12·ctg 30°..
Известно, что sin 30°=12, cos 30°=32, tg 30°=33, ctg 30°=3 и
sin 60°=32, cos 60°=12, tg 60°=3, ctg 60°=33, тогда отсюда видим, что
2·sin 30°·cos 30°=2·12·32=32, cos230°-sin230°=(32)2-(12)2=12,2·tg 30°1-tg230°=2·321-(33)=3
и ctg230°-12·ctg 30°=(3)2-12·3=33
Проведя вычисления, можно сделать вывод, что справедливость для α=30° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2α. В примере допускается применение формулы двойного угла 3π5. Тогда его необходимо преобразовать, в результате чего получим α=3π5:2=3π10. Отсюда следует, что формула двойного угла для косинуса будет иметь видcos3π5=cos23π10-sin23π10.
Представить sin 2α3 через тригонометрические функции, при α6.
Решение
Заметим, что из условия имеем 2α3=4·α6. Тогда использовав 2 раза формулу двойного угла, выразим sin2α3 через тригонометрические функции угла α6. Применяя формулу двойного угла, получим sin 2α3=2·sin α3·cos α3. После чего к функциям sin α3 и cos α3применим формулы двойного угла: sin 2α2=2·sin α3·cosα3=2·(2·sinα5·cosα6)·(cos2α6-sinα6)==4·sinα6·cos3α6-4·sin3α6·cosα6
Ответ: sin2α3=4·sinα6·cos3α6-4·sin3α6·cosα6.
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3α=sin(2α+α)=sin 2α·cos α+cos 2α·sin α=2·sin α·cosα·cos α+ (cos2 α-sin2α)·sin α==3·sin α·cos2α-sin3 α
При замене cos2α на 1-sin2α из формулы sin 3α=3·sin α·cos2α-sin3α, она будет иметь вид sin 3α=3·sin α-4·sin3 α.
Так же приводится формула косинуса тройного угла:
cos 3α=cos (2α+α)=cos 2α·cos α-sin 2α·sin α==(cos2 α-sin2 α)·cos α-2·sin α·cos α·sin α=cos3α-3·sin2α·cos α
При замене sin2 α на 1-cos2 α получим формулу вида cos 3α=-3·cos α+4·cos3 α.
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
tg 3α=sin 3αcos 3α=3·sin α·cos2 α-sin3 αcos3α-3·sin2α·cos α=3·sin α·cos2α-sin3αcos3αcos3α-3·sin2α·cos αcos3α==3·sin αcos α-sin3αcos3α1-3·sin2 αcos2 α=3·tg α-tg3α1-3·tg2α;ctg 3α=cos 3αsin 3α=cos3 α-3·sin2α·cosα3·sin α·cos2α-sin3α=cos3α-3·sin2α·cosαsin3α3·sin α·cos2α-sin3αsin3α==cos3αsin3α-3·cos αsin α3·cos2αsin2α-1=ctg3α-3·ctgα3·ctg2α-1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4α как 2·2α, тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5α в виде 3α+2α, что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.
Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).
Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.
Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника
Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co
Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.
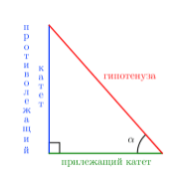
Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.
Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.
Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.
Итак,
Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.
Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.
Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.
Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.
Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.
Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.
Как найти углы в прямоугольном треугольнике, если известны стороны?
Дан треугольник АВС, угол С — прямой.
Стороны АВ, АС и ВС известны.
Т.к. угол С — прямой, он равен 90 градусам.
Другие углы можно найти, например, так:
если известен катет и гипотенуза
sinA = BC / AB,
sinB = AC / AB,
если известны два катета
tg A = BC / AC
tg B = AC / BC
Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.
Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.
Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.
sin 15° = 0,259
arcsin0,259 = 15°
Как найти углы в прямоугольном треугольнике, если известен один угол?
Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.
Еединичная окружность (единичный круг)
Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).
Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).
Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.
Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).
Координатные четверти отсчитываются так:
y
|
|
(II четверть) | (I четверть)
|
________________________ x
|0
|
(III четверть) | (IV четверть)
|
|
Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).
Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).
Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).
Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).
Например:
- углы первой четверти: 30 градусов, 85 градусов, пи/4;
- углы второй четверти: 120 градусов, 178 градусов;
- углы третьей четверти: 205 градусов, 260 градусов;
- углы четвертой четверти: 272 градуса, 305 градусов.
Тригонометрические функции
К тригонометрическим функциям относятся функции:
y = sin x;
y = cos x;
y = tg x;
y = ctg x;
y = sec x;
y = cosec x.
Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.
Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.
Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.
Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.
Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.
Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.
Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.
Как найти синус угла, если известен косинус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
sin2a = 1 − cos2a
|sin a| = КОРЕНЬ(1 − cos2a)
sin a = ± КОРЕНЬ(1 − cos2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти косинус угла, если известен синус?
Нужно воспользоваться основным тригонометрическим тождеством:
sin2a + cos2a = 1
cos2a = 1 − sin2a
|cos a| = КОРЕНЬ(1 − sin2a)
cos a = ± КОРЕНЬ(1 − sin2a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)
Как найти синус угла, если известен котангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + ctg2 a = 1/sin2 a
sin2 a = 1 / (1 + ctg2 a)
|sin a| = 1/ КОРЕНЬ(1 + ctg2 a)
sin a = ±1/ КОРЕНЬ(1 + ctg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)
Как найти косинус угла, если известен тангенс?
Нужно воспользоваться тригонометрическим тождеством
1 + tg2 a = 1/cos2 a
cos2 a = 1 / (1 + tg2 a)
|cos a| = 1/ КОРЕНЬ(1 + tg2 a)
cos a = ±1/ КОРЕНЬ(1 + tg2 a)
знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)
Тригонометрическое тождество
Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.
Основные тригонометрические тождества:
sin2a + cos2a = 1
tg a = sin a / cos a
ctg a = cos a / sin a
sec a = 1 / cos a
cosec a = 1 / sin a
Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)
- arcsin — читается: арксинус;
- arcos — читается: арккосинус;
- arctg — читается: арктангенс;
- arcctg — читается: арккотангенс.
arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.
Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:
y = arcsin x sin y = x
Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:
y = arccos x cos y = x
Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:
y = arctg x tg y = x
Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:
y = arctg x tg y = x
Например,
sin 30° = 0,5
arcsin0,5 = 30°
Синусоида и косинусоида
График функции y = sin x называется синусоидой.
График функции y = cos x называется косинусоидой.
Источники информации:
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
- В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
- docme.ru — зачем нужна тригонометрия?
- ru.wikipedia.org — Википедия — тригонометрия;
- ru.wikihow.com — как изучать тригонометрию?
Как найти угол альфа формула
Содержание
- Синус, косинус, тангенс и котангенс. Определения
- Угол поворота
- Числа
- Тригонометрические функции углового и числового аргумента
- Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α — это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α — это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят “синус угла поворота α “. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
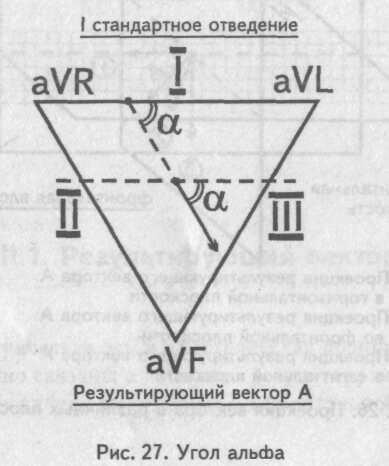
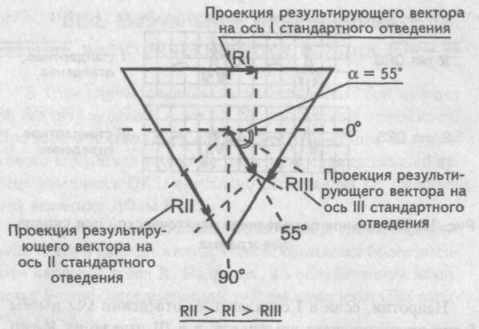
Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол альфа.
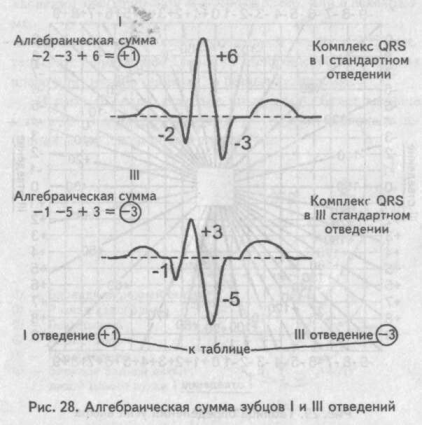
Величину угла альфа находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q + R + S) в I и III стандартных отведениях. Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (—), поскольку находятся ниже изоэлектрической линии, а зубец К — знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).
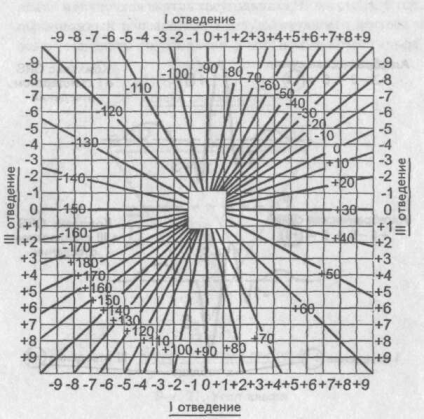
Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла альфа. В нашем случае он равен минус 70°. Таблица определения положения электрической оси сердца (по Дьеду)
Таблица определения угла альфа
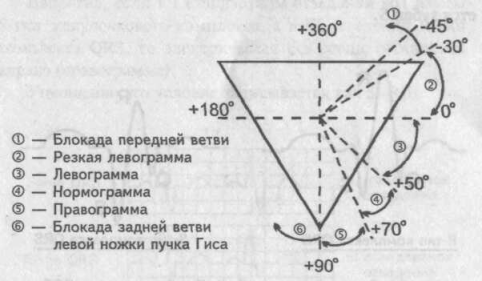
Если угол альфа находится в пределах 50—70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме. При отклонении электрической оси сердца вправо угол альфа будет определяться в пределах 70—90°. В обиходе такое положение электрической оси сердца называют правограммой.
Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса. Определяя угол альфа в пределах 50—0° говорят об отклонении электрической оси сердца влево, или о левограмме. Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме. И наконец, если значение у г л а альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса.
Пределы отклонения электрической оси сердца
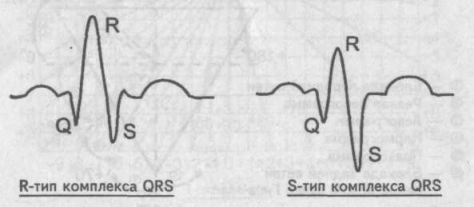
Определение отклонения электрической оси сердца по углу альфа с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой. Однако определить отклонение электрической оси сердца можно и без необходимых таблиц. В этом случае отклонение электрической оси находят по анализу зубцов R и S в I и III стандартных отведениях. При этом понятие алгебраической суммы зубцов желудочкового комплекса комплекса QRS, заменяют визуально понятием «определяющий зубец» сопоставляя по абсолютной величине зубцы R и S . Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец К. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.
Сопоставление зубцов К и 3 комплекса QRS
Если на электрокардиограмме в I стандартном отведении желудочковый комплекс представлен R-типом, а комплекс QRS в III стандартном отведении имеет форму S-типа, то в данном случае электрическая ось сердца отклонена влево (левограмма).
Схематично это условие записывается как RI-SIII.
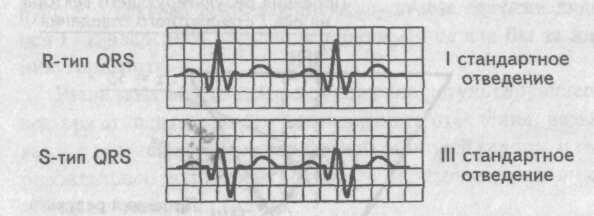
Визуальное определение электрической оси сердца
. Левограмма Напротив, если в I стандартном отведении мы имеем S-тип желудочкового комплекса, а в III отведении R-тип комплекса QRS, то электрическая ось сердца отклонена вправо (правограмма). Упрощенно это условие записывается как SI-RIII.
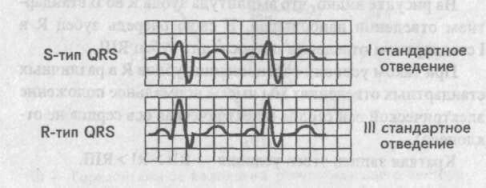
Визуальное определение электрической оси сердца
. Правограмма Результирующий вектор возбуждения желудочков расположен в норме во фронтальной плоскости так, что его направление совпадает с направлением оси II стандартного отведения.
Нормальное положение электрической оси сердца
(нормограмма) На рисунке видно, что амплитуда зубца R во II стандартном отведении наибольшая. В свою очередь зубец К в I стандартном отведении превосходит зубец RIII. При таком условии соотношения зубцов R в различных стандартных отведениях мы имеем нормальное положение электрической оси сердца (электрическая ось сердца не отклонена). Краткая запись этого условия — RII>RI>RIII.
Наиболее часто встречающиеся тригонометрические формулы:
(lacktriangleright) Основные тождества: [egin <|l|l|>hline sin^2 alpha+cos^2 alpha =1& mathrm, alpha cdot mathrm, alpha =1 &(sinalpha
e 0, cosalpha
e 0)[0.5ex] hline & mathrm, alpha=dfrac<sin alpha> <cos alpha>&mathrm, alpha =dfrac<cos alpha> <sin alpha>& 1+mathrm^2, alpha =dfrac1 <cos^2 alpha>& 1+mathrm^2, alpha=dfrac1<sin^2 alpha>& (cosalpha
e 0)& (sinalpha
e 0) hline end]
(lacktriangleright) Формулы сложения углов: [egin <|l|r|>hline & sin<(alphapm eta)>=sinalphacdot cosetapm sinetacdot cosalpha & cos<(alphapm eta)>=cosalphacdot coseta mp sinalphacdot sineta & hline & mathrm, (alphapm eta)=dfrac<mathrm, alphapm mathrm, eta><1 mp mathrm, alphacdot mathrm, eta> & mathrm, (alphapmeta)=-dfrac<1mp mathrm, alphacdot mathrm, eta><mathrm, alphapm mathrm, eta>& cosalphacoseta
e 0&sinalphasineta
e 0 hline end]
(lacktriangleright) Формулы двойного и тройного углов: [egin <|lc|cr|>hline sin <2alpha>=2sin alphacos alpha & qquad &qquad & cos<2alpha>=cos^2alpha -sin^2alpha sin alphacos alpha =dfrac12sin <2alpha>&& & cos<2alpha>=2cos^2alpha -1 & & & cos<2alpha>=1-2sin^2 alpha hline &&& mathrm, 2alpha = dfrac<2mathrm, alpha><1-mathrm^2, alpha> && & mathrm, 2alpha = dfrac<mathrm^2, alpha-1><2mathrm, alpha>&&& cosalpha
e 0, cos2alpha
e 0 &&& sinalpha
e 0, sin2alpha
e 0 hline &&& sin <3alpha>=3sin alpha -4sin^3alpha && & cos<3alpha>=4cos^3alpha -3cos alpha&&& hline end]
(lacktriangleright) Формулы понижения степени: [egin <|lc|cr|>hline &&& sin^2alpha=dfrac<1-cos<2alpha>>2 &&& cos^2alpha=dfrac<1+cos<2alpha>>2&&& hline end]
(lacktriangleright) Формулы произведения функций: [egin <|c|>hline sinalphasineta=dfrac12igg(cos<(alpha-eta)>-cos<(alpha+eta)>igg)\ cosalphacoseta=dfrac12igg(cos<(alpha-eta)>+cos<(alpha+eta)>igg)\ sinalphacoseta=dfrac12igg(sin<(alpha-eta)>+sin<(alpha+eta)>igg)\ hline end]
(lacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [egin <|l|r|>hline & sin<2alpha>=dfrac<2mathrm, alpha><1+mathrm^2, alpha> & cos<2alpha>=dfrac<1-mathrm^2, alpha><1+mathrm^2, alpha>& cosalpha
e 0 & sinalpha
e 0 hline end]
(lacktriangleright) Формула вспомогательного аргумента: [egin <|c|>hline ext<Частный случай> hline sinalphapm cosalpha=sqrt2cdot sin<left(alphapm dfrac<pi>4
ight)>\ sqrt3sinalphapm cosalpha=2sin<left(alphapm dfrac<pi>6
ight)>\ sinalphapm sqrt3cosalpha=2sin<left(xpm dfrac<pi>3
ight)>\ hline ext<Общий случай> hline asinalphapm bcosalpha=sqrtcdot sin<(alphapm phi)>, cosphi=dfrac a<sqrt>, sinphi=dfrac b<sqrt>\ hline end]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
(lacktriangleright) Вывод формулы косинуса разности углов (cos<(alpha -eta)>=cosalphacoseta+sinalphasineta)
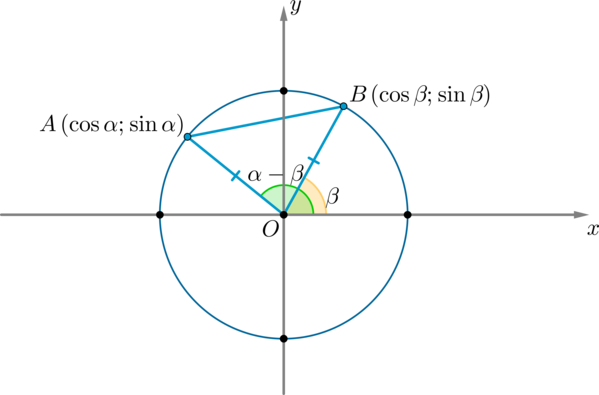
Рассмотрим тригонометрическую окружность и на ней углы (alpha) и (eta) . Пусть этим углам соответствуют точки (A) и (B) соответственно. Тогда координаты этих точек: (A(cosalpha;sinalpha), B(coseta;sineta)) .
Рассмотрим ( riangle AOB: angle AOB=alpha-eta) . По теореме косинусов:
(AB^2=AO^2+BO^2-2AOcdot BOcdot cos(alpha-eta)=1+1-2cos(alpha-eta) (1)) (т.к. (AO=BO=R) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
Таким образом, сравнивая равенства ((1)) и ((2)) :
Отсюда и получается наша формула.
(lacktriangleright) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения (sin x=cos(90^circ-x)) и (cos x=sin (90^circ-x)) :
разделим числитель и знаменатель дроби на (cosalphacoseta
e 0)
(при (cosalpha=0 Rightarrow mathrm,(alphapmeta)=mp mathrm,eta) , при (coseta=0 Rightarrow mathrm,(alphapmeta)=pm mathrm,alpha) ):
Таким образом, данная формула верна только при (cosalphacoseta
e 0) .
5) Аналогично, только делением на (sinalphasineta
e 0) , выводится формула котангенса суммы/разности двух углов.
(lacktriangleright) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) (sin 2alpha=sin(alpha+alpha)=sinalphacosalpha+sinalphacosalpha=2sinalphacosalpha)
Используя основное тригонометрическое тождество (sin^2alpha+cos^2alpha=1) , получим еще две формулы для косинуса двойного угла:
разделим числитель и знаменатель дроби на (cos^2alpha
e 0) (при (cosalpha=0 Rightarrow mathrm,2alpha=0) ):
Таким образом, эта формула верна только при (cosalpha
e 0) , а также при (cos2alpha
e 0) (чтобы существовал сам (mathrm,2alpha) ).
По тем же причинам при (sinalpha
e 0, sin2alpha
e 0) .
5) (sin3alpha=sin(alpha+2alpha)=sinalphacos2alpha+cosalphasin2alpha=sinalpha(1-2sin^2alpha)+cosalphacdot 2sinalphacosalpha=)
6) Аналогично выводится, что (cos3alpha=cos(alpha+2alpha)=4cos^3alpha-3cosalpha)
(lacktriangleright) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) (cos2alpha=2cos^2alpha-1 Rightarrow cos^2alpha=dfrac<1+cos2alpha>2)
2) (cos2alpha=1-2sin^2alpha Rightarrow sin^2alpha=dfrac<1-cos2alpha>2)
Заметим, что в данных формулах степень синуса/косинуса равна (2) в левой части, а в правой части степень косинуса равна (1) .
(lacktriangleright) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
Получим: (cos(alpha+eta)+cos(alpha-eta)=2cosalphacoseta Rightarrow cosalphacoseta=dfrac12Big(cos(alpha-eta)+cos(alpha+eta)Big))
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
3) Сложим формулы синуса суммы и синуса разности двух углов:
(lacktriangleright) Вывод формул суммы/разности функций:
Обозначим (alpha+eta=x, alpha-eta=y) . Тогда: (alpha=dfrac2, eta=dfrac2) . Подставим эти значения в предыдущие три формулы:
Получили формулу суммы косинусов.
Получили формулу разности косинусов.
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
Аналогично выводится формула суммы котангенсов.
(lacktriangleright) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
(разделим числитель и знаменатель дроби на (cos^2alpha
e 0) (при (cosalpha=0) и (sin2alpha=0) ):)
2) Так же, только делением на (sin^2alpha) , выводится формула для косинуса.
(lacktriangleright) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
Рассмотрим выражение (asin x+bcos x) . Домножим и разделим это выражение на (sqrt,) :
(asin x+bcos x=sqrtleft(dfrac a<sqrt>sin x+ dfrac b<sqrt>cos x
ight)=sqrtig(a_1sin x+b_1cos xig))
Заметим, что таким образом мы добились того, что (a_1^2+b_1^2=1) , т.к. (left(dfrac a<sqrt>
ight)^2+left(dfrac b<sqrt>
ight)^2=dfrac=1)
Таким образом, можно утверждать, что существует такой угол (phi) , для которого, например, (cos phi=a_1, sin phi=b_1) . Тогда наше выражение примет вид:
(sqrt,ig(cos phi sin x+sin phicos xig)=sqrt,sin (x+phi)) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: [<large,sin (x+phi),>> quad ext <где >cos phi=dfrac a<sqrt>] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt,cos (x-phi)]
(lacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла:
(a) sin xpmcos x=sqrt2,left(dfrac1<sqrt2>sin xpmdfrac1<sqrt2>cos x
ight)=sqrt2, sin left(xpmdfrac<pi>4
ight))
(b) sqrt3sin xpmcos x=2left(dfrac<sqrt3>2sin xpm dfrac12cos x
ight)=2, sin left(xpmdfrac<pi>6
ight))
(c) sin xpmsqrt3cos x=2left(dfrac12sin xpmdfrac<sqrt3>2cos x
ight)=2,sinleft(xpmdfrac<pi>3
ight))
Перевод градусов в радианы и обратно: формулы, примеры
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Связь между градусами и радианами
Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 р а д = 180 π ° – градусная мера угла в 1 радиан равна 180 π .
Также можно выразить один градус в радианах.
1 ° = π 180 р а д
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °
Значит, в одном радиане примерно 57 градусов
1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д
Один градус содержит 0,0175 радиана.
Формула перевода радианов в градусы
x р а д = х · 180 π °
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Пример 1. Перевод из радианов в градусы
Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.
Применим формулу перехода от радианов к градусам и получим:
3 , 2 р а д = 3 , 2 · 180 π ° ≈ 3 , 2 · 180 3 , 14 ° ≈ 576 3 , 14 ° ≈ 183 , 4 °
Аналогично можно получить формулу перевода из градусов в радианы.
Формула перевода из градусов в радианы
y ° = y · π 180 р а д
Переведем 47 градусов в радианы.
Согласно формуле, умножим 47 на пи и разделим на 180.
Центральные и вписанные углы
О чем эта статья:
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
Геометрия
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Центральный угол и градусная мера дуги
Любые две точки на окружности разбивают ее на две дуги. Чтобы отличать эти дуги, на каждой из них ставят точку, которую и указывают в обозначении дуги:
Здесь красным цветом показана⋃АСВ, а синим – ⋃ADB. Однако иногда для простоты указывают только концы дуги, то есть используют обозначение ⋃AВ. Это делается тогда, когда ясно, о какой дуге окружности идет речь. Обычно всегда подразумевается та дуга, которая меньше.
Можно заметить, что дуги отличаются по размеру, поэтому возникает потребность их измерения. Для этого используют такое понятие, как градусная мера дуги.
Для ее определения необходимо соединить концы дуги с центром окруж-ти. В результате получаются радиусы, которые пересекаются в центре окружности. Угол между ними именуется центральным углом окруж-ти.
Для каждой дуги можно построить единственный центральный угол, поэтому логично измерять дугу с помощью такого угла. Правда, обратное неверно. На рисунке видно, что центральному углу ∠АОВ соответствует сразу две дуги: ⋃АСВ и ⋃АDB:
Поэтому условно считают, градусная мера той из двух дуг, которая меньше, как раз и равна центральному углу:
Дуги, также как отрезки или углы, можно складывать или вычитать. Например, пусть есть две дуги, ⋃AВ и ⋃ВС, чьи градусные меры составляют 40° и 30°.
Как найти ⋃АС? Ей соответствует центральный угол ∠АОС, который в свою очередь равен сумме ∠АОВ и ∠ВОС:
Диаметр делит окруж-ть на две равные друг другу дуги, которые называются полуокружностями. При этом диаметр окружности можно рассматривать как угол между двумя радиусами, равный 180°. Получается, что градусная мера полуокружности составляет 180°:
Вместе две полуокружности образуют полную окруж-ть. Получается, что градусная мера всей окруж-ти составляет 180° + 180° = 360°.
Этот факт известен и из жизни – когда кто-то делает полный оборот вокруг своей оси, говорят, что он повернулся на 360°. Теперь мы можем вернуться к случаю, когда две точки делят окруж-ть на две неравные друг другу дуги. Градусная мера меньшей из них будет равна величине соответствующего центрального угла (обозначим его как α). В сумме две дуги должны дать 360°. Значит, градусная мера большей дуги будет составлять 360° – α:
Задание. Точки А, В, С и D лежат на одной окруж-ти. Известно, что ⋃АСВ составляет 107°. Какова величина ⋃ADB?
Решение. Вместе дуги ⋃АСВ и ⋃АDВ образуют полную окруж-ть, поэтому их сумма равна 360°. Это позволяет составить уравнение и найти из него ⋃АDB:
Задание. Найдите величину ∠АОС на рисунке, если известны ⋃AВ и ⋃ВС:
Решение. Сначала найдем ⋃АС, учтя, что все три дуги, показанные на рисунке, в сумме составляют 360°:
Для доказательства построим две одинаковые хорды AВ и СD в окруж-ти и соединим их концы с центром:
В результате получились ∆АОВ и ∆ОСD. У них равны все три стороны, значит, сами эти треугольники равны. Тогда
∠COD = ∠AOB
Но эти углы – центральные для дуг ⋃AВ и ⋃CD. Получается, что у этих дуг одинаковы их градусные меры, поэтому они также равны, ч. т. д.
Примечание. Всякая хорда окружности разбивает ее на две дуги – большую и меньшую. В данном правиле говорится именно равенстве меньших дуг.
Задание. На окруж-ти отмечены точки А, В и С так, что хорды AВ, ВС и АС равны. Найдите угол между радиусами окружности АО и ВО.
Дуги ⋃AВ, ⋃ВС и ⋃АС стянуты равными хордами AВ, ВС и АС. Значит, они одинаковы. Но в сумме эти три дуги образуют окруж-ть величиной в 360°. Значит, каждая из этих дуг втрое меньше:
⋃AВ = ⋃BC = ⋃AC = 360°:3 = 120°
∠АОВ – центральный для ⋃AВ, значит, он равен ее градусной мере, то есть он составляет 120°.
Вписанный угол
В окруж-ти можно построить ещё один угол, который именуют вписанным углом. Его отличие от центрального заключается в том, что его вершина лежит на окруж-ти, а не в ее центре. Сторонами же вписанного угла являются хорды окруж-ти.
Здесь дуга ⋃ВС находится внутри угла, а ее концы лежат на его сторонах. В таких случаях говорят, что ∠ВАС опирается на дугу ВС. Оказывается, что между величиной вписанного угла и дугой, на которую он опирается, есть взаимосвязь.
Обозначим вписанный угол ∠СAВ буквой α. Так как радиусы АО и ОС одинаковы, то ∆АОС – равнобедренный, и тогда углы при его основании будут одинаковы:
∠СОВ – внешний для ∆АОС. Напомним, что такой угол равен сумме тех 2 углов треуг-ка, которые с ним не смежны. В частности, в данном случае можно записать
∠СОВ = ∠OCA = ∠OAC = α + α = 2α
Но этот же угол – центральный, и его величина равна ⋃ВС:
Получается, что дуга вдвое больше вписанного угла.
Далее рассмотрим случай, когда диаметр, проведенный из вершины вписанного угла, делит его на две части:
В этом случае вписанный угол ∠СAВ можно представить как сумму углов ∠САD (обозначен как α)и ∠ВАD (обозначен как β). Мы уже доказали, что дуги, на которые опираются эти углы, вдвое больше самих углов:
Осталось рассмотреть третий случай, при котором обе стороны вписанного угла ∠ВАС лежат по одну сторону от диаметра:
Если здесь обозначить ∠САD как α, а ∠ВАD как β, то интересующий нас ∠СAВ можно представить как их разность:
Итак, во всех трех возможных случаях вписанный угол оказывается вдвое меньше дуги, на которую он опирается.
Задание. Найдите ∠ВАС на рисунке:
Задание. Найдите вписанный ∠AВС, сели прилегающие к нему дуги ⋃AВ и ⋃ВС равны 100° и 128°.
Решение. В сумме дуги ⋃АС, ⋃ВС и ⋃AВ образуют окруж-ть, поэтому их сумма составляет 360°. Тогда можно найти ⋃АС:
Задание. Найдите дугу ⋃SM на рисунке:
Решение. Сначала найдем дугу ⋃MN, она вдвое больше соответствующего ей вписанного угла:
⋃NM = 2*∠NSM = 2*35° = 70°
Заметим, что ⋃SN– это полуокружность, то есть она составляет 180°. При этом ⋃SM и ⋃MN вместе как раз образуют эту полуокружность, то есть их сумма также составляет 180°. Значит, ⋃МS можно найти, вычтя из полуокружности ⋃MN:
⋃MS = ⋃SN – ⋃MN = 180° – 70° = 110°
Заметим, что для одной дуги можно построить несколько вписанных углов. Каждый из них будет равен половине дуги, то есть все эти углы окажутся одинаковыми.
Задание. Найдите ∠АСD на рисунке:
Решение. Так как ∠ACD и ∠ABD опираются на одну дугу ⋃AD, то они должны быть одинаковыми:
∠ACD = ∠ABD = 63°
Задание. Докажите, что две дуги, находящиеся между двумя параллельными секущими окруж-ти, равны друг другу.
Нам надо доказать, что ⋃AВ и ⋃CD равны, если АС||BD. Проведем секущую ВС:
∠СВD и ∠АСВ равны, ведь они накрест лежащие. Получается, что ⋃AВ и ⋃CD являются основаниями равных вписанных углов. Отсюда вытекает, что эти дуги должны быть равными.
Напомним, что диаметр разбивает окруж-ть на две дуги по 180°. Отсюда можно сделать вывод – любой угол, опирающийся на полуокружность, должен составлять 180°:2 = 90°:
Задание. Диаметр окруж-ти AВ равен 17. Хорда ВС имеет длину 8. Какова длина хорды АС?
Так как ∠АСВ опирается на диаметр AВ, то он прямой. Значит, и ∆АСВ – прямоугольный, причем диаметр AВ в нем – гипотенуза. Неизвестный катет можно найти по теореме Пифагора:
Задание. Окруж-ть разбита на две дуги, ⋃AВС и ⋃СDA. Известно, что ∠AВС = 72°. Найдите ∠ADC.
Зная ∠AВС, мы легко найдем дугу ⋃ADC, она вдвое больше опирающегося на нее вписанного угла:
Углы между хордами и секущими
До этого мы рассматривали простые углы в окруж-ти, вершины которых лежали либо на самой окруж-ти, либо в ее центре. Однако иногда хорды и секущие пересекаются в другой точке, либо внутри, либо вне окруж-ти. Рассмотрим подобные задачи.
Более прост случай, когда необходимо найти угол между двумя пересекающимися хордами. Пусть хорды при пересечении образовали дуги ⋃AВ и ⋃СD величиной α и β. Каков угол между ними?
Проведем ещё одну хорду АD. В результате получим вписанные ∠САD и ∠ADB, которые будут равны половинам от соответствующих дуг, то есть α/2 и β/2. Интересующий нас ∠СPD оказывается внешним для ∆APD, и потому равен сумме двух углов в ∆APD (тех, которые с ним не смежны), то есть он составляет величину α/2 + β/2:
Величину α/2 + β/2 можно записать и иначе, вынеся множитель 1/2 за скобки:
Эту величину можно назвать полусуммой дуг, на которые опирается интересующий нас угол.
Задание. Найдите ∠МКВ на рисунке:
Решение. Интересующий нас угол опирается на хорды величиной 38° и 42°. Значит, он равен половине от их суммы:
∠MKB = (42° + 38°)/2 = 80°/2 = 40°
В более сложном случае необходимо найти угол между секущими, которые пересекаются вне окруж-ти. При этом известны дуги, образованные этими секущими:
Снова проведем хорду АD, чтобы у нас получились два вписанных угла, ∠ADB и ∠СAD, которые соответственно будут иметь величину β/2 и α/2:
Теперь уже ∠САD оказывается внешним для ∆ADK, а потому он является суммой двух других углов:
В итоге получили, что угол между секущими составляет половину от разности дуг, которые они отсекают от окруж-ти.
Задание. Найдите на рисунке величину∠К, если ⋃AВ и ⋃СD соответственно равны 42° и 130°:
Решение. В этой задаче просто используем доказанную теорему об углах между секущими. Искомый угол составляет половину от разности дуг, заключенных между секущими:
∠K = (130° – 42°):2 = 88°/2 = 44°
Теорема о произведении отрезков хорд
Можно заметить, что при пересечении двух хорд образуется пара подобных треугольников. Пусть хорды ADи ВС пересекаются в точке K. Добавим хорды AВ и СD и получим ∆AВК и ∆КСD:
На дугу ⋃BD опираются вписанные углы∠А и ∠С, значит, они одинаковы. Также на одну дугу АС опираются ∠D и∠В, поэтому и они одинаково. Равенство двух углов уже означает, что треугольники подобны по первому признаку подобия (дополнительно можно заметить, что ∠АКВ и ∠СКD равны как вертикальные углы).
Из подобия ∆AВК и ∆СКD вытекает пропорция между их сторонами:
Перемножив члены пропорции крест накрест, получим соотношение:
В результате нам удалось доказать следующее утверждение:
Задание. Хорды AВ и CD пересекаются в точке М. Известны, что АМ = 9, МВ = 3, МС = 2. Какова длина отрезка МD?
Хорда AВ разбивается на отрезки АМ и МВ, а хорда CD – на отрезки СМ и МD. Произведения этих отрезков одинаковы:
Подставим в это равенство известные величины
Рассмотрим ещё одну геометрическую конструкцию. Пусть из некоторой точки А к окруж-ти проведена как касательная к окружности АК, так и секущая, пересекающая окруж-ть в точках В и С:
Какие здесь есть взаимосвязи между углами и длинами отрезков? Для начала проведем хорды ВК и СК, а также радиусы ОК и ОВ. Обозначим буквой α угол ∠ВСК. Он вписанный, поэтому дуга, на которую он опирается (это ⋃ВК), вдвое больше и равна 2α. Тогда и центральный угол ∠ВОК также составляет 2α:
Теперь исследуем ∆ВОК. Он равнобедренный (ВО и ОК – одинаковые радиусы), поэтому углы при его основании совпадают:
Итак, углы при основании ∆ОВК, в частности ∠ОКВ, равны 90° – α. Заметим, что ∠ОКА – прямой, так как образован радиусом ОК и касательной АК, при этом он состоит из двух углов, ∠АКВ и ∠ВКО. Это позволяет найти ∠АКВ:
В результате мы получили важный промежуточный результат – угол между касательной и хордой, проведенной из точки касания, вдвое меньше образующейся при этом дуги.
Вернемся к картинке с секущей. Изначально как α мы обозначили ∠ВСК, но в результате получили, что и ∠АКВ = α.
Рассмотрим ∆AВК и ∆САК. У них есть общий∠А, а также одинаковые ∠AКВ и ∠ВСК, которые отмечены буквой α. Значит, ∆AВК и ∆САК подобны, поэтому мы имеем право записать пропорцию между его сторонами:
Здесь отрезок АС можно назвать секущей, а AВ – ее внешней частью. Тогда выведенное отношение можно сформулировать так:
Решение. Сначала находим длину всей секущей, пользуясь доказанной теоремой:
Решение. Проведем из точки А ещё и касательную АК к окруж-ти:
Величину квадрата касательной АК можно найти, используя секущую АС. Сначала вычислим длину АС:
Задачи на квадратной решетке
Рассмотрим несколько несложных задач, часто встречающихся на экзаменах.
Задание. Найдите ∠AВС на рисунке:
Решение. Здесь следует заметить, что расстояние между А и С составляет 8 клеток, при этом в окруж-ть как раз можно вписать квадрат со стороной 8.
Такой квадрат разобьет окруж-ть на 4 дуги, причем так как эти дуги опираются на хорды одинаковой длины, то они и сами равны. Вся окруж-ть составляет 360°, значит, каждая из этих дуг составляет 360°:4 = 90°. ∠AВС – вписанный, то есть он составляет половину дуги, на которую он опирается, а это⋃АС, равная 90°. Тогда
Задание. Найдите ∠AВС, используя рисунок:
Решение. Используя рассуждения из предыдущей задачи, легко определить, что∠А составляет 45°.При этом ∆AВС – равнобедренный, и ВС – его основание. Это следует хотя бы из того факта, что высота АН делит сторону ВН пополам.
Углы∠В и ∠С одинаковы, так как лежат при основании равнобедренного треуг-ка. Найдем их, используя тот факт, что все 3 угла в ∆AВС составляют в сумме 180°:
Задание. Вычислите ∠AВС:
Решение. Снова в окруж-ть можно вписать квадрат со стороной 8 клеток. Из этого следует что ⋃АВС составляет 90° (показана фиолетовым цветом):
Но ∠АВС опирается на синюю дугу. Так как вместе фиолетовая и синяя дуга составляют окружность, равную 360°, то синяя дуга должна быть равна 360° – 90° = 270°. ∠АВС как вписанный будет вдвое меньше, то есть он равен 270°:2 = 135°.
Задание. Чему равен ∠AВС на рисунке?
Если вписать в окруж-ть квадрат то он разобьет окруж-ти на дуги по 90°. В свою очередь точка А является серединой такой дуги, то есть она разбивает ее на две дуги по 45°.
∠AВС как вписанный будет вдвое меньше, то есть он равен 22,5°.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly
http://100urokov.ru/predmety/urok-10-ugly-v-okruzhnosti
[/spoiler]
Основные понятия. Тригонометрия довольно древняя наука, и ее первые упоминания связаны с необходимостью в практичной жизни, в земледелии, астрономии и строительстве. Впервые именно астрономы вывели такие понятия как отношение сторон треугольника. А официальные названия функций стали появляться позже, например, синус, который получил свое название первым, получил свое название от греческих математиков уже в третьем веке до н.э.. а косинус является относительно молодым, и был выведен как дополнение к синусу. История тригонометрии обширна и интересна, из древней науки о треугольниках она перешла в известную нам науку о тригонометрических функциях. Для того чтобы разобраться в формулах двойного угла, необходимо вспомнить основные понятия тригонометрии. Начнём:
Тригонометрические функции:
- Синус угла — отношение катета напротив угла к гипотенузе:
- Косинус — деление прилежащей стороны треугольника на гипотенузу;
- Тангенс — отношение синуса к косинусу или катета напротив угла к прилежащему;
- Котангенс — деление косинуса на синус, или стороны прилежащей к углу на противолежащую.
Определение
Тригонометрическая окружность — это окружность нанесённая на систему координат, имеющая радиус равный единице и центр в начале координат.
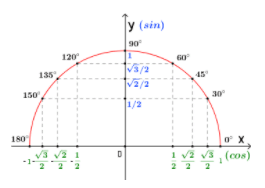
При помощи такой окружность можно наглядно разобраться в тригонометрических формулах и значениях. Например, найти числовые значения функций тригонометрии на системе координат, такие как:
[
sin 60^{circ}=frac{sqrt{3}}{2}
];
[
sin 30^{circ}=frac{1}{2}
]
Данные примеры будут использоваться далее по тексту. Мы можем посмотреть их значение на окружности на рисунке ниже.
Основное тождество в тригонометрии, звучит так:
- Синус в квадрате угла плюс косинус в квадрате угла равны единице;
- Произведение тангенса и котангенса угла равно единице;
- Тангенс угла равен, делению, синуса этого угла на косинус, а котангенс наоборот косинуса на синус.
Данные тождества также будут применены для выведения формул двойного, тройного и т.д. углов.
Формулы двойного угла в тригонометрии
Формулы двойного угла тригонометрических функций, необходимы для того чтобы выразить их, при этом угол должен иметь значение 2а, а также используя ТФ этого угла. Для отражения её на графике используют координаты с окружностью.
Список формул двойного угла
Прежде чем преступить к образованию формул двойного угла тригонометрии, давайте вспомним, что в тригонометрии углы принято писать в виде na, в такой записи п — обозначение натурального числа, а а — угол альфа. Обычно такая запись в тригонометрии используется без скобок, значит sin an, это тоже самое что sin (an). А также если рассмотреть запись sinn a, то она тоже имеет аналогичную запись вида (sin а)n . такое правило записи касается всех тригонометрических функций со степенями.
Рассмотрим какие же формулы двойного угла существуют на примерах.
Синус двойного угла формула:
sin 2 α = 2 * sin α * cos α;
Формула косинуса двойного угла:
cos 2 α = cos2α — sin2α, cos 2α = 1 − 2 * sin2α , cos 2α = 2 * cos2α−1;
Тангенс двойного угла формула:
[
operatorname{tg} 2 alpha=frac{2^{*} operatorname{tg} alpha}{1-operatorname{tg}^{2} alpha}
]
Котангенса:
[
operatorname{ctg} 2 alpha=frac{operatorname{ct}^{2} a-1}{2^{*} operatorname{ct} a}
]
Стоит не забывать, что выше приведённые формулы sin и cos, можно применять для любого значения угла. А вот если рассмотреть, формулы для тангенса, то при любых альфа где, tg 2a , имеет смысл, то есть при [a neq frac{pi}{4}+frac{pi}{2} cdot z], где z любое целое число. Что же касается формулы двойного угла котангенса, то при любом a, где ctg 2α определён на α ≠ 2 * z .
Как мы видим косинус с таким видом угла, наделён тремя вариантами записи формул, все они равноправны, а это значит, что результат их применения будет абсолютно одинаковым.
Доказательство формул двойного угла
Для того чтобы, формулы двойного угла были доказаны, вернёмся к истокам, формулам сложения. Сначала рассмотрим формулу синуса суммы, которая выглядит следующим образом:
[
operatorname{Sin}(a+b)=operatorname{Sin} a * cos b+cos a * sin b
]
Косинуса суммы:
[
operatorname{Cos}(a+b)=cos a * cos b-sin a * sin b
]
Если считать что a = b, тогда выходит:
[
operatorname{Sin}(a+a)=sin a * cos a+cos a * sin a=2 * cos a * sin a
]
И также для косинуса:
[
cos (a+a)=cos a * cos a-sin a * sin a=cos ^{2} alpha-sin ^{2} alpha
]
Таким способом мы доказали формулы синуса и косинуса двойного угла.
Формулы которые остались: cos 2α = 1 − 2 * sin2α , cos 2α = 2 * cos2α−1, выразили в таком виде благодаря приведению вместо единицы тождества суммы квадратов, cos2α +sin2α = 1. Поэтому вышло следующее:
Формулы приведения двойного угла: 1 − 2 * sin2α = cos2α +sin2α — 2 * sin2α = cos2α — sin2α.
И так же с третьих примеров формулы двойного угла.
2 * cos2α−1 = 2 * cos2α -( cos2α +sin2α ) = cos2α — sin2α.
Для того, чтобы выполнить доказательство формул для тангенса и котангенса двойного угла тоже применяется равенство следующего вида:
[
operatorname{tg} 2 alpha=frac{sin 2 alpha}{cos 2 alpha} text { и } operatorname{ctg} 2 alpha=frac{cos 2 alpha}{sin 2 alpha} .
]
Сделав замену на данные равенства получим следующие выражения:
[
operatorname{tg} 2 alpha=frac{sin 2 alpha}{cos 2 alpha}=frac{2 cdot sin alpha cdot cos alpha}{cos ^{2} alpha-sin ^{2} alpha} text { и } operatorname{ctg} 2 alpha=frac{cos 2 alpha}{sin 2 alpha}=frac{cos ^{2} alpha-sin ^{2} alpha}{2 cdot sin alpha cdot cos alpha}
]
Представленные выше выражения мы разделим на cos2α, при котором cos2α ≠ 0, а альфа имеет любое значение, когда тангенс угла альфа определён. Со вторым представленным выражением мы также произведём деление, только на sin2α, и он так же не равен нулю, и альфа имеет любое значение, при котором котангенс имеет смысл.
Получим следующие формулы:
Нет времени решать самому?
Наши эксперты помогут!
Как использовать формулы двойного угла
Рассмотрим, как применяются формулы двойного угла в решении на примерах. Такие примеры помогут закрепить и понять материалы рассмотренный ранее.
Чтобы проверить справедлива ли формула двойного угла для при значении угла альфа в тридцать градусов, необходимо применить функции тригонометрии для этих углов. Если α = 30°, тогда 2α = 60°.
Проверим: sin60° = 2 * sin30° * cos30°cos60° = cos230° — sin230°.
Следующим шагом, подставим эти значения в :
[
operatorname{tg} 60^{circ}=frac{2 cdot operatorname{tg} 30^{circ}}{1-operatorname{tg}^{2} 30^{circ}} text { и } operatorname{ctg} 60^{circ}=frac{operatorname{ctg}^{2} 30^{circ}-1}{2 cdot operatorname{ctg} 30^{circ}}
]
Так как мы знаем, что синус тридцати градусов равен одной второй, косинус этого угла, равен корню из трёх, который поделен на два, тангенс заданного угла это корень из трёх на три, котангенс корень из трёх.
Получается, что синус двойного угла, то есть шестидесяти градусов, равен корню из трёх, который поделен на два; косинус — одной второй; тангенс корню из трёх; а котангенс корню из трёх делённому на три.
Получаем следующие выражения:
Сделав все операции по вычислению, можно прийти к выводу, что справедливость для угла альфа тридцати градусов, подтверждена.
Теперь мы понимаем, что применение формул тригонометрии двойного угла, это видоизменение тригонометрических выражений. Стоит также рассмотреть пример применения формул двойного угла, в случае, когда угол не равен 2a. К примеру возьмём значение [frac{5 pi}{6}]. Имея такое значение, для решения задания, его необходимо преобразовать, поэтому получаем следующее:
[a=frac{5 pi}{6}: 2=frac{5 pi}{12}], применив данное выражение формула двойного угла для косинуса получит следующий вид:
[
cos frac{5 pi}{6}=cos ^{2} frac{5 pi}{12}-sin ^{2} frac{5 pi}{12}
]
Пример:
Необходимо, через тригонометрические функции представить [sin frac{2 a}{3} text { при } frac{a}{6}].
Решение:
Так как в условии уже [frac{2 a}{3}=4 * frac{a}{6}], то применив дважды выше обозначенную формулу удвоенного угла, что выражая [sin frac{2 a}{3}], через функции угла [frac{a}{6}], с применением формулы двойного угла, выходит , [sin frac{2 a}{3}=2 * sin frac{a}{3} * cos frac{a}{3}], затем к [sin frac{a}{3} text { и } cos frac{a}{3}]в данном примере подставим снова данную формулу удвоенного угла и получим следующее выражение:
Формулы тройного угла и более углов
Так как зачастую в тригонометрии возникает необходимость вычисления не только двойного угла, но и больше, например тройного, четверного и тд. Стоит рассмотреть примеры их вычисления. Выведение их формул аналогично с выведением формул двойного угла, но для этого будем применять формулы сложения (суммы) двойного угла.
Пример:
sin 3α = sin ( 2 α + α ) = sin 2α * cos α + cos 2 α * sin α = 2 * sin α ⋅ cos α * cos α + ( cos2α — sin2α ) * sin α =
=3 * sin α * cos2α — sin3α
Заменим cos2α, на выражение 1 — sin2α, и теперь получившаяся ранее формула тройного угла sin 3α =3 * sin α * cos2α — sin3α, примет следующий вид: sin 3α = 3 * sin α * cos2α — sin3α = 3 *sin α — 4* sin3α
Аналогично поступим и с формулами cos тройного угла:
cos 3α = cos ( 2 α + α ) = cos 2α * cos α − sin 2α *sin α = ( cos2α — sin2α ) * cos α − 2* sin α * cos α * sin α =
= cos3α − 3* sin2α * cos α
Заменяем sin2α на выражение разности единицы и косинуса, 1 — cos2α, выходит следующая формула : cos 3α =
= -3 * cos α + 4* cos3α
Так как теперь у нас есть формулы тройного угла синуса и косинуса, мы можем вывести формулы тройного угла для тангенса и котангенса, подставив полученные выражения в первичные формулы:
И так далее…
К примеру, чтобы привести формулу угла четыре альфа, для удобства лучше 4а представить, как 2 * 2а, и в результате мы получим, что для выведения формулы для 4а, нужно использовать две формулы двойного угла.
А для выведения формулы угла пятой степени, 5а, необходимо выполнить 5а как сумму тройного и двойного угла, то есть 2а+3а.
В результате мы получим выражение из суммы двух формул двойного и тройного угла. Стоит отметить, что такое же правило будет действовать если необходимо вывести формулу половинного угла.
Область применения
Для того чтобы найти значение тригонометрических функций, берётся окружность на оси координат, у которой радиус равен единице, а диаметры у неё находятся в перпендикулярном положении.
Для такого вычисления нам понадобится отложить от точки, которая принадлежит окружности различные дуги, любой длины. Соответственно если мы отложим их против часовой стрелки они примут положительное значение, а если по часовой, то отрицательное.
Допустим конец дуги имеет некую длину s, в таком случае проекция радиуса в любом выбранном значении диаметра станет значением косинуса данной дуги. Выбранная длина s, или радианная мера угла, будет считаться числом аргумента. А если этот самый аргумент, это тригонометрическая функция угла, то мы знаем, что значение может быть и в градусах.
Мы знаем, что острый угол имеет значения больше нуля, но меньше п2. В таком случае тригонометрическая функция рассматривается как катет делённый на гипотенузу. Такие названия сторон связаны с прямоугольным треугольником, в котором величина угла равна 90 градусов.
Чтобы решить задачи с функциями тригонометрии, используют теорему Пифагора. Такая теорема основана на свойствах того самого прямоугольного треугольника, в котором квадрат гипотенузы равен сумму квадратов катетов.
Так как дуга делит окружность на несколько частей, то мы можем увидеть, что углы лежащие в первой четверти больше нуля. А во второй синус меньше, а косинус больше нуля, а в третьей все функции будут меньше нуля, то есть отрицательными, четвёртая имеет значения противоположные второй. Не стоит забывать, что для построения окружности вам понадобится циркуль.
Как мы видим формулы двойного угла, не так трудно вывести, для этого необходимо знать основные тригонометрические тождества и разобраться в единичной окружности на оси координат. Также необходимо отметить, что формулы двойного угла, как и другие формулы тригонометрии используются в разных сферах жизни:
- В астрономии, учёные с помощью формул вычисляют положение небесных тел, а также расстояние до них;
- Для различного вида навигации, к примеру, морской и воздушной;
- В медицине и биологии, при построении биоритма живых организмов, а также тригонометрия служит основой работы некоторой медицинской техники;
- Архитекторам она важна при создании планов строений;
- но и это не всё, тригонометрия важна и для экономики, в производстве и создании электроники, в различных аналитических вычислениях, акустических построениях и многом другом.