Как найти альфа геодезия

 Актуальные цены на услуги геодезистов в Москве и Московской области  в 2022 году.

Решение обратной геодезической задачи онлайн

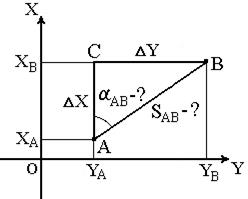
Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB  и  дирекционный угол α_AB

Ниже представлена форма в которую можно ввести исходные значения и получить искомые данные. Это простое решение, которым может воспользоваться любой кому лень разбираться с формулами.

Если же говорить о сути решения задачи, то обратная геодезическая задача решается следующим образом.

Сначала находим приращения координат:

 ΔX = X_B – X_A ;

 ΔY = Y_B – Y_A .

Величину угла r_AB определяем из отношения

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB.

Для контроля расстояние S_AB дважды вычисляют по формулам:

Решение обратной геодезической задачи

Целью решения обратной геодезической задачи является вычисление длины линии и дирекционного угла линии по известным координатам её конечных точек. Т.е. при известных координатах точек А(X_A, Y_A) и В(X_B, Y_B) необходимо найти длину S_AB и направление линии АВ: осевой румб r_AB и дирекционный угол a_AB (рис. 10).

Координаты точекА(X_A, Y_A) и В(X_B, Y_B) определяют при решении предыдущей задачи (см. п.1.4.2).

Данная задача решается следующим образом.

Сначала находим приращения координат

Рис. 10. Обратная геодезическая задача

Величину осевого румба r_AB определяем из отношения

.

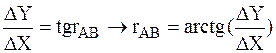По знакам приращений координат определяем четверть, в которой располагается румб, и её название (см. табл.1).

Знаки приращений координат ΔX и ΔY

Приращения координат	Четверть окружности, в которую направлена линия
I (СВ)	II (ЮВ)	III (ЮЗ)	IV (СЗ)
ΔX	+	–	–	+
ΔY	+	+	–	–

Используя зависимость между дирекционными углами и осевыми румбами (рис. 11), находим a_AB.

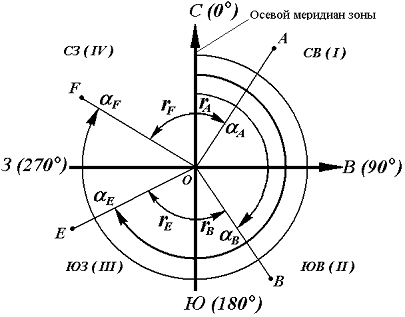
Рис. 11. Осевые румбы и дирекционные углы

Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:

I четверть (СВ) r = a ,

II четверть (ЮВ) r = 180° – a ,

III четверть (ЮЗ) r = a – 180° ,

IV четверть (СЗ) r = 360° – a .

Расстояние S_AB определяем по формуле

.

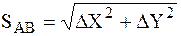Для контроля расстояние S_AB вычисляют дважды по формулам:

,

.

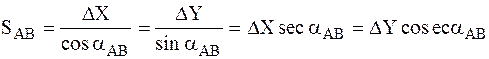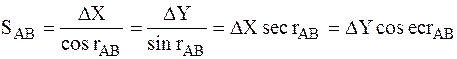Пример.Координаты точек:А(5998.650 км, 2396.750 км);

В(6000.150 км, 2395.250 км).

Вычисляем осевой румб r_AB из отношения

,

.

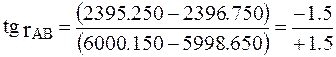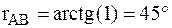По знакам приращений координат ΔX>0 и ΔY

Лучшие изречения:

Начинайте делать все, что вы можете сделать – и даже то, о чем можете хотя бы мечтать. В смелости гений, сила и магия. © Иоганн Вольфганг Гете
==> читать все изречения. 175 — | 164 —

Источник

Решение обратной геодезической задачи

Основой решения является расчетная схема рис.1.5.

1. Выписать исходную информацию (расчетная схема соответствует рис.1.10).

2. Вычислить приращения координат по формулам (1.6).

3. На микрокалькуляторе вычислить румб и длину линии по формулам (1.7)-(1.8).

4. По знакам приращений определить название румба в соответствии с рис.1.6.

5. От румба перейти к дирекционному углу по формулам связи (рис.1.4).

6. Сравнить вычисленные значения с измеренными. Расхождения не должны превышать 2 мм в длине линии и 1 0 в дирекционном угле.

Задача решается на микрокалькуляторе. Но при этом непосредственно определить угол  по формуле:=arc tg(у/х), вытекающей из уравнений (1.4), невозможно из-за неоднозначного решения задачи. Так прих отрицательном,у положительном их положительном,у отрицательном получим одинаковые значения. Для контроля вычисления можно выполнить через радианы. Связь между градусами и радианами:

r рад =r 0 / 57.29578 ;r 0 =r рад 57.29578. (1.10)

2. Приращения координат: x=X_B -X_A=6064410 — 6065675 = -1265 м,y=У_В— У_А= -188318–(- 188030) = — 288 м.

3. Румб линии через градусы, установив программу DEG:

/r/ = arc tg ( Δу / Δх )=”288” : ” 1265” = ”2ndF» tg -1 ” = 12.826 0 = 12 0 50′ .

Длина линии (программа DEG):

d=x/Cosr=“12.826“Cos”2ndF“1/x”×”1265”=1297 м. Второе вычисление:d=y/Sinr=“12.826“Sin”2ndF“1/x”×”288” = 1297 м. Расхождений в вычислениях не должно быть.

4. В соответствии со знаками приращений румб r = ЮЗ:12 0 50′.

5. Дирекционный угол = 192 0 50′.

6. Расхождение в длине линии 3 м, в румбе 10′. Расхождения допустимы.

Пример вычисления румба через радианы. Программа RAD:

arctg(Δу/Δх )=”288”:”1265“=“2ndF»tg -1 ”=»×»57.2958″=12.826 0 =12 0 50′.

Вычисления следует выполнять по разным формулам. Так, решение прямой задачи выполняется через дирекционные углы по формулам (1.4) и через румбы по формулам (1.5), кроме первой четверти. В северо-восточной части r= , контроля не будет. В этом случае, как и при решении обратной задачи, вычисления следует вести через градусы и через радианы.

Определение отметок точек

Отметки точек определяют по правилам, см. фрагмент листа карты (рис.1.1).

1. Точка лежит на горизонтали. Отметка точки равна отметке горизонтали: Н₁=152.5 м.

2. Точка лежит между разноименными горизонталями. Отметка точки определяется графической интерполяцией на глаз: Н₂=150+2.5/3=150.8 м.

3. Седловина. Отметка точки равна отметке ближней горизонтали ± полсечения рельефа: Н₃=152.5+h/2=153.8 м или 155 – h/2 = 153.8 м.

4. Определяемая точка лежит между горизонталью и точкой с подписанной на карте отметкой. Отметка определяется графической интерполяцией: Н₄=155+(156.9–155)/2=155.7 м.

5. Точка лежит на полугоризонтали: Н₅ = 155 +h/ 2 = 156.2 м.

6 и 7. Отметки вершин: H₆ =155 +h/ 2 = 156.2 м;H₇ = 156.25 (полугоризонталь)+h/4=156.8 м.

Источник

Обратная геодезическая задача.

Обратная геодезическая задача (ОГЗ) на плоскости заключается в нахождении дирекционного угла α направления с одной точки на другую и расстояния Дмежду ними по прямоугольным координатам данных точек.

Из рисунка 24 и формулировки обратной геодезической задачи известны:

α – дирекционный угол направления с точки А на точку В;

Д – расстояние (дальность) между точками А и В.

В прямоугольном треугольнике АСВ катеты АС и СВ соответствуют приращениям координат:

Таким образом, в прямоугольном треугольнике АСВизвестны два катета, по которым можно определить все его остальные элементы: острый уголСАВ, равный дирекционному углуα, и гипотенузуД(дальность).

Обратная геодезическая задача решается теми же способами и средствами, что и прямая геодезическая задача.

Огз решают в следующей последовательности:

Пусть в точке А находится огневая позиция (ОП), а в точке В – цель (Ц).

1. По известным координатам ОП и цели вычисляют приращения координат ΔХ и ΔY:

(58)

2. Определить острый угол α´(рис. 22) по формуле:

(59)

От угла α´перейти к дирекционному углуα в соответствии со знаками приращений ΔX и ΔY, согласно схеме (рис. 23), или по таблице:

Источник

Тема 3. Прямая и обратная геодезическая задача.

При производстве строительных работ создается разбивочная основа в виде строительной сетки. Пункт Государственной геодезической сети выносится на территорию строительства для обеспечения исходными данными всех геодезических работ. Решение прямой геодезической задачи позволяет определить координаты всех точек, расположенных в зоне строительства.

В геодезии принята система плос­ких прямоугольных координат, в которой относительно оси XX , совпадающей с направлением меридиана, и оси YY , перпендику­лярной к оси XX , определяют положение каждой точки, т. е. её координаты х и у; при этом счет четвертей идет по ходу часовой стрелки, согласно возрастанию азимутов и дирекционных углов .

При составлении планов ситуацию накладывают от опорных точек и линий, их соединяющих. Поэтому на бумагу сначала на­носят опорные точки по их координатам. Так как число этих точек весьма велико, то при геодезических работах часто решают прямую задачу на координаты. Она состоит в том, что по извест­ным координатам данной точки, а также дирекционному углу и горизонтальному проложению линии от этой точки до определяе­мой вычисляют координаты определяемой точки.

Решить прямую геодезическую задачу, т.е Пример

определить прямоугольные координаты точки 2 через координаты точки 1 по следующим данным:

Кординаты точки 1 — X, = 4250 м. У,=6730 м;

Расстояние между точками d =120,10 м; направление линии, т.е дирекционный угол 48°30′ =r.

Для определения координат точки 2 сначала нужно найти приращение координат –ΔХ и ΔУ,затем сами координаты Х₂;У_{2 .}

1.Определяем приращение координат ΔХ =d . cosr = 120,10 . 0,6626 =79,51 м

ΔУ= d . sinr =12,10 . 0,7490 =89,95 м

ΔУ

х₂ 2

r d

х₁ 1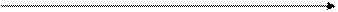

2. Определяем координаты точки 2

В практике прикладной геодезии для нужд проектирования и выноса проекта на местность приходиться определять значения дирекционного угла и длинны стороны по известным координатам её конечных точек. Это и составляет сущность решения обратной геодезической задачи.

Решение обратной геодезической задачи состоит в том, что, зная координаты опорных точек, можно вычислить дирекционный угол и расстояние между данными точками.

Пример.

Решить обратную геодезическую задачу, т.е. найти расстояниеd между точками и направление этой линии ( румб, азимут), если координаты точки1 Х₁= 320,5 м, У₁ = 780,2 м; координаты т очки 2 Х₂= 230,7 м, У₂ =900,1 м.

1. Определяем приращение координатΔХ = Х₂-Х₁ = 230,7 -320,5 = -89,8 м

ΔХ = У₂ –У₁ =900,1 – 780,2 = 119,9 м

Знаки приращений говорят, что линия расположена во второй четверти (ЮВ)

Знаки приращения координат можно определить по следующей схеме:

СЗ С х

З +ΔХ — ΔУ +ΔХ + ΔУ В

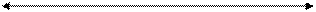
у -ΔХ — ΔУ -ΔХ + ΔУ у

Они зависят от четверти, в которой расположена линия.

2. Величина румба определяется по формуле

tg r= 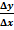= = 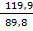1, 3352

ctgr = 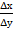= = 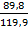0,74,89

По таблицам Брадиса находим величину румба — 53⁰ 10ʹ

3. Расстояние между точками найдем по теореме Пифагора:

d= 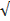ΔХ 2 + ΔУ 2 = 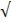89,8 2 + 119,9 2 = 22440,05 = 149,8 м

Контрольные вопросы:

1. Какие знаки у приращения координат ΔХ и ΔУ, если наименование румба ЮЗ?

а) –ΔХ, –ΔУ; б)+ ΔХ, +ΔУ; в)–ΔХ,+ΔУ; г))+ ΔХ,–ΔУ;

2. Найдите координаты точки 2, если координаты точки 1 Х= 10, У=5 и приращение ΔХ = 20, ΔУ =15.

а) 30, 20; б) 20, 30; в) 20, 40; г) 30, 40;

3. Решить обратную геодезическую задачу: найти расстояние между двумя точками и румб линии, если координаты начала и конца линии Х₁= 320,5 м, У₁ = 780,2 м; Х₂ 230,7 м,

а); 160,7 м, 60⁰ 20ʹ; б)149,8 м, 53⁰ 10ʹ; в) 120, 9 м, 58⁰ 45ʹ; г) 456,7м, 45⁰ 15ʹ;

4. Решить прямую геодезическую задачу: определить прямоугольные координаты точки 2 через координаты точки 1 по следующим данным: Х₁ = 4250м, У₁= 6730м, расстояние d – 120, 1 м, дирекционный угол — 48⁰30ʹ.

Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»

Азимут лини находится в пределах 90°-180 каково градусное значение румба?

Каково название румба линии и его величина , если азимут её определён по формуле А°-З60-r°

№	Вопросы (задания)	Ответы	Код
I	Осевого меридиана зоны	1
Ближайшего направления меридиана	2
Южного направления магнитного меридиана	3
Северного направления географического меридиана	4
II	Азимут лини находиться в пределах от 180°-270°	Сз	1
каково наименование румба?	Юв	2
Юз	3
Св	4
III	r°=А°	1
r°=180°-А°	2
r°=А°-180°	3
r°=360°-А°	4
IV	каково градусное значение азимута (А°) линии для ЮВ:r	А°=180°+r°	1
А о =360°-r°	2
А°=180°-r°	3
А°=r°	4
V	Сз:r°	1
Юз:r°	2
Юв:r°	3
Св:r°	4

Азимут лини находится в пределах 270°-360° каково градусное значение румба?

Каково название румба линии и его величина, если азимут её определён по формуле А°- 180°+r°

№	Вопросы (задания)	Ответы	Код
I	Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»	Северного направления географического меридиана	1
Осевого меридиана зоны	2
Южного	3
направления магнитного
меридиана
Ближайшего	4
направления меридиана
И	Азимут лини находиться в пределах от 0°-90° каково наименование румба?	Сз	1
Юв	2
Юз	3
Св	4
III	r°=А°	1
r°=180°-А°	2
r°=А°-180°	3
r°=360°-А°	4
IV	каково градусное значение азимута (А°) линии для Юз:ч°	А°=180°-r°	1
А°-360°-r°	2
A°=180W	3
А°=r°	4
V	Сз:r°	1
Юз:r°	2
Юв:r°	3
Св:r°	4

Азимут лини находится в пределах 180°-270° каково градусное значение румба?

Каково название румба линии и его величина , если азимут её определён по формуле А°-360°-r°

Источник

Adblock
detector

№	Вопросы (задания)	Ответы	Код
I	Какие слова нужно вставить в место точек в определении «Дирекционным углом лини называют угол, отсчитанный от. до данной прямой по направлению часовой стрелки?»	Северного направления географического меридиана	1
Южного
направления магнитного	2
меридиана
Ближайшего
направления меридиана	3
Осевого	4
меридиана зоны
И	Азимут лини находиться в пределах 90°-180 каково	Сз	8
наименование румба?	Юв	9
Юз	1
Св	2
III	r°=А°	3
r°=180°-А°	4
r°=А°-180°	5
r°=360°-А°	6
IV	каково градусное значение азимута (А°) линии для румба св: r°	А°=180°-r°	7
А°=360°-r°	8
А°=180°+r°	9
А°=r°	1
V

Обратная геодезическая задача.

Обратная
геодезическая задача (ОГЗ) на плоскости
заключается в нахождении дирекционного
угла α
направления
с одной точки на другую и расстояния Дмежду ними по
прямоугольным координатам данных точек.

Из
рисунка 24 и формулировки обратной
геодезической задачи известны:

X_А,Y_А;
X_В,Y_В
– прямоугольные координаты точек А
и В.

Требуется определить:

α –
дирекционный угол направления с точки
А на точку В;

Д –
расстояние (дальность) между точками
А и В.

В
прямоугольном треугольнике АСВ
катеты АС
и СВ
соответствуют приращениям координат:

АС
= ΔХ ; СВ =
ΔY;

Таким
образом, в прямоугольном треугольнике
АСВизвестны два катета, по которым
можно определить все его остальные
элементы: острый уголСАВ, равный
дирекционному углуα, и гипотенузуД(дальность).

Обратная
геодезическая задача решается теми же
способами и средствами, что и прямая
геодезическая задача.

Огз решают в следующей последовательности:

Пусть
в точке А
находится огневая позиция (ОП), а в точке
В –
цель (Ц).

1.
По известным координатам ОП и цели
вычисляют приращения координат ΔХ и
ΔY:

(58)

2.
Определить острый угол α´(рис.
22) по формуле:

(59)

1. От
   угла α´перейти к дирекционному
   углуα в соответствии со знаками
   приращений ΔX и ΔY, согласно
   схеме (рис. 23), или по таблице:

I четверть	ΔХ + ΔY +	 = 
II четверть	ΔХ – ΔY +	 = 30-00 – //
III четверть	ΔХ – ΔY –	 = 30-00 + //
IV четверть	ΔХ + ΔY –	 = 60-00 – //

1. Вычислить
   расстояние между ОП и Ц (из теор. Пифагора)
   по формуле:

(60)

Пример
1.

По
прямоугольным координатам огневой
позиции X_ОП
=
79 790, Y_ОП
=
16 350 и цели X_Ц
=
82 145, Y_Ц
=
17 610 вычислить дирекционный угол α
с ОП на Ц и расстояние между ними Д.

Р е ш е н и е:

1. Вычислить
   приращения координат: Х
   = 82 145 – 79 790 = + 2355;

 =
17 610 –16 350 = +1260;

1. Вычислить
   дирекционный угол α:

4-69;

1. Если
   знаки приращений координат Х+,
   +
   : значит I
   четверть, 
   = ,

дирекционный
угол будет 
= 4-69;

1. Вычислить
   расстояние
   

О
т в е т: 
= 4-69;

Д
= 2671 м.

Решение ОГЗ на микрокалькуляторе с помощью кнопок а и в: Проверим правильность решения примера 1. Вычислить приращения координат: Х = 82 145 – 79 790 = + 2355;  а = 17 610 –16 350 = +1260; Набрать приращение Х: + 2355 и нажать ; Н в абрать приращениеY: + 1260 и нажать ; Н а 2пdF ажать кнопки высветится расстояние Д: 2670,884… 2671 м (записать); Н в ажать кнопку высветится угол : 28,1481… 28,148 6 = 4,6913…= 4-69 (записать); Преобразовать угол  в соответствующую четверть. Калькулятор выдает для I и II четверти (от 0-00 до 30-00) угол с положительным знаком. В этом случае полученный результат соответствует дирекционному углу:  = . Для III и IV четверти (от 30-00 до 60-00) результат высветится с отрицательным знаком. Дирекционный угол в этом случае будет:  = (– )+360 или  = (– )+ 60-00. Дирекционный угол будет:  = 4-69; О т в е т:  = 4-69; Д = 2671 м.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  25.03.2016578.05 Кб37Uch_met_po_proizv_praktike.doc

• #
• #
• #
• #
• #
• #

Засечкой называют относительно простой метод вычисления координат некоторой точки посредством измерения на ней углов и расстояний по направлению на уже закрепленные на местности контуры.

К ней достаточно часто прибегают в различных геологических, строительных и инженерных работах за счет ее простоты и экономичности. На практике обратная засечка чаще всего используются для вычисления координат пунктов геодезической сети, выноса в натуру проектных точек и т.д.

Опытный геодезист сможет без труда провести нужные измерения при помощи теодолита, тахеометра или любого другого прибора всего за пару минут.

Виды засечек

В зависимости от местности и способов построения сетей сгущения в геодезии существует два основных вида привязки к опорным пунктам:

1. Непосредственная. Подразумевает привязку теодолитного или полигонометрического хода к триангуляционным пунктам высшего класса с возможностью выполнить измерения примычных углов. Используется в тех случаях, когда на опорных точках можно выполнить те же измерения, что и на соседних.
2. Косвенная. Проводится только при отсутствии возможности провести непосредственные измерения примычных длин и углов. К этому виду привязки и относится засечка.

По способу же построения геодезическая засечка бывает:

• линейной (полярные и биполярные по числу пунктов);
• угловой (прямая и обратная);
• комбинированной (положение точки определяют по известным углам и линейным расстояниям).

В геодезии чаще всего прибегают к комбинированию прямой и обратной засечек. Кроме того, чтобы полученные результаты были наиболее достоверными, измеряют больше величин, чем нужно, а само местоположение искомых пунктов получают посредством уравнивания.

Однократная и многократная засечка

Если для определения координат берется только один исходный пункт, то такая засечка будет называться однократной, а если более трех – многократной.

В основе обратной однократной угловой засечки лежит так называемая задача Потенота, которая была названа в честь французского математика Лорана Потенота, удачно решившего ее еще в 1692 году. Ученый предложил по известным значениям трех близлежащих точек вычислять координаты искомой.

На сегодняшний день существует уже более ста вариаций ее решения, которые были предложены многими именитыми учеными, но в геодезической практике наибольшую популярность получили формулы Жана Деламбра, Кнейссля и Гаусса.

Рисунок 1. Обратная многократная засечка

Важно отметить, что достоверные данные удается получить только в тех случаях, когда искомая точка находится в пределах треугольника, который образовали исходные пункты или же вне его, но напротив одной из его вершин.

Если же искомая точка попадает в пределы окружности, проходящей через эти точки, она становится неопределяемой. Этот ключевой недостаток в задаче Потенота, именуемый опасным кругом, приводит к необходимости определения дополнительной точки.

Обратная многократная угловая засечка как раз и подразумевает определение местоположения пункта через измерения на этом самом пункте углов или направлений как минимум на четыре твердых пункта, чьи координаты установлены. Этот метод более трудоемкий, но гарантирует надежный контроль результатов измерений. При обработке данных используют метод Гаусса-Ньютона, который в геодезии также называют параметрическим.

Способ Деламбра

Решение обратной засечки при помощи этого способа выполняется в такой последовательности:

1. Вычисляется дирекционный угол исходного направления с отметки 1 на точку «0» по формуле обратной геодезической засечки:

   (tan alpha _{1-P}= frac{(y_{2}-y_{1})ctgbeta _{1}+(y_{1}-y_{3})ctgbeta _{2}-x_{2}+x_{3}}{(x_{2}-x_{1})ctgbeta _{1}+(x_{1}-x_{3})ctgbeta _{2}+y_{2}-y_{3}} =frac{Delta y}{Delta x})

2. Значения дирекционных углов с исходных отметок Т2, Т3, Т4 получают из формул:

   (alpha _{2-P}=alpha _{1-P}+beta _{1})

   (alpha _{3-P}=alpha _{1-P}+beta _{2})

   (alpha _{4-P}=alpha _{1-P}+beta _{3})

3. Находят координаты точки Р с помощью формул тангенсов или котангенсов дирекционных углов направлений.

Комбинация 1:

(x_{P}=frac{x_{1}tgalpha_{1-P}tgalpha_{2-P}+y_{2}-y_{1}}{tgalpha_{1-P}-tgalpha _{2-P}})

(y’_{P}=y_{1}+(x_{P}-x_{1})tgalpha _{1-P})

(y”_{P}=y_{2}+(x_{P}-x_{2})tgalpha _{2-P})

Комбинация 2:

Создавайте будущее вместе с нами

Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.

(x_{P}=frac{x_{3}tgalpha_{3-P}-x_{4}tgalpha_{4-P}+y_{4}-y_{3}}{tgalpha_{3-P}-tgalpha _{4-P}})

(y’_{P}=y_{3}+(x_{P}-x_{3})tgalpha _{3-P})

(y”_{P}=y_{4}+(x_{P}-x_{4})tgalpha _{4-P})

Способ Кнейссля

Аналогично способу Деламбра последовательность формул при решении задачи обратной геодезической засечки по Кнейсслю будет иметь следующий вид:

1. Определяются вспомогательные коэффициенты:

   (k_{1}=(x_{2}-x_{1})ctgbeta_{1}+(y_{2}-y_{1}))

   (k_{2}=(y_{2}-y_{1})ctgbeta_{1}+(x_{2}-x_{1}))

   (k_{3}=(x_{3}-x_{1})ctgbeta_{2}+(y_{3}-y_{1}))

   (k_{4}=(y_{3}-y_{1})ctgbeta_{2}+(x_{3}-x_{1}))

2. Вычисляется котангенс дирекционного угла исходного направления на заданный пункт:

   (c=ctgalpha _{1-P}=frac{k_{1}-k_{3}}{k_{2}-k_{4}})

3. Приращения координаты точки Р относительно исходного пункта 1 находят при помощи нижеприведенных формул:

   (Delta y_{1-P}=frac{k_{1}-ck_{2}}{1+c^{2}}=frac{k_{3}-ck_{4}}{1+c^{2}})

   (Delta x_{1-P}=ccdot Delta y_{1-P})

4. Определяются координаты точки Р:

   (x_{P}=x_{1}+Delta x_{1-P})

   (y_{P}=y_{1}+Delta y_{1-P})
   

5. Средняя квадратическая погрешность вычисления местоположения пункта Р по трем направлениям вычисляется при помощи выражения:

   (M_{P}=frac{d_{BP}cdot m”_{beta}}{rho ”sin(varphi_{1} +varphi_{2})} sqrt{frac{d_{1}^{2}}{a^{2}}+ {frac{d_{2}^{2}}{b^{2}}}})

6. Оценивается точность обратной угловой засечки по способу Кнейссля с определением погрешности:

   (M=sqrt{M_{1}^{2}+M_{2}^{2}})

7. Допустимость в расхождениях полученных значений двух вариантов решений выполняется по формуле:

   (r+sqrt{(x’-x”)^2+(y’-y”)^2}leq 3M)

Если данное условие соблюдено, то итоговое значение координат берется как среднее арифметическое значение из результатов двух решений.

Уравнивание при помощи параметрического способа

Под определение обратной многократной угловой засечки попадает как совокупность простых однократных измерений, так и просто большое количество избыточных. Однако в обоих случаях необходимо уравнивание, которое выполняется по измеренным углам и направлениям.

К примеру, неизвестные (x_{p}) и (y_{p})  – координаты точки Р, которые в данном способе будут представлены в качестве параметров. Для этого их представляют в виде приближенных значений  (x_{0}), (y_{0}) и поправок к ним (δх) и (δу).

(left{begin{matrix}x_{p}=x_{0}+delta x
& \ y_{p}=y_{0}+delta y
&
end{matrix}right.)

В приведенном уравнении  (x_{0}) и (y_{0}) – результаты обработки однократных засечек, а (δх) и (δу) получают через уравнивание методом наименьших квадратов параметрическим способом с применением дифференциальных формул.

Этот метод подразумевает применение не только параметрического, но и коррелатного способа. Они дают одинаковые результаты, но отличаются по объему вычислений.

Однако в геодезической практике целесообразнее применять параметрический способ, поскольку при любом количестве избыточных измерений число нормальных уравнений будет аналогично числу неизвестных. При этом каждое неизвестное будет представлено в виде суммы приближенного значения и его поправки.

Сферы применения

Обратная угловая засечка нашла широкое применение в строительстве высотных зданий и сооружений, вроде опорных конструкций для мостов и дымовых труб. Кроем того, она позволяет быстро построить строительную сетку или определить местоположение точки в пространстве. В геодезии ее нередко используют в трилатерации и триангуляции.

Нельзя также не упомянуть ее огромного практического значения в навигации и военном деле. В частности, засечка по обратным дирекционным углам используется для топографогеодезической подготовки командно-наблюдательного пункта и позиции ведения огня.

Азимуты

Азимут

Это направление, измеряемое в градусах по часовой стрелке от севера на азимутальной окружности. Азимутальный круг состоит из 360 градусов. Девяносто градусов соответствует востоку, 180 градусов — югу, 270 градусов — западу, а 360 градусов и 0 градусов — северу.

Слово «азимут» иногда используется как синоним азимута для обозначения направления (показания в градусах) от одного объекта к другому. Такое использование корректно только в первом (СВ) квадранте между 0° и 90°.

Азимуты также можно считывать с юга. Национальная геодезическая служба Национального управления океанических и атмосферных исследований (NOAA) (бывшая Береговая и геодезическая служба США) всегда использует юг в качестве нулевого направления. В пожарной службе дикой природы азимут всегда считывается с северной точки.

Направление ветра

Азимут часто используется для обозначения направления ветра. Традиционно направление ветра указывается как одна из восьми точек компаса (С, СВ, В, ЮВ, Ю, ЮЗ, З, СЗ). Однако графики направления ветра и скорости часто дают значение азимута, используя 0° и 360° для севера. Ветры называются по направлению, откуда они дуют. Например, западный ветер дует с запада (или 270°), а юго-восточный ветер дует с юго-востока (135°).

Обратный азимут и обратное визирование

Обратный азимут — это проекция азимута от начала координат до противоположной стороны азимутального круга. В азимутальном круге 360 градусов, поэтому противоположное направление будет 180 градусов (половина 360 градусов) от азимута.

Обратный азимут рассчитывается путем прибавления 180° к азимуту, если азимут меньше 180°, или вычитания 180° из азимута, если он больше 180°. Например, если азимут равен 320°, обратный азимут будет 320° – 180° = 140°. Если азимут равен 30°, обратный азимут будет равен 180° + 30° = 210°.

Обратное прицеливание — это метод прицеливания, в котором используется отсчет азимута, снятый в обратном направлении.

Компас – это инструмент, используемый для навигации и ориентации. Азимутальный компас градуирован/отмечен полным кругом в 360 градусов, который называется азимутальным кругом. Компоненты компаса включают магнитную стрелку, которая всегда указывает на магнитный север, градуированную окружность для откладывания углов от истинного севера и линию визирования для продолжения линии визирования при следовании курсу направления.

Условные знаки

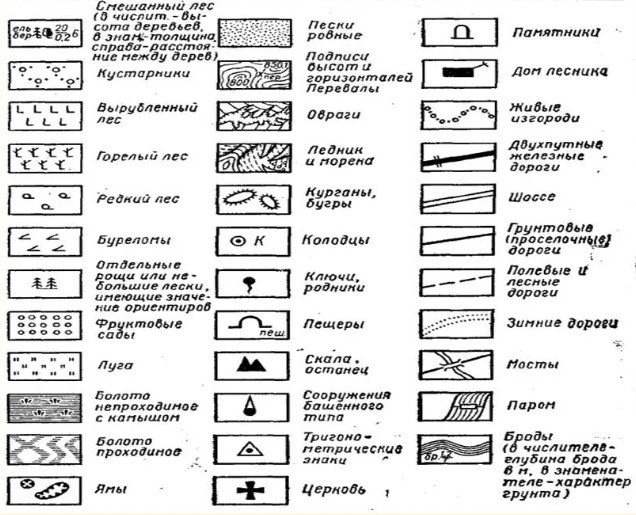
Дирекционные углы и румбы

Дирекционные углы и румбы используются для ориентирования линий.

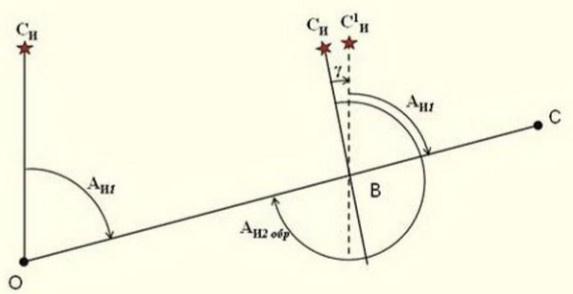
Дирекционным углом (α) линии называют угол, отсчитанный по ходу часовой стрелки от северного направления вертикальной линии километровой сетки (осевого меридиана зоны) до направления заданной линии. Пределы изменения дирекционного угла от 0º до 360º.

Румб (r)

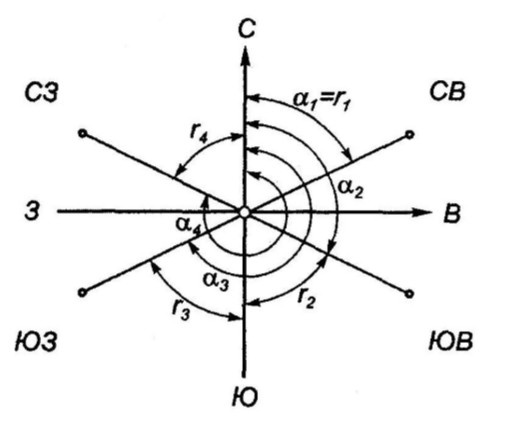
Это острый угол от ближайшего направления меридиана (северного или южного) до направления ориентирной линии. Пределы изменения румба от 0º до 90º.

Связь между дирекционными углами и румбами зависит от четверти, в которой находится заданное направление. Перевод дирекционных углов в румбы выполняется согласно таблице ниже.

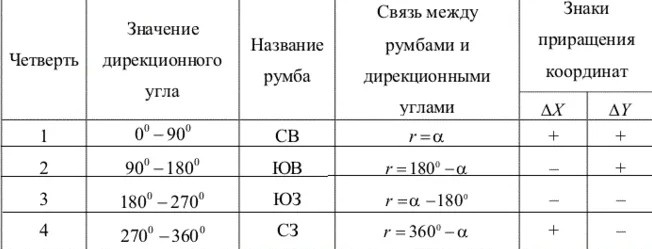
Пример перевода дирекционных углов в румбы

1. если дирекционный угол α равен 42°15′55″, тогда согласно таблице румб вычисляется по формуле r=α=42°15′55″, а название румба будет СВ;
2. если дирекционный угол α равен 100°45′11″, тогда согласно таблице румб вычисляется по формуле r=180°-α=180°-100°45′11″=79°14′49″, а название румба будет ЮВ;
3. если дирекционный угол α равен 210°17′42″, тогда согласно таблице румб вычисляется по формуле r=α-180°=210°17′42″-180°=30°17′42″, а название румба будет ЮЗ;
4. если дирекционный угол α равен 335°28′32″, тогда согласно таблице румб вычисляется по формуле r=360°-α=360°-335°28′32″=24°31′28″, а название румба будет СЗ.