Поскольку момент
пары сил равен моменту одной из ее сил
относительно точки приложения другой
силы (15)
![]() или
или
![]() ,
,
то
для пар, лежащих в одной плоскости,
момент пары можно рассматривать как
алгебраическую величину и обозначать
символом m.
При этом алгебраический момент пары
равен взятому с соответствующим знаком
произведению модуля одной из сил пары
на плечо пары:
![]() .
.
(18)
Правило
знаков здесь такое же, как и для
алгебраического момента силы:
алгебраический момент пары сил имеет
знак плюс, если пара сил стремится
вращать тело против часовой стрелки, и
знак минус, если пара сил стремится
вращать тело по часовой стрелке. Так,
для изображенной на рис. 21, а
пары
![]() ,
,![]() ,
,
момент![]() ,
,
а для пары![]() ,
,![]() ,
,
момент![]() .
.
Поскольку пара сил характеризуется
только ее моментом, то на рисунках пару
изображают часто просто дуговой стрелкой
(рис. 21,
б).
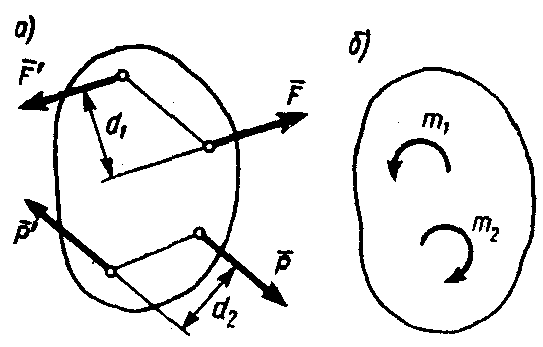
Рис.
21
Глава 3. Приведение системы сил к центру. Условия равновесия
§10. Теорема о параллельном переносе силы
В задачах на
равновесие тел сила может быть перенесена
в любую точку на линии ее действия.
Теорема: силу,
приложенную к абсолютно твердому телу,
можно, не изменяя оказываемого ею
действия, переносить из данной точки в
любую другую точку тела, прибавляя при
этом пару с моментом, равным моменту
переносимой силы относительно точки,
куда сила переносится.
Пусть
на твердое тело действует сила
![]() ,
,
приложенная в точке А (рис. 22). Действие
этой силы не изменится, если в любой
точке В тела приложить две уравновешенные
силы![]() и
и![]() ,
,
такие, что![]() ,
,![]() .
.
Полученная
система трех сил и представляет собой
силу
![]() ,
,
равную![]() ,
,
но приложенную в точке В, и пару![]() ,
,![]() с моментом
с моментом
![]() .
.
(19)

Рис.
22
Последнее равенство
следует из формулы (15). Таким образом,
теорема доказана.
§11. Приведение произвольной системы сил к центру
Теорема о приведении системы сил: любая
система сил, действующих на абсолютно
твердое тело, при приведении к произвольно
выбранному центру О заменяется одной
силой
![]() ,
,
равной главному вектору системы сил и
приложенной в центре приведения О, и
одной парой с моментом![]() ,
,
равным главному моменту системы сил
относительно центра О (рис. 23, б).
Пусть
на твердое тело действует произвольная
система сил
![]() ,
,![]() , …,
, …,![]() (рис. 23, а). Выберем точку О за центр
(рис. 23, а). Выберем точку О за центр
приведения и, пользуясь теоремой,
доказанной в §10, перенесем все силы в
центр О, присоединяя при этом соответствующие
пары. Тогда на тело будет действовать
система сил
![]() ,
, ![]() , …,
, …,![]() ,
,
(20)
приложенных в
центре О, и система пар, моменты которых
согласно формуле (19) равны:
![]() , ,
, ,
![]() , …,
, …, ![]() .
.
(21)
Сходящиеся
силы, приложенные в точке О, заменяются
одной силой
![]() ,
,
приложенной в точке О. При этом![]() или, согласно равенствам. (20)
или, согласно равенствам. (20)
![]() .
.
(22)
Чтобы
сложить все полученные пары, надо сложить
векторы моментов этих пар. В результате
система пар заменяется одной парой,
момент которой
![]() или, согласно равенствам (21)
или, согласно равенствам (21)
![]() .
.
(23)
Как
известно величина
![]() равная геометрической сумме всех сил,
равная геометрической сумме всех сил,
называется главным вектором системы
сил; величина![]() ,
,
равная геометрической сумме моментов
всех сил относительно центра О, называется
главным моментом системы сил относительно
этого центра.
Таким образом,
теорема доказана.

Рис.
23
Заметим,
что сила
![]() не является здесь равнодействующей
не является здесь равнодействующей
данной системы сил, так как заменяет
систему сил не одна, а вместе с парой.
Отметим,
что значение
![]() от выбора центра О не зависит. Значение
от выбора центра О не зависит. Значение
же![]() при изменении центра О может изменится
при изменении центра О может изменится
вследствие изменения значений моментов
отдельных сил.
Рассмотрим в заключение частные случаи:
1) если для данной системы сил
![]() ,
,
а![]() ,
,
то она приводится к одной паре сил с
моментом![]() .
.
В этом случае значение![]() не зависит от выбора центра О, так как
не зависит от выбора центра О, так как
иначе получилось бы, что одна и та же
система сил заменяется разными, не
эквивалентными друг другу парами, что
не возможно; 2) если для данной системы
сил![]() ,
,
а![]() ,
,
то она приводится к одной силе т.е.
равнодействующей, равной![]() и приложенной в центре О.
и приложенной в центре О.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Момент силы относительно точки (или центра) — вращательный эффект силы, характеризующий вращение твердого тела вокруг некоторой точки под действием приложенной силы.
Определение
Моментом силы относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы.
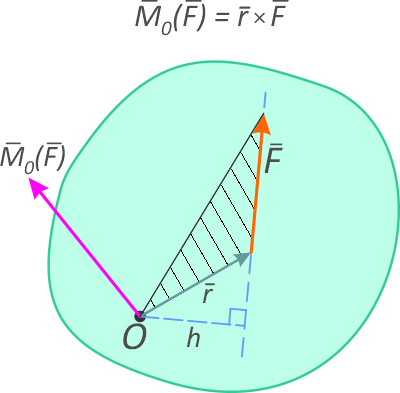
Рисунок 1.1
Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки.
Вычисление момента
Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия:
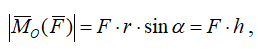
где h – плечо силы (кратчайшее расстояние от точки O – центра момента – до линии действия силы). Если сила проходит через точку, то ее момент относительно этой точки равен нулю.
Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия.
Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы.
Алгебраическим моментом силы относительно точки (или центра) называется взятое со знаком плюс или минус произведение модуля силы на плечо (рисунок 1.2).
Наш короткий видеоурок про момент силы с примерами:
Другие видео
Правило знаков
Знак плюс выбирается в том случае, если сила стремится поворачивать плоскость относительно центра момента против хода часовой стрелки.
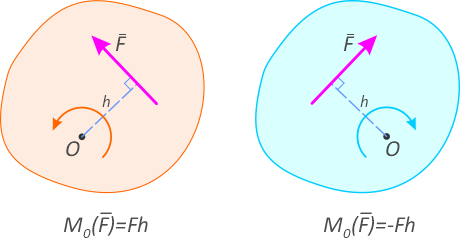
Рисунок 1.2
Если сила F задана своими проекциями на оси координат Fx, Fy, Fz и даны координаты x, y, z точки приложения этой силы, то момент силы относительно начала координат вычисляется следующим образом:
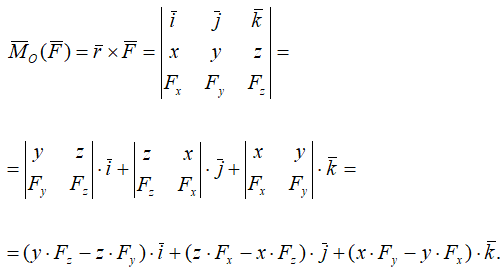
Проекции момента силы на оси координат равны:
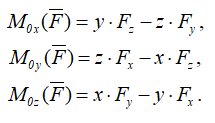
Примеры решения задач >
Момент силы относительно оси >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Содержание:
Моменты силы относительно точки и оси:
Для рассмотрения различных систем сил необходимо ввести понятия алгебраического и векторного моментов силы относительно точки и момента силы относительно оси. Введем эти характеристики действия силы на твердое тело и рассмотрим их свойства.
Алгебраический момент силы относительно точки
При рассмотрении плоской системы сил, приложенных к твердому телу, используется понятие алгебраического момента силы относительно точки.
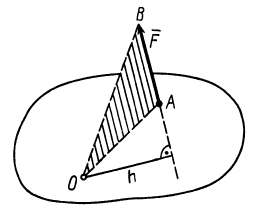
Рис. 19
Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки (рис. 19), взятое со знаком плюс или минус.
Плечом 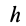
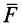 относительно точки называют кратчайшее расстояние между этой точкой и линией действия силы, т. е. длину отрезка перпендикуляра, опущенного из точки
относительно точки называют кратчайшее расстояние между этой точкой и линией действия силы, т. е. длину отрезка перпендикуляра, опущенного из точки  на линию действия силы
на линию действия силы 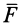 .
.
Обозначим 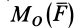 или
или 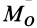 алгебраический момент силы
алгебраический момент силы 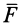 относительно точки
относительно точки  . Тогда
. Тогда

Если сила стремится вращать тело вокруг моментной точки (точки, относительно которой вычисляют алгебраический момент силы) против часовой стрелки, то берем знак плюс, если по часовой стрелке — знак минус.
Алгебраический момент силы представляет собой произведение силы на длину (в 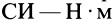 ).
).
Из определения алгебраического момента силы относительно точки следует, что он не зависит от переноса силы вдоль ее линии действия. Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю. Численно алгебраический момент относительно точки равен удвоенной площади треугольника, построенного на силе 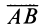 и моментной точке:
и моментной точке:
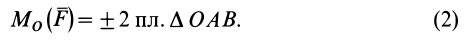
Векторный момент силы относительно точки
При рассмотрении пространственной системы сил, приложенных к твердому телу, применяется понятие векторного момента силы относительно точки.
Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки (рис. 20).
Плечом 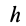 силы относительно точки
силы относительно точки  называют кратчайшее расстояние от этой точки до линии действия силы.
называют кратчайшее расстояние от этой точки до линии действия силы.
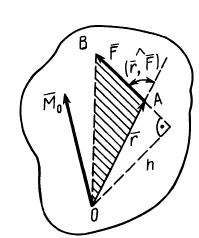
Рис. 20
Условимся векторный момент силы 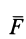 относительно точки
относительно точки  обозначать
обозначать  , а его числовую величину —
, а его числовую величину — 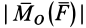 . Тогда, согласно определению,
. Тогда, согласно определению,
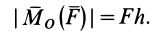
Как и для алгебраического момента, векторный момент силы относительно точки равен удвоенной площади треугольника, построенного на силе и моментной точке:
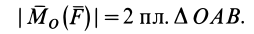
Справедлива формула

где 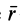 —радиус-вектор, проведенный из моментной точки
—радиус-вектор, проведенный из моментной точки  в точку приложения силы или любую другую точку линии действия силы.
в точку приложения силы или любую другую точку линии действия силы.
Чтобы убедиться в справедливости формулы (3), достаточно показать, что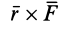 по величине и направлению выражает векторный момент силы относительно точки
по величине и направлению выражает векторный момент силы относительно точки  . По определению векторного произведения двух векторов известно, что
. По определению векторного произведения двух векторов известно, что
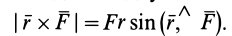
Как показано на рис. 20, 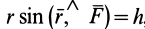 , причем это равенство справедливо для любой точки линии действия, куда проведен радиус-вектор
, причем это равенство справедливо для любой точки линии действия, куда проведен радиус-вектор 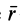 . Итак,
. Итак,
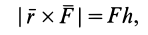
что совпадает с векторным моментом силы относительно точки  . Вектор
. Вектор 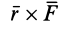 , как известно, перпендикулярен плоскости, в которой расположены векторы
, как известно, перпендикулярен плоскости, в которой расположены векторы 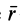 и
и 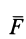 , т. е. плоскости треугольника
, т. е. плоскости треугольника 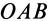 , которой перпендикулярен и векторный момент
, которой перпендикулярен и векторный момент  .
.
Направление 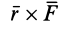 тоже совпадает с направлением
тоже совпадает с направлением  . Заметим, что векторный момент силы относительно точки считается вектором, приложенным к этой точке.
. Заметим, что векторный момент силы относительно точки считается вектором, приложенным к этой точке.
Векторный момент силы относительно точки не изменяется от переноса силы вдоль ее линии действия. Он станет равным
нулю, если линия действия силы пройдет через моментную точку.
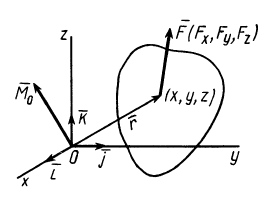
Рис. 21
Если сила 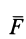 дана своими проекциями
дана своими проекциями 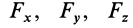 на оси координат и даны координаты
на оси координат и даны координаты 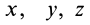 точки приложения этой силы (рис. 21), то векторный момент относительно начала координат, согласно формуле (3), после разложения по осям координат вычисляем по формуле
точки приложения этой силы (рис. 21), то векторный момент относительно начала координат, согласно формуле (3), после разложения по осям координат вычисляем по формуле
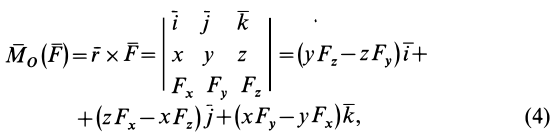
где 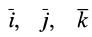 — единичные векторы, направленные по осям координат.
— единичные векторы, направленные по осям координат.
Используя формулу (4), можно выделить проекции  на оси координат:
на оси координат:
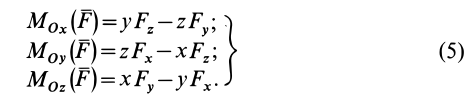
Модуль векторного момента  и косинусы углов его с осями координат определяем по формулам
и косинусы углов его с осями координат определяем по формулам
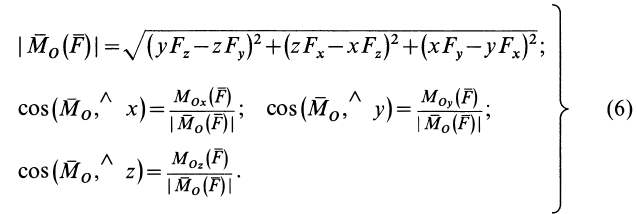
В формулах (6) числовую величину 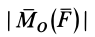 берем со знаком плюс.
берем со знаком плюс.
Момент силы относительно оси
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (рис. 22). Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси (проекция силы на плоскость является вектором), стремится вращать тело вокруг положительного направления оси против часовой стрелки, и отрицательным, если она стремится вращать тело по часовой стрелке. Момент силы, например, относительно оси  обозначим
обозначим 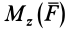 .
.
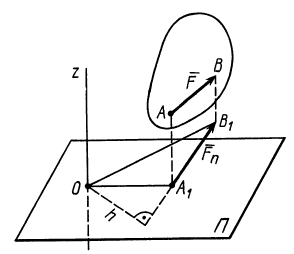
Рис. 22
По определению,
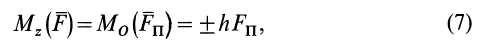
где 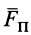 — вектор проекции силы
— вектор проекции силы 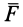 на плоскость
на плоскость  , перпендикулярную оси
, перпендикулярную оси  , а точка
, а точка  — точка пересечения оси
— точка пересечения оси  с плоскостью
с плоскостью  .
.
Из определения момента силы относительно оси следует, что введенный выше алгебраический момент силы относительно точки можно считать моментом силы относительно оси, проходящей через эту точку, перпендикулярно плоскости, в которой лежат сила и моментная точка. Момент силы относительно оси можно выразить через площадь треугольника, построенного на проекции силы 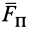 и точке пересечения
и точке пересечения  оси с плоскостью:
оси с плоскостью:
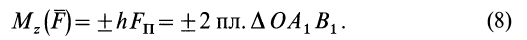
Из формулы (8) можно получить следующие важные свойства момента силы относительно оси:
- Момент силы относительно оси равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси.
- Момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось. В этом случае линия действия проекции силы на плоскость, перпендикулярную оси, проходит через точку пересечения оси с плоскостью и, следовательно, равно нулю плечо силы
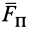 относительно точки
относительно точки  .
.
В обоих этих случаях ось и сила лежат в одной плоскости. Объединяя их, можно сказать, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Связь момента силы относительно оси с векторным моментом силы относительно точки на оси
Используя формулу (8), имеем (рис. 23)
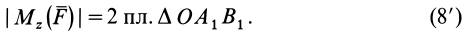
Векторный момент силы 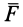 относительно точки
относительно точки  , взятой на пересечении оси
, взятой на пересечении оси  с перпендикулярной плоскостью
с перпендикулярной плоскостью  , выражается в виде
, выражается в виде
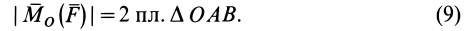
Векторный момент 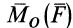 направлен перпендикулярно плоскости треугольника
направлен перпендикулярно плоскости треугольника 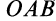 . Аналогично, для другой точки
. Аналогично, для другой точки 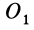 оси
оси 
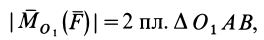
причем векторный момент 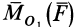 направлен перпендикулярно плоскости треугольника
направлен перпендикулярно плоскости треугольника 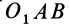 . Треугольник
. Треугольник 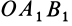 является проекцией треугольников
является проекцией треугольников 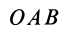 и
и 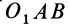 на плоскость
на плоскость  . Из геометрии известно, что площадь проекции плоской фигуры равна площади проецируемой фигуры, умноженной на косинус угла между плоскостями, в которых расположены эти фигуры. Угол между плоскостями измеряется углом между перпендикулярами к этим плоскостям. Перпендикуляром к плоскости треугольника
. Из геометрии известно, что площадь проекции плоской фигуры равна площади проецируемой фигуры, умноженной на косинус угла между плоскостями, в которых расположены эти фигуры. Угол между плоскостями измеряется углом между перпендикулярами к этим плоскостям. Перпендикуляром к плоскости треугольника 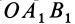 является ось
является ось  , а перпендикулярами к плоскостям треугольников
, а перпендикулярами к плоскостям треугольников 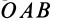 и
и 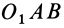 —соответственно векторные моменты
—соответственно векторные моменты 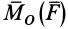 и
и 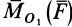 . Таким образом,
. Таким образом, 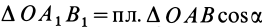 , где
, где 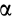 — угол между вектором
— угол между вектором 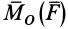 и осью
и осью  . Отсюда по формулам (8′) и (9) имеем
. Отсюда по формулам (8′) и (9) имеем
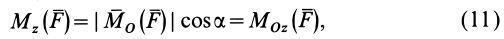
причем знак 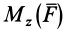 полностью определяется знаком
полностью определяется знаком 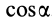 .
.
Аналогично,
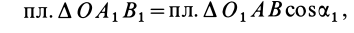
т. е.
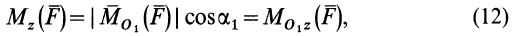
где 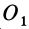 — любая точка на оси
— любая точка на оси  .
.
Формулы (11) и (12) отражают искомую связь между моментом силы относительно оси и векторными моментами силы относительно точек, лежащих на этой оси: момент силы относительно оси равен проекции на эту ось векторного момента силы относительно любой точки на оси.
Эту зависимость между моментом силы относительно оси и векторным моментом силы относительно точки на оси можно принять за определение момента силы относительно оси.
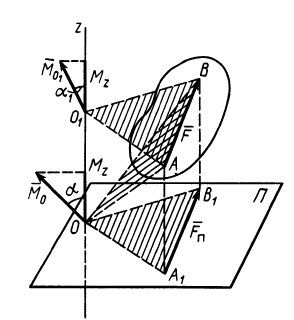
Рис. 23
Формулы для моментов силы относительно осей координат
Используя связь момента силы относительно оси с векторным моментом силы относительно точки на оси, можно получить формулы для вычисления моментов относительно осей координат, если даны проекции силы на оси координат и координаты точки приложения силы. Для оси 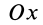 имеем
имеем
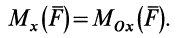
Согласно (5),
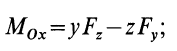
следовательно,
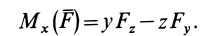
Аналогично, для осей 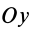 и
и 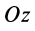
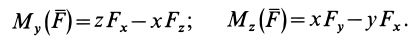
Окончательно
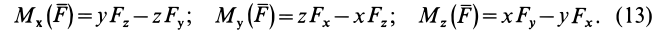
По формулам (13) можно вычислить моменты силы относительно прямоугольных осей координат.
По этим формулам получаются необходимые знаки для 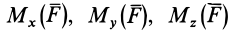 , если проекции силы
, если проекции силы 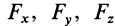 на оси координат и координаты
на оси координат и координаты 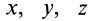 точки приложения силы подставлять в них со знаками этих величин.
точки приложения силы подставлять в них со знаками этих величин.
При решении задач момент силы относительно какой-либо оси часто получают, используя его определение, т. е. проецируя силу на плоскость, перпендикулярную оси, и вычисляя затем алгебраический момент этой проекции относительно точки пересечения оси с этой плоскостью.
Момент пары сил. Сложение пар сил. Равновесие пар сил
При изучении теоретической механики необходимо совершенно отчетливо уяснить, что в статике рассматриваются два простейших элемента: сила и пара сил. Любые две силы, кроме сил, образующих пару, всегда можно заменить одной —сложить их (найти равнодействующую). Пара сил нс поддается дальнейшему упрощению, она не имеет равнодействующей и является простейшим элементом.
Действие пары сил на тело характеризуется ее моментом — произведением одной из сил пары на ее плечо (на кратчайшее расстояние между линиями действия сил, образующих пару).
Единицей момента пары сил в Международной системе служит 1 нм (ньютон-метр = 1 н-1ж), а в системе МКГСС (технической)— 1 кГ-м.
Несколько пар сил, действующих на тело в одной плоскости, можно заменить одной парой сил (равнодействующей парой), момент которой равен алгебраической сумме моментов данных пар:
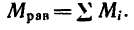
При равновесии пар сил
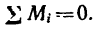
Если пары сил действуют в одной плоскости, то при решении задач достаточно рассматривать моменты пар как алгебраические величины. Причем знак момента определяется в зависимости от направления вращающего действия пары сил.
Дальнейшее изложение основано на правиле, т. е. считается момент положительным, если пара сил действует против хода часовой стрелки, если же пара сил действует на тело но ходу часовой стрелки, то момент считается отрицательным.
В том случае когда пары сил действуют на тело будучи расположенными в различных плоскостях, гораздо удобнее рассматривать пару сил как вектор, направленный перпендикулярно
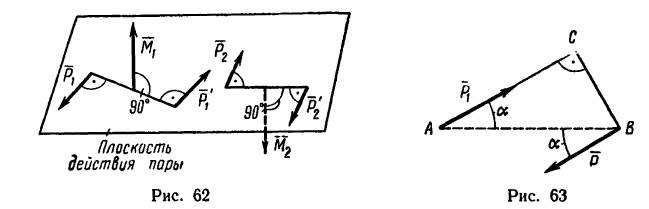
к плоскости действия пары сил (рис. 62). Направление вектора в зависимости от направления вращательного действия пары определяется по направлению движения винта с правой нарезкой.
Задача 1.
Определить момент пары сил (рис. 63), если 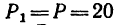 н, АВ — 0,5 м и а = 30°.
н, АВ — 0,5 м и а = 30°.
Решение.
1. При определении момента пары сил нужно прежде всего правильно определить плечо пары. При этом необходимо различать следующие понятия: плечо пары сил и расстояние между точками приложения сил нары.
Так как в механике твердого тела сила—скользящий вектор, то действие силы не изменяется при переносе точки ее приложения вдоль линии ее действия. Значит расстояние между точками приложения сил, образующих пару, можно изменять неограниченно. Но плечо пары при этом переносе остается неизменным.
В частном случае расстояние между точками приложения сил, образующих пару, может быть равно плечу.
Чтобы определить плечо данной пары из точки приложения одной из сил, например из точки В, восставим перпендикуляр ВС к линии действия другой силы. Расстояние ВС и есть плечо данной пары сил. Расстояние между точками приложения сил, образующих пару, АВ=0,5 м.
Легко видеть, что
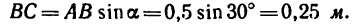
2. Найдем момент пары сил:
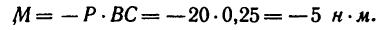
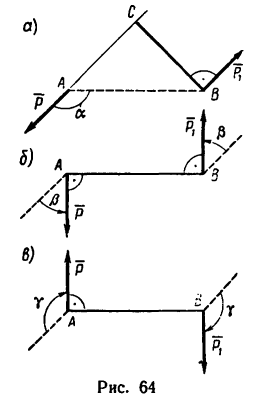
Задача 2.
Как изменится момент пары сил 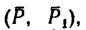 показанной на рис. 64, а (P = 50 н, AВ=0,4 м и а=135), если
показанной на рис. 64, а (P = 50 н, AВ=0,4 м и а=135), если
повернуть силы 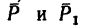 так, чтобы они стали перпендикулярными АВ? Решение.
так, чтобы они стали перпендикулярными АВ? Решение.
1. Найдем момент пары при заданном положении ее сил (рис. 64, а).
Из точки В восставим перпендикуляр ВС к линиям действия сил 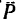 и найдем его длину:
и найдем его длину:
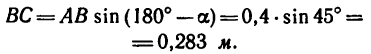
Момент пары при заданном положении сил
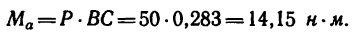
2. Повернем силы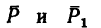 из заданного положения на угол
из заданного положения на угол 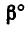 =а°— 90э в направлении против хода часовой стрелки (рис. 64, б). При таком положении сил относительно АВ плечом пары сил является расстояние между точками их приложения, поэтому
=а°— 90э в направлении против хода часовой стрелки (рис. 64, б). При таком положении сил относительно АВ плечом пары сил является расстояние между точками их приложения, поэтому
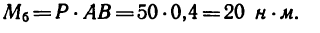
3. Сравнивая полученные результаты, видим, что после поворота сил момент пары увеличивается на 20—14,5 = 5,85 н-м.
4. Легко заметить, что силы 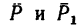 могут достичь перпендикулярного положения к АВ после их поворота на угол у в направлении по ходу часовой стрелки (рис. 64, в). В том случае плечом пары является тот же отрезок АВ, но момент пары
могут достичь перпендикулярного положения к АВ после их поворота на угол у в направлении по ходу часовой стрелки (рис. 64, в). В том случае плечом пары является тот же отрезок АВ, но момент пары
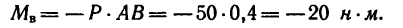
Момент пары сил изменяет свой знак.
Задача 3.
К точкам А, С и В, D, образующим вершины квадрата со стороной 0,5 м (рис. 65, а), приложены равные по модулю силы (Р = 12н) таким образом, что они образуют две пары сил
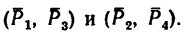 Определить момент равнодействующей пары сил
Определить момент равнодействующей пары сил
Решение 1.
Плечи у обеих пар сил равны стороне квадрата поэтому
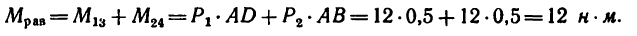
Решение 2.
1. Перенесем силы 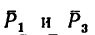 из точек
из точек 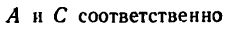 в точки В и D (рис. 65, б). В точках В и D получаются системы сходящихся сил
в точки В и D (рис. 65, б). В точках В и D получаются системы сходящихся сил 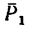 и
и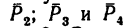 одинаковыми модулями.
одинаковыми модулями.
2. Сложим попарно эти силы у каждой из точек В и D. В обоих случаях
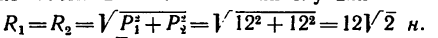
3. Силы R, модули которых теперь известны, направлены перпендикулярно к диагонали BD квадрата. Значит эта диагональ является плечом вновь образовавшейся пары сил 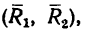 заменяющей собой две данные.
заменяющей собой две данные.
4. Найдем момент пары 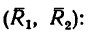
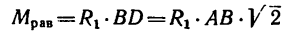
и, следовательно,
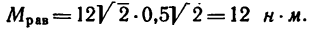
Эту пару в соответствии со вторым решением можно представить в виде пары 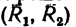 с плечом BD (диагональю данного квадрата).
с плечом BD (диагональю данного квадрата).
Но можно равнодействующую пару представить и в любом другом виде, например в виде сил Q = 24 и, приложенных к двум любым вершинам квадрата ABCD (рис. 65, в)
- Заказать решение задач по теоретической механике
Задача 4.
На прямоугольник ABCD (рис. 67) вдоль его длинных сторон действует пара сил 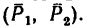 Какую пару сил нужно приложить к прямоугольнику, направив силы вдоль его коротких сторон, чтобы уравновесить пару
Какую пару сил нужно приложить к прямоугольнику, направив силы вдоль его коротких сторон, чтобы уравновесить пару 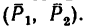
Решение.
1. Момент данной пары сил
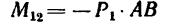
необходимо уравновесить парой, момент которой обозначим Л1м. Тогда, согласно условию равновесия,
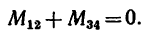
Откуда
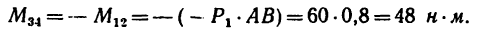
2. Обозначив силы, образующие искомую пару 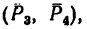 замечая, что ее плечо равно ВС, получим
замечая, что ее плечо равно ВС, получим
Отсюда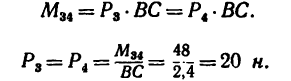
•Значит к прямоугольнику необходимо приложить пару сил с положительным (направленным против хода часовой стрелки) моментом, равным 48 н м. Силы, образующие эту пару, равняются
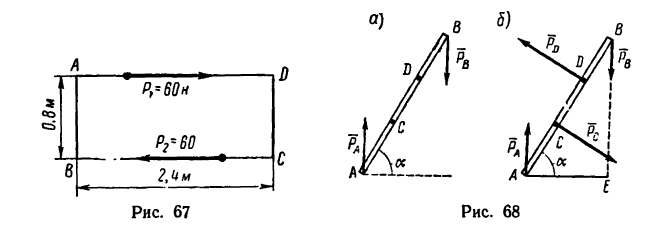
20 н каждая и одна из них должна действовать вдоль стороны АВ от А к В, вторая — вдоль стороны CD от С к D.
Задача 5.
Прямолинейный стержень АВ должен находиться в равновесии в положении, показанном на рис. 68, а (угол а = 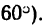 При этом в точках А и В на стержень действуют вертикальные силы
При этом в точках А и В на стержень действуют вертикальные силы 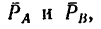 образующие пару
образующие пару 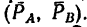 Какие две равные силы нужно приложить к стержню в точках С и D, направив их перпендикулярно к стержню, чтобы обеспечить равновесие. АВ = 3 м, CD— 1 м,
Какие две равные силы нужно приложить к стержню в точках С и D, направив их перпендикулярно к стержню, чтобы обеспечить равновесие. АВ = 3 м, CD— 1 м, 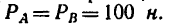
Решение.
1. Пару сил можно уравновесить только парой сил. Поэтому в точках С и D к стержню необходимо приложить две равные силы так, чтобы они образовали пару сил с моментом, равным моменту пары 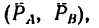 но имеющим противоположный знак.
но имеющим противоположный знак.
Так как пара 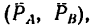 поворачивает стержень на ходу часовой стрелки, искомые силы должны поворачивать его против хода часовой стрелки (рис. 68, б).
поворачивает стержень на ходу часовой стрелки, искомые силы должны поворачивать его против хода часовой стрелки (рис. 68, б).
2. Применяем условие равновесия:
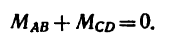
Или, подставив значения моментов,
где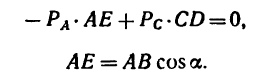
Отсюда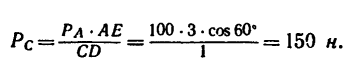
Следовательно, в точках С и D необходимо приложить силы 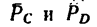 по 150 н каждая, как показано на рис. 68, б.
по 150 н каждая, как показано на рис. 68, б.
Момент силы относительно точки
Момент силы относительно точки при решении задач по статике, а затем и по динамике имеет не менее важное значение, чем проекции сил. Поэтому нужно уметь определять эту величину безошибочно. Обычно его числовое значение находят неправильно из-за ошибок, допускаемых при определении плеча.
Чтобы не допускать ошибок при определении моментов сил относительно точки, рекомендуется придерживаться следующего порядка:
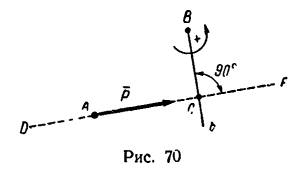
- Прежде всего нужно научиться «видеть» силу, момент которой определяем, и центр моментов – точку, относительно которой определяем момент (рис. 70 – сила
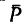 и центр моментов – точка В).
и центр моментов – точка В). - Затем из центра момента проводим прямую ВЬ перпендикулярно к линии действия силы DF. Длина перпендикуляра ВС от центра момента до линии действия силы и есть плечо.
- Потом находим знак момента. При этом если сила стремится повернуть плечо вокруг центра момента против хода часовой стрелки, то считаем момент положительным; если по ходу часовой стрелки, то отрицательным (тоже правило, что и при определении знака момента пары сил).
- Находим числовое значение момента силы относительно точки, умножив модуль силы на плечо.
По рис. 70
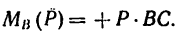
В частном случае момент силы может равняться нулю. Это происходит тогда, когда центр моментов лежит на линии действия силы, при этом плечо равняется нулю. По рис. 70 момент силы 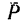 относительно точки А (или С) равен нулю.
относительно точки А (или С) равен нулю.
Задача 6.
Определить моменты шести заданных сил (рис. 71) относительно точек А, В и С, если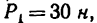
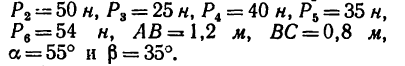
Решение 1 — определение моментов гнести заданных сил относительно точки А (рис. 71, а).
1. Центр моментов в точке А. Через точку А проходят линии действия трех сил 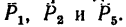 Значит для этих сил плечи равны нулю. Следовательно,
Значит для этих сил плечи равны нулю. Следовательно,
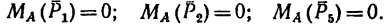
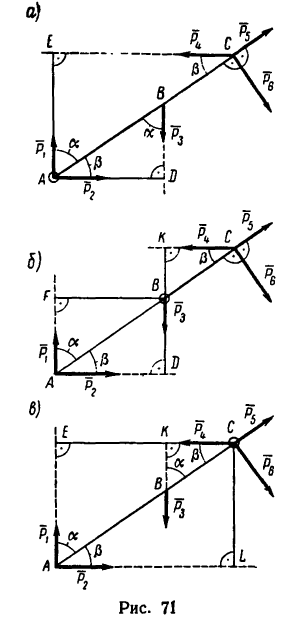
2. Находим момент силы 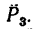 Опустив из точки А на линию действия
Опустив из точки А на линию действия
силы 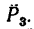 перпендикуляр AD, получим плечо силы
перпендикуляр AD, получим плечо силы 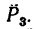 Длину AD легко найти, так как это катет треугольника ABD:
Длину AD легко найти, так как это катет треугольника ABD:
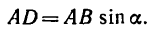
3. Величина момента отрицательная (сила 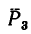 поворачивает плечо AD вокруг точки А но ходу часовой стрелки), следовательно,
поворачивает плечо AD вокруг точки А но ходу часовой стрелки), следовательно,
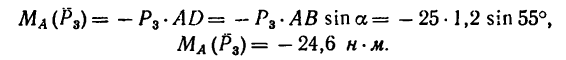
4. Находим момент силы 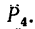 Плечом силы
Плечом силы 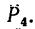 является перпендикуляр АЕ к СЕ – линии действия силы
является перпендикуляр АЕ к СЕ – линии действия силы 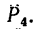 Из треугольника АСЕ
Из треугольника АСЕ
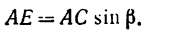
Величина момента положительная (плечо АЕ поворачивается около точки А силой 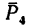 против хода часовой стрелки). Следовательно,
против хода часовой стрелки). Следовательно,
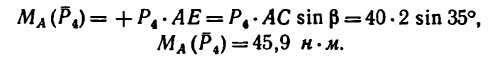
5. Находим момент силы 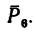 Плечом силы
Плечом силы 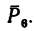 относительно точки А является отрезок АС, так как сила
относительно точки А является отрезок АС, так как сила 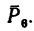 направлена к АС перпендикулярно. Величина момента отрицательная:
направлена к АС перпендикулярно. Величина момента отрицательная:
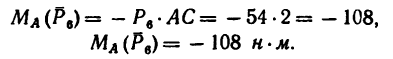
Решение 2 — определение моментов сил относительно точки В (рис. 71, б).
1. Центр моментов в точке В.
2. Через точку В проходят линии действия двух сил: 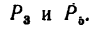 Следовательно,
Следовательно,
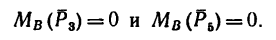
3. Находим момент силы 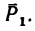 Плечо силы
Плечо силы 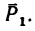
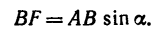
Величина момента отрицательная:
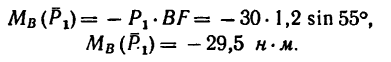
4. Находим момент силы 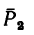 Плечо силы
Плечо силы 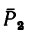
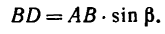
Момент отрицательный:
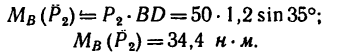
5. Находим момент силы 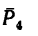 Плечо силы
Плечо силы 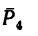
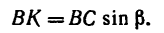
Величина момента положительная:
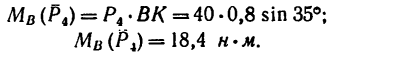
6. Находим момент силы 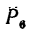 Плечом силы
Плечом силы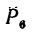 является отрезок ВС. Момент положительный:
является отрезок ВС. Момент положительный:
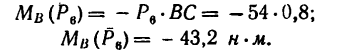
Решение 3 — определение моментов сил относительно точки С (рис. 71, в) рекомендуется выполнить самостоятельно.
Ответ. 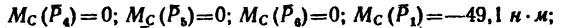
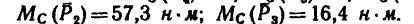
В задаче силы расположены так, что либо их плечи определяются очень просто – как катеты прямоугольных треугольников, в которых даны гипотенузы, либо плечи заданы в условии задачи (ВС и АС).
Но иногда некоторые силы заданной системы оказываются расположенными относительно выбранного центра моментов так, что определить длину плеча трудно и требуется, например, предварительно вычислить длины еще одного-двух отрезков. В таких случаях целесообразно силу разложить на две составляющие и применить для определения ее момента теорему Вариньона.
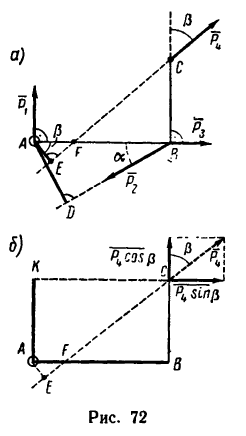
Задача 7.
Определить моменты относительно точки 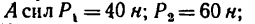
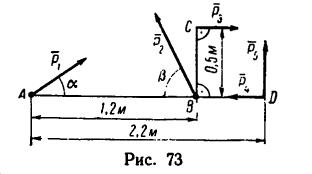
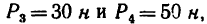 я, приложенных в точках А, В и С, как показано на рис. 72, а. Углы
я, приложенных в точках А, В и С, как показано на рис. 72, а. Углы ВС =1,5 м.
ВС =1,5 м.
Решение.
1. Относительно точки А моменты сил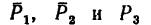 определяются аналогично
определяются аналогично
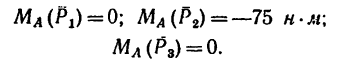
2. Находим момент силы 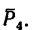 Вариант 1-й (рис. 72, а). Плечо АЕ силы
Вариант 1-й (рис. 72, а). Плечо АЕ силы 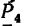 в данном случае определяем из
в данном случае определяем из 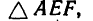 в котором известен только
в котором известен только 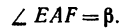 . Значит нужно предварительно определить одну из сторон. Найдем AF:
. Значит нужно предварительно определить одну из сторон. Найдем AF:
AF = AB – FB.
Величину FB находим из 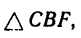 в котором
в котором 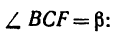
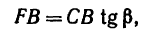
следовательно,
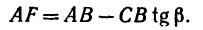
И теперь можем определить плечо АЕ:
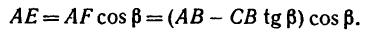
Раскрываем скобки и заменяем 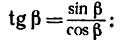
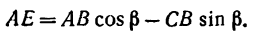
Момент положительный, следовательно:
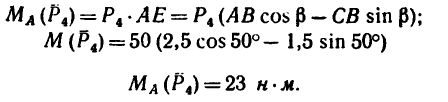
Вариант 2-й. Чтобы избежать определения плеча АЕ, которое в данном случае находится после предварительного вычисления двух отрезков (FB и AF), необходимо момент силы 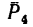 относительно точки А найти по теореме Вариньона: момент равнодействующей плоской системы сил относительно любой точки, лежащей в той же плоскости, равен алгебраической сумме моментов составляющих сил относительно той же точки.
относительно точки А найти по теореме Вариньона: момент равнодействующей плоской системы сил относительно любой точки, лежащей в той же плоскости, равен алгебраической сумме моментов составляющих сил относительно той же точки.
Разложим силу 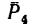 на две составляющие: одну, направленную вдоль отрезка ВС, и другую — перпендикулярно к нему (рис. 72, б).
на две составляющие: одну, направленную вдоль отрезка ВС, и другую — перпендикулярно к нему (рис. 72, б).
Модуль первой составляющей 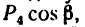 а ее плечо — отрезок АВ, длина которого задана. Модуль второй составляющей
а ее плечо — отрезок АВ, длина которого задана. Модуль второй составляющей 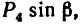 а ее плечо АК = ВС =1,5 м.
а ее плечо АК = ВС =1,5 м.
Применяя теорему Вариньона, получаем
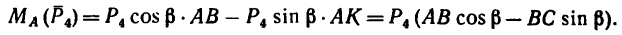
Как видно, получено точно такое же значение момента, что и в первом варианте решения:
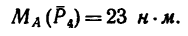
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
- Аксиомы и теоремы статики
- Система сходящихся сил
- Плоское движение тела
- Принцип виртуальных перемещений
– для произвольной системы сил.
 – для плоской системы сходящихся сил.
– для плоской системы сходящихся сил.
1.5. Момент силы относительно точки и оси
1. Алгебраический момент силы относительно точки.
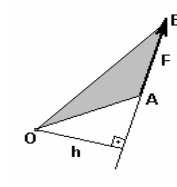
Используется при рассмотрении плоской системы сил. Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус (рис.10). Плечом h силы F называют кратчайшее расстояние между этой точкой и линией действия силы. Знак зависит от направления “вращения” тела относительно точки: при “вращении” тела против часовой стрелки будем считать момент положительным МО — (+) и наоборот МО — (-).
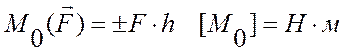
;
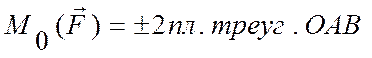
.
Рис. 10
2. Векторный момент силы относительно точки.
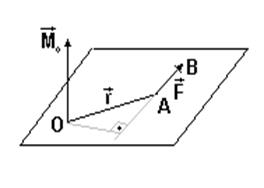 Векторным моментом силы относительно точки называют вектор приложенный в этой точке и равный по модулю (рис.11), произведению силы на плечо силы относительно этой точки. Векторный момент направлен перпендикулярно плоскости, в которой лежат сила и точка, таким образом, что с его конца можно видеть “стремление” силы вращать тело против движения часовой стрелки.
Векторным моментом силы относительно точки называют вектор приложенный в этой точке и равный по модулю (рис.11), произведению силы на плечо силы относительно этой точки. Векторный момент направлен перпендикулярно плоскости, в которой лежат сила и точка, таким образом, что с его конца можно видеть “стремление” силы вращать тело против движения часовой стрелки.
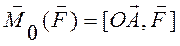
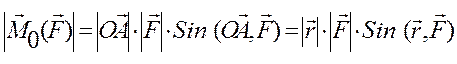
Рис. 11
Векторный момент силы относительно точки не меняется при скольжении силы по линии действия и равен нулю, если линия проходит через точку О.
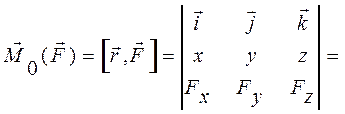
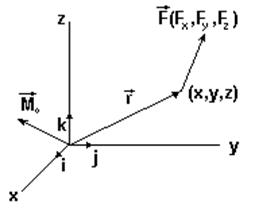 Момент силы относительно начала координат можно выразить через проекции силы на координатные оси и координаты точки приложения силы (рис.12).
Момент силы относительно начала координат можно выразить через проекции силы на координатные оси и координаты точки приложения силы (рис.12).
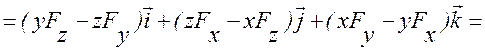
Рис. 12
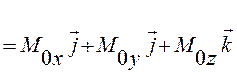
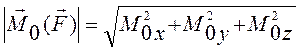
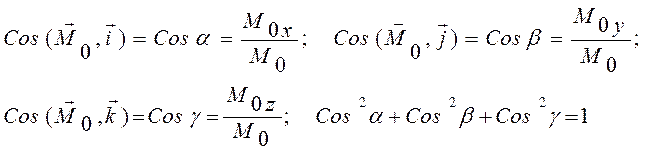
3. Момент силы относительно оси.
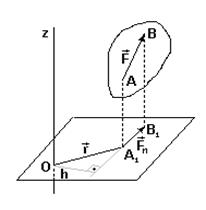 Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси (рис.13), относительно точки пересечения оси с этой плоскостью.
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси (рис.13), относительно точки пересечения оси с этой плоскостью.
Знак определяется направлением вращения (против часовой стрелки − (+), по часовой стрелки − (−)).
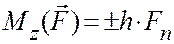
Рис. 13
Замечания: а) Mz=0, если сила параллельна оси Oz.
б) Mz=0, если линия действия пересекает ось Oz.
Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
1.6. Приведение системы сил к простейшей системе
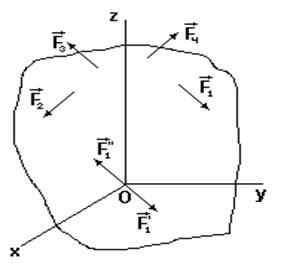 Пусть на тело действует произвольная система сил
Пусть на тело действует произвольная система сил 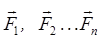 . Приведем эту систему сил к заданному центру. Выберем произвольную точку О за точку приведения (рис.14).
. Приведем эту систему сил к заданному центру. Выберем произвольную точку О за точку приведения (рис.14).
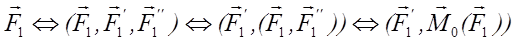 Рассмотрим одну из сил системы – F1. Добавим в точке О нулевую систему сил – (F1′, F2″). Заметим, что силы (F1, F1″) представляют пару сил, которую можно заменить вектором момента пары
Рассмотрим одну из сил системы – F1. Добавим в точке О нулевую систему сил – (F1′, F2″). Заметим, что силы (F1, F1″) представляют пару сил, которую можно заменить вектором момента пары
Рис.14
M0 (F1), приложенным в точке О (он же равен мо-менту силы F1 относительно центра О), то есть исходная сила эквилентна силе F1′ и вектору момента пары, приложенным в той же точке.
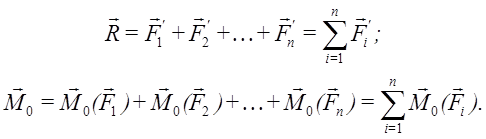 Проведя аналогичную операцию со всеми векторами исходной системы сил, мы получим два пучка векторов, приложенных в точке O – пучок сил
Проведя аналогичную операцию со всеми векторами исходной системы сил, мы получим два пучка векторов, приложенных в точке O – пучок сил 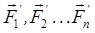 и пучок векторов моментов
и пучок векторов моментов 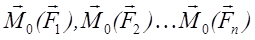 которые приводятся к эквивалентной системе двух векторов:
которые приводятся к эквивалентной системе двух векторов:
Главным вектором системы сил называют вектор, равный векторной сумме этих сил (вектор R). Значение главного вектора сил не зависит от выбора точки приведения.
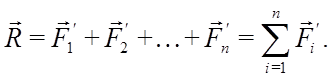
Главным моментом системы сил относительно точки О тела называют сумму векторных моментов всех сил системы относительно этой точки (вектор момента результирующей пары М0). Вектор М0 зависит от точки приведения О:
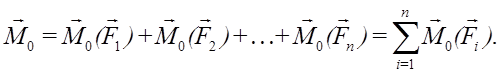
По проекциям сил можно найти модуль главного вектора и главного момента, а также косинусы их углов с осями координат.
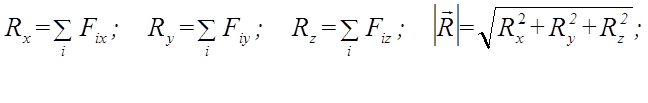
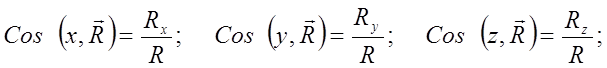
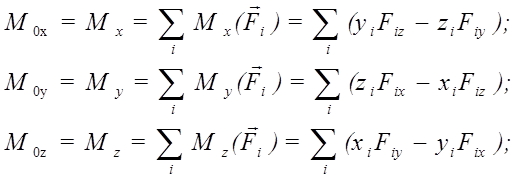
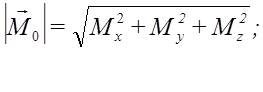
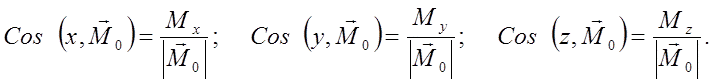
Главный момент плоской системы сил перпендикулярен главному вектору.
1.7. Условия равновесия систем сил
Пространственная система сил
Если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из главного вектора и главного момента пары. Чтобы такая система сил была эквивалентна нулю, необходимо и достаточно, чтобы выполнялось условие: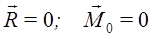 ( где О – произвольная точка)
( где О – произвольная точка)
Эти условия являются векторными условиями равновесия для любой системы сил. В аналитической форме это эквивалентно условиям: Rx=Ry=Rz=0; Mx=My=Mz=0,
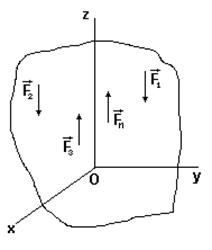 то есть в самом общем случае имеем шесть скалярных уравнений равновесия (уравнений статики).
то есть в самом общем случае имеем шесть скалярных уравнений равновесия (уравнений статики).
Система параллельных сил (рис. 15)
Пусть Fi параллельно оси Oz, тогда
Mz тождественно равно нулю и
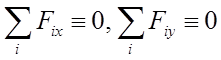 .
.
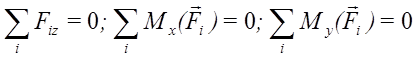 Таким образом, имеем три уравнения равновесия
Таким образом, имеем три уравнения равновесия
Рис.15
Плоская система сил (рис. 16)
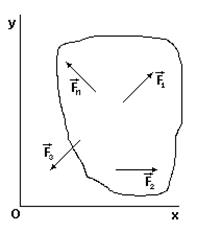 После отбрасывания тождеств:
После отбрасывания тождеств:
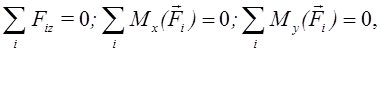
Содержание:
- Момент силы
- Момент силы относительно точки (центра)
- Момент силы относительно оси
- Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
- Моменты силы относительно координатных осей
- Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)
Момент силы (момент силы относительно точки; также: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — эо векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Момент силы
Система сходящихся сил, которая будет рассмотрена в главе 2, является особой среди
систем сил. Только в этой системе линии действия сил имеют одну точку пересечения. Поэтому для ее изучения достаточно основных понятий статики, рассмотренных в разделе 1. Для изучения других систем сил необходимо ознакомиться с понятиями момента силы и пары сил.
Понятие о моменте силы – одно из основных понятий механики, которое широко используется и в теоретических исследованиях и при практических расчетах. К понятию момента силы человечество пришло, рассматривая равновесие и движение тел, имеющих точку или ось вращения (в частности блоков и рычагов, которые использовались в практике еще до нашей эры).
Например, на неподвижный блок (рис. 3.1) действует сила  , вращающей его вокруг горизонтальной оси О. Стержень АВ (рис. 3.2), который имеет неподвижную шарнирную опору A, будет вращаться вокруг оси шарнира под действием собственной силы тяжести
, вращающей его вокруг горизонтальной оси О. Стержень АВ (рис. 3.2), который имеет неподвижную шарнирную опору A, будет вращаться вокруг оси шарнира под действием собственной силы тяжести  В обоих примерах сила обуславливает вращательное движение тела. По мере вращательного действия силы на тело является момент силы.
В обоих примерах сила обуславливает вращательное движение тела. По мере вращательного действия силы на тело является момент силы.


Момент силы относительно точки (центра)
Заданная сила  , изображена вектором
, изображена вектором  , приложенная к некоторому телу в точке А. Определим момент силы
, приложенная к некоторому телу в точке А. Определим момент силы  относительно точки О (рис. 3.3). Векторным моментом силы относительно точки О называется вектор, приложенный в точке О, равный векторному произведению радиуса вектора точки приложения силы на вектор силы:
относительно точки О (рис. 3.3). Векторным моментом силы относительно точки О называется вектор, приложенный в точке О, равный векторному произведению радиуса вектора точки приложения силы на вектор силы:

где  – радиус-вектор точки приложения силы относительно точки О.
– радиус-вектор точки приложения силы относительно точки О.
Определим величину (модуль) и направление вектора  . Согласно понятиям и свойствам векторного произведения двух векторов, величина (Модуль) момента силы
. Согласно понятиям и свойствам векторного произведения двух векторов, величина (Модуль) момента силы  относительно точки О равна:
относительно точки О равна:

Обозначим  . Поскольку
. Поскольку 
 Тогда:
Тогда:

где  (рис. 3.3) – высота
(рис. 3.3) – высота  опущенная из вершины В (с точки О) на сторону АВ этого треугольника, совпадает с линией действия силы. Короткое расстояние от точки О до линии действия силы называется плечом силы относительно этой точки. Из этого следует, что модуль (величина) момента силы относительно точки равна произведению величины силы на ее плечо относительно этой точки.
опущенная из вершины В (с точки О) на сторону АВ этого треугольника, совпадает с линией действия силы. Короткое расстояние от точки О до линии действия силы называется плечом силы относительно этой точки. Из этого следует, что модуль (величина) момента силы относительно точки равна произведению величины силы на ее плечо относительно этой точки.

Вектор  направляется по правилу векторного произведения: векторный момент силы относительно точки (Центра) является перпендикулярным к плоскости, в которой размещены сила и точка (центр) так, чтобы с его конца было видно попытки силы возвращать тело вокруг точки (Центра) против хода часовой стрелки.
направляется по правилу векторного произведения: векторный момент силы относительно точки (Центра) является перпендикулярным к плоскости, в которой размещены сила и точка (центр) так, чтобы с его конца было видно попытки силы возвращать тело вокруг точки (Центра) против хода часовой стрелки.
Заметим, что  . Поэтому:
. Поэтому:

Модуль момента силы относительно точки равен удвоенной площади треугольника, вершинами которого является точка и начало и конец вектора 
Если линия действия силы проходит через точку (центр), то h = 0, и из формулы (3.2) видно, что момент силы относительно этой точки будет равняться нулю.
Момент силы относительно точки не изменяется при переносе силы вдоль ее линии действия, поскольку неизменным остается плечо силы относительно точки (рис. 3.4).

Если на тело действует плоская система сил, то векторы моментов всех сил системы относительно некоторого центра, что лежит в плоскости действия сил, будут перпендикулярны этой плоскости, а следовательно, параллельные и их можно считать скалярными величинами, которые отличаются только величиной и знаками.
В этом случае целесообразно ввести понятие алгебраического момента силы относительно точки (центра), равный взятом со знаком «+» или «-» произведения модуля силы на плечо относительно этой точки (центра)

Будем считать момент положительным, если сила пытается вращать тело вокруг точки (центра) против хода часовой стрелки (рис. 3.5, а), и отрицательным – если по ходу часовой стрелки (рис. 3.5, б). Единицы момента силы: 

Момент силы относительно оси
Изучая пространственные системы сил, будем использовать понятие момента силы относительно оси.
Моментом силы относительно оси называется величина, равная алгебраическому моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Пусть к телу в некоторой точке А приложена сила  (Рис. 3.6). определим момент силы
(Рис. 3.6). определим момент силы  относительно произвольной оси
относительно произвольной оси  . Проведем плоскость П, перпендикулярную оси
. Проведем плоскость П, перпендикулярную оси  .
.
Точку пересечения плоскости П с осью  обозначим А. Спроектируем силу
обозначим А. Спроектируем силу  на плоскость П и получим силу
на плоскость П и получим силу 

Согласно определению 
Таким образом, чтобы определить момент силы относительно оси, необходимо:
– спроектировать эту силу на плоскость, перпендикулярную оси;
– найти точку пересечения оси с этой перпендикулярной плоскостью;
– определить алгебраический момент полученной проекции относительно точки пересечения оси с плоскостью.
Из формулы (3.5) следует, что момент силы относительно оси равен нулю, если:
1) сила параллельна оси, тогда 
2) линия действия силы пересекает ось, тогда 
Эти два условия эквивалентны одному условию: момент силы относительно оси равен нулю, когда сила и ось лежат в одной плоскости. поскольку момент силы относительно оси  , то согласно принятому правилу знаков моментов следует, что момент силы относительно оси положительный, если, смотря с конца оси, видим, что проекция этой силы на плоскость, перпендикулярную оси, пытается вращать тело вокруг оси против часовой стрелки (рис. 3.7, а). если вращение происходит в направлении хода часовой стрелки, то момент силы относительно оси будет отрицательным (рис. 3.7, б). Можно доказать, что момент силы относительно оси не зависит от выбора точки О на этой оси.
, то согласно принятому правилу знаков моментов следует, что момент силы относительно оси положительный, если, смотря с конца оси, видим, что проекция этой силы на плоскость, перпендикулярную оси, пытается вращать тело вокруг оси против часовой стрелки (рис. 3.7, а). если вращение происходит в направлении хода часовой стрелки, то момент силы относительно оси будет отрицательным (рис. 3.7, б). Можно доказать, что момент силы относительно оси не зависит от выбора точки О на этой оси.

Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
Теорема 3.1. Проекция векторного момента силы относительно точки на ось, проходящей через эту точку, равен моменту силы относительно этой оси.
Доказательство. Сила  приложена в точке А пространства. Выберем произвольную точку О и проведем оси
приложена в точке А пространства. Выберем произвольную точку О и проведем оси  (рис. 3.8). Определим момент силы
(рис. 3.8). Определим момент силы  относительно оси
относительно оси  и относительно точки О на ней.
и относительно точки О на ней.
Известно, что 

где 
Из курса элементарной геометрии известно, что 
где  – угол между плоскостями этих треугольников, а следовательно, и угол между перпендикулярами к этим плоскостей.
– угол между плоскостями этих треугольников, а следовательно, и угол между перпендикулярами к этим плоскостей.
Поскольку вектор  перпендикулярный плоскости
перпендикулярный плоскости , а ось
, а ось  перпендикулярна к
перпендикулярна к 

Учитывая равенства (3.6), (3.7), получим 
Знак  полностью определяется знаком
полностью определяется знаком  .
.
Поскольку

что и требовалось доказать.
Моменты силы относительно координатных осей
Пусть на тело действует сила  приложенная в точке А (рис. 3.9). выберем произвольную точку О и из нее проведем оси декартовой системы координат.
приложенная в точке А (рис. 3.9). выберем произвольную точку О и из нее проведем оси декартовой системы координат.
Определим момент силы  относительно этих осей. Для этого запишем выражение для момента силы
относительно этих осей. Для этого запишем выражение для момента силы  относительно точки О.
относительно точки О.

Согласно (3.1), где
где  – радиус-вектор точки А относительно точки О.
– радиус-вектор точки А относительно точки О.
Вектор силы  и радиусвектор
и радиусвектор  через проекции на оси координат выражаются:
через проекции на оси координат выражаются:

где  – координаты точки А;
– координаты точки А;  – орты выбранной системы координат.
– орты выбранной системы координат.
Тогда векторное произведение  можно записать в виде определителя:
можно записать в виде определителя:

Раскрывая этот определитель, получим

Представим векторный момент  через его проекции на оси координат:
через его проекции на оси координат:

Сравнивая правые части равенств (3.9) и (3.10), получим:

Поскольку точка О принадлежит осями  , то из формул (3.11), учитывая зависимость (3.8), получим выражения:
, то из формул (3.11), учитывая зависимость (3.8), получим выражения:

Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)
Теорема 3.2. Момент равнодействующей пространственной системы сходящихся сил
относительно некоторого центра (точки) равна векторной сумме моментов составляющих сил относительно того же центра (точки).
Доказательство. На тело действует пространственная система сходящихся сил  линии действия которых пересекаются в точке В (Рис. 3.10, а). заменим
линии действия которых пересекаются в точке В (Рис. 3.10, а). заменим
данную систему сил эквивалентной системой, все силы которой приложенные в точке В
(Рис. 3.10, б). Равнодействующую системы, прилагаемую в той же точке В, обозначим  . Найдем момент равнодействующей
. Найдем момент равнодействующей  относительно точки (центра) О. Согласно формуле (3.1),
относительно точки (центра) О. Согласно формуле (3.1),  где
где  – радиус-вектор точки приложения всех сил системы и равнодействующей относительно центра О.
– радиус-вектор точки приложения всех сил системы и равнодействующей относительно центра О.

Известно, что  . Тогда
. Тогда 
Итак, получили равенство 
Теорема доказана.
Уравнение (3.13) является математическим записи теоремы Вариньона для пространственной системы сходящихся сил.
В случае плоской системы сходящихся сил теорема Вариньона запишется так:

Итак, момент равнодействующей плоской системы сходящихся сил относительно некоторого центра (точки), лежащий в плоскости действия сил, равна алгебраической сумме моментов составляющих сил относительно этого самого центра (точки).
Рассмотрим пример на применение теоремы Вариньона.
Задача. На согнутый под прямым углом стержень АВС действуют силы  и
и  как показано на рис. 3.11. Найти моменты этих сил относительно точки А, если
как показано на рис. 3.11. Найти моменты этих сил относительно точки А, если 

Решение.

Для определения момента силы  относительно точки используем теорему Вариньона.
относительно точки используем теорему Вариньона.
Разложим силу  на две составляющие: горизонтальную
на две составляющие: горизонтальную  и вертикальную
и вертикальную  . Величины этих составляющих
. Величины этих составляющих 
 Тогда, согласно теоремой 3.2, получим:
Тогда, согласно теоремой 3.2, получим:

Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
