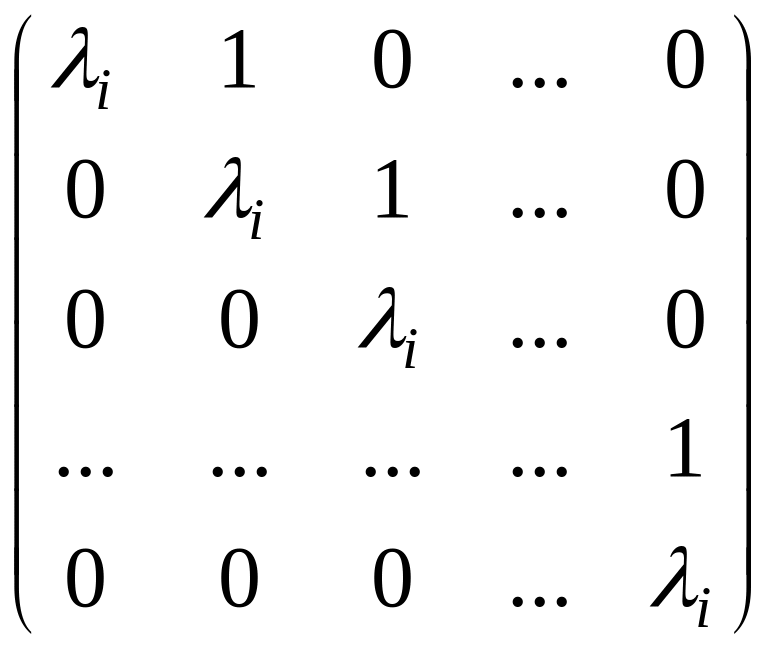Визуализация собственных значений и собственных векторов
Перевод
Ссылка на автора
Собственные значения и собственные векторы являются очень важной концепцией в линейной алгебре и машинном обучении в целом. В моем предыдущем статья Я представлял эти концепции с точки зрения анализа основных компонентов, предоставляя практические примеры. В этой статье я подробнее остановлюсь на математике, лежащей в основе этих понятий, и предоставлю геометрическую интерпретацию того, что собираюсь объяснить.
Для этого я расскажу о следующей теме:
- Линейное преобразование
- Собственные значения и собственные векторы
- Алгебраическая и геометрическая кратность
Итак, начнем с первой темы.
Линейное преобразование
Вообще говоря, преобразование – это любая функция, определенная в доменном пространстве V с выходами в кодомене W (где V и W – многомерные пространства, не обязательно евклидовы).
Преобразование, которое сохраняет операции сложения и скалярного умножения следующим образом:
Называется Linear Transformation, и теперь мы будем называть его T.
Давайте рассмотрим следующие два числовых примера, чтобы иметь это в виду. Представьте, что мы получили преобразование T, определенное в R2, с выходами в R:
Как видите, это преобразование не является линейным, поскольку не сохраняет аддитивности. А как насчет этого?
Более того:
Как видите, аддитивность и умножение на скаляр сохраняются, следовательно, преобразование является линейным. Стоит отметить, что единственными линейными преобразованиями из R2 в R являются те, которые выглядят как w = ax + by, следовательно, линейные комбинации компонентов векторов области.
Очень важное свойство линейных систем задается теоремой о представлении, которая утверждает, что линейное преобразование может быть представлено следующим образом:
Где A – это так называемая матрица представления. Мы будем использовать эту формулу, поскольку она более компактна и удобна.
Теперь каждое преобразование может влиять на направление и расширение вектора (для более ясного объяснения формы векторов в многомерном пространстве вы можете прочитать мою предыдущую статью Вот). Однако, учитывая преобразование T, существует очень интересный класс векторов, на которые это преобразование влияет только с точки зрения расширения, поскольку направление остается неизменным. Общий векторvс этим свойством таково, что:
гделямбдаявляется фактором расширения. Эти векторы называются собственными векторами, а значениелямбдасвязанный с ними называется собственное значение.
Собственные значения и собственные векторы
Как и предполагалось, собственными векторами являются те векторы, направление которых остается неизменным после преобразования через фиксированный T, а собственными значениями являются те значения коэффициента расширения, которые связаны с ними.
Чтобы быть более точным, собственные векторы являются векторами, которые не являются тривиальными, следовательно, отличаются от0, Это потому, что равенство выше всегда имеет по крайней мере одно решение, которое является тривиальнымv = 0,
Как мы можем найти наши собственные векторы и собственные значения при условии, что эти первые отличаются от тривиального вектора? Для этого давайте переосмыслим нашу линейную систему с помощью теоремы о представлении:
Как и ожидалось, эта система имеет по крайней мере одно решение, которое является тривиальным. Следовательно, мы хотим найти те значения лямбды, для которых определитель матрицы (A-лямда* I) равно нулю (в противном случае это означало бы, что из-за теоремы Крамера система имеет 1 единственное решение).
Итак, давайте установим наше уравнение:
Это уравнение называется характеристическим уравнением, а его корнями являются собственные значения. Кроме того, из-за основной теоремы алгебры«Каждый многочлен степени n имеет n решений в C (множество комплексных чисел)»мы знаем, что степень характеристического уравнения будет числом собственных значений, связанных с этой системой.
Давайте рассмотрим следующий пример:
Из характеристического уравнения мы вывели два собственных значения 3 и -1. Чтобы привести числовой пример, я собираюсь найти векторы, называемые собственными векторами, связанными слямбда= 3 (то же самое верно длялямбда= -1). Быстрый ярлык для этой цели может быть полезен, если мы рассмотрим матрицу A. Действительно, поскольку мы просили неединственность решения, мы уже знаем, что определитель матрицы (A-lI) равен 0, следовательно, пока Решив получившуюся систему, мы можем напрямую избавиться от одного из двух ограничений:
Давайте визуализируем это:
По сути, все векторы, которые лежат на этой прямой линии, являются собственными векторами, связанными с собственным значением 3: после преобразования через T они будут только расширяться / сокращаться, но не изменяться в направлении. Рассмотрим, например, следующий вектор:
Теперь давайте изменим это:
Как видите, его величина теперь в 3 раза больше, но направление остается прежним
Теперь давайте перейдем к последней теме этой статьи – алгебраической и геометрической множественности, связанной с собственными значениями и собственными векторами.
Алгебраическая и геометрическая кратность
Теперь представьте, что у вас есть характерное уравнение степениNно вы найдете только один корень. Следовательно, поскольку степеньNэтот корень, как говорят, имеет алгебраическую кратностьN, Давайте рассмотрим два следующих примера:
В первом случае мы имеем одно собственное значение, равное -2, не имеет кратности (поскольку его мощность равна 1), в то время как собственное значение -1 (из многочлена 2-й степени) будет иметь кратность, равную 2.
Теперь вопрос: уважается ли эта множественность и с геометрической стороны проблемы? Другими словами, равняется ли количество раз, когда собственное значение появляется в решении, равному размерам / степеням свободы соответствующего собственного пространства (которое является набором связанных собственных векторов)?
Ответ не всегда. Всякий раз, когда у нас есть собственное значение с кратностью, равнойNи соответствующее собственное пространство с размерами меньшеNмы называем этот коэффициент лямбда нерегулярным (в противном случае собственные значения называются регулярными).
Давайте наглядно представим это на примере выше:
Как видите, даже если у нас есть собственное значение с кратностью 2, ассоциированное собственное пространство имеет только одно измерение, так как оно равно y = 0.
Вывод
Собственные значения и собственные векторы являются фундаментальными в науке о данных и построении модели в целом. Помимо их использования в PCA, они используются, в частности, в спектральной кластеризации и сжатии изображений. Следовательно, важно иметь в виду их геометрическую интерпретацию.
Свойства собственных векторов линейных операторов (преобразований)
1. Собственные векторы линейного преобразования, принадлежащие различным собственным значениям, линейно независимы.
Аналогичное утверждение было доказано для собственных векторов матрицы (см. свойство 1).
2. Все собственные векторы линейного преобразования , принадлежащие одному собственному значению, совместно с нулевым вектором образуют линейное подпространство, инвариантное относительно преобразования
. Такое линейное подпространство называется собственным для преобразования
.
В самом деле, условие (9.5) можно записать в виде , где
— тождественное преобразование. Множество векторов
, удовлетворяющих последнему равенству, составляет ядро линейного преобразования
, т.е. является линейным подпространством
(собственное подпространство, отвечающее собственному значению
). Покажем, что это подпространство инвариантно относительно преобразования
. Действительно, любой вектор
в силу равенств
отображается в коллинеарный ему вектор
, также принадлежащий
.
3. Для собственного значения линейного преобразования
существует цепочка инвариантных подпространств
(9.8)
где ;
— некоторое натуральное число
.
Все перечисленные в цепочке (9.8) множества , являются линейными подпространствами по свойству ядра линейного преобразования. Каждое из подпространств
инвариантно относительно преобразования
, поскольку для любого вектора
его образ
, так как в силу перестановочности многочленов от одного и того же линейного преобразования (см. пункт 2 замечаний 9.3)
так как согласно определения ядра оператора.
Докажем включение . Если
, то
, при этом очевидно, что
то есть
Остальные включения доказываются аналогично.
Из цепочки (9.8) “расширяющихся” подпространств следует, что их размерности не убывают
поэтому в силу конечномерности пространства существует такое
, что
, т.е.
. Покажем, что дальнейшего “увеличения” подпространств нет, т.е.
для любого натурального
. Предположим противное. Пусть
и для некоторого
пространства не совпадают:
, то есть существует вектор
, который не принадлежит пространству
. Обозначим
. Тогда, с одной стороны,
, так как
, поскольку
. С другой стороны,
, так как
, поскольку
. Следовательно, и
и
одновременно, что противоречит предположению
.
Таким образом, в цепочке (9.8) размерности пространств , возрастают. Поэтому
.
Корневым подпространством линейного преобразования для собственного значения
называется линейное подпространство
с наименьшим натуральным показателем
, для которого
.
4. Если — собственное значение линейного преобразования
, то пространство
можно представить в виде прямой суммы
, где
— корневое подпространство, а
— инвариантное относительно
подпространство, в котором нет собственных векторов, принадлежащих собственному значению
.
В самом деле, покажем, что пересечение этих подпространств есть нулевой вектор: . Выберем вектор
. Так как вектор
, то существует такой вектор
, что
. Поскольку
, то
. Тогда
. Следовательно, вектор
, но
, так как
— корневое подпространство. Значит,
то есть
По теореме 9.1 о размерности ядра и образа получаем, что . Следовательно, пространство
можно представить в виде прямой суммы подпространств
(см. признаки прямых сумм подпространств).
Докажем, что в нет собственных векторов, принадлежащих собственному значению
. Действительно, пусть
— собственный вектор, соответствующий собственному значению
. Тогда
и в силу (9.8)
. Подпространство
имеет с
только один общий вектор (нулевой). Поэтому
, так как
. Инвариантность подпространства
следует из перестановочности операторов
и
(см. пункт 2 замечаний 9.3). В самом деле, для любого вектора
существует прообраз
. Поэтому в силу перестановочности операторов
поскольку и
. Таким образом, инвариантность подпространства
доказана, так как
.
Теорема (9.5) о разложении пространства в сумму корневых подпространств
Если все различные корни характеристического уравнения линейного преобразования
являются его собственными значениями, то пространство
можно разложить в прямую сумму инвариантных (корневых) подпространств:
(9.9)
где — корневое подпространство, соответствующее собственному значению
.
В самом деле, по свойству 4 можно “отщепить” корневое подпространство , т.е. представить пространство
в виде прямой суммы инвариантных подпространств
, причем в
нет собственных векторов, принадлежащих собственному значению
. В пространстве
определено сужение
преобразования
. Применяя свойство 4 к сужению
, аналогичным образом можно “отщепить” корневое подпространство
, т.е. представить пространство
в виде прямой суммы инвариантных подпространств:
. Этот процесс следует продолжить до тех пор, пока не исчерпаются все корни характеристического уравнения.
Следствие. Если все различные корни характеристического уравнения линейного преобразования
являются его собственными значениями, то существует базис пространства
, в котором матрица
линейного преобразования имеет блочно-диагональный вид
где — матрицы сужений
, преобразования
на корневые подпространства.
Согласно следствию из теоремы 9.2, такой базис можно получить, записывая последовательно базисы корневых подпространств (9.9).
Алгебраическая и геометрическая кратности собственных значений
Алгебраической кратностью собственного значения линейного оператора (преобразования)
называется кратность корня
характеристического многочлена
(или, что то же самое, кратность корня характеристического уравнения
).
Геометрической кратностью собственного значения линейного оператора (преобразования)
называется размерность собственного подпространства
, соответствующего этому собственному значению.
Теорема 9.6 о кратностях собственных значений оператора. Геометрическая кратность собственного значения не превосходит его алгебраической кратности.
Представим пространство в виде прямой суммы
(см. свойство 4) и обозначим
. Выбрав базис пространства
, дополним его до базиса всего пространства. В этом базисе, согласно следствию теоремы 9.5, матрица
преобразования
будет иметь блочно-диагональный вид
, где квадратная матрица
порядка
является матрицей сужения
преобразования
на подпространство
, а матрица
является матрицей сужения
. Характеристический многочлен матрицы
имеет вид (см. определитель блочно-диагональной матрицы)
где — многочлены степеней
и
соответственно. Так как сужение
не имеет собственных значений, отличных от
, то
, в силу того, что
и основной теоремы алгебры. Поскольку сужение
не имеет собственных векторов, принадлежащих собственному значению
, то
. Следовательно,
-алгебраическая кратность собственного значения
. Тогда утверждение теоремы следует из включения (9.8):
, так как
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Линейная алгебра. Как найти алгебраическую кратность собственного значения?
Ученик
(68),
закрыт
1 год назад
0x1е78 = 7800
Гений
(96126)
1 год назад
Если геометрическая кратность собст. значения суть К, то в жордановой формн матрицы А-lambda*E будет РОВНО К нулевых столбцов, правда? А стало быть ранг таеой матрицы суть n-K. Вот этот ранг и нужно найти.
Ну а алгебраическая кратность это просто сумма размеров жордановых клеток с даной лямбдой.
Noname AnonУченик (68)
1 год назад
А для чего мы находим эти кратности? Точнее, для чего нужна каждая из них? Запутался
15
ВОРОНЕЖСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Руководство к решению задач по алгебре
Часть II Жорданова форма матрицы и жорданов базис
Практическое
пособие по курсу “Алгебра и геометрия”
для
студентов по специальности
Воронеж
2003
§1. Собственные векторы и собственные значения оператора.
Жорданова
форма матрицы и жорданов базис
Рассмотрим линейный оператор в пространстве и пусть – матрица этого оператора в некотором базисе .
Определение
1.
называется характеристическим
многочленом
матрицы
(
–
единичная матрица порядка
).
Определение
2. Вектор
называется собственным вектором
оператора
,
если
,
а
– собственным значением оператора
,
соответствующим собственному вектору
.
-
Алгоритм
нахождения собственного значения и
собственного вектора оператора
1)
Найдем все корни характеристического
многочлена
,
получим
– спектр оператора (множество всех
собственных значений);
2)
подставим
в систему
,
решим
ее и найдем все собственные векторы,
отвечающие собственному значению
,
затем подставим
и т.д.
1.2. Алгебраическая и геометрическая кратности собственного значения
Определение
3. Кратность
корня
в характеристическом многочлене
называется алгебраической
кратностью собственного значения
.
Определение
4. Геометрической
кратностью
собственного значения
называется размерность собственного
подпространства оператора
.
Утверждение.
,
где
– порядок матрицы оператора
.
Теорема.
Оператор
в базисе
имеет диагональную матрицу
в том и только том случае, когда базисные
векторы
– собственные, то есть
для всех
.
-
Жорданова форма матрицы и жорданов базис
Определение
5. Жордановой
клеткой
называется клетка вида
.
(1.1)
Теорема.
Для произвольного оператора
существует базис пространства
,
в котором матрица оператора имеет
клеточно-диагональный вид, причем на
главной диагонали стоят жордановы
клетки вида (1.1).
Этот
базис называется жордановым,
а данный канонический вид матрицы
называется жордановой
формой.
Замечание.
Жорданова форма определяется однозначно
с точностью до порядка клеток (каждой
клетке с
соответствует один собственный вектор).
Алгоритм нахождения жорданова базиса для одной жордановой клетки
Рассмотрим
жорданову клетку вида (1.1). По определению
матрицы оператора в 1-м столбце стоит
вектор
,
разложенный по базису
:
,
поэтому
.
Во
2-м столбце матрицы находится вектор
,
разложенный по этому же базису и т.д.
Таким
образом, собственный вектор
находим как решение системы
,
присоединенный вектор
– как решение системы
.
Очевидно, что
.
Продолжая
аналогичные рассуждения, для вектора
получим
.
Определение
6. Вектор
называется присоединенным
вектором высоты
.
Жорданов базис
состоит из собственных и присоединенных
к ним векторов.
Утверждение.
Алгебраическая кратность собственного
значения
равна сумме размеров жордановых клеток
с этим собственным значением.
Утверждение.
Геометрическая кратность
собственного значения
равна числу клеток в жордановой форме
с собственным значением
или числу линейно независимых собственных
векторов, соответствующих собственному
значению
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Материал из Викиконспекты
Перейти к: навигация, поиск
Алгебраическая кратность
| Определение: |
| Алгебраической кратностью , отвечающей собственному значению называется порядок нильпотентности оператора (нильпотентной добавки в спектральной компоненте )
NB: – кратность корня минимального полинома NB2: – максимальный размер Жорданова блока в матрице |
Геометрическая кратность
| Определение: |
| Геометрической(спектральной) кратностью с.з называется размерность собственного подпространства, соответствующего этому с.з:
NB: равна числу Жордановых блоков в соответствующей матрице компоненты |
Полная кратность
| Определение: |
| Полной кратностью , соответствующей с.з. называется размерность ультраинвариантного подпространства, соответствующего этому с.з:
NB: – также кратность корня характеристического полинома NB2: – также размер блока, соответствующего спектральной компоненте , т.е. размер матрицы |
Теорема Гамильтона-Кэли
| Теорема (Гамильтон, Кэли): |
|
Для любого оператора общего вида выполняются три факта: Полином является аннулирующим выполняется |
| Доказательство: |
|
; ; ; поделим одно на другое: , т.е. второе утверждение верно тогда характеристический полином получается из идеала соответствующего аннулирующего полинома и тождество Кэли сохраняется: |