Амплитуда данного положения Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Эластичность ↺ | |
| Эластичность | Простое гармоническое движение (SHM) ↺ | |
| Простое гармоническое движение (SHM) | Эмпирические константы для SHM ↺ |
|
✖Угловая Частота постоянно повторяющегося явления, выраженная в радианах в секунду.ⓘ Угловая частота [ω] |
+10% -10% |
||
|
✖Период времени SHM – это время, необходимое для периодического движения.ⓘ Период времени СГМ [tp] |
+10% -10% |
||
|
✖Характеристика фазового угла периодической волны. Угловая составляющая периодической волны известна как фазовый угол. Это комплексная величина, измеряемая угловыми единицами, такими как радианы или градусы.ⓘ Угол фазы [θ] |
+10% -10% |
||
|
✖Положение частицы — это фаза колеблющейся частицы в любой момент времени — это состояние колеблющейся частицы относительно ее смещения и направления вибрации в этот конкретный момент.ⓘ Положение частицы [X] |
+10% -10% |
|
✖Амплитуда – это мера его изменения за один период.ⓘ Амплитуда данного положения [A] |
⎘ копия |
Амплитуда данного положения Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Угловая частота: 10.28 оборотов в секунду –> 10.28 Герц (Проверьте преобразование здесь)
Период времени СГМ: 0.6 Второй –> 0.6 Второй Конверсия не требуется
Угол фазы: 8 степень –> 0.13962634015952 Радиан (Проверьте преобразование здесь)
Положение частицы: 1.4 –> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.0174561426333536 метр –> Конверсия не требуется
3 Эмпирические константы для SHM Калькуляторы
Амплитуда данного положения формула
Амплитуда = (sin(Угловая частота*Период времени СГМ+Угол фазы))/Положение частицы
A = (sin(ω*tp+θ))/X
Что такое ШМ?
Простое гармоническое движение (SHM) определяется как периодическое движение точки вдоль прямой линии, так что ее ускорение всегда направлено к фиксированной точке на этой линии и пропорционально ее расстоянию от этой точки.
The maximum distance moved by a point on a vibrating body is called as amplitude. The amplitude is the vertical distance between the peak wave and the equilibrium point. The frequency and the distance traveled by the wave is an important factor to find the amplitude using the amplitude of wave calculator. Enter the required values in the amplitude calculator, it finds the amplitude of wave and prints the output within seconds. The distance can be entered for different units of measurement.
Amplitude of Wave Calculator
The maximum distance moved by a point on a vibrating body is called as amplitude. The amplitude is the vertical distance between the peak wave and the equilibrium point. The frequency and the distance traveled by the wave is an important factor to find the amplitude using the amplitude of wave calculator. Enter the required values in the amplitude calculator, it finds the amplitude of wave and prints the output within seconds. The distance can be entered for different units of measurement.
Code to add this calci to your website 

Formula:
A = D / F
Where,
A = Amplitude of Wave
D = Distance Traveled by the Wave
F = Frequency of the Wave
Example:
Find the amplitude of a sound wave where the distance traveled by the wave is 30cm and the frequency of the wave is 3 Hz.
Solution:
To Convert cm to m,
D = 30 cm
= (30 / 100) m
D = 0.3 m
A = D / F
= 0.3 / 3 = 0.1
A = 0.1dB
Related Calculators:
- Power Consumption Table
- Parallel Circuit Total Inductance Calculator
- Whip Antenna Design Calculator
- Brillouin Function Calculator
- Age Difference Calculator
- Truncated Pyramid Volume Calculator

| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
амплитуда:y=2sin(2x)+3
-
амплитуда:f(x)=sin(x)
-
амплитуда:f(x)=2cos(2x-1)+4
-
амплитуда:f(x)=cos(x)-3
-
амплитуда:y=tan(2x-5)
- Показать больше
Описание
Пошаговый поиск амплитуды периодических функций
function-amplitude-calculator
amplitude:sin(x)
ru
Блог-сообщения, имеющие отношение к Symbolab
Functions
A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Our free amplitude and period calculator is the best way to find the amplitude, period, and phase shift of the function with respect to trigonometry. You need just once a click, can calculate various amplitude-period parameters. Right now, let’s go to know how to find the period of a trig function of vibrating objects with this period and amplitude calculator.
Let’s move on!
Look at the picture showing where the amplitude, period, phase shift, and vertical shift occur on the graph.
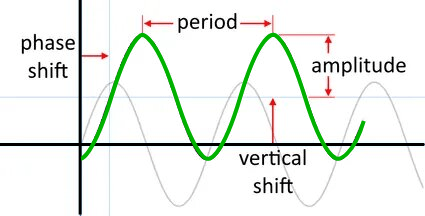
We can write such functions with the given formula
f(x) = A * sin(Bx – C) + D;
or
f(x) = A * cos(Bx – C) + D,
Where;
‘f(x)’ represents function of the sine & cosine
‘B’ represents the period
‘C’ represents the phase shift
‘D’ represents the vertical shift
Right now, you could solve the equations within the above formula and apply the formula to our amplitude period phase shift calculator online
How to Find Period?
The time required to complete one circle of the vibrating body or wave is known as the period
Formula
y = A sin(Bx + C)
Or
y = A cos(Bx + C) is 2π/|B| radians.
Explanation:
The length of the horizontal axis of the wave is the period after that function begins repeating itself. The value for a simple sine or cosine, is equal to 2π since sin(0) = sin(2π) = sin(4π) = … and the parts in between them are the same. Here, you could find the period and amplitude with the help of a period amplitude calculator.
How to Find Amplitude?
The maximum displacement covered by a point on a vibrating body or wave from its mean position is called the amplitude of the body.
Formula:
x = A sin (ωt + ϕ)
Or
x = A cos (ωt + ϕ)
Explanation:
The value of amplitude comes from the graph’s centerline. The value of sin or cosine is 1 since the centerline is 0. The function values of sin or cosine range from -1 to 1.
If you find the amplitude period and phase shift of a vibrating body, our amplitude and period calculator is beneficial for you in this regard.
How to Find Phase Shift?
Phase shift is defined as two signals which are at different points of their cycle at a given time.
Or
Inside changes on the wave or vibrating body affect the output (x-) axis value and shift the function left or right is called horizontal shift. You can also determine this particulate shift by subjecting this free and best horizontal shift calculator.
Formula:
F(x) = A sin(Bx − C) + D
Or
F(x) = Acos(Bx − C) + D
Explanation:
The phase shift or horizontal describes how far horizontally the graph moved from regular sine or cosine. If we have two functions unaltered, then its value is equal to 0.
When it comes to find amplitude period and phase shift values, the amplitude and period calculator will help you in this regard.
Vertical shift:
Outside changes on the wave or vibrating body that affect the output (y-) axis value and shift the function up or down are called vertical shifts.
Formula:
y=Asin(Bx)+D.
Or.
y=Acos(Bx)+D.
Explanation:
The vertical shift describes how far vertically the graph moved from the regular sine or cosine. The value is equal to 0 if we have the two functions unaltered.
How to find the amplitude of a function?
Now look at the following examples which are specifically solved to clarify the answer and verify the concept with this amplitude period and phase shift calculator
Example # 1
How to find the period and amplitude of the function f(x) = 3 sin(6(x − 0.5)) + 4 .
Solution
f(x) = 3 sin(6(x − 0.5)) + 4 —————- eq no 1
As the given generic formula is:
f(x) = A * sin(Bx – C) + D —————- eq no 2
When we compared eq no 1 & 2, the following result will be found
amplitude A = 3
period 2π/B = 2π/6 = π/3
phase shift = −0.5 (or 0.5 to the right)
vertical shift D = 4
Example # 2
How to find the period of a trig function of f(x)= 4sin(x)
Solution
f(x)=4sin(x) —————- eq no 1
As the given generic formula is:
f(x) = A * sin(Bx – C) + D —————- eq no 2
When we compared eq no 1 & 2, the following result will be found
Amplitude A= 4
Period B= 1
Phase shift C= 0
Vertical phase D= 0
How to use the amplitude, period, phase shift calculator?
Let this free amplitude and period calculator resolve the parameters of a trigonometric function. Let’s move on and have a look at its works!
Input
- Select the trigonometric function whether you want to calculate for sine or cosine.
- After that, enter the values of amplitude, period, phase shift, and vertical phase.
- Make a tap on the ”calculate” button
Output
The free find amplitude and period calculator does the following calculations:
- Determines the amplitude
- Determines the period
- Determines the phase shift
- Determines the vertical shift
FAQs
What is the relationship between period and frequency?
The frequency of the waves is inversely proportional to the time period.
Formula:
Frequency = 1/ time period
Or
F = 1/ T
Here you can calculate the period with respect to the amplitude-phase shift period calculator in a span of seconds.
How do you convert period to frequency?
According to the formula of frequency:
F (frequency) = 1 / T (period). f = c / λ = wave speed c (m/s) / wavelength λ (m).
What is amplitude in maths?
The value by which the graph of the function travels above and below its midline is called the amplitude of the trigonometric function.
Does phase shift affect amplitude?
There is a difference when sounds are loud, non-linear effect in the electronics and in hearing. If you have time-changing signals then phase shifts can affect the amplitude.
What does phase shift do in a signal?
Simply! Phase shift means that the two signals are at different points of their cycle at a given time. Phase shift is calculated as the angle (in degrees or radians) between two points on a circle at the same time.
Is phase shift negative or positive?
Although, phase shift could be affected by both shifting right/left and horizontal stretch/shrink. Therefore, the phase shift is positive when the shift is to the right or negative when the shift is to the left.
Is amplitude always positive?
Yes, the amplitudes of waves are always positive.
How do you calculate phase difference?
An oscilloscope’s timing markers offer the technique to calculate the phase between two signals. The time difference between two corresponding wave points on the signals represents the phase in units of time. Multiplying the ratio of this value to the period of the signals and calculating the phase in degrees.
Conclusion:
Use this online graphing trigonometric functions calculator for determining the parameters of amplitude, period, phase shift, and vertical shift. You can perform any type of calculation with respect to trigonometric functions. Although, our amplitude and period calculator find the values within a matter of seconds.
References:
From the source of Wikipedia: Amplitude, Peak amplitude & semi-amplitude, Peak-to-peak amplitude, Pulse amplitude, Amplitude normalization
From the source of khan academy: Midline, amplitude, and period
From the source of lumen learning: Amplitude and wavelength
Амплитуда колебаний, теория и онлайн калькуляторы
Амплитуда колебаний
Колебания и их амплитуда
Определение
Повторяющиеся движения или процессы называют колебаниями.
В зависимости от природы колебания могут быть механическими, электромагнитными, звуковыми и др. Разные виды колебаний описывают с помощью одинаковых уравнений и при этом используют одинаковые характеристики.
Колебания называют свободными (иди собственными), если они происходят за счет энергии, которая получена колебательной системой один раз и в дальнейшем внешних воздействий на эту систему нет.
Самым простым видом колебаний являются гармонические колебания.
Определение
Гармоническими колебаниями называют такие колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса..
Пусть происходят гармонические колебания некоторого параметра $s$, тогда эти колебания можно описать при помощи следующего уравнения:
[s=A{cos ({omega }_0t+varphi ) } left(1right),]
где $A=s_{max}$ – амплитуда колебаний; ${omega }_0$ – циклическая (круговая) частота колебаний; $varphi $ – начальная фаза колебаний (фаза при $t=0$); $({omega }_0t+varphi )$ – фаза колебаний.
Амплитудой называют максимальной значение величины, колебания которой рассматривают. Так как косинус (как и синус) изменяется в пределах от единицы до минус единицы, то величина $s$ находится в пределах $-Ale sle $+A.
Метод вращающегося вектора амплитуды колебаний
Гармонические колебания можно изображать графически (рис.1), при этом используют метод векторных диаграмм (или метод вращающегося вектора амплитуды). С этой целью, из какой – то произвольно избранной точки оси X, назовем ее точка O, под углом равным начальной фазе (угол $varphi $), откладывают вектор $overline{A}$. Длина этого вектора равна амплитуде ($A$) колебаний. Если этот вектор приводится во вращение с угловой скоростью ${omega }_0$, то проекция конца этого вектора перемещается по оси X и принимает значения от $-A$ до $A$, при этом закон колеблющейся величины будет таким, как представляет уравнение (1). Получается, что гармонические колебания можно изобразить при помощи проекции на некоторую ось вектора амплитуды $overline{A}$, который отложен из произвольной точки этой оси под углом $varphi $, вращающимся с угловой скоростью ${omega }_0$ вокруг избранной точки.
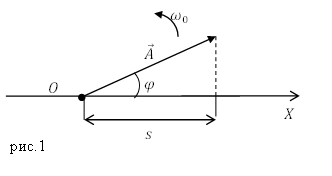
Примеры задач с решением
Пример 1
Задание. Материальная точка совершает гармонические колебания, которые описывает уравнение: $x=0,1{cos ({omega }_0t+varphi )(м) }$. Известно, что период колебаний этой точки равен T=5 c. Какова амплитуда скорости ($v_m$) и амплитуда ускорения ($a_m$) данной точки?
Решение. Прежде всего, найдем циклическую частоту колебаний точки, так как нам известен период колебаний:
[{omega }_0=frac{2pi }{T} left(1.1right).]
Зная закон изменения координаты, определим, как изменяется скорость материальной точки:
[v_x=frac{dx}{dt}=frac{d}{dt}left(x_m{cos left({omega }_0t+varphi right) }right)={-x}_m{omega }_0{sin left({omega }_0t+varphi right) }left(1.2right),]
где $x_m=0,1$ по условию задачи.
Из уравнения (1.2) следует, что амплитуда скорости колебаний точки равна:
[v_m=left|{-x}_m{omega }_0right|=x_m{omega }_0=0,1cdot frac{2pi }{T}=0,04pi left(frac{м}{с}right).]
Используя закон изменения скорости, получим закон изменения ускорения точки:
[a_x=frac{dv_x}{dt}={-x}_m{{omega }_0}^2{cos left({omega }_0t+varphi right) }left(1.3right).]
Из закона (1.3) следует, что амплитуда ускорения точки равна:
[a_m=left|{-x}_m{{omega }_0}^2right|=x_m{{omega }_0}^2=0,1{(frac{2pi }{T})}^2=0,1cdot frac{4{pi }^2}{25}=0,016{pi }^2 left(frac{м}{с^2}right).]
Ответ. $v_m=0,04pi frac{м}{с}$; $a_m=0,016{pi }^2frac{м}{с^2}$
Пример 2
Задание. К горизонтальной пружине, коэффициент упругости которой равен $k,$ прикреплен шар массой $M$. Шар находится на гладком столе, по которому может перемещаться без трения. Пуля летит горизонтально и ударяется о шар, застревает в нем. Скорость пули до удара равна $v_0$, масса пули $m$, скорость ее в момент удара направлена параллельно оси пружины. Какова амплитуда колебаний шара с пулей?
Массу пружины и сопротивление воздуха не учитывать.
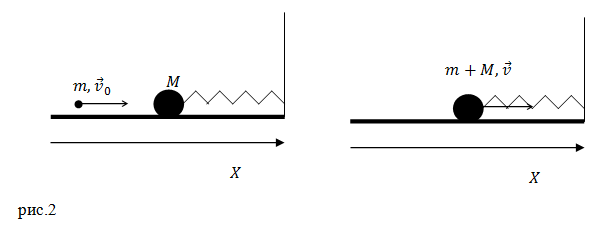
Решение. Запишем закон сохранения импульса для системы шар – пуля (до удара) и шар с пулей сразу после удара:
[overline{p}={overline{p}}’left(2.1right).]
Из рис.2 следует, что выражение (2.1) можно преобразовать к виду:
[mv_0=left(m+Mright)vleft(2.2right).]
Из (2.2) выразим скорость шара с пулей сразу после удара:
[v=frac{mv_0}{m+M}left(2.3right).]
Система пуля шар, выведена из состояния равновесия ударом пули. Она совершает свободные гармонические колебания. Кинетическая энергия переходит в потенциальную энергию сжатой пружины. Для двух состояний системы (первое состояние – максимальная скорость движения системы; второе состояние максимальное сжатие пружины) в соответствии с законом сохранения энергии запишем:
[frac{(m+M)v^2}{2}=frac{k{x_m}^2}{2}left(2.4right),]
где $x_m$ – амплитуда колебаний шара с пулей. Подставим величину скорости из (2.3) в (2.4) и выразим амплитуду:
[{left(m+Mright)v^2=k{x_m}^2to x_m=sqrt{frac{left(m+Mright)v^2}{k}}to x}_m=frac{mv_0}{sqrt{(M+m)k}}.]
Ответ. $x_m=frac{mv_0}{sqrt{(M+m)k}}$
Читать дальше: гармонические колебания.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

