Какое напряжение между фазой и нулём в отечественной электросети: 220 или 310? На самом деле и одно и другое! Всё дело в том, что в наших сетях протекает синусоидальный ток, а у синусоиды есть ряд характеристик и особенностей, которые мы попытаемся рассмотреть простым языком в этой статье.
Речь далее пойдет только о синусоидальном переменном токе или напряжении. Для тока другой формы всё сказанное далее, в принципе, справедливо, но будут отличаться формулы для вычисления и, соответственно, числовые значения.
Синусоида, её амплитуда и другие характеристики
Все мы знаем, что между фазой и нулём 220 вольт (230В по ГОСТу), но многие знают что выпрямленное и сглаженное сетевое напряжение превышает 300 вольт, да и конденсаторы в фильтры выпрямителей подбирают не ниже чем 400 вольт, откуда они берутся? Для начала рассмотрим график, на котором изображено синусоидальное напряжение в привычной всем розетке 220В.
На рисунке 1 по вертикали размечено напряжение в вольтах, а по горизонтали время. Обратите внимание, что напряжение в электросети периодично изменяется от -310 вольт, до + 310 вольт, каждый период изменений длится 20 миллисекунд, после чего повторяется.
Точно описать любую величину, изменяющуюся по синусоидальному закону можно с помощью трёх характеристик:
- Амплитуда — это высота синусоиды от нуля до верхней или нижней точки. В нашем случае это 310В. Обозначается буквами Im или Um, для тока и напряжения соответственно.
- Период — расстояние между двумя соседними максимумами или минимумами синусоиды. В электросетях РФ он равен 20 миллисекунд, так как стандартная частота — 50 Гц. Обозначается буквой T.
- Начальный фазовый угол — это величина, которая отражает насколько сдвинута синусоида по горизонтали относительно начального момента времени наблюдения (нулевой секунды). Если проще, то на графике выше фаза в начале графика начинается с 0, значит она не сдвинута, если бы начиналась с другой величины — то была бы сдвинутой на определенный угол.
При рассмотрении однофазной сети начальный фазовый угол нас не интересует, он используется при исследовании трёхфазного напряжения.
Рассмотрим этот график еще раз, но отметим на нём амплитуду и период.
График описывает формула синусоидального напряжения (для тока аналогично, но U меняется на I):
Из этого следует, что величина напряжения (или тока) в каждый конкретный момент времени разная, такая величина называется мгновенной. Соответственно и мгновенная мощность, выделяемая на активной нагрузке (R) в каждый момент будет разной:
Это подходящая формула для описания мгновенного состояния электрической цепи, но совершенно неудобная и неподходящая для измерения параметров и описания электрических цепей в общем. Поэтому используют какие-то усреднённые значения электрической мощности, напряжения и тока.
В литературе принято объяснять смысл действующих и амплитудных значений на примере силы тока. К тому же по определения, формулы и их смысл аналогичны, и для напряжения, и для тока. Поэтому я немного отойду от синусоидального напряжения, и далее пойдет речь о токе.
Действующее, среднеквадратичное, эффективное?
Теперь вы знаете, что амплитуда фазного напряжения в электросети равна 310В, но что такое 220В и откуда они берутся? Дело в том, что — 220В это действующее напряжение, его же называют среднеквадратичным или эффективным.
Это значит, что если на лампочку накаливания или нагревательную спираль подать переменный ток с действующим значением (силой) в 1 ампер, то на ней выделится та же мощность (количество тепла), как если бы через неё протекал постоянный ток в 1 ампер.
Для нахождения среднего значения переменного синусоидального тока за половину периода, необходимо проинтегрировать формулу этого тока, при этом пределами интегрирования выбирается половина периода:
Как отмечалось выше, формула для среднего переменного синусоидального напряжения (как и для ЭДС) будет аналогичной:
Но это средние величины, которые на практике не используется так часто, как действующие величины. Действующее напряжение или ток, находится подобным образом, при вычислениях интегрируется та же формула, но возведенная в квадрат, после чего извлекается корень. Пределы интегрирования уже не половина, а целый период. Кстати, поэтому действующее значение называется еще и «среднеквадратичным». Формулу действующего значения переменного синусоидального тока:
Действующий ток (Iд) или напряжение (Uд), в корень из двух раз меньше, чем амплитудное. Чтобы его вычислить, нужно амплитудное значение разделить на 1.41, или умножить на 0.707.
Uд=Um/1.41=0.707*Um
И наоборот, чтобы узнать амплитудное значение при известном действующем, нужно умножить его на 1.41 или разделить на 0.707. Приведем пример, из графика на рисунке 1, мы узнали, что амплитуда напряжения в однофазной электросети 310 вольт, найдем его действующее значение:
Uд=Um/1.41=310/1.41=219,8~220В
Мы получили привычные нам 220В. Как отмечалось ранее, действующие значения напряжения и тока удобно использовать для расчетов и описания электрических цепей, поэтому и говорят «в розетке 220В», «линейное напряжение 380В» и так далее.
Повторим пройденное: непрерывное тепловое воздействие переменного синусоидального тока на какую-то активную нагрузку за определенный период времени будет численно равно тепловому воздействию постоянного тока за тот же период, при условии, что величина постоянного тока была в 1.41 раз меньше амплитуды переменного. То есть за то же время выделится столько же теплоты.
В таком случае, при активной нагрузке (резисторы, ТЭНы, нихромовые спирали, лампы накаливания), можно приравнять действующее значение переменного тока или напряжения, к такому же по величине постоянному току или напряжению.
Какое напряжение измеряет мультиметр, амперметр или вольтметр?
В подавляющем большинстве случаев если на измерительном приборе вы выбираете режим измерения переменного тока или напряжения (U~, I~), вы измерите именно действующие значения. Однако есть и специфичные приборы, измеряющие амплитудные значения параметров в электрической сети, а также на электронных осциллографах могут выводится и действующие, и амплитудные величины измеряемых сигналов. Измерение амплитудных значений может обозначаться как Im.
При этом далеко не все приборы могут измерять переменный ток по форме отличный от синусоидального — пилообразный, прямоугольный и так далее. Вы могли видеть, что на хороших мультиметрах написано загадочное «TRUE RMS», что расшифровывается как: «True Root Mean Sqare», а переводится как — истинное среднеквадратичное значение. Такие измерительные приборы показывают действующие значения напряжений и токов любых форм (не только синусоидальных).
В завершение этой статьи, предлагаю вам закрепить знания и ознакомиться с прекрасным советским плакатом, на эту тему
2.1. Общие сведения
В электроэнергетике используют в
основном переменный ток. В настоящее
время почти вся электрическая энергия
вырабатывается в виде энергии переменного
тока. Основное преимущество переменного
тока по сравнению с постоянным током
заключается в возможности просто и с
минимальными потерями преобразовывать
напряжение при передаче энергии.
Генераторы и двигатели переменного
тока имеют более простое устройство,
надежней в работе и проще в эксплуатации
по сравнению с машинами постоянного
тока.
2.1.1. Амплитуда, частота и фаза синусоидального тока и напряжения
В современной технике широко используются
переменные токи: синусоидальные,
прямоугольные, треугольные и др. (рис.
2.1). Значение тока в любой момент времени
называется мгновеннымзначением.
Мгновенные значения тока, напряжения,
ЭДС обозначаются буквами![]() .
.

Токи, мгновенные значения которых
повторяются через равные промежутки
времени, называютпериодическими,
а наименьший промежуток времени,
через который эти повторения наблюдаются,
называютпериодомТ(рис.
2.1).
Если кривая изменения пе–
Рис. 2.1
риодического тока описывается
синусоидой, ток называется синусоидальным.
Если кривая отличается от синусоиды –
ток несинусоидальный. В электрических
цепях переменного тока наиболее
часто используют синусоидальную форму,
характеризующуюся тем, что все
напряжения и токи являются синусоидальными
функциями времени. В генераторах
переменного тока стремятся получить
ЭДС, изменяющуюся во времени по закону
синуса. Тем самым обеспечивается наиболее
выгодный эксплуатационный режим
работы электрических установок.
Все синусоидальные функции времени
(например, ток) записывают в одинаковой
форме:
![]() (2.1)
(2.1)
где
![]() –
–
мгновенное значение тока;![]() –максимальное (амплитудное)значение
–максимальное (амплитудное)значение
тока (рис. 2.2);![]() – угловая частота;
– угловая частота;![]() – начальная фаза.
– начальная фаза.
Аргумент синуса
![]() называетсяфазой.
называетсяфазой.
Угол
![]() равен фазе в начальный момент времени
равен фазе в начальный момент времени![]() =
=
0 и поэтому называетсяначальной
фазой. Фаза
с течением времени непрерывно растет
(рис 2.2). После ее увеличения на
![]() весь цикл изменения тока повторяется.
весь цикл изменения тока повторяется.
В течение периода![]() фаза увеличивается на
фаза увеличивается на![]() .
.
Поэтому отношение![]() определяет скорость изменения фазы и
определяет скорость изменения фазы и
называетсяугловой
частотой
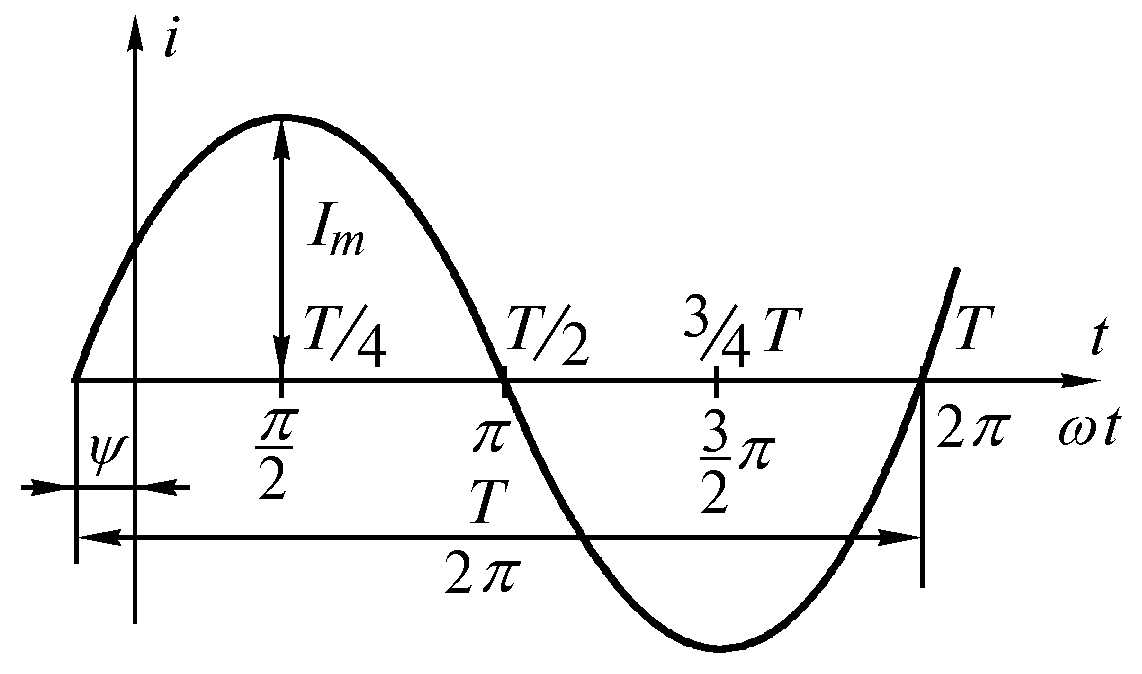
Рис. 2.2
![]() (2.2)
(2.2)
где
![]() – частота, равная числу периодов в
– частота, равная числу периодов в
секунду,Гц. При
стандартной частоте
![]() =
=
50 Гцугловая частота![]() За
За
аргумент синусоидальной функции
принимают время![]() или угол
или угол![]() .
.
Таким образом, для
определения мгновенных значений
![]() и
и![]() необходимо определить их параметры:
необходимо определить их параметры:
амплитуду, угловую частоту и начальную
фазу.
Постоянный ток
можно рассматривать как частный случай
переменного тока, частота которого
равна нулю. В современной технике
используется широкий диапазон частот
переменных токов от сотых долей до
миллиардов Герц. В электроэнергетике
нашей страны и Европы стандартная
частота 50 Гц,
США – 60 Гц.

Рис. 2.3
Синусоидальные ЭДС в современной
технике получают различными методами
в электромашинных или электронных
генераторах и других устройствах.
Наглядным примером является наведение
ЭДС за счет электромагнитной индукции
в рамке, вращающейся в однородном
магнитном поле (рис. 2.3).
Допустим, что рамка площадью
![]() содержит
содержит![]() витков и вращается с постоянной
витков и вращается с постоянной
угловой скоростью![]() в магнитном поле с индукцией
в магнитном поле с индукцией![]() .
.
Тогда потокосцепление рамки
![]() .
.
По закону электромагнитной индукции
в рамке наводится ЭДС
![]() .
.
Следовательно, ЭДС изменяется по
синусоидальному закону.
Рассмотренный способ получения ЭДС
является лишь наглядной иллюстрацией
и в технике не используется ввиду
экономической нецелесообразности
создавать достаточно сильное
равномерное магнитное поле в таком
большом воздушном промежутке.
В промышленности для получения
синусоидальных ЭДС применяют электрические
машины – синхронные генераторы,
приводимые во вращение тепловыми,
газовыми, гидравлическими и др.
двигателями.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Переменный электрический ток

Переменный ток (AC – Alternating Current) – электрический ток, меняющий свою величину и направление с течением времени.
Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC.
Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC – Direct Current – постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.
Величина тока будет равна квадратному корню из суммы квадратов двух величин – значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.
Термины AC и DC применимы как для тока, так и для напряжения.
Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:
Период T – время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота f – величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz). Частота f = 1/T

Циклическая частота ω – угловая частота, равная количеству периодов за 2π секунд.
ω = 2πf = 2π/T
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза ψ – величина угла от нуля (ωt = 0) до начала периода.
Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение – величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.
i = i(t); u = u(t)
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
i = Iampsin(ωt); u = Uampsin(ωt)
С учётом начальной фазы:
i = Iampsin(ωt + ψ); u = Uampsin(ωt + ψ)
Здесь Iamp и Uamp – амплитудные значения тока и напряжения.
Амплитудное значение – максимальное по модулю мгновенное значение за период.
Iamp = max|i(t)|; Uamp = max|u(t)|
Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) – максимальное отклонение от нулевого значения.
Среднее значение (avg) – определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение – среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) – определяется как квадратный корень из среднеарифметического квадратов всех
мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой Iamp (Uamp)
среднеквадратичное значение определится из расчёта:

Среднеквадратичное – это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов.
Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода,
что и равный по величине его среднеквадратичному значению постоянный ток.

Коэффициент амплитуды и коэффициент формы
Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой
амплитудное, среднеквадратичное и средневыпрямленное значения.
Коэффициент амплитуды – отношение амплитудного значения к среднеквадратичному.

Для синусоидального тока и напряжения коэффициент амплитуды KA = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды KA = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды KA = 1
Коэффициент формы – отношение среднеквадратичного значения к средневыпрямленному.

Для переменного синусоидального тока или напряжения коэффициент формы KФ  ≈ 1.111
≈ 1.111
Для тока и напряжения треугольной или пилообразной формы KФ  ≈ 1.155
≈ 1.155
Для переменного тока и напряжения прямоугольной формы KФ = 1
Замечания и предложения принимаются и приветствуются!
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мкс=0,001 мс = 0,000001сек =10 -6 сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами


Например, если частота тока равна 50 Гц, то период будет равен:
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2 .
.

Рисунок 2. Радиан.
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2 ). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .
). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .
? = 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник
Часть III. Цепи синусоидального тока
Тема 3. Цепи синусоидального тока
- Общие сведения и определения
- Комплексная амплитуда
- Действующие значения синусоидальной функции
- Изображение синусоидальных функций векторами. Векторная диаграмма
- Изображение синусоидальной функции комплексными числами
- Закон Ома в комплексной форме
- Уравнения элементов в комплексной форме
- § 3.1. Общие сведения и определения:
Переменный ток имеет большее распространение, чем постоянный.
- конструкция электродвигателей и генераторов переменного тока гораздо проще;
- генераторы переменного тока могут быть выполнены для более высокого напряжения;
- переменный ток легко преобразовывается с помощью трансформатора, что необходимо при распределении электроэнергии и т.д.
Переменный ток – ток, периодически меняющий свое значение и направление. Наибольшее значение переменного тока – его амплитуда.
Переменный ток характеризуется:
Амплитуда – наибольшие (положительные или отрицательные) величины.
Период – время, в течение которого происходит полное колебание тока в проводнике.
Фаза – характеризует состояние переменного тока в любой момент времени.
Основным видом переменного тока является синусоидальный (гармонический) ток. Закон изменения такого тока описывается синусоидальной функцией.
В линейных электрических цепях, в которых действуют синусоидальные источники, все электрические параметры изменяются по синусоидальному закону.
ЭДС:  .
.
Напряжение:  .
.
Ток:  ;
;
e(t), u(t), i(t) – мгновенные значения;
ω = 2π – угловая частота, [рад/с];
ƒ = 1 Т – циклическая частота, [Гц];
Любую синусоидальную функцию можно изобразить в виде графика, который называется графиком временных значений или временной диаграммой.

Расчет цепей синусоидального тока с использованием мгновенных значений требует громоздкой вычислительной работы и применим для простейших электрических цепей.
Для расчета цепей синусоидального тока синусоидальную функцию заменяют эквивалентной величиной.

где j = √ — 1 – мнимая единица.


 – комплексная амплитуда.
– комплексная амплитуда.
 – сопряженная комплексная амплитуда.
– сопряженная комплексная амплитуда.
 – поворотный множитель.
– поворотный множитель.
Последняя запись означает, что синусоидальное напряжение можно представить на комплексной плоскости в виде двух векторов, длина которых равна Um и которые равномерно вращаются со скоростями, равными ω в противоположные стороны.
- § 3.3. Действующие значения синусоидальной функции:
Действующее значение синусоидальной функции – ее количественная оценка.
Действующие значения – среднеквадратичные за период значения синусоидальной функции, то есть, если:


Аналогично и для тока I и ЭДС ε .
Часто используются выражения, связывающие между собой амплитуду и действующее значение:


Действующее значение – это постоянная величина, которую обычно обозначают той же буквой, что и амплитуду, только без индекса m.
Действующее значение тока оказывает такое же тепловое действие на проводник с сопротивлением R , что и переменный ток, в течение времени, равном периоду. Поэтому большинство электроизмерительных приборов фиксируют и реагируют на действующие значения.
- § 3.4. Изображение синусоидальных функций векторами. Векторная диаграмма:

где a – проекция вектора на ось y в момент времени t.

 рис. а рис. б
рис. а рис. б
Любому равномерно вращающемуся радиус-вектору соответствует некоторая синусоидальная функция, и наоборот.
Посмотрим, как условный графический образ синусоидальной функции – радиус-вектор – может быть применим при расчетах цепей переменного тока. Определим ток:
если:  и
и  .
.
Как известно, сумма двух синусоид одинаковой частоты ω представляет собой также синусоиду частотой ω , то есть i = Imsin (ωt + ψ ) и, следовательно, задача сводится к нахождению амплитуды Im и начальной фазы Ψ суммарного тока i. Искомые параметры Im и Ψ можно найти, воспользовавшись известными тригонометрическими преобразованиями.
Проведем решение задачи с помощью радиус-векторов I1m и I2m , вращающихся с частотой ω, положение которых для момента времени t = 0 показаны на рисунке ниже и осуществим геометрическое суммирование этих радиус-векторов по правилу параллелограмма. Результирующий радиус-вектор Im будет вращаться с частотой ω и является изображением некоторой синусоидальной функцией времени.
Следовательно, i = i1 + i2 – геометрическое изображение искомого тока.

Измерив дугу суммарного радиус-вектора и, зная выбранный масштаб, можно определить амплитуду Im тока. Непосредственно по чертежу определяется и начальная фаза Ψ.
Рассмотренная совокупность радиус-векторов, изображающих синусоидальные функции времени, называется векторной диаграммой.
- § 3.5. Изображение синусоидальной функции комплексными числами:
 Для введения комплексного изображения перенесем радиус-вектор, изображающий синусоидальную функцию времени в декартовой плоскости на плоскость комплексных чисел. Для чего совместим ось x с осью действительных чисел Re, а ось y – с Im.
Для введения комплексного изображения перенесем радиус-вектор, изображающий синусоидальную функцию времени в декартовой плоскости на плоскость комплексных чисел. Для чего совместим ось x с осью действительных чисел Re, а ось y – с Im.
Любому вектору A, расположенному на комплексной плоскости, однозначно соответствует комплексное число, которое может быть записано в трех формах:
Все три формы записи в соответствии с формулой Эйлера равнозначны:

Переход от одной формы записи к другой:

где a1 – действительная часть;
Запишем в трех формах выражение для единичных действительных и мнимых комплексных чисел ( A = 1 ):




Отношение комплексной амплитуды напряжения к комплексной амплитуде тока называется комплексным сопротивлением:

Модуль комплексного сопротивления, называемый полным сопротивлением, равен отношению амплитуды напряжения к амплитуде тока, а аргумент Ψ комплексного сопротивления – разности начальных фаз напряжения и тока:

Закон Ома в комплексной форме соответственно для амплитудных и действительных значений:
 .
.
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Источник
Содержание:
Электрические цепи синусоидального тока:
В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.
При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.
Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
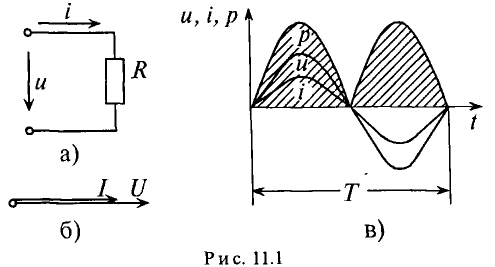
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение 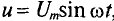
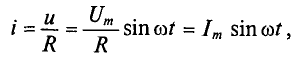
где 
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (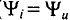 = 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 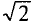 =1,41.
=1,41.
Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.
Активная мощность
Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.
Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.
Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
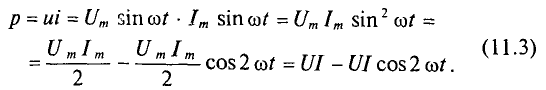
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 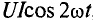 , изменяющейся с двойной частотой.
, изменяющейся с двойной частотой.
Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть
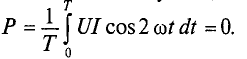
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
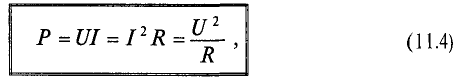
где U- действующее значение напряжения; I— действующее значение тока.
Единицей активной мощности является ватт:
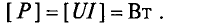
Поверхностный эффект и эффект близости
Сопротивление проводника постоянному току 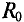 называют омическим сопротивлением и определяют выражением (2.8)
называют омическим сопротивлением и определяют выражением (2.8) 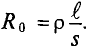 Сопротивление проводника переменному току R называют активным.
Сопротивление проводника переменному току R называют активным.
Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е. 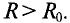
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).
На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.
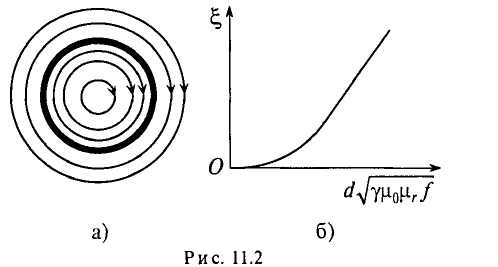
Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.
Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 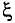 (кси)
(кси)
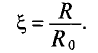
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости 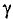 , магнитной проницаемости материала проводника
, магнитной проницаемости материала проводника 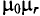 и частоты переменного тока
и частоты переменного тока  , проходящего по проводнику, показан на рис. 11.26.
, проходящего по проводнику, показан на рис. 11.26.
При токах большой частоты  (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
(радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
На величину активного сопротивления проводника R оказывает влияние и эффект близости.
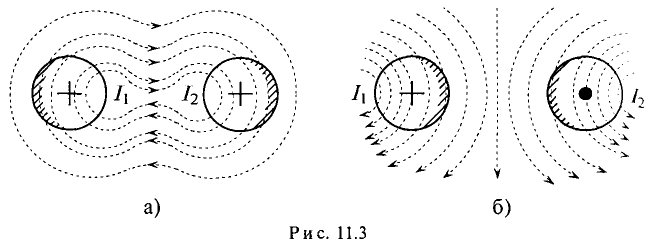
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.
Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).
Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.
Цепь с идеальной индуктивностью
Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток 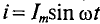 , то этот ток создает в катушке синусоидальный магнитный поток
, то этот ток создает в катушке синусоидальный магнитный поток 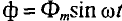 , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
, который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
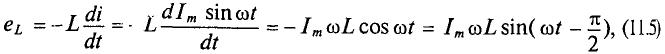
так как 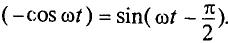
Очевидно, эта ЭДС достигает своего амплитудного значения 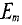 тогда, когда
тогда, когда 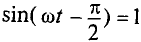 :
:
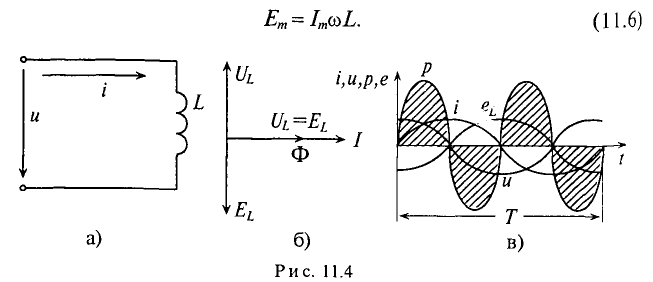
Тогда 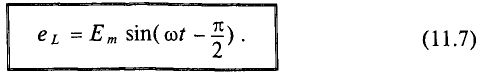
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 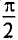 (рис. 11.46, в).
(рис. 11.46, в).
По второму закону Кирхгофа для мгновенных значений можно записать

Откуда 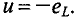
Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):
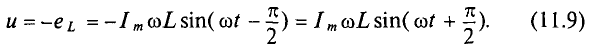
Очевидно, напряжение достигает своего амплитудного значения Um тогда, когда 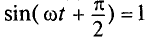 :
:

Следовательно, 
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 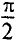 (рис. 11.46, в).
(рис. 11.46, в).
Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).
Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 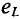 противодействует изменению тока.
противодействует изменению тока.
Если уравнение (11.10) разделить на 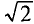 =1,41, то получается
=1,41, то получается 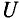 =
=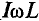 , откуда
, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.
Таким образом,

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
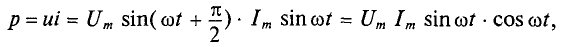
где 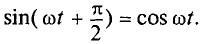
Следовательно, 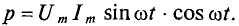
Полученное уравнение умножают и делят на 2:
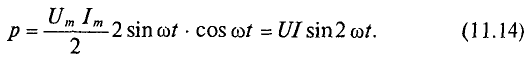
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.
Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (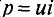 ) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно
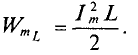
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.
Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.
Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
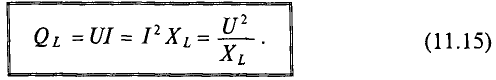
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. XL.
Цепь с емкостью
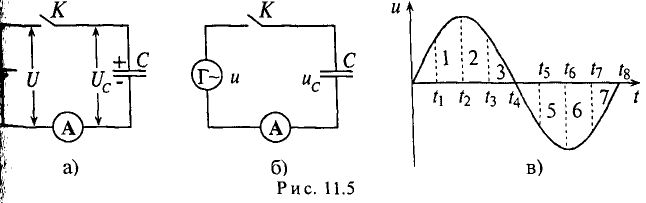
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе Uc не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).
Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе Uc отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
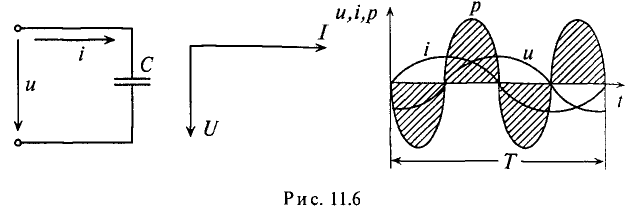
Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 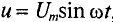 , то в цепи конденсатора проходит ток i (рис. 11.6а):
, то в цепи конденсатора проходит ток i (рис. 11.6а):
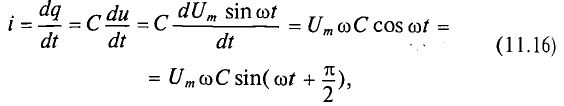
где q= Си согласно (6.3).
Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда 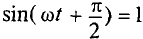 :
:

Тогда 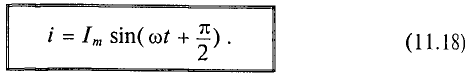
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=
Следовательно, напряжение отстает по фазе от тока на 90° =  (рис. 11.66).
(рис. 11.66).
Если уравнение (11.17) разделить на 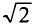 = 1,41, то получится равенство
= 1,41, то получится равенство 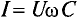 или
или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.
Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление – это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).
Реактивная мощность в цепи с конденсатором
Если в цепи конденсатора емкостью 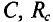 = 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
= 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
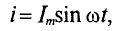
Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно
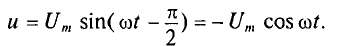
Мгновенная мощность в цепи с конденсатором
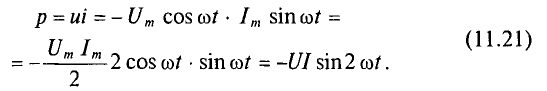
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).
Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.
Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
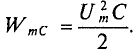
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.
Величина реактивной мощности в цепи конденсатора определяется выражением
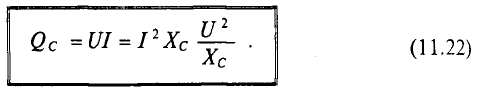
Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) – аналитическом выражении мгновенной мощности в цепи с конденсатором.
Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Хс).
Расчет линейных электрических цепей синусоидального тока
Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.
Цепь с активным сопротивлением и индуктивностью
Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 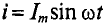 (рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки
(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки 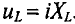
Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением XL (рис. 12.16).
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано 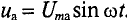 . Индуктивное напряжение
. Индуктивное напряжение 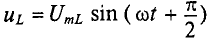 опережает ток на угол 90° =
опережает ток на угол 90° = 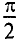 .
.
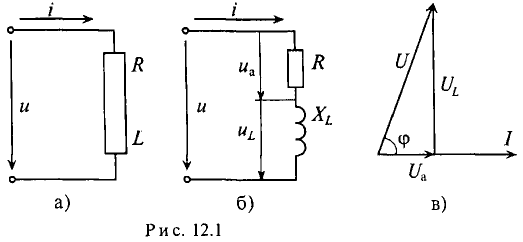
Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 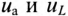 согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
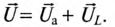
Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).
Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 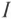 на угол ф. Мгновенное значение этого напряжения может быть записано:
на угол ф. Мгновенное значение этого напряжения может быть записано:
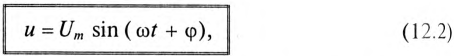
где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение
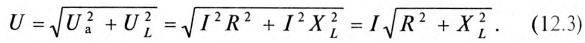
Откуда

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Zk — полное, или кажущееся, сопротивление реальной катушки.
Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.
Треугольники напряжений, сопротивлений, мощностей
Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).
Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:
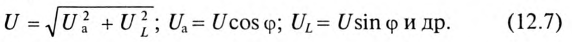
Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:
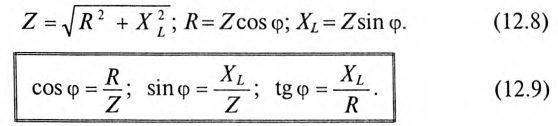
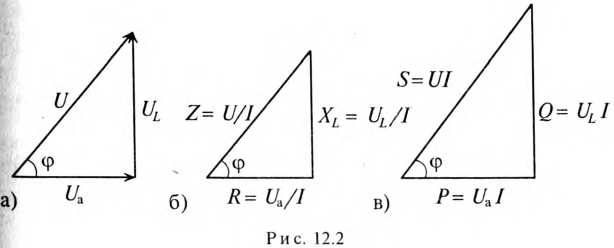
Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).
Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).
Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е. 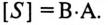
Однако потребляется в цепи только часть полной мощности – активная мощность
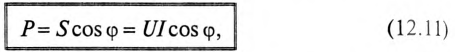
где cos ф показывает, какая часть полной мощности 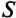 потребляется в цепи, поэтому cos ф называют коэффициентом мощности:
потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:
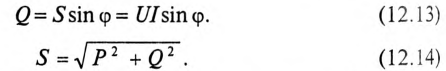
Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.
Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток 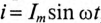 , то он создает падение напряжения на активном сопротивлении
, то он создает падение напряжения на активном сопротивлении 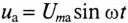 и на емкостном сопротивлении
и на емкостном сопротивлении 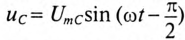 . Векторная диаграмма для этой цепи изображена на рис. 12.36.
. Векторная диаграмма для этой цепи изображена на рис. 12.36.
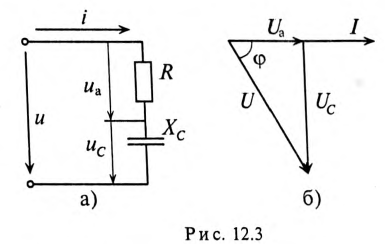
Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф < 90°, т. е.

Действующее значение напряжения U, приложенного к этой цепи, определяется по векторной диаграмме (рис. 12.3):
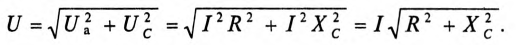
Откуда математическое выражение закона Ома для этой цепи:
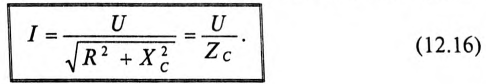
Пример 12.1
К цепи с последовательно включенными сопротивлениями R= 8 Ом и Хс= 6 Ом (рис. 12.3а) приложено напряжение U= 220 В. Определить ток цепи I, напряжение на активном 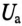 и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
Решение
Для определения тока вычислим полное сопротивление цепи
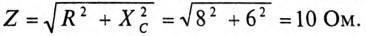
Тогда ток будет равен
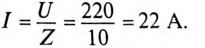
Напряжения на участках:
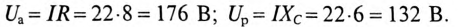
Полная мощность 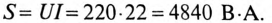
Активная мощность 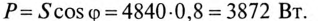
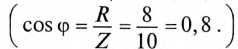
Реактивная мощность 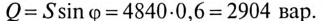
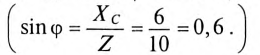
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток 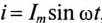 , то он создает падение напряжения на всех участках цепи:
, то он создает падение напряжения на всех участках цепи: 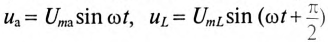 и
и 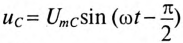 .
.
Мгновенное значение напряжения цепи определяется по формуле
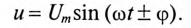
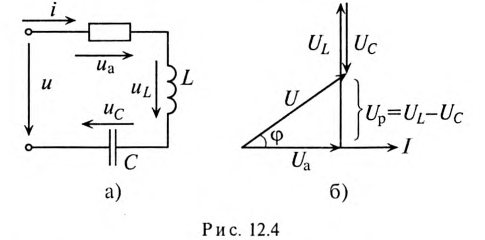
Так как в рассматриваемой цепи включены два реактивных сопротивления XL и Хс, то возможны три режима работы цепи: 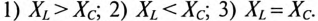
Векторная диаграмма цепи для режима 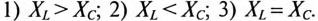 изображена на рис. 12.46.
изображена на рис. 12.46.
Знак перед углом сдвига фаз ф зависит от режима работы цепи Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т. е. 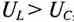 , то цепь имеет индуктивный характер и напряжение U опережает по фазе ток
, то цепь имеет индуктивный характер и напряжение U опережает по фазе ток 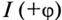 .
.
Если в цепи преобладает емкостное напряжение (сопротивление), т.е. 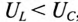 , то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
, то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
Из векторной диаграммы (рис. 12.46) следует:
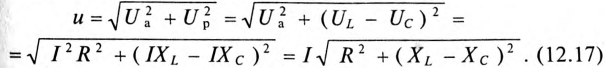
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:
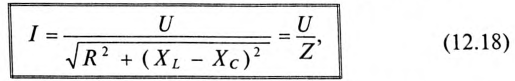
где Z — полное (или кажущееся) сопротивление неразветвленной цепи с R, L и С, т. е.
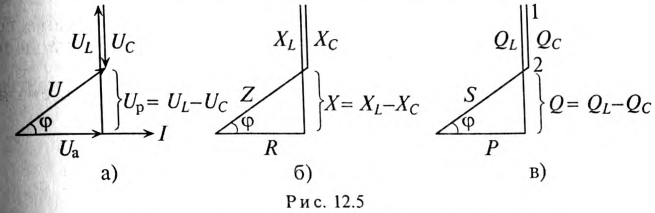
На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла ф можно определить из треугольника сопротивлений (рис. 12.56):
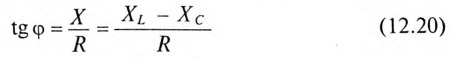
или
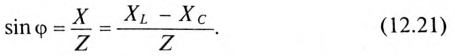
Из выражений (12.20) и (12.21) видно, что если 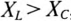 , то угол ф положителен (+ф), если
, то угол ф положителен (+ф), если 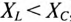 , то угол ф отрицательный (—ф).
, то угол ф отрицательный (—ф).
Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности 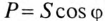 имеется реактивная мощность
имеется реактивная мощность 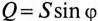 . Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
. Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= QL– Qc. Эта реактивная мощность (энергия) колеблется между источником и магнитным полем катушки индуктивности, так как 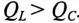
Полная мощность цепи определяется по формуле

Колебательный контур
Электрические цепи, в которых происходят периодические изменения токов, напряжений, энергии называются колебательными.
Для того чтобы исследовать резонансные явления, необходимо иметь представления о процессах в колебательном контуре, состоящем из идеальной катушки и конденсатора без потерь.
Если конденсатор емкостью С зарядить до напряжения Um, то в электрическом поле этого конденсатора накопится энергия, максимальное значение которой согласно выражению (6.21):
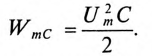
Если к заряженному конденсатору подключить индуктивность L замыканием ключа К (рис. 12.6), то конденсатор будет
разряжаться через индуктивность переменным током i. При этом в индуктивности L создается ЭДС самоиндукции eL, и в магнитном поле ее накапливается энергия, максимальное значение которой (9.12):
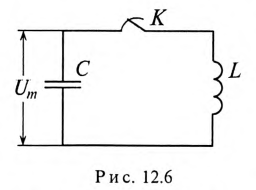
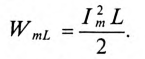
Источником энергии в этом контуре является конденсатор. Ток в контуре, состоящем из индуктивности L и конденсатора С, не прекращается даже когда конденсатор полностью разрядится. За счет ЭДС самоиндукции и энергии, накопившейся в магнитном поле индуктивности, конденсатор будет заряжаться, и энергия магнитного поля индуктивности переходит в электрическое поле конденсатора. При этом источником энергии в этом контуре является индуктивность. Дальше процесс повторяется.
Таким образом, в замкнутом контуре, состоящем из индуктивности и емкости, происходит колебание энергии между электрическим полем конденсатора С и магнитным полем индуктивности L. Поэтому такой замкнутый контур называется колебательным контуром.
Колебание энергии в колебательном контуре происходит с определенной частотой 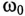 , которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
, которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
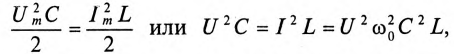
так как из (11.19) в цепи переменного тока с емкостью 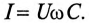
Откуда
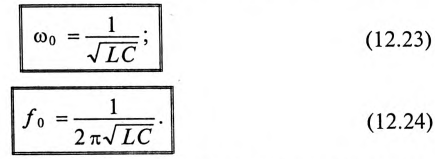
Таким образом, частота собственных колебаний колебательного контура определяется параметрами этого контура L и С.
Если в колебательном контуре отсутствуют потери (идеальный контур), то колебания в нем будут незатухающими с неизменной амплитудой. Если в колебательном контуре имеется активное сопротивление, т.е. возникают потери, то колебания энергии в нем будут затухающие, с уменьшающейся амплитудой, если эти потери не компенсируются.
Резонанс напряжений
Если в цепи синусоидального тока с последовательно соединенными конденсатором емкостью С и катушкой с сопротивлением R И индуктивностью L (рис. 12.7а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.

Из (12.25) следует 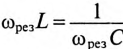 , тогда частота резонанса опреляется выражением
, тогда частота резонанса опреляется выражением

Из (12.26) следует, что резонанс напряжений имеет место в неразветвленной цепи с L и С тогда, когда частота вынужденных колебаний (частота источника) 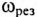 будет равна частоте собственных колебаний резонансного контура
будет равна частоте собственных колебаний резонансного контура 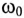 . Следовательно, добиться резонанса напряжений можно изменением частоты источника
. Следовательно, добиться резонанса напряжений можно изменением частоты источника 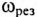 или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний
или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний 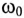 .
.
Полное (кажущееся) сопротивление цепи (рис. 12.7а) при резонансе напряжений определяется по формуле
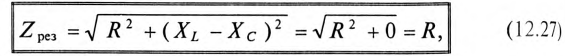
так как XL-Xc=0.
То есть полное сопротивление неразветвленной цепи при резонансе напряжений 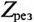 становится минимальным и равным активному сопротивлению цепи R.
становится минимальным и равным активному сопротивлению цепи R.
Следовательно, ток в неразветвленной цепи при резонансе напряжений максимальный:

Реактивные сопротивления при резонансе напряжений равны между собой, т. е.
(12.29)
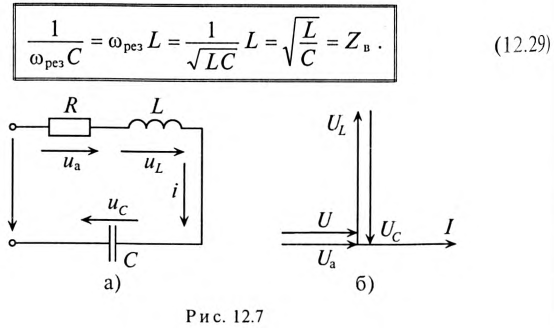
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению 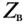 , которое называют характеристическим сопротивлением:
, которое называют характеристическим сопротивлением:
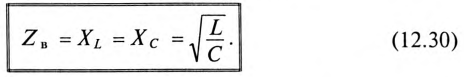
Напряжения на индуктивности UL и на емкости Uc при резонансе напряжений равны между собой, так как равны сопротивления, см. (12.25).
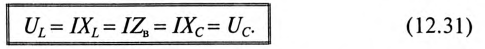
Равенство (12.31) определяет название «резонанс напряжений».
Так как UL и Uc изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении 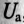 , т. е.
, т. е. 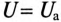 , что видно на векторной диаграмме (рис. 12.76).
, что видно на векторной диаграмме (рис. 12.76).
При резонансе напряжений каждое из реактивных напряжений UL и Uc может оказаться большим, чем напряжение цепи U.
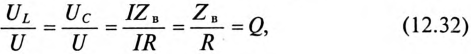
где Q — добротность резонансного контура.
Добротность контура Q показывает, во сколько раз напряжение на индуктивности UL и емкости Uc (каждое) больше напряжения цепи U.
Высокая добротность резонансного контура (при малом активном сопротивлении контура) нашла широкое применение в радиотехнике, в частности в антенном контуре.
Из векторной диаграммы (рис. 12.76) видно, что при резонансе напряжение цепи U совпадает по фазе с током 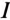 , угол между
, угол между 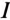 и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:
и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:

Колеблющаяся между магнитным полем индуктивности и электрическим полем емкости мощность (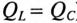 ) не является реактивной, так как не загружает источник и провода.
) не является реактивной, так как не загружает источник и провода.
Из выражения (12.33) следует, что при отсутствии активной Мощности Р (активного сопротивления R) резонансный контур становится при резонансе идеальным колебательным контуром. Следовательно, при наличии активного сопротивления R источник расходует свою мощность на компенсацию потерь в контуре, за счет чего колебания в цепи будут незатухающими.
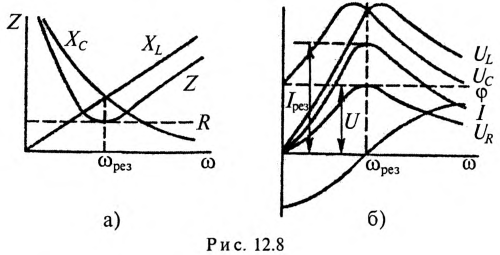
Кроме активного сопротивления R резонансной цепи и напряжения, приложенного к ней, все параметры резонансной цепи (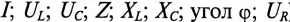 ) изменяются с изменением частоты сети
) изменяются с изменением частоты сети 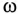 .
.
Эти изменения параметров резонансной цепи наглядно иллюстрируются резонансными кривыми, изображенными на рис. 12.8.
На резонансных кривых четко просматриваются значения этих параметров при частоте резонанса 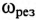 .
.
Общий случай неразветвленной цепи
Для неразветвленной цепи, содержащей несколько активных и реактивных сопротивлений различного характера (рис. 12.9а), справедливо геометрическое равенство напряжений (баланс напряжений)
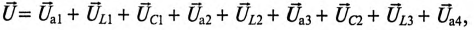
которое лежит в основе построения векторной диаграммы (рис. 12.96).
Таким образом, напряжение цепи равно геометрической сумме напряжений на всех участках этой цепи.
Из векторной диаграммы следует (рис. 12.96)
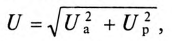
где 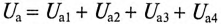 — активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи;
— активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи; 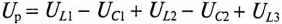 — реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
— реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
Те же рассуждения можно отнести и к сопротивлениям:
– полное сопротивление цепи 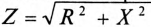 ;
;
– активное сопротивление цепи 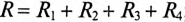 ;
;
– реактивное сопротивление цепи 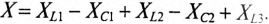
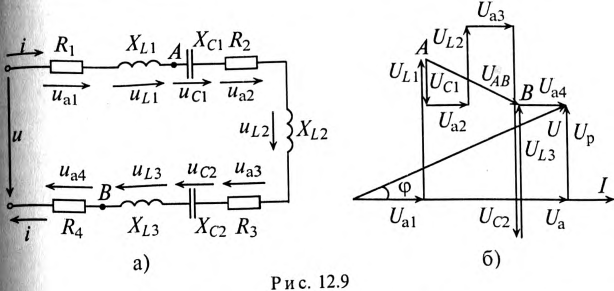
Напряжение на каком-либо участке неразветвленной цепи (рис. 12.9а), например на участке АВ, определяется так:_
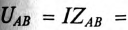
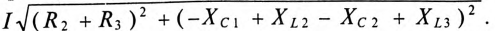
Вектор напряжения UAB показан на векторной диаграмме (рис. 12.96).
Пример 12.2
Напряжение, приложенное к неразветвленной цепи (рис. 12.10) U=220 В, частота тока сети f = 50 Гц. Начальная фаза тока 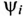 = 0.
= 0.
Сопротивление участков цепи: 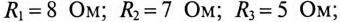
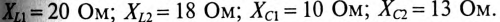
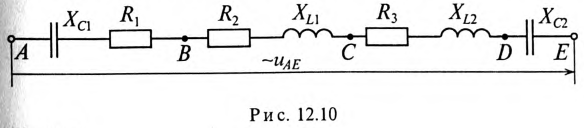
Требуется:
1. Вычислить ток цепи I и записать его мгновенное значение.
2. Записать мгновенное значение напряжения цепи иАЕ, определив предварительно угол ср и характер цепи.
3. Определить напряжение между точками АВ и CD.
4. Построить в масштабе векторную диаграмму цепи, определив едварительно напряжение на каждом сопротивлении.
5. Определить мощности S, Р и Q цепи.
6. Определить частоту, при которой в цепи наступит резонанс напряжений, и ток при резонансе.
7. Определить максимальную энергию, запасенную в магнитном поле катушек WmL и электрическом поле конденсаторов WmC. Как нужно изменить емкость конденсаторов, чтобы в цепи пил резонанс напряжений при частоте f = 50 Гц?
Решение
1. Для определения тока цепи I необходимо вычислить полное сопротивление цепи:
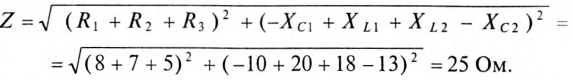
Действующее значение тока 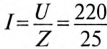 = 8,8 А, а амплитудное значение тока
= 8,8 А, а амплитудное значение тока 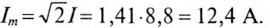
Угловая частота 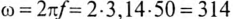 рад/с.
рад/с.
Мгновенное значение тока цепи:
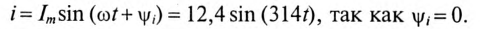
2. Угол сдвига фаз ф и характер цепи определяется через tg ф:
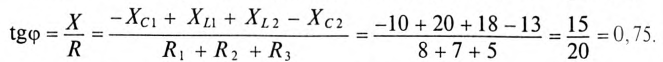
Таким образом, угол ф = 37° (из таблицы), характер цепи индуктивный (+ф).
Тогда мгновенное значение напряжения цепи
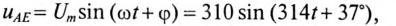
где 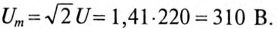
3. Напряжение на участках:
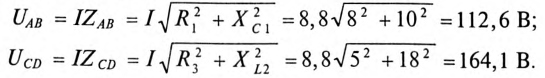
4. Для построения векторной диаграммы определяются напряжения:
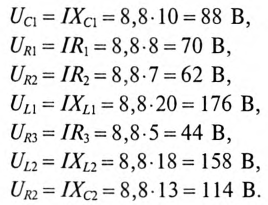
Векторная диаграмма цепи (отображает только характер участков, но не величины напряжений на них) изображена на рис. 12.11.
5. Полная мощность цепи 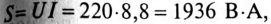 активная мощность Р=
активная мощность Р=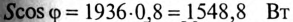 (так как
(так как 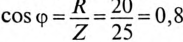 ), реактивная мощность
), реактивная мощность 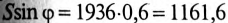 вар, (так как
вар, (так как 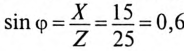 ).
).
6. Для определения частоты резонанса вычисляется индуктивность L и емкость С цепи:
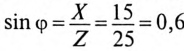
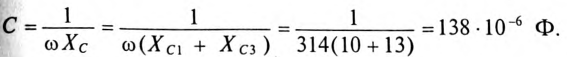
Тогда
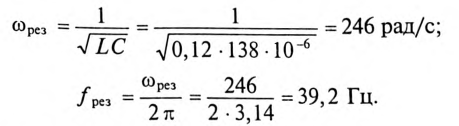
Ток цепи при резонансе 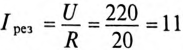 А.
А.
7. Максимальная энергия, запасенная в магнитном поле катушек:
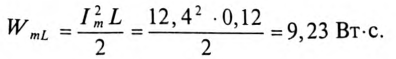
Максимальная энергия, запасенная в электрическом поле конденсаторов:
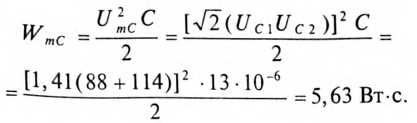
8. Условие резонанса XL = XC.
По условию задачи 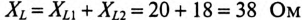 , а
, а 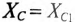
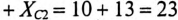 Ом. Этому Хс соответствует емкость С =
Ом. Этому Хс соответствует емкость С = 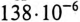 Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
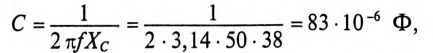
т. е. емкость конденсаторов нужно уменьшить на
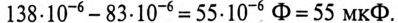
Разветвленная цепь синусоидального тока
Активный и реактивный токи:
Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.
Если к цепи, содержащей активное сопротивление R и индуктивное XL (рис. 13.1а), приложено синусоидальное напряжение 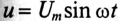 , то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в),
, то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в), 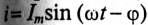 .
.
Векторная диаграмма в этом случае изображена на рис. 13.16.
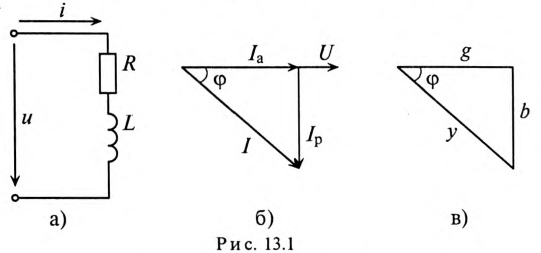
Ток цепи I (рис. 13.16) раскладывается на две составляющие, одна из которых  совпадает по фазе с напряжением, другая
совпадает по фазе с напряжением, другая  — сдвинута на 90°. Составляющая тока
— сдвинута на 90°. Составляющая тока  , совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока
, совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока  , имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
, имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
Активный и реактивный токи физического смысла не имеют. Они являются расчетными величинами, так как в неразветвленной цепи (рис. 13.1а) ток на всех участках имеет одинаковое значение. Однако понятия активный  и реактивный
и реактивный  токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
13.2. Проводимости
Из треугольника токов для рассматриваемой цепи (рис. 13.16) следует: 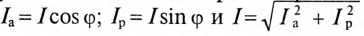 .
.
С другой стороны, известно, что 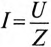 (см. (12.6)), a
(см. (12.6)), a 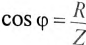 и
и 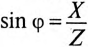 (см. (12.9)).
(см. (12.9)).
Тогда
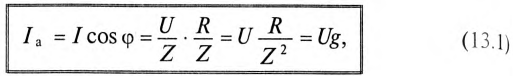
где g — активная проводимость цепи, равная

Величина, на которую умножают напряжение, чтобы получить ток, называют проводимостью.
А так как g определяет активный ток 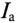 , то ее и называют активной проводимостью.
, то ее и называют активной проводимостью.
Таким образом, активная проводимость g определяется величиной активного сопротивления, деленного на квадрат полного (кажущегося) сопротивления цепи.
Величина реактивного тока определяется выражением
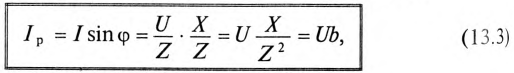
где b — реактивная проводимость цепи, равная

Величина полного тока цепи равна
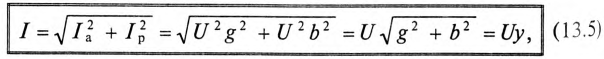
где 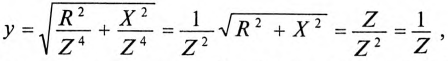 так как для цепи синусоидального тока с
так как для цепи синусоидального тока с 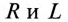 (рис. 13.1а)
(рис. 13.1а) 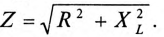
Таким образом, у — полная, или кажущаяся, проводимость цепи:

Полная (кажущаяся) проводимость цепи «у» является обратной величиной полного (кажущегося) сопротивления цепи.
Активная 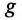 и реактивная
и реактивная 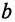 проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е.
проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е. 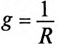 и
и 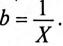
Если же в неразветвленной цепи (или ветви) включены сопротивления 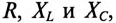 то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
Параллельное соединение катушки и конденсатора
Если к источнику синусоидального напряжения 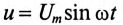 подключить параллельно реальную катушку с активным сопротивлением
подключить параллельно реальную катушку с активным сопротивлением 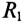 и индуктивным
и индуктивным 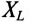 и конденсатор с активным сопротивлением
и конденсатор с активным сопротивлением 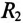 и емкостным
и емкостным 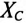 (рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
(рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
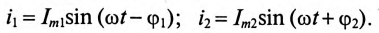
Действующие значения этих токов будут соответственно равны
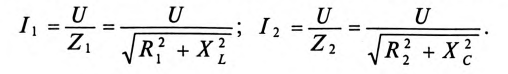
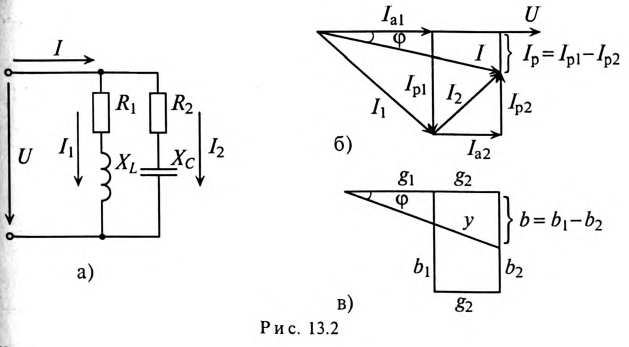
Ток в неразветвленной цепи 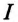 равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
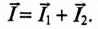
Для определения этого тока строится векторная диаграмма цепи (рис. 13.26), из которой следует:
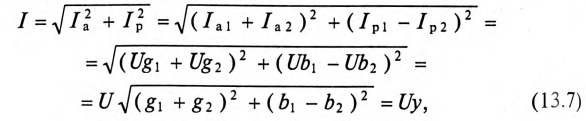
где 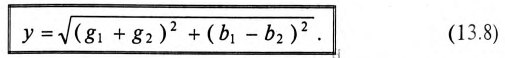
Таким образом, ток в неразветвленной части цепи 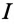 определяется произведением напряжения U и полной проводимости цепи
определяется произведением напряжения U и полной проводимости цепи 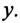
Реактивные проводимости в ветвях имеют различные знаки, так как сопротивления в ветвях различного характера (индуктивное и емкостное).
Треугольник проводимостей рассматриваемой цепи изображен на рис. 13.2в.
Характер разветвленной цепи определяется так же, как и неразветвленной. Если ток цепи 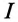 отстает от напряжения
отстает от напряжения 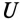 (как в рассматриваемом случае), то цепь индуктивного характера, если же ток
(как в рассматриваемом случае), то цепь индуктивного характера, если же ток 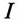 опережает напряжение
опережает напряжение 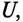 то цепь емкостного характера.
то цепь емкостного характера.
Резонанс токов
Резонанс токов в цепи (рис. 13.2а) с параллельным включением катушки и конденсатора (в различных ветвях) возникает при равенстве реактивных проводимостей в ветвях:
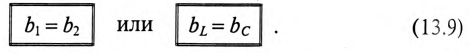
Выражение (13.9) является условием резонанса токов в разветвленных цепях синусоидального тока. Полная (кажущаяся) проводимость при этом условии
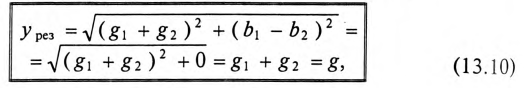
так как 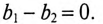
Таким образом, полная проводимость цепи при резонансе токов 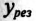 минимальна по величине и равна активной проводимости
минимальна по величине и равна активной проводимости 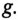 Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину
Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину

Реактивные токи в ветвях при резонансе токов равны между собой

Это равенство и определяет название «резонанс токов».
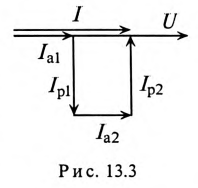
На основании равенства (13.12) строится векторная диаграмма при резонансе токов (рис. 13.3). Реактивные токи находятся в противофазе, поэтому ток в неразветвленной части цепи 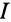 при резонансе токов равен активному току
при резонансе токов равен активному току 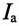 и совпадает по фазе с напряжением, т.е.
и совпадает по фазе с напряжением, т.е. 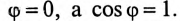 Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
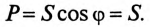
Эта активная мощность компенсирует потери на активном сопротивлении в параллельном резонансном контуре. Мощность (энергия), которая колеблется между электрическим полем конденсатора и магнитным полем индуктивности при резонансе, не является реактивной, так как не загружает источник и провода.
Частота резонанса токов в параллельном резонансном контуре может быть определена из условия резонанса токов, т. е. равенства реактивных проводимостей в ветвях 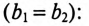
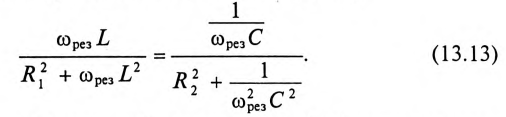
После ряда преобразований равенства (13.13) определяется частота резонанса токов
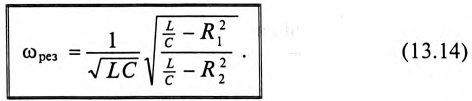
Резонансная частота зависит не только от параметров колебательного контура 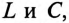 но и от активных сопротивлений в ветвях реального резонансного контура.
но и от активных сопротивлений в ветвях реального резонансного контура.
Если в резонансном контуре отсутствуют активные сопротивления в ветвях, то частота резонанса токов 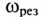 становится равной частоте собственных колебаний идеального резонансного контура
становится равной частоте собственных колебаний идеального резонансного контура
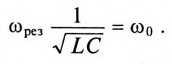
Если в резонансном контуре 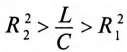 или
или 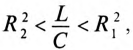 то резонанса токов добиться невозможно.
то резонанса токов добиться невозможно.
Резонанс токов нашел широкое применение в радиотехнике и выпрямительной технике (в резонансных фильтрах) и др.
Пример 13.1
Напряжение, приложенное к параллельно включенным катушке и конденсатору (рис. 13.4а), 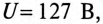 частота сети
частота сети 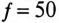 Гц. Параметры цепи:
Гц. Параметры цепи: 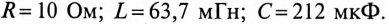 Определить:
Определить:
1) токи всех участков цепи: 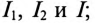
2) углы сдвига фаз этих токов относительно напряжения: 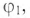
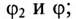
3) полную S, активную Р и реактивную Q мощности цепи;
4) частоту, при которой наступит резонанс токов в этой цепи. Построить векторную диаграмму.
Решение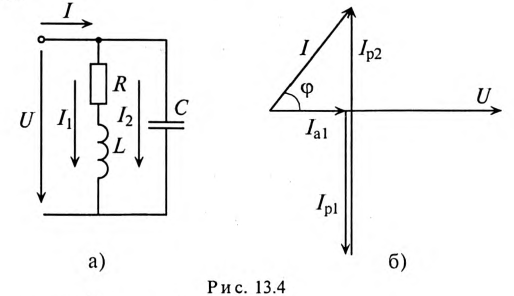
1. Сопротивление участков цепи:
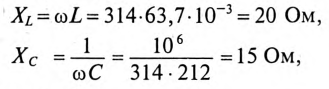
где 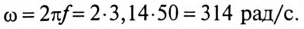
Сопротивление 1-й ветви:
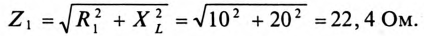
Токи в ветвях соответственно равны
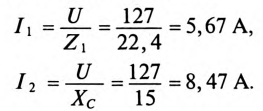
Для определения тока 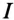 в неразветвленной части цепи определяются проводимости:
в неразветвленной части цепи определяются проводимости:
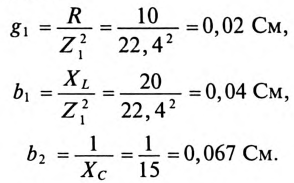
Тогда полная проводимость цепи будет равна
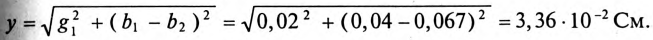
Ток в неразветвленной части цепи
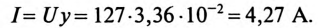
2. Углы сдвига фаз:
.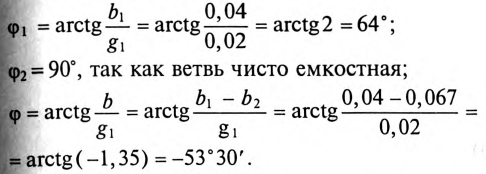
Знак «минус» перед значением угла 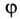 параллельного контура означает, что цепь имеет емкостной характер, так как
параллельного контура означает, что цепь имеет емкостной характер, так как 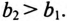
3. Полная мощность цепи 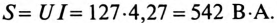
Активная мощность цепи 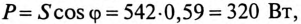 так как
так как 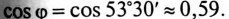
Реактивная мощность цепи 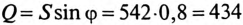 вар, так как
вар, так как 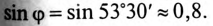
4. Угловая частота резонанса токов в цепи равна
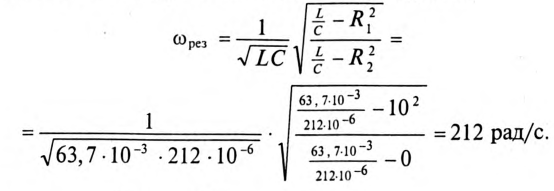
Откуда 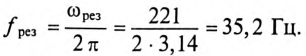
Для построения векторной диаграммы определяют активные и реактивные токи в ветвях:

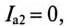 так как в ветви с емкостью отсутствует активное сопротивление, т.е.
так как в ветви с емкостью отсутствует активное сопротивление, т.е. 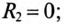
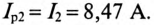
Векторная диаграмма для рассматриваемой цепи изображена на рис. 13.46.
На векторной диаграмме видно, что ток I опережает напряжение U на угол 53°30′ (цепь емкостного характера).
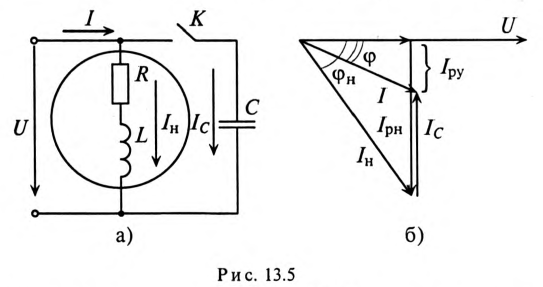
Коэффициент мощности
Номинальные параметры, т.е. мощность источника 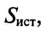 мощность потребителя
мощность потребителя 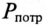 и коэффициент мощности
и коэффициент мощности 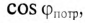 связаны следующим соотношением
связаны следующим соотношением

Из (13.15) следует, что чем меньше 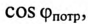 тем большую мощность
тем большую мощность 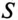 должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
Ток в цепи потребителя с определенным 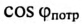 согласно выражению (12.11) равен
согласно выражению (12.11) равен
Из (13.16) видно, что чем меньше 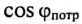 , тем больше ток потребителя
, тем больше ток потребителя 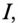 тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
Таким образом, низкий коэффициент мощности потребителя 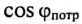 приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.
приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.  должен быть равен или больше 0,93
должен быть равен или больше 0,93 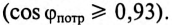
Однако  большинства электрических потребителей переменного тока меньше этой нормы. Так, например,
большинства электрических потребителей переменного тока меньше этой нормы. Так, например,  асинхронных двигателей, в зависимости от нагрузки, составляет
асинхронных двигателей, в зависимости от нагрузки, составляет 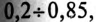 трансформаторов –
трансформаторов – 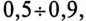 выпрямителей –
выпрямителей – 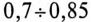 и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения 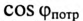 параллельно с ним подключаются конденсаторы (рис. 13.5а).
параллельно с ним подключаются конденсаторы (рис. 13.5а).
Из векторной диаграммы (рис. 13.56) видно, что с подключением конденсатора С (ключ К замкнут) появляется 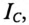 за счет которого уменьшается угол
за счет которого уменьшается угол 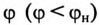 и увеличивается
и увеличивается 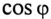 установки. При этом уменьшается ток цепи
установки. При этом уменьшается ток цепи 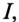 который до подключения конденсатора был равен току нагрузки
который до подключения конденсатора был равен току нагрузки 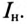
Для повышения коэффициента мощности 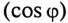 конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения
конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения 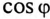 конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
Коэффициент мощности можно повысить, увеличив активную нагрузку. При этом увеличивается потребляемая энергия, что экономически нерационально (уменьшается КПД установки).
Пример 13.2
Асинхронный двигатель, включенный в сеть с напряжением 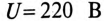 и частотой
и частотой 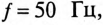 развивает на валу мощность
развивает на валу мощность 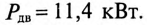 КПД двигателя
КПД двигателя 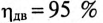 при
при 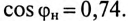 Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить
Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить 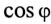 установки до 0,95.
установки до 0,95.
Решение
Мощность, потребляемая двигателем из сети:
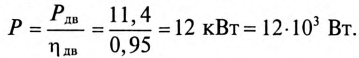
Ток нагрузки 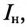 т.е. ток двигателя (рис. 13.5а), равен
т.е. ток двигателя (рис. 13.5а), равен
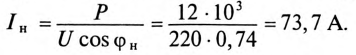
Реактивная составляющая тока двигателя 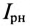 (рис. 13.56)
(рис. 13.56)
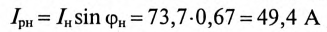
(по таблице 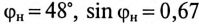 ).
).
Ток установки 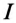 при подключении конденсатора, т. е. при
при подключении конденсатора, т. е. при 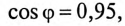 будет равен
будет равен

При 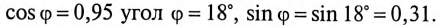 Реактивная составляющая тока установки (рис. 13.56)
Реактивная составляющая тока установки (рис. 13.56)
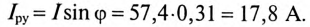
Ток конденсатора 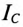 (рис. 13.56)
(рис. 13.56)
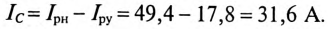
Емкостное сопротивление конденсаторов
Емкость конденсаторов, которые нужно подключить параллельно двигателю для улучшения 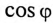 до 0,95:
до 0,95:
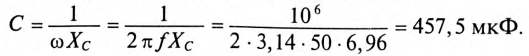
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле
