Амплитуда колебаний – это максимальное значение отклонения от нулевой точки. В физике данный процесс анализируется в разных разделах.
Он изучается при механических, звуковых и электромагнитных колебаниях. В перечисленных случаях амплитуда измеряется по-разному и по своим законам.
Амплитуда колебаний
Амплитудой колебания называют максимальную отдаленную точку нахождения тела от положения равновесия. В физике она обозначается буквой А и измеряется в метрах.
За амплитудой можно наблюдать на простом примере пружинного маятника.
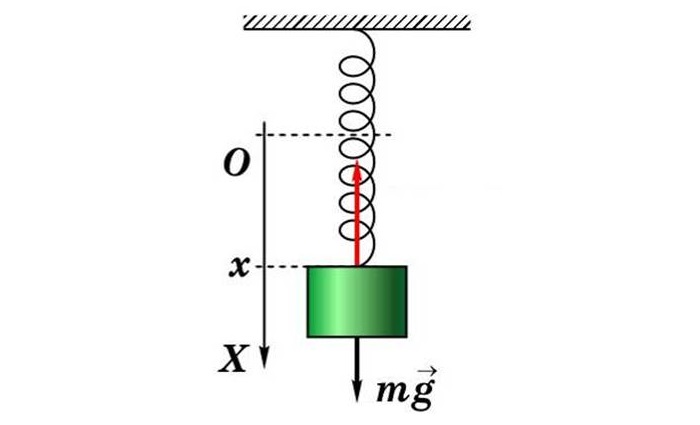
В идеальном случае, когда игнорируется сопротивление воздушного пространства и трение пружинного устройства, устройство будет колебаться бесконечно. Описание движения выполняется с помощью функций cos и sin:
x(t) = A * cos(ωt + φ0) или x(t) = A * sin(ωt + φ0),
где
-
величина А – это амплитуда свободных движений груза на пружине;
-
(ωt + φ0) – это фаза свободных колебаний, где ω – это циклическая частота, а φ0 – это начальная фаза, когда t = 0.
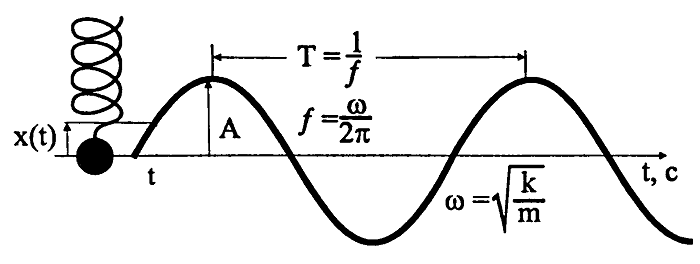
В физике указанную формулу называют уравнением гармонических колебаний. Данное уравнение полностью раскрывает процесс, где маятник движется с определенной амплитудой, периодом и частотой.
Период колебаний
Результаты лабораторных опытов показывают, что циклический период движения груза на пружине напрямую зависит от массы маятника и жесткости пружины, но не зависит от амплитуды движения.
В физике период обозначают буквой Т и описывают формулами:

Исходя из формул, период колебаний – это механические движения, повторяющиеся через определенный промежуток времени. Простыми словами периодом называют одно полное движение груза.
Частота колебаний
Под частотой колебаний следует понимать количество повторений движения маятника или прохождения волны. В разных разделах физики частота обозначается буквами ν, f или F.
Данная величина описывается выражением:
v = n/t – количество колебаний за промежуток времени,
где
-
n – это единица колебаний;
-
t – отрезок времени.
В Международной системе измерений частоту измеряют в Гц (Герцах). Она относится к точным измеряемым составляющим колебательного процесса.
Например, наукой установлена частота вращения Солнца вокруг центра Вселенной. Она равна -1035 Гц при одинаковой скорости.
Циклическая частота
В физике циклическая и круговая частота имеют одинаковое значение. Данная величина еще называется угловой частотой.
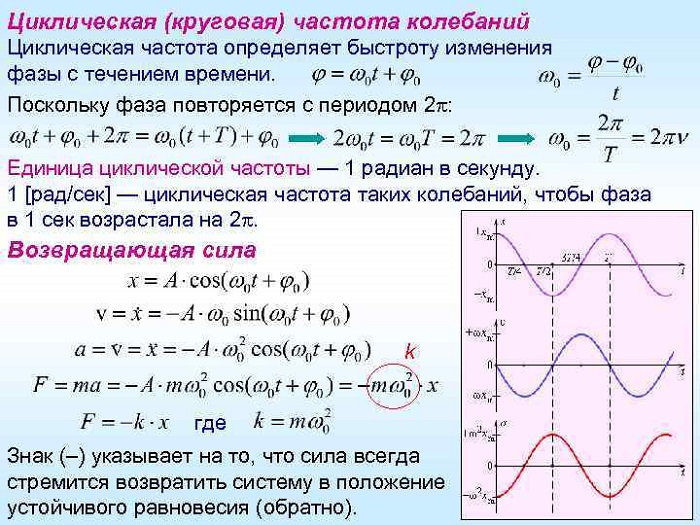
Обозначают ее буквой омега. Она равна числу собственных колебательных движений тела за 2π секунд времени:
ω = 2π/T = 2πν.
Данная величина нашла свое применение в радиотехнике и, исходя из математического расчета, имеет скалярную характеристику. Ее измерения проводят в радианах на секунду. С ее помощью значительно упрощаются расчеты процессов в радиотехнике.
Например, резонансное значение угловой частоты колебательного контура рассчитывают по формуле:
WLC = 1/LC.
Тогда как обычная циклическая резонансная частота выражается:
VLC = 1/2π*√ LC.
В электрике под угловой частотой следует понимать число полных трансформаций ЭДС или число оборотов радиуса – вектора. Здесь ее обозначают буквой f.
Как определить амплитуду, период и частоту колебаний по графику
Для определения на графике составляющих колебательного механического процесса или, например, колебания температуры, нужно разобраться в терминах этого процесса.
К ним относят:
-
расстояние испытываемого объекта от исходной точки – называют смещением и обозначают х;
-
наибольшее отклонение – амплитуда смещения А;
-
фаза колебания – определяет состояние колебательной системы в любой момент времени;
-
начальная фаза колебательного процесса – когда t = 0, то φ = φ0.
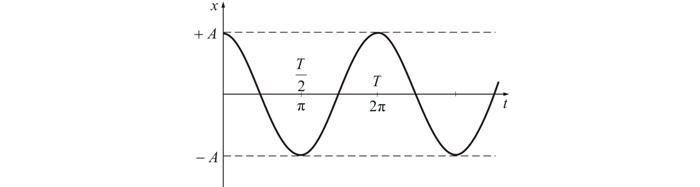
Из графика видно, что значение синуса и косинуса может меняться от -1 до +1. Значит, смещение х может быть равно –А и +А. Движение от –А до +А называют полным колебанием.
Построенный график четко показывает период и частоту колебаний. Стоить отметить, что фаза не воздействует на форму кривой, а только влияет на ее положение в заданный промежуток времени.
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.

Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):

Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):

Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Рассмотрим величины, с помощью которых можно охарактеризовать колебания.

Рис. (1). Движение пустых качелей и качелей с мальчиком
Сравним колебания двух качелей на рисунке (1) — пустых качелей и качелей с мальчиком. Качели с мальчиком колеблются с большим размахом, то есть их крайние положения находятся дальше от положения равновесия, чем у пустых качелей.
Амплитудой колебаний (A) называется максимальное отклонение колеблющегося тела от положения равновесия.
([A]=1~м)
Полным колебанием называют движение, за которое тело возвращается в исходную точку (из которой началось колебание).
За одно полное колебание тело дважды максимально отклоняется от положения равновесия, поэтому один полный путь одного полного колебания равен четырём амплитудам: (s=4A).
Период колебаний — это промежуток времени, за который тело совершает одно полное колебание.
([T]=1~с)
Пример:
ударим по столу двумя линейками — металлической и деревянной (рис. (2)) Линейки после этого начнут колебаться, но за один и тот же промежуток времени металлическая линейка (B) сделает больше колебаний, чем деревянная (A).

Рис. (2). Колебания металлической (B) и деревянной (A) линеек
Число колебаний в единицу времени называется частотой колебаний.
Обрати внимание!
Обозначается частота греческой буквой
ν
(«ню»). За единицу частоты принято одно колебание в секунду. Эта единица в честь немецкого учёного Генриха Герца названа герцем (Гц).
Период колебания (T) и частота колебаний
ν
связаны следующей зависимостью:
Свободные колебания в отсутствие трения и сопротивления воздуха называются собственными колебаниями, а их частота — собственной частотой колебательной системы.
Для описания закономерностей колебательной системы необходимо учитывать зависимость параметров колебания от параметров системы. Например, период колебаний и их частота зависят от массы груза и жёсткости пружины для физического маятника.

Рис. (3). Движение пустых качелей и качелей с мальчиком
Рассмотрим колебания двух одинаковых пустых качелей на рисунке (3). В один и тот же момент времени красные качели из положения равновесия начинают движение вперед, а зелёные качели из положения равновесия движутся назад. Движение качелей таково, что их амплитуды и периоды колебаний одинаковы. А если одинаковы периоды, то и частота колебаний совпадает. Однако, направлений движения качелей противоположно. О таких движениях говорят, что они движутся в противофазах.
Красные пустые качели и качели с мальчиком тоже колеблются с одинаковыми частотами. Направление скоростей этих качелей тоже совпадает. Это означает, что колебания происходят в одинаковых фазах, т.е. совпадают по фазе.
Фаза — физическая величина. Её используют для описания колебания тела.
Исходя из выше сказанного следует, что характеристиками колебательного движения являются:
- амплитуда,
- частота (можно использовать период),
- фаза.
Источники:
Рис. 1, 3. Движение пустых качелей и качелей с мальчиком.
Рис. 2. Колебания металлической и деревянной линеек.
Регулярное изменение физической величины вокруг центральных точек известно как колебание. Состояние меняется между двумя крайними точками.
Максимальное смещение колебания от среднего положения в обе стороны от точек известно как амплитуда колебаний. Он также указывается как величина изменения колеблющейся величины.
Постоянное перемещение любой переменной или объекта между двумя фиксированными точками называется колебанием. Пиковое значение или смещение, которого достигает колеблющийся объект, называется его амплитудой. Маятник, пружины, струны гитары – все это примеры колебаний. На приведенном выше рисунке мяч движется из точки O в точку A, а затем оттуда в точку O, затем в B. При вычислении длины между O и A или O и B мы получаем амплитуду колебаний.

Формула амплитуды колебаний
Амплитуда колебаний представлена как A. Для колебаний полного диапазона величина определяется как 2A. Поскольку колебание является периодической функцией, его волновое уравнение представляется как функция синуса или косинуса. Формула для амплитуды колебаний:
х = A sin ωt
or
х = А, потому что ωt
x – смещение частицы
A – максимальная амплитуда
ω – угловая частота
t – временной интервал
Φ – фазовый сдвиг
Частота колебаний единиц
Частота дает вам информацию о колебаниях, совершаемых за единицу секунды. Также указывается, что цикл завершается за 1 секунду. Один цикл означает одно полное колебание.
Частота представлена как f. Отношение между частотой и периодом времени определяется как;
f = 1 / T
f – частота, а T – период колебаний.
Единица измерения частоты в системе СИ обозначается как;
f = 1 цикл / 1 секунда
Следовательно, единицей измерения частоты является Герц, Гц.
Амплитуда колебательной пружины
Движение пружины – пример колебания. Когда мы нажимаем или тянем пружину, она приходит в непрерывное движение. Этот тип непрерывного движения известен как простое гармоническое движение.
Пружина может быть в двух вариантах;
- Вертикальная система
- Горизонтальная система
Вертикальная система
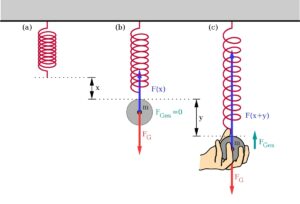
Здесь, как показано на рисунке, веревка закреплена в одной точке и свисает вертикально. Когда груз висит на пружине, она растягивается на длину y и затем начинает колебаться. На рисунке максимальное и минимальное смещение обозначено как + A и -A.
Угловая частота задается как:
т = к/м
Где;
т = 2f
Уравнение решения колебания пружины:
х = A sin ωt
Горизонтальная система
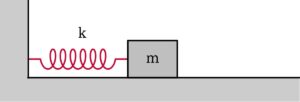
Амплитуда любого вида простого гармонического движения определяется с помощью данного уравнения;
х = A sin ωt
Компания энергия изменяется в каждой точке между кинетической и потенциальной энергия. Полная энергия всегда остается постоянной. Отсюда получаем;
Eобщий = U + к
Уравнение положения и скорости колебаний определяется как;
х = А, потому что ωt
Используя тригонометрическое тождество:
тележка2 + грех2 = 1
и
ω2 = к/м
Мы получаем:
Eобщий = 1/2 КА2
Это уравнение представляет собой соотношение между полной энергией пружинной системы и амплитудой. Следовательно, данное уравнение используется для расчета амплитуды колебаний пружины.
Амплитуда колебаний маятника
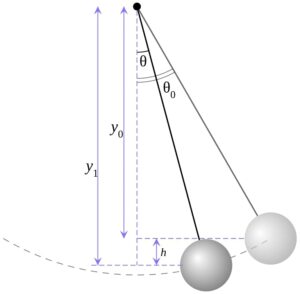
Маятник – это небольшой боб, привязанный к нитке. Он качается, чтобы вызвать колебания. Амплитуда колебаний маятника измеряется как максимальное смещение, которое боб преодолевает, начиная с центрального положения. Центральное положение – это исходное положение боба, когда он находится в исходном положении. Некоторые называют это происхождением или равновесие позиция. Маятник движется вперед и назад, начиная с этой точки. Наибольшее расстояние, которое боб преодолевает с обеих сторон, – это его «амплитуда». С обеих сторон амплитуда остается прежней. Например, если боб покрывает 3 см с левой стороны, он сместится в такой же степени с правой стороны.
Амплитуда колебаний единиц
Амплитуда – это максимальная длина, которую частица преодолевает из положения равновесия. Поскольку амплитуда – это пройденное расстояние, поэтому ее единицей является метр, то есть «м». Измеритель – это стандартная единица измерения амплитуды, но используются и другие единицы измерения. Километр-км, сантиметр-см и миллиметр-мм – это некоторые другие единицы измерения.
Амплитуда колебаний простого маятника
Простой маятник – это особый тип маятника, размер которого намного меньше, чем расстояние от центра тяжести объекта до точки подвеса. Амплитуда простого маятника никак не влияет на период времени. С увеличением амплитуды увеличивается и возвращающая сила, что нивелирует эффект.
Сравнивая колебание простого маятника с равномерным круговым движением, получаем следующее уравнение решения;
х = А, потому что ωt
x для мгновенного смещения
ω – угловая частота
t для временных интервалов.
Это уравнение используется, когда за крайнюю точку принимается начальная точка колебания маятника. В случае, если колебание начинается от среднего положения, уравнение принимает следующий вид:
х = A sin ωt
Амплитуда колебательной диаграммы
Колебание – это простое гармоническое движение, уравнение которого может быть представлено как функция синуса и косинуса. Поэтому его диаграмма изображена в виде волнового графика.

Если колеблющаяся переменная совершает регулярное движение вперед и назад, то пиковое значение, которое смещает частица, дает амплитуду переменной. Для всех типов диаграмм амплитуда остается неизменной: максимальное смещение волн.
Амплитуда колебаний частицы
Абсолютная длина колебания или смещения синусоидального колебания от положения равновесия – это его амплитуда. Это максимальный размер периодически меняющейся частицы. Отличие любой физической частицы от ее крайнего положения и среднего положения определяет ее амплитуду.
Он просто сообщает нам величину колебания частицы. Формула для синусоидальных колебаний:
у = A sin ωt
где | А | – абсолютное значение A.
Переменная амплитуда представляет собой синусоидальное колебание. Он обеспечивает отклонение частицы от средней точки до положительного или отрицательного значения. Смещение частицы – это амплитуда частицы. Поперечную волну можно описать с помощью выделенной амплитуды. Каждая частота частицы, такой как струна, маятник и пружина, имеет амплитуду.
Как найти амплитуду колебаний
Чтобы найти амплитуду колебаний, используется общая формула:
х = A sin ωt + Φ
Где,
x – смещение частицы
A – максимальная амплитуда
ω – угловая частота
t – временной интервал
Φ – фазовый сдвиг.
Например, маятник качается с угловой скоростью = π радиан и фазовым сдвигом = 0. Тогда амплитуда маятника, который покрывает 14 см за 8.50 секунд;
x = A sin ωt + Φ = A sint (0.14 * 0.85) + 0 = 146 см
Тогда амплитуду можно легко найти, изучив уравнение. В этом случае амплитуда равна 6.

Следующий случай – это график колебаний. Здесь мы видим максимальное смещение волны в обе стороны. Следовательно, амплитуда равна 5.
Частота колебаний пружинно-массой системы

В вышеупомянутой системе пружина-масса при добавлении нагрузки пружина смещается на расстояние y, а колебания растягивают ее до следующего положения x.
По закону Гука.
F = ky
Из диаграммы видно, что
Вт = мг = кы
Из диаграммы свободного тела мы видим, что вес движется вниз. Сила инерции ma действует вверх, а восстанавливающая сила k (x + y) также действует вверх.
Мы получим:
ma + k (x+y) – W = 0
Мы знаем, что W = ky, поэтому получаем:
ма + кх = 0
Делим на m:
а + к/мх = 0
Сравнивая его с уравнением SHM, получаем:
ф = 1/2 √к/м
Это частота колебаний системы пружина-масса.
Часто задаваемые вопросы (FAQ)
Что такое колебание?
Колебания происходят во всех областях физики и повседневной жизни.
Колебания – это тоже повторяющееся движение частицы, объекта или количества во времени. Колеблющиеся частицы перемещаются вокруг среднего положения к крайним точкам с обеих сторон. Простой маятник, пружина, качели на детской площадке – все это примеры колебаний.
Чем отличаются колебание от периодического движения?
Движение может быть двух типов: колебательное или периодическое.
Периодическое движение – это регулярное движение частицы через равные промежутки времени. В то же время колебания – это просто возвратно-поступательное движение вибрирующего объекта. Каждое колебательное движение периодично, но обратное не обязательно. Земля вращается вокруг Солнца, что является периодической функцией, поскольку она продолжает повторяться через определенное время. Качели – это колеблющийся объект.
Какая амплитуда колебаний?
Повторяющееся движение частицы известно как колебание.
Степень, в которой может смещаться частица, – это ее амплитуда. Смещение измеряется от среднего положения до любой стороны от крайнего положения. ‘А’ представляет собой амплитуду колебаний, стандартная единица измерения – метр.
Является ли колебание простым гармоническим движением?
Движение, пропорциональное смещению и под действием тормозящей силы, известно как простое гармоническое движение.
SHM – это колебательное движение. Или мы можем сказать, что колебание – это простые гармонические колебания. Например, пружина движется под действием закона Гука, и ее движение пропорционально смещению. Следовательно, это колебание SHM.
Что такое уравнение колеблющихся частиц?
Колебание – это простое гармоническое движение.
Уравнение колебаний следующее:
х = A sin ωt + Φ
Где,
x – смещение частицы
A – максимальная амплитуда
ω – угловая частота
t – временной интервал
Φ фазовый сдвиг
Механические колебания.
-
Гармонические колебания.
-
Уравнение гармонических колебаний.
-
Пружинный маятник.
-
Математический маятник.
-
Свободные и вынужденные колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания – это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания – это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия – это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела – это величина его наибольшего отклонения от положения равновесия.
Период колебаний – это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний – это величина, обратная периоду:
. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
к оглавлению ▴
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение
. Основная задача механики в данном случае состоит в нахождении функции
, дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них – синус и косинус – являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания – это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому
– амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина
, равная значению фазы при
, называется начальной фазой. Начальная фаза отвечает начальной координате тела:
.
Величина называется циклической частотой. Найдём её связь с периодом колебаний
и частотой
. Одному полному колебанию отвечает приращение фазы, равное
радиан:
, откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить
. Мы получаем закон косинуса:
.
График гармонических колебаний в этом случае представлен на рис. 2.
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить
. Получаем закон синуса:
.
График колебаний представлен на рис. 3.
 |
| Рис. 3. Закон синуса |
к оглавлению ▴
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы
определяются из начальных условий – по начальным значениям координаты и скорости.
к оглавлению ▴
Пружинный маятник.
Пружинный маятник – это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна
.
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось
имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и
. Наоборот, если
, то
. Знаки
и
всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
к оглавлению ▴
Математический маятник.
Математический маятник – это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство
. Воспользуемся им в формуле (11):
,
или
.
Это – уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
к оглавлению ▴
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания – это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс – явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы:
, и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний,
, а амплитуда колебаний возрастает до бесконечности при
.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
