Как найти амплитуду гармоник

Ранее
отмечалось, что любой электрический
сигнал может быть представлен в виде
суммы синусоид, каждая синусоида имеет
свою амплитуду, частоту и фазу.

где
А_к
– амплитуда f_к
– частота _к
– фаза.

Если
построить график, показывающий, как
зависит амплитуда синусоиды от частоты,
то это будет частотный спектр данного
сигнала.

U(t)
– сигнал, имеющий периодический
характер.

Частотный
спектр – зависимость А_к
от f_к.

Можно
вместо синусоиды брать косинусоиду,
частотный спектр от этого не изменится.
Выбор разложения по синусоиде или
косинусоиде зависит от выбора начала
отсчета (симметричный).

Каждая
синусоида носит название гармоника.
Поэтому представление в виде суммы
гармоник называется
гармоническим рядом.

Пусть импульсы
прямоугольной формы периодически
повторяются, амплитуда, период и
длительность – постоянны.

Выберем
начало отсчета времениt
= 0 так, чтобы картина была симметричной
относительно начала отсчета.

Тогда

– т.е. будут одни косинусоиды,

где
k
2 
f
_k
= 
_k
– частота
гармоники.

Отсутствует

_к
, т.е. все гармоники имеют нулевой фазовый
сдвиг.

Существует
косинусоида, у которой к = 0, f₀
= 0, нулевая гармоника, ей соответствует
постоянная составляющая U(t).

Частоты гармоник:

К
= 0, f
₀
= 0 – нулевая гармоника

К
= 1, f
₁
= 1/T
– первая гармоника

К
= 2, f
₂
= 2/T
– вторая гармоника и т.д.

Если Т постоянно,
т.е. сигнал периодический

Частоты
гармоник:

Амплитуды гармоник.

Определяются
из теории рядов Фурье.

Для прямоугольных
импульсов:

где
U₀
– амплитуда импульса,

К
– номер гармоники (чем больше к, тем
меньше U₀).

.

Как
следует из формулы для A_k
амплитуды гармоник идеальных прямоугольных
импульсов имеют тенденцию с ростом k
(частоты) убывать асимптотически, т.е.
формально ширина частотного спектра
идеальных прямоугольных импульсов
неограниченна.

Реальные
импульсы имеют отклонения от прямоугольной
формы и ширина их спектра не бесконечна.

Отдельно вычисляется
амплитуда нулевой гармоники.

Если к = 0 , знаком
синуса можно пренебречь и тогда:

-это
не что иное, как постоянная составляющая
напряжения U(t).

Изобразим
график частотного спектра.

Для
упрощения далее будет изображаться
только первая полуволна графика
частотного спектра – основной частотный
спектр.

Амплитуды
гармоник уменьшаются с увеличением
частоты, при этом наблюдается колебательный
характер.

Участок до первого
нуля (первая полуволна) – это основной
спектр.

Частотная
граница основного спектра определяет
ширину частотного спектра из условия:

откуда
k=k_осн=илиk_осн=q

k_осн
– количество линий в основном спектре.

Величина
F_осн=– ширина основного спектра

Часто
требуется количественная оценка ширины
частотного спектра F_c
. Для идеальных прямоугольных импульсов,
её условно принимают равной

F_c=(1..3)F_осн
или
.

Свойства
частотного спектра.

1. Чем
   больше период повторения импульсов,
   тем больше линий в основном частотном
   спектре – чаще расположены линии в
   частотном спектре.

2. Чем
   короче импульс, тем больше ширина
   частотного спектра.

3. Ширина
   ЧС определяется для прямоугольного
   импульса соотношением:

Это
соотношение справедливо для идеальных
прямоугольных импульсов.

Реальный
импульс отличается от идеального более
пологими фронтами.

Общая
формула вычисления амплитуды гармоник
для любого случая:

По
сравнению с идеальным прямоугольным
импульсом для реального импульса ЧС
имеет более определенную частотную
границу. Убывание амплитуд гармоник с
частотой может иметь монотонный характер.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #

  19.03.201580.9 Кб9Б.doc

• #
• #
• #
• #

7. Спектральный анализ периодических сигналов

7.1. Разложение периодических сигналов

       по ортогональным функциям

Электрический сигнал  (ток  или напряжение ) называют периодическим, если он существует на интервале времени от  до  и удовлетворяет условию , где  – период сигнала, а  – целое число. Примеры таких функций времени показаны на рис. 7.1.

Рис. 7.1

При расчете разнообразных сигналов удобно представить их взвешенной суммой заданных функций времени вида

,                             (7.1)

где – заданный набор (базис) функций времени,  – весовые коэффициенты, не зависящие от времени. В этом случае функция времени  может описываться набором коэффициентов , от времени не зависящих.

Рекомендуемые материалы

Чтобы разложение в ряд  (7.1) было  взаимно однозначным

144

функции  должны быть взаимно ортогональными на периоде сигнала, то есть должны удовлетворять условию

                 (7.2)

где момент начала интегрирования  выбирается произвольно исходя из удобства расчетов. При  набор функций  называют ортонормальным.

Для ортогонального базиса коэффициенты разложения  определяются выражением

.                              (7.3)

В математике и технике широко используются различные ортогональные наборы функций (базисы) и прежде всего гармонический базис

,      (7.4)

полиномы Чебышева, Лагранжа, Эрмита и др. В цифровой технике применяют ортогональные дискретные функции Уолша, Радамахера.

7.2. Ряд Фурье

Ряд Фурье для действительной периодической функции времени   является ее разложением по ортогональному базису (7.4) и имеет вид

145

           (7.5)

Компоненту ряда Фурье вида

                                  (7.6)

называют  -й гармоникой сигнала,

                                          (7.7)

– частота первой гармоники,  – постоянная составляющая сигнала,

,                                (7.8)

 – амплитуда  -й гармоники сигнала,

,                                    (7.9)

,                             (7.10)

,                             (7.11)

 – начальная фаза -й гармоники сигнала,

146

                 (7.12)

Величины  и  называют амплитудами синфазной и квадратурной составляющих -й гармоники сигнала соответственно.

7.3. Спектры амплитуд и фаз  периодического сигнала

Периодический сигнал  взаимно однозначно описывается суммой гармоник

,                   (7.13)         

то есть двумя в общем случае бесконечными наборами чисел.

Первый из них называют спектром амплитуд сигнала,

,                                (7.14)

а второй – спектром фаз,

.                                (7.15)

Спектры амплитуд и фаз не зависят от времени, а определяются формой сигнала  на периоде колебаний. Частоты гармоник  кратны частоте первой гармоники ,

,                          (7.16)

147

не зависят от формы сигнала и определяются только периодом его повторения .

Спектры сигнала можно представить в виде формулы, таблицы или графика. В качестве примера рассмотрим спектры амплитуд и фаз последова-

                       Рис. 7.2                   тельности  прямоугольных

                                                       импульсов с амплитудой , длительностью  и периодом , показанных на рис. 7.2. При расчетах целесообразно выбрать момент начала интегрирования  . Постоянная составляющая равна

,                                (7.17)

а амплитуды синфазной и квадратурной составляющих –

,  (7.18)

.                       (7.19)

Для амплитуды и начальной фазы -й гармоники получим

,                   (7.20)

                    (7.21)

148

Графики спектров амплитуд и фаз при условии , мс, мс показаны на рис. 7.3а и рис. 7.3б соответственно. Каждая гармоника отображается вертикальной линией, длина которой равна величине амплитуды или фазы.

Рис. 7.3

Переменная  является номером  гармоники. Ее можно рассматривать как нормированную частоту гармоники,

,

и спектральные диаграммы можно строить в координатах частоты гармоники, как показано на рис. 7.4 для спектра амплитуд.

Спектры имеют дискретный (линейчатый) характер, интервал частот между соседними  гармониками  одинаков  и

149

равен .

Спектр амплитуд сверху всегда ограничен линией, которая падает с ростом частоты (номера) гармоники. Вводится понятие огибающей спектра амплитуд, определяемой как непрерывная функция частоты , которая в точках  точно совпадает со значениями

              Рис. 7.4                    амплитуд  гармоник.   Формулу

                                               огибающей можно получить из выражения для спектра амплитуд, подобного (7.20), при замене номера гармоники  величиной

     ,                                    (7.22)

где  непрерывная переменная.

В примере (7.20) получим

,                         (7.23)

график показан на рис. 7.3а пунктирной линией. Характерной особенностью огибающей спектра амплитуд сигнала рис. 7.2 является наличие точек с нулевым значением (нулей огибающей), определяемых из уравнения

,                                (7.24)

решение которого имеет вид

150

,                                    (7.25)

где  – целое число. Как видно, положение нулей огибающей определяется только длительностью импульса .

7.4. Синтез сигнала по его спектру

Если известны спектры амплитуд и фаз, то с помощью ряда Фурье (7.13) можно получить сигнал как функцию времени. Бесконечная сумма на практике не реализуема и сигнал описывается конечной суммой гармоник,

.                   (7.26)

Соответствующие кривые при ,  и  показаны на рис. 7.5а, рис. 7.5б, и рис. 7.5в соответственно.

Как видно, с увеличением  форма синтезированного сигнала приближается к исходной (рис. 7.2).

7.5. Ряд Фурье в комплексной форме

Гармоники сигнала могут быть представлены своими комплексными амплитудами в виде

,                  (7.27)

тогда исходный сигнал можно представить в виде ряда Фурье,

.                          (7.28)

151

Рис. 7.5

Амплитуда -й гармоники  равна модулю комплексной амплитуды,

,                              (7.29)

а ее начальная фаза  – аргументу  с противоположным знаком,

152

     (7.30)

Комплексная амплитуда гармоники (2.27) позволяет существенно упростить расчеты спектров амплитуд и фаз за счет сокращения числа интегралов и с учетом того, что подынтегральное выражение с экспонентой часто интегрируется проще, чем с тригонометрической функцией.

Рассмотрим сигнал, показанный на рис. 7.6, тогда

 (7.31)

Как видно, в данном примере комплексная амплитуда является действительной величиной, что обусловлено формой сигнала на рис. 7.2..Спектры амплитуд и фаз совпадают с ранее полученными значениями.

7.6. Влияние формы сигнала на спектры амплитуд и фаз

Спектры амплитуд и фаз сигнала взаимно однозначно связаны с его формой, которая определяется формой импульсов и их длительностью на периоде повторения.

На рис. 7.6 показана последовательность прямоугольных импульсов  длительностью  и с амплитудой 1 на интервале периода  в нормированных координатах времени . Для этого сигнала характерны  крутые (с  нулевой  продолжи-

153

тельностью) фронт и срез  импульса. Величину

                (7.32)

называют скважностью импульсов. На рис. 7.7 приведены спектры амплитуд (рис. 7.7а) и фаз (рис. 7.7б)

      Рис. 7.6                   при .

Рис. 7.7

На рис. 7.8 приведены аналогичные зависимости при .

Рис. 7.8.

154

При фиксированном периоде повторения импульсов  увеличение скважности означает уменьшение длительности импульса , при этом согласно рис. 7.7а и рис. 7.8а, а также (7.20) амплитуды гармоник падают, спектр амплитуд становится более равномерным, положение нулей огибающей спектра амплитуд смещается в область более высоких частот (номеров гармоник).

Рассмотрим трапециидальный импульс, программа исследование которого в среде MathCAD показана на рис. 7.9. Спектральный анализ проводится с помощью стандартной процедуры спектрального анализа fft(s). Она построена на основе алгоритма быстрого преобразования  Фурье (БПФ)  и  позволяет получить комплексные коэффициенты , с помощью которых комплексная амплитуда -й гармоники определяется выражением

.                                 (7.33)

Период  сигнала выбран равным 1, – число отсчетов сигнала на периоде. Результаты расчета спектров амплитуд и фаз приведены в листинге программы на рис. 7.9 (повторите расчеты самостоятельно для различных параметров сигнала).

Как видно при сравнении графиков спектров амплитуд на рис. 7.7 и рис. 7.9, увеличение длительности фронта и среза импульса приводит к значительному ослаблению высших гармоник сигнала.

155

На рис. 7.10 показан пример программы расчета спектра амплитуд колоколообразного сигнала вида

,                           (7.34)

для которого характерно наиболее плавное изменение значений во всем интервале времени.

Рис. 7.9.

График сигнала и его спектр амплитуд показаны в листинге программы на рис. 7.10. Как видно, спектр «гладкого» сигнала сосредоточен в области нижних частот, высшие гармоники практически отсутствуют.

Полученные выводы подтверждают результаты синтеза прямоугольных импульсов по ограниченному числу  гармоник, например, показанные на рис. 7.5.

156

Рис. 7.10.

7.7. Свойства спектров сигналов

Свойства спектров сигналов часто формулируются в виде теорем.

Спектральное преобразование сигнала линейно, то есть комплексная амплитуда суммы сигналов равна сумме комплексных амплитуд гармоник каждого из суммируемых сигналов. На практике особый интерес представляет свойство (теорема) смещения сигнала во времени. Ее можно сформулировать следующим образом.

157

Взяв модули левой и правой частей (7.30), получим

,                          (7.36)

то есть спектр амплитуд не  изменяется  при  задержке  сиг-

нала во времени.

Вычислим аргументы обеих частей выражения (7.30),

,                          (7.37)

то есть начальные фазы гармоник сигнала при временной задержке уменьшаются на величину , которая зависит от номера гармоники, периода сигнала (частоты его первой гармоники) и величины задержки .

Для доказательства теоремы смещения запишем

. (7.38)

Проведем замену переменных , тогда получим

.   (7.39)

На спектральные характеристики влияют свойства симметрии сигнала.

Рассмотрим четные функции времени, удовлетворяющие условию . В этом случае амплитуда квадратурной составляющей  -й гармоники равна нулю

,                                       (7.40)

158

комплексная амплитуда -й гармоники  является действительным числом,

,                                    (7.41)

а начальная фаза равна 0 или  в зависимости от знака .

Для нечетной функции, удовлетворяющей условию , амплитуда синфазной составляющей  -й гармоники равна нулю

,                                       (7.42)

комплексная амплитуда -й гармоники  является мнимым числом,

,                                    (7.43)

а начальная фаза равна 0 или  в зависимости от знака .

Эти свойства иллюстрирует пример четного сигнала на рис. 7.2, для которого имеет место равенство (7.19). Его фазовый спектр со значениями 0 или  показан на рис. 7.3б.

Рассмотрим комплексные спектры двух сигналов  (рис.  7.11а) и  (рис. 7.11б), и их сумму  (рис. 7.11в).

Рис. 7.11.

Сигнал    получен  из    сдвигом  во  времени  на

159

величину , оба являются последовательностями прямоугольных импульсов длительностью импульса . Сигнал  оказывается последовательностью прямоугольных импульсов длительностью

Комплексная амплитуда -й гармоники  определена ранее (7.31) и равна

                                 (7.44)

По теореме смещения можно найти комплексную амплитуду -й гармоники сигнала  в виде

.                    (7.45)

Тогда согласно свойству линейности комплексная амплитуда -й гармоники сигнала  равна

 (7.46)

160

С другой стороны, при прямом вычислении (проведите расчеты самостоятельно) комплексная амплитуда -й гармоники сигнала  равна

,                    (7.47)

что полностью совпадает с (7.46).

7.8. Мощность периодического сигнала

Пусть имеется сигнал  (ток или напряжение) в сопротивлении Ом, тогда средняя мощность сигнала равна

.                            (7.48)

Эту же величину можно выразить через гармоники сигнала с помощью равенства (теоремы) Парсеваля в виде

.                 (7.49)

С помощью спектральных  характеристик  можно  определить действующее значение  сигнала в виде

.                 (7.50)

7.9. Ширина спектра

Как видно по графикам спектров амплитуд рассмотренных  сигналов,  в    целом    наблюдается    тенденция     уменьшения

161

амплитуд гармоник с ростом их номера (частоты). Графики на рис. 7.5 показывают, что форма сигнала определяется сравнительно небольшим числом гармоник. Все  это  свидетельствует

о том, что для представления (даже достаточно точного) сигнала необходимо учитывать ограниченное число гармоник, которые занимают конечный интервал частот.

Мощность сигнала определяется выражением (7.39). Для рассматриваемых видеосигналов наиболее интенсивные гармоники имеют номера от 1 до некоторой величины N, при этом их суммарная мощность равна

.                         (7.51)

Как видно, с ростом  мощность  увеличивается, и при  стремится к полной мощности .

Тогда можно определить число гармоник , при котором мощность    будет  равна  величине  , с  помощью

выражения

.                         (7.52)

В результате можно определить ширину спектра  в виде

.                          (7.53)

162

В качестве примера рассмотрим последовательность прямоугольных  импульсов, показанную  на  рис. 7.2   со  спектром амплитуд, показанном на рис. 7.3а. (скважность импульсов ) Зависимость нормированной мощности   от  числа  учитываемых  гармоник  показана  на   рис. 7.12. Как видно, функция  является неубывающей и достигает уровня  при  (, ), тогда ширина спектра сигнала определяется выражением (7.44).

Рис. 7.12

Этот же график в области значений от 0,9 до 1 показан на рис. 7.13. С ростом кривая очень медленно приближается к 1 и достигает значения 0,99 уже при .

В инженерной практике рассмотренный расчет ширины спектра проводится редко, а используется ее инженерная оценка. Для   импульсных  сигналов  с  длительностью    (на-

163

пример, рис. 7.2) ширина спектра определяется выражением

(рад/с)    или   (Гц)        (7.54)

(сравните эти величины со значениями нулей огибающей спектра амплитуд).

Рис. 7.13

Множитель от 1 до 3 косвенно характеризует долю мощности сигнала, заключенную  в  полосе  пропускания (единица примерно соответствует , а тройка –  величине , эти значения зависят от формы импульса).

Оценки ширины спектра можно выразить через число гармоник,

,                    (7.55)

где  требуемое число гармоник, равное

.                    (7.56)

164

На практике чаще всего используются соотношения с единичным множителем вида

В рассмотренном примере сигнала на рис. 7.2 скважность  и для обеспечения 90% мощности необходимо учитывать  гармоник (рис. 7.12), по оценке (7.58) требуется учитывать 10 гармоник.

7.10. Задания для самостоятельного решения

Задание 7.1. Определите и постройте графики спектров амплитуд и фаз сигналов вида:

,

,

,

,

.

Задание 7.2. Определите спектры амплитуд и фаз сигналов, показанных на рис. 7.14, постройте их графики. Проведите расчет ширины спектра при ,   и , сравните полученные результаты.

165

Рис. 7.14

Задание 7.3. С помощью теоремы смещения проведите расчет спектров амплитуд и фаз сигнала, показанного на рис. 7.14а,  воспользовавшись результатами, полученными для сигнала на рис.7.2.

Задание 7.4. Определите спектры амплитуд и фаз сигнала, показанного на рис.7.15, постройте их графики. Сравните спектр амплитуд со спектром гармонического сигнала, проанализируйте результаты.

Вычислите ширину спектра сигнала при . Чем обусловлены наблюдаемые различия в ширине спектра для сигналов, показанных на рис. 7.14а и рис. 7.15? Как в полученных результатах проявляются свойства симметрии сигнала?

Рис. 7.15

Задание 7.5. Определите спектры амплитуд и фаз сигналjd, показанного на рис.7.16, постройте их графики.

166

Рис. 7.16

Люди также интересуются этой лекцией: 2 Нефть и получение нефтепродуктов.

Задание 7.6. Определите спектры амплитуд и фаз сигнала, показанного на рис.7.17, постройте их графики.

Рис. 7.17

Проведите тот же расчет, представив сигнал на рис. 7.17 в виде суммы двух импульсных последовательностей, показанных на рис. 7.18, и используя свойство линейности.

Рис. 7.18

При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы, и как с ними работать? В этом нам и предстоит сегодня разобраться. Кроме того, мы рассмотрим важнейшее понятие – амплитудно-частотную характеристику (АЧХ) сигналов.

Гармонические и негармонические сигналы.

И для начала чуть подробнее разберемся, как классифицируются сигналы. В первую очередь, нас интересуют периодические сигналы. Их форма повторяется через определенный интервал времени T, называемый периодом. Периодические сигналы в свою очередь делятся на два больших класса – гармонические и негармонические. Гармонический сигнал – это сигнал, который можно описать следующей функцией:

Здесь A – амплитуда сигнала, w – циклическая частота, а phi – начальная фаза. Может возникнуть логичный вопрос – разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sinalpha = cos(frac{pi}{2}medspace-medspace alpha) – то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний.

Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:

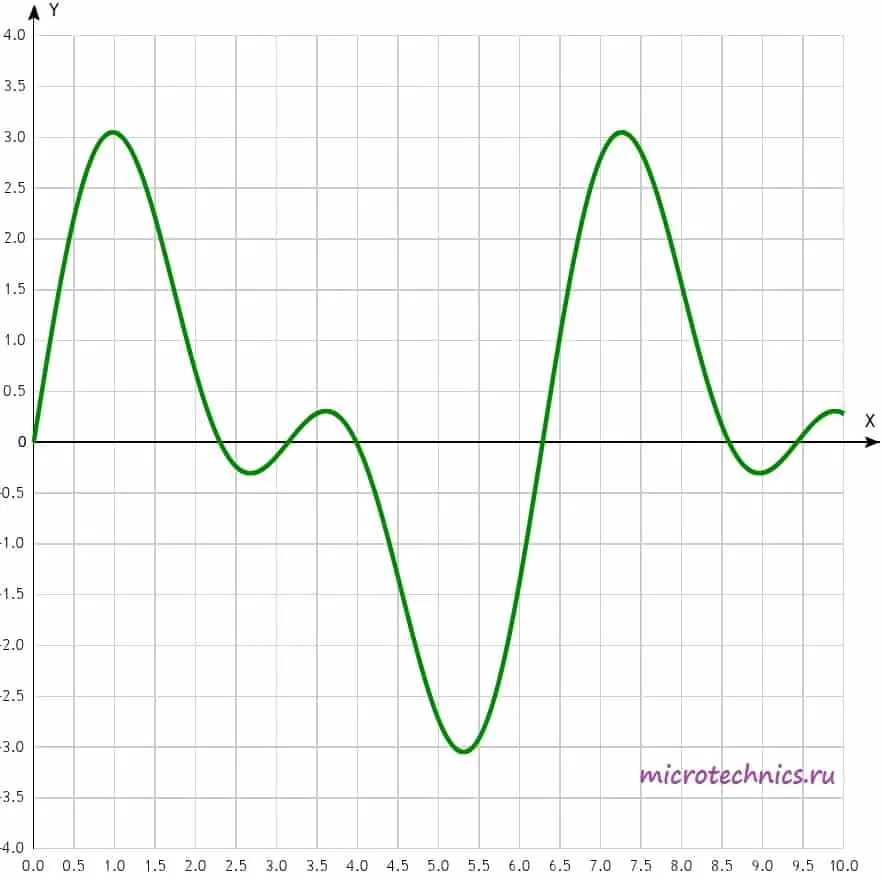
Как видите, несмотря на свой вид, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.

Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что рассмотрим практический пример и разберемся подробнее. И для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:

u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)

Давайте изобразим все эти сигналы на одном графике:

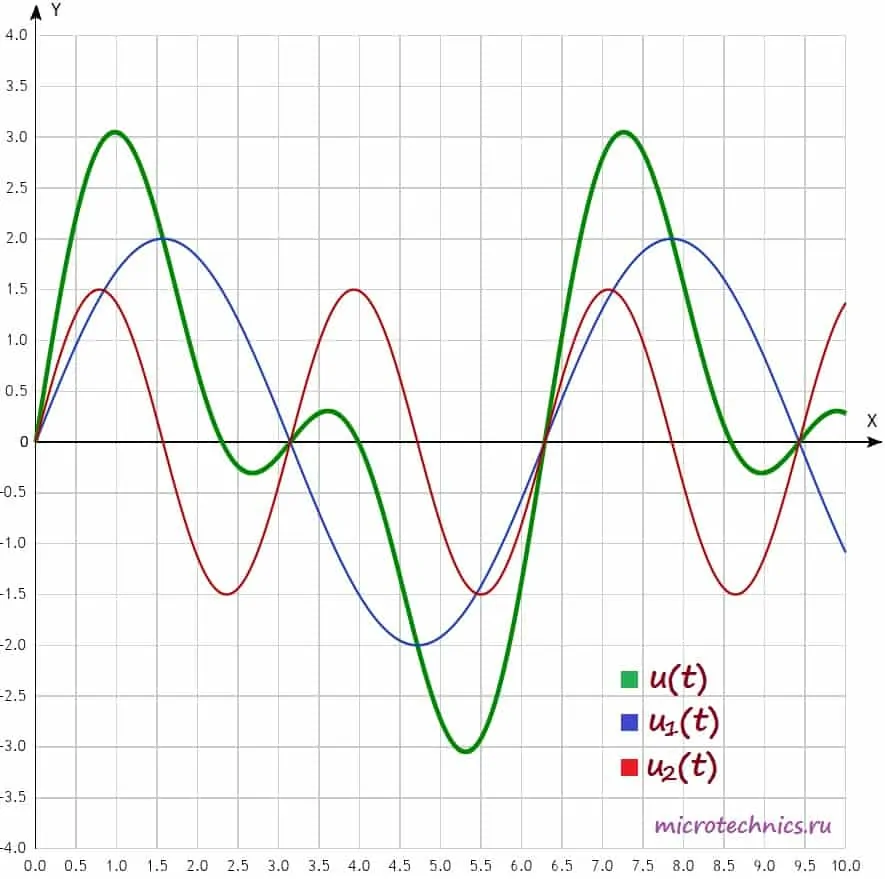
Функции u_1(t), u_2(t) называют гармониками сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой. В данном случае первой гармоникой является функция u_1(t) (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция u_2(t) = 1.5 sin(2t) представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:

u(t) = U_0 + sum_{i=0}^{infty}{U_{k}thinspace sin(thinspace kwt + phi_kthinspace )}

Здесь U_k – амплитуда, а phi_k – начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и наблюдаем в данной формуле. U_0 – это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите – среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0 👍

Амплитудный спектр сигнала.

Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:

• фазовый спектр сигнала – совокупность начальных фаз всех гармоник
• амплитудный спектр сигнала – амплитуды всех гармоник, из которых складывается негармонический сигнал

Давайте рассмотрим амплитудный спектр подробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:

При этом на горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси – амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:

u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)

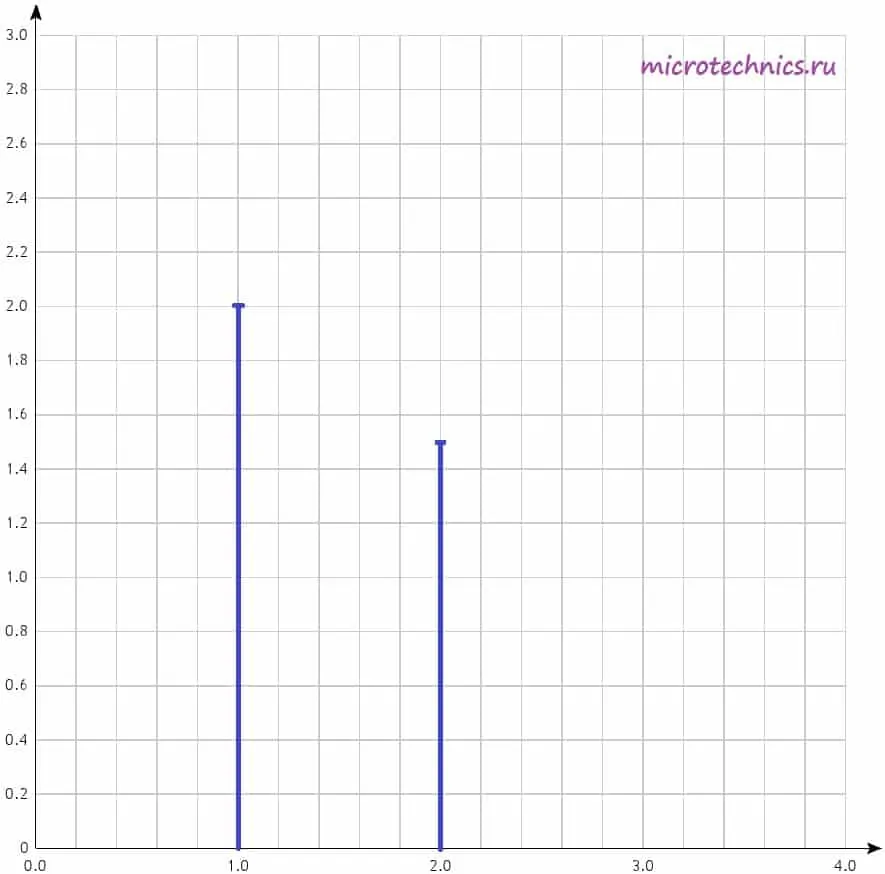
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.

Итак, с построением и анализом амплитудного спектра сигнала мы разобрались. Давайте перейдем к следующей теме сегодняшней статьи – к понятию амплитудно-частотной характеристики.

Амплитудно-частотная характеристика (АЧХ).

АЧХ является важнейшей характеристикой многих цепей и устройств – фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Проанализируем, какой смысл она в себе несет…

АЧХ – это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но мы сейчас рассмотрим, в первую очередь, аудио-сигнал, и выглядит он следующим образом:

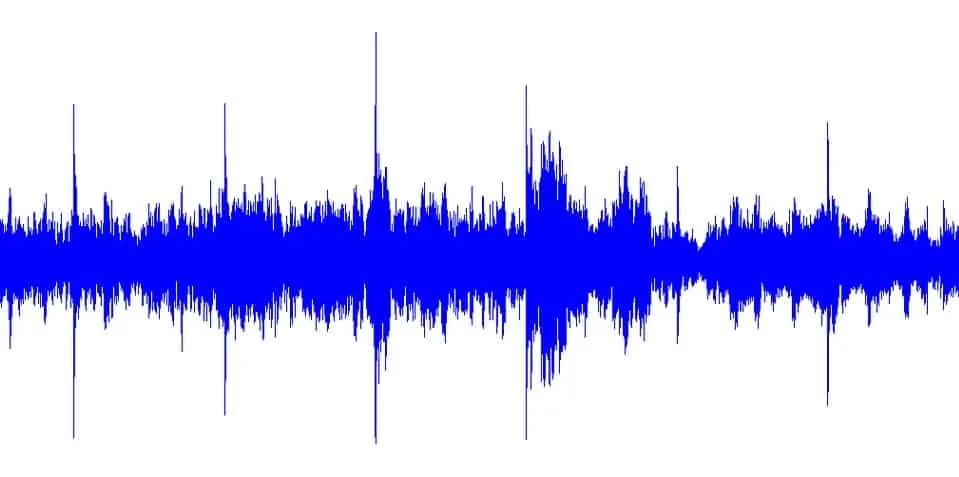
Как видите, ни о какой периодичности здесь не идет и речи. Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи. Просто примем тот факт, что они позволяют нам осуществить такое преобразование.

Соответственно, мы можем построить диаграмму амплитудного спектра такого сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте детально обсудим этот момент.

Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:

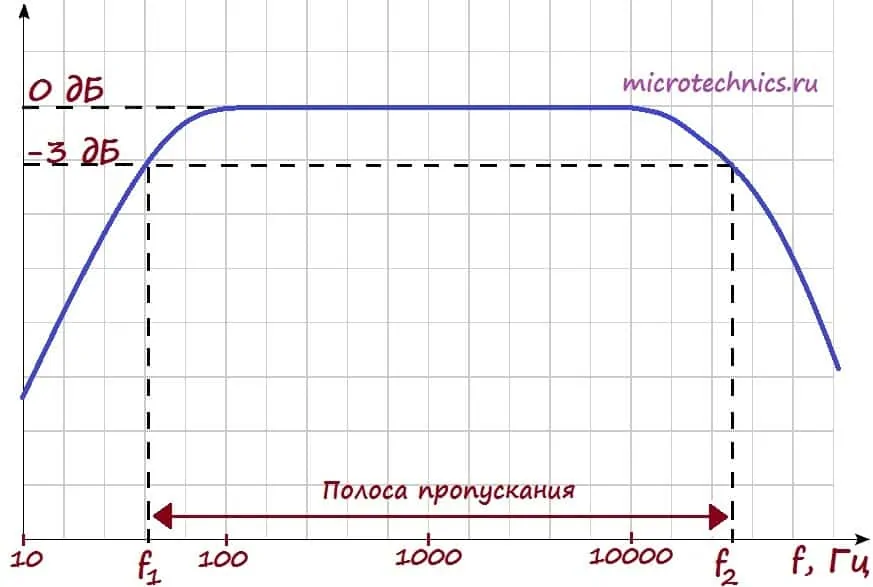
Разбираем поэтапно, что тут изображено. Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы считаем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.

По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.

На графике отдельно отмечены частоты f_1 и f_2. Их отличительной особенностью является то, что сигнал гармоник данных частот будет ослаблен в 1.41 раза (3 дБ) по напряжению. Это соответствует уменьшению по мощности в 2 раза . Полосу частот между f_1 и f_2 называют полосой пропускания. Получается следующая ситуация – сигналы всех гармоник, частоты которых лежат в пределах полосы пропускания устройства/цепи будут ослаблены менее, чем в 2 раза по мощности.

Практические примеры АЧХ аудио-устройств.

Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:

• 20 Гц – 160 Гц – область низких частот
• 160 Гц – 1.28 КГц – область средних частот
• 1.28 КГц – 20.5 КГц – область высоких частот

Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье. И в завершение статьи посмотрим на пару примеров АЧХ:

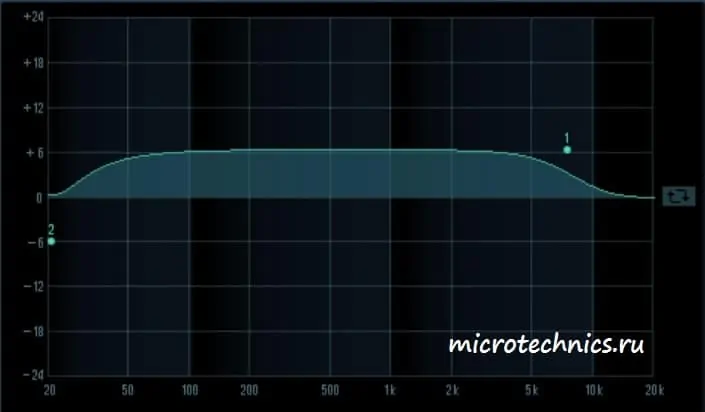
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.

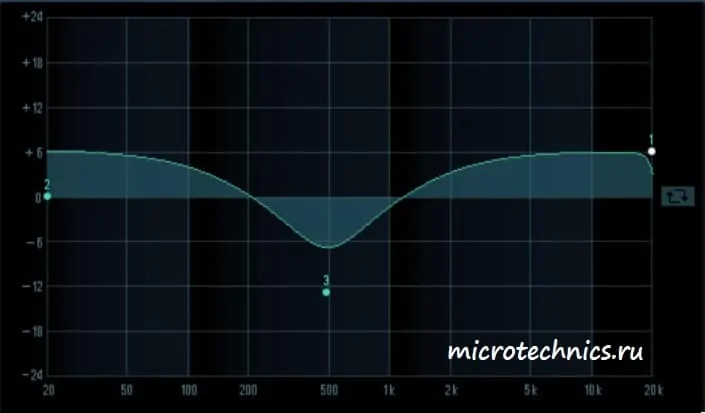
Во втором случае ситуация совсем другая – низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.

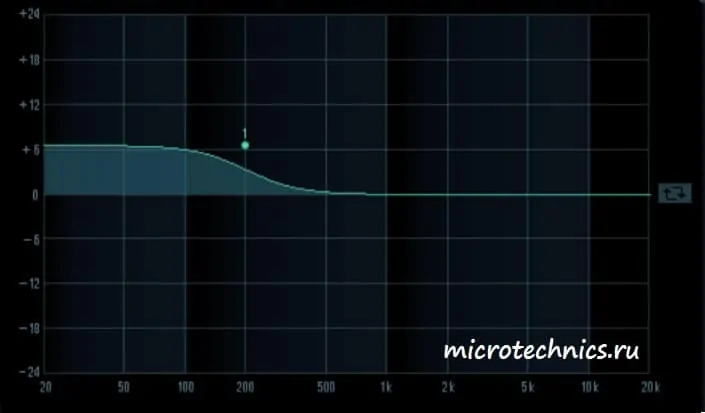
А теперь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов.

На этом мы и заканчиваем нашу сегодняшнюю статью. Спасибо за внимание и ждем вас на нашем сайте снова 🤝