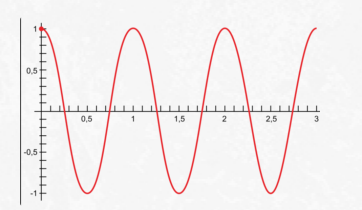
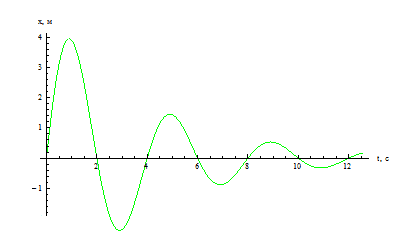
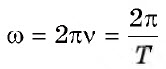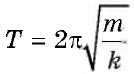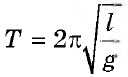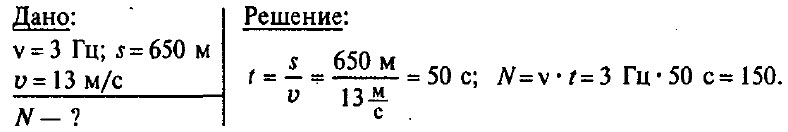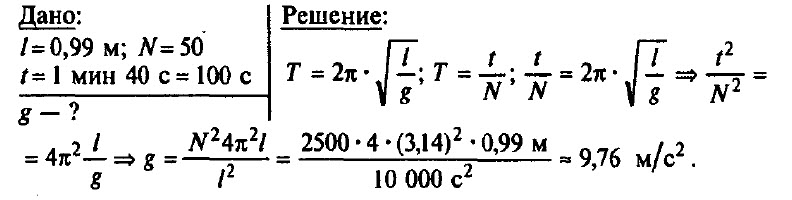Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия – достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)
Амплитуда колебаний объясняет максимальное или максимальное смещение колеблющегося тела. В статье подробно рассказывается о том, что такое амплитуда колебаний и как ее рассчитать.
Амплитуда – это величина колеблющегося тела, такая как угловая частота и период времени. Величина измеряет максимальное смещение тела по обе стороны от его среднего положения. Это означает, что он показывает нам, насколько колеблющееся тело отклоняется от своего среднего положения во время колебания.
Колебание предполагает движение тела вперед и назад от его равновесного или среднего положения. Каждое колебание имеет три основные характеристики: частота, период времени, и амплитуда. Из них мы уже обсуждали концепции частоты и периода времени в предыдущие статьи.
Давайте начнем обсуждение амплитуды колебаний или амплитуды колебаний с примера простой маятник. Маятник поворачивается под углом через свое среднее положение к максимальному расстоянию от его среднего положения. Максимальное или наибольшее расстояние колеблющегося тела от его центра или среднего положения называется его. максимальное смещение. Напротив, величина максимального смещения колеблющегося тела по обе стороны от среднего положения называется его величиной. амплитуда колебаний.
Из синусоидальный график, мы отметили, что амплитуда колебаний равна расстояние между гребнем, впадиной и средним положением.
Следовательно, амплитуда колебаний или величина максимального перемещения x равна x = Asin(ωt + Φ) …………(*)
Где А – амплитуда колебаний.
ω — угловая скорость.
Φ — фазовый сдвиг.
Мы обсудим, как вычислить уравнение амплитуды колебаний (*) из синусоидального графика в более поздней части.
Поскольку каждая волна имеет амплитуду, пики на графике показывают, что амплитуда объясняет степень или уровень изменения интенсивности в различных волны, такие как звук волны. Следовательно, это также интерпретируется как громкость звука.
Звуковые волны
На графике мы отметили, что разница между максимальным пиком амплитуды или положительным значением и самым низким пиком амплитуды или отрицательным значением называется величиной ‘размах амплитуды’ колеблющегося тела.
Узнайте больше о Простое гармоническое движение угловой частоты
Как найти осцилляция Амплитуда из графика?
Мы можем получить амплитуду колебаний из графика синусоидальной функции колеблющегося тела.
Амплитуда колебаний определяется, когда мы зарисовываем график колеблющихся переменных, таких как смещение от времени. Пики на синусоидальном графике – это амплитуда колебаний, которая описывает расстояние, на которое тело колеблется от среднего положения с каждой стороны.
В любой колебательной системе величина изменения колебательной переменной тела при каждом колебании называется амплитуда колебаний. В большинстве случаев осциллирующая переменная равна смещение. Когда мы строим график синусоидальной функции с переменным смещением колебаний в качестве вертикальной оси и временем в качестве горизонтальной оси, расстояние по вертикали между средним значением и крайними точками кривой показывает амплитуду колебаний.
(Кредит: Shutterstock)
На графике синусоидальной функции ось абсцисс рассматривается как среднее положение колеблющегося тела. Следовательно, каким бы ни было исходное положение тела, смещение измеряется от его среднего положения. Поскольку график является синусоидальной функцией, которая иллюстрирует периодические явленияпики на графике отображают параметры колеблющегося тела, такие как период и амплитуда.
сформировать график?
По пикам амплитуда колебаний рассчитывается как половина разницы между максимальным и минимальным значениями.
амплитуда = 1/2 середины макс. – середина мин.
Следовательно, величина амплитуды колебаний всегда положительна.
Мы также можем найти амплитуду колебаний и период времени из обобщенного уравнения синусоидального графика следующим образом:
у = A⋅sin (B (x + C)) + D
где мы можем найти количество колеблющегося тела следующим образом:
Амплитуда колебаний:
Период времени:2π/B
Сдвиг фазы – насколько далеко тело перемещается по горизонтали от среднего положения: C.
Вертикальный сдвиг – насколько далеко тело перемещается по вертикали от среднего положения: D.
График функции синусоидальной волны (предоставлено: математика)
Узнайте больше о Угловое уравнение движения.
Что такое амплитуда и частота колебаний?
Амплитуда и частота – это величины тел колебаний, которые определяют скорость колебаний.
Тело колеблется, когда оно перемещается из своего среднего положения в самое верхнее и возвращается в свое среднее положение. Здесь амплитуда представляет собой максимальное смещение тела от его среднего положения. В то время как частота показывает, насколько тело колеблется от своего среднего положения.
В зависимости от амплитуды и частоты колебания подразделяются на следующие три типа:
Затухающие колебания
Предположим, что тело колеблется с убывающей амплитудой из-за наличия сила сопротивления воздуха и в какой-то момент времени он останавливается, поскольку обе величины его тела рассеялись. В таком случае это называется «затухающие колебания ».
Свободное колебание
Предположим, тело свободно колеблется с постоянной амплитудой и определенной частотой из-за отсутствия силы трения. В этом случае это называется «свободное колебание », и его частота называется ‘собственная частота’ колеблющегося тела.
Принудительное колебание
Его еще называют колебанием натянутой струны или качанием. Предположим, что тело колеблется с уменьшающейся амплитудой из-за механической энергии качания, и оно приходит в состояние покоя, поскольку обе его величины рассеялись. В этом случае это называется ‘вынужденное колебание.
Возьмем, к примеру, подвешенный мяч для весла, который привязан к вашей руке.
(Кредит: просвет)
Дело 1:
Если держать руку устойчиво, мяч будет подпрыгивать вверх и вниз, включая определенное количество ударов. демпфирование (То есть, сила сопротивления воздуха применяемый).
Дело 2:
Увеличивая частоту мяча, перемещая вашу руку вверх и вниз, мяч также реагирует увеличивающейся амплитудой. Если вы ведете мяч с частотой, равной его собственной частоте, его амплитуда увеличивается при каждом колебании. Событие приведения тела в движение с частотой, эквивалентной собственной частоте, называется резонанс. В то время как тело, выполняемое на своей естественной или основной частоте, считается резонировать.
Дело 3:
если вы, кроме того, увеличиваете его частоту выше, чем его собственная частота, его амплитуда начинает уменьшаться, пока колебания почти не исчезнут. Так что движение вашей руки больше не влияет на мяч.
Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.
Определение
Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.
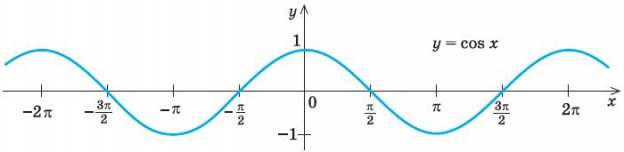
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.
Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.
Уравнение движения гармонических колебаний
Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:
ax=−kmx
Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
x″
=−kmx
Вид уравнения гармонических колебаний зависит от начальных условий. Так, на характер колебательного движения влияет амплитуда, представляющая собой расстояние, на которое изначально было отклонено тело от положения равновесия. Амплитуда обозначается как xmax. Но нельзя просто считать, что x=xmaxcost или =xmaxsint, поскольку двойная производная от этих функций будет равна:
x″=−xmaxcost=−x
Видно, что в этом случае теряется величина km, служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:
x=xmaxcos√kmt
Тогда первая производная примет вид:
x′=−√kmxmaxsin√kmt
Вторая производная примет вид:
x″
=−kmxmaxcos√kmt=−kmx
Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:
x=xmaxsin√kmt
x=xmaxcos√kmt
Обозначим постоянную величину √km, зависящую от свойств системы, за ω0:
ω0=√km
Тогда получим:
x=xmaxsinω0t
x=xmaxcosω0t
Само уравнение движения, описывающего свободные колебания, примет вид:
x″=− ω20x
Период и частота гармонических колебаний
Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:
ν=1T
Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω0T, движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:
ω0T=2π
Отсюда:
ω0=2πT=2πν
Таким образом, величина ω0 представляет собой число колебаний тела, но не за 1 секунду, а за 2π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.
Зависимость частоты и периода свободных колебаний от свойств системы
Изначально за величину ω0 мы принимали постоянную, характеризующую свойства системы:
ω0=√km
Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:
ω0=√km=2πT=2πν
Отсюда период и частота колебаний соответственно равны:
T=2πω0=2π√mk
ν=12π√km
Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной gl. Следовательно, циклическая частота для него равна:
ω0=√gl
Отсюда период и частота колебаний математического маятника соответственно равны:
T=2πω0=2π√lg
ν=12π√gl
Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.
Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.
Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.
Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?
5 мин = 300 с
Искомое число колебаний равно отношению времени к периоду колебаний:
N=tT
Период колебаний для математического маятника определяется формулой:
T=2π√lg
Тогда:
N=t2π√gl=3002·3,14√9,84,9≈68
Фаза колебаний
При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω0t. Обозначим его за ϕ и получим:
ϕ=ω0t
Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).
Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.
Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω0=2πT, фаза определяется формулой:
ϕ=ω0t=2πtT
tT — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:
| Время, t (с) | 0 |
T4 |
T2 |
3T4 |
T |
| Фаза, ϕ (рад) | 0 |
π2 |
π |
3π2 |
2π |
Можно изобразить на графике зависимость координаты колеблющейся точки не от времени, а от фазы. В этом случае графиком также будет являться косинусоида (или синусоида), но аргументом функции будет не время (период), а фаза, выражающаяся в радианах (см. рис.).
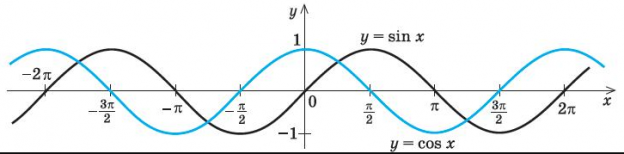
Синус от косинуса отличается только смещением аргумента на π2 (см. рис. ниже). Поэтому для описания гармонических колебаний можно использовать как синусоидальный, так и косинусоидальный закон.
Выбор закона зависит от условий задачи. Если колебания начинаются с того, что тело выводят из положения равновесия и отпускают, удобнее пользоваться косинусоидальным законом, поскольку в начальный момент времени косинусоида показывает, что это тело отклонено максимально, а не находится в положении равновесия. Если для того чтобы начались колебания, совершают толчок, удобнее использовать синусоидальный закон, так как начальному моменту времени на синусоиде соответствует положение равновесия.
Колебания, совершаемые по закону синуса и косинуса, отличаются только фазой, которая смещена на значение, равное π2. Это значение называют сдвигом фаз, или их разностью. Поэтому косинусоидальная функция также может быть записана как:
x=xmaxcosω0t=xmaxsin(ω0t+π2)
Превращение энергии при гармонических колебаниях
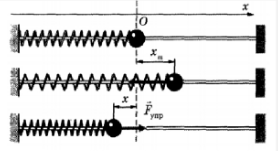
Чтобы описать превращения энергии при гармонических колебаниях, условимся, что силой трения будем пренебрегать. Для описания обратимся к рисунку ниже.
Точке О на рисунке соответствует положение равновесия шарика. Если его оттянуть на расстояние xmax, равное амплитуде, пружина получит потенциальную энергию, которая примет в этом положении максимальное значение, равное:
Wp max=kx2max2
Когда шарик отпускают, возникает сила упругости, под действием которой шарик устремляется влево. По мере уменьшения расстояния между точкой максимального отклонения и положением равновесия уменьшается и потенциальная энергия. Но в это время увеличивается кинетическая энергия шарика. Когда шарик проходит через положение равновесия в первый раз, его потенциальная энергия становится равной нулю, а кинетическая энергия обретает максимальное значение (скорость в этот момент времени тоже максимальна):
Wk max=mv2max2
После прохождения точки О расстояние между шариком и положением равновесия снова увеличивается, и потенциальная энергия растет. Кинетическая же энергия при этом уменьшается. А в крайнем положении слева она становится равной нулю, в то время как потенциальная энергия снова примет максимальное значение.
Так как мы условились пренебрегать трением, данную колебательную систему можно считать изолированной. Тогда в ней должен соблюдаться закон сохранения энергии. Согласно ему, полная механическая энергия системы равна:
W=Wp+Wk=kx2x2+mv2x2=kx2max2=mv2max2
В действительности свободные колебания всегда затухают, так как в колебательной системе действует сила трения. И часть механической энергии рассеивается в виде тепла. Пример графика затухающих колебаний выглядит следующим образом:
Пример №2. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне. Найдите отношение кинетической энергии груза к его потенциальной энергии системы в момент, когда груз находится в точке, расположенной посередине между крайним положением и положением равновесия.
Так как груз находится посередине между крайним положением и положением равновесия, его координата равна половине амплитуды:
x=xmax2
В это время потенциальная энергия груза будет равна:
Wp=kx22=k(xmax2)22=kx2max8
Согласно закону сохранения энергии, кинетическая энергия в это время равна:
Wk=W−Wp
Полная механическая энергия системы равна максимальной потенциальной энергии:
W=Wp max=kx2max2
Тогда кинетическая энергия равна:
Wk=kx2max2−kx2max8
Следовательно, отношение кинетической энергии к потенциальной будет выглядеть так:
WkWp=kx2max2−kx2max8kx2max8=kx2max28kx2max−1=4−1=3
Резонанс
Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называют вынужденными.
Работы силы над такой системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.
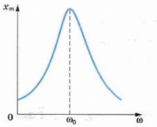
Особый интерес вызывают вынужденные колебаний в системе, способной совершать свободные колебания. Примером такой системы служат качели. Их не получится отклонить на большой угол всего лишь одним толчком. Если их толкать то в одну, то в другую сторону, тоже ничего не получится. Но если подталкивать качели всякий раз, как они сравниваются с нами, можно раскачать их очень сильно. При этом не нужно прикладывать большую силу, но на это понадобится время. Причем после каждого такого толчка амплитуда колебаний качелей будет увеличиваться до тех пор, пока не достигнет своего максимального значения. Такое явление называется резонансом.
Определение
Резонанс — резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний.
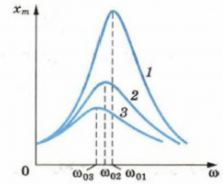
Графически явление резонанса можно изобразить как резкий скачок графика вверх (см. рис. выше). Причем высота «зубца», или амплитуда колебаний, будет зависеть от величины сил трения. Чем больше сила трения, тем меньше при резонансе возрастает амплитуда вынужденных колебаний. Это можно продемонстрировать графиками на рисунке ниже. Графику 1 соответствует минимальное трение, графику 3 — максимальное.
На явлении резонанса основан принцип работы частотомера — устройства, предназначенного для измерения частоты переменного тока. Он состоит из набора упругих пластин, которые закреплены на одной планке. Каждая пластина обладает определенной собственной частотой колебаний, которая зависит от упругих свойств, длины и массы. Собственные колебания пластин известны. Под действием электромагнита планка, а вместе с ней и пластины совершают вынужденные колебания. Но лишь та пластина, собственная частота которой совпадает с частотой колебаний планки, будет иметь большую амплитуду колебаний. Таким образом, определяется частота переменного тока.
Пример №3. Автомобиль движется по неровной дороге, на которой расстояние между буграми равно приблизительно 8 м. Период свободных колебаний автомобиля на рессорах 1,5 с. При какой скорости автомобиля его колебания в вертикальной плоскости станут особенно заметными?
Колебания автомобиля в вертикальной плоскости будут заметны тогда, когда частота наезда на бугры сравняется с частотой свободных колебаний автомобиля на рессорах. Поскольку частота обратно пропорциональна периоду, можно сказать, что резонанс будет достигнут тогда, когда автомобиль будет наезжать на бугры каждые 1,5 секунды. Зная расстояние между буграми и время, можем вычислить скорость:
v=st=81,5≈5,33 (мс)≈19,2(кмч)
Задание EF17508
Смещение груза пружинного маятника меняется с течением времени по закону x=Acos2πTt, где период Т = 1 с. Через какое минимальное время, начиная с момента t = 0, потенциальная энергия маятника вернется к своему исходному значению?
Ответ:
а) 0,1 с
б) 0,2 с
в) 0,3 с
г) 0,5
Алгоритм решения
1.Определить исходное значение потенциальной энергии шарика.
2.Сделать рисунок и определить положение шарика в начальный момент времени.
3.Определить положение шарика в момент в момент времени, когда потенциальная энергия шарика снова примет исходное значение.
4.Определить, через какое время шарик примет такое положение.
Решение
Известно, что смещение маятника меняется по закону:
x=Acos2πTt
В начальный момент времени t = 0 смещение будет равно амплитуде, поскольку косинус нуля равен «1». Следовательно, исходное значение потенциальной энергии маятника равно:
Wp0=kA22
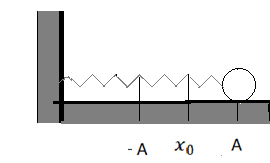
Сделаем рисунок, обозначив за x0 положение равновесия системы. Тогда A и –A будут амплитудами (максимальными смещениями от положения равновесия).
Потенциальная энергия зависит только от модуля смещения, поэтому ее значение станет таким же, как в начальный момент времени, когда смещение достигнет максимального смещения с противоположной стороны (оно составит –A). В этом легко убедиться:
Wpt=k(−A)22=kA22=Wp0
К этому моменту пройдет половина периода колебания, следовательно:
t=T2=12=0,5 (с)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17644
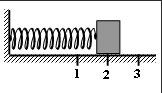
| 1) | увеличивается |
| 2) | уменьшается |
| 3) | не изменяется |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Вспомнить, от чего зависит кинетическая энергия груза маятника, и установить, как она меняется при движении груза маятника от точки 2 к точке 3.
2.Вспомнить, от чего зависит потенциальная энергия пружины маятника, и установить, как она меняется в рассматриваемый промежуток времени.
3.Вспомнить, от чего зависит жёсткость пружины, и установить, как она меняется.
Решение
Точка 2 соответствует положению равновесия, тока 3 — максимальному смещению пружинного маятника. Кинетическая энергия груза маятника зависит от скорости его перемещения:
Wk=mv22
Кинетическая энергия пружинного маятника максимально в положении равновесия и минимальная при максимальном смещении груза. Следовательно, на промежутке 2–3 она уменьшается.
Потенциальная энергия пружины маятника определяется формулой:
Wp=kx22
Так как смещение во время перемещения из точки 2 в точку 3 растет, то потенциальная энергия пружины маятника увеличивается.
Жесткость пружины зависит от природы материала. Это постоянная величина, которая с течением времени не изменяется.
Ответ: 213
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22760
Необходимо сделать нитяной маятник и с его помощью экспериментально определить ускорение свободного падения. Для этого школьник уже взял штатив с муфтой и лапкой, линейку и нить. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
Ответ:
а) секундомер
б) динамометр
в) мензурка
г) электронные весы
д) алюминиевый шарик
Алгоритм решения
1.Записать формулу, которая связывает ускорение свободного падения с периодом колебаний маятника.
2.Определить, что не хватает для проведения эксперимента и выбрать недостающие предметы из списка.
Решение
Ускорение свободного падения с периодом колебаний маятника связывает формула:
T=2π√lg
Следовательно, нужно значит не только длину нити маятника, но и период колебаний. Измерить его можно с помощью секундомера. А чтобы получить сам маятник, к нити нужно будет привязать массивный шарик. Например, алюминиевый.
Ответ: а, д
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.7k
Задачи на Механические колебания с решениями
Формулы, используемые на уроках «Задачи на Механические колебания».
Название величины |
Обозначение |
Единица измерения |
Формула |
Амплитуда колебаний |
A |
м |
|
Период колебаний |
T |
с |
T = 1 / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = 1 / T ;v = N / t |
Число колебаний за какое-то время |
N |
N = t /T ;N = vt |
|
Время |
t |
с |
t = NT ;t = N / v |
Циклическая частота колебаний |
ω |
Гц |
|
Период колебаний пружинного маятника |
T |
c |
|
Период колебаний математического маятника |
T |
c |
|
Уравнение гармонических колебаний |
x(t) = Asin(ωt+φ0) |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.
Задача № 2.
На рисунке изображен график зависимости координаты от времени колеблющегося тела.
По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.
Задача № 3.
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?
Задача № 4.
Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.
Задача № 5.
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с2.
Задача № 6.
Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.
Задача № 7.
Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?
Задача № 8.
Гармоническое колебание описывается уравнением
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?
Задача № 9.
Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π2 = 9,87.)
Задача № 10.
ОГЭ
Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?
Задача № 11.
ЕГЭ
Два математических маятника за одно и то же время совершают — первый N1 = 30, а второй — N2 = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?
Краткая теория для решения Задачи на Механические колебания.
Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.